Enzyme surface rigidity tunes the temperature dependence of catalytic rates

Significance

Faced with an exponential decrease in chemical reaction rates as the temperature is lowered, cold-adapted organisms require specialized enzymes to maintain a functional metabolism. Such enzymes catalyze their reactions with lower activation enthalpies counterbalanced by more negative entropies, yielding higher rates at low temperatures compared with mesophilic enzymes, although the rates at room temperature are often similar. The structural mechanisms behind this universal property still remain largely unknown. We attack this problem with extensive computer simulations and high-precision Arrhenius plots, showing that the protein surface rigidity outside the active site region tunes the enthalpy–entropy balance. This enables significantly higher rates at low to moderate temperatures for cold-active enzymes compared with their warm-active counterparts.

Abstract

The structural origin of enzyme adaptation to low temperature, allowing efficient catalysis of chemical reactions even near the freezing point of water, remains a fundamental puzzle in biocatalysis. A remarkable universal fingerprint shared by all cold-active enzymes is a reduction of the activation enthalpy accompanied by a more negative entropy, which alleviates the exponential decrease in chemical reaction rates caused by lowering of the temperature. Herein, we explore the role of protein surface mobility in determining this enthalpy–entropy balance. The effects of modifying surface rigidity in cold- and warm-active trypsins are demonstrated here by calculation of high-precision Arrhenius plots and thermodynamic activation parameters for the peptide hydrolysis reaction, using extensive computer simulations. The protein surface flexibility is systematically varied by applying positional restraints, causing the remarkable effect of turning the cold-active trypsin into a variant with mesophilic characteristics without changing the amino acid sequence. Furthermore, we show that just restraining a key surface loop causes the same effect as a point mutation in that loop between the cold- and warm-active trypsin. Importantly, changes in the activation enthalpy–entropy balance of up to 10 kcal/mol are almost perfectly balanced at room temperature, whereas they yield significantly higher rates at low temperatures for the cold-adapted enzyme.

Cold-adapted enzymes are able to catalyze their reactions with chemical rates comparable to and often exceeding those of their warm-active counterparts, and they are a remarkable example of how evolution can tune the biophysical properties of enzymes. Despite major efforts in the last few decades, the structural mechanisms responsible for low-temperature activity still remain largely unknown. A key problem with lowering the temperature is the exponential decrease in enzyme reaction rates, which according to transition state theory is given by

$$k_{rxn}=\kappa \left(\frac{kT}{h}\right)e^{-\frac{\mathrm{\Delta }{G}^{‡}}{kT}}=\kappa \left(\frac{kT}{h}\right)e^{\frac{\mathrm{\Delta }{S}^{‡}}{k}}\mathrm{\cdot }{e}^{\frac{-\mathrm{\Delta }{H}^{‡}}{kT}}.$$ [1]

Here, k_rxn is the reaction rate, T the temperature, $\kappa$ is a transmission coefficient, k and h are Boltzmann’s and Planck’s constants, respectively, and ∆G^‡ is the free energy of activation. Decreasing the temperature from 37 °C to 0 °C typically results in a 20- to 250-fold reduction of the activity of a mesophilic enzyme (1). Clearly, survival at low temperatures requires that both enzyme kinetics and protein stability are adapted accordingly.

A remarkable and universal feature of reactions catalyzed by cold-adapted enzymes is a lower enthalpy and a more negative entropy of activation compared with thermophilic orthologs (1–3). This enthalpy–entropy phenomenon, as indicated in Fig. 1A, coincides with the fact that psychrophilic enzymes have a reduced thermostability, and thus melt at lower temperatures than their mesophilic counterparts. It is evident from Eq. 1 that a lower activation enthalpy makes the rate less temperature-dependent, and this is believed to be the primary adaptation in psychrophilic enzymes (4–6). However, the overall activation free energies at room temperature are usually rather similar in cold- and warm-adapted enzymes (5), and the smaller activation enthalpy in the former case is thus typically compensated by a more negative value of $\mathrm{\Delta }{\mathit{S}}^{‡}$. This balance of thermodynamic activation parameters led to the controversial hypothesis that cold adaptation originates from increased flexibility of the active site (3). However, crystallographic analysis of psychrophilic and mesophilic trypsin has failed to identify any overall differences in flexibility between the two enzymes (7). Additionally, computer simulations of differently adapted citrate synthases and trypsins further showed that the flexibility of the active site residues is virtually identical in the psychrophilic and mesophilic enzyme variants (8, 9). Moreover, structural bioinformatics analysis did not reveal any global protein descriptors that uniquely correlated with cold adaptation (3).

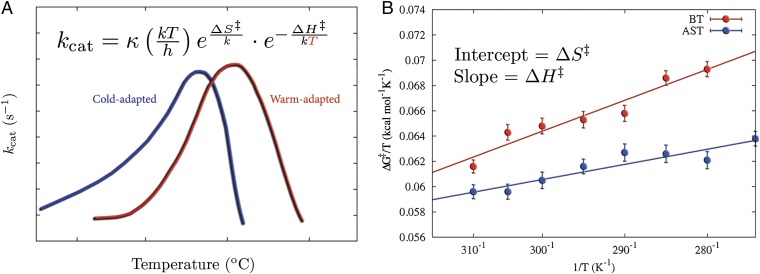
Fig. 1.

Evolutionary pressure changes the enthalpy–entropy balance to allow for enzymatic low-temperature activity. (A) Examples of k_cat vs. temperature for cold- and warm-active enzymes, showing that the exponential decrease in reaction rates with reduced temperatures is primarily counteracted by lowered activation enthalpies. (B) Comparison of computational Arrhenius plots for cold- and warm-active trypsin reveal a significantly smaller activation enthalpy (smaller slope) for the cold-adapted salmon trypsin.

Recent computer simulations of cold- and warm-adapted trypsin reactions provided new clues to the problem of the origin of the enthalpy–entropy effect (9). These calculations showed that protein rigidity well outside of the active site is what seems to control the balance between thermodynamic activation parameters (Fig. 1B), and hence also the temperature adaptation of catalytic rates (9). The results showed that it is the internal energy response of the surroundings of the active site, particularly the protein–solvent interfacial surface, that differs between the cold- and warm-adapted enzymes. The softer protein surface in the psychrophilic enzyme was found to be largely due to point mutations that disrupted extensive surface hydrogen bonding networks involving both protein residues and surface bound water molecules. A notable prediction was that single distant mutations of key residues that alter the protein–water surface interactions can significantly affect the activation enthalpy–entropy balance, without influencing the overall rate at room temperature. The same type of phenomenon has been observed in purine nucleoside phosphorylase by Schramm and coworkers (10), where distant mutations (25–45 Å from the active site) were seen to alter both thermodynamic activation parameters and kinetic isotope effects, while having virtually no effect on catalytic rate.

A direct implication of the above findings is that if it were possible to rigidify the protein surface of a psychrophilic enzyme, one would predict that it should acquire more mesophilic characteristics. In other words, rigidification of a cold-adapted enzyme surface should yield a higher enthalpy of activation for the catalyzed reaction accompanied by a less negative entropy component. Presumably, rigidification of the surface would also be reflected by a higher melting temperature, as observed experimentally for mesophilic enzymes (1). Experimentally, this type of protein engineering is not so trivial, particularly if “design” of complicated hydrogen bonding networks is needed to anchor mobile residues to the protein surface. However, it is straightforward to rigidify a protein computationally by simply applying atomic positional restraints to selected parts of the macromolecule. The key problem in terms of computer simulations is that one needs to calculate the actual experimental observables, in this case the thermodynamic activation parameters for the catalyzed reaction. However, due to the huge number of degrees of freedom involved, the extensive configurational sampling required to rigorously obtain activation enthalpies and entropies is presently beyond the scope of most quantum mechanics/molecular mechanics methods. The empirical valence bond (EVB) model (11, 12) provides a very efficient method for this purpose, because it allows extensive all-atom molecular dynamics (MD) sampling of the reaction system and can be used to directly construct computational Arrhenius plots (8, 9). This strategy has also recently been validated both for solution (13) and enzyme (14) reactions and was found to yield activation enthalpies and entropies in excellent agreement with experiment.

In this work we report extensive MD/EVB free energy simulations, yielding high-precision Arrhenius plots, to explore the effect of protein surface rigidity on the temperature dependence of peptide hydrolysis by trypsin. We show unambiguously that gradually applying positional restraints to the enzyme surface and inward causes the remarkable effect of turning psychrophilic trypsin into a variant with mesophilic characteristics, without making any changes to the amino acid sequence. We further show that just restraining a key surface loop identified previously (9) causes the same effect as the point mutation in that loop between the psychrophilic and mesophilic enzymes. The present results thus further corroborate the hypothesis that enzyme surface rigidity or softness can tune the temperature adaptation of catalytic rates.

Results

The reaction of psychrophilic anionic salmon trypsin (AST) is used as a model for exploring the role of enzyme surface rigidity in tuning the temperature dependence of the reaction rate. In the reaction with amide substrates at saturating conditions the rate-limiting step is generally the formation of the tetrahedral intermediate (15) and was simulated here using a Cys-Lys-Ala tripeptide as substrate with the MD/EVB approach as reported earlier (9). The large rate acceleration compared with the uncatalyzed reaction, which is reproduced by the simulations, is primarily accomplished by facilitating formation of the reactive anionic nucleophile (Ser195) and by transition-state stabilization (9). The backbone NH groups of Gly193 and Ser195 play a key role by forming the oxyanion hole that stabilizes the negative charge developed on the tetrahedral intermediate (16).

Protein Surface Rigidity Can Tune the Enthalpy–Entropy Balance.

The MD/EVB simulations with a water sphere of 35-Å radius surrounding the protein, centered on the substrate scissile bond, allow the entire enzyme to move freely. Calculated B-factors averaged over 100-ns simulation of the reactant state clearly show that the enzyme core is rather rigid, whereas the surface contains regions with significantly higher flexibility (Fig. S1). As noted earlier, several of these regions correspond to loops where conserved mutations between cold- and warm-adapted trypsins are found (9). The flexibility of key residues involved in the chemical reaction was also evaluated with the spherical boundary approach as well as with periodic boundary conditions using root-mean-square fluctuations (RMSF) to measure the mobility. We find no tendency of the cold-adapted enzyme to have larger active flexibility compared with the warm-adapted trypsin (Fig. S2). Interestingly, both the spherical and the periodic model yield virtually identical active site flexibilities, which shows that the spherical model does not dampen the mobility given that the radius is sufficiently large.

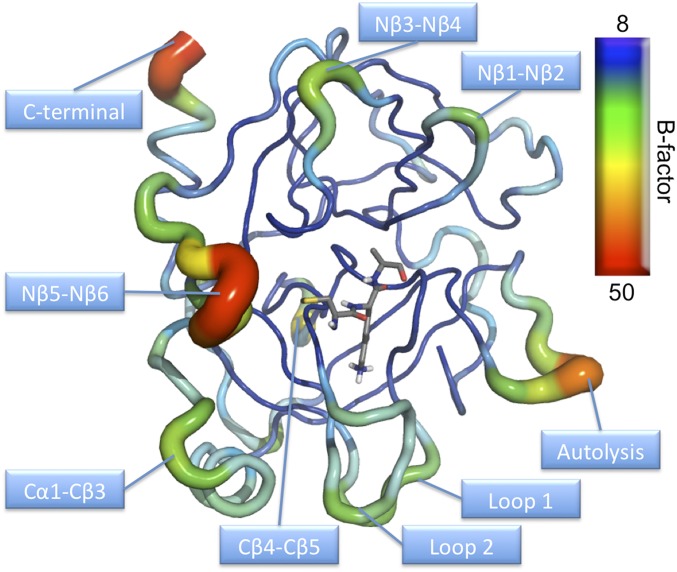
Fig. S1.

B-factor representation of AST averaged over 100-ns MD simulation at the reactant state illustrating that the enzyme core is rather rigid, whereas the surface contains regions with high flexibility.

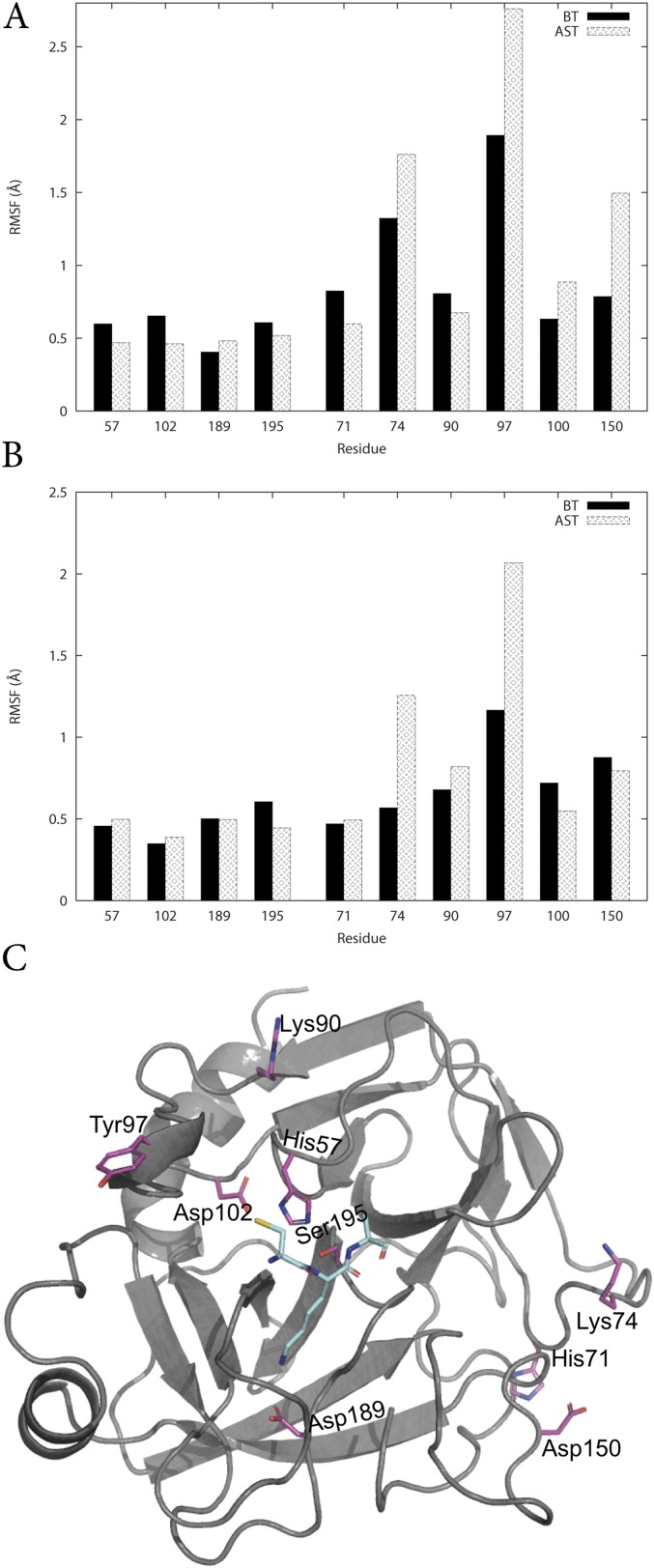
Fig. S2.

Average protein backbone RMSF of key residues using (A) periodic boundary conditions, (B) spherical boundary conditions using a radius of 35 Å, and (C) the structural positions of the residues.

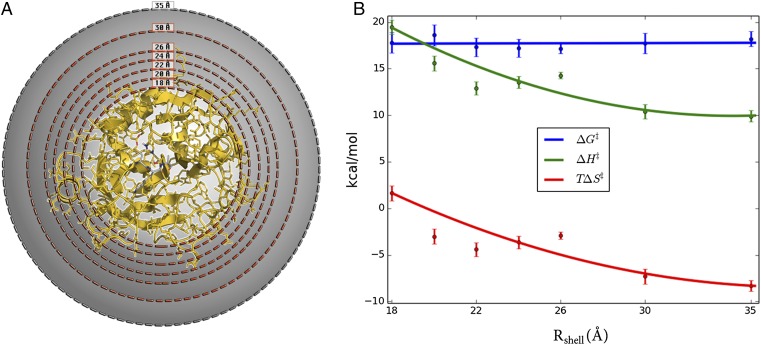
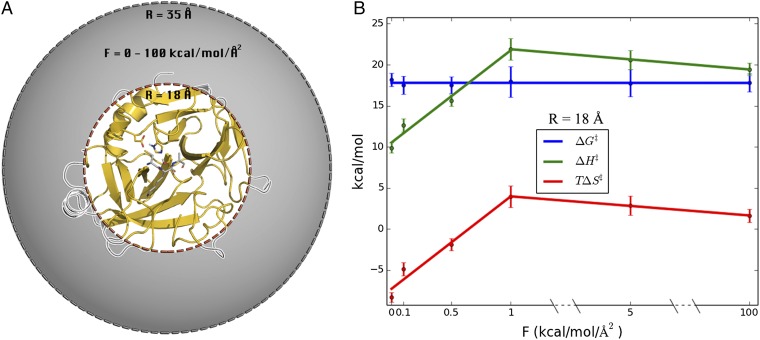
To examine the effect of surface mobility on the thermodynamic activation parameters, we carried out a series of simulations where protein restraints were applied to outer spherical shells of different thickness (Fig. 2A). Hence, a simple criterion was applied such that if r_i > R_shell for any heavy protein atom i in the crystal structure, then this atom is subjected to a harmonic restraint of 100 kcal/(mol⋅Ų) to its initial position. Seven restraining radii (R_shell) were used, and for each of these MD/EVB reaction simulations were carried out at eight different temperatures in the range 275–310 K. The number of solute atoms affected by the restraining force for each value of R_shell is presented in Table S1. Then, a computational Arrhenius plot was constructed from 800 independent free energy profiles for each restraining radius. The thermodynamic activation parameters were extracted from the Arrhenius plots by least squares linear regression of ∆G^‡/T vs. 1/T. The resulting thermodynamic data for 300 K is presented in Fig. 2B. Remarkably, we find that when the enzyme surface is gradually restrained from the outside and inward the activation enthalpy–entropy balance changes significantly, but the activation free energy remains essentially invariant. Moreover, rigidifying all atoms outside 18 Å of the active site yields activation parameters for the cold-adapted enzyme that are virtually identical to those obtained earlier for warm-adapted trypsin (Table 1). However, when restraining atoms closer than 18 Å to the active site then the mobility of the core of the protein starts to become affected (Fig. S3).

Fig. 2.

Systematic variation of protein surface flexibility and its effects on thermodynamic activation parameters. (A) Simulation sphere where solute atoms between R_shell (18, 20, 22, 24, 26, and 30 Å) and 35 Å are restrained with a force constant of 100 kcal/(mol⋅Ų). (B) Thermodynamic activation parameters (300 K) for the systems restrained in A, showing that the parameters for cold-active trypsin are gradually converted to those of the warm-adapted trypsin. See Table S1 for the number of solute atoms in each restrained shell.

Table S1.

Number of atoms in the restrained region and the percentage of the total number of atoms for simulations with R_shell from 10–35 Å

Rshell	Atoms	% Atoms
35	0	0.00
30	10	0.31
26	230	7.10
24	454	14.01
22	852	26.30
20	1,241	38.30
18	1,701	52.50
16	2,124	65.56
14	2,480	76.54
10	2,999	92.56

Table 1.

Calculated thermodynamic activation parameters for native and mutant BT and AST at 300 K

Enzyme	Force constant*	∆G‡	∆H‡	T∆S‡
BT native†	0	19.0 ± 1.4	20.4 ± 1.0	1.4 ± 1.0
BT N97Y†	0	18.4 ± 1.3	10.6 ± 0.9	−7.8 ± 1.0
AST native†	0	18.2 ± 0.8	9.9 ± 0.6	−8.3 ± 0.6
AST Y97N†	0	18.4 ± 1.1	12.0 ± 0.8	−6.4 ± 0.8
AST Nβ5–Nβ6	5	18.0 ± 0.9	12.2 ± 0.6	−5.8 ± 0.6
AST R = 18 Å	0.1	17.5 ± 1.1	12.6 ± 0.8	−4.9 ± 0.8
AST R = 18 Å	0.5	17.5 ± 1.0	15.6 ± 0.7	−1.9 ± 0.7
AST R = 18 Å	1.0	18.0 ± 1.9	21.9 ± 1.3	3.9 ± 1.3
AST R = 18 Å	5.0	17.8 ± 1.7	20.6 ± 1.2	2.8 ± 1.2
AST R = 18 Å	100.0	17.8 ± 1.1	19.5 ± 0.8	1.6 ± 0.8

^*Force constant in kilocalories per mole per square angstrom applied to protein backbone atoms.

^†Data taken from ref. 9.

Fig. S3.

Root-mean-square atomic fluctuations (backbone) at the transition state (averaged per residue) as a function of distance (Cα-atom) from the sphere center. The simulations with R_shell = 20, 18, 16, and 14 Å are plotted with gray, black, red, and blue lines, respectively.

It is further interesting to explore how strong surface restraints are really required to convert the psychrophilic enzyme into a mesophilic-like one. To examine this point we carried out four additional full sets of MD/EVB simulations (T = 275–310 K, as above) for the case with R_shell = 18 Å, with harmonic force constants varying between 0.1 and 5.0 kcal/(mol⋅Ų). With this radius it is thus still mainly surface loop regions that are restrained. It turns out that between 0 and 1.0 kcal/(mol⋅Ų) restraints the cold-adapted activation enthalpy and entropy varies approximately linearly with the magnitude of the restraining force constant, and already at 1 kcal/(mol⋅Ų) has the system reached the mesophilic characteristics (Fig. 3). Further increase of the force constant up to the strong restraints [100 kcal/(mol⋅Ų)] used to generate Fig. 2 does not affect the enthalpy–entropy balance. It is also noteworthy that, again, the activation free energy is essentially unaffected by the magnitude of the restraints. Thus, restraining the protein surface atoms to their initial positions with a force constant of 1 kcal/(mol⋅Ų) is sufficient to increase ∆H^‡ by more than 10 kcal/mol and increase T∆S^‡ by the same amount (at 300 K), indicating an almost perfect enthalpy–entropy compensation.

Fig. 3.

Alteration of the protein surface mobility by restraining protein heavy atoms outside 18 Å from the active site with different force constants. (A) Structural regions subjected to restraints are shown in gray and without in white. (B) Resulting thermodynamic activation parameters (300 K) with different force constants applied.

The calculated values of ∆H^‡ and T∆S^‡ both with a 1.0 and a 100 kcal/(mol⋅Ų) force constant, and R_shell = 18 Å, are remarkably similar to those of the warm-adapted enzyme, ∆H^‡ = 20.4 kcal/mol and T∆S^‡ = 1.4 kcal/mol (Table 1). The finding that force constants higher than 1 kcal/(mol⋅Ų) do not yield any further contributions to the thermodynamic activation parameters is not surprising because hundreds of atoms are restrained. Hence, even a weak 1 kcal/(mol⋅Ų) force constant will sum to a sizeable energetic penalty due to many atoms being restrained.

Distant Mutations Do Not Significantly Affect the Rate at Room Temperature.

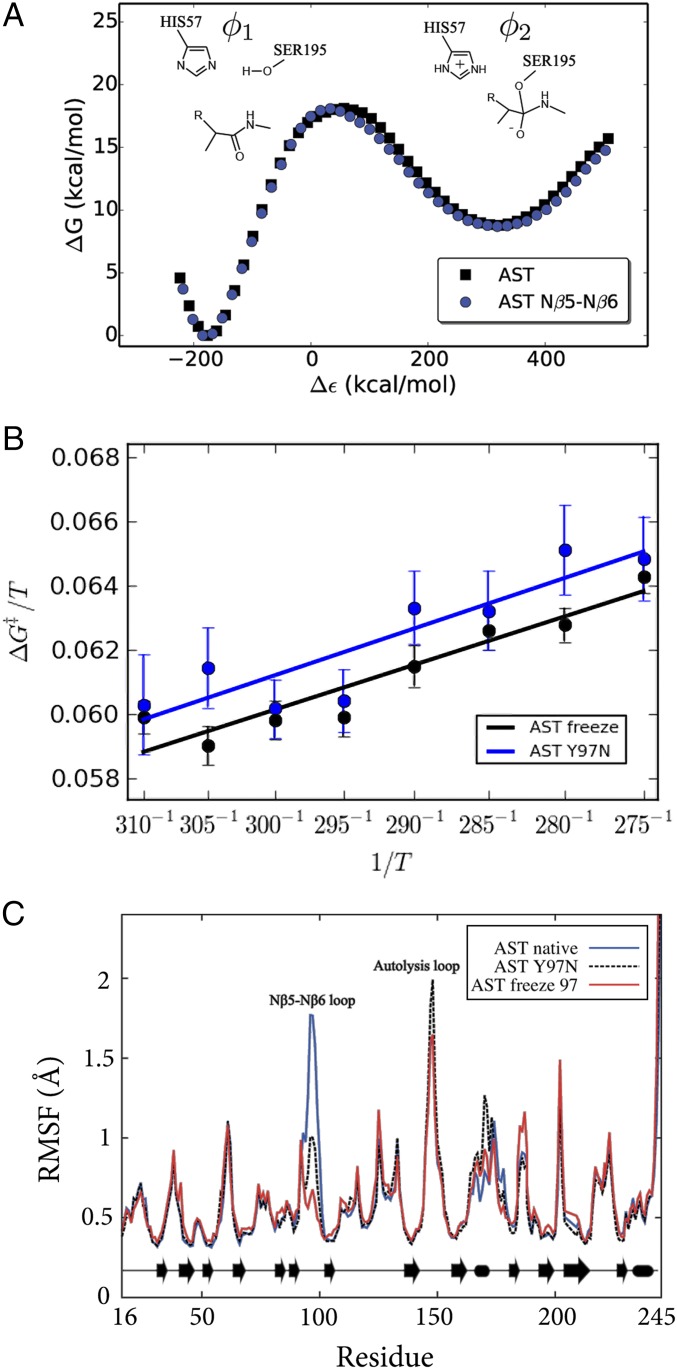
The above results clearly show that suppressing enzyme surface mobility is sufficient to turn psychrophilic trypsin into a mesophilic variant. The same effect can of course also be achieved evolutionarily by different structural mechanisms, depending on the nature of the amino acid substitutions. Earlier work (9) identified the so-called Nβ5–Nβ6 loop (residues 95–99) as being particularly important for the cold adaptation effect of AST. A key mutation here in psychrophilic trypsins is the conserved tyrosine at position 97, which in mesophilic enzymes such as bovine trypsin (BT) is an asparagine (9). The BT N97Y mutation was seen in MD simulations to significantly increase the mobility of the Nβ5–Nβ6 loop, which is also reflected by experimental B-factors in very-high-resolution (0.75–1.0 Å) crystal structures (17, 18). These structures also showed that an extensive hydrogen bond network involving surface-bound water molecules (present in BT) is disrupted in AST, which seems to explain the increased flexibility of the psychrophilic enzyme. The single N97Y (warm to cold) and Y97N (cold to warm) mutations in BT and AST, respectively, were also predicted by the computer simulations to significantly affect the thermodynamic activation parameters, thereby acting as a partial cold↔warm adaptation switch. However, it should be emphasized here that at room temperature the calculated rate differences were again small, whereas at temperatures approaching 0 °C the psychrophilic mutation was predicted to yield a rate increase of about a factor of 20.

The direct role of the Nβ5–Nβ6 loop mobility as a cold↔warm adaptation switch was examined here with extensive MD/EVB simulations where only the backbone atoms of the loop (residues 95–97) were restrained to their initial positions in AST. Note that the backbone conformation of this loop is virtually identical in AST and BT despite the changes in sequence. The resulting reaction free energy profiles (at 300 K) for the native AST enzyme and its Nβ5–Nβ6 loop-restrained variant are shown in Fig. 4A. Based on 800 additional independent MD/EVB simulations, an activation free energy of 18.0 ± 0.9 kcal/mol was obtained at 300 K for the loop-restrained enzyme. This is very similar to the previously reported activation free energy 18.2 ± 0.8 kcal/mol for wild-type AST (9). These results are also in excellent agreement with the substrate-dependent barrier of 15–20 kcal/mol (15). Hence, as expected, the calculations show that rigidifying only the Nβ5–Nβ6 loop on the enzyme surface does not affect the overall free energy of activation (Fig. 4) at room temperature, where the chemical reaction rates are similar for cold- and warm-adapted trypsin. This is also consistent with the general notion that modifications far away from the active site do not significantly affect catalytic rates near the temperature optimum (19), as was also predicted for surface mutations in ref. 9.

Fig. 4.

Key mutation (Y97N) altering surface softness in cold-active trypsin. (A) Calculated free energy profiles (300 K) for the tetrahedral intermediate formation in the acylation step for AST with the Nβ5–Nβ6 loop restrained. (B) Calculated Arrhenius plots for Y97N and the restrained Nβ5–Nβ6 loop backbone of AST demonstrating that protein surface softness regulates the enthalpy–entropy balance. (C) RMSF are virtually identical for the Y97N mutant and the restrained Nβ5–Nβ6 loop simulations.

The Y97N Enthalpy–Entropy Effect Originates from Altered Surface Rigidity.

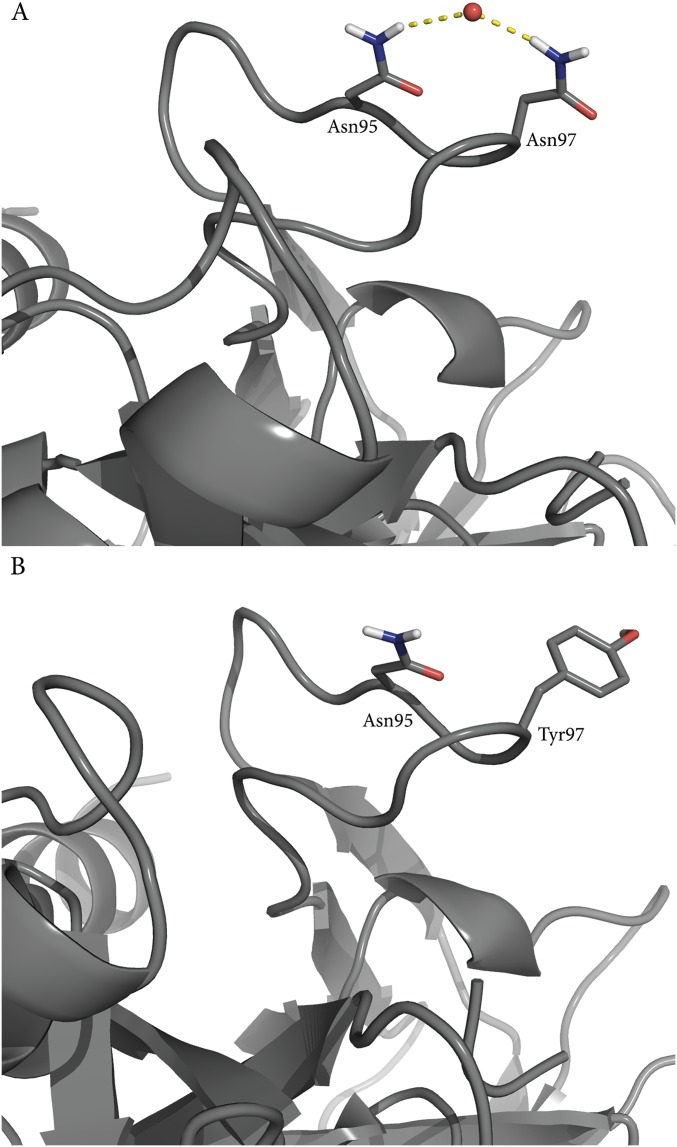
From the Arrhenius plots shown in Fig. 4B it is immediately apparent that the slopes are the same for AST carrying the Y97N mutation and the native enzyme with only the Nβ5–Nβ6 loop mobility restrained. Remarkably, the calculated values of ∆H^‡ = 12.2 kcal/mol and T∆S^‡ = −5.8 kcal/mol (300 K) for the loop-restrained AST variant are essentially identical to those obtained for the real Y97N mutation, ∆H^‡ = 12.0 kcal/mol and T∆S^‡ = −6.4 kcal/mol (Table 1). These values can be compared with those of the native AST enzyme (Table 1), which shows that a significant and similar increase of both activation enthalpy and entropy results from either mutating residue 97 or simply restraining the Nβ5–Nβ6 loop. This result thus clearly demonstrates that the mutational effect predicted for Y97N originates from altered surface rigidity. That is, freezing the Nβ5–Nβ6 loop around Y97 in wild-type AST yields the exact same shift in enthalpy–entropy balance as predicted for the Y97N mutation. As noted above, the rigidity of the Nβ5–Nβ6 loop in the native bovine enzyme (BT) can be seen from ultrahigh-resolution crystal structures to originate from extensive hydrogen bond networks that are absent in the cold-adapted enzyme, partly due to the Y97N mutation. Analysis of the MD simulations of the mutant BT N97Y shows that the water-mediated hydrogen bonding network indeed changes as a response to the mutation (Fig. S4), whereas the MD simulations of the native BT show that the network is maintained throughout the simulations.

Fig. S4.

(A) MD simulations of wild-type BT show that Asn97 forms several water-mediated hydrogen bond interactions, which are present throughout the simulations. These are disrupted in the corresponding simulations of the N97Y mutant (B), and the flexibility of the loop increases.

In addition to residue 97, two other positions behave distinctly differently when comparing the RMSFs of BT and AST (Fig. S2), namely, residue 74 in the calcium binding loop and residue 150 in the autolysis loop. Mesophilic trypsin has an asparagine and a serine, whereas psycrophilic trypsin has a lysine and an aspartic acid in positions 74 and 150, respectively. The calculated values for ∆H^‡ = 17.1 kcal/mol and T∆S^‡ = −0.4 kcal/mol (Table S2 and Fig. S5) for this triple mutant (AST K74N Y97N D150S) are very close to the corresponding values of native BT.

Table S2.

Calculated thermodynamic activation parameters for native and mutant BT and AST at 300 K

Enzyme	∆G‡	∆H‡	T∆S‡
BT native*	19.0 ± 1.4	20.4 ± 1.0	1.4 ± 1.0
AST native*	18.2 ± 0.8	9.9 ± 0.6	−8.3 ± 0.6
AST Y97N*	18.4 ± 1.1	12.0 ± 0.8	−6.4 ± 0.8
AST D150S*	18.0 ± 1.1	14.7 ± 0.8	−3.2 ± 0.8
AST K74N	17.8 ± 1.1	16.4 ± 0.8	−1.4 ± 0.8
AST 2X†	17.6 ± 1.6	18.1 ± 1.1	0.4 ± 1.2
AST 3X§	17.5 ± 0.9	17.1 ± 0.6	−0.4 ± 0.6

^*Data taken from ref. 9.

^†Two mutations: Y97N and D150S.

^§Three mutations: K74N, Y97N, and D150S.

Fig. S5.

Computational Arrhenius plots for the triple-mutated cold-adapted AST 3X (Table S2).

Discussion

It seems that all naturally occurring enzymes that have been optimized through evolution to function at low temperatures catalyze their reactions with reduced activation enthalpies and more negative activation entropies compared with their warm-active cousins. It should, however, be noted that cold-adapted enzymes generally have their temperature optimum around or above room temperature (2). This probably indicates that the evolutionary pressure acts on the effective rate at the given (low) working temperature, rather than on moving the rate optimum to low temperatures, which may also be more difficult to achieve. Hence, the adaptation seems to occur by lifting the “tail” of the rate vs. temperature curve via redistributing activation enthalpy and entropy (Fig. 1A), to yield higher rates at low temperature. Although the structural origin of this effect has remained unclear, recent studies suggested that it originates from differences outside of the active site (8, 9). Earlier work also identified a single distant surface mutation in cold-active trypsin, which was predicted to yield significant activation enthalpy–entropy changes without affecting the free energy at room temperature (9). Structurally, this mutation was found to disrupt a hydrogen bond network involving the protein and solvent, which suggested that protein surface rigidity could be involved in temperature adaptation of the enzyme.

Here, the role of surface rigidity in tuning enthalpy–entropy balances in enzymatic temperature adaptation has been investigated with extensive MD/EVB free energy simulations, for psychrophilic and mesophilic trypsin. The EVB method is particularly useful in this respect, because it allows efficient calculation of the temperature dependence of thermodynamic activation parameters. Rigidification of the enzyme surface by gradually applying positional restraints from the water–enzyme interface and inward (Fig. 2) yielded an increase in the activation enthalpy of ∼9 kcal/mol with only the outermost ∼10 Å of the enzyme surface rigidified (R_shell = 18 Å). This change in activation enthalpy is, however, fully balanced by the concomitant increase in activation entropy, making the activation free energy essentially unaltered at 300 K. It is thus noteworthy that the enthalpy–entropy balance changes significantly simply by freezing the movements of the outermost protein regions, thereby completely turning the psychrophilic trypsin into a mesophilic variant. Calculated results also show that it is sufficient to add only weak positional restraints on the outermost regions of the enzyme to achieve the effect.

The MD/EVB simulations presented here have the distinct advantage that the rigidity hypothesis can be investigated without actually introducing any mutations. Numerous comparative studies of psychrophilic, mesophilic, and thermophilic enzymes have revealed interesting differences in sequence, structure, function, and thermodynamic properties. However, identification of which amino acid substitutions are central to the process of thermal adaptation and which are merely side effects of neutral drift, or adaptation to other selective pressures, is very difficult. The cumulative effect on thermodynamic activation parameters, originating from the differences in the sequence between cold- and warm-active trypsin, seems to be fully captured by restraining the protein surface and offers a novel approach to understanding thermodynamic parameters. It should also be pointed out here that the amino acids of the active site are fully conserved in salmon and bovine trypsin, as has been found in other comparative studies of cold- and warm-active enzymes (20). From an evolutionary perspective this also makes sense, because mutations in the active site are likely to have a large negative effect on the catalytic efficiency.

Another interesting property involved in temperature adaptation is the thermostability of the enzymes. The higher catalytic activity of psychrophilic enzymes at low to moderate temperatures compared with their warm-active counterparts is always accompanied by a reduced thermostability (Fig. 1). The argument typically used to explain the trade-off between catalytic activity and thermostability is that, during evolution, interactions stabilizing the native protein structure have been tuned to obtain an optimized balance between rigidity and flexibility at their biologically relevant temperatures. This suggests that a cold-adapted enzyme working at its environmental temperatures (∼275 K) will experience thermal motions of the same magnitude as a mesophilic enzyme at its corresponding temperature (∼310 K), resulting in similar catalytic efficiencies. However, when the cold-adapted enzyme is exposed to operating temperatures of the mesophilic enzyme, thermal motions become so large that the native structure unfolds. However, the mesophilic enzyme will experience severely reduced thermal fluctuations at low temperatures, due to its rigidity, which will compromise movement along the reaction coordinate and catalytic activity.

Methods

Atomic coordinates for psychrophilic trypsin were obtained from the crystallographic structure with PDB ID code 1BZX (18). All EVB calculations were performed with the MD package Q (21) and the graphical user interface Qgui (22) using the OPLS2005 all-atoms force field (23, 24), where missing parameters and charges were assigned using Impact (25). The EVB reaction surface was calibrated using the imidazole-catalyzed methanolysis of formamide in water (26) as a reference reaction. The protein was immersed into a spherical droplet of TIP3P water molecules (27) with a radius of 35 Å centered on the Cys-Lys-Ala substrate scissile bond (9). Long-range electrostatics were treated using a multipole expansion method (28) and a direct 10-Å cutoff for nonbonded interactions. No cutoffs were applied to interactions involving the reacting fragments. All systems were heated from 1 K to the final temperature during 31 ps, using a stepwise scheme, followed by an equilibration period of 100 ps. The SHAKE algorithm (29) was used to constrain bonds and angles of solvent molecules. A time step of 1 fs was used for the production phase, and the temperature was controlled by coupling to an external bath.

To examine the effect of rigidifying the AST enzyme surface several different types of simulations were carried out. (i) Restraints on all atoms outside a given radius from the sphere center to their initial positions, with a force constant of 100 kcal/(mol⋅Ų), were used to gradually rigidified portions of the protein surface. Seven different radii in the range 18–35 Å were examined in these calculations. (ii) Simulations with different restraining force constants for heavy atoms in the protein outside 18 Å of the active site were also carried out and six different force constants in the range 0–100 kcal/(mol⋅Ų) were then examined. (iii) Movement of the Nβ5–Nβ6 loop was restrained by applying a 5 kcal/(mol⋅Ų) harmonic force constant to the backbone atoms of residues 95–99. The EVB free energy profiles were calculated using the free energy perturbation (FEP) umbrella sampling approach described elsewhere (11, 12). Each enzyme and water reaction free energy profile involved 500 ps of MD simulation and comprised 51 discrete FEP steps. Thermodynamic activation parameters were obtained from Arrhenius plots based on simulations at eight different temperatures (275–310 K) using least squares linear regression where

$$\mathrm{\Delta }{H}^{‡}=\frac{{\displaystyle {\sum }_{i=1}^n\left({\frac{1}{T}}_i-\frac{1}{\overline{T}}\right)\left(\frac{\mathrm{\Delta }{G}_i^{‡}}{T_i}-\overline{\frac{\mathrm{\Delta }{G}^{‡}}{\overline{T}}}\right)}}{{\displaystyle {\sum }_{i=1}^n{\left({\frac{1}{T}}_i-\frac{1}{\overline{T}}\right)}^2}}$$ [2]

$$\mathrm{\Delta }{S}^{‡}=\overline{\frac{\mathrm{\Delta }{G}^{‡}}{\overline{T}}}-\frac{\mathrm{\Delta }{H}^{‡}}{\overline{T}}.$$ [3]

At each temperature point 100 independent FEP simulations with different starting conditions (random seed) were carried out, resulting in a total of 9,600 individual EVB simulations, which corresponds to a simulation time of 4.9 μs.