Analyzing the electrogenicity of cytochrome c oxidase

Significance

Evaluation of voltage changes in response to charge transfer within membrane proteins can be used in studies of spectroscopically “invisible” electrogenic steps. Previous analyses of such voltage changes used qualitative macroscopic models. Here, we used a coarse-grained model, which includes an explicit description of the membrane, electrolytes, and electrodes, to interpret the observable voltage changes in cytochrome c oxidase. These calculations found that different possible electron/proton transfer (ET/PT) paths can lead to the same observed voltage changes, thus challenging the uniqueness of previous conclusions. However, our method offers a general tool for studies of a wide range of electrogenic ET/PT by combining voltage measurements with other experiments and simulations to analyze new mechanistic proposals.

Abstract

Measurements of voltage changes in response to charge separation within membrane proteins can offer fundamental information on spectroscopically “invisible” steps. For example, results from studies of voltage changes associated with electron and proton transfer in cytochrome c oxidase could, in principle, be used to discriminate between different theoretical models describing the molecular mechanism of proton pumping. Earlier analyses of data from these measurements have been based on macroscopic considerations that may not allow for exploring the actual molecular mechanisms. Here, we have used a coarse-grained model describing the relation between observed voltage changes and specific charge-transfer reactions, which includes an explicit description of the membrane, the electrolytes, and the electrodes. The results from these calculations offer mechanistic insights at the molecular level. Our main conclusion is that previously assumed mechanistic evidence that was based on electrogenic measurements is not unique. However, the ability of our calculations to obtain reliable voltage changes means that we have a tool that can be used to describe a wide range of electrogenic charge transfers in channels and transporters, by combining voltage measurements with other experiments and simulations to analyze new mechanistic proposals.

Cytochrome c oxidase (CcO) couples the four-electron reduction of O₂ to water, where the released free energy is used to pump protons from the negative (N) to the positive (P) side of the membrane (1–5), leading to an electrochemical proton gradient that drives, for example, ATP synthesis. The elucidation of the structure of CcO (6–12), combined with experimental and theoretical studies (e.g., refs. 3, 13–15), has advanced the understanding of this intriguing system. Progress has been made in defining the conditions that would allow CcO to pump protons against a pH gradient (4, 16), in estimating the electrostatic energy of possible intermediates (17–21), in evaluating the energetics of the key water chains (22, 23), and of a number of specific proton-transfer (PT) reactions (16). Furthermore, examination of the energetics of the overall pumping process has been performed by using a semimacroscopic model (16).

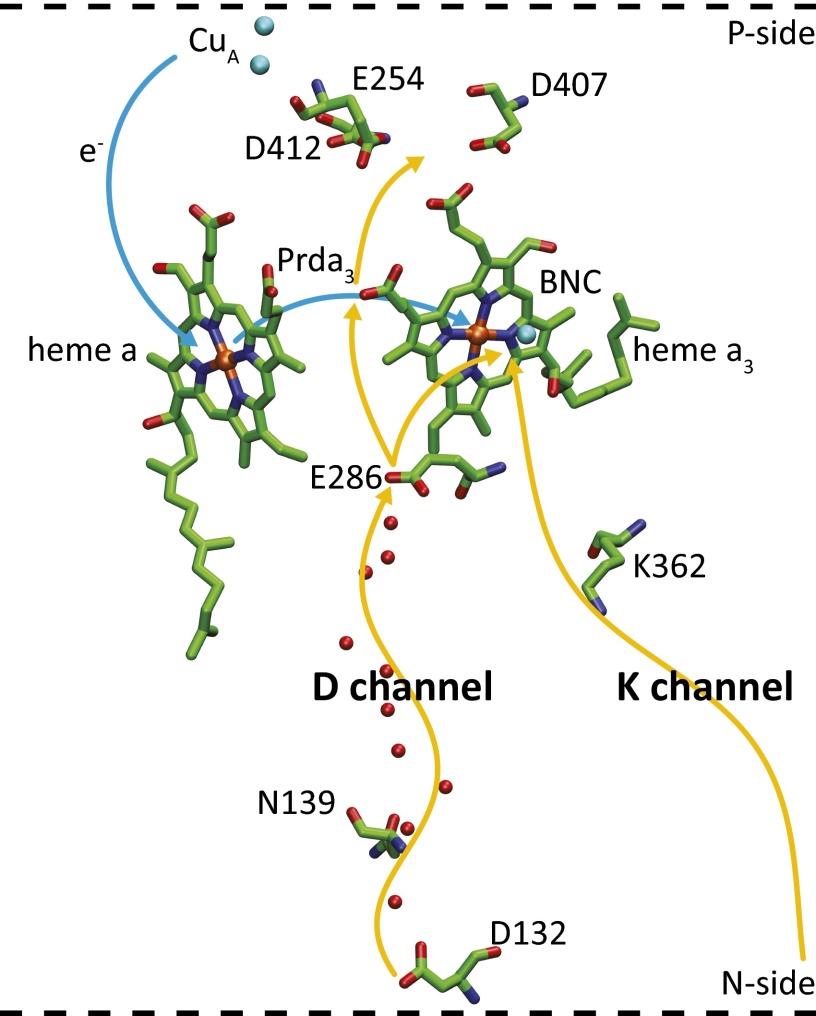
However, the relationship between protein structure, the PT energetics, and detailed PT trajectories has not been established. Furthermore, to our knowledge, a consistent proton-pumping mechanism purely based on structural information and thermodynamic considerations has not been presented. For example, we still cannot identity the primary acceptor for pumped protons, although the D propionate of heme a₃ (Prda3 in Fig. 1) is one of the most likely candidates for being at least a “transient” acceptor. Apparently, there has been some progress in using structures in functional analyses (e.g., refs. 16, 24–26). However, we still do not have a consistent model that correctly reproduces the pumping events, while preventing the back reaction. Our earlier studies of the structure–function relationship in CcO have been presented in ref. 16, with some more recent modifications (e.g., ref. 27). These and other studies (e.g., the studies mentioned in ref. 27) have not revealed the detailed features of a proton pump, and so far structure-based energy barriers have not been determined to sufficient accuracy. We note in this respect that, even though results from phenomenological analyses do provide some functional insights (28, 29), results from these studies cannot present a detailed molecular mechanism. Realizing that many problems still remain despite intriguing mutational experiments (30, 31), it is important to search for experimental information that can help in advancing our understanding of the system. In this respect, it is tempting to consider data from electrometric measurements that have been used to study time-dependent membrane potentials and to elucidate charge motions in membrane proteins. Such approaches can offer mechanistic insights into the function of membrane-bound channels and pumps (32). Monitoring the transmembrane potential may enable observation of PT steps that are typically “invisible” when using spectroscopic techniques. In recent years, Wikström and coworkers (33) have performed time-resolved measurements of voltage changes across CcO and evaluated the data in terms of sequences of PT and electron transfer (ET) events in CcO. Even though the data from these measurements offer valuable insights, correlating the observed voltage changes with the number of transferred charges and distances is challenging because the nature of the dielectric response in protein membrane systems is complex. Consequently, it is not straightforward to use macroscopic models to obtain a general and unique relationship between specific internal charge-transfer reactions and the generated potential.

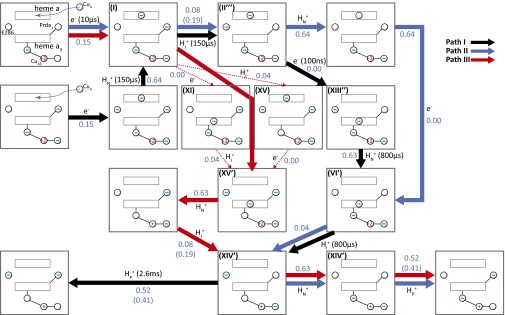
Fig. 1.

The key (D and K) proton pathways in CcO. The D pathway starts at D132, near the protein surface, and connects the site, via a number of water molecules (red spheres) with a highly conserved Glu residue, E286. Two alternative PT paths from E286 are indicated. One leads to the transient proton acceptor, propionate D (Prda₃) of heme a₃, and the other one to the catalytic site, which consists of heme a₃ and Cu_B. The K pathway starts presumably at E101 (not shown) in subunit II and leads to the catalytic site (BNC) via the conserved K362. The residue numbering is that of the Rhodobacter sphaeroides aa₃ oxidase. D407, D412, or E254 in the ionizable cluster above Prda3 could serve as the proton loading site (PLS).

The challenge of quantifying the relationship between voltage measurements and charge transport processes has been addressed in our recent work (34), where we developed a specialized coarse-grained (CG) approach (see below) and validated the method using data from measurements of charge-transfer processes in a structurally and functionally well-characterized system (photosynthetic bacterial reaction centers). In this work, we examine whether results from measurements of electrogenic events can offer unique information about the ET/PT pathways in CcO. We found that different pathways can generate the same voltage changes on the outside of the membrane, which shows that care must be exercised when using macroscopic models. We also argue, however, that combining data from electrogenic measurements with other studies and calculations might provide a way of distinguishing between different mechanistic options, thereby offering insights into the molecular mechanism of proton pumping.

Methods

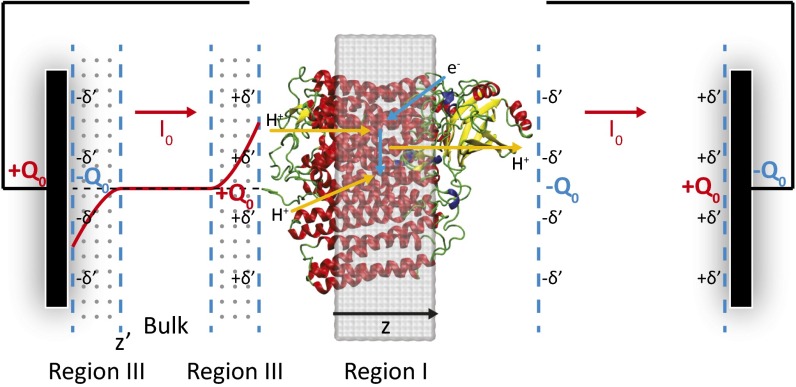
Our method is based on using the CG treatment, which is described in detail elsewhere (34–38), where we model the protein/membrane system (39) and its interaction with the external potential (Fig. 2). The use of the model for evaluating the changes in electrode potential upon charge transfer involves a novel approach of allowing the electrode potential to equilibrate with the charge transfer by selecting the lowest free energy of the complete system. More specifically, we use a CG simulation system that includes a simulation box that explicitly includes the membrane containing the protein (region I), an optional region with explicit electrolytes (region II) (38) (which is not considered in the present study), and a grid representing the electrolyte solution (region III). We also add a “bulk region” far away from both the membrane and electrode surfaces, to span the space between the membranes and the electrodes without using an enormous grid. The CG model represents the solvent implicitly, whereas the ions in the solution are considered more explicitly by using a grid-type approach where the residual charges at each grid point represent the charges of the electrolytes ($q_k^g$), which are determined self consistently, as described in ref. 35. The model allows us to evaluate the actual charge distribution of the electrolytes and the corresponding gating charge by using:

$$Q_{gate}\left(\equiv \mathrm{\Delta }{Q}_0\right)={\displaystyle \underset{-\infty }{\overset{z\text{'}}{\int }}(\mathrm{\Delta }\mathrm{\Delta }{q}_{grid}(V,Z)/\mathrm{\Delta }Z)dZ},$$ [1]

Fig. 2.

The CG model of the CcO system used in the present work: the protein/membrane system (region I), the electrolyte grid (region III), and the bulk region between the electrolyte solutions. Electrolyte charge distribution is shown as a red solid curve, resulting from the electrolyte response to charge distributions in CcO. The changes in electrode potentials (voltage generations) are measures of electrogenicity; that is, fraction of membrane potential (or dielectric distance) in the present study.

where $\mathrm{\Delta }\mathrm{\Delta }{q}_{\mathit{grid}}$ is the difference in the accumulative sum of $\mathrm{\Delta }{q}_{\mathit{grid}}$ before and after charge translocation, and Z′ is the point along the z axis (normal to the membrane plane as shown in Fig. 2), where the electrolyte charge distribution near the membrane changes sign. At this point, the integrated charge reaches a plateau and then starts to decrease. Note that the integral evaluates the electrolyte charges before they penetrate the membrane.

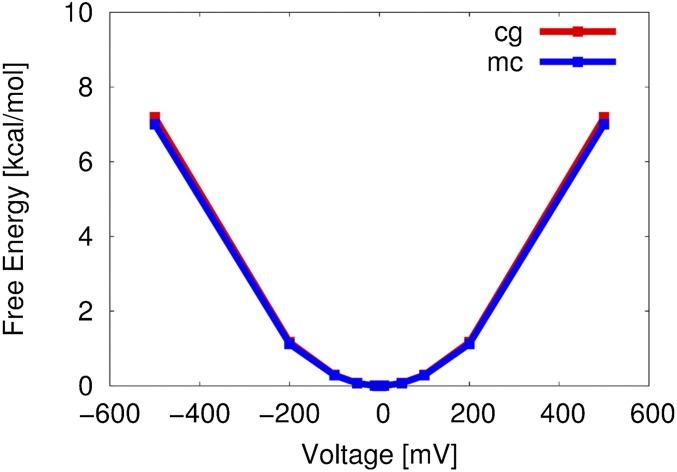
The above approach works very well when we have a fixed external potential (e.g., ref. 35). However, in the present case, we are interested in the changes in the external potential upon charge transfer. To address this challenge, we designed an approach, which is described in detail in ref. 34. In this approach, we determine the relevant potential by applying external potentials of different values, evaluate the resulting changes in the electrolyte distribution, and evaluate the total free energy of the complete protein/membrane/electrolyte/electrode system (an example of the free energy trend is given in Fig. S1). Because the system with the lowest free energy is the system that reflects the equilibration of the charges with the external potential, we take the potential that corresponds to the lowest total free energy as the relevant external potential. However, the use of our approach of searching for the lowest free energy configuration (which is, in principle, very insightful) appears to require major computational effort. Fortunately, we also found that the changes in the potential and gating charge generated after charge transfer process are independent of the applied potential (34, 37) (see also Fig. S2). Thus, we used those changes here without looking for the potential that will minimize the total free energy of the system.

Fig. S1.

Comparison of our CG semimicroscopic model of voltage coupling (CG) and macroscopic continuum (MC) electrostatic model (i.e., voltage Poisson–Boltzmann equation), applied to the evaluation of free energy of charging the membrane system (or capacitance) between two electrolytes. It turns out (by the energy conservation) that the free energy of charging the membrane is equal to the free energy of polarizing electrolytes by an externally applied voltage.

Fig. S2.

The change in electrode potential (voltage generation) for the PT from the N-side solution to E286. The number in parentheses is a fractional voltage normalized by an observed voltage generation of 2.48 mV.

In preparing the simulation system, we started with the CcO structure from PDB ID code 1M56 (10). The positioning of the membrane for the CcO was initially determined by using the OPM database (40), with a resulting membrane thickness of 30 Å. The atomistic simulation system of CcO was constructed in a similar way to that used in our previous studies of CcO (27, 41), and the system was relaxed by a short molecular-dynamics run of 10 ns for each state considered. The CG calculations used the corresponding protocol of the MOLARIS program, where we built models of the membrane protein systems (that include the electrolytes and electrodes) with a membrane thickness of 28 Å (25), in order to evaluate voltage generation upon ET/PT within the membrane. The initial protonation states of the CG model of membrane proteins were determined without electrolytes by a Monte Carlo (MC) proton transfer (e.g., ref. 42) of ∼2 million MC steps for each of nine representative simulation systems (with the redox state described in Fig. 3), reflecting different combinations of the rotameric states (χ₁) of both E286 and d-propionate of heme a3 (Prda3) (Table S1). Each system was then fed into a next step to determine the electrolyte charge distributions and the electrode potentials under an external voltage of 0.1 V. The changes in electrode potentials after the ETs/PTs were used to estimate the voltage generation (the difference in electrode potentials before and after the charge separation). The validity of our approach has been established recently in systematic works (34, 37, 38).

Fig. 3.

Three different possible PT/ET paths consistent with the electrometric experiment in ref. 33. H_N⁺, H_P, and H_I⁺ represent, respectively, the PT from the N side, the PT toward the P side, and the internal PT. e– represents ET. The spheres with the charges represent the charge state of the corresponding group. The – in spheres represents the deprotonated state for E286/Prda3 and the reduced state for heme a/a3, respectively. For example, in state I, the oxidation state of Cu_A3 is +2, and heme a is reduced. The numbers in the diagram represent the measured/calculated voltage generation (electrogenicity) associated with the corresponding PT or ET reactions. The – near Cu designates the charge on the ligands of the Cu. The Roman numeral that designate different states follow the notation of ref. 16. The reaction times are taken from ref. 33, and the time scale from the E286 to Prda3 (or E286 to BNC) transfer and the N side to E286 transfer cannot be separate. Path I (black arrows) is the path that corresponds to the proposal of ref. 33. The path starts with an ET to heme a, PT from the N side to E286, PT from E286 to the PLS, ET to heme a3, PT from E286 to the BNC, and PT to the P side. Paths II (colored in blue) and III (colored in red) are based on the options explored in ref. 16 and subsequent estimates (e.g., ref. 41). Path II starts with ET to heme a, PT to the PLS, PT from the N side to E286, ET to heme a3, PT from E286 to the BNC, PT from N to E286, and PT to the P side. Path III starts with an ET to heme a, ET to heme a3, and PT to the BNC (with two alternative paths), PT from the N side, PT to the PLS, and the same two last steps as in path II. The numbers in parentheses correspond to the fraction of membrane potentials when D412 is served as the PLS. The pathways along path III represented by thin red lines represent options that cannot be resolved at present.

Table S1.

Partial charges of ionizable residues

Residue no. (from Rb. sphaeroides)	Average	SE of mean
K27	1	0
D28	−0.99	0
R52	1	0
E54	−0.08	0
E66	−0.61	0.04
E69	−0.47	0.01
K74	1	0
E86	−0.71	0.04
D132	−0.7	0.02
R137	1	0
E182	−0.73	0.01
D188	−0.51	0.01
R216	1	0
K224	1	0
D256	−0.21	0.01
R257	1	0
D271	−0.82	0.01
E286	0	0
K307	1	0
K308	1	0
K362	1	0
E376	−0.99	0
K378	1	0
D407	−0.91	0.01
R408	1	0
D412	−0.73	0.02
K442	1	0
R446	1	0
E450	−0.93	0.02
K454	1	0
R476	1	0
R481	1	0
R482	1	0
D485	−0.09	0.01
E488	−0.24	0.03
R521	1	0
R524	1	0
E533	−0.93	0.01
D536	−0.96	0
E539	−0.37	0.02
E548	−0.94	0.01
E552	−0.86	0.01
K556	1	0
R557	1	0
E558	−0.86	0.02
D559	−0.95	0.02
E31	−0.57	0.02
R35	1	0
D58	−0.95	0.01
R82	1	0
E85	−1	0
K86	1	0
R87	1	0
K89	1	0
R93	1	0
E101	−0.62	0.02
E128	−0.46	0.01
E131	−0.37	0.02
D133	−0.61	0.06
K137	1	0
E148	−0.56	0.02
D151	−0.53	0.02
E152	−0.46	0.05
E153	−0.35	0.03
E157	−0.35	0.01
D169	−0.77	0.03
R171	1	0
E175	−0.35	0.01
E177	−0.43	0.03
E182	−0.32	0.01
R187	1	0
D188	−0.68	0.03
E189	−0.47	0.04
D195	−0.54	0.01
K204	1	0
D214	−0.41	0.02
K227	1	0
D229	−0.54	0.02
R234	1	0
R241	1	0
E243	−0.71	0.04
R244	1	0
E245	−0.23	0.02
E254	−0.4	0.02
K268	1	0
E272	−0.69	0.05
E273	−0.31	0.01
E280	−0.37	0.02
R283	1	0
E288	−0.35	0.01
K5	1	0
D8	−0.82	0.02
D61	−0.86	0.01
E65	−0.88	0.02
E68	−0.63	0.02
D70	−0.84	0.01
R76	1	0
R80	1	0
E90	0	0
K103	1	0
E112	−0.37	0.01
D117	−0.71	0.01
E123	−0.35	0.01
D129	−0.5	0.02
E158	−0.62	0.02
R161	1	0
R162	1	0
D163	−0.63	0.04
E185	−0.18	0.02
R226	1	0
R229	1	0
E235	−0.87	0.02
K236	1	0
E241	−0.81	0.01
D251	−0.02	0
D17	−0.92	0.01
E22	−0.86	0.02
K23	1	0
R30	1	0

The number is averaged over nine different combinations of rotameric states, considering three χ₁ states for each E286 and Prda3.

Results and Discussion

Because our approach has been validated in the previous study of bacterial reaction centers (34), we could turn to the CcO system with some confidence. Our study of CcO is focused on addressing the following question: Can a comparison of the calculated and observed voltage changes discriminate between different reaction pathways (i.e., exclude some possible pathways)?

Our calculations considered the system described in Fig. 2, and determined the changes in electrolyte charges and the corresponding equilibrated potentials for different elementary PT and ET steps. Our analysis has focused on the pathways summarized in Fig. 3, as well as in Table S2. In presenting the results, we note that the reported observed values must be normalized because they depend on factors such as the quantum yield, the number of proteins in the membrane (e.g., see ref. 34), and also whether or not the measurements can resolve individual charge-transfer (for example, the very large difference in the electrogenicity of the WT reported in refs. 33 and 43 indicates that we have very different analysis). Consequently, we normalized the calculated and observed results to the corresponding ratio between the given voltage and the voltage generated by a transfer of a full charge across the membrane (see ref. 43 for a related treatment). The resulting quantity is called here “fractional voltage,” which is related to the so-called “dielectric distance” (ref. 38 and references therein). We note, however, that in reporting the normalized calculated (fractional) values, we used an observed value of 2.48 mV (25, 33) (in comparison with a calculated value of 2.56 mV) for transferring a proton from the N to the P side of the membrane. We also note that the exact value used in the normalization is not so important once we compare different models.

Table S2.

Comparison of measured and calculated electrogenicity

Reaction sequences of path I (black)	Measured electrogenicity*	Calculated electrogenicity†	Calculated electrogenicity‡	Reaction sequences of path II (blue)	Calculated electrogenicity	Reaction sequences of path III (red)	Calculated electrogenicity
CuA → heme a	0.24 (0.24)	0.25 (0.25)	0.15 (0.15)	CuA → heme a	0.15 (0.15)	CuA → heme a	0.15 (0.15)
N-side → E286	0.84 (1.08)	0.54 (0.79)	0.64 (0.79)	E286 → PLS	0.08(0.23)§	heme a → heme a3	0.00 (0.15)
					0.19 (0.34)
E286 → PLS¶	0.84 (1.08)	0.10 (0.89)§	0.08 (0.87)§	N-side → E286	0.64 (0.87)	E286 → heme a3 (or CuB)	0.04 (0.19)
		0.19 (0.98)	0.19 (0.98)		(0.98)
		0.17 (0.96)	0.18 (0.97)
		0.21 (1.00)	0.22 (1.01)
Heme a → heme a3	0.00 (1.08)	0.0 (0.89)	0.00 (0.87)	Heme a → heme a3	0.00 (0.87)	N-side → E286	0.64 (0.83)
		(0.98)	(0.98)		(0.98)
		(0.96)	(0.97)
		(1.00)	(1.01)
N side → E286	0.60 (1.68)	0.54 (1.43)	0.63 (1.50)	E286 → heme a3 (or CuB)	0.04 (0.91)§	E286 → PLS	0.08 (0.91)
		(1.52)	(1.61)		(1.02)		0.19 (1.02)
		(1.50)	(1.60)
		(1.54)	(1.64)
E286 → heme a3 (or CuB)	0.60 (1.68)	0.04 (1.47)	0.04 (1.54)	N side → E286	0.63 (1.54)	N-side → E286	0.63 (1.54)
		(1.56)	(1.65)		(1.65)		(1.65)
		(1.54)	(1.64)
		(1.58)	(1.68)
PLS → P side¶	0.32 (2.00)	0.53 (2.00)	0.52 (2.06)	PLS → P side	0.52 (2.06)	PLS → P-side	0.52 (2.06)
		0.44 (2.00)	0.41 (2.06)		0.41 (2.06)		0.41 (2.06)
		0.46 (2.00)	0.42 (2.06)
		0.42 (2.00)	0.38 (2.06)
	(2.00)	(2.00)	(2.06)		(2.06)		(2.06)

^*The electrogenicity is expressed as the fractional voltage for the corresponding reactions; the numbers in parentheses are the cumulative fractional voltages. The reported values are normalized by the observed potential of 2.48 mV (25, 33) for transferring a proton from the N to P side of the membrane.

^†The electrogenicity is estimated by evaluating the simple geometric distances traveled by charge carriers perpendicular to the membrane plane.

^‡The electrogenicity is estimated by calculating the changes in the electrode potentials upon charge transfers by using our CG approach, normalized by an observed potential of 2.48 mV. In comparison, the calculated potential is ∼2.56 mV, yielding a total fraction of membrane potential of 2.06.

^§This electrogenicity is the maximum value of the fractional voltage (where the distance between E286 and Prda3 is maximum) among nine different combinations of the rotameric states (χ₁), whose minimum fractional voltage is ∼0.04.

^¶The fractional voltage for the PT from E286 to the PLS when either D412, D407, or E254 is severed as the PLS; otherwise, Prda3 is the P.

In analyzing the results of Fig. 3 and Table S2, we can start by considering the path (path I, black) that corresponds to the proposal in refs. 25 and 33. The path starts with the ET from Cu_A. The next step (which takes ∼150 μs) has been assumed (33) to correspond to the PT from the N side to Prd (the possible pump site), based on the magnitude of the measured voltage. However, this sequence of reactions is inconsistent with the earlier proposal that the first PT is from the protonated E286 (33; see also refs. 44–46). This pathway may still be possible, assuming a concerted PT from E286 to Prd and from the bulk solution to E286 (21, 26), but this sequence of events is less likely based on our earlier results (41).

To explore the possibility that the results from the measurements allows one to select among different possible paths, we examined (in addition to path I) the two feasible alternative paths that were considered in our works and depicted in Fig. 1 (paths II and III, colored in blue and red, respectively). The generated voltages in both paths also appear to be consistent with the observed voltage generation and with the voltage change obtained in path I (Fig. 3 and Table S2). Thus, one instructive conclusion from the present calculations is the observation that all three pathways considered, shown in Fig. 3 and Table S2, yield almost the same calculated accumulative voltage, and thus all are consistent with the observed voltage changes for the O to E transition (i.e., ET to the catalytic site). This finding means that the electrometric measurements cannot be used to select between different alternative paths.

In addition, our calculations indicate that, to be consistent with the experimental observations, the proton-loading site (PLS) may be located above the Prd in the cluster of ionizable residues (24), including D407, D412, or E254 (24). In fact, one of those residues (D407) is suggested in a recent study to be a candidate for the PLS (47). Here, a good fit to the observed voltage generation was obtained for each reaction step (Table S2). This conclusion is valid for the three paths. In other words, in all three models, we obtain a better fit to the observed voltage change with the PLS considered above.

Although the measured voltage does not seem to discriminate between the three paths considered for the WT, it is possible that the paths for different mutants can be discriminated by comparing the calculated and observed electrogenicity. Thus we considered here the effect of the D132N mutation (D124N in Paracoccus denitrificans CcO) on the voltage measurements. Residue D132 is located near the D pathway orifice, and removal of this protonatable residue results in blocking PT from the N-side solution to E286 (27, 48). Reprotonation of E286 through the D pathway is very slow (∼2 s⁻¹) (31). Thus, we have to consider only path III (indicated in red in Fig. 3) up to the point where the proton has been transferred to the binuclear center (BNC). The estimated observed voltage changes for the WT were 0.94 (the sum of the voltage changes originating from A→P and P→F) and 1.06 (the sum of the voltage changes of the two F→O components), respectively (43). In considering the normalization for this system, we note that it includes several transitions; the three transitions in the WT (A→P/P→F/F→O) (3.7 charges; i.e., a full oxidative cycle) (table 2 in ref. 47), whereas the reaction cycle in ref. 33 only considered the O→E transition (two charges). The F→O transition (two charges) of ref. 43 is similar to the O→E transition (two charges), but the P→F transitions generate a fractional charge of 1.33 (43), somewhat different from the F→O transition. Now, we can attempt to use the O→E transition to simulate (A→P/P→F) and to assume that averaging on the three steps of ref. 43 is similar to what is obtained in the O→E transition. At any rate, our selection of the normalization in the mutational analysis is not so important because we always compare with the WT system.

The calculated changes in fractional voltage, in the WT CcO, up to the step of protonating the BNC, were 0.82 and then 1.23 (for the protonation through the D channel); This was done with normalization to 2.00 charge transfer for paths that completed the PT/ET process (see above). Note, again, that we compare different mechanisms with the same normalization. In other words, both the calculations and experiments compare the WT and mutants in the same way. By using the data in table 1 of ref. 43, the observed results for the fast steps (i.e., A→P and P→F) in D132N (D124N) and N139V (N131V) correspond to 0.36 and 0.23, respectively, whereas the calculated result for the fast steps of the mutants (without relaxation processes that will be considered below) are 0.19. Similarly, the observed results for the slow steps are 0.38 and 0.43 for D132N and N139V, respectively, whereas the calculated result for the mutants is 0.64 (Table 1). The analysis of the above rather complex trend is given in Table 1 and Fig. 4. The analysis starts by noting that ref. 43 found that the amplitude of the fast component of D132N has larger fast amplitude (by 0.24) than those of the other two mutants. This effect was rationalized by Wikström and coworkers in ref. 43 as being due to PT from Y43 (which is located between N139 and E286) to E286. According to this argument, the replacement of the OH group by a hydrogen in Y43 of the D132N/Y43F mutant blocks this effect [similar blockage is proposed to occur in the N139V mutant (43)], and the only remaining amplitude is due to the PT form E286 to Prda3 (Fig. 4C).

Table 1.

Analyzing the electrogenicity of the mutants in different models

Mutant	Measured electrogenicity*		Calculated electrogenicity†
	Fast	Slow	Fast	Slow
WT	0.94	1.06	0.82	1.23
D132N	0.36	0.38	0.19	0.64
D132N+ (Y43→E286)	0.36	0.38	0.27	0.64
D132N+ (Y43→E286→Prda3)	0.36	0.38	0.35, 0.46‡	0.64
D132N+ (K362 relaxation)	0.36	0.38	0.23	0.64
D132N/Y43	0.24	0.43	N/A	N/A
N139V N139V+(K362 relaxation)	0.23	0.52	0.19	0.64

N/A, not applicable.

^*The experimental fractional voltages are normalized to 2.0 charge translocation (so it can be compared with the calculated results), which is essential for comparison with the calculated values, despite the fact that the observed values are assumed to reflect a transfer of 3.7 equivalent charges across the membrane (see table 2 of ref. 44). Fast and slow are defined in table 2 of ref. 44.

^†The calculated fractional voltages are normalized to 2.06 equivalent charges translocated across the membrane. The calculated splitting to slow and fast step is based on our selected path and the estimate of the corresponding transfer over time based on the relevant experimental information.

^‡D412 is served as the PLS; otherwise Prda3 is the PLS.

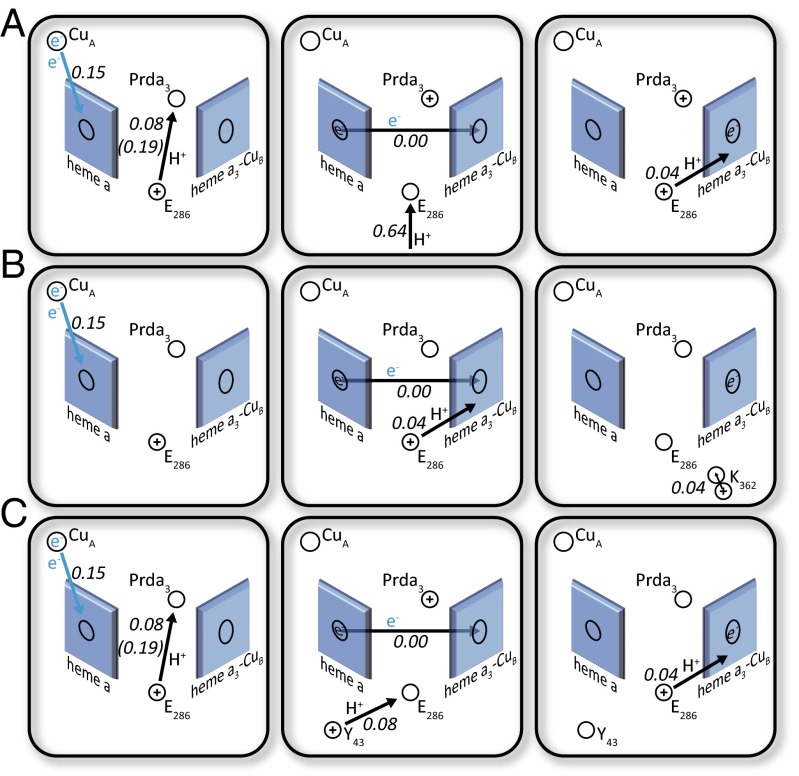
Fig. 4.

Analyzing possible effects of mutations for the fast steps. (A) A fraction of membrane potential for the WT ET and PT to the catalytic site in paths I and II. (B) A fraction of membrane potential generated for the D132N mutant fast step (defined in Table 1) with the K362 relaxation, as proposed in ref. 30. (C) A fraction of membrane potential generated for the D132N mutant fast step (defined in Table 1), as proposed by ref. 43, where a proposed PT from Y43 to E286 is added to the observed voltage change.

To explore the above option, we calculated the potential change due to a PT from Y43 to E286. The calculated change in fractional voltage is 0.08, and it is consistent with the proposed effect of Y43 in the D138N/Y43F and N139V mutants. However, the proposal of a PT to Prd in D132N is not consistent with the absence of overall proton-pumping sites in the D132N mutant. Another contentious point is the argument of Wikström and coworkers (43) that the charge shift in D132 and D132N/Y43F must include a PT from E286 to Prda₃, because the electrogenic effect for the E286 to BNC must be very small. However, as shown in Table S2, we reproduce the observed voltage change for the path that involves a PT to the BNC center.

Another interesting finding was reported in ref. 30, where it was noted that at pH 10.5 (where proton uptake through the D pathway is very slow, similar to the case with D132N), the K362M mutation leads to a reduction in the amplitude of the fast voltage change component. This finding indicates a possible charge motion in the K channel, where K362 is located. Ref. 30 argues that the effect may represent a compensation for the charge motion to the BNC by a displacement of a protonated K362 (Fig. 4B). To explore this option, we calculated the change in the potential due to transfer of a positive charge in the K channel. This calculation yielded 0.03 because of the movement of the rotamer of K362 toward the BNC. Interestingly, the idea of the effect of K362 was criticized in ref. 43, where it was stated that electrogenic events may originate from PT from Y43 without any voltage changes originating from charge transfer in the K channel. However, this argument seems not to be so relevant because the data in ref. 30 did show an effect from the K362M mutation.

Finally, we would like to clarify that the deviations observed in Table 1, between the calculated and observed trend in the electrogenicity for D132N, might reflect the assignment in ref. 43 of larger fraction of the overall voltage change to the slow process. Note that, although the overall voltage change can be reasonable, the time dependence does not correspond to the spectroscopic measurements.

Concluding Remarks

This work explored the applicability of voltage measurements in resolving mechanistic problems in CcO. The need for analysis of the type introduced in our work is dictated by major uncertainties in the use of macroscopic models and approaches in studies of membrane–electrolytes–electrode systems. Our simulations established that different charge transport pathways can give the same electrogenic results. Thus, in some cases, it is very hard to draw unique mechanistic conclusions based on electrogenic studies; this is true, not only with regard to qualitative estimates based on the distance of the transferred charge along the distance perpendicular to the membrane plane (43) or the more advanced estimates (25), but also with regard to our quantitative estimates. For example, we have shown in this work that the mechanistic conclusions drawn in ref. 33 are far from being conclusive. However, our ability to analyze the voltage change in CcO provides a very powerful tool when combined with other measurements and energy calculations. Such a combination might provide a way of distinguishing between different mechanistic options.

A case in point is the finding that the cluster with D412, D407, or E254 is likely to be the PLS. Here, although locating the PLS is not so crucial in deducing the overall mechanism (because we will obtain similar result when the PLS is Prda3), we have a demonstration of the possible usefulness of reliable calculations of voltage changes. It is also possible that better time resolution than that obtained in ref. 44 (where we get information on a single step) can make our analysis more unique. Relevant information is likely to be provided from the measurements reported in (e.g., refs. 49 and 50) Furthermore, because the voltage measurements reflect mainly the motion perpendicular to the membrane, we believe that the analysis of mechanisms, where the times of moving along different sections perpendicular to the membrane are very different, can be very useful.