Two-photon microscopy using fiber-based nanosecond excitation

Abstract

Two-photon excitation fluorescence (TPEF) microscopy is a powerful technique for sensitive tissue imaging at depths of up to 1000 micrometers. However, due to the shallow penetration, for in vivo imaging of internal organs in patients beam delivery by an endoscope is crucial. Until today, this is hindered by linear and non-linear pulse broadening of the femtosecond pulses in the optical fibers of the endoscopes. Here we present an endoscope-ready, fiber-based TPEF microscope, using nanosecond pulses at low repetition rates instead of femtosecond pulses. These nanosecond pulses lack most of the problems connected with femtosecond pulses but are equally suited for TPEF imaging. We derive and demonstrate that at given cw-power the TPEF signal only depends on the duty cycle of the laser source. Due to the higher pulse energy at the same peak power we can also demonstrate single shot two-photon fluorescence lifetime measurements.

1. Introduction

Two-photon excitation fluorescence (TPEF) microscopy [1] is a powerful technique for sensitive, high-resolution and deep tissue imaging [2]. It is a non-linear optical technique requiring high intensities. Compared to one-photon fluorescence microscopy, the non-linearity [3] has intrinsic axial sectioning capabilities and the longer wavelengths provide better tissue penetration. Current laser systems for TPEF imaging employ ultra-short pulse lasers (~100fs-10ps) in order to achieve the high intensities required for non-linear excitation. This is because the average power is limited by the sample damage threshold and most systems run at a fixed, very high pulse repetition rate (~80MHz). As a consequence, shorter pulses create higher peak powers. However, also longer pulses can be used [3–9]. Particularly, at same peak powers the repetition rate can be lowered, thus giving the same duty cycle and, hence, the same average power. In some situations lower repetition rates are even favorable for fluorescence imaging as they avoid dark states [10]. The advantage of using longer pulses, especially for fiber based beam delivery, is the narrow spectral width, so chromatic dispersion in the system has negligible effect. Further, the much smaller intensity slope prevents self-phase modulation (SPM). This holds especially true in glass fibers where long interaction lengths occur. Glass fiber based optical systems are desirable, as they provide a stable, spatially pure single mode beam quality. But more importantly, in biological imaging the tissue penetration depth is limited to ~100µm-1mm [2], so the study of deeper regions and internal organs can only be conducted by employing fiber endoscopes to overcome the penetration limit set by scattering in tissue.

Here we present a TPEF system that is fiber-based and uses 0.4-10ns pulses from a fiber master oscillator power amplifier (MOPA). This laser has freely programmable pulse repetition rates, which allows realization of duty cycles comparable to ultra-fast laser systems (10⁻⁴-10⁻⁵). We show, both theoretically and experimentally, that at comparable cw-power levels this system reaches similar TPEF signals as ultra-fast systems do. An intuitive model to understand this comparison is that a ns pulse can just be thought of as a sequence of thousand 1ps pulses all strung together to one pulse [Fig. 1].

Fig. 1.

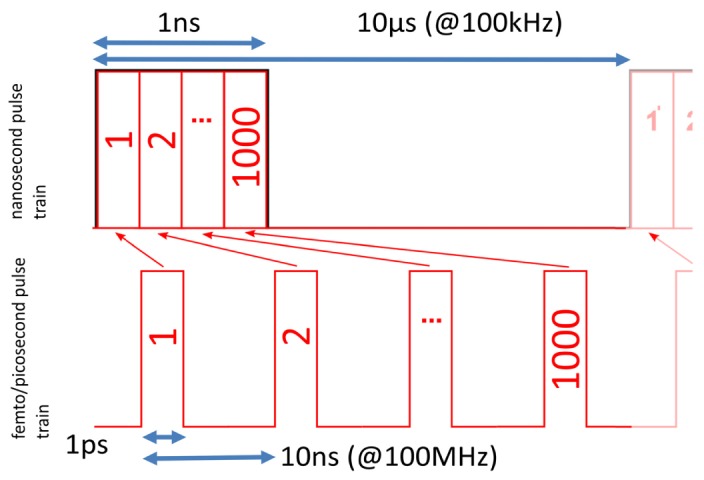
Simple sketch to visualize that at given duty cycle (here 10⁻⁴) and average power the peak power (and with it the TPEF rate) is independent of pulse duration. Ns- and ps-pulse train with same duty cycle and same average power: High repetition rate ps-pulses (bottom) versus low rep rate ns-pulses (top). A 1ns pulse can be thought of merging groups of 1000 short 1ps pulses together. Accordingly, the repetition rate is lowered from 100MHz to 100kHz.

For TPEF, high instantaneous powers are needed in order to enable the simultaneous absorption of two photons. This effect was first theoretically described by Maria Goeppert-Mayer in 1931 [11]. Only with the advent of lasers it was first experimentally observed by Kaiser and Garrett in 1961 [3].

The number of absorbed photons per fluorophore per pulse can be calculated by [1]:

$$n_a=\frac{p_0^2\delta }{{\tau }_p{f}_p^2}{\left(\frac{N{A}^2}{2\hslash c\lambda }\right)}^2=\frac{p_0^2}{{\tau }_p{f}_p^2}\times \text{S,}$$ (1)

where $p_0$ is the average power of the laser pulse train, $\delta$ the 2-photon absorption cross section, ${\tau }_p$ the pulse length, $f_p$ the pulse repetition rate, $NA$ the numerical aperture, c the speed of light, $\hslash$ the reduced Planck constant and λ the wavelength. For simplification, we assume rectangular pulses and summarize the system parameters in the factor $S=\text{δ}{\left(\frac{N{A}^2}{2\hslash c\lambda }\right)}^2$. With $p_0=p_{peak}{\tau }_p{f}_p,$ Eq. (1) can be rewritten as:

$$n_a={\text{p}}_{\text{peak}}^2\times {\mathrm{\tau }}_{\text{p}}\times \text{S}.$$ (2)

Thus, the number of absorbed photons per pulse scales quadratically with the instantaneous peak power and linearly with the pulse duration.

In practice, the average power $p_0$ is limited by the sample damage threshold, so it is useful to consider the number of TPEF photons generated per pixel. The total number $N_a$ of excited molecules over the experimental setup’s photon collection time, i.e. the pixel dwell time t_px, can be calculated by summing over all n_group pulses during t_px:

$$N_a={\displaystyle \sum }_{n_{group}}{n}_a=n_a\times f_p\times {\text{t}}_{\text{px}}=\text{S}\times \frac{p_0^2}{\text{DC}}\times {\text{t}}_{\text{px}}.$$ (3)

where the duty cycle DC = ${\tau }_p{f}_p$ was introduced, which is also the scaling factor from peak power $p_{\text{peak}}$ to average power $p_0$.

Equation (3) shows that for a given average power $p_0$ really the duty cycle matters for TPEF imaging rather than the pulse duration. Increasing the pulse width ${\tau }_p$ from 1 ps to 1 ns and simultaneously reducing the pulse frequency from 100 MHz to 100 kHz will basically lead to the same average excitation rates for linear absorption, two-photon absorption and higher order absorption processes. At a pulse width of 1 ns and a duty cycle of 10⁻⁴, a pixel dwell time of 10µs is still possible, which allows an imaging speed of 0.66s per image at 256x256 pixels.

At this point, the ideal pulse duration is not known and will most likely depend on the sample. At same DC, potential differences between TPEF microscopy with mode-locked fs-lasers and with ~0.1-3ns pulses do not arise from different excitation rates. They may be linked to the relation of pulse duration and repetition rate to the characteristic time constants of the sample. The three most important ones are: (a) the molecular S₁-state life time (~few ns), (b) the live time of long lived triplet states (many ns to > µs) and (c) the characteristic thermal diffusion time (~1 µs).

Considering point (a), a mode-locked laser’s pulse width of ~0.1-5ps is significantly shorter than the S₁ lifetime and the pulse separation of ~10ns is longer. This may be an advantage over ns-pulses since it prevents ground state depletion. However, Eq. (2) states that, at constant peak power, the pulse length contributes linearly to the excitation values and a quick estimation for a molecule with a typical TPA cross-section of $\delta$ = 10 GM (10⁻⁵⁸m⁴/s) and $p_{\text{peak}}$ = 100W, ${\tau }_p$ = 0.5ns, NA = 0.5 and $\lambda$ = 1064nm yields an excitation ratio $n_{a,ns}\approx$0.07 for a single pulse, which is far from saturation.

With respect to point (b) the long separation of ns-pulses might be an advantage, since most triplet states are cleared before the next pulse is launched. This effect can result in a significant increase in signal strength [10], but the benefit will most likely greatly depend on the sample.

The temperature increase within the focus by linear absorption referred to in (c) will relax within a microsecond, about 100-times slower than the separation of typical ~100MHz mode-locked pulses. Hence, the temperature increase is similar to cw illumination. This is not the case for ns-pulses. Here, temperatures will peak at the end of each pulse. For a 1ns pulse with 100W peak power we estimate a transient temperature increase of roughly 1°C in the focus of an NA = 1 objective, if we assume 1064nm laser wavelength and use the linear absorption coefficient of water. If transient heating is a problem, the laser can easily be adjusted to shorter pulses; durations down to 100ps should be possible with our MOPA concept in the future.

However, as will be presented, the higher energy content of longer pulses can be advantageous for another application: single pulse two-photon excited fluorescence lifetime measurements. Hence, it might even be desirable to apply more complex grouped pulse patterns. Such arbitrarily adjustable pulse patterns or sequences can easily be realized with the presented fiber MOPA.

2. Methods and results

2.1 Fiber-based two-photon microscopy

Here we present a fiber-based TPEF imaging system using nanosecond pulses and accordingly lower repetition rates. The schematic setup of the laser and the imaging system is shown in Fig. 2. The excitation light source is a homebuilt fiber MOPA laser (as described in [12]), where the light is directly modulated by an electro-optic modulator (EOM) and amplified through ytterbium doped fiber amplifiers (YDFAs). It makes this laser flexible in pulse length, repetition rate, modulation pattern, and output power. By using mainly standard fiber components, the cost of this laser is very moderate, even for a single unit. Adding the optical component costs in our case of seed diode (~1.5k$), EOM (~3k$), SM-pump diodes (2x 700$), MM-pump (~400$), Yb-fiber (~1k$) other fiber components (~3k$) we end up at roughly 10.000$. The main advantage, however, is the glass fiber propagation. Fiber-based two-photon microscopy based on ultra-short pulses has been investigated in the recent years, either by employing low-dispersion engineered fibers [13, 14] or chirp/dispersion compensation [6, 15]. In this system, we employ narrowband, longer pulses (~60pm and ~ns) to circumvent the two main problems in fiber propagation, namely temporal pulse broadening [10, 13, 14] due to chromatic dispersion and spectral broadening due to self-phase modulation (SPM) [16]. Both effects together lead to pulse breakup.

Fig. 2.

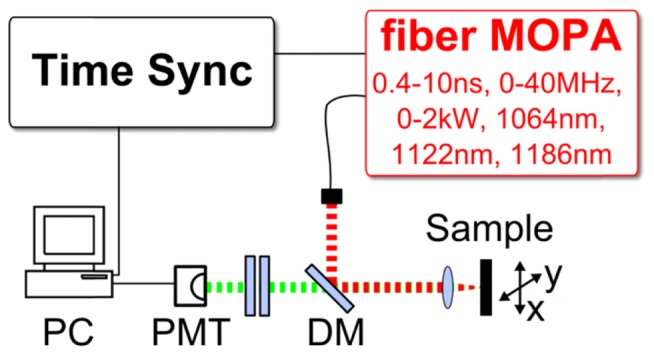
Setup of the ns-pulse TPEF microscopy system. The fiber-MOPA laser source has adjustable pulse length, repetition rate, peak power and output wavelength. The sample was either mounted on a translational stage [for Fig. 4] or galvanometric mirrors were used for scanning [Fig. 5]. The generated TPEF signal (green) passes the dichroic mirrors (DM) and is detected on a photomultiplier tube (PMT). The signals are processed on a computer (PC) equipped with an analogue-to-digital converter (ADC) card. The ADC sample clock is driven synchronously to the MOPA laser.

Additionally, we carefully analyzed two other common non-linear effects in fibers, namely stimulated Brioullin scattering (SBS) [17] and stimulated Raman scattering (SRS) [18]. We suppress SBS through the short ns-pulse length and we actually harness the SRS effect, by using the glass fiber as an optional Raman shifter. Through SRS we can shift the output wavelength from 1064nm to 1122nm and 1186nm, all by adjusting the pump and seed laser current [12]. These multiple excitation wavelengths can be switched to address different fluorophores, like e.g. Rhodamine 6G, Alexa Fluor 546 and Texas Red [19]. Advantageously, the longer wavelengths were found to cause reduced damage in biological tissue [20] and provide deeper penetration depths [13].

Two different microscopy setups were used. For first measurements and laser characterization we used a home-built microscopy setup [Fig. 2] which additionally allowed stimulated Raman imaging in forward direction [12]. We collimated the light from the fiber with an aspheric lens (Thorlabs, A280TM-C). The beam passes a dichroic mirror for separation of the multi-photon signal (Edmund Optics, 84674). The beam is focused on the sample by an aspheric lens (Thorlabs, C230TMD-C) with a numerical aperture of ~0.5. The sample was mounted on a translational stage (Thorlabs, PT3/M-Z8), allowing for raster-scanning the sample for imaging [Fig. 4]. For the first images [Fig. 4], an avalanche photodiode (Thorlabs APD110C) was used. The measurements in [Fig. 3] were recorded using a fast photomultiplier tube (Hamamatsu H12056-20).

Fig. 4.

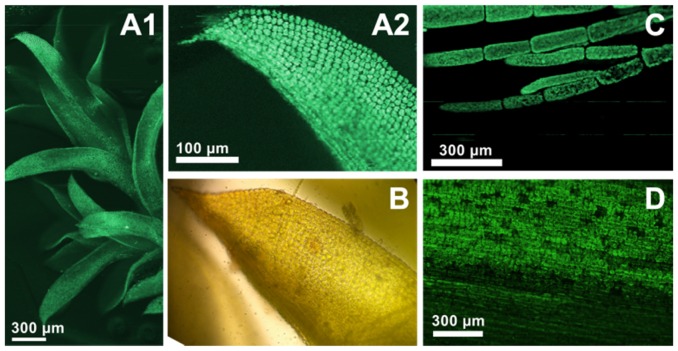
TPEF Microscopy image of endogenous autofluorescence of plant leaves. The fiber MOPA was operated at 1064nm. (A1) TPEF image of moss on a logarithmic scale. (A2) zoom-in on a leave showing the cells with high contrast against the background. (B) A standard transmission microscopy image of a moss leave. (C) TPEF image of algae. (D) TPEF image of a snowdrop plant leave.

Fig. 3.

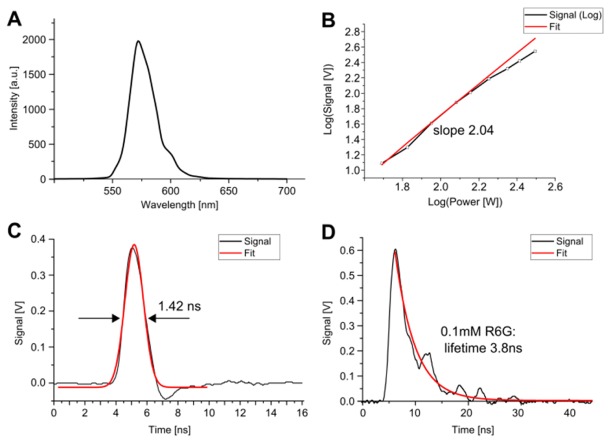
(A) TPEF spectrum of Rhodamine 6G dissolved in methanol. (B) Log-Log-Plot of the pump peak power dependency of the TPEF signal and a fitted slope of 2.04 (red), showing the quadratic dependency. (C) The SHG signal is used to determine the instrument response function (IRF) to 1.42 ns. (D) The high number of TPEF photons per single pulse and the high time-resolution allow TPEF lifetime measurements already with a single pulse. The fitted lifetime of 3.8ns for the 0.1mM Rhodamine 6G (R6G) dye in methanol agrees very well to literature values [22].

The signal from the photo-receiver was digitized by a fast analog-to-digital converter (ADC). We used a PCIe card from Alazartech (ATS9360) for the images and a 1GHz Tektronix digital real time oscilloscope (Tektronix, DPO7104C) for the measurements in Fig. 3. The ADC card has an analog bandwidth of 800MHz and a sampling rate of 1.8Gsamples per second at a resolution of 12-bit. It was operated synchronously to the laser using a phase-locked-loop at 1.6GHz, similar as described in our Time-Encoded Raman setup [12]. The high analog detection bandwidth of the ADCs enables us on the one hand to effectively suppress noise background in the TPEF images, since we only integrate the signal for a few nanoseconds. On the other hand, the fast analog bandwidth and high sampling rate also allow us to directly time resolve the fluorescence decay signal (see section 2.3) in order to perform single shot fluorescence life time measurements.

2.2 Two-photon fluorescence characterization

In order to characterize the TPEF signal, Rhodamine 6G was dissolved in methanol (δ = 10 GM at 1064nm [21]) and the fluorescence was observed as yellow, visible light. Subsequently, the spectrum of the TPEF signal was recorded [Fig. 3(A)] (Ocean Optics spectrometer USB650). Figure 3(B) is a Log-Log plot of the TPEF signal dependency on the applied pump power. The pulse length was 560ps at a repetition rate of 400kHz. The pump power was varied from 49W (log(49) = 1.7) up to 312W (log(312) = 2.5) peak power (corresponding to 11mW - 70mW average power). The fit (red) was derived using pump values up to 120 W (27mW avg) and has a slope of 2.04 thus showing the quadratic dependency on the pump power. At higher pump powers, a small deviation from the quadratic dependency is visible, indicating the onset of saturation. This curve indicates that even for strong two photon absorbers saturation is not critical even with the high energy nanosecond pulses. It also indicates that our system can generate sufficient peak power to reach an optimal, near maximum number of TPEF photons per pulse. This enables the measurement of fluorescence lifetime curves, as discussed in the following.

2.3 Single pulse fluorescence lifetime measurement

Figure 3(C) is a second harmonic generation (SHG) signal of urea crystals, used to determine the time resolution of the system. A Gaussian fit (red curve) yields an instrument response function (IRF) of 1.42ns. The large number of TPEF photons obtained by the nanosecond excitation pulses allows for fluorescence lifetime measurements already with a single light pulse (Note that the number of TPEF photons per nanosecond pulse is about 10.000-times higher than per 100-fs pulse). This type of excitation reaches an optimum balance for single pulse excitation: Considering Eq. (2), the signal per pulse can be maximized by both the peak power and the pulse length. For optimal signal generation, the peak power can only be increased to values slightly below the non-linear damage threshold. Second, the pulse length can be increased until values near fluorophore saturation are reached. This balance ensures the maximum generation of TPEF signal per pulse.

Figure 3(D) shows a non-averaged trace of the fluorescence lifetime of Rhodamine 6G (100µM solution in methanol). The excitation pulse length was 560ps and the peak excitation power ~200W. The fluorescence lifetime was fitted with an exponential decay. The IRF dependency was omitted by fitting only the decay curve after the maximum peak. The TPEF lifetime was determined to be 3.8ns, in good agreement to literature [22].

Compared to Time-Correlated Single Photon Counting (TCSPC), our direct analog detection of life-time decay curves may enable faster fluorescence lifetime imaging (FLIM). Common pulsed FLIM systems use low excitation intensities in order to statistically determine the lifetime decay. In TCSPC, typically several thousand excitation pulses per pixel are needed. Here, we use higher intensities and longer pulses, thus generating enough photons for single-pulse fluorescence lifetime measurements. This single-pulse FLIM (SP-FLIM) capability will be investigated further in the future. Further possible advantages are the synchronous driving of the fiber MOPA laser and the detection system, as described in [12], which may allow e.g. SHG, TPEF and SP-FLIM imaging in parallel, by delaying and multiplexing the signals in time, made possible by the lower repetition rates.

2.4 Two-photon microscopy results

We assessed the TPEF imaging capability of the presented system first by using the endogenous autofluorescence of plant leaves [Fig. 4]. The TPEF signal is colored green and represented on a logarithmic scale. The excitation peak power was 120W, the pulse length 560ps, the repetition rate was 415kHz. Here, the pixel dwell time was ~3ms, limited by the slow scanning speed of the sample translation stage (cf. section 2.1).

2.5 Image comparison with fs-OPO system

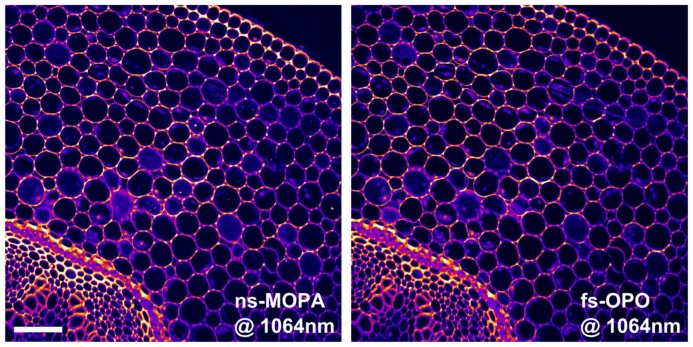
Figure 5 shows two TPEF images of a histological section of convallaria majalis stained with acridine orange, recorded on a commercial two photon microscope (Tri M scope, LaVision BioTec). The left image was created using our nanosecond laser source and the right one recorded with a state-of-the-art femtosecond OPO (Chameleon, APE). Galvanometric beam scanning achieved a pixel dwell time of 5µs. The TPEF signal was collected in epi-direction, and an objective with a numerical aperture of NA = 0.8 was used (Nikon, N16XLWD-PF). For the images (1000x1000px, 5s per image), both laser sources were operated at 1064 nm. The OPO delivered ~140fs pulses at 80MHz (DC~10⁻⁵). The repetition rate of our fiber MOPA could not be set lower than 400kHz in order to ensure at least one pulse per pixel. Unfortunately, a synchronized detection was not possible with the commercial microscope. This will be improved in a future home-built laser-scanning microscope. In order to approximately match the duty cycle, the fiber MOPA was set to 560ps pulse length, resulting in a duty cycle DC~2*10⁻⁴, hence a factor of 20 higher than the OPO system. In order to compensate for this, the average power of the MOPA was adjusted to ~135mW on the sample while for the OPO ~25mW were used, so both configurations should yield comparable numbers of fluorescence photons. We did not see any sample degradation at these powers. The two images in Fig. 5 show very similar signal levels, suggesting that the nanosecond MOPA laser is highly suited for TPEF imaging in a fiber-based microscopy system.

Fig. 5.

TPEF microscopy image comparison of convalaria majalis (scale bar represents 100µm). The images were obtained using the presented nanosecond MOPA laser (left image) and a commercial fs-OPO system (right image). For image comparison, the powers were adjusted in order to achieve same TPEF photon numbers. The images show very good agreement and almost identical TPEF signal levels.

3. Conclusion

In conclusion, we demonstrated two-photon microscopy in a long pulse/low repetition rate regime. Nanosecond pulses were used which were generated by a highly cost effective fiber based laser. The single-mode fiber output can be positioned very closely to the optics of the microscope, leading to a highly reliable, almost alignment-free imaging platform. In our experiments, continuous imaging was possible for days without beam re-adjustments. Another advantage of the presented nanosecond TPM system is that dispersion in the optical elements is negligible. No chromatic compensation or dispersion management is necessary and no detrimental self-phase modulation (SPM) in the glass-fiber occurs. Additionally, the nanosecond pulses enable single shot TPEF lifetime measurements in direct analog detection. Together, these advantages make our system the ideal candidate for future multi-photon imaging platforms employing optical fiber endoscopes in vivo.