Simultaneous nano-tracking of multiple motor proteins via spectral discrimination of quantum dots

Abstract

Simultaneous nanometric tracking of multiple motor proteins was achieved by combining multicolor fluorescent labeling of target proteins and imaging spectroscopy, revealing dynamic behaviors of multiple motor proteins at the sub-diffraction-limit scale. Using quantum dot probes of distinct colors, we experimentally verified the localization precision to be a few nanometers at temporal resolution of 30 ms or faster. One-dimensional processive movement of two heads of a single myosin molecule and multiple myosin molecules was successfully traced. Furthermore, the system was modified for two-dimensional measurement and applied to tracking of multiple myosin molecules. Our approach is useful for investigating cooperative movement of proteins in supramolecular nanomachinery.

1. Introduction

Single-molecule measurement techniques have advanced tremendously over the past two decades; such techniques include total internal reflection fluorescence microscopy [1,2], optical trapping forcemetry [3,4], and other techniques simultaneously achieving single-molecule sensitivity with nanometer and piconewton accuracy [5]. These techniques have helped deepen the understanding of the working mechanisms of linear motor proteins, such as the myosin [1,2,6], kinesin [7,8], and dynein [9,10] super-families. However, most of these studies focused on only a single molecule. Recently, there have been many studies of the cooperative function of multiple motor proteins, as the importance of cooperativity is a hot topic in biophysics [11–14]. To further understand the physicochemical mechanism of protein functioning, attention is now shifting upward through the hierarchy, from individual elements to the cooperative behavior of the supramolecular system, suggesting the need of an additional technique that transcends conventional single-molecule measurement.

Spectral precision distance microscopy (SPDM) shows great potential for simultaneous observation of multiple proteins in nanoscale beyond the diffraction limit [15–17]. In SPDM, multiple spectrally separated images are acquired at the same time using multiple fluorescent labels with different colors and multiple camera detectors. The concept of SPDM has been implemented in a variety of microscope configurations for specific or general purposes. A technique called single-molecule high-resolution colocalization (SHREC) is one successful form of SPDM specialized for single-molecule imaging that enables simultaneous tracking of two distinct protein domains within a single motor protein [18,19]. Images at two different wavelengths are separated at a dichroic mirror, and the two images are recorded on different regions of a detector surface. The position and rotation of the two images must be precisely matched. In principle, the number of separable colors can be more than two. However, because of the limited wavelength range and the difficulty of position matching and spectral unmixing, practical use is limited to two colors.

Rather than dichroic mirror-based spectroscopy, imaging polychromator-based spectroscopy is more suitable for imaging of multiple colors. Fluorescence signals from the molecules are dispersed into a continuous spectral domain. Recently, Cutler et al. reported slit-scanning confocal fluorescence microscopy with spectroscopic detection of various colors of semiconductor quantum dots (QDs) [20]. They realized observation of membrane protein dynamics and colocalization with spatial precision of ~10 nm at the video rate. However, motor protein measurement usually requires localization precision in the order of a few nanometers with the video rate or higher temporal resolution. To sustain the temporal resolution sufficient for motor protein studies, a scanless imaging scheme is more preferable.

In this study, we developed a simple and versatile microscope system for simultaneous observation of multiple fluorescent probes with high spatial precision and high temporal resolution, and we verified the performance of the microscope by tracking multiple myosin molecules. The measurement scheme is based on imaging spectroscopy of QDs of various colors under a scanless wide-field microscope. Although there have been several reports of successful works based on the same concept [21,22], this paper provides optical configurations and experimental procedures specially designed for linear motor protein studies. Recently, a similar or even more advanced optical configuration was proposed and successfully applied to single molecule localization microscopy to increase the number of different species observable at the same time [23,24]. The essential difference from our method is that in these works the separation of spatially overlapping emitters is done in the time domain via the basic manner of photoactivated localization microscopy (PALM) [25,26] or stochastic optical reconstruction microscopy (STORM) [27], while it is done in the spectral domain in our method. Since our spectral discrimination method can utilize the time domain for successive record of image frames, it is appropriate for dynamic measurement of multiple mobile molecules such as motor proteins and membrane proteins. This is the major advantage of our method over the temporal discrimination methods [23–27]. To take this advantage, in this study, we developed a microscope system in the spectral discrimination scheme for protein dynamics measurement. On the other hand, the number of spatially overlapping emitters observable at the same time is limited by the finite spectral range and spectral width of fluorescent probes used. In contrast, the temporal discrimination methods can observe, in principle, an unlimited number of overlapping emitters, and is more suited for superresolution imaging of a stationary specimen labeled with high density of fluorescent probes in a whole field of view.

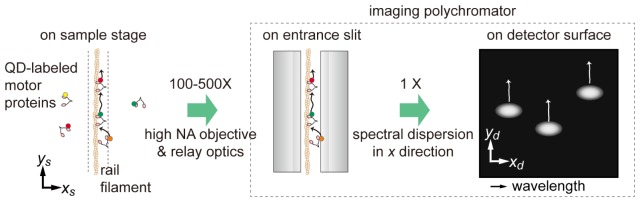
The distinctive feature of our method is that one dimension of a two-dimensional detector is dedicated to spectral discrimination of multiple QDs, and their spatial displacement along the orthogonal axis is measured. Provided that a filament of rail proteins such as filamentous actin or microtubules is oriented in parallel to the slit of the imaging polychromator, one can realize one-dimensional tracking of multiple motor proteins with nanometer precision, as schematically shown in Fig. 1. Here, we termed this microscopy one-dimensional spectrally resolved tracking microscopy (1D-SRTM). The one-dimensional tracking of protein dynamics is sufficient in many cases for biophysical discussion of linear motor proteins. Since measurement is under a non-scanning configuration, the temporal resolution should be comparable to that of conventional single-molecule tracking [6,19]. In this study, we verified the achievement of a few nanometer localization precision at the temporal resolution of 30 ms or faster.

Fig. 1.

Schematic of spectral discrimination of multiple motor proteins walking along a filament. NA: Numerical aperture.

Moreover, we also introduce a unique scheme to extend this technique to two-dimensional tracking in order to expand applicability to more general analysis of protein dynamics. The scheme of 1D-SRTM can localize the QD positions only in the direction perpendicular to the spectral dispersion because of the temporal fluctuation of the peak wavelength of fluorescence spectrum of individual QDs, which is a phenomenon known as spectral diffusion [28,29]. To circumvent the position uncertainty due to spectral diffusion, we propose a methodology for high-precision localization of two-dimensional coordinates by modifying the detection optics of the 1D-SRTM system, which is referred to as 2D-SRTM. Two-dimensional tracking would be useful for studying the steric movement of linear motor proteins [30] and other types of protein complexes, such as rotatory motors [31,32] and membrane proteins [20,33].

In the following sections, we first describe the method for 1D-SRTM and discuss the effect of spectral diffusion on the localization of the QD positions. Localization precision is discussed theoretically and experimentally, followed by discussion of two applied examples of the measurement of multiple linear motor proteins. In the last section, we introduce 2D-SRTM and how 1D-SRTM can be extended to two-dimensional tracking measurements.

2. One-dimensional tracking method: 1D-SRTM

2.1 Optical configuration

Our measurement scheme uses an imaging polychromator device at the detector position of a conventional single-molecule imaging system. The entrance slit of the imaging polychromator is placed on the image plane conjugate to the sample plane (Fig. 1). Target motor proteins are labeled with QDs of various distinct emission wavelengths. The filament orientation is controlled to be parallel to the entrance slit, which can be simply realized by a directional flow of filamentous actin solution in a flow-cell chamber (see Appendices A-1 and A-2 for details). A target filament is placed in the conjugate position of the slit by adjusting the position of the sample stage so that the fluorescence from the QDs near the filament can be transmitted through the slit. The image on the slit is then dispersed in one direction at a diffraction grating in the imaging polychromator, and the first diffraction image is focused on the surface of a camera detector. In this paper, the direction of wavelength dispersion is defined as x, and the direction parallel to the slit is y (Fig. 1). As the y coordinate at the detector (y_d; scaled for sample coordinate) directly corresponds to the counterpart coordinate at the sample (y_s), one can estimate the y_s value of fluorescence spots in the spectral dispersion image. Thus, the spectroscopic detection distinguishes multiple motor proteins along the filament, even if they are located close to each other within a sub-diffraction-limit scale.

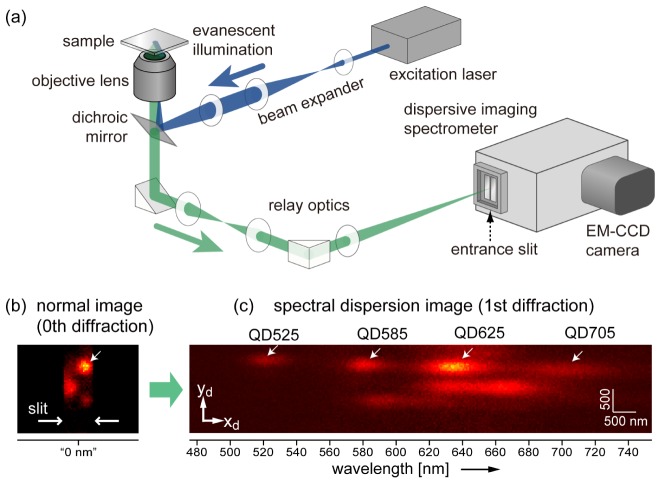
Figure 2 shows the optical configuration of our measurement system, which consists of a total internal reflection illumination fluorescence microscope and imaging polychromator (SpectraPro SP2300, Princeton Instruments, Acton, MA; grating: 50 grooves/mm, focal length: 300 mm) equipped with an electron-multiplying charge coupled device (CCD) (EM-CCD) camera detector (ProEM, Princeton Instruments). We chose a grating-based imaging polychromator with the Czerny-Turner configuration. In most experiments in this work, the size of one pixel of the CCD (16 µm) was equivalent to 37.0 nm on the sample plane as a result of the high numerical aperture (NA) objective lens (UAPON 150XOTIRF, Olympus, NA1.45, 150 × ) and magnifying relay optics. It was changed to 93.4 nm only when the effect of the pixel size on the localization precision was evaluated (Section 4). The F number of the focus on the entrance slit was ~50, which is much larger than that of the optics inside the polychromator (F = 3.9). Chromatic aberration of the relay optics was well suppressed by use of achromatic lens systems. Remaining chromatic aberration of magnification was ~0.3% in the wavelength range used in this study, which does not cause a serious problem in the measurement of the following sections. For the excitation of the multiple QDs, a semiconductor laser with a wavelength of 488 nm (Stradus 488-50, Vortran Laser Technology, Sacramento, CA) was employed.

Fig. 2.

(a) Diagram of our optical setup for 1D-SRTM, which consists of a total internal reflection illumination fluorescence microscope and an imaging polychromator. (b,c) Experimental demonstration of spectral discrimination of QDs. Four QDs in nanoscale proximity on the zeroth diffraction image (b) are discriminated by emission wavelength on first diffraction image (c). Both images are summations of 10 successive images acquired with a temporal resolution of 30 ms.

2.2 Estimation of centroid of fluorescence spot

The shape of a fluorescence spot at the detector surface is not isotropic but anisotropic, with a long axis in the x direction because of spectral dispersion of the fluorescence spectrum. A fluorescence image of a single emitter at (x_s, y_s) is theoretically given by incoherent convolution of the emission spectrum, g(λ), and the spatial profile of a fluorescence spot of a point source without a spectrometer, i.e., the point spread function (PSF), U(x,y,λ),

$$I\left(x_d,y_d|x_s,y_s\right)={\displaystyle \int U\left(x_d-x_s-x_{disp}\left(\lambda \right),y_d-y_s,\lambda \right)}g\left(\lambda \right)d\lambda$$ (1)

where x_disp(λ) is the lateral displacement of the fluorescence spot from the center of the field of view due to the diffraction grating, which is a function of the wavelength. Here, we assume that the QD is placed on the lateral center line of the field of view (x_s ~0), which corresponds to the entrance slit of the spectrometer, and that the QD is small enough to be regarded as a point source. The shape of the function x_disp(λ) is determined by various parameters including the focal length of the spectrometer and the groove density and rotation angle of the grating in the spectrometer. The function is nonlinear with respect to wavelength. However, in this particular situation, where the groove density is very low (50 grooves/mm), we can assume that the displacement is proportional to the wavelength. Indeed, the calibration coefficient of the quadratic term was six orders of magnitude smaller than that of the linear term. Thus, we do not need to consider undesired asymmetric distortion of the fluorescence spot shape.

We employed a two-dimensional elliptical Gaussian function for estimation of the centroid, which is expressed as

$$F\left(x_d,y_d\right)=C_0+C_1\exp \left\{-{\frac{\left(x_d-x_0\right)}{2s_x^2}}^2-{\frac{\left(y_d-y_0\right)}{2s_y^2}}^2\right\}$$ (2)

where C₀, C₁, x₀ (y₀), and s_x (s_y) denote the constant baseline, intensity, x_d (y_d) coordinate of the centroid, and spot width represented with the standard deviation in the x_d (y_d) direction, respectively. This function allows for accurate curve fitting to the convolution result of Eq. (1) as long as the PSF, U(x,y,λ), is close to a Gaussian function of (x,y) and g(λ) is a Gaussian function of λ. Strictly speaking, the spectral shape of QDs is not Gaussian-like, is sometimes very asymmetric along the wavelength axis, and changes over time (discussed later in Section 3). However, the precision of the y-coordinate estimation is most important and is not greatly affected by the asymmetry of the spectral shape.

For quantitative evaluation of the relationship between localization precision and photon counts, estimated intensity coefficients of fluorescence spots (C₁) were converted to photon counts through consideration of the pixel size and the gain of EM-CCD. When two fluorescence spots are closely adjacent, within about 5s_x or 5s_y, another Gaussian term is added to Eq. (2) to localize the two spots simultaneously. Since QDs exhibit random intermittency of fluorescence emission (blinking), a fluorescence spot could vanish in some sequential frames. For automation of QD localization over sequential frames, we arbitrarily preset the intensity threshold for fluorescence spot detection, and curve fitting was applied only to fluorescence spots exceeding the threshold. Nonlinear least-square curve fitting was computed by the Levenberg-Marquardt method. All computation processes used in data analysis, including curve fitting, were coded in Igor Pro (version 6.34, WaveMetrics, Lake Oswego, OR).

2.3 Quantum dots as fluorescent probes for multicolor labeling

In this study, we used various colors of commercialized QDs. We purchased the Qdot Streptavidin Sampler Kit (Q10151MP, Thermo Fisher Scientific K.K., Yokohama, Japan), which contains six types of QDs with distinct emission wavelengths: Qdot525 (QD525), Qdot565 (QD565), Qdot585 (QD585), Qdot605 (QD605), Qdot655 (QD655), and Qdot705 (QD705). In addition, Qdot625 (QD625) streptavidin conjugate (A10196) (Thermo Fisher Scientific K.K., Yokohama, Japan) was also purchased. Concentrations of the stock solutions are all 1 µM. We used some or all of the seven colors, and the number of colors used was varied according to the experiment.

In principle, any type of fluorescent probe can be used for multicolor labeling. However, QD probes are most suitable for several reasons: (1) more than eight commercially available QDs of different colors can be used, (2) all QDs can be excited by a single excitation laser, (3) high quantum efficiency of QDs leads to higher temporal resolution than molecular dyes or fluorescent proteins, and (4) a large photon budget (low photobleaching rate) allows for the tracking of a molecule for a long time.

2.4 Spectral discrimination of multiple quantum dots

Spectral discrimination of multiple QDs was demonstrated by imaging stationary QDs on a glass substrate. All seven distinct types of QDs were used for this measurement. They were randomly dispersed and immobilized on the surface of a coverslip via nonspecific adhesion (see Appendix A.3 for sample preparation details). Figures 2(b) and 2(c) show a normal fluorescence image and first-order diffraction image of QDs, respectively, on the same area of the sample. The slit width of the polychromator entrance was adjusted to have a 700-nm-wide field of view on the sample plane. The normal image was obtained as zeroth-order diffraction, that is, specular reflection of the grating. While four QDs (QD525, QD585, QD625, and QD705) colocalized within a sub-diffraction-limit scale could not be spatially resolved in the zeroth diffraction image (Fig. 2(b)), they were observed separately as distinct fluorescence spots in the first diffraction image (Fig. 2(c)). Estimation of the centroid positions reveals the relative positions of the four QDs in a nanoscale region.

3. Spectral diffusion of QDs

In contrast to the y coordinate on the detector surface (y_d), which corresponds directly to the y coordinate at the sample plane (y_s), the x coordinate at the detector (x_d) depends on both the sample coordinate x_s and the lateral displacement due to the fluorescence wavelength of the QD (x_disp) (Eq. (1)). If the fluorescence wavelength is determinable and stable, the two-dimensional coordinates on the sample plane could be estimated from a single diffraction image. However, as mentioned in Section 1, this is not realistic because of spectral diffusion, where the fluorescence spectra of individual QDs randomly fluctuate over time. The spectral diffusion of semiconductor QDs originates from the inhomogeneous crystallinity of the crystals, which leads to fluctuation of the surface electronic state [28,29].

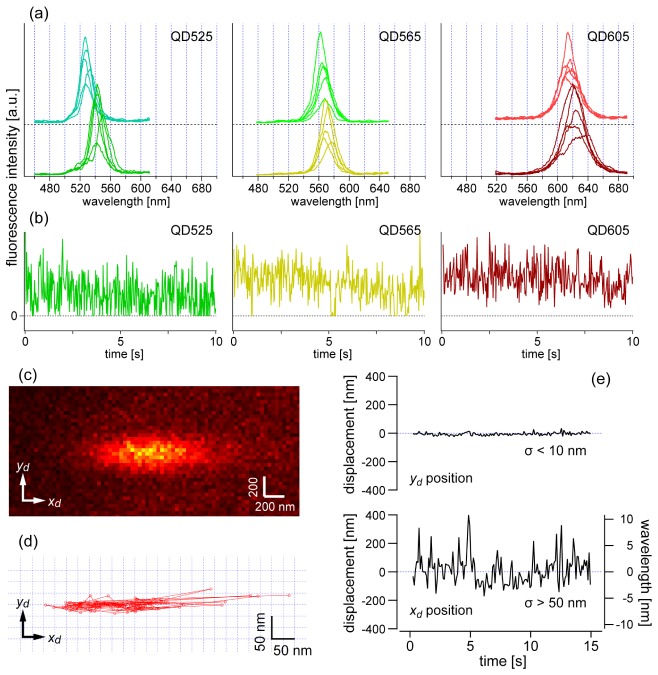
Figure 3(a) shows examples of spectral fluctuation of six QDs of three types (two individual QDs for each of QD525, QD565, QD605), which were immobilized on a glass substrate (Appendix A.3). To record fluorescence spectra with high spectral resolution, we specially used a grating with 150 grooves/mm, which is finer than the one used in the later tracking experiments. The fluorescence spectra were sequentially recorded over time with 100-ms exposure time, and five representative spectra among many are shown for each QD. In the measurement, the spectral range of the peak wavelength fluctuation was found to be a few nanometers, sometimes more than 10 nm. In addition, the comparison between the upper and lower spectra in Fig. 3(a) indicates that there is a large individual difference in peak wavelength of around 5–10 nm, even though the two QDs should have the same wavelength. Regardless of the initial peak wavelength, the wavelength fluctuates to a similar extent.

Fig. 3.

(a) Fluctuation and differences in spectral shape of QD525, QD565, and QD605. For each type of QD, two individual QDs were selected to show individual differences in the emission wavelength. For each individual QD, five spectra with characteristic shapes out of 500 serial spectra were selected to show spectral variation. These spectra were obtained with a grating of 150 grooves/mm for higher spectral resolution and more wavelength divisions than the other measurements. The exposure time for one spectrum was 100 ms. (b) Representative time traces of fluorescence intensity of QD525, QD565, and QD605, which was obtained with 30 ms exposure time. (c) Representative raw image of a fluorescence spot of a QD (QD565). The image is an accumulation of the first 10 frames obtained with a 100 ms temporal resolution. (d,e) Temporal fluctuation of the centroid position of the fluorescence spot in (c) estimated with an elliptical Gaussian function: trajectory of the position on the x–y plane (d) and separately plotted x and y coordinates relative to the mean positions as a function of time (e). The right axis of (e) represents the wavelength variation from the mean wavelength, which was calibrated from the x_d coordinate.

Figure 3(b) shows temporal change of the intensity for the same types of QDs shown in Fig. 3(a). The behavior of the blinking is dependent on the type of QDs and oxygen scavenger system. In addition, the individual difference of the intensity fluctuation is also large, similar to that of the spectral shape fluctuation (Fig. 3(a)). In this experiment, QD525 and QD565 often have zero intensity point (OFF time) during the blinking which makes average intensity low. In contrast, QD605 has relatively shorter OFF time so that we cannot see zero intensity point in the time trace obtained with the exposure time used (30 ms) (Fig. 3(b), right). Typically, under the condition of the present scavenger system (Appendix A.3), shorter wavelength QDs (QD525, QD565, and QD585) have longer OFF time while longer wavelength QDs (QD605, QD625, and QD655) have shorter OFF time. However, we found that QD705 has longer OFF time which results in lower average intensity.

We examined the influence of spectral diffusion on the localization of fluorescence spots. Temporal change of a fluorescence spot of a single QD (QD605) was recorded over 150 frames. Figure 3(c) shows a representative fluorescence spot of a single QD (QD605). The centroid of the elliptical fluorescence spot was estimated by fitting Eq. (2) to each frame. The centroid positions are plotted on an x_d-y_d plane in Fig. 3(d), where it can be seen that the spot is fluctuating largely in the x direction. The position displacement in the x and y directions were plotted as a function of time in Fig. 3(e). The standard deviation of the y_d coordinate was found to be smaller than 10 nm, which guarantees the possibility of nanometer-scale precision localization in the y direction. In contrast, because of the peak wavelength fluctuation, the standard deviation of the x_d coordinate was larger than 50 nm (Fig. 3(e), bottom). This uncertainty of the x_d coordinate makes reliable estimation of x_s almost impossible. This is why another optical configuration is necessary to achieve two-dimensional tracking with nanometer-scale precision, which will be described in Section 6.

It should be noted that QD is well known to exhibit a spectral blue shift owing to surface oxidization [22,29]. Yet, in the present case, random fluctuation of peak wavelength was predominantly observed, rather than unidirectional spectral shift. We only observed blue shift when a QD was exposed to higher laser power. This is because an oxygen scavenger system was included in our sample solution (Appendix A.3), which effectively suppressed the oxidization and corresponding blue shift [29].

4. Localization precision

4.1 Theoretical consideration

The precision of localization is different for the x and y directions because of the anisotropy of the fluorescence spot. To estimate the centroid position with elliptical Gaussian fitting using Eq. (2), the expectation of the variance in the x and y coordinates can be expressed by the following equations [34,35]:

$$\langle {(\Delta x)}^2\rangle =\frac{s_x^2}{N}+\frac{a^2/12}{N}+\frac{8\pi b^2{s}_x^3{s}_y}{a^2{N}^2}$$ (3a)

$$\langle {(\Delta y)}^2\rangle =\frac{s_y^2}{N}+\frac{a^2/12}{N}+\frac{8\pi b^2{s}_x{s}_y^3}{a^2{N}^2}$$ (3b)

where the parameters a, b, and N denote the effective pixel size of the detector scaled for the sample coordinates, the standard deviation of the background noise (due to background fluorescence from unbound QDs diffusing in the sample solution and the readout process of the detector electronics), and the total number of detected photons, respectively. The first terms are theoretical limits based on statistics; they are degraded by the second and third terms, which are related mainly to pixelation and background noise, respectively. Now, the variance of the y coordinate (Δy) depends not only on s_y but also on s_x. We can expect the localization precision in the y direction to be degraded by large s_x compared to that in conventional single-molecule imaging. At the large photon number limit, the first and second terms become dominant in Eq. (3a) and Eq. (3b), meaning that the expectation of Δy is only influenced by s_y.

4.2 Experimental examination

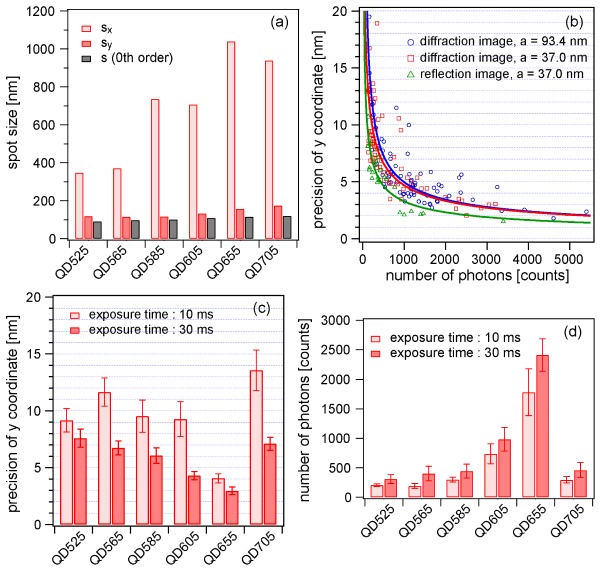
We experimentally assessed the localization precision of six types of QDs used in the subsequent experiments. We prepared six samples, each of which contained only one type of QD. The QDs were randomly dispersed and immobilized on the surface of a coverslip via nonspecific adhesion (Appendix A.3). To assess dependence on pixel size (a in Eq. (3)), we made the measurement with two different magnifications of the relay optics between the sample and the spectrometer to obtain pixel sizes of 93.4 and 37.0 nm. In addition, to examine dependence of precision on the number of detected photons (N in Eq. (3)), images were acquired with two different temporal resolutions for one frame, 10 and 30 ms. The laser intensity at the sample surface was adjusted to 2.4 kW/cm². For all six samples, a series of images was acquired over 100 frames, and then the positions of the centroids of the fluorescence spots were estimated using elliptical Gaussian fitting. For comparison with a conventional situation without spectral dispersion, we also obtained a series of images of specular reflection (zeroth diffraction). The estimate of the localization precision is defined here as the standard deviation of the estimated y coordinate over 100 frames.

Figure 4(a) compares the size of fluorescence spots on first diffraction images (s_x and s_y) and normal images (s) for the various types of QDs. It is reasonable for the s_x value to always be much larger than the s_y value (s_x >> s_y) due to the x-elongated shape of the spots. However, the s_y value was also found to be 1.2–1.5 times larger than that of a normal fluorescence spot (s) obtained without spectral dispersion (s_y > s). We attributed this significant difference to the coma and astigmatism aberration due to the normal Czerny-Turner geometry. If a polychromator with an aberration-corrected configuration [36,37] were available, the difference would be suppressed.

Fig. 4.

Experimental examination of localization precision achieved by the proposed technique. (a) Size of fluorescence spot on first diffraction images (s_x and s_y) and normal images (s) estimated by elliptical Gaussian fitting. (b) Localization precision against number of detected photons measured under three distinct conditions: diffraction image with a pixel size of 93.4 nm (blue circles), diffraction image with a pixel size of 37.0 nm (red squares), and reflection image (zeroth diffraction) with a pixel size of 37.0 nm (green triangles). Solid curves were obtained by curve fitting of Eq. (3b). (c) Summary of localization precision estimated for six types of QD at temporal resolutions of 10 and 30 ms. The pixel size was 37.0 nm. (d) Number of detected photons of different types of QD at temporal resolutions of 10 and 30 ms.

Figure 4(b) shows estimates of the localization precision plotted against the number of detected photons. For clear comparison, the theoretical function (Eq. (3b)) was fitted to the plots (solid curves). The best precision at the high photon number limit is limited by other factors, such as acoustic vibration from the environment and local fluctuation of immobilized fluorescent probes. Here, we found that there is no significant difference in localization precision between the two different pixel sizes (37.0 and 93.4 nm). The fitted curves indicate that, for example, the localization precision at N = 3000 can be approximately 3 nm. On the other hand, substitution of N = 3000 and the typical spot size in the y direction (s_y ~150 nm) into the first term of Eq. (3b) yields a precision of 2.7 nm. Thus, our microscope achieved a localization precision at nearly the theoretical limit. The precision of the present technique with diffraction imaging is slightly lower than that of conventional single-molecule imaging, which gives a precision of around 2 nm at N = 3000. This difference is mainly caused by the difference of the spot size between the zeroth and first order diffraction images even in the y direction (s_y > s) (Fig. 4(a)).

The above discussion on achievable localization precision is only valid for the specific condition of an excitation laser intensity of 2.4 kW/cm². As a matter of course, an increase in the excitation intensity would lead to a larger number of detected photons in one frame, allowing for a better localization precision. However, in addition to higher localization precision, fluorescence emission time before photobleaching would become shorter. Under the present conditions, the expected time of fluorescence emission before photobleaching is around 20 seconds, which is practical for tracking of linear motor proteins.

The estimates of the localization precision for all QDs measured under many different conditions, including six different types of QDs and two different temporal resolutions (10 and 30 ms), are summarized in Fig. 4(c). The 30 ms exposure time is expected to accumulate three times as many photons, leading to approximately √3-fold better localization precision. However, the ratios of the experimental estimates in Fig. 4(c) are not exactly √3-fold. This is because of the uneven conditions of fluorescence spot detection due to the presence of blinking and the arbitrarily preset threshold. The best precision was achieved for QD655, mainly because the number of photons detected within the exposure time was larger than those of the other QDs (Fig. 4(d)).

This result does not simply mean that the quantum efficiency of QD655 is the highest among all QDs. The number of detected photons depends not only on the quantum efficiency of the QD but also on the frequency of blinking and the spectroscopic properties of the detector and grating. In particular, the frequency of blinking is strongly dependent on the choice of oxygen scavenger system (Appendix A.3). High frequency of blinking (much faster than frame rate) could lead to reduction of temporal average number of photons. The scavenger system used this time effectively suppressed the blinking of QD655, but was not effective for QDs of shorter wavelengths. There may be better oxygen scavenger system conditions for suppressing the blinking frequency of all types of QDs, which is one of the remaining issues to be addressed.

5. Demonstration of multiple motor protein tracking

5.1 Myosins labeled with QDs

Throughout this paper, myosin-actin systems are used as test samples for demonstration of the performance of protein dynamic measurements. Among the myosin super-family, we chose myosin V (M5) and myosin VI (M6), which are processive linear motor proteins movable along an actin filament. They convert the chemical energy of ATP hydrolysis to the physical energy of force generation [38,39] and act as vesicle transporters in biological cells. They form homodimers and exhibit a walking-like behavior through beautiful coordination with each other [6,19,40,41]. The translational movement of M5 and M6 along actin filaments was observed in subsequent sections.

For labeling of the myosins with QDs, we used biotinylated myosins that were bound with QD-streptavidin conjugates. The same concentrations of the various colors of QDs were mixed in a solution, which was then mixed with myosins. The myosins were randomly bound to one color of QD with almost the same probability, which is about 1/7 when seven types of QDs were used together. Under the microscope, a certain fluorescence spot is expected to originate from one color of QD with the same probability as well. When we observe two fluorescence spots at the same time, we can expect that they represent different colors with ~86% probability.

The preparation protocol is described in detail in Appendices A-4 and A-5.

5.2 Actin filament labeled with dye

Filamentous actin works as a rail for myosin motors. In this study, we used actin filaments labeled with the fluorescent dye tetra-methyl-rhodamine (TMR), which was necessary to observe the distribution and orientation of the actin filaments. Before addition of the QD-labeled myosins, actin filaments were immobilized on a glass surface inside a flow chamber (See Appendices A-1 and A-2 for details on the flow chamber and chemical treatment of actin filament). Most of the actin filaments were oriented well in a direction of injection flow, which helped us to find actin filaments parallel to the entrance slit of the polychromator. In one-dimensional tracking measurements, the orientation of the flow chamber was adjusted such that the actin filaments were parallel to the entrance slit. To identify a suitable filament for a tracking experiment, fluorescence images of TMR dye were observed. Just after the position of the filament was set, the TMR dyes were purposely photobleached by strong illumination of excitation light to avoid spectral overlap of fluorescence between TMR and the QDs.

5.3 Two heads of a myosin

To demonstrate dynamic imaging, we performed multiple-molecule tracking of a motor protein system consisting of M5 and an actin filament, which has been widely studied by single-molecule tracking experiments [2,6]. First, we observed the walking behavior of a double-headed M5 molecule. We labeled both heads of M5 with QDs of two distinct colors. The dual labeled QD-M5 was prepared by mixing biotinylated M5 molecules and streptavidin-conjugated QDs of two types (QD525 and QD585) in a solution (Appendix A.4). The solution used in this measurement contains 1% β-mercaptoethanol which is effective to suppress the intensity fluctuation of QD525 and QD585. The ATP concentration was 5 µM. The laser intensity at the sample surface was adjusted to 0.71 kW/cm². An actin filament oriented in the slit direction was positioned at the lateral center of the slit (Fig. 5(a)). The slit width of the polychromator entrance was adjusted to have a 1700-nm-wide field of view on the sample plane. The movement of the QDs along an actin filament immobilized on a glass substrate was observed with a 30-ms temporal resolution. Figure 5(b) shows an example of the spatiotemporal variation of two fluorescence spots originating from the two QDs (QD525 and QD585), which corresponded to movement of the two heads of a single M5 molecule. The image in Fig. 5(b) is composed of raw first diffraction images at 0 and 7 s and kymographs of the two columns at the spectral peak wavelengths (around 525 and 585 nm) of the two QDs. The two kymographs indicate gradual displacement of the two heads at almost the same speed. We estimated the centroids of the two fluorescence spots over 0–7 s and obtained the trajectories of the positions of two QDs on the x_d–y_d plane, as shown in Fig. 5(c). Temporal profiles of the y_d displacement of the QDs are shown in Fig. 5(d), where y_d is regarded to be identical to the y coordinate at the sample plane (y_s). A stepwise hand-over-hand profile is clearly observed in Fig. 5(d). The distance of both heads was ~36 nm during the walk, which is consistent with previous studies of M5 using conventional single-molecule imaging [6].

Fig. 5.

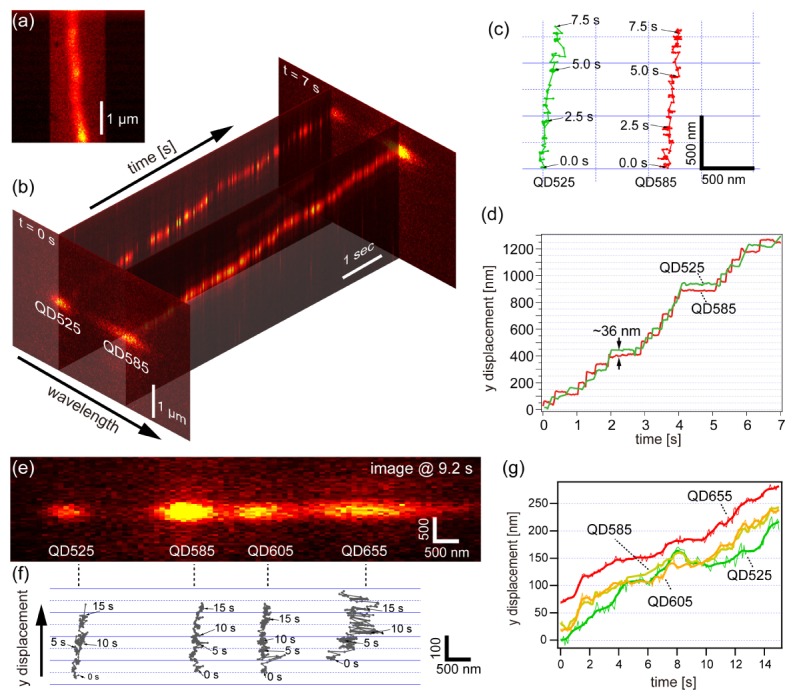
Simultaneous nanometry of two heads of an M5 molecule by 1D-SRTM. (a) A fluorescence image of a TMR-labeled actin filament oriented parallel to the slit direction, which was obtained by zeroth order imaging. (b) Spatiotemporal variation of two fluorescence spots originating from two QDs (QD525 and QD585) attached to two heads of M5, composed of the first diffraction images at 0 and 7 s and two kymographs at the peak wavelengths of the two QDs. The image set was acquired with a temporal resolution of 30 ms. (c) Trajectories of the movement of the two spots. (d) Temporal profile of the displacement of the two QDs in the y direction. (e,f) Demonstration of tracking of four QD-M6 at sub-diffraction-limit scale. (e) Representative first diffraction image of the four fluorescence spots originating from four different QDs (QD525, QD585, QD605, and QD655). (f) Trajectories of the four spots in (e). (g) Temporal profile of the displacement of the four QDs in the y direction, made by the same data set as (f). Raw traces are shown with thin lines, whereas smoothed traces (binomial, n = 3) are shown with thick lines.

5.4 Four myosins

To demonstrate the ability to discriminate more than two molecules, we also performed a similar tracking experiment with a higher concentration of motor proteins. In this experiment, we used M6 instead of M5 [41] (Appendix A.5). The ATP concentration was set to 50 µM, which is higher than that in the previous measurement (5 µM). Figures 5(e) and 5(f) show simultaneous tracking of the fluorescence spots of four QD-M6 samples. Figure 5(e) shows a representative frame in the movie. Four QDs with different wavelengths attached to myosins were found to be moving along a common actin filament. Figure 5(f) shows the trajectories of the four QDs on the x_d–y_d plane, where four of the QDs in nanometric proximity were successfully recognized and tracked at the same time.

We made time traces of the four QDs, as shown in Fig. 5(g). Four different traces were successfully obtained, where four myosin VI with different QDs moved in the same direction with almost the same speed. Compared to the one in Fig. 5(d), it is difficult to recognize sharp steps. However, several unique behaviors can be seen. Around the time 8 s, the myosin with QD525 made a backward step after a forward step, which is a characteristic feature of myosin VI [41]. An interesting phenomenon is that a myosin with QD605 and that with QD525 are chasing each other back and forth. Another unique phenomenon is that QD605 and QD585 are moving together with a few nanometer distance over the whole time range. This is conflicting with a fact that distance between two QDs cannot be smaller than sum of the two QDs’ radii. Although actual geometry of the two particles is unclear, most probably they are on top of each other. Since the current study focuses on the introduction of an optical methodology, we do not go into the detail of biological interpretation of these phenomena. This result verifies the capability of simultaneous nanometry of more than three molecules in one dimension, and indicates the possibility of measurement of cooperativity or interaction of multiple motor proteins.

6. Extension to two-dimensional tracking measurement: 2D-SRTM

6.1 Optical configuration

As mentioned earlier, the optical configuration must be modified to achieve localization of two-dimensional coordinates with nanometer-scale precision. Figure 6(a) shows the modified version of the optical system for 2D-SRTM, where one optical path was added in the detection optics. The fluorescence image from the sample is divided by a non-polarizing half-mirror and undergoes the same magnification on both paths. One of the optical paths (path I in Fig. 6(a)) transfers the fluorescence image without rotation, whereas the other (path II) transfers the image with rotation by 90°. Two images are focused on the slit, one (path I) on the upper half and the other (path II) on the lower half, and their spectral dispersion images are acquired by the EM-CCD detector at the same time. Figure 6(b) shows what a raw zeroth-order image looks like. For two-dimensional tracking, the slit width is set wider than that for the one-dimensional tracking experiment. Note that, in our current optical system, the fluorescence image is not simply rotated by 90° but inverted with respect to the y = −x line (Fig. 6(b)), which does not affect the essential mechanism. The upper and lower images provide estimates of y_s and x_s, respectively, which are combined to determine the two-dimensional coordinates (x_s, y_s). Although the precision of position estimation is degraded by the decrease in the number of fluorescence photons at one spot, we can estimate the two-dimensional coordinates of multiple QDs without the need for spatial or spectral scanning.

Fig. 6.

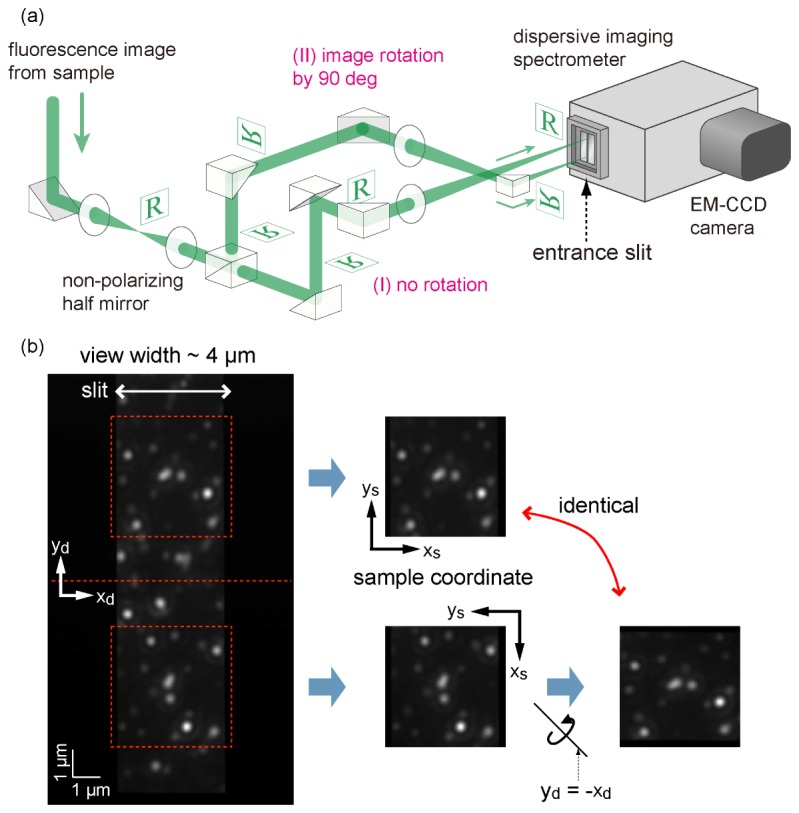
2D-SRTM. (a) Configuration of the relay optics of the detection path for two-dimensional tracking. Path I lets an image pass without rotation, whereas path II rotates the image by 90°. (b) Left: normal fluorescence image obtained as zeroth diffraction (specular reflection of the grating). Areas inside of the red dashed squares are the same sample areas with different orientations. We defined the direction of the x_d and y_d axes of the upper view to be identical to those of the x_s and y_s axes on the sample plane, which yields the relationship between the x_d and y_d axes seen in the lower view and the x_s and y_s axes, as shown on the right.

6.2 Pairing of fluorescence spots

There is one important issue in finding pairs of QDs. Because the emission wavelengths of all the QDs are unknown, it is not easy to correctly find pairs of fluorescence spots originating from the same QD among many spots using only the estimated positions. To address this issue, we found that the correlation coefficient could tell us the correct pairing. Emission spectra of QDs fluctuate randomly in time owing to blinking and spectral diffusion (Fig. 3). The wavelength and intensity of two fluorescence spots originating from the same QD have to fluctuate in synchrony. For quantitative evaluation of the synchronization of the fluctuation, Pearson’s correlation coefficients of intensity time courses were calculated for all possible pairs of fluorescence spots, which enabled us to correctly find pairs for tracing the two-dimensional coordinates of the QDs.

7. Demonstration of two-dimensional localization and tracking

7.1 Stationary QDs

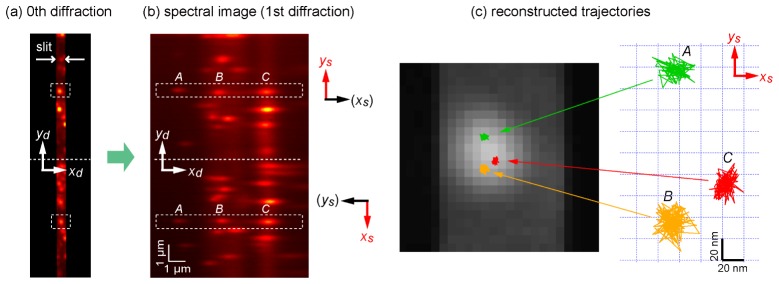
To demonstrate two-dimensional localization using the optical system of 2D-SRTM, we first used a sample of stationary QDs on a glass surface. Figures 7(a) and 7(b) show a normal fluorescence image (zeroth diffraction) and first diffraction image, respectively, of the same area of the sample. To show the spectral discrimination performance, our attention was focused on fluorescence spots at the center of the field of view, which are indicated by dashed squares in the upper and lower views of Fig. 7(a). These two fluorescence spots originated from the same cluster of QDs. In the diffraction image, the fluorescence spots were divided into three spots in both the upper and lower views corresponding to QD525 (labeled A), QD585 (labeled B), and QD655 (labeled C). The position coordinates y_s and x_s of these three QDs were estimated from the upper and lower views by elliptical Gaussian curve fitting to the six spots. This process was repeated for serial frames of a movie. Consequently, two-dimensional coordinate tracing of the three QDs within a sub-diffraction-limit scale was achieved, as depicted in Fig. 7(c). Because the QDs are immobilized on the substrate surface, the position fluctuation of the traces in Fig. 7(c) indicates the localization precision. From this result, the localization precision was found to be approximately 8 nm, which is less precise than that of the one-dimensional case owing to the division of fluorescence photons into two paths.

Fig. 7.

Demonstration of estimation of two-dimensional coordinates of stationary QDs by 2D-SRTM. Representative raw images of (a) zeroth diffraction and (b) first diffraction of many QDs. Three QDs in an aggregate indicated by the dashed squares in (a) are separately recognized in the first diffraction image (b). The three QDs labeled A, B, and C represent QD525, QD585, and QD655, respectively. Both images are summations of 100 successive images acquired with a temporal resolution of 30 ms. The y and x coordinates are estimated from the upper and lower views of the first diffraction image, respectively. (c) Trajectories of the estimated two-dimensional coordinates of the three QDs plotted on a close-up of the zeroth diffraction image of the aggregate.

7.2 Dynamic movement of myosins

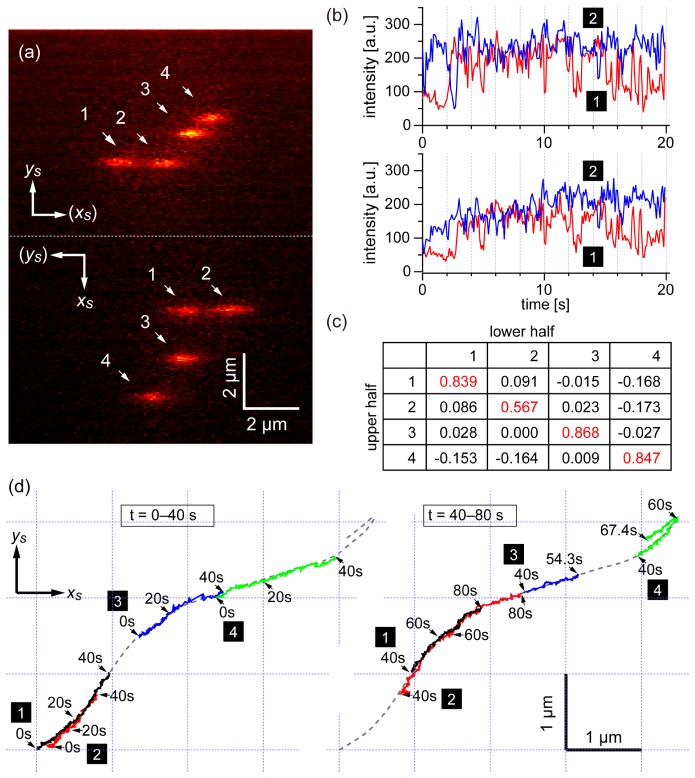
Using this measurement system, we observed M6 moving along an actin filament (Appendix A.5). In this measurement, the slit width was set to be equivalent to 4 µm in the sample coordinates to widen the field of view. The laser intensity at the sample surface was adjusted to 0.71 kW/cm². To demonstrate two-dimensional tracing, we intentionally adjusted the orientation of the flow-cell chamber so that actin filaments in the field of view were not parallel to the direction of the entrance slit. Figure 8(a) is a representative diffraction image, in which we can see four fluorescence spots in both the upper and lower views. Figure 8(b) shows temporal profiles of intensity fluctuation of the fluorescence spots labeled 1 and 2 in the first 20 s, where it is obvious that the same QDs have synchronous fluctuation in the upper and lower images. The Pearson’s correlation coefficients for all possible pairs of fluorescence spots are shown in Fig. 8(c). Correct pairs have high correlation coefficients, whereas false pairs have low correlation coefficients. The statistical significance of the correlation coefficient (r) can be evaluated by the t-test of a value given by t = r√(n-2)/√(1-r²) which follows Student’s t-distribution with a degrees of freedom n-2 [42]. If we set the level of statistical significance for the positive correlation to be p = 0.01, the correlation coefficient should be larger than 0.6 at n = 17 and 0.5 at n = 25. In general molecular tracking experiment, a series of more than a few tens of frames is recorded. Thus, the correlation coefficient analysis gives a correct paring with high reliability. With the help of this analysis, we correctly identified pairs for drawing two-dimensional trajectories of the QD-M6 samples.

Fig. 8.

(a) Representative first diffraction image containing four fluorescence spots in both the upper and lower views, which is one frame in a movie obtained with a temporal resolution of 100 ms. (b) Temporal fluctuation of intensity of two fluorescence spots labeled 1 and 2 observed in both views. (c) Pearson’s correlation coefficients of temporal profile of intensity for all 16 possible pairs of four fluorescence spots in both upper and lower halves of (a). (d) Reconstructed two-dimensional trajectory of the four QDs on the sample coordinates (x_s, y_s), where we found that they are moving along a single actin filament.

Figure 8(d) shows two-dimensional trajectories of the four QD-M6 samples on the x_s–y_s plane, which were derived from a set of serial images in the time range of 0–80 s. The temporal resolution was set to 100 ms per frame to accumulate a sufficient number of photons. The ATP concentration was 50 µM. The first half (0–40 s) and second half (40–80 s) of the time range are separately plotted on the left and right sides of the figure, respectively. Two-dimensional dynamic behaviors of the four QD-M6 samples moving on a common actin filament were successfully observed. The figure shows that the two QDs labeled 1 and 2 are very close, within the sub-diffraction-limit scale, most of the time, and we can see they are chasing each other back and forth. This result indicates the ability of our technique to track multiple motor proteins even on a two-dimensional plane.

8. Conclusions and future perspectives

In conclusion, we introduced spectrally resolved tracking microscopy, SRTM, which is a simple and versatile technique for simultaneous tracking of multiple motor proteins even if they are adjacent at the sub-diffraction-limit scale. The key concept is that only one-dimensional displacement of proteins along a filament axis is measured, and its orthogonal dimension is dedicated to spectral discrimination to separately detect the proteins (1D-SRTM). A localization precision of less than 5 nm was achieved at a temporal resolution of 30 ms. This microscopy is straightforward for observation of movement of linear translational motor proteins (myosin, kinesin, and dynein) on a rail protein filament (actin filament and microtubule). We also showed how the method can be extended to two-dimensional measurement (2D-SRTM). We believe that this measurement scheme would be useful for understanding the cooperativity of multiple motor proteins working in close proximity. While the current study only employed isolated molecules of processive linear motors for demonstration, the developed microscopy is also applicable to other subjects involving linear motor proteins, including cooperative transport of a single cargo by multiple linear motors [43–45] and cooperativity among multiple myosin-II heads on a thick filament of muscle [46,47]. Aside from linear motor proteins, measurement of multiple proteins in a rotatory motor system [31,32] and molecular complexes of membrane proteins [20,33] could also be potential applications. It is also possible to combine this method with three-dimensional tracking techniques [29,48]. Further optimization of the optical setup and localization algorithm would enhance the capabilities of this technique.

Appendix.

A.1 Flow-cell chamber

A flow-cell chamber was made by assembling two pieces of glass microscope coverslips (22 mm × 32 mm microcover glass and 18 mm × 18 mm microcover glass, no. 1 thickness, Matsunami, Osaka, Japan) with double-sided transparent tape (Scotch, Saint Paul, MN).

A.2 Preparation of actin filaments immobilized on coverslip

Actin-immobilized glass substrates were prepared by the procedure described below. Rabbit-derived actin was purified by a procedure described in the literature [49]. G-actin stock at a concentration of 5.7 mg/mL was diluted to 0.9 mg/mL in 10 mM HEPES-KOH (pH 7.0) and 100 mM KCl and then kept at room temperature for 30 min. Buffer [400 µL; 10 mM HEPES-KOH (pH 7.0) and 100 mM KCl] was added, and then 0.1 mM tetra-methyl-rhodamine (TMR) phalloidin (Life Technologies, Carlsbad, CA) was added for fluorescent staining of actin filaments and structure stabilization. TMR labeling was necessary for easily finding the filaments during observation. The mixture was kept overnight at 4°C.

Before the actin was injected, 10 µL of α-actinin (1.5 mg/mL in AB) was injected into a flow-cell chamber and incubated for 3 min to allow for tight adsorption. Unbound α-actinin was removed by washing with 20 µL of AB. Actin stock (10 µL), diluted 200 times in AB, was then injected and incubated for 3 min to allow for tight adsorption. Excess actin was removed by washing with 20 µL of AB. The flow cell was then incubated with 10 µL of 5 mg/mL α-casein in AB (C6780, Sigma-Aldrich, St. Louis, MO) for 3 min to reduce QD adhesion. Excess solution was removed by washing with 20 µL of AB.

A.3 Preparation of stationary quantum dots

Assay buffer [AB; 20 mM HEPES-KOH (pH 7.8), 25 mM KCl, 5 mM MgCl₂, and 1 mM EGTA] was prepared. An oxygen scavenger system (0.2 mg/mL glucose oxidase, 4.5 mg/mL glucose, 36 µg/mL catalase) was added to the AB. Seven types of QDs were added so that the final concentration of all QDs was reduced by 10,000-fold. The solution was injected into the flow-cell chamber described above, which was then sealed with nail polish. QDs were directly deposited on the surface of the coverslip via nonspecific adhesion.

A.4 Preparation of double-labeled myosin V

Recombinant myosin V fused with a HaloTag® (DHA, Promega) fragment at the N-terminus was mixed with HaloTag PEG-Biotin Ligand (Promega) for biotinylation [50]. Streptavidin conjugates of QD525 and QD585 (1 µL) were mixed with 1 µL of biotinylated M5 (~1 µM). Calmodulin (2 µL, 2.0 mg/mL) was added to stabilize the myosin structure. The mixture was incubated for 1 h on ice.

The mixture of QDs and M5 was diluted 400 times in a motility buffer (AB plus 5 µM ATP, 0.2 mg/mL glucose oxidase, 4.5 mg/mL glucose, 36 µg/mL catalase, 1% v/v β-mercaptoethanol, 5 µM calmodulin, 2 µM phosphocreatine, and 0.1 mg/mL creatine phosphokinase, final pH 7.8). This mixture (20 µL) was injected into a flow cell, which was sealed with nail polish.

A.5 Preparation of myosin VI molecules

Recombinant myosin VI fused with a HaloTag® (DHA, Promega) fragment at the N-terminus was mixed with HaloTag PEG-Biotin Ligand (Promega) for biotinylation [19]. Streptavidin conjugates of the seven QD solutions (0.5 µL) were mixed with 4 µL of the biotinylated M6 (~1 µM). Calmodulin (2 µL, 2.0 mg/mL) was added to stabilize the myosin structure. The mixture was incubated for 1 h on ice.

The mixture of QDs and M6 was diluted 100 times (for the experiment in Figs. 5(e) and 5(f)) or 400 times (for the experiment in Fig. 8) in a motility buffer (AB plus 50 µM ATP, 0.2 mg/mL glucose oxidase, 4.5 mg/mL glucose, 36 µg/mL catalase, 5 µM calmodulin, 2 µM phosphocreatine, and 0.1 mg/mL creatine phosphokinase, final pH 7.8); this buffer is similar to that used for the M5 sample (Appendix A.4) except for a higher ATP concentration and the absence of β-mercaptoethanol. This mixture (20 µL) was injected into a flow cell, which was sealed with nail polish.