Depth-resolved analytical model and correction algorithm for photothermal optical coherence tomography

Abstract

Photothermal OCT (PT-OCT) is an emerging molecular imaging technique that occupies a spatial imaging regime between microscopy and whole body imaging. PT-OCT would benefit from a theoretical model to optimize imaging parameters and test image processing algorithms. We propose the first analytical PT-OCT model to replicate an experimental A-scan in homogeneous and layered samples. We also propose the PT-CLEAN algorithm to reduce phase-accumulation and shadowing, two artifacts found in PT-OCT images, and demonstrate it on phantoms and in vivo mouse tumors.

1. Introduction

Molecular imaging is widely used in pre-clinical studies, for example in drug discovery [1], and to study biological processes [2]. Multiple imaging modalities have been developed for in vivo molecular imaging, each on different field-of-view and resolution scales, and each with their own advantages and disadvantages. Whole body imaging techniques include magnetic resonance imaging (MRI) [3], computed tomography (CT) [4] and positron emission tomography (PET). These whole body imaging techniques have no limit on imaging depth, but are usually high cost methods, with poor sensitivity to the molecular contrast agent (CT, MRI) and/or involve the use of ionizing radiation (CT, PET). Ultrasound and photoacoustic [5] imaging have a penetration depth of up to 10 cm and have the advantage of being low cost, with equipment already available in the clinic. Ultrasound can image contrast agents such as microbubbles [6] and some nanoparticles [7] while photoacoustic imaging can image absorbers such as blood, melanin and a wide array of metallic nanoparticles. However, both ultrasound and photoacoustic imaging do not allow simultaneous multi-modality imaging since they use an ultrasound transducer, which complicates the coupling of multiple imaging techniques in one instrument and can also complicate the coupling of the instrument to the subject. Finally, optical techniques are limited to low imaging depths but allow for both large field-of-views with low resolution (e.g. whole body bioluminescence imaging [8]) and small field-of-views with very high resolution (e.g. fluorescence microscopy [9]).

There is a need for an optical molecular imaging technique with a large field-of-view and high resolution to fill the gap between microscopy and bioluminescence imaging, and complement non-optical techniques. Photothermal optical coherence tomography (PT-OCT) is an emerging technique [10, 11] that would allow the imaging of contrast agents in vivo with a field-of-view (>25mm²), imaging depth (>1mm) and resolution (<15μm transverse) comparable to traditional OCT. In PT-OCT, a laser is used to heat the contrast agent embedded in the sample, which in turn heats the sample locally, and thus causes an elastic expansion and a change in the index of refraction of the medium. This causes a local variation in optical path length that is then detected by a phase-sensitive OCT system. PT-OCT thus offers similar sources of contrast as photoacoustic imaging, while allowing multiplexing with other functional OCT modalities (such as speckle variance OCT [12]). Additionally this method does not require the instrument to be in contact with the sample.

PT-OCT has been demonstrated in vitro [10], ex vivo [13] and in vivo [14] on a multitude of contrast agents, such as gold nanospheres [10], gold nanoshells [13, 15], gold nanorods [12, 14, 16, 17], carbon nanotubes [18], indocyanine green [19, 20] and blood [21, 22]. However, PT-OCT images are still affected by two artifacts: phase-accumulation (signal becoming brighter with depth) and shadowing below high intensity regions. A method has been proposed to correct those artifacts [23] but this method also drastically decreases the signal-to-noise ratio of the image.

A theoretical model of PT-OCT would allow for a better understanding of the photothermal signal, give indications on how to optimize the imaging procedure, and would be a tool toward solving the problem of phase accumulation and shadowing. Separate components of the photothermal process have been modeled in the past, including the sample heating through the bio-heat conduction equation [14], the change in optical path length due to the change in temperature [23], the reflectivity of a sample with specific optical characteristics [24] and the phase sensitivity as a function of the signal-to-noise ratio in OCT [25].

We propose a model that assembles those individual components and includes the evolution of the photothermal signal with depth. This is the first model to replicate reliably a PT-OCT A-scan for a homogenous sample and for a layered heterogeneous sample. This model can be customized to the specific instrument (spectral-domain or swept-source OCT), imaging parameters, and sample characteristics. Furthermore, we have used the model to implement a variation of the CLEAN algorithm [26] which successfully eliminated the effect of phase accumulation and shadowing in phantom images and in images of heterogeneous tumors acquired in vivo. This paper will present the equations necessary to implement this analytical model of PT-OCT and our version of the CLEAN algorithm. Experimental validations in phantoms will also be presented in each section.

2. Theory

2.1 Model of photothermal signal generation

PT-OCT relies on photothermal heating of contrast agents by a laser illumination source. For the contrast agent to be heated, the photothermal laser light must first reach the contrast agent. The photothermal laser power P(z) was generated using a Monte Carlo simulation [27] that took into the absorption and scattering coefficient of the sample, respectively μ_a and μ_s (cm^-1) and z (μm), the distance travelled within the sample. Once the power that reaches the contrast agent is known (and the laser spot size is known), we can calculate how much heat will be emitted. The bio-heat conduction equation is used to model how the temperature will vary in the sample surrounding the contrast agent when it is illuminated. The bio-heat conduction equation with a heat source is the following [14]:

$$\frac{\partial T}{\partial t}=\frac{\phi {\mu }_a}{\rho c}+\alpha {\nabla }^{2}T$$ (1)

where T (K) is the temperature, t (s) is the time, φ (W/m²) is the photothermal laser fluence rate, ρ (kg/m³) is the density of the sample, c (J/kg*K) is the specific heat of the sample and α (m²/s) is the thermal diffusivity of the sample (α = k/ρc where k (W/m*K) is the thermal conductivity of the medium). In the case where the laser spot size is small compared to the absorption depth, radial heat transfer dominates the heat conduction equation, which can then be solved in cylindrical coordinates. The temperature ΔT at the center of the laser beam (r = 0) will rise and fall over one modulation period (2t_L) of the photothermal laser in the following way [14]:

$$\Delta T(t,r=0)=\frac{P(z){\mu }_a}{4\alpha \pi \rho c}\ln \left(1+\frac{t\alpha }{{\omega }^2(z)/8}\right),t<t_L$$ (2)

$$\Delta T(t-t_L,r=0)=\frac{P(z){\mu }_a}{4\alpha \pi \rho c}\ln \left(1+\frac{t_L\alpha }{\frac{{\omega }^2(z)}{8}+\alpha \left(t-t_L\right)}\right),t\ge t_L$$ (3)

where t_L (s) is the dwell time of the photothermal laser on the sample before an acousto-optic modulator reduces the laser power to zero (square waves modulation, 50% duty cycle) and $\omega (z)={\omega }_0\sqrt{1+{\left(z/z_0\right)}^2}$ is the 1/e² beam radius (ω₀ (μm) is the waist size inside the tissue estimated with a Monte Carlo simulation [28] and z₀ (μm) is the Rayleigh range of the objective). The change in temperature will cause the sample to undergo two changes: elastic expansion and change in index of refraction. Combined, these phenomena will cause a change in the optical path length (ΔOPL) detected by the OCT system. The change in OPL over a set amount of time (Δt) at each depth z can be calculated as follows [23]:

$$\Delta OPL(z)=OP{L}_{T_0+\Delta T}-OP{L}_{T_0}={\displaystyle \underset{0}{\overset{z}{\int }}\left(\left[n(T_0)+\frac{dn}{dT}\Delta T\right]·\left[1+\beta \Delta T\right]-n(T_0)\right)dZ}$$ (4)

where T₀ (K) is the initial sample temperature, n is the index of refraction, dn/dT (K⁻¹) is the thermo-optic coefficient that is assumed to be constant for this model and β (K⁻¹) is the thermal expansion coefficient of the sample. In our sample, dn/dT>0 and β<0 thus both effects act against each other. Over multiple photothermal excitation cycles, the variation in OPL will cause a change in phase ΔΦ (mrad) in the OCT signal, which will be detected by our instrument [25]:

$$\Delta \Phi (z)=\frac{4\pi n\Delta OPL(z)}{{\lambda }_0}$$ (5)

where λ₀ (nm) is the center wavelength of the OCT laser and the average index of refraction for the sample n = n(T₀) is used.

2.2 Model of photothermal signal detection

Once the photothermal signal is generated inside a sample, the signal is detected using an OCT system. The signal I(z), collected from one A-scan with a sub-resolution change in reflector position ΔΦ(z), is calculated as [25]:

$$I(z)=\frac{\delta }{2e}S\Delta t\sqrt{R_s(z)R_R}{e}^{i\Delta \Phi (z)}·\sin \text{c}(az)$$ (6)

where δ (A/W) is the detector responsivity, e (C) is the electronic charge, S (W) is the power of the OCT laser source at the sample, Δt (μs) is the time to acquire one A-scan, R_s(z) is the reflectivity at the sample as a function of depth inside the sample, and R_R is the reflectivity of the reference arm. The sinc function accounts for the spectrometer fall-off with depth, and the scaling constant a is determined experimentally. We use the following equation to calculate the reflectivity of the sample arm R_s(z) [24]:

$$R_s(z)=\frac{{\mu }_b\pi {\omega }^2(z)L_c{e}^{-2({\mu }_s+{\mu }_a)z}}{4{(nz)}^2\left[1+{\left(\frac{\pi {\omega }^2(z)}{4\lambda nz}\right)}^2{\left(1-\frac{nz}{n^{2}f}\right)}^2\right]}$$ (7)

where μ_b (cm⁻¹) is the backscattering coefficient of the sample, L_c (μm) is the coherence length of the OCT laser and f (μm) is the focal position of the OCT beam. Reflectivity models specific for phase-sensitive detection [24, 25] were chosen over other models [29], because PT-OCT is a phase-sensitive technique.

The experimental signal also contains additive, uncorrelated Gaussian white noise, divided here into shot noise A_shot(z) [25] and environmental noise A_env(z):

$$A_{shot}(z)=\sqrt{\frac{\delta }{e}S\Delta t{R}_R}{e}^{-i{\varphi }_{rand}}$$ (8)

$$A_{env}(z)=A_0{e}^{-i{\varphi }_{rand}^{\prime }}$$ (9)

where φ_rand and φ’_rand are uniformly distributed random phases between -π and π and A₀ is an experimentally determined magnitude that includes other sources of noise (electronic, vibrational, thermal, etc.). The experimental phase change ΔΦ_exp(z) is then calculated as the phase of the signal and noise terms added together.

$$\Delta {\Phi }_{\exp }(z)=\angle \left[I(z)+A_{shot}(z)+A_{env}(z)\right]$$ (10)

The experimental phase change ΔΦ_exp(z,t) is acquired over time (in practice 1000 repeated A-scans at the same location inside a sample), then a Fourier transform is used to go from the time domain to the frequency domain.

$$p(z,f)=FT(\Delta {\Phi }_{\exp }(z,t))$$ (11)

The photothermal signal is then defined as the magnitude of the signal at the laser modulation frequency f₀ = 500Hz, The photothermal signal is also weighted by the OCT laser wavelength λ, the average index of refraction n and the laser modulation frequency f₀ in order to have units of nm (same as ΔOPL). (See [14] for full derivation).

$$PTOCT(z)=\frac{\left|p(z,f_0)\right|\lambda }{4{\pi }^2{f}_{0}n\Delta t}$$ (12)

The photothermal noise is calculated following the same equation but where p(z,f₀) is replaced by the mean magnitude of nearby frequencies.

2.3 Model for heterogeneous samples

The model described in the previous sections is only valid for homogenous samples. However, quasi-heterogeneous samples can be created by superposing layers of different homogenous samples. First the power P(z) is simulated for a multi-layer sample using the Monte Carlo method [27]. Then the temperature change ΔT and reflectivity R_s(z) are calculated for each layer separately and combined as one continuous function vs depth. The beam waist ω(z) is again estimated using a Monte Carlo simulation of a focused Gaussian beam in a multi-layered sample [28]. The following calculation steps to obtain the PT-OCT signal are then the same as in the one-layer case.

2.4 PT-CLEAN algorithm to eliminate phase accumulation and shadowing

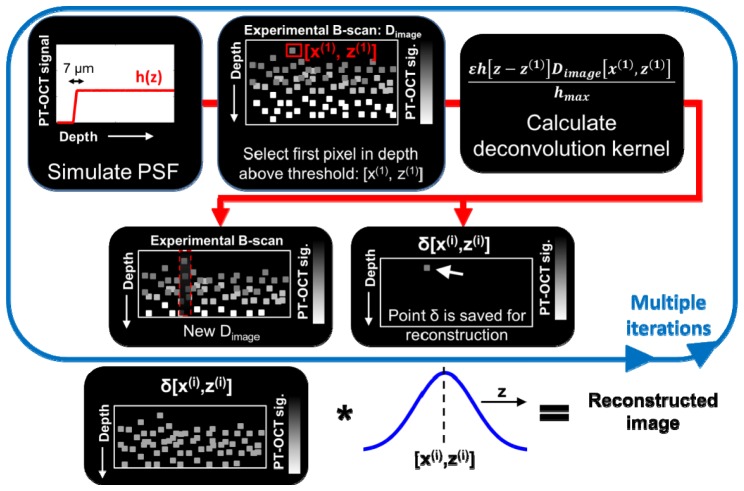
The CLEAN algorithm was invented in the 1970s with applications in radio astronomy [30] before being adapted for microwave imaging [31]. It was then adapted for OCT to reduce speckle noise, cancel coherent artifacts and improve resolution [26, 32]. The CLEAN algorithm relies on a basic procedure: deconstruct an image point-by-point using the point-spread function (PSF) proper to the instrument, then re-construct the image point-by-point using a modified PSF to improve image quality. In the case of PT-OCT, we want to correct for phase accumulation and shadowing, thus a PSF without those two artifacts will be used for reconstruction.

First, our analytical model of PT-OCT is used to create the PSF of our system. Using the theoretical model for this step is more practical than to image a thin, homogeneous absorber (<10 μm) that could be approximated as a point. For the PSF, a 7 μm thick absorbing and scattering layer of tissue (thickness on the order of the OCT axial resolution) is simulated and serves as a 1D PSF of PT-OCT, denoted h(z). This PSF can be generated with approximated values for the scattering and absorption coefficients since it will be normalized in the next step of the algorithm. Second, the original experimental PT-OCT B-scan is considered, and the first pixel in depth to have a photothermal signal above a certain threshold (ΔOPL = 2 nm) is selected (coordinates [x⁽¹⁾, z⁽¹⁾]). Third, the following deconvolution kernel is subtracted from the original image [26]:

$$\epsilon h\left[z-z^{(1)}\right]D_{image}\left[x^{(1)},z^{(1)}\right]/h_{\max }$$ (13)

where ε<1 is the loop gain, or fraction of the image that is removed at each iteration of the algorithm, h[z-z⁽¹⁾] is the PT-OCT PSF centered at [x⁽¹⁾, z⁽¹⁾], D_image[x⁽¹⁾, z⁽¹⁾] is the intensity of the selected pixel in the original PT-OCT B-scan and h_max is the maximum value of the PSF. A point of intensity δ[x⁽¹⁾, z⁽¹⁾] = ε∙D_image[x⁽¹⁾, z⁽¹⁾] at position [x⁽¹⁾, z⁽¹⁾] is then saved for the final image reconstruction.

The next iteration then starts by finding the first pixel in depth to have a photothermal signal above threshold in the remaining image (original image minus deconvolution kernel):

$$D_{image}-\epsilon h\left[z-z^{(1)}\right]D_{image}\left[x^{(1)},z^{(1)}\right]/h_{\max }$$ (14)

then we proceed as described for the previous iteration. The iterative process is stopped when the brightest pixel is below the noise floor of the original image. The final CLEANed image is obtained by convoluting each points δ[x⁽ⁱ⁾, z⁽ⁱ⁾] with a Gaussian function of 7 μm in width at half maximum. What is left of D_image after the iterative process can be added to the CLEANed image to provide a realistic-looking noise floor. The PT-CLEAN algorithm takes into account the decreasing SNR of the image with depth since the PSF also has a decreasing SNR with depth. Additionally, a speckle-correction algorithm can be used if necessary in combination with the PT-CLEAN algorithm to improve data visualization.

A summary of the PT-CLEAN algorithm can be seen in Fig. 1

Fig. 1.

Flow diagram of the PT-CLEAN algorithm to remove phase accumulation and shadowing. A point spread function is created using the analytical model. The first pixel in depth with a PT-OCT signal above threshold is then selected to calculate the deconvolution kernel. Two new images are created; a B-scan from which the deconvolution kernel was subtracted and a new image where the selected pixel is recorded. The final image is reconstructed by convoluting each of the individual saved pixels to a 1-D Gaussian along the depth dimension.

3. Methods and instrumentation

3.1 Instrumentation

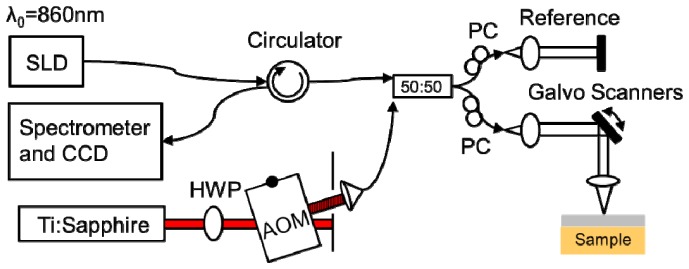
A commercial spectral-domain OCT system (Bioptigen, Inc.) was altered for photothermal imaging (Fig. 2). A superluminescent diode imaging laser (SLD, Fig. 2) with λ₀ = 860 nm central wavelength and 40 nm bandwidth (Superlum) was used as the OCT imaging beam. The light from the SLD was split between the sample and reference arms using a 50:50 fiber coupler (50:50, Fig. 2). Photothermal heating was provided by a wavelength tunable Titanium:Sapphire laser (Coherent). The wavelength of the PT laser was tuned to match the absorption peak of the contrast agent used (λ_PT = 750 nm for indocyanine green and brown human hair, λ_PT = 740 nm for gold nanorods). The PT laser intensity was modulated by an acousto-optic modulator (Brimrose) (AOM, Fig. 2) following a square wave with frequency f₀ = 500 Hz. The light of the PT laser was combined to the superluminescent diode and sent to the reference and sample arms using the 50:50 fiber coupler. A telecentric lens (Bioptigen) was used to focus the light onto the sample (1/e² beam radius ω₀ = 28 μm in air, 36 μm simulated in tissue). The returning light was directed to the spectrometer and the CCD integrated to the Bioptigen system using a circulator (AC photonics).

Fig. 2.

PT-OCT instrumentation. The light from a superluminescent diode (SLD) is split between a reference and sample arm using a 50:50 fiber coupler (50:50). The photothermal excitation is provided by a Titanium:Sapphire laser (Ti:Sapphire) that is amplitude modulated by an acousto-optic modulator (AOM). HWP: Half-wave plate. PC: Polarization compensation.

3.2 Phantom fabrication

Clear silicone (Quantum Silicones) was used to create solid homogeneous phantoms. The silicone consists of two parts (base and curing agent) that need to be mixed in a 10:1 ratio. For all phantoms, rutile titanium dioxide (TiO₂, <5μm, Sigma Aldrich) was first added to the silicone base for a final concentration of 2.05mg/g (μ_s≈50cm⁻¹). The base and TiO₂ were then mixed for two minutes and degassed for two minutes using a planetary centrifugal mixer (Thinky USA). In phantoms where indocyanine green (ICG) was added, it was first dissolved into 800 μL of 70% ethanol then added to the curing agent of the silicone. It was then mixed and degassed for two minutes each in the planetary centrifugal mixed (when ICG was not used, this step was skipped). Finally, the base and curing agent were mixed together and degassed. This final mixture was then poured into a petri-dish and placed under vacuum at 29 inches of Hg for five minutes with brief returns to standard pressure every minute.

To make layered phantoms, the final silicone mixture for each of the layers was poured between two glass slides with 115 μm spacers attached on both sides. The layers were then cured at 70°C for 12h and superimposed after curing. For single-layer phantom the silicone mixture was poured into a petri-dish and then cured following the same procedure.

A phantom was made using a human brown hair as a thin absorbing layer. A silicone mixture was prepared as described above (no ICG). Then, a single hair was attached to both sides of the petri-dish so it would form the hypotenuse of a right triangle of known height (petri dish depth) and length (petri-dish diameter). The silicone mixture was then poured into the petri-dish, covering part of the hair strand. Using trigonometry, it was thus possible to know the depth of the hair as it progressively penetrated the silicone. The phantom was then cured.

3.3 Imaging parameters and signal processing for phantom experiments

For every phantom experiment, the SLD power at the sample was 2 mW, with a 36 μm 1/e² beam radius at the focus (in silicone). The photothermal laser power at the sample was varied in between 2 mW and 16 mW depending on the experiment. For each 1D depth-resolved PT-OCT A-scan, 1000 OCT A-scans were recorded over time with every OCT A-scan lasting Δt = 100 μs. Each OCT-A scan was resampled from a linear wavelength space to a linear wavenumber space, then corrected for dispersion and background subtracted [14]. A Chirp-Z transform was used to convert the wavenumber data to depth-resolved data. The phase data at each point in depth was then used for the rest of the analysis. The temporal derivative of the phase at each point was calculated and a Fourier-transform was taken in the temporal dimension. The data was then treated exactly like the data generated by the analytical model (see Eq. (12)).

For each experimental validations of the model, one B-scan (4 mm in length) containing 400 PT-OCT A-scans was averaged to produce one noise-reduced PT-OCT A-scan and facilitate data visualization . The same method was used with the data generated by the model.

3.4 In vivo imaging

All animal work was approved by the Vanderbilt IACUC committee, and all surgical procedures were performed using aseptic techniques. One nude female mouse (Foxn1^nu/ Foxn1^nu, The Jackson Laboratory) underwent dorsal skinfold surgery to enable imaging of MDA-MB-231 (human, breast) tumors. Following baseline (pre-injection) PT-OCT imaging (no signal detected), gold nanorods (AuNRs) coated with methoxy-terminated poly(ethylene glycol) (PEG) were injected (200 μL injection, 9 nM) with a retro-orbital injection. The mouse was imaged again 17h post-injection with PT-OCT while under anesthesia (isofluorane mixed with air, 1.5-2%). The full protocol, including AuNRs synthesis and surgical procedure is described in detail in [12]. For this experiment, the photothermal laser was set to λ_PT = 740 nm, with 70 mW of power at the sample. The SLD delivered 6.6 mW of power at the sample. B-scans were acquired and processed as in section 3.3.

3.5 Input parameters for the analytical model

Two different samples were simulated using the PT-OCT theoretical model: a one layer, 5 mm thick silicone phantom containing TiO₂ (2 mg/g) and ICG (0.09 mg/g), and a silicone phantom containing TiO₂ (2 mg/g) and a human brown hair. The different variables that were used to implement the theoretical model for those two samples can be seen in Table 1.

Table 1. Input parameters for PT-OCT analytical model.

Optical properties	5mm ICG phantom	Human hair phantom
Scattering coefficient μs (cm−1)	50 [33]	(Silicone) 50
		(Hair) 55 [34]
Absorption coefficient μa (cm−1)	11 [35]	(Silicone) 0.005 [36]
		(Hair) 50 [34]
PT laser power P0 (mW)	0-16	15
PT laser wavelength (nm)	750	750
Back-scattering coefficient μb (cm−1)	1a,b	1a,b
Thermal conductivity k (W/K)	0.18 [36]	0.25 [37]
Specific heat c (J/kg*K)	1200 [36]	1602 [37]
Density of medium ρ (kg/m3)	1020 [36]	1100 [37]
Laser beam radius ω0 (μm)	36 [28]	36
Rayleigh length z0 (μm)	1000	1000
Depth of focus zf (μm)	400	400
Dwell time of PT laser tL (ms)	1	1
Index of refraction n	1.44 [36]	(Silicone) 1.44
		(Hair) 1.55 [34]
Thermo-optic coefficient dn/dT (K−1)	−340 x 10−6 [38]	−110 x 10−6 [23]a
Thermal expansion coefficient β (K−1)	275 x 10−6 [36]	100 x 10−6 [23]a
OCT wavelength λ0 (nm)	860	860
OCT power S (mW)	2	2
OCT coherence length (μm)	15.1	15.1
Detector responsivity δ (A/W)	0.2	0.2
A-scan acquisition time Δt (μs)	100	100

^aApproximate value since exact values were not found in the literature.

^bIf necessary, the backscattering coefficient can be more precisely determined with published methods [39].

4. Results

4.1 Demonstration of the analytical model

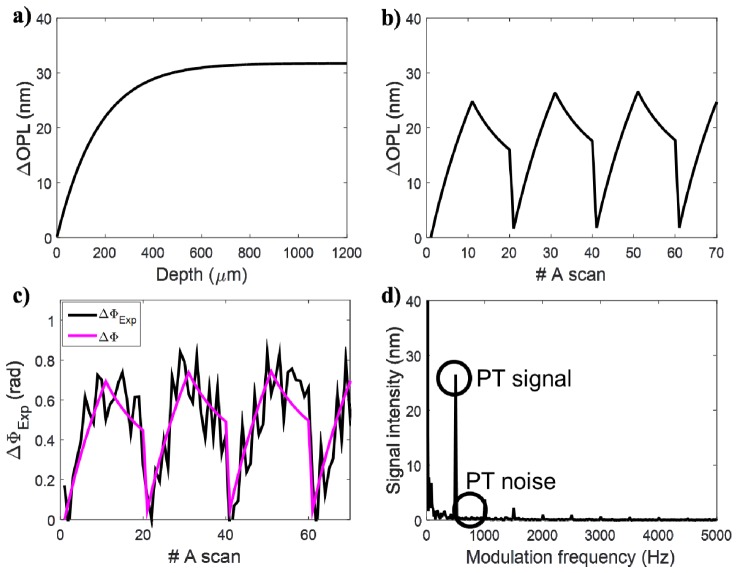
The parameters for a thick silicone phantom containing TiO₂ and ICG (Table 1, first column) were used to visualize the model output at different steps of the simulation. The first behavior illustrated by the model is the change in OPL Eq. (4) which is a result of the cyclic variations in temperature caused by the photothermal laser and contrast agent. Our model simulates both the change in OPL at different depths inside the sample (Fig. 3(a)) and at a fixed depth over time (Fig. 3(b)). At this step, only the physical change in the sample is simulated. We still need to detect the change in OPL using an OCT system. This step is done using Eq. (10), which calculates the experimental change in phase detected by a realistic OCT system. The experimental phase change is shown over time (Fig. 3(c)) at the same sample location depicted in Fig. 3(b) (z = 400 μm). A Fourier transform is then performed on the experimental phase change signal (Eq. (11), Eq. (12)) and the PT-OCT signal is taken as the amplitude of the peak at the modulation frequency f₀ = 500 Hz (Fig. 3(d)).

Fig. 3.

Demonstration of the PT-OCT analytical output signal. (A) The change in optical path length produced in the sample by the photothermal effect is plotted as a function of depth and at a fixed depth z = 400 μm over repeated A-scans (B). (C) The change in optical path length is detected as a noisy change in phase by the OCT system. The noiseless change in phase is overlaid in magenta to guide the eye. (D) A Fourier transform of the phase signal is taken to isolate the PT signal and PT noise.

Two characteristics of the signal can be observed from Fig. 3(a)) for ΔOPL and Eq. (5) for ΔΦ(z): phase accumulation and shadowing. Phase accumulation describes the fact that ΔΦ increases with depth for a homogenous sample, and thus the photothermal signal will be detected as increasing, even though the amount of contrast agent in the sample is constant with depth. Experimentally, this causes images to become brighter with depth even though the sample is homogeneous. Shadowing designates a region of high intensity in a region of the sample not containing any absorbers, simply because it is directly below a high absorbing region. Those two phenomena happen because, as seen in Eq. (4), when ΔT≥0, ΔOPL can only increase or remain stable with depth. ΔΦ is a function of optical path length which integrates with depth. Since we are never cooling the sample below its initial temperature, ΔOPL and ΔΦ can never decrease with depth, which causes phase accumulation and shadowing. Both phase accumulation and shadowing are detrimental to the image quality of PT-OCT.

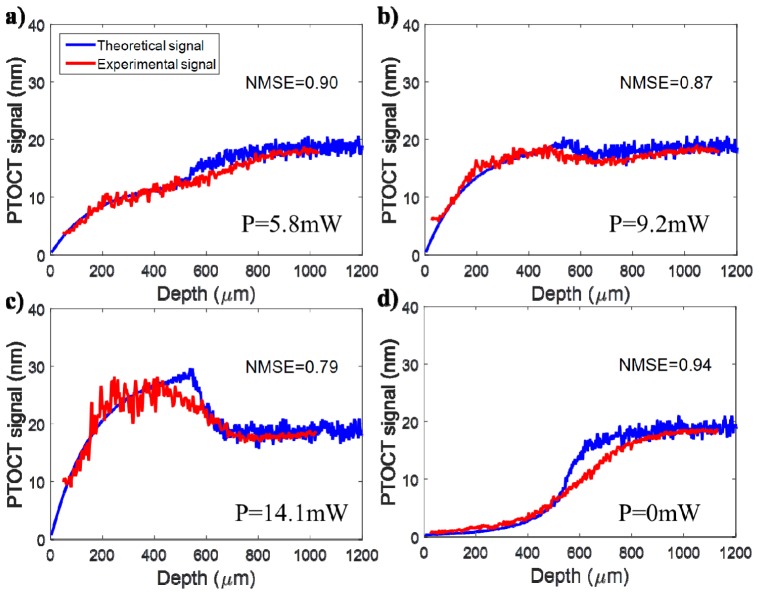
4.2 Validation of the analytical model (monolayer)

A thick, one layer silicone phantom with 90 μg of ICG per gram of silicone was imaged to validate the result predicted by the theoretical model (parameters from Table 1, first column). The power of the photothermal laser at the sample was varied between 0 mW and 16 mW. The resulting average PT-OCT signal can be seen in Fig. 4 for both the analytical model(blue) and the experimental validation (red). The two signals overlap throughout the field of view of the OCT system, for all powers of the PT laser. In each case, both the experimental and theoretical signal initially increases with depth, a result of phase accumulation. However, the signal becomes dominated by noise between 500 μm and 600 μm in depth, a result of the low reflectivity of the sample. This region in depth shows poor agreement between the theoretical signal and the experimental signal. However, this region of poor agreement corresponds to a region already dominated by noise (i.e. SNR is equal to or less than 1). Thus, the model will not routinely be used to interpret data at these low SNR levels. Contrary to intuition, the noise floor (caused by the shot noise) is situated at 18 nm in PT-OCT signal (see Fig. 4(d)). This is because the noise follows a 1/f behavior and happens to have a value of 18 nm at f = 500 Hz. When the SNR approaches one, the PT-OCT signal invariably increases or decreases to reach 18 nm.

Fig. 4.

Validation of the PT-OCT analytical model over an A-scan in a single layer homogeneous sample. The theoretical signal (blue) was generated from the model based on the optical properties listed in Table 1 (5mm ICG phantom). The experimental signal (red) is the average A-scan obtained experimentally by performing PT-OCT on a silicone phantom containing ICG as an absorber. The photothermal laser power at the sample was fixed at (A) 5.8 mW, (B) 9.2 mW and (C) 14.1 mW to show the behavior of the signal in relation to the noise floor. The noise floor can be seen in (D) when the photothermal laser is turned off. NMSE: Normalized Mean Square Error.

4.3 Validation of the analytical model (multi-layer) and PT-OCT imaging depth

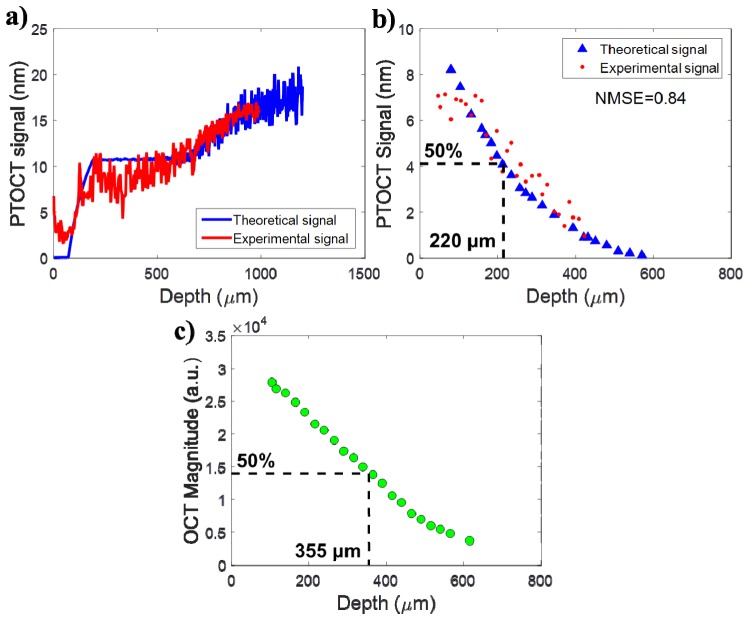
A second experiment was used to investigate the maximum imaging depth of PT-OCT and validate the multi-layer model. The silicone phantom containing the human brown hair was imaged in such a way that the hair is at a different known depth (between 0 and 450 μm from the surface of the phantom to the center of the hair) every B-scan. The hair was considered to be 130 μm in thickness. An A-scan showing the experimental signal (Fig. 5(a), red) from a hair at 80 μm in depth and the corresponding theoretical signal (Fig. 5(a), blue) are shown to validate the multi-layer analytical model. The model input to generate the analytical signal can be found in Table 1, second column.

Fig. 5.

Validation of the PT-OCT analytical model over an A-scan in a multi-layered heterogeneous sample. (A) Theoretical (blue) and experimental (red) A-scan of a human brown hair 80 μm deep inside a scattering silicone phantom. (B) Average theoretical and experimental photothermal signal for different hair depths. Each hair depth was produced by a separate simulation or recorded on a separate B-scan. The signal has decreased by 50% when the hair is 220 μm in depth inside the phantom. (C) Experimental average OCT intensity for a section of scatterer at different depths inside the sample. The signal has decreased by 50% when the scatterers are 355 μm in depth inside the phantom.

To observe how the PT-OCT signal intensity decreases with the absorber depth, results from multiple hair depths were compared. For each hair depth, the PT noise was subtracted from the PT signal and this resulting signal was averaged over the cross section of the hair. The result was then recorded vs the hair depth (see Fig. 5(b), red). The same value was generated by the analytical model (Fig. 5(b), blue). The experimental and theoretical values overlapped for most of the hair positions. The normalized mean square error (NMSE) was calculated between theoretical and experimental values at matched depth to quantify theagreement between the model predictions and the experimental result. (NMSE = 0.84, perfect agreement when NMSE = 1).

We compared the evolution of the PT signal with depth and the evolution of the OCT signal intensity with depth (Fig. 5(c)). For this we measured the average OCT intensity of an area of scatterer inside the phantom, progressively choosing areas at greater depths inside the sample. By comparing the point where the experimental PT signal and the experimental OCT signal have decreased by 50% of their initial value, it was determined that for this specific sample, the PT signal had decreased by half at 220 μm inside the sample, while the OCT intensity had decreased by half at 355 μm inside the sample. This indicates that PT-OCT has a smaller imaging depth than OCT, but of similar order.

4.4 PT-CLEAN algorithm

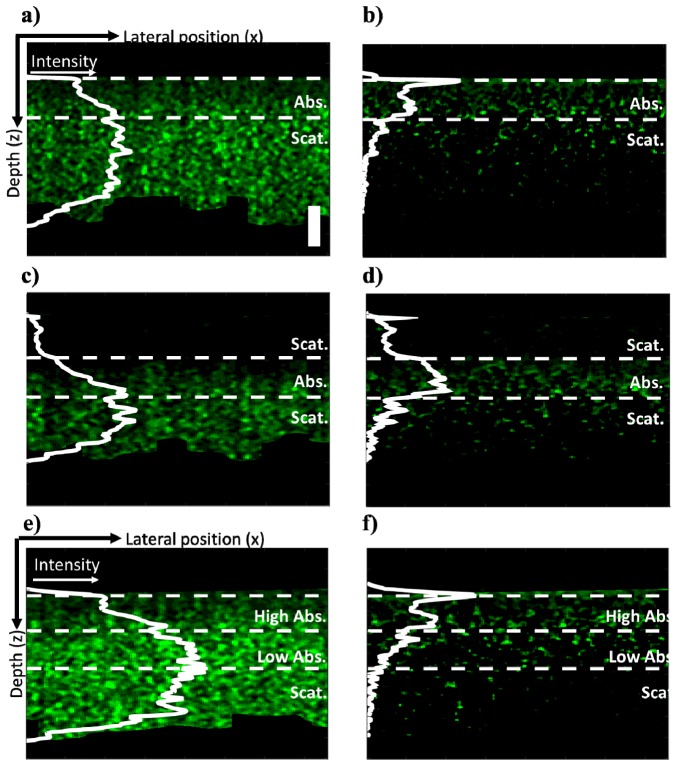
To demonstrate the PT-CLEAN algorithm, multi-layered silicone phantoms containing only TiO₂ (2.05 mg/g) or both TiO₂ and ICG were created. First, a thin layer (115 μm) of ICG phantom was deposited on top of a thick (>5 mm) phantom containing only TiO₂. The sample was imaged with 15 mW of PT laser power at the sample and intensity modulated at 500 Hz. A single B-scan with 400 A-scans/B-scan was acquired (see Fig. 6(a)). Some phase accumulation can be seen in the absorbing (ICG) layer. A large amount of signal is also present in the non absorbing layer from the effect of shadowing. The PT-CLEAN algorithm was applied to the B-scan with a loop gain of 0.01 and photothermal threshold of 2 nm. Those parameters were chosen experimentally to optimize accuracy, run-time and reduce speckle. The resulting B-scan is displayed in Fig. 6(b). In the PT-CLEAN image, the signal inside the absorbing layer is more constant with depth (reduced phase accumulation) and the signal in the scattering layer decreases rapidly to the noise floor (reduced shadowing) (the row-averaged mean signal is indicated as the solid white line on Fig. 6(a)-6(f)). The signal peak at the surface of the CLEANed image stems from the fact that the first pixels in depth are all chosen first by the PT-CLEAN algorithm before it progresses to the rest of the sample. The phantom layer location on each B-scan was determined based on the OCT B-scan that was simultaneously acquired.

Fig. 6.

Demonstration of the PT-CLEAN algorithm and comparison to traditional PT-OCT B-scans. (A) Thin ICG phantom on thick scattering (TiO₂) layer and (B) resulting B-scan after performing the PT-CLEAN algorithm. The horizontal dashed white lines indicate the limit of each layer. The solid white line is the average signal intensity vs. depth. (C) Thin ICG layer between a thin and a thick scattering layer and (D) after application of the PT-CLEAN algorithm. (E) Layer with a high ICG concentration, over a low ICG concentration layer, both over a scattering phantom and (F) after application of the PT-CLEAN algorithm. Scale bar: 100 μm.

To test the robustness of the PT-CLEAN algorithm, a thin layer of phantom with TiO₂ and no ICG was added on top of the sample described previously and imaged with the same parameters (see Fig. 6(c)). The PT-CLEAN algorithm was applied with the same parameters and the resulting B-scan can be seen in Fig. 6(d). Again, the PT-CLEAN signal is more constant over depth in the absorbing layer and close to the noise floor in the scattering layers.

An additional test for the PT-CLEAN algorithm is to differentiate between multiple concentrations of absorbers. Two thin layers of phantom were made with TiO₂ and respectively 11 μg and 45 μg of ICG per gram of silicone. Both layers were then mounted on top of a thick phantom with only TiO₂ with the high concentration layer on top (see Fig. 6(e)).The imaging parameters and the PT-CLEAN parameters were the same as for the previous two experiments. The PT-CLEAN images can be seen in Fig. 6(f). When the absorber concentration goes from high to low with depth (Fig. 6(e) and 6(f)), the traditional PT B-scan displays an increase in signal with depth throughout both absorbing layers, which is due to phase accumulation. However, the PT-CLEAN image shows a decreasing signal with depth that is proportional to the absorption from both layers. This shows the advantage of the PT-CLEAN algorithm over the traditional PT-OCT processing.

The PT-CLEAN algorithm was also applied to a true heterogeneous sample: a mouse tumor xenograft imaged in vivo using a dorsal window 17h after systemic injection of gold nanorods. Both the original PT-OCT B-scan and the PT-CLEANed scan can be seen in Fig. 7(a) and 7(b). Phase accumulation and shadowing are shown to be reduced by the PT-CLEAN algorithm even in a truly heterogeneous sample. A median filter was also applied to the original PT-OCT B-scan (Fig. 7(a)) and the PT-CLEANed B-scan (Fig. 7(b)) to demonstrate the use of a speckle-correction technique in combination with the PT-CLEAN algorithm.

Fig. 7.

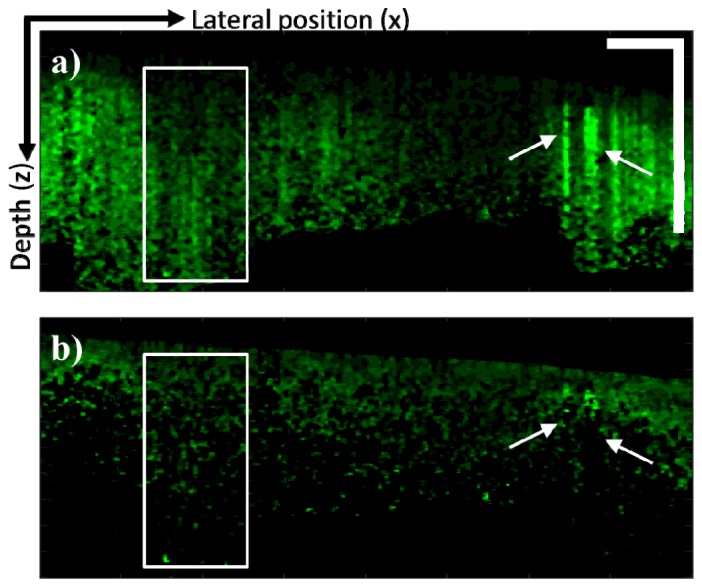
Demonstration of the PT-CLEAN algorithm on in vivo tumor sample. (A) In vivo PT-OCT B-scan of a tumor xenograft after retro-orbital injection of gold nanorods. Both phase accumulation (boxed area) and shadowing (arrows) are visible. (B) B-scan after application of the PT-CLEAN algorithm. Both phase accumulation and shadowing are reduced. Scale bar: 500 μm.

5. Discussion

PT-OCT is an emerging technique for pre-clinical molecular imaging. It has been experimentally demonstrated in vitro, ex vivo and in vivo in the past and parts of its signal had been modeled. However, this is the first time that a comprehensive, customizable analytical model of a PT-OCT A-scan is presented for homogeneous and quasi-heterogeneous samples. We have validated our model against experimental data acquired in a homogeneous silicone phantom containing TiO₂ (scatterer) and ICG (absorber) at various photothermal laser powers, and in a multi-layer phantom containing TiO₂ and a human hair (absorber). Previous models of PT-OCT only described the general shape of the photothermal signal with depth and did not take into consideration the effect of noise. Our model is the first to match the data directly instead of being mathematically fitted to the experimental data points. Our model can also predict the A-scan obtained for different instrument design, imaging parameters, and sample composition.

By layering different sections of homogeneous samples, a heterogeneous sample was approximated. For in vivo drug delivery and molecular imaging experiments, it is expected that the contrast agent will diffuse through the sample and form a heterogeneous distribution. As a first step toward re-creating this situation, we created a three-layer phantom experiment and simulation: two large sections of scattering silicone surrounding a thin layer (130 μm) of absorber. A human brown hair was used as the thin absorption layer. This choice of absorber allowed us to easily vary the position of the absorbing layer in depth inside the sample and to assure that no leaking of the absorber into the scattering layer occurred. We measured the photothermal signal as a function of the hair depth and determined that the photothermal signal decreases with depth slightly more rapidly than OCT. This experiment also validated our model for a multi-layered sample, as the experimental values agreed with the theoretical values (NMSE = 0.84). The maximum imaging depth for PT-OCT is strongly dependent on the type of sample being imaged, how many absorbing layers it has and where they are located. With our analytical model, we can now predict the imaging depth that will be obtained in practice for a given sample, which could not be done theoretically before. We can also select imaging parameters (e.g. photothermal laser power, photothermal modulation frequency, or the integration time of the detector) to maximize the signal strength in a specific sample. In the future, this model can be used to simulate a multi-layered sample that is a better approximation of a heterogeneous distribution of contrast agents inside a tissue sample.

Using our analytical model, we were able to simulate the PT-OCT signal from a homogeneous 7 μm thick absorber, which would be impractical to do without a model. This provided a point-spread function for our PT-OCT system. It was then possible to implement a modification of the CLEAN algorithm, which relies on the PSF of an instrument to improve image resolution and quality. The PSF should be generated with realistic optical parameters for the sample and instrument used to re-create the most accurate PT-OCT image. With the PT-CLEAN algorithm, we have demonstrated that phase accumulation and shadowing can be reduced in different layered samples and in a heterogeneous in vivo tumor sample, which is an improvement over traditional photothermal B-scans. Additionally, PT-CLEAN preserves the units of change in optical path length proper to PT-OCT and does not require any assumption on the signal shape or the sample composition, which allows its application to homogeneous and heterogeneous samples. In comparison with an algorithm proposed before [23], PT-CLEAN does not assume that the change in optical path length is proportional to the geometrical depth inside the medium (as seen in Fig. 3(a), ΔOPL levels off with depth). It is therefore appropriate for complex, heterogeneous samples, and was thus the first algorithm of its kind to be applied to in vivo PT-OCT B-scans. Axial resolution for PT-OCT used to be difficult to define, since a small region of absorber could create a large shadow once the B-scan was processed. With the PT-CLEAN algorithm, the shadowing is eliminated and the effective axial resolution of PT-OCT is improved.

In conclusion, we have presented and validated the first analytical model of PT-OCT that can predict signal intensity with depth in homogeneous and multi-layered samples. We have also presented the PT-CLEAN algorithm to reduce phase accumulation and shadowing, effectively improving the axial resolution of PT-OCT.