Super-resolved thickness maps of thin film phantoms and in vivo visualization of tear film lipid layer using OCT

Abstract

In optical coherence tomography (OCT), the axial resolution is directly linked to the coherence length of the employed light source. It is currently unclear if OCT allows measuring thicknesses below its axial resolution value. To investigate spectral-domain OCT imaging in the super-resolution regime, we derived a signal model and compared it with the experiment. Several island thin film samples of known refractive indices and thicknesses in the range 46 – 163 nm were fabricated and imaged. Reference thickness measurements were performed using a commercial atomic force microscope. In vivo measurements of the tear film were performed in 4 healthy subjects. Our results show that quantitative super-resolved thickness measurement can be performed using OCT. In addition, we report repeatable tear film lipid layer visualization. Our results provide a novel interpretation of the OCT axial resolution limit and open a perspective to deeper extraction of the information hidden in the coherence volume.

1. Introduction

Optical coherence tomography (OCT) is a noninvasive imaging modality based on low coherence interferometry. It is currently used in a wide range of industrial and medical applications and has become a standard tool in ophthalmology for diagnosis and monitoring of several ocular diseases [1].

Key performance indicators of an OCT system are its axial (along the probe beam direction) and lateral (in the perpendicular plane) resolution values. Whereas the lateral resolution is given by the focus spot size and is determined by the optics of the system, the axial resolution in an ideal dispersion-matched system depends only on the property of the light source, namely the bandwidth of the light source’s power spectrum. The axial resolution value is in fact defined as half the coherence length of the light source [2]. From the imaging point of view, it corresponds to the axial length of the smallest feature in a sample that can be resolved in the OCT image. In an ultrahigh resolution OCT (UHR-OCT) system, it is around 1 μm.

Several optical methods have been used to measure sub-micron thicknesses of thin films. Quantitative phase imaging (QPI) can be used to measure the optical thickness of objects in transmission or reflection configuration [3]. Spatial light interference microscopy (SLIM) implementation of QPI uses an enhanced commercial phase contrast microscope with an additional module allowing one to obtain nanoscale topography of several biological samples, and measure thicknesses with nanometer accuracy [4]. Synthetic optical holography (SOH) was proposed to perform QPI with an optical setup using a He-Ne laser and a point detector allowing for sub-nanometer axial resolution surface topography [5]. Unlike QPI which uses the field phase for measuring the optical thickness, several methods relying on the reflectance and transmittance were used. Andrade et al. [6] used optimization applied to transmittance measurements for determining submicron thickness of a thin film stack. Reflectometry uses broad bandwidth reflectance to retrieve the thicknesses of thin films, using models requiring a priori knowledge about the refractive indices of the different layers of the samples under study [7–9]. Reflection interference contrast microscopy (RICM) [10] was used to analyze the surface profile of stratified media for wetting studies and for membrane topography [11]. De Groot recently reviewed interference microscopy for the measurement of surface topography [12]. Surface topography should not be confused with thin film thickness measurement. Coherence scanning interferometry (also known as white-light scanning interferometry) mechanically scans the sample and allows sub-nanometer surface topography, and, combined with model-based analysis allows measurements of thin film thicknesses [13, 14]. Recently, coherent diffractive imaging (CDI) was used to measure accurately a thickness of 32.7 nm using coherent extreme ultraviolet light generated from a Ti:Sapphire laser using high-harmonic up-conversion [15]. The authors used phase retrieval algorithms to recover the 2D thickness maps of a fabricated sample. Methods based on polarization measurement were also reported. For example, ellipsometry, which is widely used for measuring thin film thickness [16]. Using a laser confocal microscope combined with a polarization-based differential interference contrast microscope (LCM-DIM), Wen et al. were, with an optical method, able to resolve single layers of gold atoms, corresponding to a height step of 0.25 nm [17].

It is currently unclear if UHR-OCT allows to measure the thickness of layers below 1 μm. The technology seems to be limited by its axial resolution value which sets the minimal axial feature that can be resolved. But on the other hand, several other optical methods are able to measure submicron thicknesses without the spectral bandwidth that would be required by the OCT resolution criterion.

Here we report super-resolved thickness measurements using a spectral-domain UHR-OCT system. We start with recalling the basic working principles of single thin film reflectometry. The model of the OCT signal of two reflectors in resolved and super-resolved regimes is presented. The results of a simulation of this mathematical model are compared with an experiment that was realized using an interferometer containing a mirror mounted on a piezoelectric stack which allows for accurate setting of the axial position. Super-resolved thickness measurements of several custom fabricated thin film layers on silicon are shown. A comparison with atomic force microscope (AFM) measurements is presented. Finally, we demonstrate the visualization of the tear film lipid layer based on in vivo measurements of the anterior eye segment in several healthy subjects.

2. Optical setup and samples fabrication

The spectral-domain UHR-OCT system is composed of a broadband light source, a Michelson interferometer and a spectrometer. Three different interferometers were used for performing the experiments. The first interferometer was used for investigating the OCT signal in super-resolution regime using a piezoelectric stack for accurately controlling the axial position of a reflector. The second interferometer was used for measuring fabricated samples of known thicknesses. The third interferometer was used for in vivo measurements of the front surface of the eye in humans. The light source and spectrometer were the same for all experiments. The light source was a Ti:Sapphire laser (Integral OCT; Femtolasers Produktions GmbH, Vienna, Austria) providing 170 nm full-width-at-half-maximum (FWHM) spectral bandwidth at a central wavelength λ_c ∼ 800 nm. The spectrometer has already been described in detail elsewhere [18]. The custom acquisition software was done in Labview 2014 (National Instruments, Austin, TX, USA). The post-processing was performed using Matlab R2015b (The MathWorks Inc., Natick, MA, USA).

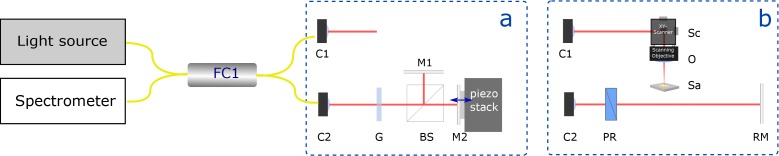
For investigating the OCT signal in super-resolution regime, we used the interferometer depicted in Fig. 1(a). This interferometer was designed in a way that two peaks are present in the OCT amplitude signal. The position of one peak can be controlled continuously using the piezoelectric stack. The glass plate used in the interferometer was a coverslip of 150 μm thickness. The piezoelectric stack was driven by a closed-loop controlled piezoelectric amplifier (E-665; Physik Instrumente (PI), Karlsruhe, Germany) using an input signal provided by an analog function generator. The used waveform was a sawtooth with 10 Hz frequency. The signal model of this interferometer is derived in section 3.7 and the comparison with the experiment is shown in section 4.

Fig. 1.

Schematic diagram of the UHR-OCT system with the different interferometer implementations. Interferometer used : (a) for validating the OCT signal model, (b) for measuring the fabricated samples of known thickness. C: collimators; G: coverslip glass plate; PR: prism pair for dispersion compensation; M: mirror; RM: reference mirror; Sc: two-axis galvanometric scanner; Sa :fabricated sample; FC1: 50/50 Fiber-coupler

The interferometer used for measuring the fabricated samples with known thickness (section 5.1) is schematically depicted in Fig. 1(b). The lateral resolution was approximately 20 μm. The axial position of the reference mirror was adjusted so that the sample’s interfaces were imaged within the depth range of the spectrometer. A prism pair was used for compensating the group velocity dispersion (GVD) mismatch. The two galvanometric scanners were controlled by a field-programmable gate array (FPGA) (NI PCIe-7851R; National Instruments, Austin, TX, USA) for synchronizing with the acquisition. The setup used for the in vivo measurements was described in detail elsewhere [19].

The samples were fabricated as follows: crystalline silicon was first cleaned using acid solution (3 parts sulphuric acid + 1 part hydrogen peroxide) for 5 minutes. This was followed by a rinse in acetone, then a rinse in isopropanol, and finally drying in nitrogen. The resist used was SU-8 2000.5 (MicroChem, Westborough, MA, USA), diluted with cyclopentanone (Sigma-Aldrich, St. Louis, MO, USA), to a ratio of 1:2. The diluted resist was spin coated on to the silicon substrate for 35 s at different speeds for each sample (8933, 3254 and 1802 RPM for samples A, B and C respectively). After spin-coating, the resist was cured (soft-baked) at 90°C for 60 s. For the lithography a Raith Voyager (Raith GmbH, Dortmund, Germany) system was used, and the resist was exposed with an electron dose of 2 μC/cm². After exposure, a second curing was required to cross-link the polymer chains in the exposed region. This was again performed at 90 °C, but this time for 90 s. The development solution was Microposit EC solvent (Rohm & Haas Electronic Materials, Philadelphia, PA, USA), used for 60 s, which dissolves the non-exposed regions. A rinse in isopropanol was used to stop the developer and remove any residue. Finally, the sample was placed on a 150°C hotplate for 2 minutes to hard-cure the polymer.

3. Theory

In section 3.1, a model of the reflectance of a thin film with monochromatic illumination is developed. Thickness-dependent modulations of the reflectance due to the constructive/destructive interferences are predicted. OCT uses a broad bandwidth light source and therefore the model of section 3.1 is not directly applicable. In section 3.5 we define a quantity called OCT reflectance that can be calculated from the OCT signal. Using the Parseval identity, we establish the link between the OCT reflectance, the spectral shape and the reflectance at each wavelength. Finally, in section 3.7, a model of the OCT signal of a reflector pair separated by a variable distance is derived.

3.1. Reflection coefficient and reflectance of a thin film with monochromatic illumination

Light reflection takes place at the interfaces between media. The Fresnel equations allow to compute the reflection coefficient r and the transmission coefficients t of a monochromatic electric field plane wave traveling from medium 1 to medium 2. At normal incidence, the Fresnel equations are written as [20]:

$$r_{12}=\frac{n_1-n_2}{n_1+n_2}$$ (1)

$$t_{12}=\frac{2n_1}{n_1+n_2}=r_{12}+1$$ (2)

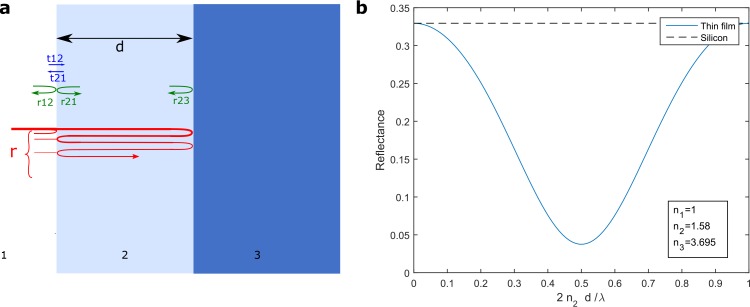
Consider a thin film of fixed thickness d deposited on a substrate. Let n₁, n₂ and n₃ be the refractive indices of the air, the film and the substrate, respectively (Fig. 2). Posing p = exp(i2π n₂2d/λ) and q = r₂₁r₂₃ p. The total reflection coefficient at normal incidence can be written as a series

$$r=r_{12}+t_{12}{r}_{23}p(1+q+q^2+q^3+\dots )t_{21}$$ (3)

Each term corresponds to a propagation path (Fig. 2(a)). The geometric series (1 + q + q² + q³ + ...) can be summed to 1/(1 − q), as |q| < 1. Eq. (3) is often called the Airy’s Formula [20] and is in agreement with other expressions of the reflection coefficient of a thin film layer found in the literature [21].

Fig. 2.

(a) Schematic diagram of a thin film of thickness d (medium 2) on a substrate (medium 3) and of the propagation paths contributing to the total reflection coefficient. (b) Reflectance at normal incidence of an SU-8 photoresist film deposited on a silicon substrate.

The reflectance R is given by the square-modulus of the reflection coefficient r:

$$R={\left|r\right|}^2$$ (4)

If the reflectance is plotted as a function of the film thickness, modulations corresponding to the constructive/destructive interferences are observed (cf. Fig. 2(b)). These modulations of the reflectance have a periodicity d_p of λ/(2n₂). For most of the OCT light sources, d_p is smaller than the axial resolution value. The basic idea of our approach is to exploit these modulations of the reflection coefficient in order to measure thicknesses below the OCT axial resolution.

The model of Eq. (3) is simplified and not unrestrictedely applicable to OCT because it considers monochromatic illumination while OCT uses light sources with a broad bandwidth. However, when the reflectors are in the coherent regime (below the resolution by definition), this model gives a good overview of the situation: the amplitude of the peak is modulated as a function of the thickness of the film.

3.2. Measured spectral array

In spectral domain OCT, the detection provides the spectral array s[m] which corresponds to discretization of the interferometer’s output power spectrum. The spectral array is composed of a sum of terms. Each term corresponds to a back-reflector pair in the interferometer. The expression of the spectral array is derived in the appendix A.2 and is written as

$$s[m]=a[m]\sum _{(k,l)\in D}{r}_k{r}_l^{*}\text{exp}\left(i\mathrm{\Delta }{\phi }_{kl}[m]\right)+n[m]$$ (5)

where D is the set of detected back-reflector pairs within the depth range of the spectrometer, a[m] is the spectral shape array corresponding to light source power spectrum, r_k is the reflection coefficient of the back-reflector k. The noise vector n[m] represents the different noise sources [22]. Each term of Eq. (5) is either resolved or in the super-resolution regime. Each resolved term corresponds to a distinct peak in the OCT amplitude signal.

3.3. OCT signal

The OCT signal is obtained after applying Fourier transformation to the rescaled measured spectral signal s[m] [23]. Here we use discrete-time Fourier transform (DTFT) [24]

$$\mathrm{\Gamma }(t)=\text{DTFT}\left\{s[m]\right\}=\sum _{m=0}^{M-1}s[m]e^{-itm}$$ (6)

where m = 0,...M − 1 is the spectrometer pixel index. The domain of the continuous variable t is [−π, π] rad/sample. The discrete Fourier transform (DFT) corresponds to a discretization of the DTFT. The OCT amplitude signal |Γ(t)| corresponds to the modulus of the complex-valued OCT signal Γ(t).

3.4. Spectral shape and point-spread function

Let a[m] be the light source’s spectral shape. The axial point spread function (PSF) A(t) corresponds to the Fourier transform of the spectral shape [23]:

$$A(t)=\text{DTFT}\left\{a[m]\right\}$$ (7)

According to the Fourier transform convolution theorem, the multiplication with a[m] in Eq. (5) corresponds to a convolution with A(t) in the OCT signal Eq. (6). The axial resolution (AR) is defined as the FWHM of the central lobe in A(t) [1].

Apodization (or windowing) and its effect on the AR, SNR and spectral leakage is investigated in the appendix A.1.

3.5. OCT reflectance

Consider a reflector pair formed by a reference mirror of constant reflectivity r₀ and a sample reflector with a reflectivity r₁[m]. The corresponding term in the measured spectral array can be written as [Eq. (5)]

$$s_1[m]=a[m]r_0^{*}{r}_1[m]\hspace{0.17em}\hspace{0.17em}\text{exp}\hspace{0.17em}\hspace{0.17em}\left(i\mathrm{\Delta }{\phi }_{01}[m]\right).$$ (8)

Let Γ₁(t) be the OCT signal corresponding to s₁[m]

$${\mathrm{\Gamma }}_1(t)=\text{DTFT}\left\{s_1[m]\right\}.$$ (9)

Using the Parseval equality [Eq. (23)], one gets

$$E_1=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{\left|{\mathrm{\Gamma }}_1(t)\right|}^{2}dt=R_0\sum _{m=0}^{M-1}a{\left[m\right]}^2{R}_1[m]$$ (10)

where R₀ = |r₀|² and R₁[m] = |r₁[m]|².

Equation (10) establishes the link between the integral of the squared OCT amplitude signal and the weighted sum of the spectral reflectance. To the best of our knowledge, this is the first time that the quantity E₁ is analyzed in the OCT field. In the following, E₁ will be referred to as OCT reflectance. As it can be shown that the contribution to the integral of Γ₁(t) is negligible outside a certain range, the OCT reflectance can be calculated from single resolved terms or mixture terms (i.e. terms in the super-resolution regime).

Matrix transfer theory can be used for modeling single wavelength reflectance R₁[m] of arbitrary thin film structures [20]. In section 3.1, we derived the reflectance R₁[m] of a single thin film corresponding to the fabricated samples. Details about the numerical computation of the OCT reflectance from the OCT signal measurement Γ₁(t) are provided in section 5.1.

3.6. Spectral phase accumulated through propagation of thickness d

In a weakly dispersing medium, the spectral phase Δφ[m] = k[m]d accumulated during propagation through a thickness d is linear in m [20]

$$\mathrm{\Delta }{\phi }_d[m]=2\pi \left(\frac{d}{d_0}+\frac{d}{d_1}m\right)=\varphi +\tau \hspace{0.17em}\hspace{0.17em}m$$ (11)

The pixel index is m = 0,...M − 1. The constant term ϕ ∈ [−π, π] corresponds to the phase. The coefficient multiplying m corresponds to the dimensionless group delay τ ∈ [−π, π]. Aliasing occurs if |τ| > π. The spectral phase accumulated propagating through several media is the sum of each medium’s contribution. The analytical expressions of the parameters d₀ and d₁ are derived in the appendix A.5. Briefly, d₁ is equal to the spectrometer depth range divided by the group index of the medium, and in air d₀ corresponds to the wavelength.

3.7. OCT signal of a reflector pair separated by a variable distance

In this section, the OCT signal corresponding to the interferometer shown in Fig. 1(a) is derived. Let term 1 correspond to interferences between the mirror M1 and the mirror M2 and let term 2 correspond to the interferences of each interface of the glass plate G. Using Eq. (5), the discrete spectral signal corresponding to these two terms can be written as

$$s_{12}[m]=s_1[m]+s_2[m]=a[m]\text{exp}\left(i\mathrm{\Delta }{\phi }^{(1)}[m]\right)\left[1+r_0\text{exp}\left(i\mathrm{\Delta }{\phi }^{(p)}[m]\right)\right]$$ (12)

Δφ⁽¹⁾[m] is the spectral phase difference associated with the term 1 [Eq. (11)], and Δφ^(p)[m] = Δφ⁽²⁾[m] − Δφ⁽¹⁾[m] = ϕ_p + τ_p m is the supplement of spectral phase of the term 2 relative to the term 1, r₀ is the ratio between the two terms’ reflectivity.

Using Eqs. (7) and (11), and the DTFT shifting theorem [Eq. (22)], one gets

$${\mathrm{\Gamma }}_{12}(t,d)=e^{i{\varphi }_1}\left(A(t-{\tau }_1)+r_0{e}^{i{\varphi }_p}A(t-{\tau }_1-{\tau }_p)\right)$$ (13)

Posing u = t − τ₁ and taking the square modulus of Eq. (13) leads to

$${\left|{\mathrm{\Gamma }}_{12}(u,d)\right|}^2={\left|A(u)+r_0{e}^{i{\varphi }_p(d)}A(u-{\tau }_p(d))\right|}^2$$ (14)

Equation (14) describes the OCT amplitude signal of two terms as a function of the distance d between the two corresponding peaks. In the next section, simulation and measurement of |Γ₁₂(u, d)|² will be compared.

4. Model validation

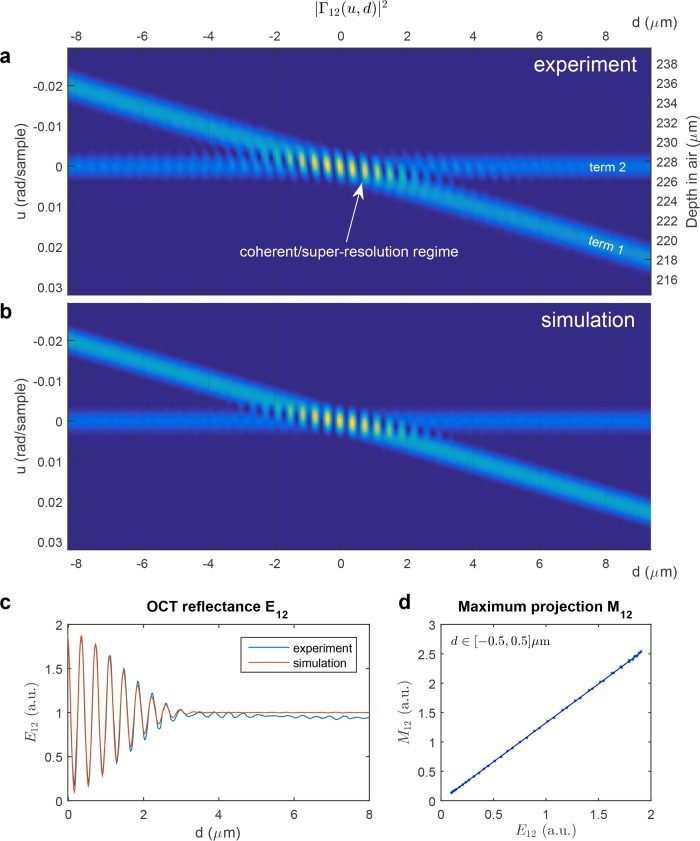
Figure 3(a) shows measurements of the OCT amplitude signal of two terms separated by a variable distance, obtained using the interferometer presented in Fig. 1(a). The term 1 physically corresponds to interferences between the mirror M1 and the mirror M2 and the term 2 corresponds to the interferences of each interface of the glass plate G (cf. Fig. 1(a)). One peak is fixed and another is moving, driven by a piezoelectric stack. When the peaks are in the super-resolution regime, they cannot be resolved based on the OCT A-scan; one mixture peak is formed and modulations of the OCT signal are observed. The quantity d corresponds to the equivalent air thickness separating the two OCT terms.

Fig. 3.

OCT signal of two terms in incoherent and coherent/super-resolution regime. d is the distance between the two peaks. (a) Experimental OCT signal measured with the interferometer presented in Fig. 1(a). The term 1 corresponds to interferences between the mirror M1 and the mirror M2 and the term 2 corresponds to the interferences of each interface of the glass plate G. One peak is fixed and another is moving, driven by a piezoelectric stack. (b) Simulated OCT signal according to the signal model presented in Eq. (14). (c) OCT reflectance $E_{12}={\int }_U{\left|{\mathrm{\Gamma }}_{12}(u,d)\right|}^{2}du$ as a function of the distance d in experiment and simulation (cf. section 3.5). (d) Comparison between the maximum projection M₁₂ = max_u |Γ₁₂(u, d)|² and the OCT reflectance E₁₂ in the region where d ∈[−0.5, 0.5] μm.

Figure 3(b) shows the corresponding simulated data according to the signal model of |Γ₁₂(u, d)|² formulated in Eq. (14). The axial PSF A(t) used in this model is estimated from the experimental data. To estimate A(t), the power spectrum was averaged to obtain a vector, then low-pass filtering was applied and Eq. (7) was used to obtain the axial PSF. The phase ϕ_p(d) and the dimensionless delay τ_p(d) in Eq. (14) were calculated using the estimated traveled distance, obtained from the calibration of the delay axis and using the results for the parameters d₀ and d₁ obtained in the appendix A.5. A good agreement between simulation and experiment can be observed. Analyzing the signal model in Eq. (14), one can see that the modulations are driven by the phase difference between the two terms ϕ_p(d) = ϕ₂ − ϕ₁(d). Without the phase factor e^iϕ_p(d) in Eq. (14), no modulation would be present.

In Fig. 3(c), curves of the OCT reflectance $E_{12}={\int }_U{\left|{\mathrm{\Gamma }}_{12}(u,d)\right|}^{2}du$ as a function of the distance d between the two peaks in experiment and simulation, respectively, are shown (cf. section 3.5). When the peaks are in the super-resolution regime, modulations of the OCT reflectance are observed.

In Fig. 3(d), a comparison between the maximum projection M₁₂ = max_u |Γ₁₂(u, d)|² and the OCT reflectance E₁₂ is presented. The comparison is performed using the simulated data in the region d ∈[−0.5, 0.5] μm. It can be seen that in this region, M₁₂ and E₁₂ are almost proportional (r² = 0.9999). Later in this paper, this maximum projection estimator will be used, because it offers a much shorter computation time than E₁₂ (cf. section 5.1).

Although the spectral phase used in the model is simplified, it accurately describes the OCT signal in coherent and incoherent regimes. Good agreement between experimental data [Fig. 3(a)] and simulation [Fig. 3(b)] is observed. The main difference between both data sets is a slight tilt of the isoamplitude curves in the experimental coherent regime area, while in the simulation they are perfectly vertical. We believe that this is due to the fact that in the experiment, slight second order dispersion occurs in the glass plate, which is not considered in the simulations as the spectral phase formula given in Eq. (11) takes only the zero and first order dispersion terms into account. The OCT reflectance curves seem, however, not to be influenced much by this slight second order dispersion. The domain of integration U corresponds to the range u ∈ [−0.03, 0.03]. The modulation of the amplitude of the mixture peak in the coherent regime is consistent with the modulation of the reflectance as a function of the thickness with coherent illumination presented in section 3.1.

5. Results

5.1. Measurements of thin film samples

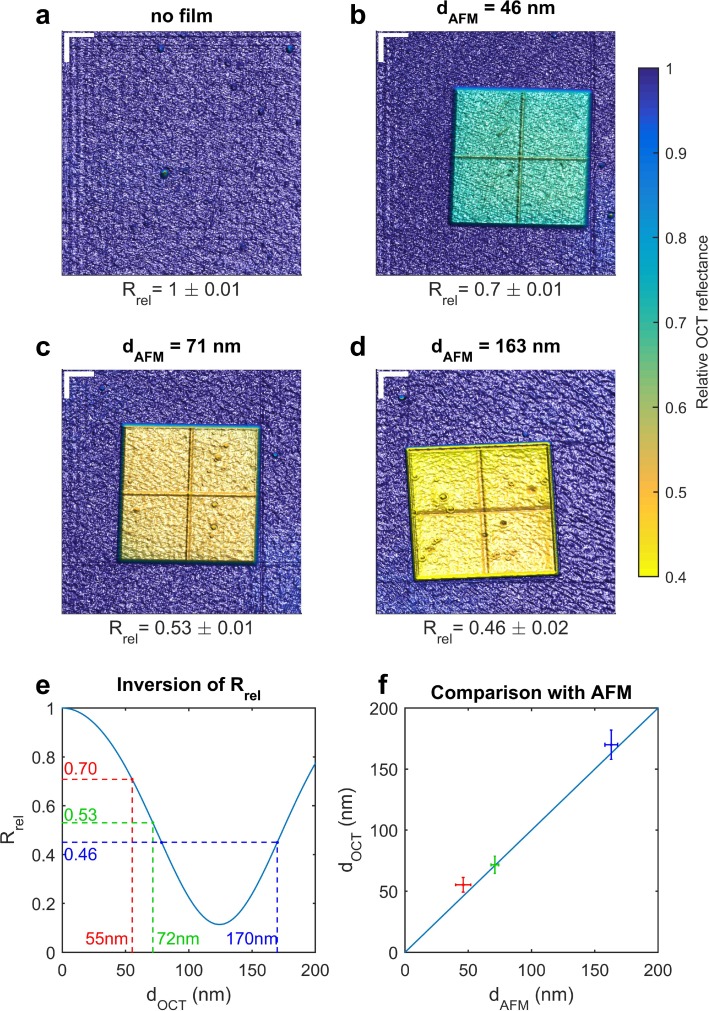
Several fabricated samples with a photoresist film (SU-8) of known thickness and refractive index were imaged. The thickness of this film layer is below the OCT resolution limit of the system. The reference thicknesses were measured using an AFM. A contrast difference of the OCT reflectance of the different samples can clearly be observed comparing the measurements in Fig. 4. These results indicate that the OCT reflectance can be used to visualize thickness maps below the axial resolution limit.

Fig. 4.

(a–d) En face OCT reflectance maps of fabricated samples: (a) silicon substrate only, (b–d) island of SU-8 photoresist film (1 mm × 1 mm) deposited on silicon substrate. Film thicknesses are (b) 46 ± 6 nm (b) 71 ± 2 nm (c) 163 ± 5 nm, as measured with the AFM (mean ± roughness). Comparing the maps (b–d), differences in the OCT reflectance can clearly be observed. (e) Inversion of R_rel to obtain the OCT thickness value. (f) Comparison between the AFM and OCT thicknesses values. Error bars correspond to OCT thickness uncertainty (vertically) and to AFM roughness (horizontally). Lateral scale bar (top-left corner in Fig. 4(a–d)) corresponds to 225 μm. The color scale is the same for each sample. The cross seen on the islands is an artifact of the fabrication process.

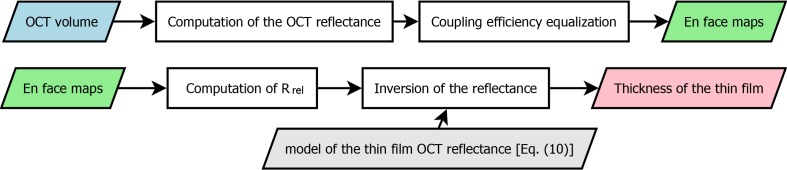
The computation of the OCT reflectance as defined in the left member of Eq. (10) is heavily time consuming as it requires numerical computation of the integral of a continuous function. Several approaches can be used to decrease the computation time. Firstly, Fast Fourier Transform (FFT) can be used instead of DTFT, for which the Parseval identity is written as a sum instead of an integral [24]. Secondly, it can be shown that in the super-resolution regime, the OCT reflectance E₁ is proportional to the maximum value of |Γ₁(t)|² (see Fig. 3(d)). Therefore, for a small thickness, computing only the maximum projection of the squared OCT amplitude signal might be used as a fast estimator of the OCT reflectance. For obtaining the en face OCT reflectance maps in Fig. 4, we used this fast maximum projection estimator applied to DTFT. The full spectrum was used to calculate the OCT reflectance of these samples. Two-pass coupling efficiency equalization was applied to the raw en face reflectance measurements. The goal of this processing step was to obtain uniform OCT reflectance maps by compensation of the spatial variation of the coupling efficiency. This processing step assumes that the coupling efficiency γ(x, y) is a product function (γ(x, y) = X(x)Y(y)). The raw reflectance function was divided by the estimated coupling efficiency along each direction. The coupling efficiency along one direction was estimated using the median in one band with a width of 30 pixels for the first-pass and of the whole background for the second-pass. The last step consisted of dividing the OCT reflectance map by the median background reflectance in order to compare the different measurements with a single colorscale. Even with this equalization, some fluctuations due to galvo-scanner motion can be seen in the left part of Fig. 4(a–c). In Fig. 4(a–d), 3D-rendering of the maps is depicted and a single colorscale is used for all images. The relative OCT reflectance median value R_rel was calculated by dividing the median reflectance of the sample by the median reflectance of the background. This calculation of R_rel is done automatically. The standard deviation of the relative OCT reflectance over the thin film island is indicated after the R_rel value and is influenced by inhomogeneity of the sample. The cross seen in the middle of the islands is an artifact due to the fabrication process. In Fig. 5, the post processing steps needed for generation of the en face OCT reflectance maps depicted in Fig. 4(a–d) and for obtaining the thickness values are shown.

Fig. 5.

Flowchart of the processing steps to obtain the maps depicted in Fig. 4 and the thickness of each thin film.

AFM measurements were carried out using a JEOL SPM-5200 and silicon cantilever probes from Bruker (TESP). The scan area was 25 × 25 μm² and included the border of the probes in order to measure the thickness as the height difference between the substrate and the film top. The instrument calibration was used in order to convert the AFM signal into a thickness. Fig. 4(e) shows the OCT thickness measurement using the inversion of the OCT reflectance model, which is build using the right member of Eq. (10). In Fig. 4(f), the comparison between the AFM and OCT measured thickness is presented. The error bars of the AFM thickness measurements correspond to the measured roughness on the scanned area. The error bars of the OCT thickness measurements correspond to the estimated uncertainty of the measurements. The uncertainty on the OCT thickness was estimated using the uncertainty propagation formula and assuming uncertainties of 0.01 on refractive indices of the film and substrate and of 15 nm on the spectrometer calibration and taking the uncertainties on the measured OCT reflectance and on surface roughness into account. The influence of the surface roughness on the Fresnel reflection coefficient can be modeled using the Debye - Waller factor [16], and was used for calculating the uncertainty. Taking the uncertainties into account, the AFM and OCT thickness are in agreement [Fig. 4(f)].

The OCT reflectance shows a strong dependence on the film thickness but its inversion is a difficult problem. As we will see in the next section, the range for which the OCT reflectance can be easily inverted is one period of oscillation d_p = λ_c/(2n₂). In our current approach, a priori knowledge about the thickness range of the layer is used in order to obtain the thickness from OCT. We assumed that the measured thin film samples had thicknesses in the range [0,250] nm.

5.2. Post-processing wavelength-swept reflectometry

In the last section, we showed maps of the OCT reflectance calculated with the full broadband light source’s spectral shape [Fig. 4]. In post-processing, using several narrower spectral bands, one can gain additional information about the spectral dependence of the OCT reflectance. We will see that this spectral dependence can easily be used to exclude thickness aliases in the thickness range [0, λ_c/(2n₂)].

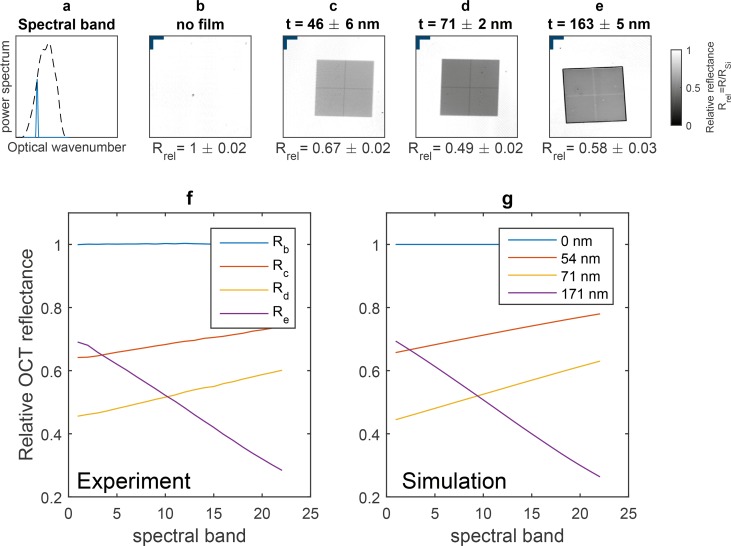
To investigate the spectral dependence of the OCT reflectance, we compared simulations of OCT reflectance to the measured spectral dependence. Twenty-three spectral bands covering the whole light source’s spectral shape were successively used to compute the OCT reflectance maps of each sample. The results for one of these spectral bands are shown in Fig. 6(b–e), for 4 different samples. The used spectral shape is indicated by the blue smooth curve in Fig. 6(a). The comparison of simulations and measurements of the OCT reflectance spectral dependence is shown in Fig. 6(f–g). The spectral band sweeping on the OCT reflectance is presented in the attached [ Visualization 1 ^{(1.6MB, AVI)} ].

Fig. 6.

Post-processing wavelength-swept optical coherence reflectometry ( Visualization 1 ^{(1.6MB, AVI)} ). (a) Dashed curve, full light source’s spectral shape; smooth blue curve, narrower spectral band used for calculating the OCT reflectance. (b) Silicon substrate with (c) 46 ±6 nm, (d) 71 ±2 nm and (e) 163 ±5 nm photoresist film layer. (f) Measured relative OCT reflectance as a function of the spectral band. (g) Simulation of the OCT reflectance spectral dependence for each thickness indicated in the legend. Lateral scale bar (top-left corner in Fig. 6(b–e)) corresponds to 225 μm.

In the thickness range [0, λ_c/(2n₂)], each thickness can be associated with a single thickness alias (i.e. another thickness with the same full-spectrum OCT reflectance value). The spectral dependence of the OCT reflectance can be used to discriminate these aliases. To illustrate, consider the sample with 163 nm AFM thickness, which has a relative OCT reflectance value of 0.46. In the range [0, λ_c/(2n₂)], this OCT reflectance value corresponds to 78 nm and 170 nm. Investigating the experimental data, one observes that the measured OCT reflectance is decreasing with spectral band number [R_e in Fig. 6(f)], therefore one can exclude 78 nm, as its OCT reflectance increases with spectral band number [Fig. 6(g)]. This approach can also be applied to other thickness ranges, as for example [λ_c/(2n₂), λ_c/n₂].

5.3. In vivo visualization of the tear film lipid layer

In the conventional model, the tear film is composed of three layers [25]. The mucous layer contains the cornea-spanning glycocalyx and soluble mucins of different origins. The middle layer, the aqueous layer, consists of water, proteins and electrolytes mainly secreted by the lacrimal glands [26]. It is 3 – 8 μm thick in healthy subjects. The lipid layer is the outermost layer and is in direct contact with the air. Meibomian glands located at the inner rim of the eye lids produce the meibum, a mixture containing cholesterol esters and wax esters [27]. Since these molecules are hydrophobic in nature, they alone would not be able to coat the aqueous layer due to surface tension, but form droplets [28]. Phospholipids or (O-acyl)-ω-hydroxy fatty acids (OAHFAs) could work as a surfactant and make a thin spread possible [29].

The functions of the tear film lipid layer have not yet been fully elucidated. Although for a long time it has been accepted that its main purpose is retarding evaporation [30], in vitro studies struggle to affirm this [29, 31]. Nevertheless, the lipid layer is suspected to play a role in evaporative dry eye [30, 32]. The stability-providing function of the lipid layer is especially interesting and research on the viscoelastic properties of the lipid layer do not seem to support the anti-evaporation theory [33].

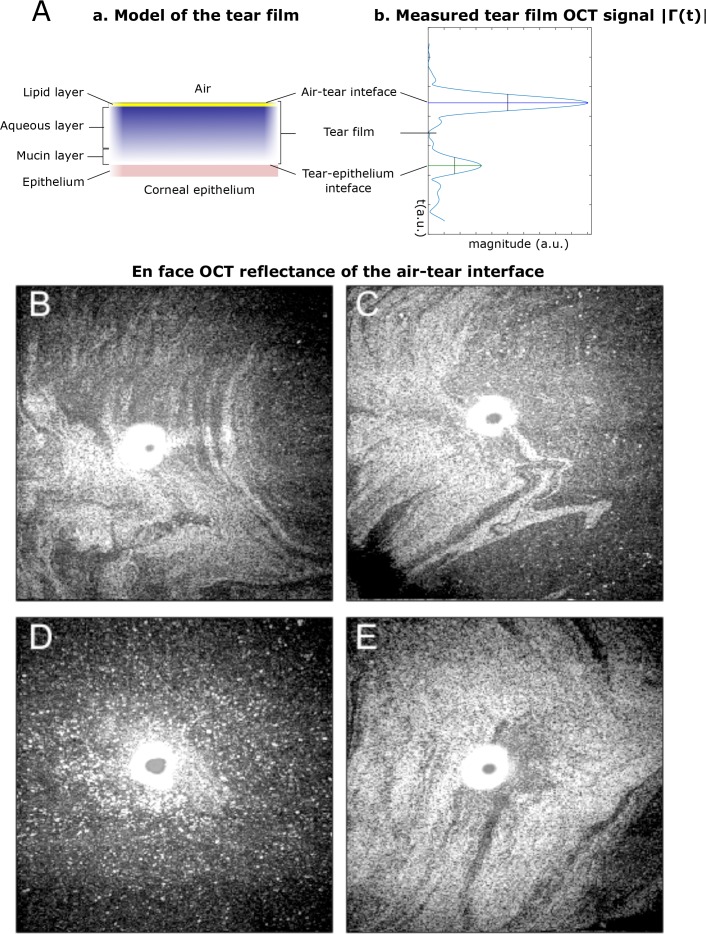
While the aqueous layer can be resolved with OCT [18, 19], the lipid layer, which has a thickness estimated to be in the range 40 – 80 nm [34, 35] cannot be resolved. The lipid of the tear film has a refractive index estimated to be 1.482 [36], while the aqueous layer has a refractive index close to 1.333 at 800 nm [19].

We acquired 10 volumes of 256 × 256 × 2048 voxels corresponding to 4 × 4 × 1.2 mm³ within approximately 12 s, in 4 different subjects in vivo. For each volume, we calculated the full-spectrum OCT reflectance of the air-tear interface peak using the maximum projection estimator presented above. The maps are shown in log scale. Videos of the measured OCT reflectance in the successive volume can be found in the attached Visualization 2 ^{(1.4MB, AVI)} , Visualization 3 ^{(1.4MB, AVI)} , Visualization 4 ^{(1.4MB, AVI)} , and Visualization 5 ^{(1.4MB, AVI)} .

In Fig. 7(B–E), the OCT reflectance of a single volume is presented for each subject. Light and dark areas corresponding to higher and lower OCT reflectance can be observed. Over the range 0 – 125 nm, the reflectance is a monotonous function of the lipid thickness [9]. Thus, if one assumes locally constant coupling efficiency, the OCT reflectance maps indicate the local variation of the lipid quantity. These patterns are similar to the ones observed with other interferometric techniques [9,37]. In OCT, the coherence gating allows to select the contribution of the air-tear interface only and filter out the contribution of the deeper layers of the cornea. The white zone in the center of each image corresponds to a zone where the camera is saturated. We believe that the white dots in Fig. 7(D) correspond to small bubbles, as also reported recently by Braun et. al [31].

Fig. 7.

(A) Comparison between a model of the tear film layers (a) and an in vivo OCT A-scan of the tear film (b). (B–E) In vivo measurements of the raw en face OCT reflectance (in log scale) of the air-tear interface obtained from the front surface of the central cornea in 4 healthy subjects (4 × 4 mm²). Observation of the lipid layer of the tear film, which has a thickness below 150 nm, far below the OCT axial resolution value of 1.2 μm. ( Visualization 2 ^{(1.4MB, AVI)} , Visualization 3 ^{(1.4MB, AVI)} , Visualization 4 ^{(1.4MB, AVI)} , and Visualization 5 ^{(1.4MB, AVI)} ).

To obtain quantitative lipid layer thickness measurements, the measured OCT reflectance value needs to be converted to an absolute thickness value. Results presented in Fig. 4 show that this is possible for thin film samples in vitro. To transfer this approach to the in vivo situation might be possible in the future, but requires some additional work. After coupling efficiency equalization, there is still a global unknown factor linking the reflectance measured via OCT to the modelled OCT reflectance of the lipid layer. To determine this factor, one would need either to know the exact back-coupling of the cornea, or to assume that there is a point with known thickness (e.g. where lipid layer thickness equals zero), which currently cannot be assumed free of doubt. The measurement of a cornea-shaped interface of known reflectance could be used to obtain the unknown factor. An alternative way to overcome this problem would be to use another interface within the cornea as reference signal. The investigation of the feasibility of this approach does, however, require further in vitro and in vivo studies.

6. Discussion

In this paper, we describe the visualization of super-resolved structures in OCT. Using a contrast mechanism based on sample OCT reflectance, features with thicknesses smaller than the axial resolution value of the system can be visualized.

The model of the OCT signal of two terms in the super-resolution regime [Eq. (14)] was compared to the experiment. We observed a good agreement. Our model predicts that in the super-resolution regime, modulation of the OCT reflectance occurs, driven by the phase difference between the two terms. To the best of our knowledge, this is the first time that the OCT signal is analytically investigated in the super-resolution regime. Using the Parseval identity, we established the link between the OCT reflectance that can be calculated from the OCT amplitude signal and the single wavelength reflection coefficient that can be modeled using matrix transfer theory. This model allows us to predict the OCT reflectance value of any thin film structure. The OCT signal measurements in super-resolution regime obtained using our interferometer [Fig. 1(a)] are in agreement with recently reported measurements of the air wedge between two glass surfaces [38].

Measurements of fabricated thin film samples of known thickness and refractive index were performed. The samples appeared with uniform relative OCT reflectance corresponding to their uniform thickness [Fig. 4(b–d)]. Thickness contrast visualization has been demonstrated. To determine if quantitative thickness measurement could be performed, a model of the OCT reflectance, requiring a priori knowledge about the refractive indices of the samples, was used. The inversion of the modeled OCT reflectance yielded values close to those measured by the AFM [Fig. 4(f)]. These in vitro experiments indicate that structures can be visualized below the OCT axial resolution limit and that the relative OCT reflectance can be used for quantitative thickness measurements. Limitation of these measurements are discussed in a later paragraph.

In vivo measurements of the precorneal tear film showed that qualitative contrast of the lipid layer can be obtained [Fig. 7]. Multiple volumes were successively acquired and analysis of the reflectance provided similar lipid layer maps over time. To the best of our knowledge, this is the first time that en face visualization of the tear film lipid layer in vivo using OCT is reported. Quantitative lipid layer thickness measurement would require coupling efficiency equalization and the inversion of the OCT reflectance model. Recently, Napoli et al. [39] used a lipid-based tracer, containing an oil-in-water emulsion to enhance the OCT signal of the lower tear meniscus.

Using a maximum likelihood (ML) approach, Huang et al. [40] proposed an algorithm for super-resolved OCT measurement and applied it to an in vitro tear film phantom measurement. To the best of our knowledge, our approach based on measurements of the OCT reflectance to obtain super-resolved thickness maps is new in the OCT field. Our lipid layer maps are similar to the ones obtained with colorimetric [41, 42] and reflectometric approaches [9, 37]. OCT provides two advantages in comparison to the other reported methods for visualizing the lipid layer. Firstly, the coherent amplification of the sample reflectivity by the reference mirror reflectivity helps to increase the sample SNR [43]. Secondly, thanks to the coherence gating, OCT allows to select the contribution of the air-tear interface only and to eliminate contributions of the deeper layers of the cornea. Bousi et al. [44] reported deconvolution methods applicable to time-domain OCT [45] and to swept-source OCT. Deconvolution is used to inverse the convolution with the PSF in the OCT signal [cf. Eq. (5) and Eq. (7)]. Liu et al. [46] reported two-dimensional deconvolution methods to deblur OCT images. Recently, Liu et al. [38] reported on the use of an auto-regressive-moving-average spectral analysis technique for obtaining axial super-resolution of the OCT signal. This approach allows decreasing the width of the peaks by a factor of approximately 4.7, but requires to have uniform spectral shape and sufficient SNR. The equalization of the spectral shape can lead to decreased SNR, as discussed in the appendix A.1.

Further development of the algorithm is needed for automated quantitative thickness measurement over the whole range of possible layer thicknesses. As we showed, our approach allows to obtain the thickness from OCT over a range of lengths λ/(2n₂), known a priori. The combined use of spectral analysis (e.g. Burg, Yule-Walker methods etc.) for improving axial resolution with our approach could potentially be used for quantitative thickness measurement over the whole range of thicknesses. However, the application seems to be limited to well-defined structures with a known number of terms and not to complex scattering tissues with speckle.

The discrepancy between the retrieved thickness and the AFM reference thickness can be explained by the measurement uncertainties and by the influence of the surface roughness, which is also a problem in reflectometry [16]. However, we believe that due to spatial coherence, the influence of surface roughness is even stronger in OCT as compared to measurements with a thermal light based setup. If the wavefront is modified by the roughness of the surface, the coupling efficiency and, thus, the measured reflectance decreases [47], which is a limitation of the method for measuring the thickness of rough samples.

Further steps for the presented approach include the comparison of our lipid layer maps with the measurements obtained with a commercial system (Lipiview, TearScience Inc., Morrisville, NC, USA). Furthermore, the model [Eq. (14)] will be improved for including higher dispersion orders and to allow the imaging of more than two reflector pairs. Finally, the OCT signal phase, which is left unused by our approach could also be employed for thickness estimation.

7. Conclusion

In conclusion, we presented thickness measurements below the OCT axial resolution limit. Our approach allowed for a quantitative thickness measurement of fabricated samples and qualitative measurements of the tear film lipid layer in vivo. Our results provide a novel interpretation of the OCT axial resolution limit and open a perspective to extract information hidden in the coherence volume.

A. Appendix

A.1. Apodization vs. axial resolution and SNR

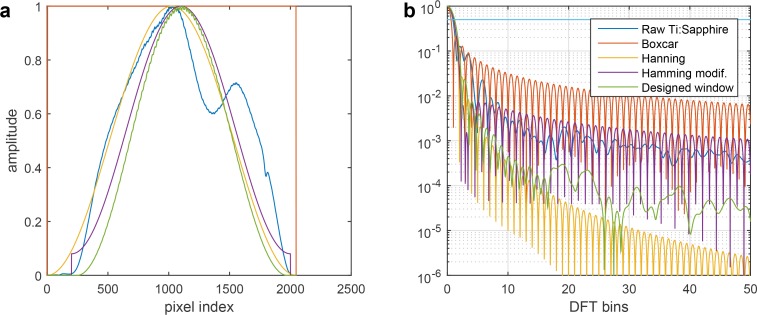
The axial PSF A(t) has one main lobe which FWHM corresponds to the axial resolution but it has also some sidelobes, which can cause artifacts in the image and impair the contrast. Apodization (or spectral windowing) can be used to decrease the level of sidelobes. However apodization is often done at the expense of impairing the axial resolution. Apodization consists of multiplying the measured spectral signal by an appropriate window before doing the Fourier transformation that leads to the OCT signal. The sidelobes are a consequence of the spectral leakage, which occurs because of the finite-range of the analyzed signal [48].

We analyzed the effect of apodization on several quantities. Table 1 contains the axial resolution value (FWHM), the highest sidelobe level and the mean SNR in a test measurement of the different windows we considered. The values of the axial resolution and sidelobe level were calculated using our custom Matlab script. The calculated values of the Boxcar, Hanning and Hamming windows were compared with the literature [24, 49] and a very close agreement was found. The mean SNR was calculated as the average SNR of the air-tear interface in 9 in vivo measurements of the central cornea composed of 512 B-scans, each composed of 1024 A-scans. For each tested single B-scan, the ranking of the windows according to SNR performance was the same. The best SNR is obtained with the raw spectrum of the light source (Raw Ti:Sapphire in Fig. 8). The sidelobe levels are, however, poor with the raw spectrum [Fig. 8(b), Table 1].

Fig. 8.

Spectral shape and axial PSF A(t) (a) Spectral shapes investigated. (b) Corresponding axial PSF A(t).

Table 1.

Analysis of the effect of windowing on the axial resolution, the highest sidelobe level and the average SNR of a test measurement. The FWHM axial resolution is expressed in DFT bins. The measured spectral array is multiplied in order to obtain the following window. Raw: raw Ti:Sapphire spectral array; Boxcar: 2048-pixels rectangular window; Hann.: 2048-pixels Hanning window; Hamm.: 2048-pixels Hamming window; Hamm. cent. : 1800-pixels Hamming window centered on the raw spectrum.; Designed wind. : designed window based on a modified Hanning window used for most of the experimental measurement presented in this paper.

	Raw	Boxcar	Hann.	Hamm.	Hamm. cent.	Designed wind.
FWHM (DFT bins)	1.78	1.21	2.00	1.81	2.07	2.21
1-sidelobe level (dB)	−18	−13	−31	−41	−41	−31
Test SNR (dB)	64.4	44.3	59.7	50.3	62.4	63.6

To decrease the level of sidelobes without impairing axial resolution, one might be tempted to correct the measured spectrum in order to get, for example, a Hamming spectral shape, which provides a good axial resolution and low highest-sidelobe level [Table 1]. However signal amplification in the low intensity zone will lead to a decrease of the SNR in the image (−15.1 dB in comparison with raw spectrum) [Table 1]. No window is perfect and a compromise has to be found between the level of sidelobes, the axial resolution and the SNR. A good compromise is provided by the spectrum-centered Hamming window, which yields slightly impaired axial resolution (2.07 bins), low highest-sidelobe level (−41 dB) and a good SNR (−2.0 dB in comparison with the raw spectrum), however, the long-range sidelobe level is high [Fig. 8(b)]. We used a spectrum-centered Hanning window, which provides a slightly impaired axial resolution (2.21 bins), but better long-range sidelobe level and SNR (−0.8dB in comparison with the raw spectrum).

A.2. Detected spectral array

Let H(ω) be the frequency response of the interferometer. Using H(ω), the complex electric field at the output E_out(ω) can be linked to the complex electric field at the input E_in(ω)

$$E_{\mathit{out}}(\omega )=E_{\mathit{in}}(\omega )H(\omega )$$ (15)

where ω is the optical angular frequency. H(ω) can be decomposed as a sum of terms

$$H(\omega )=\sum _{j\in B}{r}_j(\omega )\hspace{0.17em}\hspace{0.17em}\text{exp}(i{\phi }_j(\omega ))$$ (16)

B = {back-reflectors of the interferometer}, r_j(ω) is the reflection coefficient and φ_j(ω) is the spectral phase of the back-reflectors j. The output power spectrum S_out(ω), which is proportional to |E_out(ω)|² can be written as

$$S_{\mathit{out}}(\omega )=S_{\mathit{in}}(\omega ){\left|H(\omega )\right|}^2$$ (17)

Using Eq. (16), one gets

$$S_{\mathit{out}}(\omega )=S_{\mathit{in}}(\omega )\sum _{(i,j)\in B^2}{r}_i(\omega )r_j{\left(\omega \right)}^{*}\hspace{0.17em}\hspace{0.17em}\text{exp}\left(i\left[{\phi }_i(\omega )-{\phi }_j(\omega )\right]\right)$$ (18)

The discretisation of Eq. (18) leads to

$$s[m]=a[m]\sum _{(k,l)\in D}{r}_k[m]r_l{\left[m\right]}^{*}\hspace{0.17em}\hspace{0.17em}\text{exp}\left(i\mathrm{\Delta }{\phi }_{kl}[m]\right)+n[m]$$ (19)

where m = 0,... M − 1 is the pixel index. Low-pass filtering is physically applied before discretization, because of the finite spectral resolution of the detection [40]. This low-pass filtering leads to a finite depth range [1]. Therefore, not every reflector pair contributes to the measured spectral array. The spectral shape a[m] corresponds to the discretization of the input power spectrum. n[m] is the noise vector and models the different additive noise sources corrupting the measurement [22].

A.3. Depth range of the spectrometer

The domain of the continuous variable t in the DTFT of the OCT signal [Eq. (6)] is [−π, π] rad/sample [24]. The angular optical frequency vector can be written as ω[m] = ω_min + m δω. The optical delay τ_o is linked to t according to the following relationship τ_o = t/δω. Thus, the air depth range is

$$z_{\mathit{air}}\in \left[-c\pi /\delta \omega ,c\pi /\delta \omega \right].$$ (20)

Then, the expression of the full depth-range in air (FDR) is

$$\mathit{FDR}=c\hspace{0.17em}\hspace{0.17em}2\pi /\delta \omega$$ (21)

A.4. DTFT basic properties

The DTFT shifting theorem states that [24]

$$\text{DTFT}\left\{e^{i{t}_{0}m}a[m]\right\}=A(t-t_0).$$ (22)

For the DTFT as defined in Eq. (6), the Parseval’s equality can be written as

$$\sum _{m=0}^{M-1}{\left|x\left[m\right]\right|}^2=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{\left|X(t)\right|}^{2}dt$$ (23)

where DTFT{x[m]} = X(t).

A.5. Spectral phase characteristic lengths

The spectral phase accumulated through propagation of thickness d in a medium of optical wavenumber k(ω) can be written as

$$\mathrm{\Delta }\phi =k(\omega )d$$ (24)

In a weakly dispersing medium, the dispersion relation k(ω) = n(ω)ω/c can be written as a linear function of ω

$$k(\omega )=k_0+k_1(\omega -{\omega }_0)$$ (25)

where ω₀ is the central angular frequency of the power spectrum. One has k₀ = 2πn₀/λ and k₁ = N_g/c, where n₀ and N_g are respectively the refractive index and the group index at ω₀ [20].

The spectrometer calibration provides the optical frequency ω[m] associated with each pixel m = 0,... M − 1

$$\omega [m]={\omega }_{\mathit{min}}+m\hspace{0.17em}\hspace{0.17em}\delta \omega$$ (26)

the samples are uniformly spread over the frequency axis and separated by δω (after rescaling).

The d-dependence of the discrete spectral phase can be written as

$$\mathrm{\Delta }{\phi }_d[m]=2\pi \left(\frac{d}{d_0}+\frac{d}{d_1}m\right),$$ (27)

where d₀ and d₁ are the characteristic lengths of the zero order and first order. Using Eqs. (24), (25), (26) and (27), one can obtain the expressions of the characteristic lengths:

$$d_0=\frac{2\pi }{k_0+k_1({\omega }_{\mathit{min}}-{\omega }_0)}.$$ (28)

In vacuum (n(ω) = 1), the expression of d₀ can be simplified to d₀ = λ_min.

For the first order, one obtains

$$d_1=\frac{2\pi }{\delta \omega \hspace{0.17em}\hspace{0.17em}{k}_1}=\frac{2\pi \hspace{0.17em}\hspace{0.17em}c}{\delta \omega \hspace{0.17em}\hspace{0.17em}{N}_g}=\frac{\mathit{FDR}}{N_g},$$ (29)

using the definition of k₁ and Eq. (21). One sees that d₁ corresponds to the expression of the full depth-range (FDR) divided by the group index of the medium N_g.