Learning layer-specific edges for segmenting retinal layers with large deformations

Abstract

We present an algorithm for layer-specific edge detection in retinal optical coherence tomography images through a structured learning algorithm to reinforce traditional graph-based retinal layer segmentation. The proposed algorithm simultaneously identifies individual layers and their corresponding edges, resulting in the computation of layer-specific edges in 1 second. These edges augment classical dynamic programming based segmentation under layer deformation, shadow artifacts noise, and without heuristics or prior knowledge. We considered Duke’s online data set containing 110 B-scans of 10 diabetic macular edema subjects with 8 retinal layers annotated by two experts for experimentation, and achieved a mean distance error of 1.38 pixels whereas that of the state-of-the-art was 1.68 pixels.

1. Introduction

In the recent practice of ophthalmology, spectral domain optical coherence tomography (SD-OCT) has attained a crucial place for early diagnosis of pathologies [1,2]. SD-OCT acquires cross-sectional information regarding the retina and cornea at µm resolution [3]. This helps in the early diagnosis and prognosis of diseases through analyzing layer-width profiles [4–6]. Visually delineating the OCT image and keeping track of the width profiles along each image in a 3D stack is a burden on ophthalmologists. To reduce this burden, automated layer delineation approaches compute the width profiles along each column of the OCT image [7, 8]. This transforms a 3D stack to width maps, which are clinically referred to as the retinal nerve fiber layer (RNFL) quadrants, and clock hours. Such automated width maps allow ophthalmologists to select a representative image for diagnosis [9]. There has been growing interest in the exploration of multiple retinal layers for mapping the individual layer width or the relation between the layer widths to various pathologies [6,10]. This resulted in the need for more robust delineation algorithms that can handle layers that have a similar intensity as their adjacent layers and deviations of the layer information (morphology and intensity) due to pathology, higher-order noise, etc [11,12].

The delineation of retinal layers is a challenging and evolving problem in biomedical image processing. Numerous approaches have been proposed, ranging from the A-scan to graph-based retinal layer segmentation [13,14]. Graph-based approaches [15–18], especially dynamic programming approaches, have been widely employed due to their performance, limited computational complexity, and resilience to noise.

Conventional graph-based retinal delineation algorithms vary, based on the features [18,19], heuristics [13], and regularizer [19,20], that are used to construct the graph edges. Such edges are used to find the shortest path from the extreme left node to the extreme right node on the image graph through dynamic programming.

The fundamental graph approach [15], treats vertical gradients as edges and uses heuristics (viz., the layer arrangement and average width) to constrain the search space of dynamic programming. A method based on the fuzzy search space with a shape regularizer has demonstrated an improved performance with shadowed artifacts spanning a few A-scans [19]. Alternatively, iterative layer delineation has been proposed for exhaustive layer delineation in low-computational facilities [17]. Moreover, limiting the search space through traditional heuristics results in failed delineation due to the emergence of less frequent patterns. To accommodate all patterns, graph edges are learned through probabilistic graphical models which have an intrinsic regularizer; however, they fail when the layers incur large deformations [20]. Diabetic macular edema (DME) is one such pathological condition with greatly deformed layers. Recently, kernel regression has been employed for feature quantification in order to model various layers through support vector machines (SVM) to strengthen fundamental graph approach [15]; this has resulted in improved performance for cases with deformed layers [18]. Kernel regression surpassed previous methods in terms of layer segmentation in DME subjects, and its performance is regarded to be comparable with state-of-the-art methods [18]. Moreover, recent and successful approaches have employed learning or modeling of image graph edges [18–20].

The majority of learning approaches for retinal-layer segmentation or delineation are anchored around classical learning methods (e.g., SVM and random forests). However, such algorithms are designed for single value prediction and are not suitable for 2D space (image) predictions. This lead to structural learning methods (structured SVM and structured random forests) and resulted in improved image segmentation [22], and image edge detection [23]. Structured random forests [24], have been widely employed for structural learning and displaying optimal structural risk minimization along with all the qualities of random forests, including robust to irrelevant data, missing data, and noise in data. It also holds advantage over structured SVM when provided ample amount of data. The approach proposed in this paper equips classical image edge learning [23], to predict object specific edges, because it has been established that such integration improves multi-object segmentation [21]. The resulting algorithm can predict the object type as well as the edge. Such information avoids fusion of edges from different layers, suppresses artifact induced edges, shows resilience to shadow artifacts, prevents dynamic programming from jumping (between layers) across paths in case of feeble layers, and latches on to the edge even under large deformation. For current applications, the proposed algorithm models layer-specific edges as opposed to modeling the edges of all layers. It is to be noted that a layer-specific edge implies only the contour (i.e., upper boundary) of a layer.

Graph-edge learning methods involve predicting layers, from which the graph edges are then computed. However, the proposed approach predicts the layer edges, therefore the layer edge can be treated as a graph edge for dynamic programming without the inclusion of such computations. The learned edge is compatible with any off-the-shelf graph optimization algorithms. In other words, the proposed approach reinforces the existing graph optimizers, and it should not be considered as a competitive alternative. For experimentation, Duke University’s Retina OCT Data set [18], was used to evaluate the proposed algorithm against a dynamic programming-based segmentation approach (AN) where the image graph edges are constructed based on vertical gradients [15]. The kernel regression-guided dynamic programming algorithm (AD) [18], is another algorithm that is considered for the evaluation, because it is similar to the proposed approach and its performance is regarded as the current benchmark.

The remainder of this paper is organized as follows. Section 2 provides a brief introduction to random forests and the modifications needed to make structured random forests. Section 3 introduces the workflow for the proposed approach method along with the image results at each block of the prediction phase. In section 4, the data sets and metrics used to evaluate the proposed method are defined. In section 5, the image results, governing parameters, limitations, and future scope of the proposed approach are discussed.

2. Preamble to structured random forests

Classical supervised classification algorithms [25], use a set of feature vectors $\left(f\in {ℝ}^{11}\right)$ and corresponding targets (l $\subset${1, 2, ...,8}) to construct a hypothesis (h). Given a test feature vector (f_test), such a hypothesis is capable of estimating the target $\left(f_{test}\to \hat{l}\right)$. This can be extended to image segmentation [26,27], by constructing hypothesis from a feature vector quantified at each pixel and corresponding layer label (i.e., label image). Given a test image, the feature vectors are computed at each pixel and the corresponding labels are predicted using the hypothesis. Supervised classification ranges from the Bayes classifier to support vector machines, out of which decision trees are robust to noise and class imbalance (the number of pixels annotated as background is greater than the number of pixels annotated as retinal pigment epithelium). The random forests method refers to an ensemble of decision trees, where each tree is trained with different subsets of training data such that each tree constructs a decorrelated hypothesis [29]. During prediction, the label predicted by the majority of trees is treated as the random forests prediction. The random forests method has been widely employed owing to its modeling capabilities and rapid predictions [27]. For image segmentation, however, random forests generally result in inconsistent predictions and unappealing image segmentation [24]. This has been improved by appending conditional random fields [28], wherein the neighborhood pixel predictions (i.e., pair-wise energy) are considered along with a feature vector for label prediction (i.e., unary energy). Nevertheless, this approach forbids end-to-end training due to architectural incompatibility. Structured random forests [24], transform classical random forests by predicting a small 2D patch (i.e., the label patch) based on a feature vector rather than a label, as shown in Fig. 1. During training, structured random forests consider a 2D patch (i.e., the label patch) from the label image corresponding to the location of the feature vector, rather than a single variable (i.e., the label at that pixel). During prediction, the hypothesis generates a label patch for a given feature vector. During segmented-image reconstruction, all label patches are arranged based on the location of the corresponding feature vectors, while the overlapping regions are averaged.

Fig. 1.

Random forest predictions and structured random forest predictions for given feature maps.

Major scientific programming environments like MATLAB and Python are equipped with random forests. However, predicting a label patch using random forests renders decision-tree learning computationally unfeasible. To address this issue, each possible label patch pattern is mapped to an index. In essence, this means training the random forests with feature vectors and their corresponding indexes. One computational pitfall, however, is that a 16 × 16 2D label patch leads to 2^{16 × 16} patterns if each pixel has two states. Thus, a limited number of label patches with distinct patterns are identified through clustering. Such expert intervened clustering does not consider the underlying manifolds (non-Euclidean space) of the label space. Structured forests for semantic segmentation are intended to avoid clustering and include structural information of the label by reducing label patch space through random sampling at each node of decision tree [24]. Random sampling induces noise during training; this prevents learning algorithm from overfitting. Structured forests for edge (SFE) introduced intermediate mapping which assigns each label pattern to a distinct binary vector code (z) based on unique pixel pairs so that similarity can be computed on the Euclidean space [23]. The 16 × 16 binary label patches result in 32640 unique pixel pairs. Random sampling (256 dimensions) is included to reduce dimensions of z. A reduced intermediate mapping assigns z (256 dimensions) for each label patch [23]. Training a SFE (ensemble of decision trees) requires feature vectors, label patches and edge patches, as shown in Fig. 2(a) (feature vectors are reshaped for visualization); where, each tree is trained with different data. Training a tree involves constructing decision node (indicated by circles in Fig. 2(c)) rules and leaf node (indicated by rectangles in Fig. 2(c)) decisions. Decision tree training is initialized from the top node. Initially, reduced intermediate mapping assigns z to all label patches, then principle component analysis based clustering (2 class) of z assigns provisional class (blue and orange) to each label patch and corresponding feature vector (Fig. 2(b)) [23]. Gini impurity is employed to construct rules based on feature vectors and class information. Feature vectors are split towards the left branch or right branch based on the constructed rule. At each branch, label patches corresponding to feature vectors are retrieved from the input data. Subsequently, class information of the feature vectors and label patches is removed. Then, each branch is appended with another node. The z construction, clustering, rule construction, splitting, class information removal, and node appending are repeated for individual branches until the dissimilarity between label patches falls below a tolerant level (left branch in Fig. 2(b)). The last node of an individual branch is regarded as the leaf node. For each leaf node, a representative label patch that is the least distant to other label patches is identified as shown in Fig. 2(c). Such representative label patches are leaf node decisions and corresponding edge patches are retrieved from input data. Given a test feature vector, each tree in SFE directs towards a leaf node based on decision node rules, as shown in Fig. 2(d). The edge patch corresponding to leaf node is treated as tree decision. The mean of tree decisions is treated as SFE decision, i.e., mean of edge patches. The rules (gini impurity) are constructed based on feature patch (arbitrary size) and corresponding provisional class (scalar) at each node, while the class depends on z, which can be constructed for label patch of any size. Therefore, the feature patch size and label patch size are not required to be identical. It is to be noted that for visualization purposes, all patches in Fig. 2 are kept the same. During prediction, input feature patch size for SFE is required to be the same as the training feature patch size, and SFE estimates the edge patch with same size of training edge patches. For the application considered in this paper, the edges should be layer-specific. To the best of our knowledge, such a dimension has not been explored by other methods involving SFE. SFE can be equipped to predict layer specific edges by training it as 'one vs. rest' (multiclass classification) through appending layer ‘n’ selection block. Another workaround is replacing binary z with multivalued z. Proposed method considered first approach as it does not involve modifying training and prediction process and hence can be extended to any other structured learning algorithm. To depict that the proposed workflow is not subjective to features considered, the same features as in [23], are employed. Given an image (Fig. 3(a)), the difference between the predictions of SFE and those of the proposed method are illustrated in Fig. 3(b) and Fig. 3(c).

Fig. 2.

Training and prediction process of structured forest for edge. (a) Required data, (b) decision construction, (c) training, and (d) prediction of a structured forest for edge.

Fig. 3.

Predictions of edges with and without layer information. (a) Input image, (b) structured forests for edge prediction, and (c) proposed method prediction.

3. Method

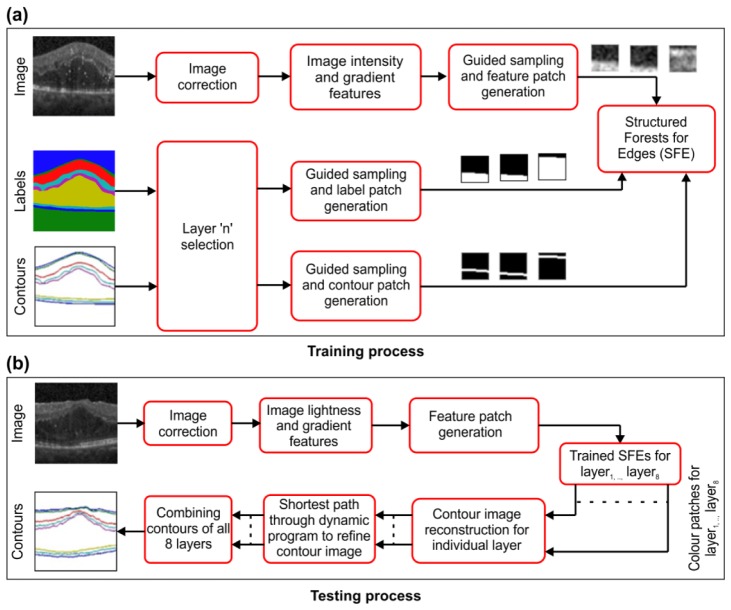
The proposed algorithm involves two phases (see Fig. 4): training the Structured forests for edge for each layer (Fig. 4(a)) and predicting the edge maps for the upper boundaries of each layer (Fig. 4 (b)), which can be included in any graph-based segmentation technique.

Fig. 4.

Flow of the processing blocks for proposed algorithm. (a) During training, and (b) during prediction.

Training: The training phase employs an input image $\left(I\in {ℝ}^{m\times n}\right)$ with a corresponding label image (L, where$\forall$L(x, y){0, 1, ...,8}) and contour image (C) with pseudo-colors, as shown in Fig. 5(a), Fig. 5(b), and Fig. 5(c). The (x,y) indicate the spatial coordinates.

Fig. 5.

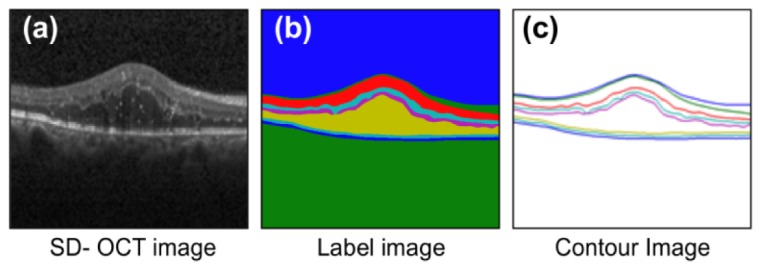
Required images for preparing training data set. (a) Input image, (b) label image, and (c) contour image.

The label image is constructed by replacing every pixel from the input image with its corresponding layer label. The contour image is constructed by replacing only the upper boundary pixels in the input image with their corresponding layer labels, while suppressing the other pixels. The DME data set comprises manual annotations for the inner limiting membrane, nerve fiber layer, inner plexiform layer, inner nuclear layer, outer plexiform layer, outer nuclear layer, inner segment myeloid, retinal pigment epithelium, and Bruch’s membrane, which are hereafter referred to as Layer 1, Layer 2, Layer 3, Layer 4, Layer 5, Layer 6, Layer 7, and Layer 8, respectively.

The image-correction process involves the conversion of the dynamic range of the input image$\left(I\in {ℝ}^{m\times n}\right)$ from [0,255] to [0,1]. The image-acquisition protocol chisels the acquired A-scans to predefined B-scans, resulting in saturated values along the boundaries. To overcome this, all values in I that are equal to 1 are replaced with 0.01.

The process for extracting the image intensity and gradient features involves computing the intensity (i.e., luminance) and the gradient channels that are commonly employed for edge detection in computer vision [23]. The SD-OCT image information is treated as an intensity map (I). Normalized gradient magnitudes are computed at each pixel by employing a 9 × 9 window and are treated as a magnitude map (M). A histogram of the oriented gradients is then computed (employing 4 orientation bins and a 9 × 9 window) based on M, resulting in 4 histogram maps (H); one map for each orientation. To simulate multiscale properties, the input image is downscaled and upscaled by a factor of 2, using bilinear interpolation resulting I_0.5. The M and H feature maps are computed on I_0.5, producing the maps M_0.5 and H_0.5. Each feature map is then filtered using a triangular filter. Given an image $I\in {ℝ}^{m\times n}$, each feature map is of the same size. Upon concatenating all the feature maps (I, M, H, M_0.5, and H_0.5) along the third dimension, a feature tuple $F\in {ℝ}^{m\times n\times 11}$is generated.

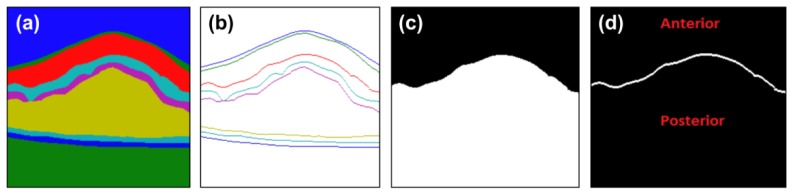
The ‘n’ layer selection process creates a contour binary mask (B_C(x, y) = 1 _$\forall$C(x, y) = n), with only the top boundary of layer ‘n’ (n$\subset${1, 2, ...,8}) as the foreground. In other words, every spatial location (x,y) in B_C is ‘1’ if the corresponding location in C is ‘n’ and all other locations of B_C are ‘0’. This information is used as a guide for sampling the feature, label, and contour patches. This process also creates a label binary mask (B_L(x, y) = 1 $\forall$L(x, y)> = n), where the anterior region of B_C is the background and its posterior is the foreground. Given a label image (Fig. 6(a)) and contour image (Fig. 6(b)) construed B_L (Fig. 6(c)) and B_C (Fig. 6(d)) for Layer 3 is illustrated in Fig. 6.

Fig. 6.

Processed outputs of layer ‘n’ selection block for Layer 3. (a) Label image, (b) contour image, (c) processed label binary mask, and (d) processed contour binary mask.

The guided sampling process involves morphologically dilating B_C with a disk of radius r (16), which results in B_DC. Then, the positive spatial locations (Y = {(x1,y1), (x2,y2),...}$\forall$B_DC = 1) are identified. Spatial locations other than Y are treated as N. Partial locations of Y and N are retained. The process for generating feature patches involves the extraction of patches from F (feature tuple) based on Y and N, resulting in a set of feature patches $\text{{}{P}_F^1,P_F^2,\mathrm{..}{P}_F^j,\mathrm{..}\text{}}$, where each patch size is 32 × 32 × 11. Each feature patch $P_F^j$(where P represents patch, F represents feature, and j represents index of the patch) is flattened (into a 1D array) by lexicographically arranging its elements.

Next, the process for generating label patches involves extracting patches from B_L based on Y and N, resulting a set of label patches$\text{{}{P}_L^1,P_L^2,\mathrm{..}{P}_L^j,\mathrm{..}\text{}}$with each patch size being 16 × 16. Finally, the process for generating contour patches involves repeating the above extraction process on B_C, resulting in a set of label patches $\left\{P_C^1,P_C^2,\mathrm{..}{P}_C^j,\mathrm{..}\right\}$with each patch size being 16 × 16. The index j is required to retain the correspondence between feature patches, labels patches, and contour patches during the construction of rules and decisions of SFE.

The SFE block trains an ensemble of decision trees, wherein each tree is designed to construct rules and decisions (Section 2) to predict the contour patch based on a flattened feature patch. During training, the SFE stores representative label patches and corresponding contour patches.

The training process is repeated for each layer (i.e., n = {1, 2, .., 8}) and the corresponding SFEs are stored.

Edge prediction: During the edge-prediction phase, given an image $\left(I_{test}\in {ℝ}^{a\times b}\right)$, the process of correcting the image and the quantified features are the same as during the training phase. The patch-generation process generates overlapping patches (32 × 32) using a sliding window approach (only along the X and Y axes) with a single pixel shift, resulting in (a − 31) × (b − 31) patches with dimensions of 32 × 32 × 11. SFE trained with layer_n, predicts layer ‘n’ contour patch for each flattened feature patch. This step results in 16 × 16 layer ‘n’ contour patches for each location in the test image. Contour image reconstruction averages

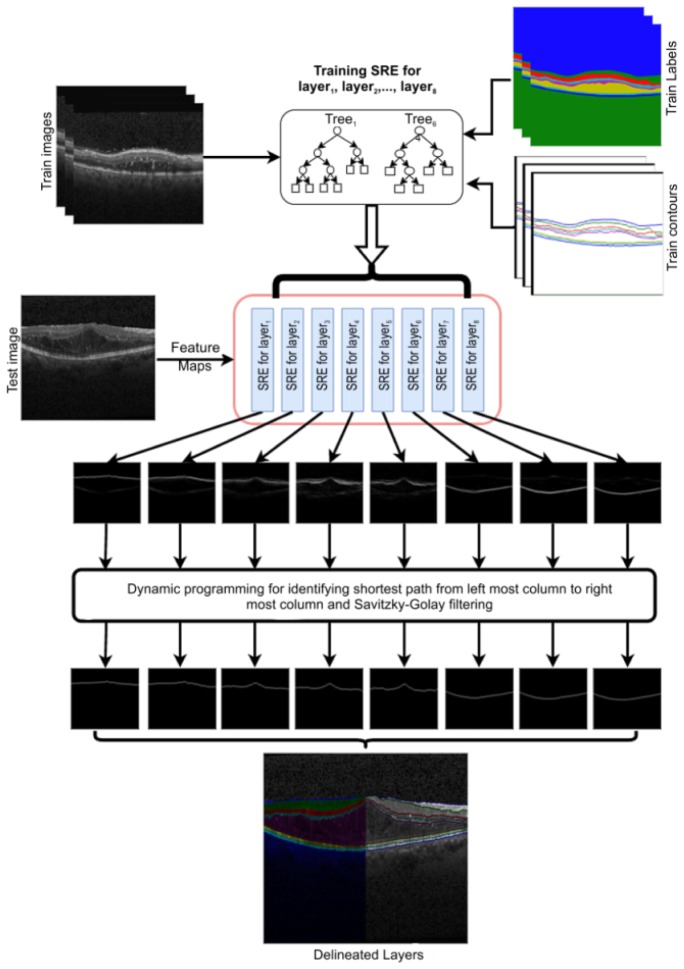
overlapping layer ‘n’ contour patches for each location in the test image. This results in a probability map (with a size of a × b) for the upper boundary of layer ‘n’, which is considered as graph edge for delineating the upper boundary of layer ‘n’ from its upper (anterior) layer. The process by which the shortest path is determined initially appends a column with 1e⁻¹⁵ on either side (left and right) of the probability map. Then, dynamic programming is performed to identify the shortest path from the top pixel of the left column to the bottom pixel of the right column, which is the approach employed by Chiu et al. [15]. The path is smoothened using the Savitzky–Golay filter [30]. The shortest path is considered the contour (i.e., the upper boundary) of layer ‘n’. Upon repeating SRE prediction to smoothen the shortest path for all layers, eight layer contours are achieved, which are then fused for the layer delineation result. Figure 7 shows the block diagram of the training and testing phases with the image results during prediction.

Fig. 7.

Block diagram illustrating image inputs during training, and the resulting images at each block during testing.

4. Experimentation and results

The Duke DME data set [18], comprises 110 OCT images from 10 subjects (110 images in all), accompanied with the upper boundaries of eight layers annotated by two experts. The experiment was performed in a MATLAB environment. Two external MATLAB toolboxes (Piotr’s image and video toolbox and the edges toolbox) were used for guided sampling, patch-space reduction, and the structured random forests. The two external toolboxes are available at: https://github.com/pdollar/toolbox and https://github.com/pdollar/edges. During training, a workstation with 112 GB of RAM was used. For the edge prediction phase, however, 4–8 GB of RAM is sufficient. The proposed method source code has been released for reproducibility and is available at: https://github.com/ultrai/Chap_1. The performance of the proposed algorithm was compared to that of dynamic programming-based retinal segmentation [15], and kernel regression-guided dynamic programming [18].

The data preparation for training involved the following:

• • Preprocessing of all OCT images (images for training only);
• • Averaging the contour locations provided by experts;
• • Interpolating (1D) the intermediate location values with “nan” (not a number);
• • Construction of a contour image by considering each averaged location as a row value and by allotting the layer indices {1,..,8} to the pixel;
• • Construction of the label image from each contour image by allotting pixels between the contours with their corresponding layer indices;
• • Consideration of only columns from 120 to 650 in the input image, label image, and contour image, owing to lack of expert edge locations.

The training phase for layer ‘n’ involved the following:

• • Selection of five subjects—i.e., 55 images;
• • Thresholding of the pixels in the contour image and the label image based on the label value of layer ‘n’;
• • Construction of feature maps for individual images by employing Piotr’s image and the video toolbox;
• • Performing guided sampling (Y = 1 × 10⁶ and N = 1.5 × 10⁶) on the feature maps, contour image, and label image;
• • Training of the ERF with 6 trees, where each tree used 25% of the patches.

Six trees are identified as it balances underfitting and overfitting of ERF.

Given a test image, layer ‘n’ contour prediction involves the following: preprocessing, constructing F, extracting feature patches for all locations, predicting edge patch, averaging overlapping regions; this results in a layer-specific probability map for layer ‘n’ and leads to the detection of the shortest path.

Shortest paths from all layers are combined to depict the layer segmentation result. Figure 8 illustrates the delineation of all eight layers under various deformations.

Fig. 8.

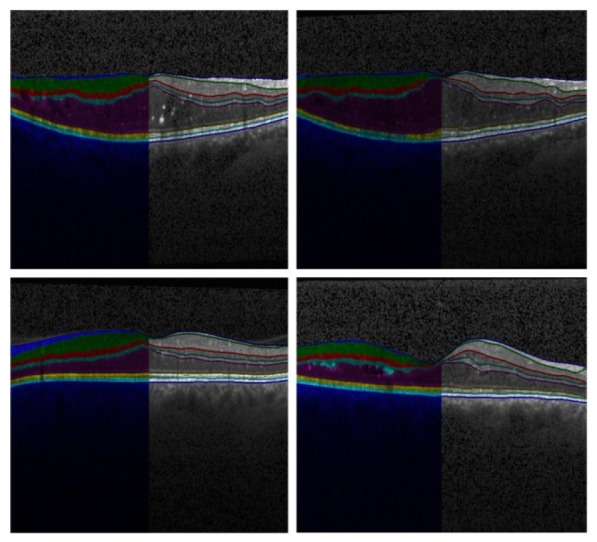
Predictions of proposed approach on test images with various deformations.

Testing was performed on the remaining 50% of the data. The following three metrics were employed for a comparison with the state of the art method.

• • Metric 1: Mean absolute difference between the predicted contour and the expert contour along the column
• • Metric 2: Mean absolute difference in layer widths
• • Metric 3: $F-score=\frac{2\times \text{True positive}}{2\times \text{True positive}+\text{False positive}+\text{False negative}}$

The first metric (i.e., the mean-prediction difference) is more relevant from a computational perspective, because it is a surrogate for the mean absolute error. The second metric (i.e., the mean layer-width difference) is more pertinent from a clinical perspective, because the layer width profiles translate to pathologies. Indeed, a poor prediction of a single contour is reflected in the profile of the widths of the adjunct layers. The third metric (i.e., the F-score) is employed by the image-processing community as dice coefficient measure to compare segmentation results. Kernel regression based segmentation [18], has established a benchmark (AD) by guiding the classical approach (AN) for robust segmentation. The proposed approach was evaluated against AD and AN across two expert annotations. The performance results for Metrics 1, 2, and 3 are shown in Tables 1, 2, and 3, respectively. The results clearly demonstrate the effectiveness of the proposed approach.

Table 1. Metric 1: comparison of the classical graph approach, kernel-guided graph approach, and the proposed approach.

	Expert 1 vs				Expert 2 vs
	Expert 2	AN	AD	Proposed	AN	AD	Proposed
Layer 1	1.14	1.099	1.319	0.969	1.024	1.189	0.906
Layer 2	1.683	3.962	1.708	1.625	4.25	1.91	1.826
Layer 3	1.681	5.936	2.013	1.698	6.03	2.092	1.853
Layer 4	1.752	5.598	2.168	1.704	5.816	2.431	1.753
Layer 5	1.959	5.311	2.486	2.146	5.317	2.406	2.125
Layer 6	1.103	1.125	1.064	0.863	1.037	1.043	0.901
Layer 7	1.273	1.042	1.185	1.086	1.271	1.328	1.229
Layer8	1.191	1.348	1.182	0.863	1.623	1.399	1.112

Table 2. Metric 2: comparison of the classical graph approach, kernel-guided graph approach, and the proposed approach.

	Expert 1 vs				Expert 2 vs
	Expert 2	AN	AD	Proposed	AN	AD	Proposed
Layer 1	2.013	4.034	1.742	1.764	4.483	2.076	2.055
Layer 2	2.336	4.045	2.321	2.25	4.286	2.604	2.533
Layer 3	2.17	1.994	2.277	2.195	2.413	2.575	2.264
Layer 4	2.291	2.633	2.384	2.315	2.708	2.539	2.25
Layer 5	2.241	5.507	2.649	2.314	5.559	2.683	2.303
Layer 6	1.537	1.328	1.49	1.268	1.476	1.603	1.327
Layer 7	1.542	1.323	1.496	1.231	1.726	1.812	1.429

Table 3. Metric 3: comparison of the classical graph approach, kernel-guided graph approach, and the proposed approach.

	Expert 2	AN	AD	Proposed	AN	AD	Proposed
Layer 1	0.864	0.778	0.853	0.874	0.768	0.85	0.868
Layer 2	0.903	0.772	0.895	0.909	0.764	0.887	0.9
Layer 3	0.797	0.652	0.757	0.807	0.649	0.751	0.802
Layer 4	0.747	0.67	0.747	0.77	0.65	0.728	0.756
Layer 5	0.941	0.868	0.931	0.944	0.869	0.933	0.944
Layer 6	0.862	0.878	0.872	0.889	0.868	0.864	0.878
Layer 7	0.829	0.823	0.824	0.868	0.791	0.803	0.845

5. Discussion

In the proposed algorithm, the individual layer contour is trained and predicted independently of the other layer contours. This makes the algorithm’s phases (viz., training and prediction) parallelizable and scalable. During training it can be scaled up to eight machines with eight threads (i.e., Layer 1 trained on Machine 1 with Tree 5 on Thread 5) to reduce the training time. During prediction each layer contour can be estimated on individual thread of a single machine.

The governing parameters—such as the number of samples, number of trees, and width of the label path—affect the performance. For the DME data set, the parameters were set to 2.5 × 10⁶, 6, and 16, in order to balance the computational complexity with the performance. The reason for using a high computational workstation for training and a commonly available computational facility for prediction is that when using random forests, an increase in model complexity does not hamper the prediction phase complexity by the same order, because random forests construct decision rules that can be literally translated to if–else conditions. This will facilitate the incorporation of the prediction phase into the clinical pipeline. By limiting the number of patches to 1 × 10⁶ and training only 1decision tree, the performance of the proposed algorithm was comparable to kernel-guided dynamic programming and required only a 48-GB RAM machine for training. Moreover, the label patch size can be further reduced; however, this result in degradation of the performance, given that it leads to the minimization of the structural contribution, resulting in the algorithm being reduced to a classical learning process.

Predicting a layer-specific probability map requires approximately 1 s per class on an 8-GB RAM machine. Because ordinary processors support 8 threads, the prediction of all 8 probabilities can be computed in parallel, resulting in a computation time of 1s in total. Computing the shortest path requires 2.5 s, which can be reduced to 0.5 s on a downsampled probability map. Because the primary objective is the construction of the edge map, we did not experiment with the complexity for detecting the shortest path.

During training (individual SFE) 2.5 × 10⁶ patches of size 16 × 16 are extracted per layer from 55 images out of which 1 × 10⁶ are along the layer contour. So training data is equipped with possible variations of contours in 16 × 16 region. This minimizes the risk of misclassification even with less number of images. This further allows the model to be independent of layer flattening and prior layer information. Indeed, the primary objective of this study is to report on the impact of the proposed algorithm on reinforcing graph-based segmentation.

The robustness of the proposed framework against the influence of artifacts and magnified representations is illustrated in Fig. 9(a). The results include its performance under deformation due to pathology, imaging-protocol-induced noise, shadows due to blood vessels, and low gradients due to signal attenuation in the posterior retina. The framework is capable of accompanying deviations in expert annotations, as illustrated in Fig. 9(c) and Fig. 9(d). The prediction of the proposed approach have more agreeability with expert annotations in comparison to AD, both visually (Fig. 9(b)) and statistically (Table 3).

Fig. 9.

Illustration of Layers delineation in the presence of deformation (red), noise (yellow), shadows (orange) and low gradients (blue). (a) Proposed, (b) AD, (c) expert 1, and (d) expert 2.

Given that the proposal is robust to deformed layers, it is generalizable. This allows for the extension of the proposed algorithm to layer delineation with several pathologies that have corresponding expert annotations. It has been reported that the consideration of neighboring images improves the accuracy of graph-based segmentation [13]. Thus, 3D structured learning is a future research direction for the proposed algorithm. Another direction is the fusion of the proposed delineation with abnormality prediction. This shall be pursued by color-coding individual pixels on the layer contour, based on the degree of abnormality, for rapid screening though retinal nerve fiber layer quadrants. For future scope, the training time can be reduced by allotting multi valued z rather to binary values, thereby allowing single SRE to model all layer contours.

The effectiveness of the proposed algorithm is exploring the potentiality of SFE to predict layer information along with edges. However, the employment of HoG features has one particular disadvantage—they are gradient-dependent. Therefore, a diminished gradient between the layers can disrupt the results. In its current setup, structured random forests can only handle missing gradients (i.e., shadowed artifacts) that are 16 pixels wide.

6. Conclusion

This paper proposed an algorithm capable of predicting layer-specific edge maps. The proposal can be integrated with any graph-based retinal layer delineation method, and it is robust to large-grade deformations. A layer selection block was appended to classical structured learning algorithm and trained with histogram of oriented gradients (HoG) features to learn layer-specific edges. This contributes to localizing the upper boundary of the intended layer. Along with the advantages to classical learning approaches, structured learning prediction involves correcting the prediction (i.e., by averaging overlapping edge patches) based on neighboring predictions. This resolves missing edges by linking the prediction of the neighboring edge patch (i.e., edge linking). The predicted edge map is used for the edges of graph-based (dynamic programming) retinal-layer delineation. The results of our experiment clearly demonstrate the feasibility of our novel attempt to combine layer-specific edges and structured learning with reduced time and cost complexity during the test phase.