Abstract
Characterization of anatomical change and other differences is important in sequential computed tomography (CT) imaging, where a high-fidelity patient-specific prior image is typically present, but is not used, in the reconstruction of subsequent anatomical states. Here, we introduce a penalized likelihood (PL) method called reconstruction of difference (RoD) to directly reconstruct a difference image volume using both the current projection data and the (unregistered) prior image integrated into the forward model for the measurement data. The algorithm utilizes an alternating minimization to find both the registration and reconstruction estimates. This formulation allows direct control over the image properties of the difference image, permitting regularization strategies that inhibit noise and structural differences due to inconsistencies between the prior image and the current data.Additionally, if the change is known to be local, RoD allows local acquisition and reconstruction, as opposed to traditional model-based approaches that require a full support field of view (or other modifications). We compared the performance of RoD to a standard PL algorithm, in simulation studies and using test-bench cone-beam CT data. The performances of local and global RoD approaches were similar, with local RoD providing a significant computational speedup. In comparison across a range of data with differing fidelity, the local RoD approach consistently showed lower error (with respect to a truth image) than PL in both noisy data and sparsely sampled projection scenarios. In a study of the prior image registration performance of RoD, a clinically reasonable capture ranges were demonstrated. Lastly, the registration algorithm had a broad capture range and the error for reconstruction of CT data was 35% and 20% less than filtered back-projection for RoD and PL, respectively. The RoD has potential for delivering high-quality difference images in a range of sequential clinical scenarios including image-guided surgeries and treatments where accurate and quantitative assessments of anatomical change is desired.
Keywords: computed tomography, cone-beam CT, model-based image reconstruction, statistical image reconstruction, prior image-based reconstruction, penalized likelihood estimation, image-guided radiotherapy
1. Introduction
Many diagnostic imaging studies such as myocardial function analysis (Pourmorteza et al 2012), lung nodule surveillance (Hasegawa et al 2000), and image-guided therapy tasks including image-guided surgeries (Siewerdsen et al 2009, Cleary and Peters 2010, Navab et al 2010, Dang et al 2012) and radiotherapy (Jaffray et al 2002, Dawson and Jaffray 2007) involve acquiring a sequence of CT images over time. However, in many cases, image information from previous studies is conventionally ignored, and images of the current anatomical state are estimated based solely on the latest set of measurements. Adhering to the notion of acquiring CT scan at as low as reasonably achievable (ALARA) radiation dose has significantly reduced the average radiation exposure in the past decade (Kalender 2014). A number of prior-image-based reconstruction algorithms have been proposed that seek to leverage the rich patient-specific anatomical information found in prior imaging studies to improve image quality or reduce radiation exposure. Prior image constrained compressed sensing (PICCS) (Chen et al 2008) and PICCS with statistical weightings (Lauzier and Chen 2013) use a linearized forward model and the concept that sparse signals can be recovered via an l1 optimization strategy. Prior image registration, penalized likelihood (PL) estimation (PIRPLE) (Stayman et al 2013) uses patient-specific prior images in a joint registration-reconstruction objective function that includes a statistical data fit term with a nonlinear forward model, and a generalized regularization term to encourage sparse differences from a simultaneously registered prior image. Other prior image methods include prior-based artifact correction (Heußer et al 2014) and the use of prior images for patch-based regularization (Xu and Tsui 2013). These methods have demonstrated dramatic improvements in the trade-off between radiation dose and image quality in the reconstruction of the current anatomy.
In many sequential imaging tasks, however, the ultimate goal is to characterize the difference between the prior and current anatomy. Examples scenarios include the monitoring of growth or shrinkage of a tumor during or after image-guided radiotherapy (IGRT), localizing and visualizing a surgical tool, implant, or treatment during image-guided surgery (IGS) (Siewerdsen et al 2009), visualizing contrast agents (as in perfusion CT (O’Connor et al 2014) and digital subtraction angiography studies (Davis et al 2013, 2015)) or in monitoring results of spinal (Libicher et al 2005) or dental (Wouters et al 2011) surgeries. Prior work that has sought direct reconstruction of difference (RoD) includes (Lee et al 2012), where PL estimation was used to reconstruct projections formed from the difference between prior and current CT projections. This method presumes the subtraction of noisy projections is Poisson and introduces additional complexity when these projection differences are negative.
In this work, we introduce a PL method to directly reconstruct the anatomical difference image from the current projections and a forward model that includes the prior image. We refer to this method as the RoD approach. Because RoD allows direct control and regularization of the anatomical difference image (as opposed to the current anatomy), the approach can have improved control over the image properties of the difference image. Moreover, if changes are known to be local and spatially limited, RoD allows local acquisition and reconstruction techniques that offer superior computational speed and dose reduction. In contrast, traditional model-based approaches generally require full reconstruction support even if only a small volume of interest is sought. Manduca et al reported a magnetic resonance imaging local reconstruction algorithm that incorporates a priori information of object spatial support into a compressive sensing algorithm (Manduca et al 2010). Local acquisition dose-saving becomes important especially in dynamic imaging scenarios to reduce or eliminate unnecessary radiation exposures to the regions of the body that are not of diagnostic interest for the imaging task. One such example is 4D cardiac imaging in which the motion of the heart, which lies in the central region of the scan field of view, is of interest and the background is stationary but is scanned multiple times.
In this paper we present the development of the framework for RoD, test its performance in reconstruction of low-fidelity projections using simulations and test-bench measurements, and demonstrate the potential for dose reduction and improvement of image quality in the formation of difference image estimates.
2. Methods
2.1. Overview
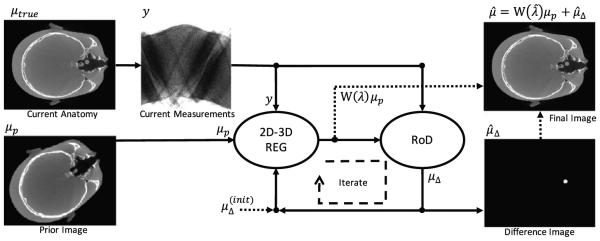
A simplified flowchart for the RoD approach is presented in figure 1. The methodology presumes that a previously acquired image volume, μp, is available to serve as a prior image. A subsequent acquisition of tomographic projection data, y, is available where the current anatomy is presumed to share many similarities with the prior image. The current anatomy and the prior image are not necessarily registered. Thus, a 2D-to-3D registration is conducted to form an appropriately transformed prior image, W (λ)µp, where the registration operator, W, is parameterized by the vector λ. As opposed to traditional reconstruction methods where one attempts to reconstruct the true current anatomy, µtrue, from y, we instead propose to reconstruct only the difference, µΔ, between the current anatomy and the prior image. The RoD estimator takes the raw data and the transformed prior image as an input to produce an estimate of µΔ. The difference image itself is often of interest; however, if desired, one may compute μ from µΔ, and µp. We allow the possibility of alternating optimizations between the 2D-to-3D registration and the RoD estimation to permit for possible refinement.
Figure 1.
Overview of the reconstruction of difference approach. The inputs to the algorithm are projection measurements for the current anatomy and an unregistered prior image volume. The approach alternates between registration updates and image updates to estimate the change between the current and prior anatomy. While the output is a difference image, which is valuable in many imaging scenarios, one may also form a traditional image of the current anatomy by adding the prior image to the difference image.
A detailed discussion of the algorithm follows in section 2.2 where we introduce the general RoD framework and the likelihood-based joint reconstruction and registration objective function. Next, the optimization of the objective function and its numerical implementation is explained in 2.3. Finally, a series of cone-beam CT simulation and test-bench experiments are described in sections 2.4 and 2.5.
2.2. Forward model and objective function
Consider the following model for the mean measurements of a transmission tomography system
| (1) |
where bi is a gain term associated with the number of unattenuated photons (x-ray fluence) and detector sensitivities, μ is vector of attenuation coefficients representing the current anatomy, A is the system matrix, and [Aµ]i is the line integral associated with the ith measurement. We presume that yi is independent and Poisson distributed.
We model the current image volume as the sum of a registered prior image, μp, and a difference image, μΔ, such that
| (2) |
where W is a general transformation operator with parameters λ and could potentially represent deformable registration. In this work we parameterized W as a rigid transform as explained in detail in Stayman et al (2012). With this object model, we can rewrite all the measurements from (1) in the following vector form
| (3) |
where the · operator denotes an element-by-element vector multiplication. Furthermore, we may combine the first two terms of (3) into a single gain parameter, g, such that
| (4) |
Equation (4) is convenient since it reduces the difference forward model to the same form as the traditional forward model in (1). This formulation will permit the use of standard reconstruction algorithms with only a redefinition of the gain term. Similarly, the factorization in (4) separates the dependence of λ on µΔ, and suggests that the registration may also be easily decoupled from the reconstruction.
We choose the following PL objective for the reconstruction of the difference image:
| (5) |
with the implicitly defined estimator:
| (6) |
The (Poisson) log-likelihood function is denoted with L. Our objective function uses two regularization terms leveraging sparsity in multiple domains. This is akin to other work that regularizes in multiple domains (Dutta et al 2012, Xu et al 2014). The second term in (5) is a traditional edge-preserving roughness penalty term that encourages smooth solutions and whose strength is controlled by the scalar regularization parameter βR. In this work, we chose Ψ to be a local pairwise voxel difference operator for a first-order neighborhood. To ensure a differentiable objective, the l1 norm is approximated using a Huber penalty function (Huber 1964) with a small δ parameter. The parameter δ controls the location of the transition between the quadratic and linear portions of the Huber function. In this work we used δ = 10−4 mm−1 for all reconstructions. The third term in (5) is a magnitude penalty on μΔ with strength βM that encourages the difference image itself to be sparse (e.g. the change in anatomy is local and relatively small).
While the roughness penalty is fairly intuitive in its control of the noise-resolution tradeoff, the function of the magnitude penalty is more complex. This penalty controls the amount of prior image information used in image formation. A large βM forces the difference image to be closer to zero, enforcing smaller allowable differences from the prior image. A small βM permits larger differences from the prior image and therefore a greater reliance on the current projection data; however, this increased reliance on the measurement data can also lead to attenuation differences due to noise. Thus, a proper balance and control of prior information inclusion must be selected. This trade-off is investigated in following sections.
2.3. Algorithm and implementation
We propose to solve the optimization in (6) using a two-step alternating approach to jointly solve for and . That is, the registration parameters λ are updated using a traditional gradient-based approach with a fixed attenuation estimate, and the difference image µΔ is estimated iteratively using a tomography-specific image update with fixed registration.
Mathematically, we may write the registration step of the problem as
| (7) |
Equation (7) represents a 2D-to-3D likelihood-based rigid registration approach. This same form of registration was discussed in detail in Stayman et al (2012). In short, the W operator in (2) is parameterized using B-spline kernels to ensure its differentiability. This allows us to use a quasi-Newton update method using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) (Liu and Nocedal 1989) updates to optimize the objective function (7). The required function and gradient evaluations are straightforward to compute and may be derived from (5) by eliminating factors dependent only on attenuation (including the regularization terms). The bracketed superscript, [n], denotes the nth estimate of the parameter vector, formalizing that the nth alternation of registration updates depends on the previous, (n − 1)th alternation of image updates.
For the image volume updates, we may write the optimization part of the problem as:
| (8) |
which includes a transformed prior with fixed λ from the previous set of registration updates. The roughness and magnitude penalty terms satisfy the five criteria in (Erdogan and Fessler 2002) for finding paraboloidal surrogates. Therefore, we may adopt the separable paraboloidal surrogates (SPS) approach introduced by Erdogan and Fessler in 1999 with ordered-subsets subiterations for improved convergence rates. The difference image µΔ represents the change in attenuation coefficients between scans and could have positive or negative values. Consequently, traditional non-negativity constraints on the reconstruction are not applied. The SPS image update equation can be readily derived:
| (9) |
where ci are optimal curvatures, is the derivative of the Huber penalty function, and calculated according to Erdogan and Fessler (2002). The derivatives of marginal log-likelihoods were defined as with .
Table 1 depicts pseudocode for the alternating joint registration and image update approach. The outer loop iterates over registration and image updates each with their own inner loops over BFGS and ordered subsets iterations, respectively.
Table 1.
Pseudo code for the proposed reconstruction of difference approach.

|
The simultaneous image update in (9) can be easily parallelized for efficient computation on a graphical processing unit (GPU). We implemented all routines in Matlab (The Mathworks, Natick, MA) with calls to custom external libraries for the separable-footprint (Long et al 2010) projectors and back-projectors in C/C + + using CUDA libraries for execution on GPU. We have not directly compared the computational efficiency of this implementation to un-parallelized methods in this work; however, details of its computation efficiency and other possible speedup techniques are discussed in Wang et al (2014).
2.4. Simulation studies
We simulated growth of a spherical lesion in the nasal cavity of an anthropomorphic head phantom. We formed a digital phantom from relatively low-noise cone-beam CT (CBCT) measurements (100 kVp, 453 mAs, 720 projections over 360°) using a CBCT test-bench (explained in detail in the next section) and a PL reconstruction with 0.5 mm isotropic voxel size. This image was used as the prior image µp for subsequent studies. A spherical lesion with 10.5 mm diameter and 0.02 mm−1 attenuation (simulating a tumor, mucocele, or other abnormality to be detected in the RoD image) was digitally added to the nasal cavity, as seen in figure 4(A), to create the ground truth image for the current anatomy. Simulated new measurements were then created by projecting this ‘with lesion’ volume for 720 angles over 360°. Acquisitions with different levels of x-ray fluence were simulated by adding various levels of Poisson noise to the noiseless measurements. These data sets were used to investigate sensitivity to the regularization parameters (2.4.1), local versus global reconstruction (2.4.2), and performance of RoD with varying data fidelity (2.4.3). A separate dataset was simulated by rigid transformation of the prior image with a set of known λ to investigate the performance of the registration step on image quality in section 2.4.4. In all experiments, the root-mean-square error (RMSE) between the RoD estimate and the ground truth difference image was used as a measure of image quality. The error was calculated over a large (100 × 100 voxel) neighborhood around the spherical lesion in order to include the boney structures in the background as well as the air and soft tissue of the nasal cavity.
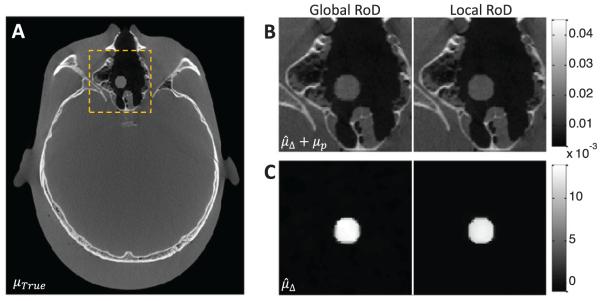
Figure 4.
Results of global and local RoD with best penalty coefficients in terms of RMSE; A: ground truth image for the current anatomy. The dashed square shows the 100 × 100 ROI reconstructed with local RoD. B: summed current anatomy images reconstructed with global and local approaches of RoD. C: Difference images reconstructed with global and local RoD.
2.4.1. Regularization investigation
The objective function in (5) has two coefficients βR, βM that control the strength of the roughness and prior magnitude penalty, respectively. We studied trends in optimal penalty strength by performing the reconstruction with an exhaustive 2D sweep of the coefficients for one slice of the volume. The coefficients were varied linearly in the exponent from 100 to 105 with a 101/2 step size. The fluence (104 photons) and number of projections (180) were fixed for all reconstructions. The coefficient values that produced the smallest RMSE were chosen as the optimal settings.
2.4.2. Local versus global reconstruction of difference
The RoD methodology has a potential advantage over other model-based reconstruction methods. If the change in anatomy is known to be local and inside a relatively small ROI, we can assume μΔ is zero everywhere else. Thus, unlike traditional model-based methods that require a full parameterization of the entire imaging volume or have to resort to interior tomography solutions (Wang and Yu 2013), RoD can be employed to reconstruct only those regions where there is anatomical change. This can significantly reduce the required support size for the RoD algorithm and lead to computational speedups. Similarly, as long as all anatomical change is covered in the projection data, truncated acquisitions can also be obtained permitting additional possibilities for dose reduction.
We simulated the local approach by truncating the rays that did not intersect with the 100 × 100 ROI around the lesion (simulating a dynamically collimated truncated data set) and choosing 100 × 100 voxel support for image reconstruction. For comparison, a global RoD was performed over the full FOV (512 × 512 voxels) without data truncation. The prior image used in both approaches was not truncated. We exhaustively searched for the optimal penalty coefficients as explained in the previous section and RMSE was calculated over the same 100 × 100 anatomical ROI in the local and global approaches.
2.4.3. RoD performance versus data fidelity
Prior-image-based reconstruction methods have been used in many scenarios to overcome poor data fidelity including situations involving poor signal-to-noise ratio and sparse sampling. We have investigated both of those situations here. Specifically, we consider the effects of noise on RoD using measurements with simulated fluence ranging from 102 to 105 (photons per pixel) swept linearly in the exponent with a 101/2 step size and using 180 projections over 360°. For comparison, these measurements were also reconstructed with an ordinary PL approach (without a prior image model) with the same form of roughness penalty as used in RoD. The PL roughness penalty coefficient was also swept from 102 to 105 with a 101/2 step. We also performed a similar experiment that studied the dependence of RoD and PL on data sparsity. For this experiment, we subsampled the 720 projections with factors of 2, 4, 8, 16, 30, and 45 at a fixed fluence (104 photons per pixel). We used local RoD as explained in the previous section while the PL reconstruction was performed on the full FOV. All penalty coefficients were determined through exhaustive search.
2.4.4. Performance of likelihood-based registration
While the previous experiments have focused on preregistered prior images, it is important to understand the sensitivity to misregistration. Toward this end, we performed a registration experiment where we transformed the prior volume by a known amount, λtrue, and estimated the transformation parameters, λΔ, using RoD likelihood-based rigid registration.
For each of the six transformation parameters, 50 values were randomly selected from a bimodal distribution while the rest of the parameters were fixed at zero. The translations (in mm) were chosen from a bimodal distribution defined by (−40, 15) + (40, 15) and the rotations (in degrees) were selected from (−45, 22.5) + (45, 22.5) where (m, s) is the Gaussian distribution with mean m and standard deviation s. We calculated the error in transformation parameter estimation as well as the RMSE between the estimated image and the ground truth. The images were reconstructed at 256 × 256 × 241 matrix size with 1 mm isotropic voxels.
We define capture range of a parameter as the interval within which the RMSE is within (±0.0005 mm−1) of the RMSE of the RoD image reconstructed from a perfectly pre-registered prior. Additionally, we tested the performance of the registration algorithm when the prior image was transformed by ten sets of λ’s with nonzero elements, which were created by a combination of single translations and rotations along all axes randomly selected within their determined capture ranges.
2.5. Test-bench studies
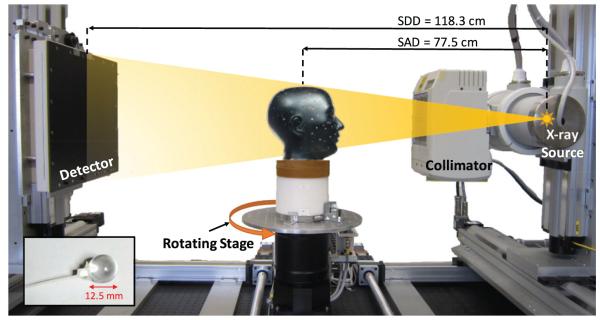
In addition to the previous simulation experiments, we acquired physical CBCT measurements using the test-bench setup in figure 2. The bench consisted of a Rad-94 x-ray source (Varian Medical Systems, Palo Alto, CA), a Varian PaxScan 4030CB flat-panel detector with 40 × 30 cm2 total size and 0.388 mm pixel pitch after 2 × 2 binning, and a motion control system (Parker Hannifin, Mayfield Heights, OH). The bench geometry was chosen to simulate a C-arm system with a 118 cm source-to-detector distance and 77.4 cm source-to-axis distance.
Figure 2.
CBCT test-bench with stationary flat panel detector (left) and x-ray tube (right), and the anthropomorphic head phantom on a rotating stage. The inset shows the acrylic sphere placed in the nasal cavity of the phantom to mimic a tumor.
We placed an acrylic sphere with 12.5 mm diameter inside the nasal cavity of an anthropomorphic head phantom (The Phantom Laboratory, Salem, NY) to simulate a tumor growth (see inset in figure 2). Two scans were performed at 100 kVp and 453 mAs with 720 projections over 360° with and without the sphere inserted. The phantom was not moved during the removal of the sphere and between scans. We used a PL reconstruction of the scan with no sphere as the prior; similarly a PL reconstruction of the scan with the sphere inserted was used as the ground truth for the current anatomy.
We examined the performance of RoD in reconstructing a 3D volume, with an unregistered prior, to that of FBP and PL algorithms in a noisy scan. We created a rigid transformation matrix to form a misregistered prior image. The registration parameters (λ: −4, 5, and −10 mm shifts and 10°,−7°, and 30° rotations for x, y, and z axes respectively) were within the capture range of translations and rotations calculated from the results of the experiment explained in 2.4.4. Poisson noise was added to the projections of the ‘with tumor’ measurements to simulate fluence of 5000 photons and the penalty coefficients were chosen based on the results of the exhaustive search of the simulated data described in section 2.4.1.
3. Results
3.1. Investigation of regularization parameters
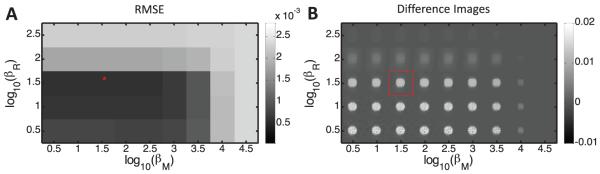
We explored the effects of the penalty coefficients βR, βM on reconstructed image quality as explained in section 2.4.1. Figure 3(A) shows the RMSE (relative to truth) as a function of both regularization parameters, while figure 3(B) shows the zoomed ROI difference images that result from the (global) RoD approach. As expected, increasing βR resulted in less noisy difference images by forcing the reconstruction to be spatially smooth; coefficient values larger than 102 completely blurred the difference image. Similar to the roughness penalty coefficient, large values of βM also created less noisy images but by different means: the magnitude penalty forces the reconstructed image to be sparse. In the extreme, βM larger than 104.5 forced the reconstructed image to be completely sparse (i.e. zero everywhere). In this case βR, βM = 101.5 produced the best image quality in terms of RMSE. Exhaustive search of the 2D βR, βM space may be time-consuming especially in the case of large 3D volume reconstructions; however, the basic trend in RMSE map suggests that it is possible to find the optimum point by starting from low regularization levels and performing 1D searches first along the βR, and next along the βM axes. This is somewhat similar to the results found and reported in Dang et al (2014b).
Figure 3.
Results of regularization investigation. A: RMSE (mm−1) for results of the exhaustive search for penalty coefficients. The asterisk denotes the point with lowest RMSE. B: zoomed ROI illustrating the difference reconstructions associated with each regularization strength pair. The asterisk (A) and rectangle (B) correspond to the image estimate that minimized RMSE.
3.2. Global versus local reconstruction of difference
The results of the global and local RoD experiment described in section 2.4.2 are summarized in figure 4. Both the summed current anatomy volume, , and the difference volume, are shown for the local and global approaches. Images reconstructed were with RMSE-optimal penalty coefficients (though omitted for brevity, penalty coefficient RMSE maps for the local and global RoD showed similar trends.) RMSE was 4.02 × 10−4 (mm−1) for the local and 4.19 × 10−4 (mm−1) for the global protocols. The results indicate that the performance of local and global RoD were comparable, and there was slight improvement in RMSE when local RoD was used. This is possibly due to the fact that local RoD enforces zero difference image values outside the ROI, whereas global RoD must estimate those voxel values outside the ROI with some potential propagation of error/noise from the outside into the ROI where RMSE is computed. Since local RoD was faster to compute and at least as accurate as the global approach, we used the local approach for the remainder of the simulation experiments.
3.3. Performance as a function of data fidelity
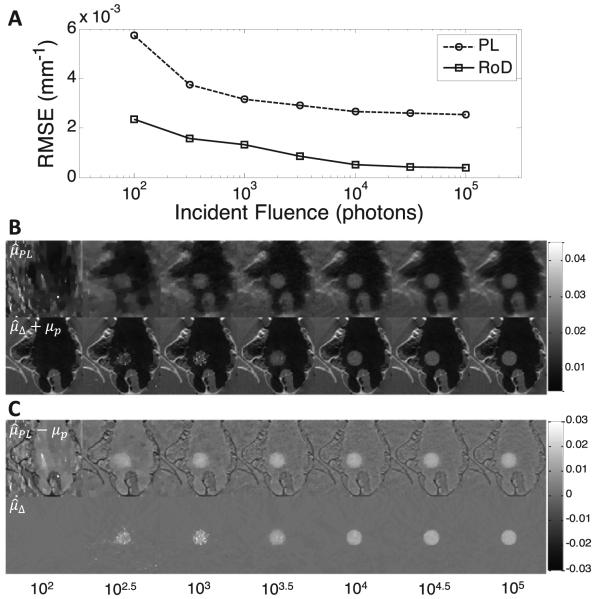
We tested the performance of RoD under different levels of data fidelity. We changed the fidelity of the measurements by: (1) simulating noisy measurements, and (2) subsampling the number of projections. The results of the performance of RoD compared to PL in reconstructing measurements with decreasing photon fluence are presented in figure 5. The performance of both methods deteriorated as the photon fluence decreased to the point that at fluence of 100 (photons per pixel) both methods failed to reconstruct the difference; however, RoD performed consistently better than PL. The PL anatomical change images were calculated by subtracting the prior image from the PL estimate and show structural differences in the background.
Figure 5.
Effects of noise on RoD. (A) RMSE (mm−1) measured as a function of incident photon fluence (for 180 projections) for noisy projections reconstructed with PL and RoD. (B) Current anatomy images reconstructed at different noise levels using PL (, top row) and local RoD ( + μp, bottom row). (C) Change in anatomy estimated by subtracting the prior image from the PL reconstruction ( − μp, top row) and estimated directly using RoD (, bottom row).
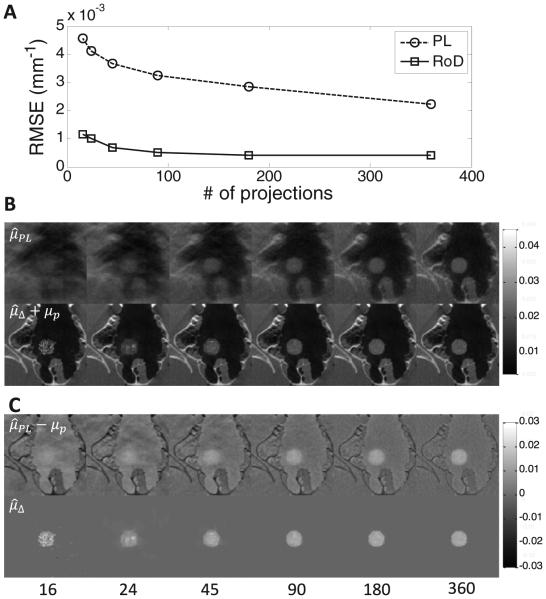
Note the significant amount of anatomical structure in the PL difference images (particularly due to bones near the sinus cavity) as opposed to RoD which does not exhibit such structure and yields an image much closer to the true anatomical difference. This performance difference is due, in part, to the differing regularization between the prior image and the PL reconstruction, whereas the regularization in RoD can be adjusted to mitigate the appearance of such differences. Figure 6 shows a similar trend in the performance of PL and RoD methods at different levels of data sparsity. The structural differences are also present in the background of subtracted PL images. Furthermore, the performance of RoD does not decline much compared to PL when the number of projections is reduced from 360 to 90.
Figure 6.
Effects of data sparsity on RoD. (A) RMSE (mm−1) measured as a function of number of projections (fluence = 104) reconstructed with PL and RoD. (B) Current anatomy images reconstructed at different projection angle subsampling levels using PL ( top row) and local RoD ( bottom row). (C) Change in anatomy estimated by subtracting the prior image from the PL reconstruction (, top row) and estimated directly using RoD (, bottom row).
3.4. Performance of likelihood-based registration
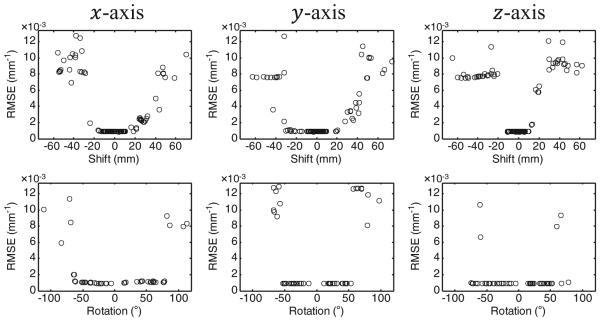
We tested the performance of the likelihood-based rigid registration of the global RoD algorithm under various random single translations and rotations in 3D as explained in 2.4.4. These results are summarized in figure 7. The RMSE in reconstruction for ensembles of random translation is shown in the top row, and for ensembles of random rotation in the bottom row. There is a fairly well-defined limit beyond which the RMSE rises dramatically. The capture range (defined as the range for which RMSE differs by < ±0.0005 mm−1 of that in preregistered reconstruction) for translations along the x, y, z axes were [−16 10], [−29 9], and [−11 10] (in mm), respectively. The translation capture ranges were limited by the prior image being cropped by moving outside the reconstructed volume by the transformation; theoretically the translation capture range can be improved by using a large enough reconstruction FOV. The capture range for a single random rotation about any axis was at least ±50°. Overall, this is a broad capture range consistent with robust rigid registration and suggests that the method can handle large errors in initialization in the alternating optimization.
Figure 7.
Root-mean-square error of RoD image after a single shift (top row) or rotation (bottom row) of the prior image.
For the multivariate registration experiment, where we tested the performance of the registration algorithm using 10 sets of random λ with nonzero elements, the mean and standard deviation of the RMSE was 0.02 ± 0.0005 mm−1. That is, all cases converged to essentially the same results in terms of registration and image quality (though there were minor differences due to noise).
3.5. Test-bench data
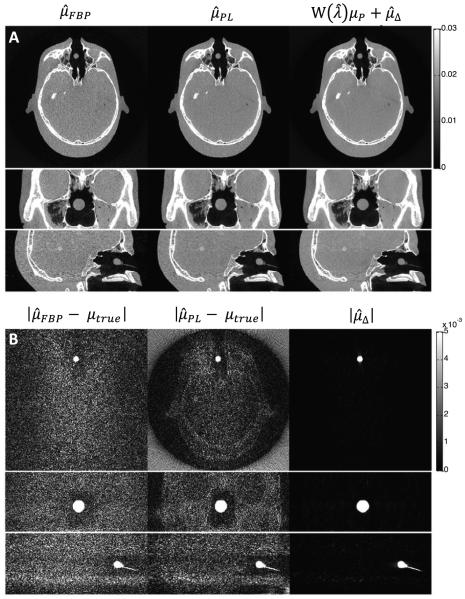
Figure 8 shows the results of the 3D reconstruction of the physical CBCT test-bench data. Reconstructions using FBP, PL, and RoD with an unregistered prior image are presented. Both current anatomy volumes and (absolute) difference volumes are presented for each method. The RMSE was (1.27, 1.57, 1.97) × 10−3 mm−1 for RoD, PL, and FBP reconstructions, respectively. The difference images for the PL and FBP change images included high levels of noise in the background. Moreover, the PL reconstruction exhibited highly structured noise showing anatomical boundaries (in particular the boundary between water and bone) as seen and described in previous studies. In contrast, the RoD does not show much noise outside the actual change and yields a much more accurate reconstruction of the difference image.
Figure 8.
Results of 3D reconstruction of cone-beam CT test bench data in axial, coronal, and sagittal views. A: current anatomy images reconstructed with FBP, PL, and RoD. Bottom row: absolute value of anatomical change.
4. Discussion
In this paper we introduced a novel prior-image-based reconstruction method to directly estimate change in anatomy in sequential scans. The proposed method directly reconstructs the difference image by incorporating the prior image into the forward model and directly regularizing the difference image. Our simulation experiments showed the utility and predictability of image roughness and magnitude penalties in regularizing the RoD image. Furthermore, we found that it is possible to reconstruct the image using local reconstruction methods (potentially with truncated acquisitions) which presents additional opportunities for computational speedup and radiation dose reduction. The performance of the proposed RoD method was superior to that of a PL method in low-fidelity acquisitions. In future studies, it will be important to compare RoD with other prior image based reconstruction methods.
In joint registration and reconstruction studies, we found the capture ranges of the like-lihood-based registration to be largely limited by the range in which the prior image was cropped outside the field of view. The capture range for rotations was similarly large (±50°) and suggests a high degree of robustness to errors in registration initialization. The physical experiments using CBCT test-bench data reproduced many of the observations seen in the simulation studies. This demonstrated the feasibility of RoD reconstruction in real data featuring realistic non-idealities in detector noise, x-ray scatter, etc and suggests that the method may offer a valuable approach to estimating the anatomical change in clinical sequential imaging scenarios such as IGS and IGRT, perfusion CT scans, spectral CT, and 4D cardiac studies.
While this paper has introduced a general framework for RoD, there are many areas for potential improvements. For example, the penalty coefficients were chosen to be scalar values determined through exhaustive search. A precalculated space-variant map of penalty coefficients, similar to the one reported in Dang et al (2014a) which adjusts the strength of regularization at different locations of the image volume, may have additional value. There are also ongoing efforts to prospectively estimate the penalty coefficients with respect to an image quality metric (Dang et al 2015).
The lesion simulated in this study was of relatively high contrast. Although there are many applications where high contrast change is present (e.g. DSA, and perfusion CT) it is worth investigating the performance of RoD in detecting low contrast change.
Another area for potential improvement is in the registration approach. In this work, we used a likelihood-based rigid registration algorithm in this study, however, the modular (alternating) design of the RoD registration and reconstruction algorithm allows for any projection-to-volume or potentially a 3D volume-to-volume registration algorithm. While the head motion experiments of this paper were easily modeled with a rigid transformation, other imaging applications (e.g. abdominal imaging) may require use of more challenging non-rigid transformations as was successfully performed for the initial experiments of dPIRPLE technique (Dang et al 2014b). We plan to further investigate the use of non-rigid registration in RoD. In addition, there are scenarios such as spectral imaging using photon counting detectors (Taguchi and Iwanczyk 2013), dual source, fast kilovolt (KV) switching, or dual-layer detector technology (Marin et al 2014) where the acquisitions are performed (almost) simultaneously and are, inherently, registered. In other cases such as digital subtraction angiography and perfusion imaging, a rigid registration algorithm may be sufficient.
Direct regularization and reconstruction of the difference image has distinct advantages as seen in the very clean reconstructions. Not only does this allow better visualization of change, one can still form volumetric images of the current anatomy by adding the RoD estimate to the prior image, if desired. Additionally, for efforts that involve quantification and/or localization of anatomical change (e.g. measuring tumor growth/shrinkage, doubling times, changing tumor boundaries for radiotherapy, etc)—especially approaches that rely on isolation of change via methods like segmentation—the RoD images may present an improvement. The absence of noise and structure due to mismatches between the current and prior image can easily confound such quantitation and localization whereas RoD can largely mitigate such contamination. These properties of RoD suggest potential application in sequential studies where quantitative measures are desired or clear delineation of change boundaries is required.
Acknowledgments
This work supported in part by an academic-industry partnership with Elekta (Stockholm, Sweden) and the National Institutes of Health grant R01EB017226. The authors thank Drs Junghoon Lee and John Wong (Department of Radiation Oncology, Johns Hopkins University) for collaboration and valuable conversations.
References
- Chen G-H, Tang J, Leng S. Prior image constrained compressed sensing (PICCS): a method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med. Phys. 2008;35:660–3. doi: 10.1118/1.2836423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleary K, Peters TM. Image-guided interventions: technology review and clinical applications. Annu. Rev. Biomed. Eng. 2010;12:119–42. doi: 10.1146/annurev-bioeng-070909-105249. [DOI] [PubMed] [Google Scholar]
- Dang H, Otake Y, Schafer S, Stayman JW, Kleinszig G, Siewerdsen JH. Robust methods for automatic image-to-world registration in cone-beam CT interventional guidance. Med. Phys. 2012;39:6484–98. doi: 10.1118/1.4754589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dang H, Siewerdsen JH, Stayman JW. Regularization design and control of change admission in prior-image-based reconstruction. SPIE Med. Imaging (Int. Soc. Opt. Photon.) 2014a;9033:90330O. doi: 10.1117/12.2043781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dang H, Wang AS, Sussman MS, Siewerdsen JH, Stayman JW. dPIRPLE: a joint estimation framework for deformable registration and penalized-likelihood CT image reconstruction using prior images. Phys. Med. Biol. 2014b;59:4799. doi: 10.1088/0031-9155/59/17/4799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dang H, Siewerdsen JH, Stayman JW. Prospective regularization design in prior-image-based reconstruction. Phys. Med. Biol. 2015;60:9515. doi: 10.1088/0031-9155/60/24/9515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis B, Oberstar E, Royalty K, Schafer S, Strother C, Mistretta C. Volumetric limiting spatial resolution analysis of four dimensional digital subtraction angiography (4D-DSA) SPIE Med. Imaging (Int. Soc. Opt. Photon.) 2015;9412:94121B. doi: 10.1117/1.JMI.3.1.013503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis B, Royalty K, Kowarschik M, Rohkohl C, Oberstar E, Aagaard-Kienitz B, Niemann D, Ozkan O, Strother C, Mistretta C. 4D digital subtraction angiography: implementation and demonstration of feasibility. Am. J. Neuroradiol. 2013;34:1914–21. doi: 10.3174/ajnr.A3529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson LA, Jaffray DA. Advances in image-guided radiation therapy. J. Clin. Oncol. 2007;25:938–46. doi: 10.1200/JCO.2006.09.9515. [DOI] [PubMed] [Google Scholar]
- Dutta J, Ahn S, Li C, Cherry SR, Leahy RM. Joint L1 and total variation regularization for fluorescence molecular tomography. Phys. Med. Biol. 2012;57:1459. doi: 10.1088/0031-9155/57/6/1459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erdogan H, Fessler JA. Ordered subsets algorithms for transmission tomography. Phys. Med. Biol. 1999;44:2835–51. doi: 10.1088/0031-9155/44/11/311. [DOI] [PubMed] [Google Scholar]
- Erdogan H, Fessler J. Monotonic algorithms for transmission tomography. 5th IEEE EMBS Int. Summer School on Biomedical Imaging, 2002. 2002:14. doi: 10.1109/42.802758. (IEEE) [DOI] [PubMed] [Google Scholar]
- Hasegawa M, Sone S, Takashima S, Li F, Yang ZG, Maruyama Y, Watanabe T. Growth rate of small lung cancers detected on mass CT screening. Br. J. Radiol. 2000;73:1252–9. doi: 10.1259/bjr.73.876.11205667. [DOI] [PubMed] [Google Scholar]
- Heußer T, Brehm M, Ritschl L, Sawall S, Kachelrieß M. Prior-based artifact correction (PBAC) in computed tomography. Med. Phys. 2014;41:21906. doi: 10.1118/1.4851536. [DOI] [PubMed] [Google Scholar]
- Huber PJ. Robust estimation of a location parameter. Ann. Math. Stat. 1964;35:73–101. [Google Scholar]
- Jaffray DA, Siewerdsen JH, Wong JW, Martinez AA. Flat-panel cone-beam computed tomography for image-guided radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 2002;53:1337–49. doi: 10.1016/s0360-3016(02)02884-5. [DOI] [PubMed] [Google Scholar]
- Kalender WA. Dose in x-ray computed tomography. Phys. Med. Biol. 2014;59:R129. doi: 10.1088/0031-9155/59/3/R129. [DOI] [PubMed] [Google Scholar]
- Lauzier PT, Chen G-H. Characterization of statistical prior image constrained compressed sensing (PICCS): II. Application to dose reduction. Med. Phys. 2013;40:21902. doi: 10.1118/1.4773866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Stayman JW, Otake Y, Schafer S, Zbijewski W, Khanna AJ, Prince JL, Siewerdsen JH. Volume-of-change cone-beam CT for image-guided surgery. Phys. Med. Biol. 2012;57:4969. doi: 10.1088/0031-9155/57/15/4969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Libicher M, Vetter M, Wolf I, Noeldge G, Kasperk C, Grafe I, Da Fonseca K, Hillmeier J, Meeder PJ, Meinzer HP. CT volumetry of intravertebral cement after kyphoplasty. Comparison of polymethylmethacrylate and calcium phosphate in a 12 month follow-up. Eur. Radiol. 2005;15:1544–9. doi: 10.1007/s00330-005-2709-x. [DOI] [PubMed] [Google Scholar]
- Liu DC, Nocedal J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989;45:503–28. [Google Scholar]
- Long Y, Fessler J, Balter JM. 3D forward and back-projection for x-ray CT using separable footprints. IEEE Trans. Med. Imaging. 2010;29:1839–50. doi: 10.1109/TMI.2010.2050898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manduca A, Trzasko JJD, Li Z. Compressive sensing of images with. SPIE Med. Imaging. 2010;7622:762223–7. [Google Scholar]
- Marin D, Boll DT, Mileto A, Nelson RC. State of the art: dual-energy CT of the abdomen Radiology. 2014;271:327–42. doi: 10.1148/radiol.14131480. [DOI] [PubMed] [Google Scholar]
- Navab N, Heining S-M, Traub J. Camera augmented mobile C-arm (CAMC): calibration, accuracy study, and clinical applications. IEEE Trans. Med. Imaging. 2010;29:1412–23. doi: 10.1109/TMI.2009.2021947. [DOI] [PubMed] [Google Scholar]
- O’Connor JPB, Tofts PS, Miles KA, Parkes LM, Thompson G, Jackson A. Dynamic contrast-enhanced imaging techniques: CT and MRI. Br. J. Radiol. 2011;84:112. doi: 10.1259/bjr/55166688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pourmorteza A, Schuleri KH, Herzka DA, Lardo AC, McVeigh ER. A new method for cardiac computed tomography regional function assessment: stretch quantifier for endocardial engraved zones (SQUEEZ) Circ. Cardiovasc. Imaging. 2012;5:243–50. doi: 10.1161/CIRCIMAGING.111.970061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siewerdsen JH, Daly MJ, Chan H, Nithiananthan S, Hamming N, Brock KK, Irish JC. High-performance intraoperative cone-beam CT on a mobile C-arm: an integrated system for guidance of head and neck surgery. SPIE Med. Imaging (Int. Soc. Opt. Photon.) 2009;7261:72610J. [Google Scholar]
- Stayman JW, Dang H, Ding Y, Siewerdsen JH. PIRPLE: a penalized-likelihood framework for incorporation of prior images in CT reconstruction. Phys. Med. Biol. 2013;58:7563. doi: 10.1088/0031-9155/58/21/7563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stayman JW, Otake Y, Prince JL, Khanna AJ, Siewerdsen JH. Model-based tomographic reconstruction of objects containing known components. IEEE Trans. Med. Imaging. 2012;31:1837–48. doi: 10.1109/TMI.2012.2199763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taguchi K, Iwanczyk JS. Vision 20/20: Single photon counting x-ray detectors in medical imaging. Med. Phys. 2013;40:100901. doi: 10.1118/1.4820371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang AS, Stayman JW, Otake Y, Kleinszig G, Vogt S, Gallia GL, Khanna AJ, Siewerdsen JH. Soft-tissue imaging with C-arm cone-beam CT using statistical reconstruction. Phys. Med. Biol. 2014;59:1005. doi: 10.1088/0031-9155/59/4/1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G, Yu H. The meaning of interior tomography. Phys. Med. Biol. 2013;58:R161. doi: 10.1088/0031-9155/58/16/R161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wouters V, Mollemans W, Schutyser F. Calibrated segmentation of CBCT and CT images for digitization of dental prostheses. Int. J. Comput. Assist. Radiol. Surg. 2011;6:609–16. doi: 10.1007/s11548-011-0556-6. [DOI] [PubMed] [Google Scholar]
- Xu Q, Sawatzky A, Anastasio MA, Schirra CO. Sparsity-regularized image reconstruction of decomposed K-edge data in spectral CT. Phys. Med. Biol. 2014;59:N65. doi: 10.1088/0031-9155/59/10/N65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Tsui BM. C-arm CT image reconstruction from sparse projections. Proc. of Int. Meeting on Fully 3D Image Reconstruction in Radiology and Nuclear Medicine. 2013:34–7. [Google Scholar]