Abstract
Genes encode components of coevolved and interconnected networks. The effect of genotype on phenotype therefore depends on genotypic context through gene interactions known as epistasis. Epistasis is important in predicting phenotype from genotype for an individual. It is also examined in population studies to identify genetic risk factors in complex traits and predicting evolution under selection. Paradoxically, the effects of genotypic context in individuals and populations are distinct and sometimes contradictory. We argue that predicting genotype from phenotype for individuals based on population studies is difficult and, especially in human genetics, likely to result in underestimating the effects of genotypic context.
Introduction
The importance of genotypic context has been recognized almost from the beginning of modern genetics, when William Bateson coined the term epistasis to describe the departures from expected Mendelian ratios he observed in experimental crosses (Bateson, 1907). In the hundred years since Bateson’s work, the idea of genotypic context has taken on a broader meaning, to include any situation where the phenotypic manifestation of the genotype at a locus depends on the genotypes present at one or more other loci in the genome. Genotypic context is an important consideration because it underlies, among other things, how genetic risk factors contribute to complex diseases (Wei et al., 2014), the elusive missing heritability not accounted for by known genetic risk factors (Zuk et al., 2012), genetic breeding values in agricultural contexts ( Meuwissen et al., 2001; Hayes et al., 2009; Desta and Ortiz, 2014), and the short-term and long-term evolutionary trajectories of traits under natural or artificial selection (Hill et al., 2008). Genotypic context, therefore, has wide ranging implications for understanding the relationship between genotype and phenotype across much of biology.
But the concept of genotypic context is more complex than first appears because there are two distinct and in some sense contradictory ways to think about it. One perspective, which has been called physiological epistasis (Cheverud and Routman, 1995), focuses on the effects of genotypic context in determining phenotypes in an individual. This perspective is common in formal genetic analysis of mutants in Drosophila, nematodes, yeast, and other model organisms, where the term epistasis refers to a gene interaction in which the genotype of one gene results in a phenotype that masks the effects of another gene (Reiger et al., 1968). In evolutionary genetics, the term has taken on a broader meaning to refer loosely to any kind of gene interaction other than additive (Weinreich et al., 2013; Hartl, 2014). As Weinreich et al. (2013) put the matter, “epistasis can be regarded as our surprise at the phenotype when mutations are combined, given the constituent mutations’ individual effects.” This loose definition of epistasis allows for all sorts of nonadditive interactions among two or more nonallelic genes. This definition has been used extensively in describing alleles in natural populations whose phenotypic effects are not necessarily clear, and it also encompasses one of many mechanisms that can lead to incomplete penetrance or variable expressivity. We use the term physiological epistasis to include both the narrow and loose definitions, as both focus on the effects of gene interactions in a particular individual.
Another, different, definition of epistasis applies in quantitative genetic analysis of complex traits. In this case the focus of attention is often on causes of genetic variation including variance from a predicted phenotype due to additive contributions of alleles, variance due to dominance effects, and variance due to epistasis. This definition of epistasis has a precise and unambiguous meaning; however, the quantitative genetic perspective on epistasis differs from physiological epistasis in that epistatic variance is a function of the allele frequencies in a population (Hill et al., 2008). The effect of epistasis on the genetic variance at the population level effects has been called statistical epistasis (Cheverud and Routman, 1995), and its definition is elaborated further below.
With two distinct definitions of epistasis (physiological and statistical) referring to effects of genotypic context on the level of an individual or a population, one might well expect some confusion especially among geneticists with different backgrounds. The distinct perspectives on epistasis reflect the fact that genotypic context is a grand concept with differing implications in different fields of genetics. Both ways of looking at the subject have their own set of strengths and liabilities. Consequently, genotypic context should be considered from each point of view because, taken together, they are synergistic and offer a vantage point for comprehensive understanding of the biology underlying complex traits, inferring phenotype from genotype, and predicting evolutionary response.
Why care about genotypic context?
A focus on the genotypic context is particularly timely given a number of recent developments driven by the current technological revolution in biology. As acquiring whole genome sequencing data from humans, model organisms, and agriculturally important animals and plants becomes increasingly easy, the need to understand how to predict phenotypes and disease risk from genetic data becomes ever-more important. However, our ability to do this depends on understanding genotypic context from a variety of perspectives.
Increasingly inexpensive sequencing technology holds the promise that whole genome sequencing will be a routine part of medical care in the near future, with all the potential for personalized medicine that entails. Indeed, building upon the success of the 1000 Genomes Project (Altshuler et al., 2015), several projects to sequence tens or hundreds of thousands of individuals are now or will soon be underway. However, to realize the potential of personalized medicine requires an ability to predict an individual’s disease risk from genetic data, and this implies that understanding the role of genotypic context in shaping phenotypes will become increasingly important in medicine. To the extent to which the molecular details of how alleles interact in disease pathways are known, personalized medicine entails an understanding of physiological epistasis. However, especially in human genetics, statistical epistasis is equally crucial, because the accuracy of predictive models of disease risk derived from population-level studies depends on understanding the estimation and magnitude of statistical epistasis.
The genomics revolution has had a striking impact in other fields as well. In animal breeding, the ability to predict the short-term response to selection from whole genome data has had a profound impact of the efficiency of agricultural improvement programs, and genome prediction (using all markers to predict the response to selection on a trait) has rapidly become a key technique in both animal and plant breeding (Hayes et al., 2009; Desta and Ortiz, 2014). Genome prediction is also being used increasingly in human disease studies (de los Campos et al., 2010), albeit with important caveats (Wray et al., 2013). A remaining challenge is to incorporate information about non-additive effects, including statistical epistasis, into these modeling approaches. Understanding the relative importance of statistical epistasis in explaining the genetic variation in traits is thus of crucial to the continued improvement of genomic prediction models in both agricultural and medical contexts.
A final context where understanding genotypic context will be increasingly important is genome editing. Ultimately, if we are ever going to safely modify genes in humans or other animals, we will need a detailed understanding of how the modifications we would like to make will behave in more than one genetic background. This may not be as simple as it appears, even in the case of restoring a wild-type allele, as the phenotypic effects of a particular mutation may depend on the genotypic context, which could involve both the network-level interactions captured by physiological epistasis and the higher-order effects of non-additive interactions generally, as described by statistical epistasis.
Ultimately, in all these cases – personalized medicine, crop and livestock improvement, and genome editing – the goal is to predict some kind of phenotypic response at the individual or population level. Reliable prediction will require careful accounting of how and why genetic context impacts phenotype, and often will involved understanding the role of epistasis at multiple levels. In the rest of this perspective, we first define and give examples of physiological and statistical epistasis, and then return to the question of predicting phenotype from genotype to assess what an understanding of epistasis reveals.
Physiological epistasis: Genotypic context in individuals
Bateson’s (1907) classical definition of epistasis is by far the least ambiguous and most well suited to formal genetic analysis of simple Mendelian (mostly laboratory) mutants. In this classical definition, the phenotypic effect of a particular mutation is masked by a mutation at a different locus. In this way, the effect of the first mutation is dependent on the allelic state (genotypic context) elsewhere in the genome. This type of masking epistasis is far more common among laboratory mutants in model organisms than in natural populations, however it has great utility in the genetic analysis of biosynthetic pathways, developmental pathways, and other genetic networks (see, for example, Cairns et al., 1992; Van Driessche et al., 2005; Huang and Sternberg, 2006; Ririe et al., 2008; Gupta et al., 2012). More broadly, physiological epistasis refers to any situation in which the genotype at one locus modifies the phenotypic expression of the genotype at another locus. Such genotypic effects have been recognized since the origin of modern genetics.
Some of the clearest demonstrations of the effect of genotypic context come from studies in model organisms where the same mutation has been expressed in a large number of genetic backgrounds. Two recent papers (He et al., 2014; Chow et al., 2015) used this approach to show that mutations which reduce eye size in a standard laboratory background express a highly heritable, quantitative distribution of eye phenotypes when expressed in the > 150 natural genetic backgrounds represented by the Drosophila Genetic Reference Panel (Mackay et al., 2012). Other studies have measured the phenotypes of a large number of mutations in two different backgrounds (Vu et al., 2015) and similarly concluded that, for a large fraction of null mutations, the phenotypic expression of the mutation varies according to genetic background. A final example is the expression of the scalloped-wing mutation in D. melanogaster, in which genotypic context affecting the global transcriptome results in differences in phenotype that can be as large as the main effects of the mutation (Dworkin et al., 2009). In all these examples, the key point is that the phenotypic expression of a particular mutation varies tremendously and heritably, depending on the set of interacting alleles that happen to be present.
The role of physiological epistasis can also be understood in classical genetic terms by considering the phenotypic outcomes of a simple cross between two individuals heterozygous at two independent loci (a dihybrid cross). If each of the two loci have a dominant allele, and if epistatic interactions are absent, classical Mendelian segregation would predict 9 : 3 : 3 : 1 phenotypic ratio, describing the proportions of offspring that manifest both dominant phenotypes, one or the other dominant phenotype, or the recessive phenotype. With complete dominance there are four genotypic classes and, in principle, from 1–4 possible phenotypes. All possible mappings of phenotypes onto genotypes yields exactly 11 distinct phenotypic ratios in the F2 generation of a dihybrid cross (Hartl and Maruyama, 1968). Dropping the assumption of complete dominance results in 9 genotypic classes and, in principle, from 1–9 possible phenotypes. In this case, all possible mappings of phenotypes onto genotypes yields a total of 147 distinct F2 phenotypic ratios (Hartl and Maruyama, 1968). Our point is that, even at the level of two genes with only two alleles of each, the possible varieties of physiological epistasis are impressive. A perennial issue is how best to quantify these effects at the level of the individual organism, which we discuss in more detail in Box 1. As we shall emphasize later, genotypic effects at the level of the population are measured very differently than those at the level of the individual.
BOX 1. Measuring physiological epistasis.
The effects of physiological epistasis on the phenotype of an individual can be formalized with a quantitative model, which we expand on here. Table 1 gives an example of physiological epistasis for the nine genotypes with two alleles at each of two loci. In each box, wij indicates the phenotype of the corresponding genotype, with the subscripts indicating the number of A and B alleles in the genotype (i, j = 2, 1, or 0). These phenotypes can also be expressed completely equivalently in terms of the main effects of the A gene (m1) and B gene (m2), their dominance effects (d1 and d2), and also five epistatic effects, eij, that are assigned arbitrarily to the genotypes that are either homozygous for both genes or heterozygous for both genes. In this example, we consider a binary phenotype that can be either +1 or −1, and assign the +1 phenotype to individuals with A–B– genotypes and −1 to all others. (The dash “−” is a “wild card” that can represent either the uppercase or lowercase allele of either gene.) The type of physiological epistasis specified by the genotype-phenotype correspondences in Table 1 is known as complementary epistasis (Crow and Kimura, 1970), which in the F2 generation of a dihybrid cross would yield a 9 : 7 ratio of phenotypes. In this example, it is clear that m1 = m2 = +1, d1 = d2 = 0, e11 = e02 = e00 = +1, and e22 = e20 = −1. The epistatic effects in this example are very large, in fact equal to the main effects of the alleles, and the phenotypes of five of the genotypes deviate substantially from what they would be were there no gene interactions.
Increasing the number of genes results in an exponential increase in the number of possible epistatic interactions. Even with only two alleles per gene, for n genes the genotype-phenotype correspondences, parameterized as in Table 1, have n main effects, n dominance effects, and 3n - 2n possible epistatic interactions (even more if parent-of-origin effects are included). Some of these will be two-gene interactions, others three-gene, four-gene, and so forth on up to n-gene interactions. Given the exponentially large number of possible effects, systematically characterizing multigene interactions remains a significant challenge, although possible in some limited cases (i.e., haploid organisms or homoyzgous diploids) (Heckendorn and Whitley, 1997; Iglesias et al., 2008; Weinreich et al., 2013).
Physiological epistasis has often been presumed to be ubiquitous given that many genes interact in complex ways with other genes. However, the daunting number of possible interactions (Box 1) has made explicit measurements of the prevalence of higher-order epistatic effects rare. One exception is the work of Weinreich and collaborators (2013), who estimated higher-order epistasis in 14 experimental data sets as well as simulated data from two theoretical fitness landscapes. They find that, in most cases, the magnitude of the effects of second-order and each higher-order level of epistasis can be as great or greater than those of the main effects themselves (see Fig. 1 in Weinreich et al., 2013). In most of the examples the mutant sites are amino acid replacements in the same protein molecule, where significant higher-order interaction effects might be expected, but the data also include fitness of visible mutant genes in D. melanogaster and Aspergillus niger as well as beneficial mutations that arise in populations of Methalobacterium extorquens and E. coli. Likewise, Young and Durbin (2014) have estimated that pairwise and higher-order interactions account for an average of nearly 25% of the phenotypic variance across 46 traits in laboratory crosses of S. cerevisiae. Also in yeast, the effects of higher-order epistasis on fitness appear as diminishing-returns epistasis among beneficial mutations (Kryazhimskiy et al., 2014).
Statistical epistasis: Genotypic context in populations
In model organisms, or those used in agriculture, physiological epistasis can be studied directly in genetic crosses, with transgenes or DNA editing, or by other experimental approaches. In human genetics, direct studies are rarely possible, and inferences about physiological epistasis instead rely on estimates of statistical epistasis in populations. This is problematical because as we discuss in more detail below, the failure to detect statistical epistasis does not imply that physiological epistasis is absent or unimportant.
Physiological epistasis arises from the network structure of cellular metabolic and signaling pathways and the interactions within and among the proteins and other components that make up and regulate these pathways. The complexity of biological systems and the need of organisms to interact with their environment and to adjust, acclimatize, or maintain homeostasis implies that physiological epistasis is likely to be pervasive. This inference is often misleading when extrapolated to statistical epistasis because there is an asymmetry in their implications. On the one hand, high levels of statistical epistasis always imply substantial physiological epistasis, but on the other hand physiological epistasis can be pervasive and still result in negligible levels of statistical epistasis.
To illustrate why this is so, we first need to briefly discuss how statistical epistasis is estimated. This concept originates with R. A. Fisher’s analysis of sources of genetic variation that drive evolutionary change (Fisher, 1918, 1930; Moran and Smith, 1966), in which he partitioned the genetic variance of a trait into several different components by fitting an additive model of the genotypic values. In this framework phenotypic values are predicted by an additive a model of gene action in which each allele of each gene has a phenotypic effect on the trait, and the phenotypic effects are additive (that is, heterozygote genotypes have a phenotype exactly intermediate between the alternate homozygotes) (Falconer and Mackay, 1996; Lynch and Walsh, 1998). The variance among the predicted phenotypic values in an additive model is called the additive genetic variance (VA). In cases in which the heterozygous genotypes have a phenotype that is not exactly intermediate between the corresponding homozygous genotypes, the variance due to deviations of the heterozygous genotypes from the additive model is the dominance variance (VD). Finally, the variance due to the deviations of each multilocus genotype from the additive model allowing for dominance is the epistatic or interaction variance (VI). This is what we have been calling the statistical epistasis. These variance components can be estimated from covariances among relatives. For example, in the absence of epistasis, the additive genetic variance can be estimated as twice the covariance in phenotype between parent and offspring.
Because there are many possible combinations of multi-locus epistasis among genes, it is tempting to infer that statistical epistasis must be important, but there are three reasons for challenging this inference. The first is the hierarchical manner in which the variance components are estimated from the genotypic values. Since an additive model is fit by least squares, some of the effects of dominance become incorporated into the additive variance, and likewise some of the effects of epistasis are tallied with the additive variance and some with dominance variance (See Figure 1 and related text below). This means that, in their contribution to the genetic variance, many of the effects of physiological epistasis are allocated to the additive and dominance components of variation and do not contribute to statistical epistasis. Second, the contribution of physiological epistasis to statistical epistasis depends on the population frequencies of the multilocus genotypes, and the greater the number of interacting genes, the smaller the population frequency of the multilocus genotypes. Finally, as emphasized by Hill et al. (2008), the distribution of allele frequencies in natural populations is typically J-shaped or U-shaped, so that multilocus genotypes are even more rare than one might naively expect from uniform allele frequencies. In other words, given the allele distributions in the human population, the chance of a sample including enough individuals of each genotype to give significant effects may be very small.
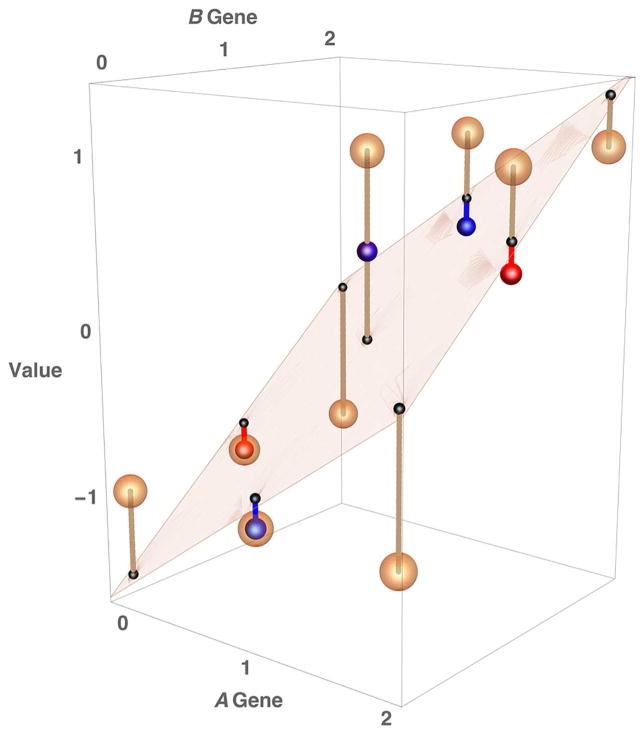
Fig. 1.
Hierarchical fitting of variance components obscures physiological epistasis in population studies. (A) Genotype-phenotype correspondence in a model of complementary epistasis, in which the phenotypes of genotypes A– B– are assigned values of +1 and genotypes aa ––, –– bb, and aa bb are assigned values −1 (as in Table 1). Genotypes are represented as brown spheres, and the deviation of each phenotypic value from the population mean is shown as a brown dashed line. The frequencies of A and B both set equal to 0.459, as in Crow and Kimura (1970, p. 176). The average of the squared deviations is the total genetic variance, in this case equal to 1.000. (B) The plane is the least-squares fit to an additive model of gene action. The black spheres are the predicted phenotypes based on an additive model, and the additive genetic variance is the variance among these predicted phenotypes (in this example 0.582). (C) The red spheres depict the predicted phenotypes based on a model that includes additive as well as dominance effects, but no epistasis. The dashed red lines are the deviations from the additive model due to dominance. The dominance variance equals the average of these squared deviations, in this case 0.247. After allocating the additive and dominance variance, the remaining variance is the epistatic variance (statistical epistasis), which is a mere 17.1% of the total genetic variance.
The typical J- or U-shaped distribution of allele frequencies is a serious limitation in human population studies because statistical epistasis is usually maximized for allele frequencies that are nearly equal. In model and agricultural organisms, experimental populations can be contrived that have nearly equal allele frequencies, and this is one reason why high levels of statistical epistasis are much more often reported in these organisms than in humans. This is true even with statistical methods designed specifically for increased power to detect statistical epistasis in human populations (Deng et al., 2014). Furthermore, J-shaped or U-shaped distributions of allele frequencies imply that many combinations of alleles that might potentially be strongly epistatic in the physiological sense will be rare or nonexistent in samples typical of those studied in human populations.
As a simple example of how the hierarchical apportionment of genetic variance can allocate nonadditive interactions to the additive genetic variance, consider the effect of dominance. When a dominant allele is rare, almost all of the genetic variance contributed by dominance is additive variance, which may seem paradoxical. However there is an intuitive explanation: when a dominant allele is rare, the genotypic value of the heterozygous genotype is transmitted from parent to offspring, and a high parent-to-offspring correlation implies a high additive variance. At the other end of the spectrum, when a dominant allele is nearly fixed, it reduces the parent-to-offspring correlation and hence the additive variance to nearly zero, basically because most offspring of any parent have the same phenotype. The same sort of reasoning applies to statistical epistasis, as the hierarchical nature of estimating the variance components and the typically J- or U-shaped distribution of allele frequencies means that much of the genetic variance due to statistical epistasis is allocated to the additive and dominance components of variance.
The principles of statistical epistasis are illustrated in Fig. 1 for two genes each with two alleles exhibiting physiological epistasis, where the y axis depicts the phenotypic values of the 9 possible genotypes. In this example, genotypes A– B– have phenotypic values of +1 whereas genotypes aa–– and –– bb have phenotypic values of −1. This specific type of physiological epistasis is complementary epistasis as in Table 1. In the classical terminology of epistasis, aa is epistatic to B– and bb is epistatic to A–. In Fig. 1A, each dashed line represents the deviation (distance) of each phenotypic value from the population mean. We assume random mating and linkage equilibrium with allele frequencies of A and B both equal to 0.459 so that the mean phenotypic value in the population equals 0. The average of the squared deviations equals the total genetic variance, which in this example equals 1.0. (The example is taken from Crow and Kimura (1970, p. 126), where the calculations of the variance components are described in detail.)
Table 1.
Phenotypic values with complementary epistasis at two diploid loci
| AA | Aa | aa | |
|---|---|---|---|
| BB |
w22 m1 + m2 + e22 1 |
w12 m2 + d1 1 |
w02 m2 ? m1 + e02 −1 |
| Bb |
w21 m1 + d2 1 |
w11 d1 + d2 + e11 1 |
w01 −m1 + d2 −1 |
| bb |
w20 m1 − m2 + e20 −1 |
w01 −m2 + d1 −1 |
w00 −m1 −m2 + e00 −1 |
In Fig. 1A it is obvious that much of the total genetic variance results from the physiological epistasis between the two genes. If this were a simple Mendelian trait with contrasting phenotypes (for example, of +1 corresponded to purple flowers and −1 to white flowers), then classical genetic crosses would reveal the genotype-phenotype correspondence and the physiological epistasis would be revealed.
With multifactorial quantitative traits in natural populations, the genotype-phenotype correspondence is unknown. Any genetic effects of a gene (or a pair of genes) on a trait must be inferred from population studies, in particular from correlations between relatives. Prominent among these is the parent-to-offspring correlation, which is a function of the additive genetic variance of the trait, which as indicated above is the variance among the phenotypic values predicted by an additive a model of gene action in which each allele of each gene has a phenotypic effect on the trait, and the phenotypic effects are additive with heterozygote genotypes having a phenotype exactly intermediate between the alternate homozygotes. The predicted phenotypic values in an additive model are shown by the black spheres in Fig. 1B, which lie on a plane that, in practice, is fitted to the actual phenotypic values by least squares. The additive genetic variance is the variance among these predicted values, which in this case equals 0.582. The deviations from the additive model are again shown as brown dashed lines, and on average they are much shorter than in Fig. 1A. This means that more than half of the variance among genotypes in Fig. 1A is included in the additive genetic variance, even though in this example all of the phenotypic variability derives from physiological epistasis
In population studies, the correlation between certain types of relatives, such as siblings, is a function of the additive genetic variance but also of the dominance variance. As noted above, the dominance variance is the variance among the phenotypic values predicted by a model of gene action in which the heterozygous genotypes can have a phenotype that is not exactly intermediate between the corresponding homozygous genotypes. Such a model for our example is shown in Fig. 1C, in which the dashed red lines depict the deviations from the additive model due to dominance. The dominance variance is the average of the squares of these deviations. In this example the dominance variance equals 0.247, and so almost a quarter of the variance among genotypes in Fig. 1A is included in the dominance variance.
Note in Fig. 1C that the lengths of the dashed brown lines are very much diminished from those in Fig. 1A. It is these lines that depict the statistical (epistatic) variance. In this example, the statistical variance is only 0.171. What’s worse, in a more realistic model of complementary epistasis in a complex disease in which the population frequency of −1 phenotypes is 1%, the epistatic variance equals a mere 0.25% of the total genetic variance. In other words, although the genotypes exhibit a great deal of physiological epistasis (Fig. 1A), there is relatively little statistical epistasis. The statistical epistasis is minimized owing to the hierarchical allocation of variance components, the first share is allocated to the additive genetic variance, the next portion to dominance variance, and the leftovers to the epistatic variance (statistical epistasis).
Low values of statistical epistasis are not unique to any particular type of physiological epistasis. Hill and colleagues (Hill et al., 2008; Mäki-Tanila and Hill, 2014) have analyzed several models of multilocus epistasis including multilocus complementary epistasis; duplicate factor epistasis, in which a particular phenotype results from homozygosity at two or more loci; and diminishing-returns epistasis based on a model in which the phenotype is proportional to the flux of substrate through a linear metabolic pathway. For two loci and a U-shaped distribution of allele frequencies, each of these models of epistasis results in the additive variance accounting for a high proportion (70–90%) of the total genetic variance; however as the number of loci increases this proportion decreases, in extreme cases to 0. But as the authors point out, the extreme models do not explain the covariance between siblings (which requires a nonzero additive variance), the approximate linear response to artificial selection, or the near linear decrease in fitness with degree of inbreeding (inbreeding depression) (Hill et al., 2008). The overall conclusion is that physiological epistasis is unlikely to produce much statistical epistasis because much of the variance due to physiological epistasis is allocated to the additive genetic variance.
Does statistical epistasis account for missing (“phantom”) heritability?
Since virtually anyone will concede that physiological epistasis is important and pervasive, why does it matter whether statistical epistasis is or is not a significant part of the genetic variance? It matters because of the assumption that tracing the sources of genetic variation will reveal metabolic and regulatory networks for complex diseases to improve disease risk prediction and also highlight new drug targets for prevention or therapeutic intervention. Genome-wide association studies have already identified more than 6000 genetic factors associated with more than 500 quantitative traits and complex diseases in humans (Robinson et al., 2014). Yet for most complex diseases, the genetic risk factors result in a modest (10–50%) increase in risk, and in the aggregate they account for only part (typically less than 50%) of the phenotypic variation attributable to the additive effects of genes (i.e., the heritability) (Manolio et al., 2009). For example, the top 40 gene contributing to variation in adult human height account for less than 10 percent of the heritability (Manolio et al., 2009), and a total of 697 genetic factors with statistically significant effects on adult height explain only about 20 percent the heritability (Wood et al., 2014a).
The part of the heritability not accounted for by identified genetic risk factors has become known as the “missing heritability,” and many explanations have been offered. Among the hypotheses put forward to account for the missing heritability are lack of sufficiently powerful statistical methods to detect causal variants (Golan et al., 2014; Yang et al., 2015), common variants with effects too small to detect with typical sample sizes (Manolio et al., 2009), rare variants with large effects (Manolio et al., 2009), dominance (Zhu et al., 2015), physiological epistasis (Manolio et al., 2009; Hemani et al., 2013; Zuk et al., 2012), tandem repeat polymorphisms (Hannan, 2010), and epigenetic effects (Trerotola et al., 2015).
Some authors argue that the missing heritability is not really missing but “phantom” owing to an overestimation of heritability from phenotypic correlations among relatives, notably comparison of identical versus same-sex fraternal twins (Zuk et al., 2012). Estimates of heritability from family studies can be biased upward by interactions between genes (physiological epistasis), by genotype-by-environment interactions in which some genotypes are more sensitive than others to environmental influences, and by unrecognized correlations in environments among relatives.
Other authors argue that the fraction of the heritability that went missing is in reality rather small. The evidence is that, when all genetic factors are taken into account, including those whose effects do not reach statistical significance, then a high proportion of the heritability for complex traits and diseases can be explained (Lee et al., 2011; Yang et al., 2013). Hundreds or thousands of genetic factors of small effect might therefore contribute to complex traits and diseases. In one study, Yang and colleagues (2015) used genetic relationship matrices stratified by minor allele frequency and linkage disequilibrium to impute about 17 million causal variants affecting adult height and body mass index among 44,126 unrelated individuals. Taking into account the likely overestimate of heritability based on family studies, the imputed genetic factors accounted for 80–90% of heritability for adult height and 70–90% of heritability for body mass index (Yang et al., 2015). Some 25–50% of the genetic variation in these traits could be attributed to common variants.
The approach of Yang et al. (2015) has been criticized on grounds that its heritability estimates are inaccurate even when the model assumptions are met exactly, and that they are biased and unstable in the presence of population stratification and measurement error in either the phenotype or the genetic relatedness matrix (Krishna Kumar et al., 2016a). Yang et al. (2016) rebut the first criticism by showing that Krishna Kumar et al. (2016a) incorrectly impute assumptions not required by the model, and they also suggest that the second criticism arises from failure to remove cryptic relatedness. The debate continues about the accuracy of procedures to remove related individuals, the effects of noisy estimates of the genetic relatedness matrix on filtering cryptic relatedness, and ultimately on estimates of heritability (Krishna Kumar et al., 2016b).
Estimates of heritability and the contribution of genotypic effects to complex traits are more easily carried out in model organisms such as Drosophila or yeast. In Drosophila, for example, studies of various quantitative traits such as life-history traits, olfactory response, or startle behavior in crosses or in artificial laboratory populations derived from sequenced inbred lines indicate that, while most of the genetic variation is additive, the majority of genetic factors influencing each trait participated in at least one epistatic interaction (Huang et al., 2012). The type of epistasis is largely suppressing epistasis (Swarup et al., 2012), in which the common variant buffers against the effects of new mutations. Most of the genetic factors associated with such traits do not replicate across populations (Mackay and Moore, 2014), suggesting that genetic background effects are common, although it is difficult to rule out the possibility that this could be due in part to false positives and lack of statistical power. Epistasis also figures importantly in some of the 46 quantitative traits studied among the progeny of a yeast cross (Bloom et al., 2013); while genetic factors with significant effects accounted for most of the additive genetic variance, some traits also showed significant epistatic variation. It must be emphasized, however, that in both Drosophila and yeast the artificial populations are contrived to have nearly equal allele frequencies at all segregating loci, which contrasts markedly with the U-shaped or J-shaped allele-frequency distributions expected in natural populations (Hill et al., 2008). This distinction alone would make statistical epistasis more readily detectable in artificial populations of model organisms than in natural human populations.
In any case, statistical epistasis is not difficult to find in artificial populations of model organisms, which is unsurprising given the ubiquity of physiological epistasis. However, there is little evidence that statistical epistasis is readily detectable in human populations, despite considerable attention to this problem (reviewed in Wei et al., 2014). Even when significant statistical epistasis can be identified, as in a recent study searching for associations between pairs of SNPs and gene expression in peripheral blood in a large cohort (Hemani et al., 2014), alternative additive explanations are difficult to rule out completely (Wood et al., 2014b). Taken as a whole, the search for statistical epistasis affecting complex traits in humans strongly suggests that interaction effects of similar magnitude to main (additive) effects do not exist. Although methods for detecting epistasis are generally underpowered (Wei et al., 2014), and it is difficult to rule out very weak pairwise interactions, there is little evidence that statistical epistasis contributes a substantial amount to the total genetic variance (Wei et al., 2014). Even in twin studies, for the majority of traits, the observed twin correlations can be ascribed to a simple model with only additive variance and are inconsistent with large effects due to shared environment, dominance, or epistatic variance (Polderman et al., 2015). The finding that, when all contributing genetic factors are taken into account for complex traits, most of the missing heritability reappears, is also consistent with a model of largely additive genetic variance. (Full disclosure: the additive genetic variance also includes the additive-by-additive components of the epistatic variance, if any.) Considering all the data presently available from genome-wide association studies of a large number of quantitative and complex traits, Fisher’s (1918) model of genetic correlations being due to the additive effects of a large number of genes of mostly small effect was singularly prescient. A low level of statistical epistasis found in population studies does not imply that physiological epistasis is unimportant. It is still critically important for disease understanding, prediction, prognosis, prevention, and treatment. But it does imply that the interactions underlying physiological epistasis are unlikely to be discovered by looking for statistical epistasis.
Conclusions
The importance of genotypic context and understanding the various modes of epistasis is increasingly important given the clear relevance to personalized medicine (Collins, 2010). We argue that understanding the biology of genotypic context requires clearly distinguishing between physiological epistasis that affects the expression of particular genotypes in individuals and statistical epistasis that describes genetic variation in populations.
To date, there is relatively little evidence for substantial amounts of statistical epistasis in human populations or most natural populations of other organisms. This conclusion is supported by a number of lines of evidence, including the observation that genome prediction models, which typically do not include higher-order interactions (although this is changing, e.g., Hu et al., 2011), are remarkably efficient at predicting population-level phenotypes in both human disease (e.g., Lee et al., 2011; Yang et al., 2013) and agricultural contexts (e.g., Hayes et al., 2009; Desta and Ortiz 2014).
In contrast, in model organisms or those used in agriculture, studies of genetic crosses and experimental populations reveal substantial statistical epistasis, in some cases amounting to 25% or more of the total phenotypic variance. What accounts for the difference? Are humans different from other organisms? Not likely. In our opinion, the difference between natural and artificial populations lies in the typically J-shaped or U-shaped distribution of allele frequencies, which minimizes the effects of statistical epistasis. When the allele frequencies are more nearly equal, as they are in artificial populations, the effects of statistical epistasis are maximized. It is also possible that the genetic basis of human disease traits differs qualitatively from the genetic basis of quantitative traits. For example, genetic variation in disease traits may be maintained largely by mutation-selection balance whereas genetic variation for quantitative traits is maintained by stabilizing selection for an intermediate optimum. This may be true but irrelevant if, as we believe, statistical epistasis is low in human populations because the effects of physiological epistasis largely vanish under hierarchical variance partitioning.
Importantly, a low level of statistical epistasis in human populations does not imply that physiological epistasis is either weak or rare. In fact, evidence from model organisms in particular suggests that physiological epistasis is ubiquitous (Dworkin et al., 2009; Corbett-Detig et al., 2013; He et al., 2014; Chow et al., 2015; Vu et al., 2015), often encompassing more than pairwise gene-by-gene interactions to include higher-order effects (Weinreich et al., 2013; Hartl, 2014) and even gene-by-genome interactions. But then, with so little statistical epistasis detectable in human populations, on what basis can one predict how genotypic context influences phenotypic expression in a particular individual? The low level of statistical epistasis is a conundrum and a disappointment. Probably the best that one can do under the circumstances, using present methods, is to make predictions based on the main, additive effects of alleles, recognize the uncertainty of such predictions, and hope for the best.
Acknowledgments
This work was supported by NIH grants AI106734 and AI099105 to DLH. We are very grateful to Daniel M. Weinreich, Shamil R. Sunyaev, C. Brandon Ogbunugafor, Christopher L. Hartl, and three anonymous reviewers for their comments and suggestions for improving the manuscript.
Footnotes
Conflicts of interest: None for either author
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Timothy B. Sackton, Informatics Group, 38 Oxford Street, Harvard University, Cambridge MA 02139
Daniel L. Hartl, Department of Organismic and Evolutionary Biology, 16 Divinity Avenue, Harvard University, Cambridge MA 02139.
References
- Altshuler DM, Durbin RM, Abecasis GR, Bentley DR, Chakravarti A, Clark AG, Donnelly P, Eichler EE, Flicek P, Gabriel SB, et al. A global reference for human genetic variation. Nature. 2015;526:68–74. doi: 10.1038/nature15393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bateson W. The progress of genetics since the rediscovery of Mendel’s paper. Progressus Rei Botanicae. 1907;1:368–382. [Google Scholar]
- Bloom JS, Ehrenreich IM, Loo WT, Lite TLV, Kruglyak L. Finding the sources of missing heritability in a yeast cross. Nature. 2013;494:234–237. doi: 10.1038/nature11867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cairns BR, Ramer SW, Kornberg RD. Order of action of components in the yeast pheromone response pathway revealed with a dominant allele of the STE11 kinase and the multiple phosphorylation of the STE7 kinase. Genes Dev. 1992;6:1305–1318. doi: 10.1101/gad.6.7.1305. [DOI] [PubMed] [Google Scholar]
- Cheverud JM, Routman EJ. Epistasis and its contribution to genetic variance components. Genetics. 1995;139:1455–1461. doi: 10.1093/genetics/139.3.1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chow CY, Kelsey KJ, Wolfner MF, Clark AG. Candidate genetic modifiers of retinitis pigmentosa identified by exploiting natural variation in Drosophila. Hum Mol Genet. 2015;25:651–659. doi: 10.1093/hmg/ddv502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins FS. Has the revolution arrived? Nature. 2010;464:674–675. doi: 10.1038/464674a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbett-Detig RB, Zhou J, Clark AG, Hartl DL, Ayroles JF. Genetic incompatibilities are widespread within species. Nature. 2013;504:135–137. doi: 10.1038/nature12678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow JF, Kimura M. An Introduction to Population Genetics Theory. New York: Harper & Row; 1970. [Google Scholar]
- de los Campos G, Gianola D, Allison DB. Predicting genetic predisposition in humans: the promise of whole-genome markers. Nat Rev Genet. 2010;11:880–886. doi: 10.1038/nrg2898. [DOI] [PubMed] [Google Scholar]
- Deng WQ, Asma S, Paré G. Meta-analysis of SNPs involved in variance heterogeneity using Levene’s test for equal variances. Eur J Hum Genet. 2014;22:427–430. doi: 10.1038/ejhg.2013.166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desta ZA, Ortiz R. Genomic selection: genome-wide prediction in plant improvement. Trends Plant Sci. 2014;19:592–601. doi: 10.1016/j.tplants.2014.05.006. [DOI] [PubMed] [Google Scholar]
- Dworkin I, Kennerly E, Tack D, Hutchinson J, Brown J, Mahaffey J, Gibson G. Genomic consequences of background effects on scalloped mutant expressivity in the wing of Drosophila melanogaster. Genetics. 2009;181:1065–1076. doi: 10.1534/genetics.108.096453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falconer DS, Mackay TFC. Introduction to Quantitative Genetics. 2. London: Longman; 1996. [Google Scholar]
- Fisher RA. The correlation between relatives on the supposition of Mendelian inheritance. Phil Trans R Soc Edinburgh. 1918;52:399–433. [Google Scholar]
- Fisher RA. The Genetical Theory of Natural Selection. Oxford: Oxford University Press; 1930. [Google Scholar]
- Golan D, Lander ES, Rosset S. Measuring missing heritability: Inferring the contribution of common variants. Proc Nat Acad Sci USA. 2014;111:E5272–E5281. doi: 10.1073/pnas.1419064111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta BP, Hanna-Rose W, Sternberg PW. WormBook: The Online Review of C. elegans Biology [Internet] Pasadena (CA): 2012. Morphogeneis of the vulva and the vulval-uterine connection. doi:101895/wormbook11521. Available from: http://wwwwormbookorg/chapters/www_vulvamorph/vulvamorphhtml. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hannan AJ. Tandem repeat polymorphisms: modulators of disease susceptibility and candidates for ‘missing heritability’. Trends Genet. 2010;26:59–65. doi: 10.1016/j.tig.2009.11.008. [DOI] [PubMed] [Google Scholar]
- Hartl DL. What can we learn from fitness landscapes? Curr Opinion Microbiol. 2014;21:51–57. doi: 10.1016/j.mib.2014.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartl DL, Maruyama T. Phenogram enumeration: The number of genotype-phenotype correspondences in genetic systems. J Theoret Biol. 1968;20:129–163. doi: 10.1016/0022-5193(68)90186-0. [DOI] [PubMed] [Google Scholar]
- Hayes BJ, Bowman PJ, Chamberlain AJ, Goddard ME. Invited review: Genomic selection in dairy cattle: Progress and challenges. J Dairy Sci. 2009;92:433–443. doi: 10.3168/jds.2008-1646. [DOI] [PubMed] [Google Scholar]
- He BZ, Ludwig MZ, Dickerson DA, Barse L, Arun B, Vilhjálmsson BJ, Park SY, Tamarina NA, Selleck SB, Wittkopp PJ, et al. Effect of genetic variation in a Drosophila model of diabetes-associated misfolded human proinsulin. Genetics. 2014;196:557–567. doi: 10.1534/genetics.113.157800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckendorn RB, Whitley D. Predicting epistasis from mathematical models. Evol Comput. 1997;7:69–101. doi: 10.1162/evco.1999.7.1.69. [DOI] [PubMed] [Google Scholar]
- Hemani G, Knott S, Haley C. An evolutionary perspective on epistasis and the missing heritability. Plos Genetics. 2013;9 doi: 10.1371/journal.pgen.1003295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hemani G, Shakhbazov K, Westra HJ, Esko T, Henders AK, McRae AF, Yang J, Gibson G, Martin NG, Metspalu A, et al. Detection and replication of epistasis influencing transcription in humans. Nature. 2014;508:249–253. doi: 10.1038/nature13005. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Hill WG, Goddard ME, Visscher PM. Data and theory point to mainly additive genetic variance for complex traits. PLoS Genet. 2008;4:e1000008. doi: 10.1371/journal.pgen.1000008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu T, Sinnott-Armstrong NA, Kiralis JW, Andrew AS, Karagas MR, Moore JH. Characterizing genetic interactions in human disease association studies using statistical epistasis networks. BMC Bioinformatics. 2011;12 doi: 10.1186/1471-2105-12-364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang LS, Sternberg PW. WormBook, The. C elegans Research Community, WormBook, [Internet] Pasadena (CA): 2006. Jun 14, Genetic dissection of developmental pathways. doi:101895/wormbook1882. http://wwwwormbookorg/chapters/www_epistasis2/epistasishtml. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang W, Richards S, Carbone MA, Zhu DH, Anholt RRH, Ayroles JF, Duncan L, Jordan KW, Lawrence F, Magwire MM, et al. Epistasis dominates the genetic architecture of Drosophila quantitative traits. Proc Nat Acad Sci USA. 2012;109:15553–15559. doi: 10.1073/pnas.1213423109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iglesias M, Verschoren A, Vidal TC. Higher order functions and Walsh coefficients revisited. Bull Belg Math Soc Simon Stevin. 2008;15:385–568. [Google Scholar]
- Krishna Kumar S, Feldman MW, Rehkopf DH, Tuljapurkar S. Limitations of GCTA as a solution to the missing heritability problem. Proc Nat Acad Sci USA. 2016a;113:E813–E813. doi: 10.1073/pnas.1520109113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishna Kumar S, Feldman MW, Rehkopf DH, Tuljapurkar S. Response to commentary on “Limitations of GCTA as a solution to the missing heritability problem”. bioRxiv. 2016b doi: 10.1073/pnas.1520109113. preprint first posted online Feb. 17, 2016; http://dx.doi.org/2010.1101/039594. [DOI] [PMC free article] [PubMed]
- Kryazhimskiy S, Rice DP, Jerison ER, Desai MM. Global epistasis makes adaptation predictable despite sequence-level stochasticity. Science. 2014;344:1519–1522. doi: 10.1126/science.1250939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Wray NR, Goddard ME, Visscher PM. Estimating missing heritability for disease from genome-wide association studies. Am J Hum Genet. 2011;88:294–305. doi: 10.1016/j.ajhg.2011.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Walsh B. Genetics and Analysis of Quantitative Traits. Sunderland, MA: Sinauer; 1998. [Google Scholar]
- Mackay TF, Richards S, Stone EA, Barbadilla A, Ayroles JF, Zhu D, Casillas S, Han Y, Magwire MM, Cridland JM, et al. The Drosophila melanogaster Genetic Reference Panel. Nature. 2012;482:173–178. doi: 10.1038/nature10811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay TFC, Moore JH. Why epistasis is important for tackling complex human disease genetics. Genome Med. 2014;6:42. doi: 10.1186/gm561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mäki-Tanila A, Hill WG. Influence of gene interaction on complex trait variation with multilocus models. Genetics. 2014;198:355–367. doi: 10.1534/genetics.114.165282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen THE, Hayes BJ, Goddard ME. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001;157:1819–1829. doi: 10.1093/genetics/157.4.1819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran PAP, Smith CAB. Commentary on R.A. Fisher’s paper on the correlation between relatives on the supposition of Mendelian inheritance, Eugenics Laboratory Memoirs XLI. Cambridge, UK: Cambridge University Press; 1966. [Google Scholar]
- Polderman TJC, Benyamin B, de Leeuw CA, Sullivan PF, van Bochoven A, Visscher PM, Posthuma D. Meta-analysis of the heritability of human traits based on fifty years of twin studies. Nat Genet. 2015;47:702–709. doi: 10.1038/ng.3285. [DOI] [PubMed] [Google Scholar]
- Reiger R, Michaelis A, Green MM. A Glossary of Genetics and Cytogenetics. New York: Springer-Verlag; 1968. [Google Scholar]
- Ririe TO, Fernandes JS, Sternberg PW. The Caenorhabditis elegans vulva: a post-embryonic gene regulatory network controlling organogenesis. Proc Natl Acad Sci USA. 2008;105:20095–20099. doi: 10.1073/pnas.0806377105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson MR, Wray NR, Visscher PM. Explaining additional genetic variation in complex traits. Trends Genet. 2014;30:124–132. doi: 10.1016/j.tig.2014.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swarup S, Harbison ST, Hahn LE, Morozova TV, Yamamoto A, Mackay TFC, Anholt RRH. Extensive epistasis for olfactory behaviour, sleep and waking activity in Drosophila melanogaster. Genet Res. 2012;94:9–20. doi: 10.1017/S001667231200002X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trerotola M, Relli V, Simeone P, Alberti S. Epigenetic inheritance and the missing heritability. Hum Genomics. 2015;9:17. doi: 10.1186/s40246-015-0041-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Driessche N, Demsar J, Booth EO, Hill P, Juvan P, Zupan B, Kuspa A, Shaulsky G. Epistasis analysis with global transcriptional phenotypes. Nat Genet. 2005;37:471–477. doi: 10.1038/ng1545. [DOI] [PubMed] [Google Scholar]
- Vu V, Verster AJ, Schertzberg M, Chuluunbaatar T, Spensley M, Pajkic D, Hart GT, Moffat J, Fraser AG. Natural variation in gene expression modulates the severity of mutant phenotypes. Cell. 2015;162:391–402. doi: 10.1016/j.cell.2015.06.037. [DOI] [PubMed] [Google Scholar]
- Wei WH, Hemani G, Haley CS. Detecting epistasis in human complex traits. Nat Rev Genet. 2014;15:722–733. doi: 10.1038/nrg3747. [DOI] [PubMed] [Google Scholar]
- Weinreich DM, Lan Y, Wylie CS, Heckendorn RB. Should evolutionary geneticists worry about higher-order epistasis? Current Opinion Genet Develop. 2013;23:700–707. doi: 10.1016/j.gde.2013.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood AR, Esko T, Yang J, Vedantam S, Pers TH, Gustafsson S, Chun AY, Estrada K, Luan J, Kutalik Z, et al. Defining the role of common variation in the genomic and biological architecture of adult human height. Nat Genet. 2014a;46:1173–1186. doi: 10.1038/ng.3097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood AR, Tuke MA, Nalls MA, Hernandez DG, Bandinelli S, Singleton AB, Melzer D, Ferrucci L, Frayling TM, Weedon MN. Another explanation for apparent epistasis. Nature. 2014b;514:E3–5. doi: 10.1038/nature13691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wray NR, Yang J, Hayes BJ, Price AL, Goddard ME, Visscher PM. Pitfalls of predicting complex traits from SNPs. Nat Rev Genet. 2013;14:507–5015. doi: 10.1038/nrg3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Lee SH, Wray NR, Goddard ME, Visscher PM. Commentary on “Limitations of GCTA as a solution to the missing heritability problem”. bioRxiv. 2016 preprint first posted online Jan. 20, 2016 http://dx.doi.org/2010.1101/036574.
- Yang J, Bakshi A, Zhu Z, Hemani G, Vinkhuyzen AAE, Lee SH, Robinson MR, Perry JRB, Nolte IM, van Vliet-Ostaptchouk JV, et al. Genetic variance estimation with imputed variants finds negligible missing heritability for human height and body mass index. Nat Genet. 2015;47:1114–1120. doi: 10.1038/ng.3390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Lee T, Kim J, Cho MC, Han BG, Lee JY, Lee HJ, Cho S, Kim H. Ubiquitous polygenicity of human complex traits: Genome-wide analysis of 49 traits in Koreans. Plos Genet. 2013;9:e1003355. doi: 10.1371/journal.pgen.1003355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young AI, Durbin R. Estimation of epistatic variance components and heritability in founder populations and crosses. Genetics. 2014;198:1405–1416. doi: 10.1534/genetics.114.170795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu ZH, Bakshi A, Vinkhuyzen AAE, Hemani G, Lee SH, Nolte IM, van Vliet-Ostaptchouk JV, Snieder H, Esko T, Milani L, et al. Dominance genetic variation contributes little to the missing heritability for human complex traits. Am J Hum Genet. 2015;96:377–385. doi: 10.1016/j.ajhg.2015.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuk O, Hechter E, Sunyaev SR, Lander ES. The mystery of missing heritability: Genetic interactions create phantom heritability. Proc Nat Acad Sci USA. 2012;109:1193–1198. doi: 10.1073/pnas.1119675109. [DOI] [PMC free article] [PubMed] [Google Scholar]