Abstract
Wolbachia is a maternally inherited and ubiquitous endosymbiont of insects. It can hijack host reproduction by manipulations such as cytoplasmic incompatibility (CI) to enhance vertical transmission. Horizontal transmission of Wolbachia can also result in the colonization of new mitochondrial lineages. In this study, we present a 15‐year‐long survey of Wolbachia in the cherry fruit fly Rhagoletis cerasi across Europe and the spatiotemporal distribution of two prevalent strains, wCer1 and wCer2, and associated mitochondrial haplotypes in Germany. Across most of Europe, populations consisted of either 100% singly (wCer1) infected individuals with haplotype HT1, or 100% doubly (wCer1&2) infected individuals with haplotype HT2, differentiated only by a single nucleotide polymorphism. In central Germany, singly infected populations were surrounded by transitional populations, consisting of both singly and doubly infected individuals, sandwiched between populations fixed for wCer1&2. Populations with fixed infection status showed perfect association of infection and mitochondria, suggesting a recent CI‐driven selective sweep of wCer2 linked with HT2. Spatial analysis revealed a range expansion for wCer2 and a large transition zone in which wCer2 splashes appeared to coalesce into doubly infected populations. Unexpectedly, the transition zone contained a large proportion (22%) of wCer1&2 individuals with HT1, suggesting frequent intraspecific horizontal transmission. However, this horizontal transmission did not break the strict association between infection types and haplotypes in populations outside the transition zone, suggesting that this horizontally acquired Wolbachia infection may be transient. Our study provides new insights into the rarely studied Wolbachia invasion dynamics in field populations.
Keywords: endosymbiont, horizontal transmission, infection dynamics, modelling, selective sweep
Introduction
Heritable endosymbionts play an important role in the ecology and evolution of animals (McFall‐Ngai et al. 2013). The alphaproteobacterium Wolbachia infects a broad range of arthropods and filarial nematodes and is probably the most common endosymbiont (Werren et al. 2008). It is mostly maternally inherited and spreads by increasing reproductive fitness of infected females (Engelstädter & Hurst 2009). The most common phenotype of reproductive manipulation by Wolbachia is the induction of cytoplasmic incompatibility (CI; e.g. Hoffmann & Turelli 1997) that results in embryonic death in matings between infected males and uninfected females, while reciprocal matings are compatible. This reproductive advantage of Wolbachia infected over uninfected females enhances the spread of Wolbachia within a population (Turelli & Hoffmann 1991). However, in certain cases Wolbachia can be retained within a population with little or no reproductive manipulation (e.g. Hamm et al. 2014). Although Wolbachia is one of the best studied endosymbionts, only few studies describe its spatial dynamics in field populations (Turelli & Hoffmann 1991; Jaenike et al. 2006; Narita et al. 2006; Hoffmann et al. 2011; Kriesner et al. 2013; Schuler et al. 2013; Atyame et al. 2015) and over extensive periods of time (Riegler et al. 2005; Weeks et al. 2007), limiting the understanding how this bacterium invades new populations.
Horizontal transmission of Wolbachia across species boundaries explains the broad distribution of this bacterium. Incongruence between Wolbachia and host phylogenies (Baldo et al. 2008; Zug et al. 2012) and the occurrence of closely related Wolbachia strains in unrelated hosts (Baldo et al. 2006) are an indirect evidence for the ability of Wolbachia to move among species. The evolutionary time spans of Wolbachia–host associations are very diverse. For example, the association between bees of the genus Nomada and their Wolbachia has persisted over 1.7 million years (Gerth et al. 2013). An intermediate time span was identified via whole‐genome sequencing of 290 Drosophila melanogaster lines and their Wolbachia, showing a perfectly congruent phylogeny and suggesting a single ancestral infection event followed by approximately 8000 years of vertical transmission, co‐evolution with its host and some cases of Wolbachia loss due to incomplete transmission (Richardson et al. 2012). Analysing the Wolbachia infection of the North American Eastern cherry fruit fly, Rhagoletis cingulata, a recent invader in Europe, showed that Wolbachia switched from the European endemic Rhagoletis cerasi to R. cingulata in Europe in a time frame of <20 years (Schuler et al. 2013). Additionally, two other studies on Hymenoptera demonstrated that intraspecific horizontal Wolbachia transmission can also play an important role for the spread of Wolbachia in new host populations (Kraaijeveld et al. 2011; Reumer et al. 2012).
Very few examples of ongoing Wolbachia invasions into new host populations are documented in field populations (Turelli & Hoffmann 1991; Schuler et al. 2013). The dynamics of a newly introduced Wolbachia within a host population were studied mainly theoretically by modelling the spread of Wolbachia infections due to CI (Turelli et al. 1992; Turelli & Hoffmann 1995; Barton & Turelli 2011; Fenton et al. 2011; Hancock et al. 2011) and tested for a small number of host species in the field, for example Drosophila simulans (Kriesner et al. 2013) and Aedes aegypti (Hoffmann et al. 2011). One of the key factors for the successful establishment of a new strain is its ability to induce CI in combination with a high maternal transmission frequency (Hoffmann & Turelli 1997), with possible fecundity advantages of infected over uninfected females (e.g. Fast et al. 2011). However, Wolbachia can also persist in a population without inducing CI. The examples of persistence of wMel in D. melanogaster (Hoffmann et al. 1998), wAu in D. simulans in Australia (Hoffmann et al. 1996; Kriesner et al. 2013) and wSuz in Drosophila suzukii in the USA (Hamm et al. 2014) show that Wolbachia is able to be maintained with minimal or without manipulation of host reproduction. Maternal Wolbachia transmission is rarely perfect and can lead to a continuous emergence of uninfected females, hindering fixation of a Wolbachia strain (Kriesner et al. 2013; Hamm et al. 2014). This leakage may, on the other hand, be compensated by selective effects such as CI or beneficial effects of Wolbachia provided to its host, including the protection against pathogens (Hedges et al. 2008; Fenton et al. 2011).
The acquisition of Wolbachia can influence the genetic diversity of the maternally transmitted mitochondria (Turelli et al. 1992; Hurst & Jiggins 2005); this is of significant importance as mitochondrial DNA (mtDNA) sequences are often used for inferences on species identity, phylogeny and population structure. In populations where infected individuals gain any fitness or reproductive advantage from Wolbachia, the mitochondrial genomes of these initially infected individuals will hitchhike with the spreading Wolbachia, reducing the haplotype diversity and replacing the haplotypes found in uninfected individuals (Narita et al. 2006; Charlat et al. 2009; Atyame et al. 2011). Therefore, populations recently infected by Wolbachia can display a different or fewer mitochondrial lineages than uninfected ones (e.g. Jiggins 2003; Hurst & Jiggins 2005).
The European cherry fruit fly R. cerasi is a model host system to study Wolbachia infections in natural populations. It is a serious pest of cherry orchards (Fimiani 1989; Daniel & Grunder 2012). Rhagoletis cerasi has a univoltine life cycle and infests cherries, mainly Prunus avium and Prunus cerasus, and honeysuckle, Lonicera xylosteum (Boller & Bush 1974; Schwarz et al. 2003). Crossings of males from southern and central European populations with females from northern and eastern European populations showed an egg mortality of 98%, while the reciprocal crosses were fully compatible (Boller et al. 1976). Riegler & Stauffer (2002) identified Wolbachia as cause of this unidirectional incompatibility. All R. cerasi individuals were infected by wCer1, and most central and southern European populations harboured an additional strain, wCer2. In between these two blocks of populations was a transition zone that contained populations with individuals that were either infected by wCer1 or both strains. The geographic distribution of the wCer2 infection closely matched the occurrence of incompatible populations detected by Boller et al. (1976) (Riegler & Stauffer 2002; Fig. 1a). A major exception to this pattern was a population 500 km north of the expected transition zone in Germany that was infected by wCer2 in 1998 (Riegler & Stauffer 2002), indicating that wCer2 had either progressed significantly since 1976 or experienced an anthropogenic introduction to northern Germany. Using more sensitive detection techniques, three additional Wolbachia strains, wCer3, wCer4, and wCer5, were found at different frequencies in almost all European populations (Arthofer et al. 2009b). The prevalence of wCer3 was the lowest and without a clear distribution pattern. The abundance of wCer4 was homogenous across Europe. wCer5 showed differences in spatial distribution not consistent with the distribution of the unidirectional CI phenotype (Arthofer et al. 2009b).
Figure 1.
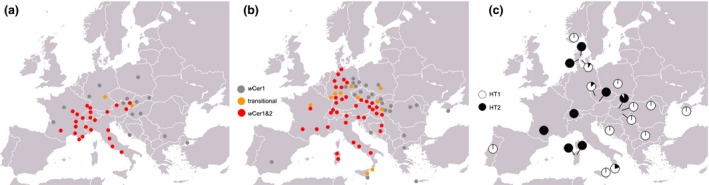
(a) Distribution of unidirectional incompatible southern (red) and northern (grey) R. cerasi populations in 1974 with two transitional (orange) populations (Boller et al. 1976). (b) Distribution of wCer1 (grey dots), wCer1&2 (red dots) and transitional populations with singly and doubly infected flies (orange dots), modified from Riegler & Stauffer (2002), with inclusion of a subset of representative populations from Fig. 3a,b; (c) prevalence of mitochondrial haplotypes of R. cerasi populations in Europe (white HT1, black HT2).
Here, we studied the infection dynamics of Wolbachia, the distribution of mitochondrial haplotypes and microsatellite allele frequencies in R. cerasi in Europe. Furthermore, we focused on the expansion history of wCer2 in R. cerasi populations in Germany over a time period of over 15 years and pinpointed the transition zone in which wCer2 introgressed into wCer1‐infected populations (Riegler & Stauffer 2002). Besides establishing a mitochondrial haplotype framework for European populations, we looked at the infections of German field samples from four different collection periods (1998/1999, 2000/2001, 2008 and 2014) in more detail. The previously reported shift in the Wolbachia distribution in Germany, between Boller et al. (1976) and Riegler & Stauffer (2002), as well as the expected transition zone in central Germany represent an ideal opportunity to study both the spread of the endosymbiont and its influence on the mitochondrial and nuclear genetic structure of R. cerasi. A CI‐driven invasion by a new Wolbachia strain such as wCer2 was expected to result in a sweep of the infected mitochondrial haplotype and a replacement or reduction of mitochondrial diversity (Turelli et al. 1992; Hurst & Jiggins 2005). Thus, a clear association between the spreading wCer2 and a specific mitochondrial R. cerasi haplotype would be in support of the expression of CI and reliable maternal inheritance, while a random association would suggest frequent horizontal transmission or loss of Wolbachia. Analysis of the nuclear diversity of singly and doubly infected populations would demonstrate whether Wolbachia has an impact on the genome of its host. We compared our empirical data with quantitative analyses of the frequency dynamics of Wolbachia and associated mitochondrial haplotypes and analysed the invasion front and shifts in the transition zone between the different years.
Materials and methods
Rhagoletis cerasi collection
Populations of R. cerasi were collected from infested Prunus (59 populations) and Lonicera (33 populations) plants between 1998 and 2014 (Table S1, Supporting information). The fruits were placed in plastic trays at room temperature, and emerging larvae were allowed to pupate and stored in absolute ethanol at −20 °C. DNA extracts of 188 individuals from 20 European populations studied by Riegler & Stauffer (2002) (Fig. 1a, Table S1, Supporting information) were re‐analysed, and one population from Portugal was additionally probed in 2009. Collections from Germany included 103 individuals from 11 populations in 1998/1999 (1‐1 to 1‐11), 226 individuals from 22 populations in 2000/2001 (2‐1 to 2‐22), 468 individuals from 34 populations in 2008 (3‐1 to 3‐34) and 39 individuals from four populations in 2014 (4‐1 to 4‐4; Table S1, Supporting information). Total DNA of single pupae was extracted using a salting‐out method (Miller et al. 1988) and dissolved in 50 μL TE buffer.
Screening for Wolbachia
Wolbachia screening was performed using wCer1‐ and wCer2‐specific primers, targeting specific regions of the Wolbachia surface protein wsp (Arthofer et al. 2009b). PCR amplification was performed in a total volume of 10 μL using 1× NH4 Buffer (Thermo Scientific), 2 mm MgCl2, 100 μm dNTPs, 0.2 μm of each primer, 0.25 U Taq polymerase (Thermo Scientific) and 0.8 μL template DNA. PCR amplification conditions were 94 °C for 1 min followed by 35 cycles of 94 °C for 30 s, 55 °C for 45 s and 72 °C for 1 min, followed by 72 °C for 10 min. Electrophoretic separation of the PCR products was carried out on 2% ethidium bromide‐stained agarose gels. For the purpose of this study, and in accordance with Riegler & Stauffer (2002), we refer to wCer1‐infected individuals as singly infected, and wCer1&2‐infected individuals as doubly infected. Populations fixed for wCer1 are referred to as singly infected populations, and populations fixed for wCer1&2 as doubly infected populations, while populations with both infection types are transitional populations. Given that an initial screening of the three other Wolbachia strains in R. cerasi showed a distribution inconsistent with the distribution of CI (Arthofer et al. 2009b; data not shown), we did not survey wCer3, wCer4 and wCer5 in this study.
Mitochondrial genotyping
A 546‐bp fragment of the mitochondrial COI gene was amplified using the primers Pat and Dick (Simon et al. 1994), and amplicons were Sanger sequenced by a commercial provider. In total, six to 10 individuals from nine European populations outside Germany (Table S1, Supporting information), six individuals from each of seven German populations from 2008 (3‐3, 3‐7, 3‐9, 3‐10, 3‐18, 3‐22, 3‐33), and all 39 individuals from four German populations in 2014 were sequenced. Sequences were aligned using CodonCode Aligner (CodonCode Corporation). All 152 individuals from these 20 populations showed only two haplotypes separated by one polymorphic site. Therefore, in all other individuals (except for the populations from 1998/1999 for which not enough DNA was available) the mitochondrial haplotype was determined by PCR‐RFLP: 0.5 μL of the PCR product was incubated with 0.5 U HaeIII (Thermo Scientific) at 37 °C for 4 h and loaded on an agarose gel. Haplotype 2 (HT2) was cut into a 342‐ and 204‐bp fragment while haplotype 1 (HT1) remained undigested. DNA extracts of flies with confirmed single and double infections were used as control. Amplicons showing unclear results after PCR‐RFLP were sequenced.
Nuclear genotyping
Nuclear genotyping was performed on individuals from ten German populations representing different Wolbachia infection status, geographically different origins and different host plants (3‐1, 3‐2, 3‐3, 3‐6, 3‐10, 3‐18, 3‐22, 3‐28, 3‐30, 3‐33; Table S1, Supporting information). Seven to 16 individuals per population were genotyped using the seven microsatellite loci RcMic76‐1, RcMic76‐7, RcMic82‐46, RcMic83‐16, RcMic83‐26, RcMic83‐44 and RcMic84‐42 (Arthofer et al. 2009a). PCRs were carried out in a total volume of 10 μL containing 1× NH4 Buffer, 1.5 mm MgCl2, 100 μm dNTPs, 0.2 μm FAM/HEX/NED fluorescent‐labelled M13 primer, 0.02 μm M13 tailed forward primer, 0.2 μm reverse primer, 0.25 U Taq polymerase (Thermo Scientific) and 0.8 μL template DNA. Amplification conditions were 94 °C for 5 min followed by 35 cycles at 94 °C for 30 s, 60 °C for 1 min and 72 °C for 45 s with a final extension at 68 °C for 20 min. Fragment separation was performed by capillary electrophoresis on an ABI 3100 sequencer (Applied Biosystems). The electropherograms were visualized with PeakScanner (Applied Biosystems), and alleles were called manually. The overall genetic diversity of the different populations, total number of alleles, number of alleles per population, observed and expected heterozygosity, and deviations from Hardy–Weinberg equilibrium were calculated using genalex ver. 6.5 (Peakall & Smouse 2006), and sequential Bonferroni–Holm corrections (Rice 1989) were performed manually in microsoft excel ®. Weir & Cockerham's (1984) F ST was calculated separately for the global data set and for each possible pair of populations using fstat ver. 2.9.3.2 (Goudet 1995); the latter approach was chosen as the software only calculates confidence intervals for global, not for pairwise F ST. The genotype data were then merged to four regional classes (singly infected, population 3‐10; doubly infected north, populations 3‐1, 3‐2, 3‐3; doubly infected south, populations 3‐28, 3‐30, 3‐33; transition zone, populations 3‐6, 3‐18, 3‐22), and this classification was used for amova in genalex. Another amova was computed merging the populations according to their host plant (Lonicera, population 3‐18; Prunus, all other populations). Nei distances were used as input for a principal coordinate analysis (PCoA) and, together with the geographic distances between populations, for a Mantel test in genalex.
Microsatellite results were used as input for the Bayesian clustering algorithm implemented in structure ver. 2.3.3 (Pritchard et al. 2000). The admixture model with correlated allele frequencies was used, with default settings and 120 000 iterations of the Markov chain, discarding the first 20 000 iterations as burn‐in. For each K in [1, 10], 10 runs were performed. To identify the best K, similarity coefficients and ΔK were calculated following the protocol of Evanno et al. (2005) as implemented in structuresum ver. 2009 (Ehrich 2006).
Results
Distribution of wCer1 and wCer2 across Europe
All 1032 R. cerasi individuals analysed in this study were infected with wCer1 (Fig. 1, Table S1, Supporting information). The screening with wCer2‐specific primers confirmed the results of Riegler & Stauffer (2002) that showed fixation of this strain in most parts of southern and central Europe (Fig. 1). Within Germany, our fine‐scale sampling showed fixation of wCer2 in northern and southern Germany (Fig. 2). In contrast, central Germany formed a belt of singly infected populations bordered by transition zones consisting of both singly and doubly infected individuals surrounded by doubly infected populations in the south and the north. These transitional populations contained few to many individuals infected with wCer2 (Fig. 2, Table S1, Supporting information). In contrast to Boller et al. (1976) and across the three sampling periods, wCer2 covered all tested populations in Denmark (populations Dan1, Dan2, Dan3), Schleswig‐Holstein (1‐1, 1‐2, 1‐3, 2‐1), Hamburg (3‐1), Bremen (2‐2), Lower Saxony (1‐4, 2‐3, 2‐4, 2‐5, 3‐2, 3‐5, 3‐7, 4‐1, 4‐2), and Witzenhausen in Hesse (1‐8, 2‐8, 3‐9, 4‐3). The portion of wCer2‐infected flies increased in the area around Hamburg (1‐2, 1‐3, 3‐1) and Witzenhausen (1‐8, 2‐8, 3‐9, 4‐3) between 1998 and 2014. Witzenhausen showed differences in the infection status of R. cerasi deriving from different host plants: in Lonicera‐infesting flies, wCer2 expanded from 14% in 1998 to 43.8% in 2008, while Prunus‐infesting flies were already completely invaded by wCer2 in 2000 and 2014.
Figure 2.
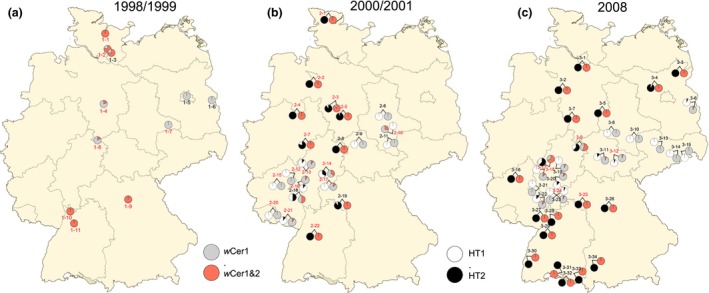
Geographic distribution of Wolbachia and mitochondrial haplotypes of R. cerasi. (a) Wolbachia and mitochondrial haplotype frequencies in 1998/1999, (b) in 2000/2001, and (c) in 2008. White = proportion of individuals from HT1, black = proportion of individuals from HT2, grey = proportion of wCer1 singly infected flies and red = proportion of wCer1&2 doubly infected flies; black numbers represent flies collected from Prunus while red numbers represent populations from Lonicera. Population localities and numbers are listed in Table S1 (Supporting information).
Association of Wolbachia with mitochondrial haplotypes of Rhagoletis cerasi
The mitochondrial diversity of R. cerasi with two detected haplotypes, HT1 (GenBank KJ488948) and HT2 (GenBank KJ488949), was generally very low. Both haplotypes were only separated by a single synonymous transition at a third codon position. Outside Germany, 116 individuals from 15 European populations singly infected with wCer1 were exclusively associated with HT1; in contrast, individuals from doubly infected European populations were almost perfectly associated with HT2, with the exception of one individual from a transitional Danish population on honeysuckle associated with HT1 (Odense; Table S1, Supporting information). This suggests an overall strict association of Wolbachia and mitochondrial haplotypes in R. cerasi across Europe. In Germany, for which we had more samples and a higher spatial resolution than the rest of Europe, most singly infected individuals were also linked to HT1 and most doubly infected individuals to HT2 (Fig. 3). This association was perfect for all 121 singly infected individuals collected in 2000/2001 that were associated with HT1. In 2008, 236 of 237 wCer1‐infected individuals were associated with HT1, and only one (0.4%) was associated with HT2. In 2014, however, three of 25 wCer1‐infected flies (12%) from a single population (Höhnstedt 4‐4) were associated with HT2.
Figure 3.
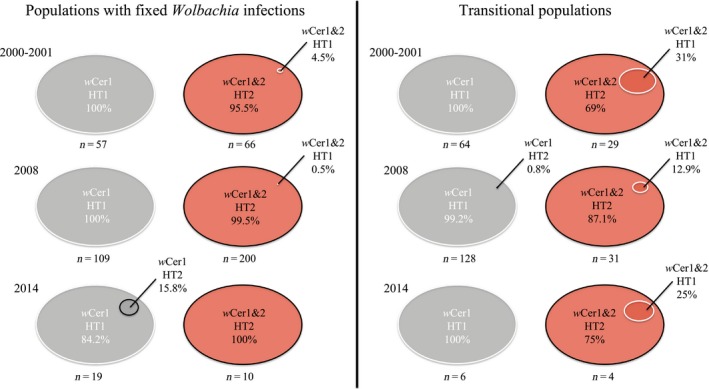
Comparison of the association of wCer1 (grey) and wCer1&2 (red) infections with the two different haplotypes (HT1 white encircled, HT2 black encircled) between populations of Germany outside the transition zone (left) and population from the transition zone (right) collected in 2000/2001, 2008 and 2014. Size of the ovals represents relative abundance of the different Wolbachia–haplotype combinations.
Outside the transition zones, the strict association of Wolbachia and haplotypes was nearly complete: all wCer1 individuals (except Höhnstedt 4‐4) were associated with HT1. The wCer1&2 association with HT2 was also strong, with 63 of 66 (95.5%) individuals in 2000/2001, 199 of 200 (99.5%) individuals in 2008, and 10 of 10 individuals in 2014 (Fig. 3). Within the transition zone, 197 of 198 (99.5%) wCer1 individuals also had HT1, supporting the same pattern as for populations with fixed infection status. The wCer1&2 individuals within the transition zone, however, were different (Fig. 3). In 2000/2001, the association of wCer1&2 with HT2 occurred in only 20 of 29 (69%) individuals, and this was different from populations with fixed infection status (Fisher's exact test, P < 0.001). In 2008, this association occurred in 27 of 31 individuals from the transition zone (87.1%; P = 0.001), and in 2014 in three of four individuals from the transition zone (75%; P = 0.029) (Fig. 3). In total, 21.9% (14 of the 64) wCer1&2 individuals from the transition zone were associated with HT1. This is in sharp contrast to populations outside the transition zone where just four of 276 (1.5%; P < 0.001) doubly infected individuals were associated with HT1. Additionally, the haplotype association of doubly infected flies differed between host plants: while 12 of 47 (25.5%) wCer1&2 flies from Lonicera were associated with HT1, just two of 17 (11.8%; P = 0.53) wCer1&2 flies from Prunus showed this association.
No association of Wolbachia with nuclear genome of Rhagoletis cerasi
Of 116 individuals screened at seven nuclear microsatellite loci, 89.7% of the reactions amplified successfully. Eleven locus–population pairs showed significant deviation in the chi‐square tests for Hardy–Weinberg equilibrium, and one pair retained significance after sequential Bonferroni–Holm correction (Table S2, Supporting information). Both global F ST = 0.019 (Table S3, Supporting information) and population pairwise F ST (min. −0.032, max. 0.076, Table S4, Supporting information) were low, and, with two exceptions (population pairs 3‐10/3‐18, 3‐18/3‐30), the confidence interval for F ST included zero. Infection‐based amova allocated 0% variation among the infection classes (singly infected, doubly infected north, doubly infected south, transition zone), 3% among populations, 20% among individuals and 77% within individuals, respectively (Table S3, Supporting information). The Mantel test (R = −0.053, P = 0.409) rejected geographic structuring of the genotypes. Host plant‐based amova allocated 3% variation among the host plant classes (Lonicera and Prunus), 1% among populations, 20% among individuals and 76% within individuals (Table S5, Supporting information). The first three axes of the PCoA explained cumulatively 68.25% of the total variation, and no obvious clusters were observed (Table S6, Supporting information). Evanno analysis of the structure data resulted in a maximum of ΔK at K = 2. This method is unable to identify K = 1 as best estimation of K, but visual inspection of the structure box plots and the distribution of Ln P(D) did not show population structuring (Fig. S1, Supporting information). Summarizing, several distance‐, frequency‐ and Bayesian inference‐based analysis methods applied on this data set agreed that there was no pronounced nuclear population structure in Germany.
Mathematical modelling and quantitative analysis
The data set was analysed quantitatively using mathematical models (see Appendix I for detailed model descriptions). First, we followed Hoffmann et al. (1990) and described the spread of CI‐inducing Wolbachia in a panmictic population by a nonlinear recursion equation. Three parameters were included: the level of cytoplasmic incompatibility (l CI), the maternal transmission rate (1 − µ) and the relative fecundity of infected females in comparison with uninfected females (F). In order to simulate the spread of wCer2 in a wCer1 population, we had to estimate parameter values. Based on crossing studies by Boller et al. (1976), we assumed unidirectional CI with a CI level of 0.98 between doubly (wCer1&2) and singly (wCer1) infected individuals. For transmission, we assumed 100% maternal transmission. This is because field data of R. cerasi indicated high infection prevalence for wCer2 and a low number of singly infected individuals with HT2. As we had no information about potential fitness costs of the Wolbachia infection in Rhagoletis, we assumed no fecundity reduction due to Wolbachia.
Next, we investigated the spatial spread of wCer2 in Europe. In general, CI‐inducing Wolbachia are predicted to spread spatially as a travelling wave (Turelli & Hoffmann 1991; Schofield 2002, see discussion for alternative model approaches). Let σ be the variance of the individual dispersal probability. Under the assumption of a Gaussian dispersal kernel, 100% maternal transmission rate and no fecundity cost of infection (F = 1), the width of the transition zone (defined as the geographic range in which Wolbachia frequency increases from 5% to 95%) is predicted as (Turelli & Hoffmann 1991). This theoretical prediction was compared with the empirical data. To obtain a good estimate of the transition zone's width and because sampling coverage was highest for this region, we focused on the situation in Germany. First, we noted that the spread of wCer2 most likely happened along a north–south axis (Fig. 2). Therefore, a lower bound for the transition zone width Δx was given by the latitudinal distance between the most northern and the most southern populations that contained both singly and doubly infected individuals. For 1999, the latitudinal distance between Ahrensburg (1‐2) and Witzenhausen (1‐8) was 260 km, which was set as a lower bound for the transition zone width. For 2008, the latitudinal distance between Witzenhausen (3‐9) and Stockstadt (3‐22) was 170 km. However, wCer2 spread from both north and south into the transition zone. Therefore, a lower bound of Δx was given by half of this distance, that is Δx > 130 km for 1999 and Δx > 85 km for 2009. These two lower bounds were then used to estimate minimal values of σ. Using equation for a CI level of 0.98 yields lower estimates for the dispersal kernel of σ > 43 km for 1999/2000 and of σ > 28 km for 2008. However, adult cherry flies are estimated to fly a maximum distance of 4 km (Boller & Remund 1983). This suggests that long‐distance migration of adults or dispersal of infested fruits is key for understanding the spatial spread of wCer2.
Some doubly infected individuals in the transition zone have haplotype HT1 (21.8%; Fig. 3), but this combination was uncommon outside the transition zone. This high incidence of unexpected Wolbachia–haplotype combination could be the result of either paternal (e.g. Hoffmann & Turelli 1988) or intraspecific horizontal transmission of Wolbachia. To examine this further, we analysed three extensions of the basic CI model: (i) paternal transmission, (ii) horizontal transmission with subsequent vertical transmission (heritable horizontal transmission) and (iii) somatic horizontal transmission with no vertical transmission (transient horizontal transmission) (see Appendix I for details). Within this theoretical framework, we analysed the population dynamics of Wolbachia and the mitochondrial haplotypes. As expected, the Wolbachia–haplotype combination wCer1&2‐HT1 was formed in all three models (Fig. 4a–c). Differences between the three models occurred with respect to the long‐term dynamics. The mismatched combination continued to persist in the model with paternal transmission (Fig. 4a) and heritable horizontal transmission (Fig. 4b), but went to extinction in the model with somatic horizontal transmission (Fig. 4c). In conclusion, all three models could explain the data within the transition zone, but only the model with somatic horizontal transmission could explain the absence of the mismatched Wolbachia–haplotype combination wCer1&2‐HT1 outside the transition zone (Fig. 4d).
Figure 4.
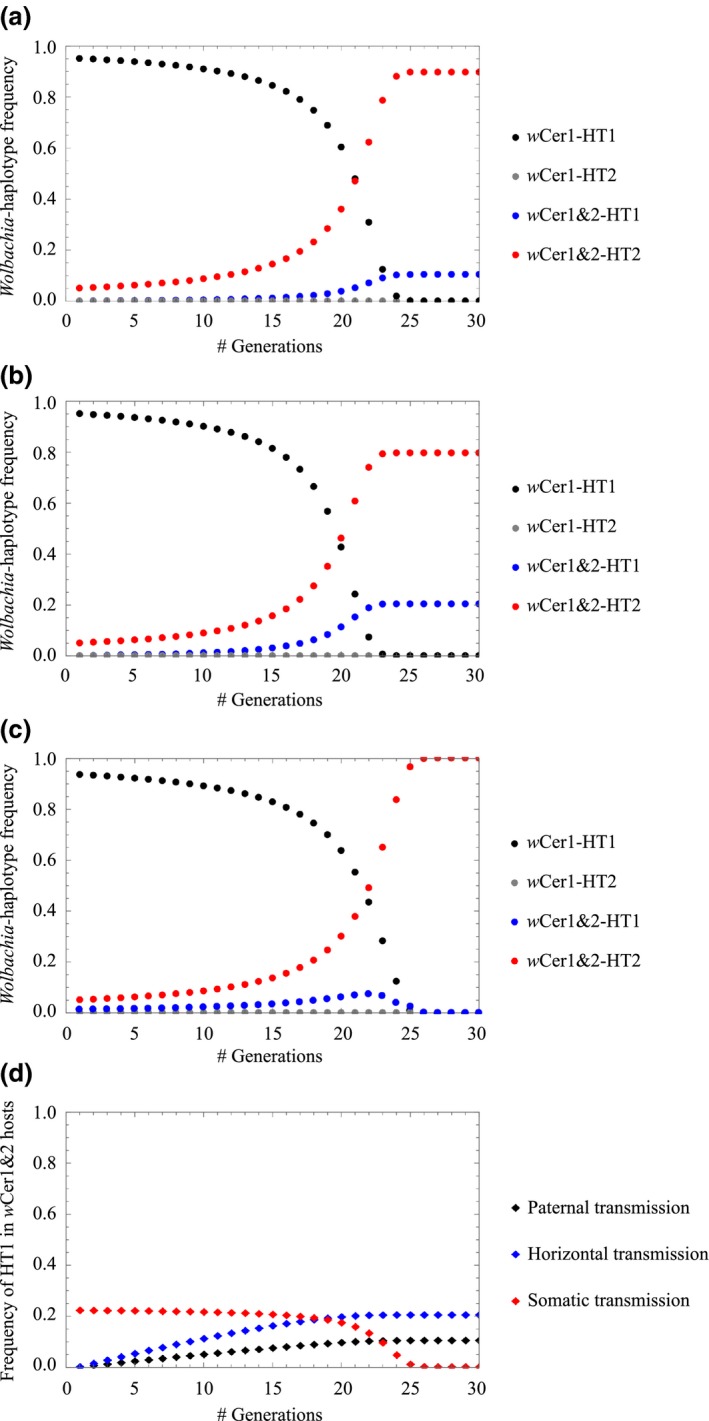
Codynamics of Wolbachia and mitochondrial haplotypes. (a) Model with paternal transmission (b) model with heritable horizontal transmission, (c) model with somatic horizontal transmission, (d) dynamics of Wolbachia–haplotype mismatch for all three models. Wolbachia–haplotype combination frequencies were determined using equations (A8), (A9), (A10), (A11), (A12), (A13), (A14), (A15), (A16), (A17), (A18), (A19). Parameters: l CI = 0.98, µ = 0, F A = F B = 1 for all graphs; τ = 0.3, β = 0 for model with paternal transmission; τ = 0, α = 1, β = 0.015 for model with horizontal transmission; τ = 0, α = 0, β = 0.3 for model with somatic transmission.
Discussion
We investigated the dynamics of the Wolbachia strain wCer2 and its co‐inheritance with haplotype HT2 in R. cerasi in Europe over a time period of over 15 years. A special focus was on central Germany, where wCer2 was previously reported to spread into wCer1 singly infected populations (Riegler & Stauffer 2002). Our theoretical analysis of the transition zone based on distributional shifts within this time frame shows a large transition zone of wCer2, which may be driven by long‐distance migration of R. cerasi. We further investigated mitochondrial diversity of the German R. cerasi populations and found a strong association of the infection status of wCer1 and wCer1&2 with the two mitochondrial haplotypes HT1 and HT2, respectively. However, in transitional populations we detected 21.8% of wCer2‐infected individuals with HT1, suggesting a high degree of intraspecific somatic horizontal transmission. Mathematical modelling in combination with the evidence for the strong Wolbachia–haplotype associations in populations outside the transition zone suggests that the horizontal acquisition of wCer2 detected in the transition zone is most likely transient. Finally, we found no impact of the wCer2 spread on nuclear diversity of its host.
A rapid spread of wCer2
The Wolbachia strain wCer1 was fixed in all populations confirming previous findings (Riegler & Stauffer 2002; Arthofer et al. 2009b). Riegler & Stauffer (2002) found mostly geographic congruence between the distribution of mating incompatibilities described by Boller et al. (1976) and the occurrence of wCer1 and wCer1&2 after 26 years (1976–2002). However, this previous study also demonstrated that populations in Austria with previously reported incompatibilities (Boller et al. 1976) have become completely invaded by wCer2 (Fig. 1). Further comparison of the sampling locations of incompatible populations in the 1970s and the occurrence of wCer2 in the late 1990s established that the range of wCer2 has expanded further from Austria to Western Hungary, and it was also detected in Bosnia‐Herzegovina (Riegler & Stauffer 2002; Fig. 1). While the incompatibility caused by wCer2 originally seemed to be restricted to the southern and central European populations, Riegler & Stauffer (2002) described a population in northern Germany (Kiel) infected by wCer1&2. Here, we further confirm this by describing wCer2 in three Danish populations and by our fine‐scale screening of populations of the German transition area in 1998/1999, 2000/2001, 2008 and 2014. It is not entirely clear how wCer2 expanded into populations of Denmark and northern Germany. The accidental release of wCer1&2 individuals from southern populations due to the transport of infested cherries to the north could be the origin of the double infections in the north.
An interesting finding is the large width of the transition zone with lower estimates of 260 km for 1999 and 170 km for 2008. Under the assumption of a Gaussian dispersal kernel, the quantitative analysis yields lower estimates of the average dispersal probability of 43 km for 1999 and 28 km for 2008. These lower bounds are in stark contrast to empirical studies of R. cerasi that estimate maximal migration distances of single individuals around 4 km (Boller & Remund 1983), suggesting that long‐distance migration or passive movement of flies plays an important role. The latter could be possibly facilitated by human transport of infested cherry fruits. It could also be possible that previous mark/recapture studies (Boller & Remund 1983) underestimated the migration of R. cerasi, although a migration of adults more than 20 km seems unlikely.
Studies of Wolbachia in natural host populations showed that this endosymbiont can experience different patterns of range expansions in the field: field released A. aegypti mosquitos that have been artificially infected with wMel (Hoffmann et al. 2011) suffer small but significant fitness costs that can hinder the spread of Wolbachia outside the released areas (Hoffmann et al. 2014). This was tested, and low‐frequency introduction into surrounding areas did not result in Wolbachia establishment, suggesting structured host populations and bistable dynamics with unstable equilibrium frequencies. In contrast, the spatial spread of wRi in D. simulans in California (Turelli & Hoffmann 1991) and Australia may follow a Fisherian wave (Kriesner et al. 2013). For this system, it was shown that wRi increases female fecundity, resulting in a spread from low initial infection frequencies. Kriesner et al. (2013) argued that this promotes the spatial spread of Wolbachia because rare long‐distance migration can result in the establishment of Wolbachia‐infected satellite populations. This is different from situations with bistable dynamics where long‐distance migration has no significant effect on spatial spread because low Wolbachia infections are quickly lost. For the quantitative analysis of our data, we chose the ‘standard model’ of Barton & Turelli (2011) because we do not have data about potential fecundity effects of wCer2. Without available data about potential fitness benefits, an important factor for Wolbachia spread from initial low frequencies (Fenton et al. 2011; Kriesner et al. 2013), alternative approaches that evaluate the spread based on Fisherian dynamics (Kriesner et al. 2013) are not suitable for our data. Future studies are necessary to characterize the phenotypic effects of wCer2 on its host (other than CI) in conjunction with continued monitoring in a number of sites over a series of years. All of these efforts will be needed to analyse the spread of wCer2 in R. cerasi more comprehensively.
Low mitochondrial diversity and the association of specific haplotypes with Wolbachia
Characterizing the mtDNA of 733 R. cerasi individuals from different populations in Germany and 196 individuals from other European populations revealed only two closely related haplotypes. This remarkably low mitochondrial diversity in widely distributed populations of R. cerasi is therefore best explained by two consecutive sweeps, first of wCer1 and then of wCer1&2. This first invasion by wCer1 is expected to have begun from a single or very few founder individuals that had acquired this strain horizontally from another species. Subsequent fitness and/or reproductive advantages of wCer1‐infected individuals, for example due to the induction of CI, resulted in the spread of wCer1 and the elimination of uninfected haplotypes. Due to the fact that wCer1 reached fixation in all R. cerasi populations, a comparison of mtDNA diversity between infected and uninfected populations (e.g. Atyame et al. 2011) is not possible for R. cerasi.
The origin of HT2 remains an unresolved issue, with two possible scenarios. First (and perhaps most likely), invasion of wCer1 had occurred long enough prior to the invasion of wCer2 to allow the evolution of new mitochondrial diversity within wCer1‐infected populations. Second, wCer1 invaded independently two different and uninfected R. cerasi haplotypes HT1 and HT2, resulting in the extinction of all but these two haplotypes. HT2 later acquired wCer2 and since then has hitchhiked with wCer2 through European populations. Both scenarios require that HT2, when acquiring wCer2, was a spatially isolated haplotype, as otherwise singly infected HT2 populations should have been detected; furthermore, the spread of wCer2 and HT2 must have been fairly recent. Current data do not discriminate between the two scenarios, rendering a determination of the age of the spread based on molecular clock calculations (e.g. Rasgon et al. 2006) impossible. However, both hypotheses indicate that the spread of both wCer1 and wCer2 started from just a few, if not one single individual, thus driving the mitochondrial genome of R. cerasi through a severe genetic bottleneck.
Nearly perfect maternal transmission
Because both mitochondria and Wolbachia are cytoplasmically inherited, their association provides information about the efficiency of the Wolbachia spread. The detection of only four of 415 genotyped individuals (0.96%) with mitochondrial HT2 not being infected by wCer2 suggests that this strain induces very strong CI and probably has high transmission efficiency. We assume that rare associations of wCer1 singly infected individuals with HT2 seen in the field are due to imperfect transmission of wCer2, and we also assume that this haplotype–Wolbachia strain association is transient: in case of a male individual, the association is already in a dead end; singly infected females, on the other hand, may likely fail in finding a compatible mate. Of HT2 individuals from within the transition zone only 1.96% (one of 51) were not infected by wCer2. This further supports the view of strong CI induction capacity and high transmission efficiency of wCer2. Our theoretical predictions are supported by studies of Boller et al. (1976) that showed nearly complete cytoplasmic incompatibility of 98% (Riegler & Stauffer 2002).
Frequent intraspecific transient horizontal transmission
An unexpected finding, however, was the presence of wCer2 in HT1 individuals (Fig. 3). Considering just populations from the transition zone, 21.9% of the wCer2‐infected individuals were associated with HT1. We cautiously interpret this observation as evidence for repeated intraspecific horizontal transmission events of wCer2 into singly infected HT1 flies, without transmission into the next generation. Although horizontal transmission of Wolbachia is commonly found on an evolutionary timescale (O'Neill et al. 1992; Vavre et al. 1999; Baldo et al. 2008; Kraaijeveld et al. 2011; Gerth et al. 2013) and rarely observed in real time in the field (Schuler et al. 2013), it does not necessarily lead to a successful establishment in new populations. In line with our observations, recent studies on Australian tephritid fruit flies sharing host plants and parasitoids demonstrated that identical Wolbachia was detected across fruit fly and parasitoid species (Morrow et al. 2014), however at an overall low prevalence within most species (Morrow et al. 2015). This suggests that Wolbachia can readily move between closely interacting species even if prevalence and maternal transmission is low; yet, this Wolbachia spillover may be transient and not passed on to the next generation (Morrow et al. 2015). Thus, a contribution of parasitoids to the transmission of wCer2 into HT1 seems plausible under the assumption that at least some flies survive the parasitoid attack. It should be noted, however, that none of the mtDNA sequenced individuals gave any hints for the presence of parasitoid DNA. Another route for intraspecific horizontal transmission could be cannibalism by differently infected larvae that co‐inhabit the same host fruits.
An alternative explanation for the findings of wCer2 in HT1 individuals could be paternal transmission of Wolbachia (e.g. Hoffmann & Turelli 1988). The strong CI caused by wCer2 minimizes the number of progeny from wCer2‐HT2 male and wCer1‐HT1 female crosses and thus the likelihood that offspring inherits HT1 from the mother and wCer2 from the father. This is supported by theoretical predictions showing that in case of paternal wCer2 transmission more than 10% of the individuals would be permanently associated with HT1 (Fig. 4c).
The question remains whether transferred wCer2 ever reaches the germline of HT1 flies (and is eventually inherited) or remains a somatic infection. Successful and permanent invasion of the germline would result in a permanent association of 20% wCer2‐infected individuals with HT1 (Fig. 4a); however, this was in discordance with our empirical data that found wCer1&2‐HT1 individuals almost exclusively in the transition zone (Fig. 2). Such findings of potentially transient, not inherited somatic infections, are further evidenced by laboratory studies demonstrating that Wolbachia, even if successfully transferred by microinjection, can be lost in a few generations due to insufficient maternal transmission (e.g. Riegler et al. 2004). We therefore assume that in our case infections acquired by intraspecific horizontal transmission either do not invade the host's germline or suffer from poor maternal transmission (Riegler et al. 2004). Theoretical analyses of our data support this scenario and demonstrate that temporarily more than 20% of the individuals can show the wCer1&2–HT1 association that will be lost after complete invasion of (maternally transmitted) wCer2 (Fig. 4c).
A potential role of the host plant in the wCer2 invasion
While within the transition zone, 25.5% wCer1&2‐infected flies from Lonicera were associated with HT1, just 11.8% wCer1&2‐infected flies from Prunus were associated with HT1, suggesting a potential role of the host plant in horizontal transmission. Smaller size of Lonicera berries may increase the likelihood of cannibalism between larvae that share a fruit resulting in horizontal transmission of Wolbachia. Alternatively, if indeed parasitoids are involved in horizontal Wolbachia transmission (Gehrer & Vorburger 2012; Ahmed et al. 2015), adult parasitoids emerging from the earlier occurring cherry host could provide high wCer2 loads to the later attacked honeysuckle‐infesting larvae. In contrast, the first emerging parasitoids of each year, attacking the cherry host, would not yet have had a chance to acquire wCer2.
An interesting case was found in the northern transition zone at Witzenhausen (populations 1‐8, 2‐8, 3‐9, 4‐3). The samples from 1999 to 2008 were collected from honeysuckle, while in 2000 and 2014 cherry had been sampled, and the results revealed another possible host plant effect: On honeysuckle, wCer2 prevalence increased from 17% in 1999 to 56% in 2008, while on cherry wCer2 had reached fixation already in 2000 (and stayed fixed in 2014). Such a delayed increase on honeysuckle could indicate that wCer2 faces a number of challenges when invading populations of R. cerasi. The potential for host race formation of R. cerasi on cherry and honeysuckle has previously been discussed (Boller et al. 1998; Schwarz et al. 2003) and could impede a Wolbachia invasion due to host plant phenology, with cherries becoming available prior to honeysuckle berries and female host plant preference being determined by previous female experience (Boller et al. 1998; but see results of our microsatellite analysis). Furthermore, R. cerasi is a univoltine insect with an obligatory diapause and a portion of pupae undergoing prolonged dormancy. These overlaying pupae emerge in the subsequent year(s) (Vallo et al. 1976; Moraiti et al. 2014) and could thus act as reservoir of singly infected flies that delay wCer2 fixation.
To further investigate the role of the wCer2 spread on its host, we characterized the nuclear diversity of singly and doubly infected R. cerasi populations using previously developed microsatellite loci (Arthofer et al. 2009b). Characterization of different populations of R. cerasi showed that neither the different Wolbachia infection, nor geographic separation resulted in any nuclear genetic structure of R. cerasi. Furthermore, we could not detect genetic differences in sympatrically overlapping Prunus‐ and Lonicera‐infesting host forms, concluding that wCer2 did not sufficiently inhibit gene flow to result in population divergence. This is in line with a previous study that showed that unlike large effects on mtDNA the spread of Wolbachia has little effects on nuclear genomes (Turelli et al. 1992). However, our observation of at least some differences at the Wolbachia invasion front between Prunus and Lonicera might be an additional indication (besides data presented by Boller et al. 1998; Schwarz et al. 2003) of the formation of host races in R. cerasi and merits further investigation.
Conclusion
We studied the infection dynamics of Wolbachia in R. cerasi in Europe and focussed on the invasion history of wCer2 over a time period of 15 years. The comparison of our data with studies from the 1970s and our fine‐scale analysis of populations from Germany show that wCer2 is currently invading wCer1‐infected populations from the south and from the north. Our quantitative analysis yielded a large transition zone of wCer2 that suggests a spreading wCer2 infection in Germany. Furthermore, we show low mitochondrial diversity and a high level of mitochondrial haplotype association in this host species. wCer1 singly infected populations are almost perfectly associated with HT1 and populations with fixed wCer2 infections perfectly associated with HT2. The transitional zone, remarkably, showed a large proportion of HT1 flies infected by wCer2, suggesting a high frequency of intraspecific horizontal transmission. However, as the wCer2–HT1 association appears to be almost exclusive to the transition zone, we assume that this combination is due to horizontal transmission of wCer2 that seems to be transient. Theoretical modelling supports this assumption. The rare reciprocal wCer1–HT2 combination suggests nearly perfect maternal transmission of wCer2. In summary, our study constitutes a new example of a Wolbachia spread in natural populations and provides novel insights into the dynamics of natural Wolbachia invasion in the field.
The project was conceived and designed by M.R., C.S., W.A. and H.S. The data collection and analysis were performed by H.S., M.R., W.A., S.D.H., K.K., B.R. and S.K. A.T. designed the mathematical model and conducted the quantitative analysis. Materials and specimens were supplied by M.R., K.K., D.S., T.H. and C.S. The manuscript was written by H.S., A.T., C.S., W.A. and M.R. with contributions from all other authors.
Data accessibility
Mitochondrial DNA sequences have been submitted to GenBank: Accession numbers: KJ488948 (HT1) and KJ488949 (HT2). Mitochondrial DNA sequence chromatograms, microsatellite raw data, genalex, fstat, and structure data and result files have been deposited at Dryad: Provisional DOI: 10.5061/dryad.gs8r.2.
Supporting information
Fig. S1 Results of structure analysis of microsatellite data.
Table S1 Locality information, frequency of Wolbachia infections (wCer1, wCer1&2), frequencies of different haplotypes, and association of Wolbachia with the respective haplotype.
Table S2 Summary of microsatellite data chi‐square tests for Hardy–Weinberg Equilibrium.
Table S3 Results from amova analysis based on infection status.
Table S4 Results from pairwise F ST analysis.
Table S5 Results from amova analysis based in R. cerasi host plants.
Table S6 Principal coordinate analysis (PCoA) of different R. cerasi populations, based on Nei distances.
Table S7 Mating table used to derive model (A4), (A5), (A6), (A7). Modified from Turelli et al. (1992).
Acknowledgements
We thank Glen R. Hood, Jeffrey L. Feder, Martin Schebeck, subject editor Jacob A. Russell, Ken Kraaijeveld, and three anonymous referees for helpful comments on the manuscript and D. Pilarska, I. Sredkov, M. Subchev, Bulgaria; K. Zanic, Croatia; J. Viktorinov, Czech Republic; U. Holz, D. Mohr, M. Hommes, P. Baumjohann, E. Hummel, A. Trapp, M. Stark, C. Scheer, I. Toups, H. Vogt, Germany; A. Pulvirenti, M. Porto, Italy; G. Jaastad, G.K. Knudsen, Norway; J. Szymura, Poland; J.P. Luz, R. Paiva, Portugal; A. Diaconu, Romania; V. Mitrofanov, Ukraine for providing R. cerasi samples. Financial support was provided by the Austrian Science Fund FWF (P‐14024‐BIO; P‐19206‐B17 and Erwin Schrödinger Fellowship J‐3527‐B22 to H.S.), the Hochschuljubiläumsstiftung of the City of Vienna, and the European Union 7th Framework Programme FP7 2007–2013 (KBBE 2009‐3) under grant agreement 245268 ISEFOR.
Appendix I. Mathematical modelling and quantitative analysis
Infection dynamics of CI‐inducing Wolbachia
CI dynamics in a panmictic population
We followed Hoffmann et al. (1990) and describe the infection dynamics of CI‐inducing Wolbachia in a panmictic host population by a nonlinear recursion equation. Host generations are discrete and nonoverlapping. Let p w and p′w denote the frequency of Wolbachia‐infected hosts in subsequent generations. Then, the intergenerational change in infection frequency is described by
| (A1) |
where F denotes the relative fecundity of infected females in comparison with uninfected ones, (1 − μ) the maternal transmission rate of Wolbachia, and l CI the level of cytoplasmic incompatibility, defined as offspring loss in incompatibility matings (i.e. infected male and uninfected female) in comparison with the other possible matings. Note that model (A1) does not allow for paternal or horizontal transmission of Wolbachia.
Spatiotemporal model
The spatiotemporal spread of CI‐inducing Wolbachia was previously modelled using partial differential equations (Turelli & Hoffmann 1991; Schofield 2002). Let p = p (x, t) denote the frequency of Wolbachia at point and time . Under the basic assumptions of model (A1) with respect to transmission, fecundity reduction and CI, the spatial dynamics of Wolbachia is described by
| (A2) |
where is the instable fix point of model (A1) for µ = 0 and σ is the variance of the individual movement probability distribution of host individuals. Analytical solutions exist for µ = 0. For p* < 0.5, Wolbachia is expected to spread as a travelling wave,
| (A3) |
where is the wave speed and the wave width, such that the Wolbachia frequency is expected to go from p ≈ 0.5 to p ≈ 0.9 over Δx = 3w (Turelli & Hoffmann 1991). We refer to Δx as to the transition zone width.
Codynamics of CI‐inducing Wolbachia and mitochondrial haplotypes
Model with paternal transmission
Turelli et al. (1992) analysed an extension of model (A1) to investigate the effect of paternal transmission of Wolbachia on the codynamics of Wolbachia and mitochondrial haplotypes. There are two mitochondrial haplotypes (M 1 and M 2), and individuals can be either infected with Wolbachia (W) or not (Ø). The model describes the intergenerational change in frequency of the four Wolbachia–haplotype combinations (denoted by p W1, p W2, p 01 p 02). It is derived using table S7 and computes to
| (A4) |
| (A5) |
| (A6) |
| (A7) |
where (1 − μ) and τ are the maternal and the paternal transmission rates of Wolbachia, respectively, H = 1 − l CI the relative hatch rate in incompatibility matings, F i the relative fecundity of Wolbachia‐infected females with haplotype M i relative to uninfected females, and the average fitness defined as the sum of all terms on the right‐hand side of equations (A4), (A5), (A6), (A7). The original model analysed by Turelli et al. (1992) is the special case of (A4), (A5), (A6), (A7) for F 1 = F 2.
Model with horizontal transmission
We extended model (A4), (A5), (A6), (A7) to incorporate horizontal transmission of Wolbachia. Horizontal transmission follows the mass action principle and is described by parameter β. All horizontally transmitted Wolbachia establish a somatic infection in the new host, but only the fraction α of these enters the germ line and is inherited to future generations. Somatic infections are not further transmitted and a dead end for Wolbachia. Horizontally transmitted Wolbachia can neither induce CI nor protect against it.
Let denote the Wolbachia–haplotype frequencies in the germline in subsequent generations among adults during mating. The change in frequency is described as follows. First, we calculate the frequencies among offspring, denoted by . These compute to
| (A8) |
| (A9) |
| (A10) |
| (A11) |
where all parameters and are defined as in model (A4), (A5), (A6), (A7).
Next, horizontal transmission takes place. We first consider only somatic infections of Wolbachia. Let denote the Wolbachia–haplotype frequencies for host individuals that are infected at germline and/or soma. Then, it holds that
| (A12) |
| (A13) |
| (A14) |
| (A15) |
where 0 ≤ β ≤ 1.
The fraction α of somatic infections enters the germline. Accordingly, the Wolbachia–haplotype frequencies in the next generation compute to
| (A16) |
| (A17) |
| (A18) |
| (A19) |
where 0 ≤ α ≤ 1.
References
- Ahmed MZ, Li SJ, Xue X et al (2015) The intracellular bacterium Wolbachia uses parasitoid wasps as phoretic vectors for efficient horizontal transmission. PLoS Pathogens, 10, e1004672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arthofer W, Krumböck S, Schuler H et al (2009a) Thirteen new microsatellite loci in Rhagoletis cerasi (Diptera: Tephritidae), a model host species for Wolbachia symbiosis in field populations. Molecular Ecology Resources, 9, 1460–1466.21564933 [Google Scholar]
- Arthofer W, Riegler M, Schneider D, Krammer M, Miller WJ, Stauffer C (2009b) Hidden Wolbachia diversity in field populations of the European cherry fruit fly, Rhagoletis cerasi (Diptera, Tephritidae). Molecular Ecology, 18, 3816–3830. [DOI] [PubMed] [Google Scholar]
- Atyame CM, Delsuc F, Pasteur N, Weill M, Duron O (2011) Diversification of Wolbachia endosymbiont in the Culex pipiens mosquito. Molecular Biology and Evolution, 28, 2761–2772. [DOI] [PubMed] [Google Scholar]
- Atyame CM, Labbe P, Rousset F et al (2015) Stable coexistence of incompatible Wolbachia along a narrow contact zone in mosquito field populations. Molecular Ecology, 24, 508–521. [DOI] [PubMed] [Google Scholar]
- Baldo L, Dunning Hotopp JC, Jolley KA et al (2006) Multilocus sequence typing system for the endosymbiont Wolbachia pipientis . Applied and Environmental Microbiology, 72, 7098–7110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baldo L, Ayoub NA, Hayashi CY, Russel JA, Stahlhut JK, Werren JH (2008) Insight into the routes of Wolbachia invasion: high levels of horizontal transfer in the spider genus Agelenopsis revealed by Wolbachia strain and mitochondrial DNA diversity. Molecular Ecology, 17, 557–569. [DOI] [PubMed] [Google Scholar]
- Barton NH, Turelli M (2011) Spatial waves of advance with bistable dynamics: cytoplasmic and genetic analogues of Allee effects. American Naturalist, 178, E48–E75. [DOI] [PubMed] [Google Scholar]
- Boller E, Bush GL (1974) Evidence for genetic variation in populations of the European cherry fruit fly, Rhagoletis cerasi (Diptera: Tephritidae) based on physiological parameters and hybridization experiments. Entomologia Experimentalis et Applicata, 17, 279–293. [Google Scholar]
- Boller EF, Remund U (1983) Field feasibility study for the application of SIT in Rhagoletis cerasi L. in Northwest Switzerland (1976–79) In: Fruit Flies of Economic Importance. Proceedings of the CEC/IOBC International Symposium Athens, November 1982(ed. Calvalloro R.), pp. 366–370. Balkema, Rotterdam. [Google Scholar]
- Boller EF, Russ K, Vallo V, Bush GL (1976) Incompatible races of European cherry fruit fly, Rhagoletis cerasi (Diptera: Tephritidae), their origin and potential use in biological control. Entomologia Experimetalis et Applicata, 20, 237–247. [Google Scholar]
- Boller E, Katsoyannos BI, Hippe C (1998) Host races of Rhagoletis cerasi L. (Dipt., Tephritidae): effect of prior adult experience on oviposition site preference. Journal of Applied Entomology, 122, 231–237. [Google Scholar]
- Charlat S, Duplouy AMR, Hornett EA et al (2009) The joint evolutionary histories of Wolbachia and mitochondria in Hypolimnas bolina . BMC Evolutionary Biology, 9, 64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniel C, Grunder J (2012) Integrated management of European Cherry Fruit Fly Rhagoletis cerasi (L.): situation in Switzerland and Europe. Insects, 3, 956–988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehrich D (2006) aflpdat: a collection of R functions for convenient handling of AFLP data. Molecular Ecology Notes, 6, 603–604. [Google Scholar]
- Engelstädter J, Hurst GDD (2009) The ecology and evolution of microbes that manipulate host reproduction. Annual Review of Ecology Evolution and Systematics, 40, 127–149. [Google Scholar]
- Evanno G, Regnaut S, Goudet J (2005) Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Molecular Ecology, 14, 2611–2620. [DOI] [PubMed] [Google Scholar]
- Fast EM, Toomey ME, Panaram K, Desjardins D, Kolaczyk ED, Frydman HM (2011) Wolbachia enhance Drosophila stem cell proliferation and target the germline stem cell niche. Science, 334, 990–992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenton A, Johnson KN, Brownlie JC, Hurst GDD (2011) Solving the Wolbachia paradox: modeling the tripartite interaction between host, Wolbachia, and a natural enemy. American Naturalist, 178, 333–342. [DOI] [PubMed] [Google Scholar]
- Fimiani P (1989) Mediterranean region In: Fruit Flies. Their Biology, Natural Enemies and Control, Vol. 3A (eds Robinson AS, Hooper G.), pp. 39–50. Elsevier, Amsterdam. [Google Scholar]
- Gehrer L, Vorburger C (2012) Parasitoids as vectors of facultative bacterial endosymbionts in aphids. Biology Letters, 8, 613–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerth M, Röthe J, Bleidorn C (2013) Tracing horizontal Wolbachia movements among bees (Anthophila): a combined approach using MLST data and host phylogeny. Molecular Ecology, 22, 6149–6162. [DOI] [PubMed] [Google Scholar]
- Goudet J (1995) FSTAT version 1.2: a computer program to calculate F‐statistics. The Journal of Heredity, 86, 485–486. [Google Scholar]
- Hamm CA, Begun DJ, Vo A et al (2014) Wolbachia do not live by reproductive manipulation alone: infection polymorphism in Drosophila suzukii and D. subpulchrella . Molecular Ecology, 23, 4871–4885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock P, Sinkins SP, Godfray HCJ (2011) Population dynamic models of the spread of Wolbachia . American Naturalist, 177, 323–333. [DOI] [PubMed] [Google Scholar]
- Hedges LM, Brownlie JC, O'Neill SL, Johnson KN (2008) Wolbachia and virus protection in insects. Science, 322, 702. [DOI] [PubMed] [Google Scholar]
- Hoffmann AA, Turelli M (1988) Unidirectional incompatibility in Drosophila simulans: inheritance geographic variation and fitness effects. Genetics, 126, 933–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA, Turelli M (1997) Cytoplasmatic incompatibility in insects In: Influential Passengers: Inherited Microorganisms and Arthropod Reproduction (eds O'Neill SL, Hoffmann AA, Werren JH.), pp. 42–80. Oxford University Press, Oxford. [Google Scholar]
- Hoffmann AA, Turelli M, Harshman LG (1990) Factors affecting the distribution of cytoplasmic incompatibility in Drosophila simulans . Genetics, 126, 933–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA, Clancy D, Duncan J (1996) Naturally‐occurring Wolbachia infection in Drosophila simulans that does not cause cytoplasmic incompatibility. Heredity, 76, 1–8. [DOI] [PubMed] [Google Scholar]
- Hoffmann AA, Hercus M, Dagher H (1998) Population dynamics of the Wolbachia infection causing cytoplasmic incompatibility in Drosophila melanogaster . Genetics, 148, 221–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA, Montgomery BL, Popovici J et al (2011) Successful establishment of Wolbachia in Aedes populations to suppress dengue transmission. Nature, 476, 454–457. [DOI] [PubMed] [Google Scholar]
- Hoffmann AA, Iturbe‐Ormaetxe I, Callahan AG et al (2014) Stability of the wMel Wolbachia infection following invasion into Aedes aegypti populations. Plos Neglected Tropical Diseases, 8, e3115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurst GDD, Jiggins FM (2005) Problems with mitochondrial DNA as a marker in population, phylogeographic and phylogenetic studies: the effects of inherited symbionts. Proceedings of the Royal Society of London B: Biological Sciences, 272, 1525–1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaenike J, Dyer KA, Cornish C, Minhas MS (2006) Asymmetrical reinforcement and Wolbachia infection in Drosophila . PLoS Biology, 4, 1852–1862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiggins FM (2003) Male‐killing Wolbachia and mitochondrial DNA: selective sweeps, hybrid introgression and parasite population dynamics. Genetics, 164, 5–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraaijeveld K, Franco P, De Knijff P, Stouthamer R, van Alphen JJM (2011) Clonal genetic variation in a Wolbachia‐infected asexual wasp: horizontal transmission or historical sex? Molecular Ecology, 20, 3644–3652. [DOI] [PubMed] [Google Scholar]
- Kriesner P, Hoffmann AA, Lee SF, Turelli M, Weeks AR (2013) Rapid sequential spread of two Wolbachia variants in Drosophila simulans . PLoS Pathogens, 9, e1003607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McFall‐Ngai M, Hadfield MG, Bosch TCG et al (2013) Animals in a bacterial world, a new imperative for the life sciences. Proceedings of the National Academy of Sciences of the United States of America, 110, 3229–3236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller SA, Dykes DD, Polesky HF (1988) A simple salting out procedure for extracting DNA from human nucleated cells. Nucleic Acids Research, 16, 1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moraiti CA, Nakas CT, Papadopoulos NT (2014) Diapause termination of Rhagoletis cerasi pupae is regulated by local adaptation and phenotypic plasticity: escape in time through bet‐hedging strategies. Journal of Evolutionary Biology, 27, 43–54. [DOI] [PubMed] [Google Scholar]
- Morrow JL, Frommer M, Shearman DC, Riegler M (2014) Tropical tephritid fruit fly community with high incidence of shared Wolbachia strains as platform for horizontal transmission of endosymbionts. Environmental Microbiology, 16, 3622–3637. [DOI] [PubMed] [Google Scholar]
- Morrow JL, Frommer M, Royer JE, Shearman DCA, Riegler M (2015) Wolbachia pseudogenes and low prevalence infections in tropical but not temperate Australian tephritid fruit flies: manifestations of lateral gene transfer and endosymbiont spillover? BMC Evolutionary Biology, 15, 202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narita S, Nomura M, Kato Y, Fukatsu T (2006) Genetic structure of sibling butterfly species affected by Wolbachia infection sweep: evolutionary and biogeographical implications. Molecular Ecology, 15, 1095–1108. [DOI] [PubMed] [Google Scholar]
- O'Neill SL, Giordano R, Colbert A, Karr T, Robertson H (1992) 16S Ribosomal‐RNA phylogenetic analysis of the bacterial endosymbionts associated with cytoplasmic incompatibility in insects. Proceedings of the National Academy of Sciences of the United States of America, 89, 2699–2702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peakall R, Smouse PE (2006) GenAlEx 6: genetic analysis in Excel. Population genetic software for teaching and research. Molecular Ecology Notes, 6, 288–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P (2000) Inference of population structure using multilocus genotype data. Genetics, 155, 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasgon JL, Cornel AJ, Scott TW (2006) Evolutionary history of a mosquito endosymbiont revealed through mitochondrial hitchhiking. Proceedings of the Royal Society of London B: Biological Sciences, 273, 1603–1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reumer BM, van Alphen JJM, Kraaijeveld K (2012) Occasional males in parthenogenetic populations of Asobara japonica (Hymenoptera: Braconidae): low Wolbachia titer or incomplete coadaptation? Heredity, 108, 341–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice WR (1989) Analyzing tables of statistical tests. Evolution, 43, 223–225. [DOI] [PubMed] [Google Scholar]
- Richardson MF, Weinert LA, Welch JJ et al (2012) Population genomics of the Wolbachia endosymbiont in Drosophila melanogaster . PLoS Genetics, 8, e1003129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riegler M, Stauffer C (2002) Wolbachia infections and superinfections in cytoplasmically incompatible populations of the European cherry fruit fly Rhagoletis cerasi (Diptera, Tephritidae). Molecular Ecology, 11, 2425–2434. [DOI] [PubMed] [Google Scholar]
- Riegler M, Charlat S, Stauffer C, Merçot H (2004) Wolbachia transfer from Rhagoletis cerasi to Drosophila simulans: investigating the outcomes of host‐symbiont coevolution. Applied and Environmental Microbiology, 70, 273–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riegler M, Sidhu M, Miller WJ, O'Neill SL (2005) Evidence for a global Wolbachia replacement in Drosophila melanogaster . Current Biology, 15, 1428–1433. [DOI] [PubMed] [Google Scholar]
- Schofield P (2002) Spatially explicit models of Turelli‐Hoffmann Wolbachia invasive wave fronts. Journal of Theoretical Biology, 215, 121–131. [DOI] [PubMed] [Google Scholar]
- Schuler H, Bertheau C, Egan SP et al (2013) Evidence for a recent horizontal transmission and spatial spread of Wolbachia from endemic Rhagoletis cerasi (Diptera: Tephritidae) to invasive Rhagoletis cingulata in Europe. Molecular Ecology, 22, 4101–4111. [DOI] [PubMed] [Google Scholar]
- Schwarz D, McPheron BA, Hartl G, Boller E, Hoffmeister TS (2003) A second case of genetic host races in Rhagoletis? A population genetic comparison of sympatric host populations in the European cherry fruit fly, Rhagoletis cerasi . Entomologia Experimentalis et Applicata, 108, 11–17. [Google Scholar]
- Simon C, Frati F, Beckenbach A, Crespi B, Liu H, Flook P (1994) Evolution, weighting, and phylogenetic utility of mitochondrial gene‐sequences and a compilation of conserved polymerase chain‐reaction primers. Annals of the Entomological Society of America, 87, 651–701. [Google Scholar]
- Turelli M, Hoffmann AA (1991) Rapid spread of an inherited incompatibility factor in California Drosophila . Nature, 353, 440–442. [DOI] [PubMed] [Google Scholar]
- Turelli M, Hoffmann AA (1995) Cytoplasmic incompatibility in Drosophila simulans: dynamics and parameter estimates from natural populations. Genetics, 140, 1319–1338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turelli M, Hoffmann AA, McKechnie SW (1992) Dynamics of cytoplasmic incompatibility and mtDNA variation in natural Drosophila simulans populations. Genetics, 132, 713–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vallo V, Remund U, Boller E (1976) Storage conditions of stockpiled diapausing pupae of Rhagoletis cerasi for obtaining high emergence rates. Entomophaga, 21, 251–256. [Google Scholar]
- Vavre F, Fleury F, Lepetit D, Fouillet P, Bouletreau M (1999) Phylogenetic evidence for horizontal transmission of Wolbachia in host‐parasitoid associations. Molecular Biology and Evolution, 16, 1711–1723. [DOI] [PubMed] [Google Scholar]
- Weeks AR, Turelli M, Harcombe WR, Reynolds KT, Hoffmann AA (2007) From parasite to mutualist: rapid evolution of Wolbachia in natural populations of Drosophila . PLoS Biology, 5, e114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir BS, Cockerham CC (1984) Estimating F‐statistics for the analysis of population structure. Evolution, 38, 1358–1370. [DOI] [PubMed] [Google Scholar]
- Werren JH, Baldo L, Clark ME (2008) Wolbachia: master manipulators of invertebrate biology. Nature Reviews Microbiology, 6, 741–751. [DOI] [PubMed] [Google Scholar]
- Zug R, Koehncke A, Hammerstein P (2012) Epidemiology in evolutionary time: the case of Wolbachia horizontal transmission between arthropod host species. Journal of Evolutionary Biology, 25, 2149–2160. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. S1 Results of structure analysis of microsatellite data.
Table S1 Locality information, frequency of Wolbachia infections (wCer1, wCer1&2), frequencies of different haplotypes, and association of Wolbachia with the respective haplotype.
Table S2 Summary of microsatellite data chi‐square tests for Hardy–Weinberg Equilibrium.
Table S3 Results from amova analysis based on infection status.
Table S4 Results from pairwise F ST analysis.
Table S5 Results from amova analysis based in R. cerasi host plants.
Table S6 Principal coordinate analysis (PCoA) of different R. cerasi populations, based on Nei distances.
Table S7 Mating table used to derive model (A4), (A5), (A6), (A7). Modified from Turelli et al. (1992).
Data Availability Statement
Mitochondrial DNA sequences have been submitted to GenBank: Accession numbers: KJ488948 (HT1) and KJ488949 (HT2). Mitochondrial DNA sequence chromatograms, microsatellite raw data, genalex, fstat, and structure data and result files have been deposited at Dryad: Provisional DOI: 10.5061/dryad.gs8r.2.


