Original Research: Sickle cell anemia and pediatric strokes: Computational fluid dynamics analysis in the middle cerebral artery

Abstract

Children with sickle cell anemia (SCA) have a high incidence of strokes, and transcranial Doppler (TCD) identifies at-risk patients by measuring blood velocities in large intracerebral arteries; time-averaged mean velocities greater than 200 cm/s confer high stroke risk and warrant therapeutic intervention with blood transfusions. Our objective was to use computational fluid dynamics to alter fluid and artery wall properties, to simulate scenarios causative of significantly elevated arterial blood velocities. Two-dimensional simulations were created and increasing percent stenoses were created in silico, with their locations varied among middle cerebral artery (MCA), internal carotid artery (ICA), and anterior cerebral artery (ACA). Stenoses placed in the MCA, ICA, or ACA generated local increases in velocity, but not sufficient to reach magnitudes > 200 cm/s, even up to 75% stenosis. Three-dimensional reconstructions of the MCA, ICA, and ACA from children with SCA were generated from magnetic resonance angiograms. Using finite element method, blood flow was simulated with realistic velocity waveforms to the ICA inlet. Three-dimensional reconstructions revealed an uneven, internal arterial wall surface in children with SCA and higher mean velocities in the MCA up to 145 cm/s compared to non-SCA reconstructions. There were also greater areas of flow recirculation and larger regions of low wall shear stress. Taken together, these bumps on the internal wall of the cerebral arteries could create local flow disturbances that, in aggregate, could elevate blood velocities in SCA. Identifying cellular causes of these microstructures as adhered blood cells or luminal narrowing due to endothelial hyperplasia induced by disturbed flow would provide new targets to treat children with SCA. The preliminary qualitative results provided here point out the critical role of 3D reconstruction of patient-specific vascular geometries and provide qualitative insight to complex interplay between vascular geometry and rheological properties possibly altered by SCA.

Introduction

Sickle cell anemia (SCA) is one of the most common blood disorders in the world with 300,000 babies born each year¹; amongst them, 11% of children with this genetic disease will have a major stroke by the age of 16 years; and up to 37% will have a silent stroke impairing mental function and cognitive abilities by age 14.^2,3 After the first stroke, the risk of recurrent strokes is elevated significantly to 50–90%.^4,5 During the major clinical trial STOP, Transcranial Doppler ultrasound was used to measure the highest time averaged mean blood flow velocity in the internal carotid artery (ICA), middle cerebral artery (MCA), or the anterior cerebral artery (ACA).The study concluded that children with time-averaged maximum mean velocities (TAMMV) greater than 200 cm/s had greater than 50% chance of developing a stroke, but chronic transfusions significantly reduce the risk of primary stroke^5,6; patients in the conditional range from 170 to 199 cm/s are at increased risk as well and have high probability of conversion to the abnormal range.⁷ The mechanisms that cause sickle cell-mediated strokes are still being clarified, but altered hemodynamics may be responsible as indicated by the elevated velocities. Deoxygenation causes a conformational change in the hemoglobin protein that exposes the mutant valine on the surface of the β-globin subunit that drives polymerization into stiff hemoglobin fibers that deform the red blood cell (RBC) membrane into the sickle shape. The repetitive polymerization and melting of hemoglobin fibers in the RBCs as they travel throughout oxygenated and deoxygenated circulation cumulatively damage the membrane, increasing its viscosity and RBC density, which can ultimately change bulk flow properties in unexpected ways. RBC density, viscosity, and stiffness increase with each sickling, increasing viscosity of sickle cell blood by as much as 3–7 times greater than non-sickle blood at an equivalent hematocrit.^8–11 However, people with SCA have a reduced hematocrit of only ∼25% compared to 45% of those without the genetic disease.

The interplay between the altered rheological properties induced by the sickle cells and the hemodynamics is not trivial and needs to be properly modelled with mathematical and numerical tools. While the change of the shape and mechanical properties of the red cells induces an increment of the apparent viscosity which slows down the blood, we notice increased velocity in children that needs to be properly addressed and explained by such complex interplay. It is also worth pointing out that while it is expected to find elevated centerline velocities through stenotic regions of arteries, abnormalities may not be detected by MRAs although an elevated velocity may be measured by TCD.¹² The objective of this study is to provide preliminary insight into these inconsistencies by determining in silico scenarios by which pathological, elevated blood velocities can occur in the MCA, ICA, and ACA of children with SCA. Utilizing the computational fluid dynamics (CFD), blood flow was simulated in both two- and three-dimensional computational reconstructions rendered from actual patient angiograms, then manipulated to determine virtual stenotic scenarios in the cerebral arteries capable of reproducing the elevated velocities measured by TCD to locate regions where stenosis may not yet be detected by magnetic resonance angiography. Further, these scenarios will provide key insight into hemodynamics that is counterintuitive to the general assumptions made about flow in tubes and at branches. Reconstructions from patients with and without SCA were then compared for their hemodynamic properties to investigate inherent differences in geometry or anatomy that could be key to altering hemodynamics. This is a first work toward a progressively more accurate assessment of the rheological properties of patients affected by SCA by using computational tools and their consequences on the hemodynamics.

Materials and methods

System of equations

The finite element method was implemented to simulate blood flow in the cerebral arteries. The commercial package, Comsol 4.4, and an open-source software, LifeV (www.lifev.org)⁵³ were used to perform simulations in both two and three dimensions, respectively. The governing model used for the study consisted of the classical Navier–Stokes equations for incompressible fluids following from mass and momentum conservation principles. At this first level of investigation, we assumed blood to be a Newtonian fluid, so that viscous effects are explained by a constant viscosity μ multiplying the shear stress. By denoting v the velocity, P the pressure, ρ the (constant) density, the equations read

$$\nabla ·v=0$$ (1)

$$\rho \frac{\mathrm{Dv}}{\mathrm{Dt}}-\nabla P+\mu {\nabla }^{2}v=0$$ (2)

where $\frac{D}{\mathrm{Dt}}$ denotes the material or Lagrange derivative, and ${\nabla }^2$ is the Laplace operator. The region where we assume these equations to hold is the vascular lumen, delimited by the vascular walls and inflow/outflow sections. On the walls we postulate rigid displacement and consequently we take null velocity (or no-slip) conditions. Conditions on the inflow and outflow sections will be specified later on. As for any time-dependent problems, we need to specify an initial condition for the velocity, whose impact is, however, got rid of by simulating an appropriate number of heart beats that guarantee periodicity in the simulation. Since the initial conditions typically do not match the prescribed boundary conditions (typically we prescribe zero-velocity initial conditions, while inflow velocity is not zero at the beginning), this inconsistency may generate some numerical instabilities. To avoid these spurious effects, before the computation of the heart beats, we perform a “pre-load” phase, when the initial conditions are gradually made consistent with the boundary data, by solving the Navier–Stokes equations for a certain number of fictitious time steps. At the end of this stage, the velocity and pressure fields at the beginning of the (physical) heart beat are perfectly consistent with the prescribed boundary data.

Characteristics and properties of two-dimensional simulations in Comsol

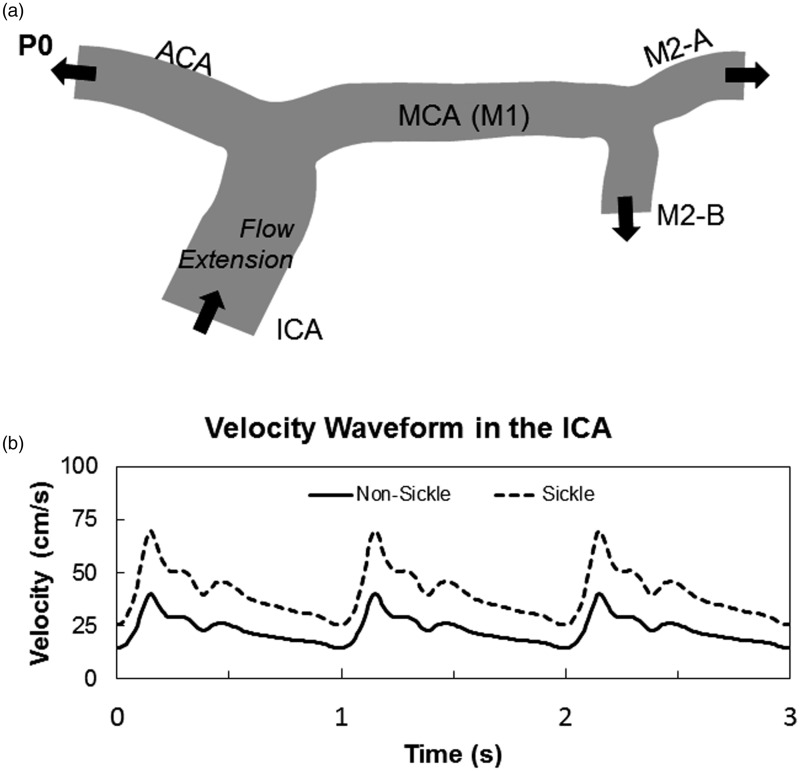
Arterial segments containing the distal ICA, the ACA, the MCA, and segments from the first bifurcation of the MCA, known as M2, were used for models in blood flow simulations (Figure 1(a)). These segments were chosen because of their diagnostic importance in determining stroke risk in SCA by TCD.^13–15 The two-dimensional model was created from a representation previously published of a 71-year-old female subject (P0),¹⁶ and used to perturb fluid properties, initial conditions, and stenoses placements (Figure 1(a)). The representative figure was scanned into SolidWorks, where an outline of the model was produced and scaled to the appropriate size. As for the boundary conditions, beyond nonslip null velocity conditions at the rigid walls, we prescribe an inflow waveform illustrated in Figure 1. These conditions are prescribed by postulating an arbitrary parabolic velocity profile fitting the flow rate. To mitigate the impact of this arbitrary choice on the final results, as common practice we add a flow extension, i.e. a fictitious portion of the ICA upstream the real one. This is taken to be as long as 10 diameters of the 2D ICA. The mesh for the 2D simulations was created in Comsol using the program’s in-house mesh generator, where a mesh containing ∼21,000 elements was applied to the geometry.

Figure 1.

Outline of two-dimensional cerebral artery model. A 2D representation of the MCA from a 71-year-old female subject was used for the two-dimensional simulation (a). Comparison velocity profiles over three cardiac cycles found in the ICA of SS and AA individuals. The elevated velocity profile caused by anemia in SCA was used as the inlet boundary condition for all simulations (b)

Simulated fluid properties were that of healthy blood (μ = 3 cP, and ρ = 1060 kg/m³). Artery walls were assumed to be rigid, thus no-slip condition velocity along the wall was assumed to be zero. Flow extensions at the ICA-inlet were added to the original geometry to guarantee that velocity profiles entering the ICA during the simulation were laminar and parabolic. The outlet arteries (ACA, M2-A, and M2-B) had an open boundary, and Comsol’s suppression algorithm was used to prevent backflow at the outlets, preventing the need for flow extensions at these arteries.

Individuals with HbAA blood (RBC containing only normal hemoglobin) have a maximum mean velocity of 40 cm/s in the ICA, based on values found in literature,^17,18 therefore to simulate conditions in a person with HbSS blood (RBC containing only sickle hemoglobin), this maximum mean velocity at the inlet was changed to 70 cm/s. This was based on values found clinically and represents the elevated blood velocities caused by anemia in an individual with SCA.^15,19 After the maximum mean velocity of the profile was increased, the rest of the waveform was scaled accordingly. These two velocity waveforms over three cardiac cycles are shown in Figure 1(b).

Simulations were run for three consecutive heart beats (1 Hz frequency) with a step of 0.1 s. Post-processing of data for the 2D simulations were completed in Comsol. The maximum velocity during systole was calculated across the entire model for all simulations, and the time-averaged velocity was taken across cross-sectional slices at the proximal and distal ends of the MCA. The shear stress by definition reads

$$\tau =\mu (\nabla v+\nabla v^T)$$ (3)

On the boundaries (walls), it is well known that the wall shear stress (WSS) has a clinical significance.^20,21 The latter is defined as the tangential projection of the normal component of the shear stress

$$\mathrm{WSS}=\tau ·n-(\tau ·n)n$$

where n is the outward unit vector normal to the wall.

Characteristics and properties of three-dimensional simulations with VMTK, Netgen, and LifeV

Magnetic resonance angiograms (MRAs) were used to create 3D models of the cerebral arteries for each subject. Amongst the subjects, one did not have SCA (P1) (Figure 2(a)), while the remaining two (P2 and P3) were afflicted with the disease. No identifying information was provided, other than P2 had no history of stroke (Figure 2(b)), while P3 had a previous overt stroke that affected the left side of the brain (Figure 2(c)). Using the reconstructive software, Vascular Modeling Toolkit (VMTK),²² 2D MRA slices taken in the coronal plane were stacked together to produce a 3D layered object.²³ Arterial branches were segmented out from the layered object and used to reconstruct the vascular tree. Once the vascular network was created, only the segments of interest were kept, and all the other vessels were removed. Re-meshing and smoothing algorithms from VMTK were applied to remove irregular artifacts created during the reconstructive process. The finished models include flow extensions at the inlets and outlets with lengths equal to 10 times the diameter. Flow extensions have a twofold purpose. As for the 2D case, at inflow boundaries they are intended to take the effect of the arbitrary velocity profile used to compensate the lack of patient specific data away from the region of interest, so to mitigate (or even discard) its impact on the solution; at the outflow they are not strictly needed, but they contribute to reduce the risks of backflows – the latter are well known to be a source of numerical instabilities at outlets.²⁴ The flow extensions basically reduce the impact of the arbitrary choice for the velocity profile in the region of interest.²⁵ The third subject, P3, contains a slightly longer ICA due to a stenosis featured in that arterial segment.

Figure 2.

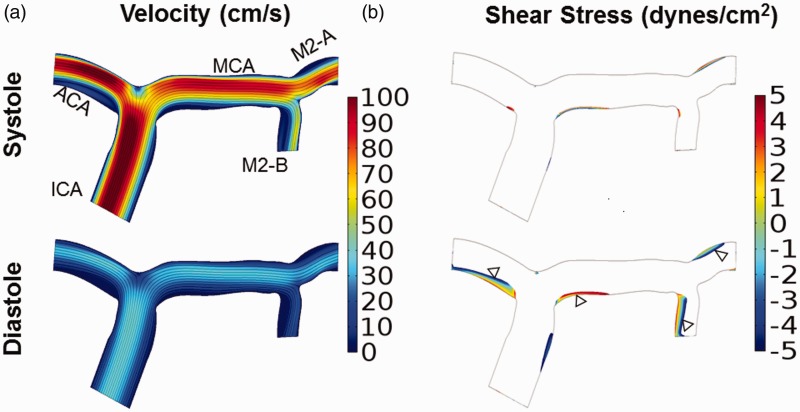
Elevated internal carotid artery velocities caused by sickle cell anemia does not generate velocities greater than 200 cm/s in the middle cerebral artery. Velocity and shear stress profiles were calculated for a 2-D arterial model with the TAMMV of the ICA inflow velocity set to those of a patient with SCA (70 cm/s). (a) Velocity during systole and diastole. Velocity was highest in the ICA and ACA, and the maximum velocity in the MCA did not exceed 90 cm/s. (b) Regions of low wall shear stress during systole and diastole are depicted with a maximum threshold of ± 5 dynes/cm² . The affected regions correlate to regions with low velocities (a), and include the apex of the terminal end ICA bifurcation and inner curvature of bifurcations

A mesh of approximately 75,000 elements was applied to each of the three-dimensional artery models. While for more accurate quantitative assessments, more refined meshes may be needed, and at this preliminary qualitative stage of analysis, this mesh size is fine enough for a qualitative analysis of blood flow in view of comparative discussion. Meshes for the 3D simulations were first produced in the open-source software, Netgen²⁷ before being imported into LifeV⁵³ The latter is an open source Object Oriented C++ Finite Element solver developed as a joint initiative of Department of Mathematics at EPFL, Lausanne CH, Department of Mathematics at Politecnico di Milano, Milan, IT and the Department of Mathematics and Computer Science at Emory University, Atlanta, GA, USA. The same velocity waveforms from 2D simulations were applied in 3D. Again, the properties of Newtonian blood were assumed, and the artery walls were assumed to be rigid with a blood velocity of zero at the wall. In the 3D models, a lumped parameter (or 0D) model was used at each individual outlet to relate the outgoing artery velocity to the pressure of the outlet – usually called 3-element Windkessel Model.²⁷ While not the same as the boundary conditions used in the 2-D model, by applying this boundary equally to all outlets, the resistances on the system acted similarly to the open boundary condition. Simulations were run in parallel on a local Linux cluster. Free software Paraview was used for postprocessing and in particular for computing maximum systolic velocity. Average velocity was taken across cross-sectional slices at the proximal and distal ends of the MCA, using a script developed in Matlab that integrated individual velocity points across a surface. Lastly, wall shear stress (WSS) was calculated during diastole from the velocity profile using LifeV.

Results

MCA-elevated velocities indicative of stroke risk could not be generated in a two-dimensional computational fluid dynamic model

First, we tested the hypothesis that an elevated velocity profile at the ICA-inlet caused by anemia would be sufficient to produce time-averaged mean velocities in the MCA greater than 200 cm/s, the magnitude that is indicative of stroke risk. Despite elevated inlet velocities approximately 40% greater than individuals with AA blood, the velocities in the MCA only reached a maximum speed of 90 cm/s during systole (Figure 2(a)). Diastole values were of course lower, reaching only a maximum of 40 cm/s (Figure 2(b)). Under these conditions, higher fluid velocities were observed in the ACA (100 cm/s) as compared to the MCA.

Since the elevated inlet blood velocity was insufficient to generate threshold velocity values indicative of stroke risk, shear stress was determined to identify regions of low or oscillatory shear stress. Such regions are known to cause endothelial cell responses that promote proteolytic mediated vascular remodeling leading to the formation of intimal hyperplasia that could possibly form stenoses in the artery.^28–30 Wall shear stress values were calculated from the velocity profiles, and areas of the artery wall exposed to shear stress in the range of ± 5 dynes/cm² are found to occur preferentially along the inner curvature of bifurcations (Figure 2(c) and (d)). The length of the wall region exposed to this low, and in some cases oscillatory shear stress, is shorter in systole than diastole.

Effects of stenosis placement and size on velocities in the MCA

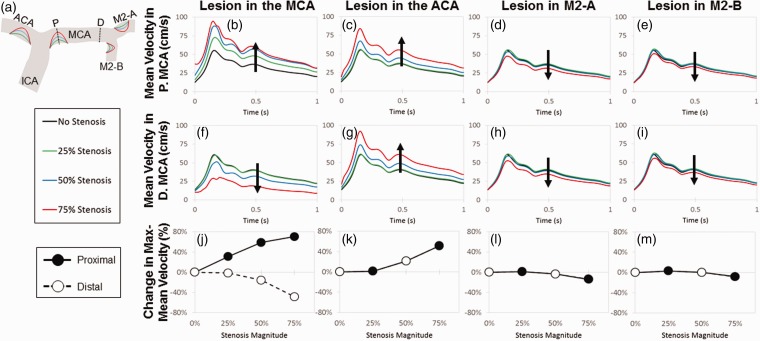
The original model was modified to simulate the development of intimal hyperplasia and vascular lesions that would occur at sites exposed to low wall shear stress, and these regions were informed by the sites of low wall shear stress from the previous model (Figure 2(d)). To test the hypothesis that stenoses formed by such lesions could produce an elevated time-average maximum-mean velocity greater than 200 cm/s, vascular lesions were placed one at a time, in either the ACA, the proximal MCA, the M2-A, or the M2-B. This was to determine the percent stenosis necessary to generate elevated velocities. Simulations were performed over a range of stenosis magnitudes: 25% (green), 50% (orange), or 75% (red) of the artery diameter (Figure 3(a)).

Figure 3.

A lesion at the entrance of the middle cerebral artery produces the largest difference in the proximal and distal velocities. Lesions of increasing size from 25% to 75% of the artery diameter were placed at the entrance of MCA, ACA, MCA-1, and MCA-2 (areas affected by low WSS) in order to produce stenotic lesions (a). Dotted lines represent slices where the mean velocity was measured in the proximal (top panel) and distal (middle panel) MCA. Mean velocity in the proximal MCA increased with lesion magnitude when narrowing occurred at the entrance of the MCA (b) and ACA (c). Lesions in M2-A and M2-B had a negligible effect on velocity, despite lesion magnitudes of 75% (d, e). In the distal end of the MCA, the mean velocity decreased with increasing MCA stenosis (f). Increasing the magnitude of the ACA lesion led to an increased velocity in the distal MCA (g), and stenoses in the M2-A and M2-B did not affect velocity (h, i), matching observations seen in the proximal MCA. In the bottom panel, percent change in the maximum mean velocity was calculated in respect to lesion magnitude and location. A lesion in the MCA entrance produced the greatest difference in percent change, increasing and decreasing in the proximal and distal MCA velocity, respectively (j). Lesions in the ACA, MCA-1, and MCA-2 entrances have the same effect on both the proximal and distal velocities (k–m)

The mean velocity was calculated at the proximal and distal ends of the MCA, and the effects of stenosis magnitude and location on mean blood velocity in the proximal and distal MCA were determined. As the magnitude of a stenosis in the MCA increased from 0% to 75% the artery diameter, the mean velocity also increased in the proximal MCA, reaching a maximum-mean velocity of about 90 cm/s (Figure 3(b)). A similar effect was observed when a stenosis was placed in the ACA; however, the velocity at the proximal MCA only increased from stenoses sizes ranging between 50% and 75%, with the 25% lesions having little to no effect on blood velocities at proximal MCA site (Figure 3(c)). Stenoses in both the M2-A and M2-B had minimal effect on velocity in the proximal MCA despite large stenoses that filled 75% of the artery diameter (Figure 3(d) and (e)).

Stenosis placement in the ACA and the downstream arteries of the MCA, the M2-A and M2-B, had similar effects on velocity calculated at the distal MCA site (Figure 3(g) to (i)), but when the stenosis was placed at the entrance to the MCA, the results were different (Figure 3(f)). There was a decrease in mean velocity at the distal MCA site from 60 cm/s to 25 cm/s which was opposite of what occurs to velocities measured at the proximal MCA location. Taken together, these data could be plotted as the percent change in the maximum mean velocity to distinguish differences between velocities at the proximal or distal end of the MCA (Figure 3(j) to (m)). Only for stenoses placed at the entrance of the MCA can a stark difference in maximum-mean velocities be generated along the length of the MCA. The percent change in velocity increased as a function of percent stenosis for velocities measured at proximal MCA, but conversely decreased with percent stenosis at the distal end. This has important implications for determining patient stroke risk. It could be that when averaging velocities measured by TCD over the length of the entire MCA, an incorrect and significantly lower velocity reading might be obtained, misleading clinicians to think that the patient is safe, although a large stenosis may be present and the patient is at high risk. Despite this interesting disparity for proximal MCA lesions, the mean MCA velocity never exceeded a 100 cm/s, regardless of lesion size and location.

Mean velocity is elevated in 3D patient-specific cerebral artery geometries of individuals with SCA

The inability to reach high pathological MCA velocities indicative of stroke risk in individuals with SCA in the 2D simulations maybe due to a lack of features only available in three dimensions, therefore the importance of using full 3D models was investigated. Three subjects were compared to determine if anatomical differences between sickle and non-sickle individuals could influence the hemodynamic properties. ICA, ACA, and MCA vessels were reconstructed as described in the Materials and Methods sections from MRAs (Figure 4). Simulations were run with similar fluid properties and inlet values for all three subjects as can be seen with velocities in the ICA (Figure 5).

Figure 4.

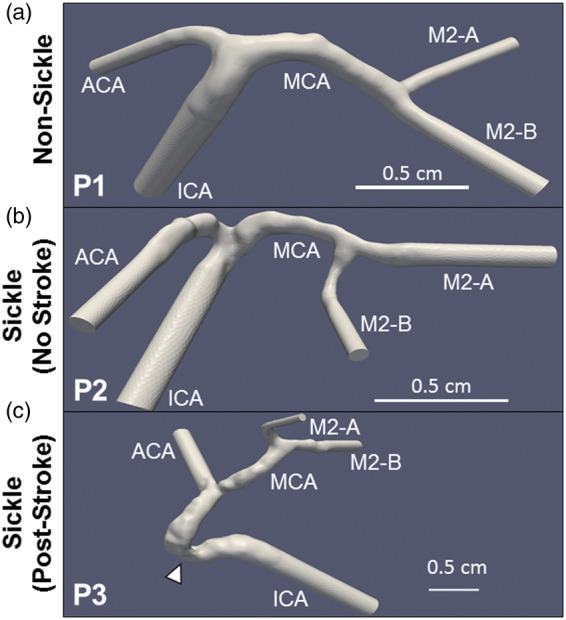
Reconstructed geometries of sickle and non-sickle cerebral arteries. Three-dimensional models were generated from MRAs of one non-sickle subject (P1) (a) and two sickle patients: one with no history of stroke (P2) (b), and another post-stroke (P3) (c). The model of Patient 3’s artery is extended due a stenosis in the ICA (arrowhead). Scale bar is shown

Figure 5.

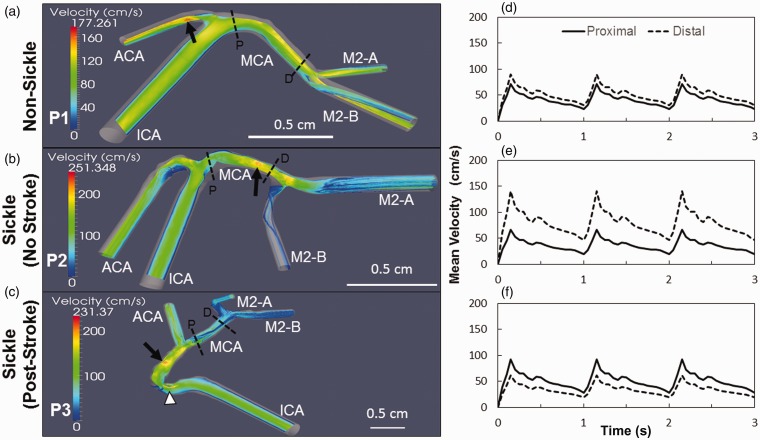
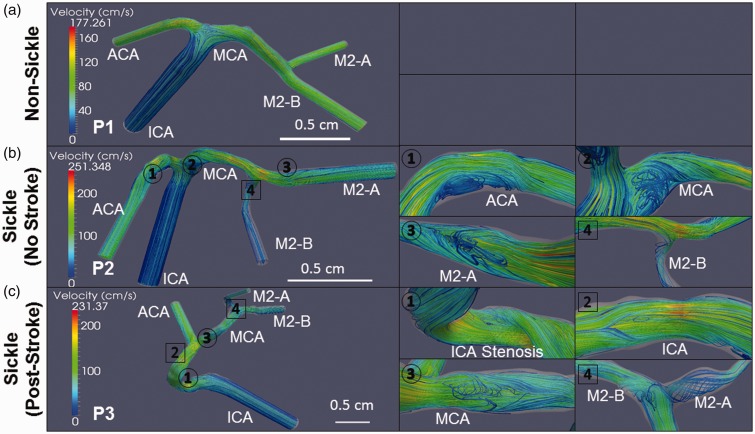
Velocity profiles in the middle cerebral are elevated in individuals with sickle cell anemia. Slices of the velocity streamlines are depicted for the each subject during systole. The maximum velocity in the non-sickle patient (P1) is highest in the ACA (arrow), and the MCA presents a consistent profile that peaks at ∼150 cm/s (a). In the sickle patient with no stroke (P2), the velocity is highest in the MCA (arrow), increasing from the proximal to the distal end with a maximum speed of 251 cm/s (b). The sickle subject with a previous history of stroke (P3) has the highest velocity occurring along the ICA prior to the bifurcation (arrow) and at the stenosis (arrowhead). The maximum velocity in the MCA reaches approximately 180 cm/s at the proximal end and decreases towards the distal MCA bifurcation (c). The velocity in the MCA of P1 has the least variance with the velocity at the proximal and distal ends reaching 72 and 90 cm/s, respectively (d). The velocity profile in the MCA of P2 has the largest variance amongst all the subjects with velocity increasing from the proximal end at 66 cm/s to the distal end at the 141 cm/s (e). Subject P3 has its velocity in the MCA decrease from 92 cm/s at the proximal side to 61 cm/s at the distal end (f). Scale bar is shown

A slice of the velocity streamlines during systole are shown for each subject: (P1) non-sickle cell; (P2) sickle patient with no history of stroke; and (P3) sickle cell patient who had a previous stroke (Figure 5(a) to (c)). Maximum velocities differ for each of these reconstructed cerebral artery trees with P1, the non-sickle subject maximum reaching 170 cm/s in the ACA, up to 230 cm/s in the ICA of P3, the sickle patient post-stroke, and then the highest max value of 250 cm/s occurs in P2, the sickle patient no history of stroke (arrows, Figure 5(a) to (c)). The velocity in the MCA remains consistent throughout the entire length of subject P1 (Figure 5(a)). Velocity in the MCA of P2 gradually increased starting at 120 cm/s at the proximal side before reaching a maximum toward the distal end (Figure 5(b)). The velocity profile slowed across the length of the MCA for P3 with the proximal end reaching a maximum value of approximately 180 cm/s, and gradually decreased to ∼90 cm/s at the distal MCA. Subject P3 also had a localized increase in velocity occurring at the stenosis in the ICA (arrowhead, Figure 5(c)).

The mean velocities in the proximal and distal ends of the MCA were calculated for each subject. Subject P1 had the greatest consistency across the length of the MCA with the proximal end reaching a TAMMV of 72 cm/s and the distal end as high as 90 cm/s (Figure 5(d)). Subject P2 had the largest variance between both ends of the MCA. The proximal MCA was much lower reaching 66 cm/s, with the distal end having a maximum mean velocity of 140 cm/s, but there appeared to be a stenosis right at the bifurcation to the M2-B that may be causal (Figure 5(e)). P3 fell in between the other subjects, for both velocity and maximum speed and variance in the MCA; however, the velocity was much higher at the proximal end. This subject had a TAMMV of 92 cm/s and 61 cm/s for both the proximal and distal ends, respectively (Figure 5(f)).

Areas of flow recirculation and low shear stress are more prevalent in reconstructed cerebral arteries of individuals with SCA

Post-stenotic regions are subject to flow separation and flow reversal during the cardiac cycle,³¹ which also impose oscillatory shear stress on the endothelial cells lining the arteries that contributes to endothelial dysfunction and vascular remodeling.^32–34 With identification of elevated velocity regions in the cerebral arteries of these three subjects due to their individual geometry differences and not unique fluid inlet profiles, we next determined where regions of flow separation and low shear stress could influence biological remodeling. Velocity streamlines for each subject during systole is displayed in Figure 6, to display areas affected by disturbed flow with particular interest in regions of flow separation and recirculation. Magnified images of flow recirculation (circles) and vortices (square) are labeled to distinguish the differences (Figure 6). P1, The individual without sickle cells disease, did not show regions of disturbed flow (Figure 6(a)); however, subjects with SCA, P2 and P3, both demonstrated fluid recirculation along multiple locations despite given the same inlet profile as P1. For P2, sickle with no history of stroke had regions of recirculation along the inner curvature of bifurcations in the ACA, MCA and M2-A (Figure 6(b)). P3, sickle post-stroke, had regions of flow recirculation at MCA along the inner curvature of the ICA bifurcation, and at the ICA stenosis (Figure 6(c)).

Figure 6.

Recirculation of velocity streamlines is more prevalent in sickle cell anemia. Patient-specific velocity streamlines during systole are depicted for the 3-D vascular models with recirculations (circles) and vortexes (squares) magnified for easier viewing. The non-sickle subject’s (P1) artery is completely void of any regions of fluid recirculation (a). The first sickle subject (P2) has fluid recirculating at multiple locations near the inner curvature of bifurcations: specifically at the ACA (1), MCA (2), and M2-A (3) arterial segments. A vortex is also observed in the M2-B segment (4) (b). The second subject has recirculation occurring at the ICA stenosis (1), and the MCA (3) following the ICA bifurcation. Vortexes are observed along the ICA (2) and at the MCA bifurcation (4) (c). Scale bar is shown

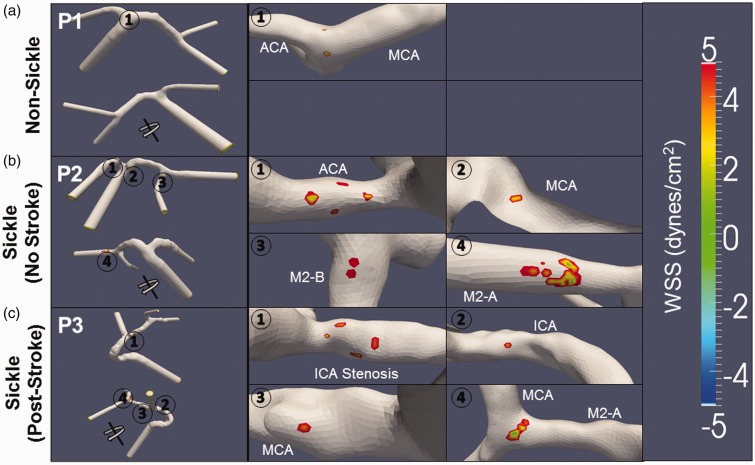
In addition to velocity, the wall shear stress (WSS) profiles were calculated during diastole. Areas of low shear stress (±5 dynes/cm²) appeared near the recirculation zones, as expected (Figure 6). The front and back views of the model for subject P1 show areas of low shear stress to be located at the apex of the internal carotid bifurcation (Figure 7(a)). In both subjects with SCA (P2 and P3), regions of low WSS were found in multiple locations that encompass a larger area as compared to the non-sickle subject. In the first individual with SCA (P2), regions of low WSS occurred along the inner curvature of the ICA and MCA bifurcations at the ACA, MCA, and M2-A (Figure 7(b)). P3 had regions of low WSS along the ICA and MCA arterial segments (Figure 7(c)).

Table 1.

List of nomenclature used and their associated values

Variables	Nomenclature	Value
µ	Viscosity	3 cP
P	Pressure	1060 kg/m3
uentr	Average inlet velocity	70 cm/s
Dt	Time step	0.01 s
T	Total time	3 s
uint	Initial velocity	0 cm/s
pint	Initial pressure	0 dynes/cm2

Figure 7.

Areas of low shear stress are greater in sickle cell anemia arteries. Low WSS (±5 dynes/cm²) during diastole were calculated from the velocity profiles of the non-sickle and sickle subjects. The locations of these low WSS (circles) are magnified in the images to the right for easier viewing. In the non-sickle subject (P1), two spots of low stress areas of low shear stress occur at the apex of the internal carotid bifurcation (1) (a). The sickle subject with no history of stroke (P2) has regions of low WSS occur along the inner curvature both bifurcations in the ACA (1), MCA (2), M2-B (3), and M2-A (4) (b). The second subject (P3) has multiple regions of low WSS. Two occur in the ICA, first at the stenosis (1) and then preceding the ICA bifurcation (2). Low shear areas also occur along the length of the MCA, one following the ICA bifurcation (3), and the other at the apex of the MCA bifurcation (4) (c)

Discussion

The maximum velocities measured in the 3D simulations ranging between ∼180 and 250 cm/s were much higher than in 2D, where only a max velocity of 100 cm/s was achieved. The 3D models therefore offered a better representation of the fluid profiles. While none of the mean velocities surpassed the 200 cm/s threshold value indicative of stroke risk, velocities in the simulations created from individuals with SCA (P2 and P3) were higher than the reconstruction without the sickle mutation (P1). Therefore, despite the same boundary conditions across all simulations, the patient-specific geometries were sufficient to produce elevated velocities. This is an important result given that only a percentage of children with SCA will have a major or silent stroke; the patient-specific differences responsible for this variability may include the individual anatomy.

The mean velocity in the distal MCA for both sickle subjects P2 and P3 were greater than the non-sickle subject P1, and greater changes in magnitudes of the velocities occurred at the proximal vs. distal ends of MCA (Figure 4). In the proximal MCA, the mean velocity for subject P2 was greater than the mean velocity for P1; however, the sickle subject P3 was the lowest. This lower velocity in the sickle subject may be due to the presence of a small stenosis occurring in the distal end of the artery. Along the length of the MCA, subject P1 (non-sickle) had lower velocities, compared to SS subjects P2 and P3 (Figure 5). This may be due to the surface texture of the endothelial surface in the arteries from sickle cell patients as they presented a “bumpy” appearance not seen in the non-sickle patient. These patient-specific geometries may be indicative of cellular or pathophysiological phenomena that should be studied as causative phenomena for elevated velocities and stroke risk. Autopsies of patients who passed away from strokes indicated vascular remodeling characterized by fragmented elastic lamina, intimal hyperplasia, and luminal occlusion.^35–37 Significant stenoses are not detected in these children by MRA until much higher percent stenoses. The luminal narrowing may cause the high blood velocities indicative of stroke risk, but it is unknown if it acts as the main contributing mechanism to the pathology. Additionally, an array of other pathological mechanisms, including increased red blood cell (RBC) and leukocyte adhesion, inflammation, and increased viscosity of individual red blood cells may be responsible for the bumpy texture and also provide biological mechanisms to be investigated as novel mechanisms that accumulate to cause sickle cell-mediated strokes.^38–41

Although the TAMMV of the MCA did not exceed 200 cm/s in the 3D simulations, subjects with SCA when compared to the non-sickle patient were found to have higher streamline velocities. Additionally, both individuals with SCA had altered hemodynamic profiles, characterized by greater regions of flow reversal (Figure 6) and large areas affected by low WSS (Figure 7). These regions of low shear stress also correlated to zones of fluid recirculation, and occurred preferentially at the inner curvature of bifurcations or following stenoses, as seen in subject P3, corroborating findings from the atherosclerosis literature and previous studies.^20,21,42 Subjects with SCA were affected by low shear stresses over a larger surface area compared to the non-sickle patient, indicating that those individuals may be subject to shear stress-mediated vascular remodeling. This result also illustrates the power of CFD as shear stress cannot be directly measured. CFD could potentially be used to predict stroke risk by allowing clinicians to look for signs of altered blood flow, as these altered hemodynamics may precede the large stenosis formation that can cause high streamline velocities. Vascular remodeling may precede stroke formation, but difficult to detect with MRA, until larger stenoses occur that unfortunately coincide with stroke, as seen in subject P3. The next step will be to compare predicted flow velocities in patient 3D MRA reconstructions to the actual TCD values measured clinically and merge the MRA anatomy predictions with the confirmatory TCD. More simulations will need to be performed in the future to show statistical significance correlating disturbed flow profiles to stroke risk, but these current results show promise.

Higher MCA velocities could be achieved in silico by manipulating the ICA-inlet boundary condition, as the 70 cm/s maximum velocity chosen for this study was the lowest measured value acquired from a sickle patient in a cohort of six individuals. In general, sickle patients will have higher velocities caused by anemia.^15,43 Thus, the lower, but still elevated value of 70 cm/s, was deemed an appropriate input value for this study. An interesting phenomenon observed in the 2D stenotic simulations and in both of the 3D sickle models was the occurrence of a velocity gradient, which varied along the length of the MCA. This finding poses a question on the precision of TCD and the potential for misdiagnosis. Currently, TCD cannot perform the precise measurements taken from the simulations, as averages are taken across an area which can spans a width of 4 mm to 1.5 cm.⁴⁴ Measurements typically are made at 2-mm intervals, and thus only approximate values that extend over an entire arterial segment. This can potentially lead to incorrect diagnoses, as localized regions with high elevated velocities are in the same frame of measurement as regions with significantly lower velocities.

This study does have limitations. In particular, geometries are rigid, we do not have patient-specific boundary conditions, and viscosity is assumed to be constant and tuned to literature values. Blood is a non-Newtonian fluid, and we did perform some simulations with a Carreau model of non-Newtonian fluid dynamics without finding significant differences in the hemodynamics. Shear rates in those simulations exceeded 1000 Hz, a range where both the Newtonian and non-Newtonian models had the same viscosity (data not shown). Our simulations are for the large arteries, not the smaller vessels such as capillaries, where shear rates are lower and produce differences in viscosity between Newtonian and non-Newtonian models.

After this qualitative assessment, we plan to perform a campaign of numerical simulations – possibly with patient-specific boundary data and certainly with more refined meshes – for a more quantitative analysis of the interplay of rheology and fluid patterns. The follow-up of the study is exactly to retrieve pediatric data of sickle vs. non-sickle age-matched geometries, and reproduce the results obtained here with a precise quantitative assessment. Although we highlight pediatric strokes as the main motivation for this work, adults with SCA also have elevated cerebral artery velocities associated with stroke risk.^45,46 The ultimate goal is to find a precise correlation between the altered rheological properties and the stroke risk in young people with SCA. As for the rheological models, another important aspect of CFD is the solution of rigorous data assimilation problems for a patient-specific quantification of apparent viscosity in diseased patients. This means that we systematically compare numerical results with available measures for different values of the viscosity to find the value that best describes measurements. This can be done by performing rigorous numerical procedures of what is called “variational data assimilation”.^47–49

Currently, few researchers are examining the fluid dynamics in large arteries associated with SCA, and the difficulty in doing so is not minimal. Blood rheology is affected by red cells in two ways: rouleaux formation at low shear rates and inelastic collisions at high shear rates.⁴¹ The altered shapes, density, and membrane viscosity, and associated variability among the RBCs in sickle cell disease as they progress from reticulocytes to irreversibly sickled cells over the 9–10 days of their lifespan⁵⁰ probably affects both of these aspects. The impact of the shape on the effects of the collision (with consequent altered energy balance) may require some sophisticated rheology based on differential models. However, all these models require the quantitative tuning of many parameters (beyond the viscosity) which at this stage is out of reach. We plan to have data assimilation techniques soon to perform more precise quantitative assessments. There are investigations of the cerebral anatomy in the MCA and ICA by other groups, and they have found tortuosity to be implicated in stenosis formation.⁵¹ This is interesting to note as certain tortuosity and curvature have been associated with aneurysm formation and rupture.⁵² As demonstrated in this paper, geometrical differences in the arteries themselves between sickle and non-sickle individuals can have drastic effects on the hemodynamics. Quantifying these differences may allow clinicians to predict patients who are at risk of stroke prior to the elevated velocities used currently, enabling patients to get treatment sooner.

Authors’ Contributions

All authors participated in the design, interpretation of the studies and analysis of the data and review of the manuscript; CPR and AV conducted the numerical experiments, REW selected patient angiograms for analysis and provided critical clinical feedback, CPR and MOP conceived the project and all authors contributed to the writing of the manuscript.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.