Abstract
In this paper a Computer Aided Detection (CAD) system is presented to automatically detect Cerebral Microbleeds (CMBs) in patients with Traumatic Brain Injury (TBI). It is believed that the presence of CMBs has clinical prognostic value in TBI patients. To study the contribution of CMBs in patient outcome, accurate detection of CMBs is required. Manual detection of CMBs in TBI patients is a time consuming task that is prone to errors, because CMBs are easily overlooked and are difficult to distinguish from blood vessels.
This study included 33 TBI patients. Because of the laborious nature of manually annotating CMBs, only one trained expert manually annotated the CMBs in all 33 patients. A subset of ten TBI patients was annotated by six experts. Our CAD system makes use of both Susceptibility Weighted Imaging (SWI) and T1 weighted magnetic resonance images to detect CMBs. After pre-processing these images, a two-step approach was used for automated detection of CMBs. In the first step, each voxel was characterized by twelve features based on the dark and spherical nature of CMBs and a random forest classifier was used to identify CMB candidate locations. In the second step, segmentations were made from each identified candidate location. Subsequently an object-based classifier was used to remove false positive detections of the voxel classifier, by considering seven object-based features that discriminate between spherical objects (CMBs) and elongated objects (blood vessels). A guided user interface was designed for fast evaluation of the CAD system result. During this process, an expert checked each CMB detected by the CAD system.
A Fleiss' kappa value of only 0.24 showed that the inter-observer variability for the TBI patients in this study was very large. An expert using the guided user interface reached an average sensitivity of 93%, which was significantly higher (p = 0.03) than the average sensitivity of 77% (sd 12.4%) that the six experts manually detected. Furthermore, with the use of this CAD system the reading time was substantially reduced from one hour to 13 minutes per patient, because the CAD system only detects on average 25.9 false positives per TBI patient, resulting in 0.29 false positives per definite CMB finding.
Keywords: Computer Aided Detection, Cerebral Microbleeds, Traumatic Brain Injury, Susceptibility Weighted Imaging
Highlights
-
•
We present an automated detection system for microbleeds in MRIs of trauma patients.
-
•
When using the system, detection time goes down from one hour to 13 min.
-
•
The system enables the user to detect a significantly higher number of CMBs.
-
•
The inter-observer variability for detecting CMBs is very large in TBI patients.
1. Introduction
To determine the severity of Traumatic Brain Injury (TBI) and patient prognosis, the Glasgow Coma Scale (GCS) together with the assessment of large hemorrhages and fractures seen on Computed Tomography (CT) are widely used. The GCS is a neurological scale to determine the level of consciousness of a patient. Using three measures; motor response, verbal performance, and eye opening, a scale between 3 and 15 is determined, where 3 indicates deep unconsciousness of a patient (Teasdale and Jennett, 1974). The prognostic precision of these two assessments is low, most likely because less acute damage such as diffuse axonal injury is not evaluated. Therefore research is focusing on Magnetic Resonance (MR) imaging to identify prognostic markers which are less or not visible on CT scans, such as Cerebral Microbleeds (CMBs). CMBs are thought to be related to Diffuse Axonal Injury (DAI) and to clinical prognosis (Werring, 2011). Studies evaluating the clinical and prognostic value of the individual location and size of CMBs in TBI do not exist, mainly due to the amount of time required to exhaustively annotate every CMB in a TBI scan.
CMBs are hemosiderin deposits in the brain caused by leakage of small blood vessels. CMBs can be detected on both T2* GRE and Susceptibility Weighted Imaging (SWI) scans, where it has been shown that the sensitivity of SWI outperforms the sensitivity of T2* GRE imaging in finding CMBs (Geurts et al., 2012, Nandigam et al., 2009, Tong et al., 2003, Cheng et al., 2013, Liu et al., 2014). On an SWI scan CMBs appear as spherical hypointense lesions and are considered to have a diameter smaller than ten millimeters (Greenberg et al., 2009). Fig. 1 shows an example of a single CMB on an SWI scan, Fig. 2 shows a TBI patient with many CMBs.
Fig. 1.
Example of a CMB on an SWI scan. From left to right: axial, sagittal and coronal view.
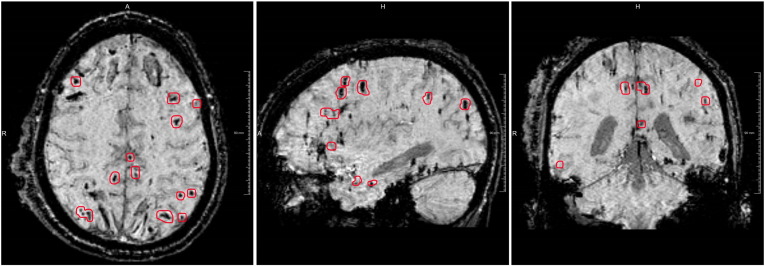
Fig. 2.
Example of a TBI patient with many CMBs encircled in red and two large hemorrhages located bifrontal. From left to right: axial, sagittal and coronal view. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The observer variability for the detection of CMBs is large (Geurts et al., 2012, Kuijf et al., 2012). Additionally, manual detection of CMBs is a time consuming task, which can take more than one hour per TBI patient. A Computer Aided Detection (CAD) system can alleviate these drawbacks. Several CAD systems have been developed for the detection of CMBs in other patient populations (stroke patients Seghier et al., 2011, Dou et al., 2016), Alzheimer patients Barnes et al., 2011, Fazlollahi et al., 2014, patients with arterial disease Kuijf et al., 2012, patients with radiation damage Bian et al., 2013, and the elderly Ghafaryasl et al., 2012), but to the authors knowledge this is the first CAD system designed for TBI patients. These existing CAD systems report several false positive (FP) detections per CMB. Since the number of CMBs in our TBI patient population is a factor larger than what is commonly seen in the population for which these systems were designed, these CAD systems would result in large amounts of false positive detections. This would reduce the possible time gain that could be achieved with the use of a CAD system compared to manual annotation, as it would require extensive manual false positive reduction.
In this paper we present a CAD system that automatically detects CMBs in TBI patients.
2. Material and methods
A schematic overview of our work is given in Fig. 3. In short, a preprocessing step was performed to identify the brain, the different modalities were registered, the bias field was corrected and the images were normalized. Next, a voxel classifier identified CMB candidates. Subsequently false positive detections were removed by a second, object-based, classifier taking the shape of the detected CMBs.
Fig. 3.
Schematic overview of our work.
candidates into account. Next, four experiments were performed. First, the observer variability was measured. Second the CAD system was optimized. Third, the optimized CAD system was manually evaluated by a neuroradiologist. Last, the performance of the CAD system was compared to the annotations of six independent experts.
2.1. Data
2.1.1. Patient data
This study includes 33 patients with moderate (GCS 9–12) to severe (GCS 3–8) Traumatic Brain Injury (mean age 33 years, sd 14 years, 21 male, 12 female) and 18 healthy subjects (mean age 37 years, sd 16 years, 12 male, 6 female). For every TBI patient and healthy subject an SWI scan (TR: 27 ms, TE: 20 ms, flip angle: 15°, BW: 120 Hz/pixel, voxel size: 0.98 × 0.98 × 1 mm3) and a T1 MP-RAGE scan (TR: 2300 ms, TE: 2.98 ms, flip angle: 9°, BW: 240 Hz/pixel, voxel size: 1 mm isotropic) have been made on a 3 T MRI scanner (Siemens Magnetom Trio). The average time between the trauma and the acquisition of the scan was 28 weeks with a standard deviation of 3 weeks. The local ethics committee waived the need for review board approval and written informed consent, considering the retrospective character of this study.
2.1.2. Annotations
Manually annotating CMBs in TBI patients is a very time consuming task. Therefore, only one trained expert manually annotated the CMBs in all 33 patients. A subset of ten TBI patients was later annotated by six experts for evaluation of the CAD system and to measure user performance characteristics. The annotations were made following the Microbleed Anatomic Rating Scale (MARS) guidelines (Gregoire et al., 2009). The MARS guidelines identify CMBs as either definite or possible. Definite CMBs are defined as small, rounded or circular, well-defined hypointense lesions with clear margins within the brain parenchyma. Possible CMBs are defined as not strictly rounded or circular, less well-defined, and less hypointense lesions.
2.2. Preprocessing
2.2.1. Brain mask
Since CMBs only occur in brain tissue, a brain mask was made for both the T1 and the SWI scan. A brain mask defines which voxels belong to the brain and which voxels belong to the skull and air surrounding the brain. The brain mask was made in three steps. Firstly, the gray matter, white matter, and spinal fluid were segmented into three probability maps using SPM12b (Ashburner and Friston, 2005). Secondly, these three probability maps were summed and thresholded to create a mask. The segmentation algorithm of SPM has not been developed for the segmentation of SWI scans. Therefore, the susceptibility effects were erroneously segmented as air, which resulted in small cavities in the mask. These cavities were removed by applying region growing from the edge of the scan. All dark areas connected to the edge of the brain mask are not CMBs, since per definition CMBs are not connected to the meninges. The inverse of the region growing algorithm result was used as the final SWI brain mask.
2.2.2. Registration
The T1 and SWI scans were made during the same scanning session, but minor patient movements between the scans can occur. To correct for this movement the T1 scan was registered to the SWI scan using the rigid body registration of FSL FLIRT (Jenkinson and Smith, 2001, Jenkinson et al., 2002).
2.2.3. Bias field correction
The performance of the automated detection system is degraded by inhomogeneities caused by the bias field. For this reason the T1 scan was bias field corrected, using FSL FAST (Zhang et al., 2001). Since FSL FAST is not designed to correct the inhomogeneities in SWI scans the N3 algorithm was used to correct the bias field in these scans (Sled et al., 1998).
2.2.4. Normalization
Similar to intra-patient inhomogeneities, inter-patient intensity variation negatively impacts the performance of a classification system. Therefore, the SWI and T1 data was normalized by dividing the data by the median intensity of the voxels inside the brain mask.
2.3. Voxel classifier
A set of features characterizing each voxel, was specifically chosen for the task of CMB recognition. By means of supervised machine learning CMB candidate locations were identified.
2.3.1. Initial candidate detection
Not all the voxels in the brain mask were used to train the classifier. CMBs appear as hypointense spherical structures. We utilized these two characteristics to identify candidates for training.
Only local minima of the SWI scan (in a 3 × 3 × 3 voxel neighborhood), that have an intensity below the mean intensity of the voxels inside the brain are selected for training.
Positive samples were defined as the initial candidates located inside annotated CMBs, marked as “definite”. Negative samples were defined as initial candidates in the healthy subjects. This important step was taken, because CMBs in the TBI patients could have been missed by the expert, leading to false negatives in the training data. By taking local minima from the SWI data of healthy controls as negative samples, this risk is negated. The number of negative samples in the healthy subjects was much higher than the number of positive samples in the TBI patients. The number of negative samples was randomly downsampled to obtain a one to ten ratio between the positive and negative samples. This downsampling was necessary to train a reliably classifier, further reduction of the amount of negative samples resulted in a worse performance.
2.3.2. Feature extraction
The voxel-based features can be divided into two groups: intensity features and local shape features. Table 1 gives an overview of all features that are used for voxel classification.
Table 1.
Overview of the voxel-based features.
| Based on | Feature | Modality | Scale |
|---|---|---|---|
| Intensity | Intensity value | SWI and T1 | Single voxel |
| Mean intensity | SWI and T1 | Kernel size of 7 × 7 × 7 voxels | |
| Standard deviation | SWI and T1 | Kernel size of 7 × 7 × 7 voxels | |
| Local shape | Spherical kernel | SWI | Kernel size of 7 × 7 × 7 voxels |
| Laplacian | SWI | Max response of σ is 1, 1.5 and 2 mm | |
| Determinant of Hessian matrix | SWI | Max response of σ is 1, 1.5 and 2 mm | |
| Eigenvalues of Hessian matrix | SWI | σ is 2 mm | |
| Vesselness | SWI | σ is 1 mm | |
| Deviation from sphericalness | SWI | σ is 1.5 mm |
The first group consisted of three intensity-based features that were calculated on both the SWI and the T1 scan. The combination of the intensity features captures the relation between the darker voxel and its brighter surroundings. The intensity of the T1 scan is included, because this sequence contains extra information about structures in the brain that are not visible on the SWI scan (e.g. the gray-white matter boundary). The scales of the kernel-based features are reported in voxels, where one voxel in our data corresponds to 0.98 × 0.98 × 1 mm.
The second group consists of six local shape features which are only calculated on the SWI scan, as this modality best depicts the CMBs. The first feature is the response of a convolution of the image with a spherical kernel. The inside of this spherical kernel is negative and the edge of the kernel is positive. These negative and positive areas are normalized, so the convolution will give no response if the total intensity inside the kernel is equal to the total intensity at the edge of the kernel. The other five shape features are based on the Hessian matrix. The Hessian matrix is shown in formula (1).
| (1) |
Where Lnn is computed by a convolution of the image with a second order Gaussian derivative. The scale of the Hessian matrix is therefore determined by σ of the Gaussian filter kernel G that is applied as:
| (2) |
The Laplacian feature is defined by the sum of the diagonal of the 3D Hessian matrix (the trace). The determinant and the three eigenvalues of the Hessian matrix are used as features that describe the spherical nature of CMBs. The vesselness feature vf is defined by Eq. (3), where λ1, λ2, and λ3 represent the eigenvalues of the 3D Hessian matrix with a σ of 1 mm (Sato et al., 1998).
| (3) |
As suggested by Sato et al. (1997) we define α1 = 0.5 and α2 = 2.
The last feature is the so-called deviation from sphericalness (ter Haar Romeny, 2011). This feature captures the spherical appearance of a neighborhood by considering the local curvature of the SWI scan. The two principal curvatures (k1 and k2) are given by the eigenvalues of the 2D Hessian matrix:
| (4) |
| (5) |
The two principal curvatures are equal when 4Lxy2 + (Lxx − Lyy)2 is zero. This happens in so-called umbilical points. In umbilical points the curvature direction is undefined and the surface is locally spherical. The term 4Lxy2 + (Lxx − Lyy)2 can be interpreted as ‘deviation from sphericalness’ in 2D. This feature is computed in all orthogonal directions with a σ of 1.5 mm.
The scales of the features were determined by approximation of the volumes of the manually annotated CMBs, marked as “definite”. To be able to approximate the diameter of the annotations, the shape of a CMB was assumed to be a sphere. Resulting in a distribution of diameters as shown in Fig. 4. The median diameter of the definite annotated CMBs is 4.7 mm (sd 0.72 mm). A few annotations include multiple CMBs, causing the positive skewness (0.96) of this distribution. For the kernel-based features a kernel size of 7 × 7 × 7 voxels is used, which is slightly bigger than the average CMB and thus also captures the surroundings of the CMB. As mentioned the scale of the Hessian matrix is determined by σ of the Gaussian filter kernel G as shown in formula (2). The scales (σ) of the features were defined by the observation that a σ of 1.5 mm gives the highest response for CMBs with a diameter between 3.8 and 5.4 mm. A σ of 1 mm was used to detect the smaller CMBs present in the data and a σ of 2 mm was used to detect the larger CMBs present in the data.
Fig. 4.
Histogram with the approximated diameters of the definite annotations.
2.3.3. Training and classification
For classification an OpenCV implementation of the Random Forest Classifier (RFC) (Breiman, 2001) with 100 trees was used. The initial candidates (Section 2.3.1) together with the above mentioned features (Section 2.3.2) were used to train the classifier.
For testing, all voxels inside the brain mask below the mean intensity of the SWI voxels were classified. The test set was not limited to local minima of the SWI, because CMBs with an attached darker structure might not contain a local minimum and would therefore be missed. The final result of the voxel classifier was a likelihood map, where every voxel inside the brain mask gets a likelihood of that voxel being a CMB.
2.4. Object classifier
Despite the use of the vesselness feature, the result of the voxel classifier still contains numerous false positives inside blood vessels. Blood vessels also appear dark on SWI scans. The local variation in a blood vessel's diameter and orientation can cause hypointense spherical structures to appear in the SWI scan at these positions. Fig. 5 shows an example of such a structure inside a blood vessel. These structures look similar to CMBs at voxel level, but can be distinguished from CMBs by looking at its surroundings. To remove these false positives an object-based approach was used to distinguish between spherical shaped CMBs and elongated shaped blood vessels.
Fig. 5.
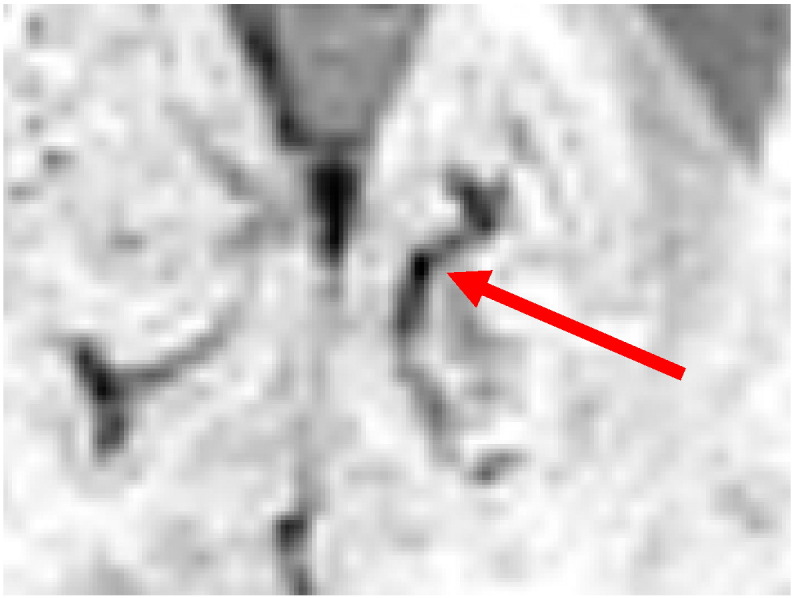
An example of a spherical like structure inside a blood vessel.
2.4.1. Segmentation
For segmentation a region growing-based algorithm was used. The results of the voxel classifier were used as seed points for this algorithm. A subvolume around each seed point was taken to improve computational speed. The size of this subvolume can contain two CMBs with a diameter of ten millimeters. The intensity threshold of the region growing algorithm is iteratively increased until the volume of the segmentation exceeds the volume of a sphere with a diameter of ten millimeters. During each iteration only voxels attached to the segmentation, that have a gray value between the intensity values of the previous and current iteration, are added to the segmentation. The iteration prior to the largest volume increase is taken as the final threshold for the segmentation.
2.4.2. Feature extraction
Prior to feature extraction all segmentations with a volume smaller than four voxels were marked as false positives of the voxel detector, because these segmentations were considered too small to be a CMB. From the segmentations with a minimum size of four voxels seven features were considered. See Table 2 for an overview of the object-based features.
Table 2.
Overview of the object-based features.
| Object feature |
|---|
| Probability of the voxel classifier |
| Intensity threshold of the region growing algorithm |
| Volume of the segmentation |
| Number of voxels intersecting the boundary of the subvolume |
| Elongation measure |
| Overlapping voxels with sphere centered at seed point |
| Overlapping voxels with sphere centered at center of gravity of the segmented object |
The first feature is the probability of our voxel classifier in the seed point. The second feature is the final intensity threshold of the region growing algorithm. The third feature is the volume of the segmentation. The fourth feature is the number of voxels that intersect with the boundary of the subvolume around the seed point. If a segmentation intersects with the boundary of the subvolume it will probably not be a CMB. The fifth feature is an elongation measure em defined by:
| (6) |
where λ1 and λ2 are eigenvalues of the segmented object. The sixth and seventh feature describe the percentage of voxels of the segmented object that overlap with a sphere with the same volume as the segmented object. The sixth feature describes the overlap of the sphere centered at the seed point of the segmentation and the seventh feature locates the center of the sphere at the center of gravity of the segmented object.
2.4.3. Training and classification
The object classifier was trained on the local maxima of the probability map (in the 3 × 3 × 3 voxel neighborhood), that have a voxel classifier likelihood above a certain threshold. This threshold is chosen such that the sensitivity of the voxel classifier would be as high as possible, but the number of FP detections would not exceed 100 FP per healthy subject. In this way the object classifier maintains an acceptable computation time, because the segmentation algorithm needs to be computed for each voxel classifier result above this likelihood. As positive samples, local maxima within the definite annotated CMBs were used. Negative samples were local maxima in healthy subjects. For each sample the seven features, described in Section 2.4.2, were computed for training and classification. For classification an RFC with 100 trees is used. The result of the object classifier defines a likelihood for every local maximum within the voxel classifier probability map.
2.5. Experiments
Four different experiments were performed during this study. First, the inter-observer variability was measured with the Fleiss' kappa statistics. Second, optimization of the CAD system was performed using the data of all 33 TBI patients and 18 healthy subjects. Third, one trained expert manually evaluated the CAD system output with a newly designed guided user interface. Last, the CAD system performance was evaluated using the subset of ten TBI patients that was manually annotated by six trained experts.
2.5.1. Observer variability
This study included 33 TBI patients, but because of the laborious nature of manually annotating CMBs only a subset of ten TBI patients was annotated by six experts. Within this subset of ten TBI patients the inter-observer variability was computed using Fleiss' kappa statistics.
2.5.2. CAD system optimization
Optimization of the CAD system was performed based on FROC analysis. In an FROC analysis the sensitivity is plotted against the average number of false positive detections. The curve was computed by varying the likelihood threshold of the classifier result. In the voxel- and object classifier, an annotated CMB, marked as “definite”, as described in Section 2.1, is considered a true positive if a local maxima (in a 3 × 3 × 3 voxel neighborhood) of the probability map is present within 1 mm of the annotation. Since the annotations in all 33 TBI patients were made by a single expert, it is likely that not all CMBs were detected, which could potentially lead to an over estimation of the amount of false positives in the TBI patient dataset. For this reason, the number of false positives for each classifier was computed on the data of the healthy subjects. All results present within 1 mm of an annotated CMB, marked as “possible” (Section 2.1), were ignored and thus not counted as true positives nor as false positives. Only the definite CMB were taken into account during evaluation, because the possible CMBs lower the agreement between raters and therefore it is recommended to only report definite CMBs for research studies (Werring, 2011).
Both the voxel classifier and the object classifier were evaluated using a leave-one-out cross validation. To avoid bias in the training data of the object classifier, the voxel classifier was tested using a leave-two-out cross validation, which is schematically presented in Fig. 6. In this example patient 1 is used for testing the object classifier (shown in red). Patients 2 through 33 and healthy subjects H1 through H18 are used testing the voxel classifier and for training the object classifier (shown in orange). To test the voxel classifier on patient 2, the voxel classifier is trained on patients 3 through 33 and healthy subjects H1 through H18 (shown in green).
Fig. 6.
A schematic representation of the leave-two-out cross validation. Green is the dataset that is used for training the voxel classifier. Orange is the dataset that is used for testing the voxel classifier and for training the object classifier. Red is the dataset that is used for testing the object classifier. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
2.5.3. CAD system evaluation
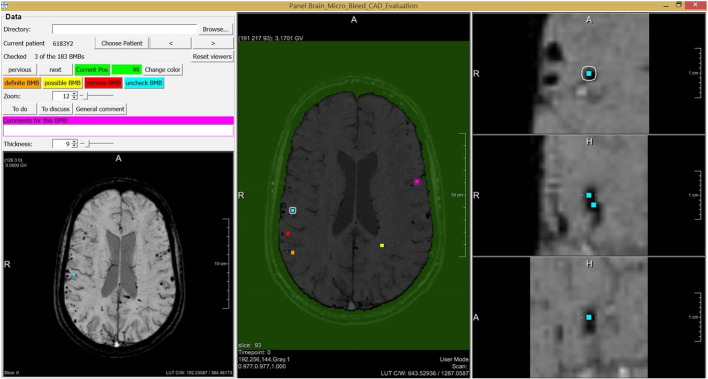
One operating point in the FROC curve was chosen for manual evaluation of the CAD system output. This manual evaluation was performed by one neuroradiologist, using a guided user interface shown in Fig. 7. The manual evaluation consisted of two steps. First, the brain mask was checked for mistakes. Second, every detected location was manually checked and divided into three categories; definite CMB, possible CMB, and no CMB. The evaluation expert was blind to the annotations made by the other experts.
Fig. 7.
The guided user interface that is used for manual evaluation of the CAD system result.
The guided user interface was constructed for fast evaluation of the detected locations. For every detected location an overview of the entire brain in axial direction was shown to determine its location in the brain. A zoomed-in version of the location was visible in axial, coronal, and sagittal direction, to be able to analyze the shape of the detected object in 3D. The amount of zoom could be manually adjusted and the expert could scroll through the surroundings of the location in all three directions. Also a Minimal Intensity Projection (MinIP) over a user definable number of slices in axial direction was presented, to be able to quickly detect blood vessels. Per location a comment was made if the category of a detection was equivocal to the expert. These detections were discussed with a second neuroradiologist.
During the evaluation of the CAD system the neuroradiologist detected some obviously missed CMBs. After the evaluation of the CAD system the neuroradiologist went through all the SWI scans to manually add these CMBs that were missed by the CAD system. These CMBs were manually added to the final result.
2.5.4. CAD system performance
The CAD system performance was evaluated on the subset of ten TBI patients which were manually annotated by six independent experts. The CAD system performance was compared to the performance of each individual expert using FROC analysis. The ground truth was made by combining the annotations of the other five experts using majority voting. A location was considered as a definite CMB when at least three out of the five experts annotated the location as a definite CMB. A location was considered as a possible CMB when it was not marked as a definite CMB by the above mentioned criteria, and at least three of the five experts annotated the location as either a possible or definite CMB. For the CAD system an FROC curve was made, where an annotated CMB, marked as “definite”, is considered a true positive if a local maxima (in a 3 × 3 × 3 voxel neighborhood) of the probability map is present within 1 mm of the annotation in the ground truth. All results present within 1 mm of an annotated CMB, marked as “possible”, were ignored and thus not counted as true positives nor as false positives.
For each expert the sensitivity and number of FPs was computed. An annotated CMB, marked as “definite”, was considered a true positive if the annotation in the ground truth overlapped with an annotation of the expert. All results that overlapped with an annotated CMB, marked as “possible”, in both the ground truth and the evaluated expert annotations, were ignored and thus not counted as true positives nor as false positives.
3. Results
3.1. Observer variability
The annotations of the single expert in all 33 TBI patients resulted in a total of 523 (sd) definite CMBs and 104 (sd) possible CMBs. No CMBs were identified in the healthy subjects. In the subset of ten TBI patients each expert detected on average a total of 136.0 (sd 27.9) definite CMBs and 44.8 (sd 43.2) possible CMBs, with a Fleiss' kappa value of 0.24.
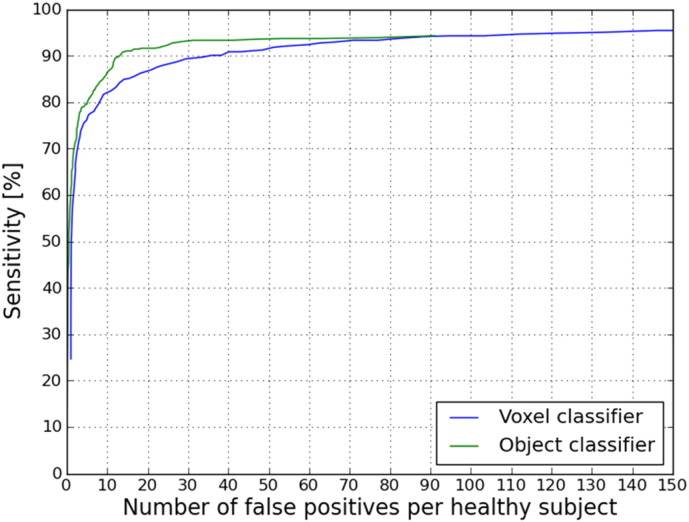
3.2. CAD system optimization
In all 33 TBI patients on average 15.8 definite CMBs (sd 22) were annotated per TBI patient by one expert. The performance of our CAD system considering these definite annotated CMBs as a reference standard is visualized in Fig. 8. It can be seen that including the object classifier after the voxel classifier improved the result of the CAD system at every point in the FROC curve. At a sensitivity of 90.8% compared to the expert annotations, the CAD system detects 13.9 FPs per healthy subject (that is 0.88 FPs per CMB). Other operating points of the object classifier FROC curve are presented in Table 3.
Fig. 8.
FROC curve of the CAD system result. The average number of false positives per healthy subject is plotted on the x-axis. The sensitivity compared to the expert annotation is plotted on the y-axis. In blue, the result after voxel classification. In green, the result after voxel- and object classification. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Table 3.
FROC curve operation points after object classification.
| Sensitivity | Nr of FPs per CMB | Nr of FPs per healthy subject |
|---|---|---|
| 86.5% | 0.64 | 10.1 |
| 90% | 0.82 | 13.1 |
| 90.8% | 0.88 | 13.9 |
3.3. CAD system evaluation
The operating point for manual evaluation of the CAD system was chosen at a sensitivity of 90.8%. This operating point was chosen in agreement with the expert who performed the manual evaluation. At this operation point the CAD system detected on average 13.9 locations per healthy subject and 79.8 locations per TBI patient. Detections of the CAD system in both the TBI patient and the healthy subjects were manually evaluated as explained in Section 2.5.3. The results of the manual evaluation are shown in Table 4.
Table 4.
Result after manual evaluation of the CAD system.
| Category | Mean per TBI patient (sd) | Mean per Healthy subject (sd) |
|---|---|---|
| Definite CMB | 57.5 (99.1) | 0 (0) |
| Possible CMB | 9.8 (20.6) | 0.78 (1.4) |
| No CMB | 12.5 (9.2) | 13.2 (9.1) |
| Total | 79.8 (124.9) | 13.9 (10.0) |
The manual evaluation for the 79.8 locations per TBI patient into the three categories took on average 13 minutes per TBI patient. This also includes the time needed for discussion of equivocal cases.
The computation time of the CAD system per patient was approximately 17 minutes, from which the preprocessing took 14 minutes (laptop with 64-bit Intel Core i7 2.4 GHz CPU and 12 GB RAM). The computation of the CAD system can be performed offline, without any manual interaction, so the expert does not need to spend time on the CAD system during this period.
After the evaluation of the CAD system the second expert went through all the SWI scans to manually add CMBs marked as “definite” that were obviously missed by the CAD system. During this process on average 4.8 CMBs per TBI patient were added to the final result, leading to an average of 62.4 definite CMBs per TBI patient.
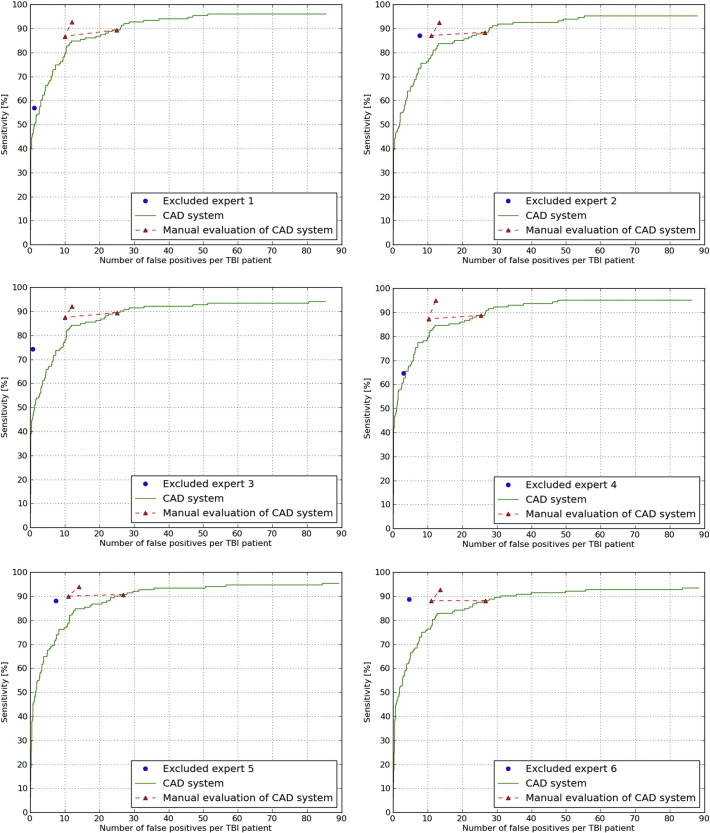
3.4. CAD system performance
In the subset of ten TBI patients each expert detected on average a total of 136.0 (sd 27.9) definite CMBs. The FROC curves are shown in Fig. 9 and the corresponding operating points are presented in Table 5.
Fig. 9.
Comparison of the six experts to the CAD system using FROC analysis. In blue, the result of the excluded expert. In green the result of the CAD system. In red, the evaluated operating point, the result of the manual CAD evaluation and the manually added obvious missed CMBs. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Table 5.
Operation points of the FROC curves for the subset of ten TBI patients.
| Performance of | Average sensitivity (sd) | Average number of FPs (sd) per TBI patient |
|---|---|---|
| The experts | 76.7% (12.4%) | 4.1 (2.8) |
| Chosen operating point of the CAD system | 89.1% (0.8%) | 25.9 (0.8) |
| CAD system after manual evaluation | 87.8% (1.1%) | 10.6 (0.5) |
| CAD system after obviously missed CMBs were added | 93.2% (1.0%) | 12.9 (0.8) |
4. Discussion
In this work we have developed a CAD system for automated detection of CMBs in TBI patients. Experiments shown that the CAD system has significantly higher sensitivity than an expert observer in detecting CMBs and with the use of this CAD system the reading time is substantially reduced.
4.1. Observer variability
The Fleiss' kappa value of 0.24 shows that the inter-observer variability is very large. During manual detection a lot of CMBs are overlooked. This also emphasizes the need of a CAD system that not only decreases reading time, but also aids the detection of CMBs.
4.2. CAD system optimization
The FROC curves in Fig. 8 show that the CAD system performance improves when the object classifier is included. This means that the object classifier removed FPs (mostly caused by blood vessels). Table 3 shows that our CAD system achieves a sensitivity of 90.8% based on one expert in all 33 TBI patients and detects 13.9 FPs per healthy subject. Table 4 shows that after manual evaluation 12.5 FPs per TBI patient are detected. A two-sampled t-test shows that there is no significant difference (p = 0.79) between the number of FPs in the TBI patients and healthy subjects, which confirms that taking negative samples from healthy subjects is a valid approach for the CAD optimization when lacking a ground truth of multiple expert annotations. The FPs that remain after object classification are mainly parts of blood vessels that appear as spherical like structures due to the partial volume effect or a strong curvature and are therefore detected as CMBs.
4.3. CAD system evaluation
The CAD system detected on average 79.8 locations per TBI patient, of which 57.5 detections were evaluated as definite CMB by the second expert. After manual evaluation of the CAD system's detections the expert added on average another 4.8 CMBs marked as “definite” that were obviously missed by the CAD system, bringing the total number of detected CMBs marked as “definite” to 62.4 CMBs.
During manual evaluation, no false positives were detected around skull injuries and subdural and epidural hematomas. This shows that the CAD system is very robust for trauma often seen in this patient group.
4.4. CAD system performance
The sensitivity of the experts in the subset of ten TBI patients was on average 76.7% (sd 12.4%) with on average 4.1 FPs (sd 2.8) per TBI patient. This large inter-observer variability underlines the difficult task of manually detecting CMBs in TBI patients. The sensitivity of the CAD system for the chosen operating point within the subset of ten TBI patients was on average 89.1% (sd 0.8%) with on average 25.9 FPs (sd 0.8) per TBI patient. After manual evaluation of this CAD system result the average sensitivity remained almost the same at 87.8% (sd 1.1%), but the average number of FPs drastically decreased to 10.6 FPs (sd 0.5) per TBI patient. So when the CAD system presents a location, the expert is able to distinguish the CMBs from the FPs. When the expert manually added the obviously missed CMBs the average sensitivity increases to 93.2% (sd 1.0%) with on average 12.9 FPs (sd 0.8). A paired t-test shows that the sensitivity of 93.2% per TBI patient is significantly higher (p = 0.03) than the average sensitivity of 77% per TBI patients that the six experts manually detected. It can be concluded that a single expert using this CAD system can reach a high sensitivity with a low number of FPs and can reduce reading time from one hour to 13 minutes per patient.
4.5. Comparison to other CAD systems
It is not possible to make a fair comparison between our CAD system and other (semi-) automated methods simply by comparing reported results, since major differences exist in the patient population, MR acquisition protocols, MR system field strengths and datasets. Nonetheless, we give a short overview of the results from two other contributions in the field.
At a sensitivity of 89% our CAD system detects 25.9 FPs per 88.5 definite CMBs, resulting in 0.29 FPs per CMB. At a sensitivity of 86.5% Bian et al. (2013) reported 1.5 FPs per CMB in patients with radiation damage, which resulted in 44.9 FPs per patient. Our CAD system outperforms this in terms of sensitivity, number of false positives per CMB and per patient. The paper of Ghafaryasl et al. (2012) reported 1.8 FPs per CMB in elderly patients at a sensitivity of 90%. While 1.8 FPs per CMB is a lot higher than our CAD system, the elderly patient population that Ghafaryasl used for evaluation only contained 2.3 CMBs per patient, resulting in only 4 FPs per patient.
A fair comparison between our CAD system and these existing CAD systems can only be made by applying these different CAD systems to the same patient population. However, because these systems were designed for different patient populations we assume that their performance for the detection of CMBs in TBI patients would be suboptimal.
4.6. Study limitations
During this research a number of limitations of the study were encountered. First, due to the time-consuming nature of manually annotating CMBs in TBI patients only ten of the 33 TBI patients were annotated by all six experts, while only one expert manually annotated CMBs all TBI patients, which led to CMBs being overlooked. For the optimization of the CAD system we therefore computed false positives on the data of healthy subjects, who did not present CMBs. To avoid contamination of the negative samples used for classifier training, we also obtained negative samples from the data of healthy subjects. Retraining the classifier with additional “definite” CMBs could further improve the performance.
Second, the proposed method is developed to detect hypointensities caused by CMBs on our specific SWI images, this implies that when the parameters of the acquisition change, also the parameters (such as kernel sizes, scales of derivatives and thresholds in the object classifier) likely need to be changed. The overall framework however, and the types of features can remain the same.
Lastly, during this research it was not needed nor possible to test complicated normalization algorithms, because the data used in this research was acquired from the same MRI scanner using the same sequence. The influence of different normalization algorithms on the CAD system have to be tested when data from other scanners is available.
4.7. Improvements and future work
Improvements of the CAD system can be accomplished by using an MRI sequence that will give information about blood flow (e.g. magnetic resonance angiography). In this way the CAD system would be able to discriminate more easily between flowing blood in the blood vessels and non-flowing blood deposits in CMBs. Unfortunately, this kind of data was not acquired for the patient population in this research.
Other classifiers such as support vector machine, Gentleboost and Adaboost might improve the classification result of the voxel and object classifier. This can be evaluated in future work.
This system is deemed valuable for further research to investigate the relationship between CMBs and clinical outcome of TBI patients, the relationship between CMBs and the Glasgow Coma Scale and the relationship between CMBs and diffuse axonal injury. All this further research would be more, if not too time-consuming to perform without the use of a well performing CAD system.
5. Conclusions
In this paper we presented a CAD system for the detection of CMBs in TBI patients. With the use of this CAD system the sensitivity of an expert was on average 93% which was significantly higher (p = 0.03) than a fully manual annotation performed by a single expert which had an average sensitivity of 77%. The CAD system only detects 25.9 false positives per TBI patient and with the newly developed user interface reading time is drastically decreased. In future research the relations between the number, size, and location of CAD detected CMBs and diffuse axonal injury, Glasgow Coma Scale and patient outcome, should be investigated.
References
- Ashburner J., Friston K.J. Unified segmentation. NeuroImage. 2005;26(3):839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- Barnes S.R., Haacke E.M., Ayaz M., Boikov A.S., Kirsch W., Kido D. Semiautomated detection of cerebral microbleeds in magnetic resonance images. Magn. Reson. Imaging. 2011;29(6):844–852. doi: 10.1016/j.mri.2011.02.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bian W., Hess C.P., Chang S.M., Nelson S.J., Lupo J.M. Computer-aided detection of radiation-induced cerebral microbleeds on susceptibility-weighted MR images. NeuroImage Clin. 2013;2:282–290. doi: 10.1016/j.nicl.2013.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L. Random forests. Mach. Learn. 2001;45(1):5–32. [Google Scholar]
- Cheng A.L., Batool S., McCreary C.R., Lauzon M.L., Frayne R., Goyal M., Smith E.E. Susceptibility-weighted imaging is more reliable than T2*-weighted gradient-recalled echo MRI for detecting microbleeds. Stroke. 2013;44:2782–2786. doi: 10.1161/STROKEAHA.113.002267. [DOI] [PubMed] [Google Scholar]
- Dou Q., Chen H., Yu L., Zhao L., Qin J., Wang D., Mok V.C., Shi L., Heng P.-A. Automatic detection of cerebral microbleeds from MR images via 3D convolutional neural networks. IEEE Trans. Med. Imaging. 2016;35(5):1182–1195. doi: 10.1109/TMI.2016.2528129. [DOI] [PubMed] [Google Scholar]
- Fazlollahi A., Meriaudeau F., Villemagne V.L., Rowe C.C., Yates P., Salvado O., Bourgeat P. Biomedical Imaging (ISBI) 2014. Efficient machine learning framework for computer-aided detection of cerebral microbleeds using the Radon transform; pp. 113–116. (Vol. 11th IEEE International Symposium). [Google Scholar]
- Geurts B., Andriessen T., Goraj B. The reliability of magnetic resonance imaging in traumatic brain injury lesion detection. Brain Inj. 2012;26(12):1439–1450. doi: 10.3109/02699052.2012.694563. [DOI] [PubMed] [Google Scholar]
- Ghafaryasl B., van der Lijn F., Poels M., Vrooman H., Ikram M.A., Niessen W.J., van der Lugt A., Vernooij M., de Bruijne M. Biomedical Imaging (ISBI) 2012. A computer aided detection system for cerebral microbleeds in brain MRI; pp. 138–141. (Vol. 9th IEEE International Symposium). [Google Scholar]
- Greenberg S.M., Vernooij M.W., Cordonnier C., Viswanathan A., Salman R.A.-S., Warach S., Launer L.J., Van Buchem M.A., Breteler M.M. Cerebral microbleeds: a guide to detection and interpretation. Lancet Neurol. 2009;8(2):165–174. doi: 10.1016/S1474-4422(09)70013-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregoire S.M., Chaudhary U.J., Brown M.M., Yousry T.A., Kallis C., Jäger H.R., Werring D.J. The microbleed anatomical rating scale (MARS) reliability of a tool to map brain microbleeds. Neurology. 2009;73(21):1759–1766. doi: 10.1212/WNL.0b013e3181c34a7d. [DOI] [PubMed] [Google Scholar]
- Jenkinson M., Smith S.M. A global optimisation method for robust affine registration of brain images. Med. Image Anal. 2001;5(2):143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- Jenkinson M., Bannister P.R., Brady J.M., Smith S.M. Improved optimisation for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17(2):825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Kuijf H.J., de Bresser J., Geerlings M.I., Conijn M.M., Viergever M.A., Biessels G.J., Vincken K.L. Efficient detection of cerebral microbleeds on 7.0 T MR images using the radial symmetry transform. NeuroImage. 2012;59(3):2266–2273. doi: 10.1016/j.neuroimage.2011.09.061. [DOI] [PubMed] [Google Scholar]
- Liu J., Kou Z., Tian Y. Diffuse axonal injury after traumatic cerebral microbleeds: an evaluation of imaging techniques. Neural Regener. Res. 2014;9(12):1222–1230. doi: 10.4103/1673-5374.135330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nandigam R.N., Viswanathan A., Delgado P., Skehan M.E., Smith E.E., Rosand J., Greenberg S.M., Dickerson B.C. MR imaging detection of cerebral microbleeds: effect of susceptibility-weighted imaging, section thickness, and field strength. Am. J. Neuroradiol. 2009;30(2):338–343. doi: 10.3174/ajnr.A1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato Y., Nakajima S., Atsumi H., Koller T., Gerig G., Yoshida S., Kikinis R. 3D multi-scale line filter for segmentation and visualization of curvilinear structures in medical images. CVRMed-MRCAS. 1997:213–222. doi: 10.1016/s1361-8415(98)80009-1. [DOI] [PubMed] [Google Scholar]
- Sato Y., Nakajima S., Shiraga N., Atsumi H., Yoshida S., Koller T., Gerig G., Kikinis R. Three-dimensional multi-scale line filter for segmentation and visualization of curvilinear structures in medical images. Med. Image Anal. 1998;2(2):143–168. doi: 10.1016/s1361-8415(98)80009-1. [DOI] [PubMed] [Google Scholar]
- Seghier M.L., Kolanko M.A., Leff A.P., Jäger H.R., Gregoire S.M., Werring D.J. Microbleed detection using automated segmentation (MIDAS): a new method applicable to standard clinical MR images. PLoS One. 2011;6(3):e17547. doi: 10.1371/journal.pone.0017547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sled J.G., Zijdenbos A.P., Evans A.C. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. Med. Imaging. 1998;17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Teasdale G., Jennett B. Assessment of coma and impaired consciousness: a practical scale. Lancet. 1974;304(7872):81–84. doi: 10.1016/s0140-6736(74)91639-0. [DOI] [PubMed] [Google Scholar]
- ter Haar Romeny B. Biomedical Image Processing. Springer; Berlin Heidelberg: 2011. Multi-scale and multi-orientation medical image analysis; pp. 177–196. [Google Scholar]
- Tong K.A., Ashwal S., Holshouser B.A., Shutter L.A., Herigault G., Haacke E.M., Kido D.K. Hemorrhagic shearing lesions in children and adolescents with posttraumatic diffuse axonal injury: improved detection and initial results. Radiology. 2003;227(2):332–339. doi: 10.1148/radiol.2272020176. [DOI] [PubMed] [Google Scholar]
- Werring D.J. Cambridge University Press; 2011. Cerebral Microbleeds: Pathophysiology to Clinical Practice. [Google Scholar]
- Zhang Y., Brady M., Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imaging. 2001;20(1):45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]