Soft computing modelling of moisture sorption isotherms of milk-foxtail millet powder and determination of thermodynamic properties

Abstract

Moisture sorption isotherms of spray-dried milk-foxtail millet powder were determined at 10, 25 and 40 °C. Sorption data was fitted using classical and soft-computing approaches. The isotherms were of type II, and equilibrium moisture content (EMC) was temperature dependent. The BET monolayer moisture content decreased from 3.30 to 2.67 % as temperature increased from 10 to 40 °C. Amongst the classical models, Ferro-Fontan gave the best fit of EMC-a_w data. However, the Sugeno-type adaptive neuro-fuzzy inference system (ANFIS) with generalized bell-shaped membership function performed better than artificial neural network and classical models with RMSE as low as 0.0099. The isosteric heat of sorption decreased from 150.32 kJ mol⁻¹ at 1 % moisture content to 44.11 kJ mol⁻¹ at 15 % moisture. The enthalpy-entropy compensation theory was validated, and the isokinetic and harmonic mean temperatures were determined as 333.1 and 297.5 K, respectively.

Electronic supplementary material

The online version of this article (doi:10.1007/s13197-016-2242-8) contains supplementary material, which is available to authorized users.

Introduction

In the present era of specialized and personalized foods, the importance of milk-malted millet beverages and products is well-recognized. Milk, being deficient in select minerals, vitamins and soluble fibers, is often supplemented with minor millets (Singh et al. 2008). Once milk is supplemented with the targeted millet(s), the blends can be extensively used as weaning food, infant food and in various supplementary food formulations (Malleshi et al. 1989; Livingstone et al. 1993; Balasubramanian et al. 2014).

Foxtail millet (Setaria italica) is one of the commonly cultivated minor millets in India. It is a cheap source of micronutrients, and is nutritionally competitive to other cereals such as wheat, rice and maize that form our daily diet. The millet contains 70–76.5 % carbohydrates, 10–13.5 % proteins, 2.5–5.0 % fat, 0.5–3.0 % minerals and 3.5–21.0 % total dietary fibres (Devisetti et al. 2014). It is reported to be one of the richest sources of fibre (6.7 g 100 g⁻¹) and thiamine (0.59 mg 100 g⁻¹) among cereals and grains (Saleh et al. 2013). It can be blended with milk to produce weaning and geriatric foods that are rich in vitamins, fibre and iron. Several such milk-malted millet foods have been developed to cater various consumer groups (Shah et al. 1987; Salooja and Balachandran 1988; Sharma et al. 2014). One of the most common methods of producing malted foods is by spray drying.

Spray-dried milk-foxtail millet powder, because of its hygroscopicity, will adsorb moisture during storage, resulting in various physicochemical changes. Most of these physicochemical changes are undesirable and may seriously affect the end use of the powder. Controlling the a_w of food prevents chemical deterioration, ensuring food safety and extended shelf-life (Labuza 1968). Therefore, it is necessary to determine the moisture sorption of milk-foxtail millet powders and the associated thermodynamics of sorption. Properties such as isosteric heat of sorption, net integral enthalpy and entropy and spreading pressure are important for understanding the energy requirement during dehydration, the food microstructure, physical phenomena on the food surfaces and sorption kinetic parameters (Rizvi and Benado 1984).

Many traditional empirical and semi-empirical models are reported in literature for describing the sorption behaviour of food powders. However, in recent times, artificial neural network (ANN) and adaptive neuro-fuzzy inference system (ANFIS) models have been successfully used in the prediction of moisture sorption behaviour of processed foods (Siripatrawan and Jantawat 2008; Sharma et al. 2014). The ANN is a soft-computing approach that imitates the human neural system that can perform spontaneously. It is designed by interconnecting to neurons, operating in parallel and simulating the pattern of biological networks (Bishop 1994). The self-learning and adaptive ANN models thus have the inherent ability to understand complex patterns in biological systems and have the capability to describe and predict such nonlinear relationships. The combination of ANN and fuzzy inference systems (FIS) leads to an integrated multi-layered system called ANFIS which has the advantage of both ANN and FIS.

Al-Mahasneh et al. (2012) modelled the sorption isotherms in roasted green wheat using neuro-fuzzy technique and reported that the predictions were superior to conventional nonlinear least square regression methods. Sharma and Sawhney (2015) studied the moisture sorption characteristics in dried acid casein and reported that the connectionist model outperformed conventional empirical models. Sharma et al. (2014) reported that neural network models were superior as compared to the conventional sorption models. As described above, the moisture sorption isotherms and its thermodynamics of milk-foxtail millet powder has not been reported. Considering the importance of milk-malted millet foods, this study was proposed (1) to determine the moisture sorption of milk- foxtail millet powder at different temperatures and (2) to determine the thermodynamics governing sorption.

Materials and methods

Preparation of malted foxtail millet

Foxtail millet was procured from the local market of Bengaluru, India and was malted as per the procedure outlined by Nirmala et al. (2000). After soaking the grains in water at 40 °C for 24 h, the water was drained and the wet grain was allowed to germinate at ambient condition (25–30 °C) for 72 h. The germinated seeds were taken out and dried in hot air oven at 50 °C for 12 h, and the vegetative part was removed manually. De-vegetated grains were ground using an ultra-centrifugal mill (model: ZM 200, Retsch GmbH, Haan, Germany) to get flour of 200 µ particle size.

Preparation of wort and optimization of alpha-amylase

Wort was prepared from ground flour using the infusion method proposed by Rao et al. (1976) with minor modifications. The millet flour (50 g) was blended with 360 mL of water. The blends thus prepared were kept in a water bath at 45 °C for 30 min. Then the supernatant liquid solution (150 mL) of each sample was collected separately in a bowl to retain the native enzyme. The mixture in the beaker was heated to 90 °C in a water bath. After cooling to 50 °C, the supernatant solution was added back. To this sample, 1 mL of alpha-amylase enzyme (Sigma Aldrich Co. LLC, Bengaluru) was added, and the contents were incubated at 40 °C for 24 h to achieve the complete hydrolysis of starch present.

Spray drying

Fresh cow milk, procured from the farm of Southern Regional Station, ICAR-National Dairy Research Institute, Bengaluru, was pasteurized and concentrated in a rotary evaporator (model: R-3, BÜCHI Labortechnik AG, Flawil, Switzerland) under vacuum at 45 °C to 22 % total solids (TS). Foxtail millet wort also was concentrated in the rotary evaporator to 22 % TS, and was blended with concentrated milk at 1:1 ratio. This blend was spray-dried into a powder using a lab-scale dryer (model: LU-222 advanced, LabUltima Pvt. Ltd., Mumbai, India) at inlet temperature of 185 ± 2 °C, outlet temperature of 80 ± 2 °C, aspiration rate of 45 N m³ h⁻¹ and feed rate of 6 mL min⁻¹.

Chemical analyses

The moisture content of milk-foxtail millet powder was determined by AOAC method 927.05 (AOAC 2012). Exactly 2 g of sample was used, and the moisture content was expressed in dry basis (d.b). Fat content was determined by AOAC method 922.09 while the protein content was estimated by Micro-Kjeldahl method 930.29 (AOAC 2012). The total ash content of the sample was determined gravimetrically by AOAC method 930.30, while the carbohydrate content was calculated from the difference to 100. All the chemical analyses were done in triplicate.

Determination of moisture sorption isotherms and fitting of models

The moisture sorption isotherms of spray-dried milk-foxtail millet powder were determined by isopiestic method using nine different saturated salt solutions, ranging in a_w from 0.11 to 0.96 at temperatures of 10, 25 and 40 °C. About 1 g of sample was taken and weighed to 0.1 mg precision using an electronic balance (model: CPA224S, Sartorius Mechatronics India Ltd., Bengaluru), transferred and spread evenly at the base of a 25 mL beaker. Each of these 25 mL beakers was placed inside another beaker of 50 mL capacity. This was done to reduce experimental errors by avoiding splashing of salt solution and condensation of water on the sample beaker. Before placing the sample, the beakers were equilibrated to the respective relative humidity (RH) conditions.

The samples were equilibrated for 40 days at the respective temperatures, and the final equilibrated weights of the samples were recorded to calculate the equilibrium moisture content (EMC). The experiment was carried out with six replications at each temperature. The model parameters were determined by regression analysis using SAS 9.3 (SAS Institute, Cary, USA).

Artificial neural network modelling

Artificial neural network (ANN) model was used to fit the sorption data. A multilayer feed-forward (MLFF) neural network trained by a back propagation (BP) algorithm was developed. The input layer of the model consisted of two neurons which corresponded to two independent variables (temperature, water activity) while the output layer had one neuron which represented the dependent variable (EMC). To train the network, a Bayesian Regularization process was used. The sum of squares of network errors was used as the performance function for training the feed-forward neural network. Weights and biases were randomly initialized. The network was trained for 5000 epochs. The transfer function for the hidden and output layers was logarithmic sigmoid (logsig)/tangent sigmoid (tansig) and linear (purelin), respectively.

The data sets obtained from the experiments were randomised using the RAND function in Microsoft Excel 2007. The randomized data sets were divided into two disjoint subsets namely, training set containing 75 % of observations and testing set comprising of the remaining 25 % (total 162 observations). Due to the different ranges of input and output data, the inputs and output were normalised into the interval [0, 1] before feeding into the network. At the end of training, simulations were done with the trained model in order to validate the proposed back propagation neural network. A MATLAB program was written to develop the ANN model (ver. R2008a, The MathWorks Inc., Natick, Massachusetts, USA). The network performance was evaluated using root mean square error (RMSE).

ANFIS modelling

The Sugeno-type ANFIS model also was used to predict the EMC using Fuzzy Logic Toolbox in MATLAB (ver.R2008a, The MathWorks Inc., Natick, Massachusetts, USA). The following rule:

Rule ‘r’:

IF temperature was ‘x’ and water activity was ‘y’,

THEN EMC was $Z_{jr}=ax+by+c$. If there were ‘R’ fuzzy inference rules, the output (Z_jr) of observation ‘j’ from each rule ‘r’ would be weighed to give the final output. The Sugeno-type ANFIS architecture used in this study consisted of five layers, viz. fuzzification (I), rule (II), normalization (III), defuzzification (IV) and output layer (V). As in the case of ANN, the randomized data sets were divided into two subsets (75 % training and 25 % testing). The input factors for the model were temperature and water activity while EMC was the output. The grid partitioning technique was utilized in framing the rules. The fuzzy rules are derived from the membership functions (MF), which in turn are defined based on input–output data. In this study, the ANFIS model was developed by fixing the number of MFs as three (corresponding to the three regions of the sorption isotherm).

Eight types of MFs were tried for the input factors, while the output factor was assigned as constant or linear. The training of the FIS was optimized using hybrid algorithm (combination of least squares and back propagation), by fixing the learning epochs and error tolerance as 500 and 0.0001, respectively. After fixing the threshold values for error, the consequent model parameters were calculated, and if the error was larger than the threshold value, the premise parameters would be updated. The process would be terminated when the error became less than the threshold value. The trained ANFIS model was then used to predict the EMC (at different a_w) using the testing data to further check if it achieved good generalization. Thus, in the training step, the model would be compared with actual system for validation. The performance of the developed models was evaluated based on RMSE. The ANFIS model yielding the lowest RMSE value during testing was chosen as the best.

Evaluation of model performance

The performances of the classical regression and soft computing models were evaluated and compared using RMSE as shown below in Eq. (1).

$$RMSE=\sqrt{\frac{\sum _{i=1}^N{\left(M_{iexp}-M_{i\mathrm{pre}}\right)}^2}{N}}$$ 1

where, ‘N’ was the number of observations, ‘M_iexp’, and ‘M_ical’ were experimental and predicted EMC values, respectively (Rao et al. 2006).

Thermodynamics of sorption

Isosteric heat of sorption

The net isosteric heat of sorption represents the difference between the latent heat of sorption and the latent heat of condensation of pure water at a particular moisture content and temperature (Gabas et al. 1999). It can be calculated from the Clausius–Clayperon equation as shown below:

$$\frac{\mathit{\partial }ln(a_w)}{\mathit{\partial }ln\left(\frac{1}{T}\right)}=-\frac{\mathrm{\Delta }{h}_d}{R}$$ 2

where, ‘a_w’ was the water activity, ‘T’ was the absolute temperature, ‘R’ was the universal gas constant [8.314 kJ (mol K)⁻¹]. Plotting the natural logarithm of a_w against $1/T$ at specific moisture content yielded several slopes, which were used to determine the net isosteric heat of sorption. This approach assumed that heat of sorption was independent of temperature and moisture content was constant with varying time (Tsami et al. 1990).

Enthalpy–entropy compensation theory

The enthalpy-entropy compensation theory or isokinetic relationship hypothesizes a linear relationship between ∆h_d and ∆S_d as follows:

$$\mathrm{\Delta }{h}_d=T_{\mathit{\beta }}(\mathrm{\Delta }{S}_d)+\mathit{\alpha }$$ 3

where, ‘T_β’ was the isokinetic temperature and ‘α’ was the constant. The isokinetic temperature represents the temperature at which all reactions proceed at the same rate. To corroborate the compensation theory, Krug et al. (1976) proposed a statistical analysis involving comparison between isokinetic temperatures (T_β) and harmonic mean temperature (T_hm) as given below

$$T_{hm}=\frac{n}{{\sum }_{i=1}^n\frac{1}{T}}$$ 4

where, ‘n’ was the total number of isotherms used and ‘T’ was the absolute temperature in K.

Spreading pressure

The spreading pressure or surface potential represents the surface excess free energy and it gives information about the increase in surface tension of bare sorption sites due to sorbed molecules (Fasina et al. 1999). The spreading pressure was calculated from the GAB model at different temperatures using Eq. (5) below (Pushpadass et al. 2014).

$$\mathit{\varphi }=\frac{K_{B}T}{A_m}ln\left[\frac{1-K_g{a}_w+K_g{C}_g{a}_w}{1-K_g{a}_w}\right]$$ 5

where, ‘K_B’ was Boltzmann constant (1.38 × 10⁻²³ JK⁻¹), ‘A_m’ was the area of a single water molecule at monolayer, and ‘K_g’ and ‘C_g’ were GAB model constants. The sorption data was analyzed using randomised complete block design (RCBD) to find the effect of temperature on spreading pressure, keeping a_w as blocking factor. The spreading pressure was plotted against a_w at each sorption temperatures to obtain the spreading pressure isotherms.

Net integral enthalpy and entropy

At constant spreading pressure, the net integral enthalpy (∆h_in) and net integral entropy (∆S_in) were determined from the slope and intercept of ln(a_w) versus $1/T$ plot, and the values were plotted against moisture content.

$${\left.-ln{a}_w^{\ast }\right|}_{\mathit{\varphi }}=\frac{\mathrm{\Delta }{h}_{in}}{RT}+\frac{\mathrm{\Delta }{S}_{in}}{R}$$ 6

where, ‘a_w’ was the geometric mean water activity obtained at constant spreading pressure at different temperatures.

Results and discussion

Composition and sorption isotherms of milk-foxtail millet powder

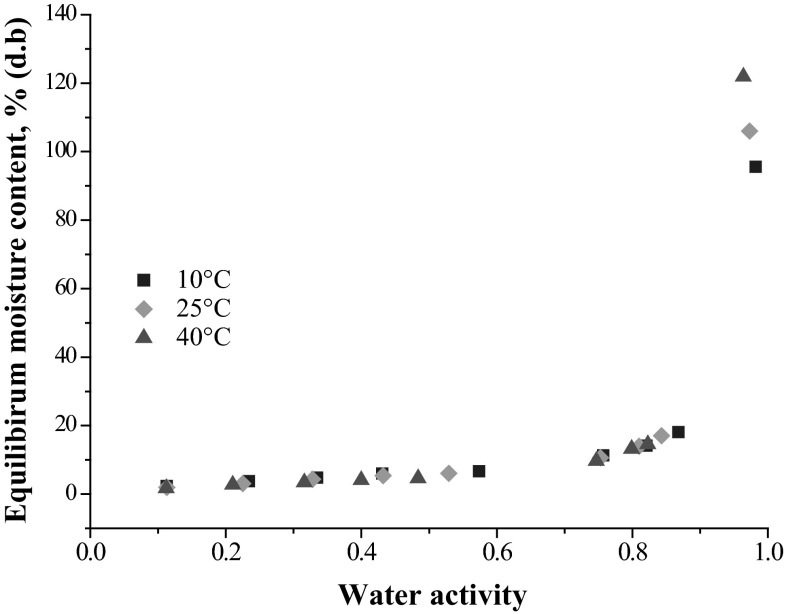
Proximate composition analyses of spray-dried milk-foxtail millet powder showed that it contained 49.2 % carbohydrates, 23.5 % proteins, 20.4 % fat, 4.7 % ash and 2.2 % moisture (d.b). The presence of carbohydrates and proteins affects the physicochemical properties and moisture adsorption of the powder. The moisture sorption isotherms for the entire range of a_w at 10, 25 and 40 °C are presented in Fig. 1. The isotherms were of sigmoidal shape, and belonged to type II of BDDT (Brunauer–Deming–Deming–Teller) classification. The sorption behaviour was in agreement with that of spray-dried whole milk powder (Jouppila and Roos 1994) and gulabjamun mix (Pushpadass et al. 2014). A slight depression in EMC was observed in the range of 0.44–0.57 a_w, likely due to the crystallization of lactose. The isotherms were characterized by two bending regions in the ranges of 0.03–0.05 and 0.799–0.861 a_w. The moisture uptake was stable till 0.8 a_w, followed by an impulsive rise in the region III of the isotherm. Such isotherms are common in foods containing sugars (Mrad et al. 2012). The milk-foxtail millet powder contained considerable amount of sugars released from conversion of starch during malting. The BET monolayer moisture content decreased from 3.30 to 2.67 % as sorption temperature increased from 10 to 40 °C.

Fig. 1.

Moisture sorption isotherms of spray dried milk-foxtail millet powder at different temperatures

The temperature range of 10–40 °C was selected in this study because the product was a powder, and would likely be stored at this temperature. In addition, as sorption is exothermic and higher temperatures favour desorption rather than adsorption, the maximum temperature of this study was limited to 40 °C. It may also be noted that such desorption data obtained at higher temperatures would not be useful to spray-dried milk-malted foxtail millet powder having moisture content below 2.2 %. Moreover, in biological systems, irreversible changes and phase transformations invariably occur at elevated temperatures, rendering the sorption data and the thermodynamic properties irrelevant (Rizvi 2005).

Sorption temperature affects the mobility of water and the dynamic equilibrium between vapour and food (Sawhney et al. 1991). Figure 1 also shows the effect of temperature on the moisture sorption behaviour of milk-malted foxtail millet powder. The EMC decreased with increasing temperature at constant water activity. The EMC was expected to decrease with increasing temperature, since the Gibb’s free energy ($\mathrm{\Delta }\text{G}$) was equal to $\left(\mathrm{\Delta }{\text{h}}_{\text{d}}-\text{T}·\mathrm{\Delta }{\text{S}}_{\text{d}}\right)$. As adsorption is an exothermic process, the water molecules get excited at higher sorption temperature, and tend to break away from the water binding sites, lowering the EMC. The isotherms, however, crossed over at a_w above 0.82. This was attributed to the increased dissolution of sugars, which were produced during malting of the millet.

Fitting of classical sorption models

BET, Caurie, Halsey, Iglesias and Chirife, Kühn, Henderson, GAB, Ferro-Fontan, Lewicki, modified GAB, modified Mizrahi and Peleg models were fitted to the EMC-a_w data. The first six are two-parameter models while rest of the models have three or more parameters. The goodness of fit was evaluated by comparing the RMSE values. The estimated model parameters are summarized in Table 1. Amongst the classical models, Ferro-Fontan gave the best fit of the sorption data at all temperatures with RMSE of 0.051–0.095, closely followed by modified GAB (RMSE of 0.053–0.143). The Ferro-Fontan and GAB models were reported to fit the sorption behaviour of many food products (Delgado and Sun 2002). The conventional three-parameter GAB model was well-suited for the a_w range of 0–0.9, but it failed to predict adsorption adequately in the a_w region of 0.9–1.0. It is well-known that the GAB model has inherent limitations in the capillary condensation region, even though it has described the sorption behaviour over a complete range of a_w in many foods. Iglesias and Chirife (1995) recommended the use of Ferro-Fontan model as an alternative to GAB model.

Table 1.

Parametric constant of various classical sorption models

Model	T (°C)	Model parameters				RMSE
BET	10	Wm = 3.301	C = 27.383			0.106
	25	Wm = 3.161	C = 9.578			0.056
	40	Wm = 2.669	C = 13.155			0.049
GAB	10	Wm = 3.371	Cg = 18.111	Kg = 0.955		0.265
	25	Wm = 3.284	Cg = 10.387	Kg = 0.971		0.265
	40	Wm = 2.638	Cg = 13.345	Kg = 1.005		0.151
Caurie	10	Mo = 3.601	C = 1.342			0.298
	25	Mo = 2.935	C = 1.346			0.391
	40	Mo = 2.188	C = 1.260			0.501
Modified Mizrahi	10	a = −1.585	b = −6.407	c = 6.384		0.097
	25	a = −2.590	b = 0.391	c = −0.687		0.184
	40	a = −4.398	b = 12.043	c = −12.472		0.415
Halsey	10	A = 6.020	B = 1.273			0.116
	25	A = 3.388	B = 1.034			0.196
	40	A = 1.906	B = 0.823			0.328
Henderson	10	A = −1.574	B = 0.457			0.626
	25	A = −1.384	B = 0.392			0.659
	40	A = −1.178	B = 0.327			0.694
Iglesias and Chirife	10	A = 1.210	B = 3.079			0.385
	25	A = 1.030	B = 3.352			0.407
	40	A = 0.842	B = 3.579			0.466
Peleg	10	a = 1.50	b = 0.951	c = 118.879	d = 20.279	0.114
	25	a = 12.488	b = 0.967	c = 154.700	d = 18.259	0.093
	40	a = 11.544	b = 1.072	c = 219.342	d = 18.630	0.154
Ferro-Fontan	10	a = 0.993	b = 10.355	c = 0.665		0.088
	25	a = 0.986	b = 7.113	c = 0.738		0.095
	40	a = 0.976	b = 4.794	c = 0.804		0.051
Lewicki	10	a = 4.363	b = 0.774	c = −0.273		0.158
	25	a = 2.663	b = 1.023	c = −6.537		0.198
	40	a = 1.736	b = 1.281	c = −4.575		0.117
Modified GAB	10	A = 2.678	B = 0.990	C = 2.75 × 106		0.143
	25	A = 2.693	B = 1.002	C = 1.02 × 104		0.119
	40	A = 2.442	B = 1.017	C = 5.85 × 103		0.053
Kühn	10	A = −1.672	B = 3.964			0.384
	25	A = −2.867	B = 1.060			0.117
	40	A = −4.512	B = −2.917			0.691

Prediction of sorption using ANN

The ANN model was used for estimation of EMC of spray dried milk-foxtail millet powder. The total number of observations used for predicting EMC was 162, which was categorized into two datasets namely, training (122) and testing (40). The neural network comprised one hidden layer and the number of neurons in this layer was varied from 4–12 to obtain better prediction of the sorption phenomenon. Transfer function comprising 2-4-1 topology (2 inputs, 4 neurons in the hidden layer and 1 output) gave the lowest RMSE for logsig–purelin (0.09063) as compared to tansig–purelin (0.09488) (Table 2). Further increase in the neurons did not yield any significant reduction or increase in the RMSE values. From the network architecture and RMSE values, it could be stated that the 2-4-1 topology was very simple and efficient. Aghbashlo et al. (2012) observed that increase in number of neurons not only enhanced the training time but also complicated the ANN topology.

Table 2.

Predictive performance of ANN models

No. of neurons	Approximation function	No. of epochs	RMSE
			Training	Testing
4	Tansig–Purelin	1105	0.09008	0.09488
4	Logsig–Purelin	390	0.09592	0.09063
6	Tansig–Purelin	349	0.08840	0.09579
6	Logsig–Purelin	384	0.08884	0.09538
8	Tansig–Purelin	1744	0.08792	0.09673
8	Logsig–Purelin	452	0.08787	0.09697
10	Tansig–Purelin	577	0.08786	0.09661
10	Logsig–Purelin	927	0.08757	0.09673
12	Tansig–Purelin	798	0.08719	0.09610
12	Logsig–Purelin	1579	0.08605	0.09517

Prediction of sorption using ANFIS

The inputs and output of ANFIS models and the dataset for training and testing remained same as that of neural network model. Various ANFIS models were developed using membership functions such as trimf (triangular), trapmf (trapezoidal), gbellmf (generalized Bell), gaussmf (Gaussian), gasuss2mf (Gaussian combination), pimf (pi-shaped), dsigmf (difference between two sigmoidal) and psigmf (product of two sigmoidal). The ‘gbellmf’ MF is the standard for ANFIS because of its smoothness and concise notation. The ANFIS model predicted EMC as a function of temperature and a_w.

As there were three regions in the sorption isotherm, the number of MFs was fixed as three. Another reason to keep the number of MFs small was that a large number in the premise part of the rules could produce a large number of fuzzy rules, which could cause the learning complexity of ANFIS to suffer exponential explosion. The predictive performance of the models is summarized in Table 3. The shape of MF was a key parameter in tuning the ANFIS. The ‘gbellmf’ with constant MF gave the best fit of the EMC data with RMSE as low as 0.0099. The prediction accuracy of this ANFIS model was as high as 99.94 %. The fuzzy rules premise and antecedent parameters were directly dependent on the type (shape) of MF and its parameters. Also, it could be said that the constant MF for output (Table 3) showed better fit than linear MF. The plot between predicted and experimental EMC showed that the computed EMC values were very close to the observed values at the same temperature.

Table 3.

Predictive performance of Sugeno-type ANFIS models

Number of input MF	Input MF type	Output MF type	Training RMSE	Testing RMSE
3 each	Triangular MF	Constant	0.0129	0.0148
	Trapezoidal MF	Constant	0.0216	0.0249
	Generalised bell MF	Constant	0.0058	0.0099
	Gaussian MF	Constant	0.0152	0.0181
	Gaussian combination MF	Constant	0.0253	0.0181
	Pi shaped MF	Constant	0.0091	0.0121
	Difference between two sigmoidal MF	Constant	0.0156	0.0184
	Product of two sigmoidal MF	Constant	0.0156	0.0184
3 each	Triangular MF	Linear	0.0121	0.0139
	Trapezoidal MF	Linear	0.0068	0.0105
	Generalised bell MF	Linear	0.0052	0.0100
	Gaussian MF	Linear	0.0061	0.0102
	Gaussian combination MF	Linear	0.0077	0.0111
	Pi shaped MF	Linear	0.0057	0.0100
	Difference between two sigmoidal MF	Linear	0.0059	0.0101
	Product of two sigmoidal MF	Linear	0.0059	0.0101

MF membership function

Performance evaluation of different models

The prediction capabilities of classical regression, ANN and ANFIS models were compared using RMSE values. The predictive performance of ANN was better than the Ferro-Fontan model. However, amongst the three computing approaches, ANFIS gave a much superior prediction of the EMC. The developed ANFIS model consisting of three MF and generalized Bell shape would be simple and efficient. ANFIS gave superior prediction because it was more powerful than ANN and classical regression models, and hence, it could learn about the dataset and computed the MF parameters that allowed the associated FIS to track the given input/output data (Jang 1993).

The EMC could not be predicted by classical models when temperature changed. Hence, the classical model had to be revised for each temperature. Similar superior performance of ANFIS model over connectionist and GAB models in predicting sorption was reported by Sharma et al. (2014) for milk-pearl millet-based fortified powder. Al-Mahasneh et al. (2012) reported that the neuro-fuzzy technique provided much better fit as compared to classical nonlinear regression methods.

Thermodynamics of sorption

Isosteric heat of sorption

The net isosteric heat of sorption (differential enthalpy) is an indicator of the strength of intermolecular bonding between water molecules and adsorbing surfaces, and hence, it varies with the amount of water adsorbed by the substrate (Pushpadass et al. 2014). The isosteric heat of sorption at the mean temperature of 25 °C declined from as high as 150.32 kJ mol⁻¹ at 1 % moisture content (d.b) to 44.11 kJ mol⁻¹ at 15 % moisture content (d.b). The latent heat of vapourization of pure water at 25 °C is 43.97 kJ mol⁻¹. Similar trends were reported by Rao et al. (2006) for chhana podo, Abdenouri et al. (2010) for spray-dried milk powder and Cano-Higuita et al. (2015) for spray-dried milk-mango powder. The closeness of heat of sorption to that of pure water at moisture contents above 15 % suggested that water molecules were loosely bound to the powder molecules. It also could be the beginning of condensation in the capillaries of the powder particulates. The second bending region of the adsorption curves, which represented the major shift in water binding in the food, corresponded to a moisture content of 14–16 % at the temperature range tested.

Enthalpy–entropy compensation theory

The enthalpy (∆h_d) and entropy (∆S_d) values at different moisture contents were calculated using Eq. 2. It was assumed that at specific moisture content, both ∆h_d and ∆S_d were invariant of temperature. The plot of ∆h_d versus ∆S_d for the spray-dried milk-foxtail powder was linear (Fig. not shown). The linear relationship between the two thermodynamic quantities confirmed the existence of compensation theory, which was demonstrated by Ferro-Fontan et al. (1982) for several foods, Abdenouri et al. (2010) for spray-dried milk powder and Pushpadass et al. (2014) for gulabjamun mix. The isokinetic temperature and harmonic mean temperature were calculated from Eqs. (3) and (4). The T_β and T_hm were calculated as 333.1 and 297.5 K, respectively.

To test the validity of the compensation theory, the T_β was compared with T_hm. It is evident that T_β differed appreciably from T_hm. Gabas et al. (1999) reported that, if T_β > T_hm, the sorption process was enthalpy driven, and when the contrary condition existed (T_β < T_hm), the process was entropy-controlled. Since the two temperatures were not equal and T_β was greater than T_hm, it could be concluded that the sorption thermodynamics of this product was enthalpy-driven in the range of moisture content studied.

Spreading pressure

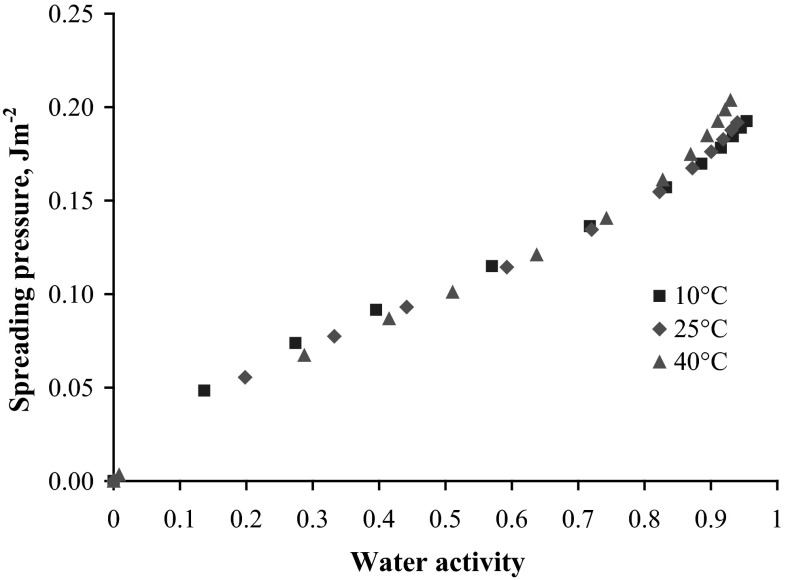
The spreading pressure isotherms of spray-dried milk-foxtail millet powder were plotted against a_w at each temperature (Fig. 2). The spreading pressure lied in the range of 0–0.25 J m⁻², and it increased with a_w regardless of the temperature. The effect of temperature on spreading pressure was statistically significant (p < 0.05). The spreading pressure decreased with increasing temperature, but the trend reversed above 0.8 a_w where crossover of the isotherms occurred. The values for spreading pressure obtained were comparable with those determined by Martinez-Monteagudo and Salais-Fierro (2012) for Mexican Mennonite-style cheese and Pushpadass et al. (2014) for gulabjamun mix.

Fig. 2.

Spreading pressure isotherms of spray dried milk-foxtail millet powder

Net integral enthalpy and entropy

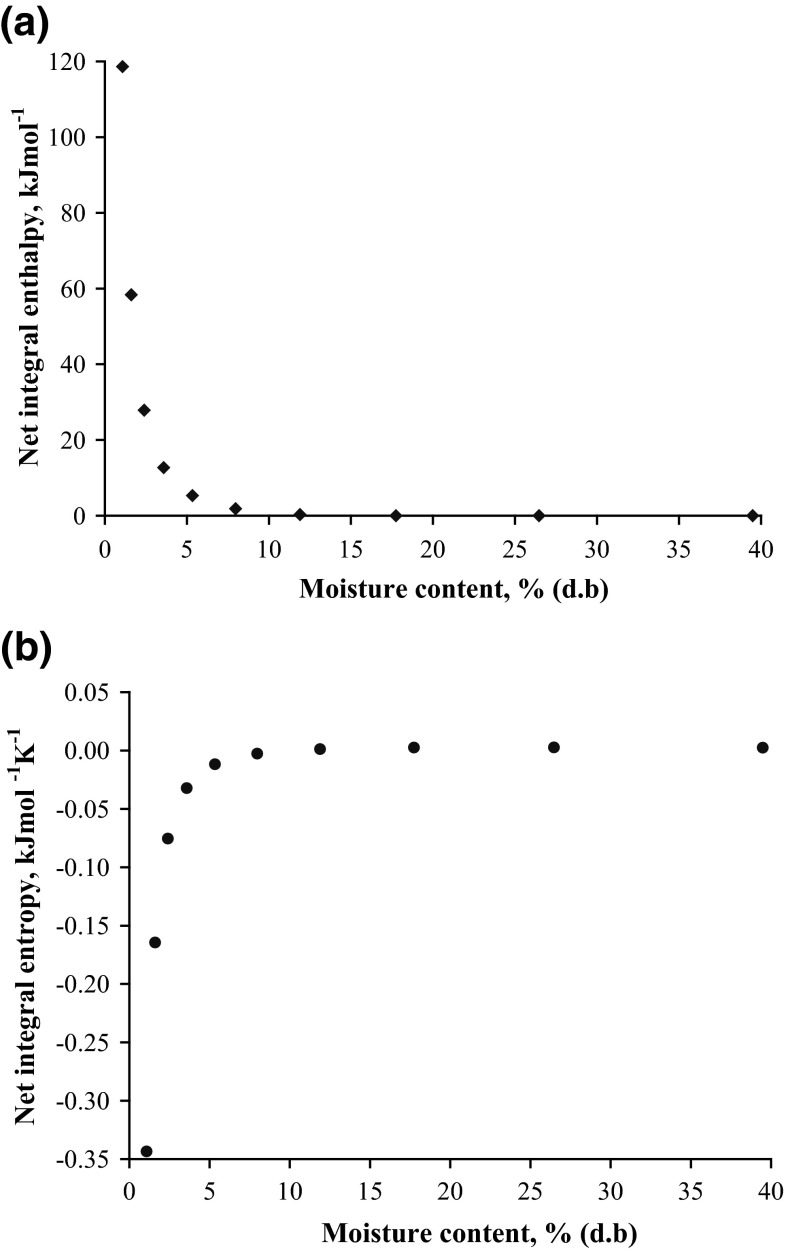
The net integral enthalpy was calculated by plotting ln(a_w) versus $1/T$ for a specific spreading pressure using Eq. (5). The net integral enthalpy of sorption was plotted as a function of moisture content (Fig. 3a). The enthalpy declined exponentially with increasing moisture content. The maximum enthalpy value of 118.63 kJ mol⁻¹ was observed at 1.08 % moisture content, which approached nearly zero at a moisture content of 11.9 %. At lower moisture contents, the water was adsorbed on the easily accessible locations on the powder particles. However, as the moisture content increased, the net integral enthalpy decreased because the ‘less favourable’ sorption sites became associated with water and multiple layers of sorbed water were formed.

Fig. 3.

Thermodynamic properties of sorption a net integral enthalpy and b net integral entropy

The net integral entropy ranged from −0.344 to 0.002 kJ (mol K)⁻¹. As the first layer was covered and when the sorbed water became increasingly localised, the entropy reached the minimum at 1.09 % moisture content (Fig. 3b). The a_w at which minimum integral entropy was observed could be interpreted as the point where the product has the best stability. The subsequent increase in magnitude reflected on the formation of multi-layers and more freely held water molecules, approaching that of free water (Rizvi 2005).

Conclusions

The moisture sorption isotherms of spray-dried milk-foxtail millet powder at 10, 25 and 40 °C were of sigmoidal shape and belonged to type II of BDDT classification. The moisture sorption behaviour was adequately described by Ferro-Fontan and Modified GAB classical models. However, amongst the three prediction approaches, the Sugeno-type ANFIS model using ‘gbellmf’ membership function provided superior prediction of the sorption data with RMSE as low as 0.0099. ANFIS proved to be a simple and efficient technique for predicting complex nonlinear relationships in foods. The energy of binding of water reached close to that of pure water at moisture contents above 15 %. The enthalpy-entropy compensation theory proved that the sorption mechanism of milk-foxtail millet powder was basically enthalpy-driven. Spreading pressure increased with increasing water activity but decreased significantly with sorption temperature. The results of this study would be valuable for determining the end point of spray drying, the shelf-life of the dried powder and for design of packaging systems.

Electronic supplementary material

Below is the link to the electronic supplementary material.

List of symbols

a_w

Water activity

a^*_w

Geometric mean water activity (at constant spreading pressure)

C_g

GAB model constant

A_m

Area of water molecule (m²)

K_B

Boltzmann constant (1.38 × 10⁻²³ J K⁻¹)

K_g

GAB model constant

M_iexp

Experimental moisture content (% d.b)

M_iexp

Predicted moisture content (% d.b)

N

Number of observations

n

Number of isotherms

R

Universal gas constant (8.314 kJ mol⁻¹ K⁻¹)

T

Absolute temperature (K)

T_hm

Harmonic mean temperature (K)

α

Constant

φ

Spreading pressure (J m⁻²)

∆h_in

Net integral enthalpy (kJ mol⁻¹)

∆S_d

Differential entropy (kJ mol⁻¹ K⁻¹)

∆S_in

Net integral entropy (kJ mol⁻¹ K⁻¹)