Efficient Queries of Stand-off Annotations for Natural Language Processing on Electronic Medical Records

Abstract

In natural language processing, stand-off annotation uses the starting and ending positions of an annotation to anchor it to the text and stores the annotation content separately from the text. We address the fundamental problem of efficiently storing stand-off annotations when applying natural language processing on narrative clinical notes in electronic medical records (EMRs) and efficiently retrieving such annotations that satisfy position constraints. Efficient storage and retrieval of stand-off annotations can facilitate tasks such as mapping unstructured text to electronic medical record ontologies. We first formulate this problem into the interval query problem, for which optimal query/update time is in general logarithm. We next perform a tight time complexity analysis on the basic interval tree query algorithm and show its nonoptimality when being applied to a collection of 13 query types from Allen’s interval algebra. We then study two closely related state-of-the-art interval query algorithms, proposed query reformulations, and augmentations to the second algorithm. Our proposed algorithm achieves logarithmic time stabbing-max query time complexity and solves the stabbing-interval query tasks on all of Allen’s relations in logarithmic time, attaining the theoretic lower bound. Updating time is kept logarithmic and the space requirement is kept linear at the same time. We also discuss interval management in external memory models and higher dimensions.

Background and Motivation

Electronic medical records (EMRs) normally include some well-structured tabular data such as laboratory measurements and medication orders, but a large portion of each patient’s record is in the form of narrative sentences (eg, pathology reports, discharge summaries, progress notes, clinicians’ notes, and comments) or snippets (eg, medical problem listings and medical test items).^1–4 EMRs are being widely adopted, providing valuable repositories of historical patient data that enable clinicians and researchers to study profound biological and clinical questions.^5–11 To make effective use of these natural language data, we typically run multiple interpretive algorithms over the text, each generating annotations of portions of the text.^3,4

Many early natural language processing (NLP) systems and corpora used in-line annotations where annotations are marked and embedded in the text (eg, i2b2 de-identification and smoking challenge corpora^12,13). Figure 1 shows an example sentence with in-line annotations of Private Health Information (PHI) and Unified Medical Language System (UMLS) semantic types (STs) in XML style markups. In comparison, stand-off annotations identify the starting and ending positions of the text to which it applies and contain various types of additional information specific to the type of annotation. Stand-off annotations have the benefit that the original document is never altered or directly marked up by NLP steps (see Box1), hence more human readable. Stand-off annotations can be stored in data structures that make their retrieval fast and management efficient. This eliminates the need to maintain multiple versions of a document depending on what markups have been made on it, and it eliminates the often tedious task of other language processing systems to generate a flat file representation of intermediate analysis results, followed immediately by the need to reparse those at files into an internal representation that support the next processing step. More recent biomedical NLP systems and corpora gradually adopted the stand-off annotation or its variants, eg, cTAKES,¹⁴ current version of MetaMap,¹⁵ and the i2b2/VA 2010 challenge.¹⁶ Example stand-off annotations are also shown in Figure 1. Note that we can introduce additional STs due to alternative taxonomies/ontologies, including SNOMED-CT (www.ihtsdo.org/snomed-ct), LOINC (loinc.org), and ARTEMIS.¹⁷ These STs share the start and end positions, thus would be cumbersome for in-line annotation format but cleanly separated using stand-off annotations.

Figure 1.

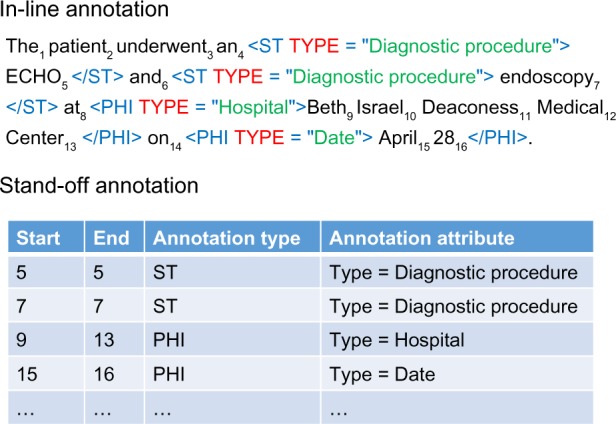
Comparison of in-line annotation and stand-off annotation. The annotations marked in the sentence are PHI and UMLS ST. For example, there are over 30,000 UMLS ST annotations that can be mapped to the category of medical problems in the i2b2/VA corpus.

In general, there can be many thousands of annotations per EMR document. As an example in the typical EMR setting, for the corpora in the i2b2/VA 2010 challenge,¹⁶ after basic syntactic (tokenization, part-of-speech tagging, sentence parsing, phrase chunking, etc.) and semantic analysis (concept recognition, assertion recognition, relation recognition, etc.), we have on average about 10,000 annotations per document and millions of annotations in total. Such a large amount of annotations can be space consuming to store and time consuming to search through. Thus, it is important to store and retrieve these annotations efficiently.

Further analysis of the text often requires retrieval of different types of annotations pertaining to different segments of the text. For example, a program may need to find all the sentences within a specific document section, or all the PHI annotations within a sentence or phrase. Another program may need to extract features for relation classification between two concept annotations (named entities such as medical problems and treatments), which can require querying syntactic, lexical, and semantic annotations that are before, between, or after the two concept annotations in a record (eg, the time of relation between <ST TYPE = "Diagnostic Procedure"> endoscopy7 </ST> and <PHI TYPE = "Date">April₁₅ 28₁₆ </PHI> in Fig. 1). Viewing annotations and text segments as intervals (with attributes) in the text, most annotation queries may then be formally stated as interval queries.

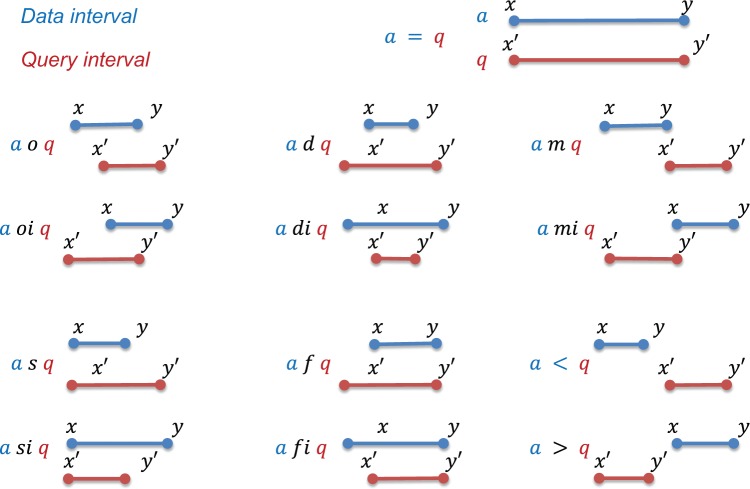
An interval is defined by its starting and ending positions. There are only three possible relations between two positions in a document, namely, = , <, or >. However, as Allen¹⁸ has shown that, for temporal intervals, there are 13 possible relations between two intervals, as defined in Table 1. We adopt this insight and terminology here, though referring to spatial rather than temporal intervals. Temporal intervals mining and reasoning is itself an active area of research.^19,20 We note that the algorithms we present in this paper apply directly to temporal intervals. If we consider two intervals, α and q, with starting and ending positions x and y, as well as x′ and y′, respectively, they may have any of the 13 relationships defined in Table 1 and illustrated in Figure 2. In the special case where some intervals are degenerated (ie, x = y), it is possible for more than one of the above relations to be satisfied. For example, given a degenerated α whose start and end coincide with a nondegenerated q′s x′, we could say that α m q or that α s q. The scenarios of the 13 relations of Allen’s interval algebra arise frequently in NLP on EMRs. For example, one may need to find all noun phrase annotations after a verb phrase annotation in a sentence, extract all automatically identified PHI annotations that overlap with those in ground truth to calculate partial matches, or find all noun word annotations within a certain medical concept annotation. The distribution of these query types is task and corpus dependent. In this paper, we propose to solve the problem of efficiently retrieving all intervals satisfying each of the 13 interval relationship with respect to a given query interval. The task of retrieving all intervals satisfying certain relationship with the given query is called a stabbing-interval query or stabbing query for short. Note the difference between stabbing-interval query and stabbing-point query, where a (time or spatial) point rather than interval is given as the probe.

Table 1.

Possible relations among intervals, according to Allen’s interval algebra.

SYMBOL	DESCRIPTION	DEFINITION	INVERSE
=	α and q span the same text	x = x′ ∧ y = y′
<, >	α is completely to the left (right) of q	y < x′	x > y′
m, mi	α meets (is met by) q	y = x′	y′ = x
d, di	α is during q (vice versa)	x > x′ ∧ y < y′	x′ > x ∧ y′ < y
s, si	α starts q (q starts α)	x = x′ ∧ y < y′	x = x′ ∧ y > y′
f, fi	α finishes q (q finishes α)	x′ < x ∧ y = y′	x′ > x ∧ y = y′
o, oi	α overlaps q (is overlapped by)	x < x′ < y < y′	x′ < x < y′ < y

Note: In our notation, α and q are intervals, x, x′ are the start positions, and y, y′ are the end positions.

Figure 2.

Allen’s interval algebra. In our notation, a and q are intervals, x, x′ are the start positions, and y, y′ are the end positions. In typical applications, we are given a query interval q to find from a collection of intervals (many α’s) those that satisfy certain relation with q.

Box 1. Common natural language processing steps.

Common Natural Language Processing Steps

Tokenization automatically decides where words in a sentence begin and end. Part -of-speech (POS)tagging assigns a part-of-speech tag for each word in the sentence (eg, VBD for “underwent” in thesentence in Fig. 1). Sentence parsing is the process of assigning a syntactic structure to a sentence(eg, the constituency or dependency structure obtained by Stanford Parser). Phrase chunking refers togrouping multiple words into a phrase (eg, the noun phrase of “Beth Israel Deaconess Medical Center” in Fig. 1). The results from tokenization, POS tagging and sentence parsing can provide features forrecognizing typed concepts (concept recognition), negations and uncertainty of concepts (assertionrecognition), semantic relations between concepts (relation recognition).

Stabbing-interval queries and stabbing-point queries are typically solved by using a data structure called an interval tree.²¹ It is known that the stabbing-point query has an optimal structure in both the internal memory model (in which the cost of an algorithm depends on the total number of accesses to memory locations) and the external memory model (in which different levels of a memory hierarchy are characterized by different accessing costs).²² A related problem formulation is the stabbing-max point query, in which each interval is associa ted with a priority score and the task is to retrieve the interval containing the query point and having the maximum priority. There are also near optimal²³ and optimal²⁴ structures for stabbing-max point queries in the internal memory model. Let n be the total number of intervals and k be the number of reported intervals. Under the big O notation that gives an upper bound for a function to within a constant factor,²⁵ there are structures that support O(log n + k)-time stabbing-interval queries on the overlap relation. However, among all the 13 relations in Allen’s interval algebra, there are relations on which a stabbing-interval query is hard to achieve O(log n + k) time.

In the rest of this paper, we first describe a baseline interval tree, requiring O(log n) update time and O(n) space, which runs a stabbing-interval query in O(log n + k) time on the overlap relation and runs stabbing-max point query in O(log² n) time. We then describe Allen’s interval algebra and explain why certain relations are hard. “Interval tree with embedded secondary tournament trees” and “Interval tree with large fan-out base tree” sections recapitulate two linear space interval trees, one with near logarithmic time²³ and the other with logarithmic time²⁴ on stabbing-max query. “Solve Allen’s interval algebra in logarithmic time” section proposes efficient stabbing-interval queries on hard Allen relations, based on modifications of interval trees in the study by Agarwal et al.²⁴ and query reformulations. We then review interval management in the external memory model and higher dimensions. We conclude our paper with suggestions for future work and a discussion.

Basic Interval Tree

A centered interval tree IT₀ with secondary data structures can be defined as follows. The set S of intervals is stored in a balanced binary tree T_p, in which interval end points are stored in leaves. The T_p starts in the root r with range σ_r = [–∞, ∞] and repeatedly divides and distributes a node v′s range to its two children v_l and v_r. The dividing point x_v is used as search key for node v. The endpoints in the leaves of the subtree rooted at v fall in its range. The node v is the allocation node for an interval s (s is called v′s associated interval) if x_v ∈ s and x_p(v) ∉ s, where p(v) denotes the parent of v. The set S(v) consists of v′s associated intervals. Two secondary balanced search trees (BSTs) T_l(v) and T_r(v) store left and right endpoints of S(v), respectively. S = Y_v S(v) is the set of all intervals. We refer the reader to Cormen et al.²⁵ for more detail on basic interval tree and its variations. Note that interval tree is related to range tree that holds a list of points. Their difference and connection is beyond the scope of this paper and we refer the reader to the study by Lueker²⁶ for more detail.

In the rest of this paper, we let n be the total number of intervals. When inserting or deleting an interval s = [x, y] to the tree T_p, we first find the lowest common ancestor (lca) u of x and y and then update T_l(u) and T_r(u), taking O(log n) time. Considering possible rotation, an update takes O(log n) amortized time.²⁵ Amortized time is the time required to perform a sequence of operations averaged over all the operations performed.²⁵ It is also clear that stabbing-max query takes O(log² n) time, as the secondary trees of all nodes on the search path of q need to be searched. The data structure takes O(n) space. IT₀ runs stabbing-interval query on the overlap relation as follows. Let s = [x, y] be the query interval. Starting from root, for each node v visited, if x_v ∈[x, y], report all intervals in S(v). If x_v < x, descend to right child v_r of v. If x_v > y, descend to left child v_l of v. The query time is clearly O(log n + k).

Challenges for Stabbing-Interval Queries on Allen’s Interval Algebra

To solve the stabbing-interval query problem under Allen’s interval algebra, the IT₀ that works for general overlap relation will not suffice for some Allen’s relations in that it cannot achieve O(log n + k) query time and O(log n) update time under O(n) space. For example, let the query interval be s = [x,y], for oi query (ie, find s′ such that s′ oi s), the IT₀ will work as follows. At a node v,

• – If x_v < x, then no interval s′ in v or in subtree rooted at v_l satisfy s′ oi s. Search the subtree rooted at v_r.

• – If x_v > y, then interval s′ with x < x′ < y satisfy s′ oi s, no intervals in subtree rooted at v_r satisfy s′ oi s. Search the subtree rooted at v_l for additional s′ such that s′ oi s.

• – If x_v ∈[x, y], we need x′ > x and y′ > y.

We run into problems if x_v ∈[x, y]. For the two constraints, if we search T_l(v) and T_r(v) separately and intersect the result set, then we cannot prevent T_l(v) or T_r(v) from returning more than desired intervals and exceeding the theoretically desirable O(log n + k) query time bound. This is different from the general overlap query, for which all s′ ∈S_v can be returned and the query time is O(log n + k). In fact, the worst case for oi query can be O(log² n), as shown in the next section. It is easy to see that the o query has a worst-case time complexity of O(log² n) too.

However, for the di query, the pruning that works for x_v < x or x_v > y in the oi query will not work, and it is hard to analyze time complexity for this query by such reasoning. We give a tight time complexity analysis in the next section.

Tight Time Complexity Analysis on Solving Allen’s Algebra Using Basic Interval Tree

Despite the nonoptimal performance, solving Allen’s algebra using basic interval tree (IT₀) is appealing in the sense that the implementation is simple. For example, one can use a red–black tree as T_p. As stated in the previous section, it is hard to perform accurate time complexity analysis on stabbing-interval queries with respect to some interval relations. In this section, we use query rewriting to reduce those queries into stabbing-max queries and give a tight time complexity analysis.

For the o query, it can be translated into the following equivalent query, “find all intervals s′ = [x′,y′] such that y ∈ s′ and w(s′) = x′ > x.” In the above notation, w(s′) = x′ > x means that the weight of s′ is x′, and we require that x′ > x. The new query is similar to the stabbing-max query, except for that we report all intervals with priority >x instead of reporting only the maximum priority interval. Note that this does not take extra time to scan the secondary trees in IT₀, so the time complexity is O(log² n). Also note that O(log² n) is not output sensitive time complexity, and this corresponds to the worst-case scenario in the example analysis of the previous section.

Of all Allen relations, three (ie, o, oi, and d) can be reformulated into stabbing-max point queries. The reformulations of the three Allen’s relation queries are presented in Table 2. Thus, all above queries have a time complexity of O(log² n).

Table 2.

Reformulations for stabbing-interval queries on some Allen’s relations.

ALLEN’S RELATION	REFORMULATION
s = [x,y] o s′ = [x′,y′]	y ∈ s′ and w(s′) = x′ > x
s = [x,y] oi s′ = [x′.y′]	x ∈ s′ and w(s′) = y′ > x
s = [x,y] d s′ = [x′,y′]	y ∈ s′ and w(s′) = –x′ > –x

The stabbing-interval queries given interval s on the rest of Allen’s relations are relatively straight forward with stabbing-max reformulation. For s di s′ query, we descend the interval tree with queries x and y in O(log n) time. For all the nodes hanging right off the search path ∏_x for x and hanging left off the search path ∏_y for y, we report all the associated intervals. It remains to check the leaf node of ∏_y for intervals s′ such that s di s′, or equivalently x < x′. The leaf node can be linearly scanned in O(log n) time. Thus, the total query time is O(log n + k).

The s < s′ or s > s′ queries are like s di s′ query, even simpler. For s < s′ query, we follow the search path ∏_y in the interval tree, report all the associated intervals of the nodes hanging right off the path. We scan the leaf of ∏_y in O(log n) time and report intervals whose x′ > y. It is clear that the query takes O(log n + k) time. The analysis is analogous for s < s′ query.

In Allen’s interval algebra, specifically for m, mi, s, si, f, fi, and = , duplicate end points are allowed. We only store one representative of the duplicate end points and keep pointers from the copy to all intervals. We require that the number of representative end points in a leaf node is O(log n).

For s m s′ query, we simply follow the search path ∏_y in O(log n/log log n) time to the leaf and do an O(log n) time linear scan of the end points and report intervals whose left endpoints x′ = y. The overall query time is O(log n). The s mi s′ query is analogous. The queries on the s, si, f, fi, and = relations can all be analyzed in a similar fashion, yielding O(log n + k) query time.

For combined queries, such as <m (< or m) and >mi (> or mi), we can simply perform the individual queries and union the results, the query time is still O(log n + k).

The above asymptotic time complexities are tight, given the IT₀ data structure, except for the d query. To show that O(log² n) time complexity is also tight for the d query, we show that one can rewrite stabbing-max query and reduce it to d query. This can be done by expanding query point q into an interval s = [q, q + δ], where δ is small so that no stored interval endpoints falls into [q, q + δ]. Then, the stabbing-max query can be done by stabbing-intervals s′ such that s d s′ and keeping track of the max priority one. As bookkeeping does not take additional time for stabbing-interval query, if the d query takes less than O(log² n) time, so does the stabbing-max query on IT₀. This contradicts that O(log² n) is tight bound for stabbing-max query on IT₀, hence O(log² n) is a tight bound for the d query given the IT₀.

Interval Tree with Embedded Secondary Tournament Trees

In the next two sections, we describe two augmented interval trees that can be used to efficiently perform stabbing-interval query on hard Allen’s relations. By augmenting secondary trees into tournament trees and embedding them into T_p, Kaplan et al.²³ reduced stabbing-max query time to O(log n) in the worst case, insertions to O(log n) amortized time, and deletions to O(log n log log n) amortized time.

Using tournament tree

A tournament tree is a complete binary tree that can be operated as a min (max) heap.²⁵ The name is coined after the imaginary tournament: every leaf node corresponds to one player and every internal node correspond to the winner of one match. Each node a of the secondary BSTs T_l(v) or T_r(v) uses a tournament tree to maintain the maximum priority of the intervals in its subtree, denoted by m(α). The stabbing-max query can be performed as $ma{x}_q(S)=\underset{v\in {\prod }_{\mathrm{q}}}{\max }ma{x}_q(S(v))$, where ∏_q is the search path of q in T_p and recall that S = ∪_v S(v) is the set of all intervals. We abuse the notation and let max_q (.) denote both the maximum priority and the corresponding interval in a set. By keeping a backtrack pointer, max_q(.) operator also returns the max priority interval. If q < x_v in T_p, all the intervals whose left endpoints are <q will contain q. Thus $ma{x}_q(S(v))=\underset{\alpha \in {\prod }_q^l}{\max }m(\alpha )$, where ${\prod }_q^l$ consists of nodeshanging left off ∏_q, as shown in Figure 3. The case where q > x_v is analogous. This two-step procedure takes O(log² n) time.

Figure 3.

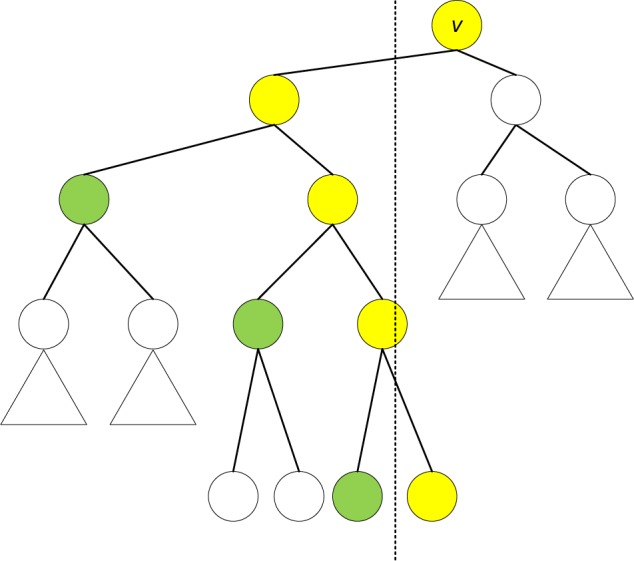
Secondary tournament tree T_l(v). ∏_q is highlighted in yellow, while ${\prod }_q^l$ is highlighted in green.

Embed tournament tree

To embed the tournament trees into T_p, the tree T_l(v) (resp. T_r(v)) is redefined to be a tree isomorphic (hence a bijection δ is defined) to a subtree in T_p whose leaves store the left endpoints of S(v) (resp. the right endpoints of S(v)). Let p^k(v) denote v’s ancestor and recall that δ(.) is the bijection defined by the isomorphism between T_l(v) (resp. T_r(v)) and a sub-tree in T_p. Two additional data structures h_l(v) and h_r(v) are maintained, where h_l (v) = {α | ∃u = p^k(v)st.α ∈ T_l (u) and δ(α) = v} and h_r(v) is symmetrically defined. The h_l(v) and h_r(v) are maintained as max-heaps that have m(α) as the node α’s key. They are of size O(log n) and their maxima are M_l(v) and M_r(v), respectively. By definition, the set of intervals in h_l(v) is the set of intervals associated with v’s ancestors while having left endpoints in the range σ_v. The h_r(v) has symmetric definition. One stops maintaining secondary structures for low-level node v ∈ LL = {v | depth(v) < log n}. Let HL = {v | depth(v) $ log n}, HL has height O(log n – log log n). Denote the improved data structure to be IT₁. As they only maintain a O(log n) secondary structure for each of the Θ(n/log n) nodes, the space complexity of IT₁ is O(n).

Query and update

Let s′ be the interval with an endpoint at the leaf of ∏_q, and let w′ be the priority of s′ (if q ∈ s′, otherwise 0). The stabbing-max query can then be performed by $\underset{q}{\max }(S)=\max (\underset{v\in {\prod }_q^l}{\max }{M}_l(v)$, $\underset{v\in {\prod }_q^r}{\max }{M}_r(v)$,w′, where M_l(v) and M_r(v) are introduced in “Embed tournament tree” section. This is illustrated in Figure 4. We can keep track of the interval achieving max_q(S) by storing backtracking pointers at the roots of h_l(v) and h_r(v). For all v ∈ HL, M_l(v) and M_r(v) now have O(1) access time. For all v ∈ LL, $\underset{v\in {\prod }_q^l,v\in LL}{\max }$ M_l(v) and $\underset{v\in {\prod }_q^l,v\in LL}{\max }$ M_l(v) can be found by a linear scan of O(log n) end points in O(log n) time. Thus, stabbing-max query now runs in O(log n) time.

Figure 4.

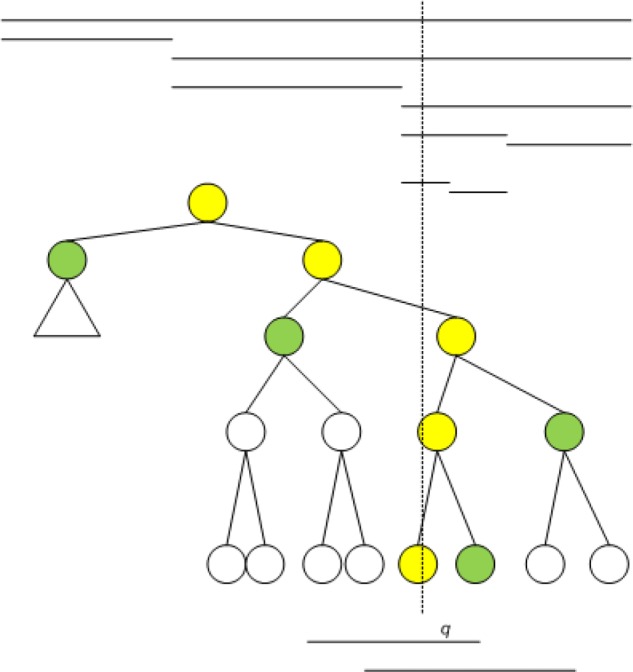
Stabbing-max query in T_p with data structure IT₁. Line segments on top denote range of relative nodes. Line segments at bottom are example intervals of the two nodes hanging right of the search path. The search path ∏_q is highlighted in yellow, the nodes hanging left off ${\prod }_q({\prod }_q^l)$ and hanging right off ${\prod }_q({\prod }_q^r)$ are highlighted in green.

Kaplan et al.²³ showed that insertions and deletions can both be done in O(log n log log n) time. If we only maintain secondary structure for the nodes in the top O(log n – log log n) levels of the tree, amortized time is reduced to O(log n) for insertion but not for deletion. Intuitively, after deletion, all remaining intervals are candidates for the maximum interval, hence O(log log n) time is still required to update each of the O(log n – log log n) secondary structures (under top-only secondary structure maintenance) on a search path in T_p (O(log log n)⋅O(log n – log log n) = O(log n log log n)).

Interval Tree with Large Fan-Out Base Tree

Agarwal et al.²⁴ increased the fan-out of T_p from 2 to $\sqrt{\log n}$, and cut redundant storage at secondary data structure. As a result, their data structure, denoted by IT₂, achieved O(log n) query and update time with O(n) space.

Structure of large fan-out interval tree

The data structure of Agarwal et al.²⁴, denoted by IT₂, consists of n/log n fat leaves, each containing log n consecutive endpoints. The children of a node are stored in a BST that allows O(log log n) search time. For internal node v and its children v_i’s, the range σ_v associated with v is divided into ranges ${\sigma }_{v_i}$ associated with v_i’s (called slabs). The intersecting point of two slabs $x_{v_i}={\sigma }_{v_{i–1}}\cap {\sigma }_{v_i}$ is called a boundary. A multislab is defined as the union of several consecutive slabs $\sigma [i:j]={\cup }_{{{}_l}_{=}{}_i}^i{\sigma }_{v_i}$. Let f be the fan-out of the tree, then there are $\left(\begin{array}{c}f\\ 2\end{array}\right)=O(\log n)$ multislabs in v. The node v is called the allocation node for an interval s if there exists an i, such that its children’s dividing points are in the interval $\left(x_{v_i}\in s\right)$, but its parent’s dividing point is not in the interval (x_p(v) ∉ s) (similar to the binary case IT₁). The main tree T_p is maintained as a weight-balanced B-tree where split instead of rotation is used to balance the tree.

There are $O\left(\frac{n}{\log n}\right)/\sqrt{\log n}=O\left(n/{\log }^{\frac{3}{2}}n\right)$ internal nodes in T_p. Any interval s = [x,y] such that $x\in {\sigma }_{v_i}$ and $y\in {\sigma }_{v_j}$ can be divided into the left interval $s^l=[x,x_{v_{i+1}}]$, the middle interval $s^m=[x_{v_{i+1}},x_{v_j}]$ (degenerated if j = i + 1) and the right interval $s^r=[x_{v_j},y]$. In the sequel, we define v’s left interval set as $s_v^l={\cup }_{s\in S_v}{s}^l$ and T_p’s left interval set as $s^l={\cup }_{v\in T_p}{s}_v^l$. We also define $S_v^m$, S^m, $S_v^r$, S^r analogously.

Secondary data structures M_v, L_v, and R_v are maintained for $S_v^m$, $S_v^l$, and $S_v^r$ respectively, as explained below. The structure M_v consists of O(log n) max-heaps storing multislabs (formerly $H_v^{ij}=\{[x,y]|x\in {\sigma }_{v_i},x\in {\sigma }_{v_j},[x,y]\in S_v\})$ and $O\left[\sqrt{\log n}\right]$ max-heaps storing slabs (formerly $H_v^l=\{\max (H^{ij})|i\le l\le j\}$). Overall, M_v uses $O\left(\left|S_v^m\right|+{\log }^{\frac{3}{2}}n\right)$ space. As there are $O\left(n/{\log }^{\frac{3}{2}}n\right)$ internal nodes and hence this many M_v’s, they use O(n) space in total. The secondary structure L_v stores a high-level tournament tree for intervals in the set ${\cup }_{u=p^k(v)}{S}_v^l$ of intervals that have left end points in the node v’s slab σ_v. More precisely, let ψ(u = p^k(v), v) be the left intervals (s^l′s) with allocation node being v’s ancestor and with left end point being in the slab σ_v. Let ψ(p^k(v), v) be the maximum priority interval in the set ψ(u = p^k(v),v). Also, define the set Φ(v) = ∪_k≥2 ψ(u = p^k(v),v) to be the left intervals associated with v’s indirect ancestors and the interval ϕ(v) = max_k$2ψ(p^k(v),v) to be the max priority interval in the set. Only ϕ(v)’s are actually stored. Let L_v be the tournament tree used to store ϕ(v)’s, it has height and search time O(log log n). In order to update L_v, two additional structures are maintained, a BST T_u for the internal node u and a max-heap H_v for the node v. Roughly speaking, T_u corresponds to T_l(u) in IT₁, except that a small tournament tree for each leaf is maintained to enable O(log log n) search time at leaves. In addition, the operator for retrieving the max priority and the associated interval, namely, m(α) in IT₁, has been extended into ψ(u, v) here. For the node v and all its indirect ancestors (ie, ∀u = p_k(v), k ≥ 2), we denote H_v to be a max-heap used to store ψ(u, v). By definition, ϕ(v) is at the top of the max-heap H_v. It is easy to see that the space complexity of tournament trees is ${\sum }_{u\in T_p}\left|T_u\right|\text{=}O(n)$ and the space complexity of max-heaps is ${\sum }_{v\in T_p}\left|H_v\right|\text{=}O(n)$ because each Ψ(u, v) is stored once and each left interval is stored in exactly one tournament tree associated with a leaf node of T_p. The total space requirement is thus O(n). The secondary data structure R_v for $S_v^r$ can be analogously defined and analyzed.

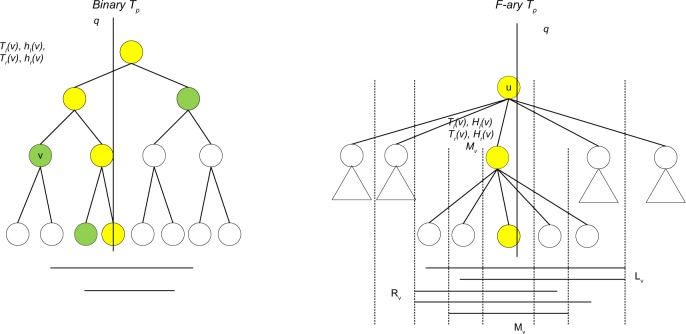
Binary versus N-ary primary tree

Figure 5 shows the differences and connections between the IT₁ and IT₂ on the primary tree (T_p) level. Compared with IT₁’s secondary structure, IT₂ has extra max-heaps M_v due to large fan-out. In the tree IT₁, the intervals containing a position q can be extracted using the operators h_l(.) and h_r(.) on the nodes hanging left and right off the search path. In IT₂, the intervals containing a position q can be extracted using the data structures L_v’s, R_v’s, and M_v’s on the search path. Nevertheless, together with intervals containing position q and having end points in the leaf nodes of the search path ∏_q, they form a partition (off-path and on-path) of all relevant intervals. This extra layer of complexity is necessary for IT₂ to be used for stabbing-interval queries on hard Allen’s relations as enumerated in “Tight time complexity analysis on solving Allen’s algebra using basic interval tree” section.

Figure 5.

The difference between the IT₁ (on left) and IT₂ (on right). Yellow indicates search path.

The major difference is that IT₂ has larger fan-out $\sqrt{\log n}$; therefore, the height of T_p has been reduced to O(log n/log log n), allowing query and update time to be O(log log n) for secondary data structures and O(log n) in total.

Another difference is that IT₂ has smaller heap size for max-heaps H_v’s than h_l(v) in IT₁, this is why IT₂ has O(n) space requirement even without top-only secondary structures maintenance as in IT₁.

Query and update

For stabbing-max query, the number of secondary structures for nodes on the search path ∏_q that need to be searched can be up to O(log n/log log n); thus, we need query time on secondary structures to be O(log log n) so that the total search time is O(log n). On the other hand, update (insertion and deletion) is more complicated as rebalancing the tree may be necessary. An analysis on secondary data structures is first presented, followed by an intuitive explanation on update in primary tree is presented below.

Recall the definition of the S as the union of left, middle, and right intervals (ie, S = S^l ∪ S^m ∪ S^r), thus max(S) = max(max S^l, max S^m, max S^r), the stabbing-max query can be performed in a divide-and-conquer fashion. In addition, the interval collections S^l, S^m, and S^r can be separately queried and updated.

Stabbing-max point query on intervals in S^m requires querying all O(log n/log log n) internal nodes on the search path and reporting the maximum. Stabbing-max query for intervals in $S_v^m$ associated with an internal node v requires finding a slab of σ_v containing q (this takes O(log log n) time) and then retrieving the max interval from the max-heap of this slab (this takes O(1) time). Total time is O(log n). The update on S^m requires searching down the balanced B-tree T_p in O(log n) time and updating on $S_v^m$ for identified node v. The update on $S_v^m$ requires updating a multislab max-heap in O(log n) time and then updating $O\left(\sqrt{\log n}\right)$ affected slab max-heaps (each taking O(log log n) time) in O(log n) time (as $O\left(\sqrt{\log n}\cdot \log \log n\right)$ ≤ O(log n)). Thus, the total update time is O(log n).

The stabbing-max point query on the left intervals in S^l requires following the search path ∏_q in T_p and querying for each node on the path $\left(v\in {\prod }_q\right)$ the left intervals associated with it (the secondary tournament tree L_v introduced in “Structure of large fan-out interval tree” section). Each tournament tree has O(log log n) search time, hence all O(log n/log log n) nodes on the search path ∏_q require O(log n) search time. The fat leaves can be searched in O(log n) time by linear scan. Thus, the total search time is O(log n). When updating L_v, for v’s ancestor u (ie, u = p^k(v)), we need to update the BST T_u. The ancestors of v need to be traversed bottom up along a path of length O(log n/log log n). Each T_u of size O(log n) needs to be updated in O(log log n) time. Thus, the update on T_u takes O(log n) time in total for all ancestors of v. Similarly, updating H_v also takes O(log n) time. Finally, updating L_v itself takes O(log log n) time. Hence, the total update time is O(log n). The stabbing-max point query and update times on S^r have analogous analysis.

The stabbing-max point query time and update time are O(log n) on all data structures S^l, S^m, and S^r; hence, the query and update time on S are O(log n).

Solve Allen’s Interval Algebra in Logarithmic Time

In this section, we solve the problem of efficient stabbing-interval queries on all Allen’s relations. That is, the query has O(log n + k) worst-case time, the update has O(log n) amortized time and the space requirement is linear. We extend the data structure IT₂ to build two interval trees, $I{T}_2^{le}$ and $I{T}_2^{re}$, using values of left end points and right end points as priorities, respectively. The new data structure is called IT₂’.

For the o query, as explained in “Tight time complexity analysis on solving Allen’s algebra using basic interval tree” section, it can be translated into the following equivalent query, “find all intervals s′ = [x′,y′] such that y ∈s′ and w(s′) = x′ > x.” The new query is similar to the stabbing-max query, except for that we report all intervals with priority larger than x instead of reporting only the maximum priority interval. This change requires some modifications to the IT₂ querying algorithm.

For the middle interval set S^m, we still query all O(log n/log log n) internal nodes on the search path. Query for the middle interval set for a node $v\left(S_v^m\right)$ requires first finding a slab σ_v containing q (in O(log log n) time). For the max-heap corresponding to σ_v’s slabs, we traverse all nodes in the heap having key > x. For each traversed node v′ in σ_v’s slab max-heap, we traverse all nodes having key > x in the multislab max-heap whose max is stored in v′. For each traversed node in the multislab max-heap, we report the corresponding interval. For each valid interval (eg, s′ such that s o s′), we traversed one node in the slab max-heap and one node in the multislab max-heap; thus, the query time on the middle interval set S^m is $O\left(\frac{\log n}{\log \log n}\cdot \log \log n+k\right)=O(\log n+k)$.

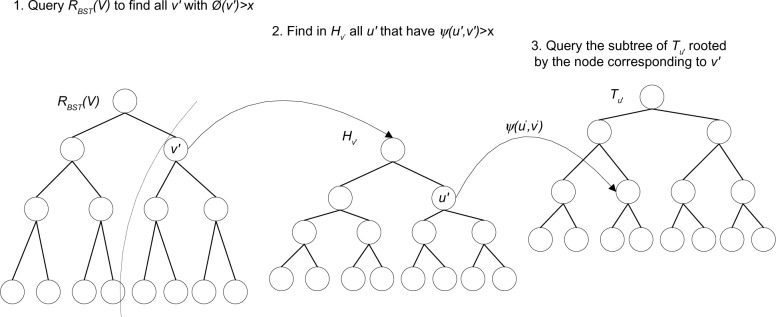
For the right interval set S^r, we still follow all O(log n/log log n) internal nodes on the search path. As shown in Figure 6, let R_BST(v) be the BST associated with a node v hanging right off the search path ∏_y. We query the BST R_BST(v) to find all v′ with ∏(v′) > x. Note that the newly introduced R_BST(v) is a BST version of the tournament tree R_v. The BST R_BST(v) allows identifying all node v′’s in O(log log n) time without adding asymptotic update time to the overall O(log n) bound. For each such v′, we find in the max-heap H_v′ all u′ that have (u′,v′) > x where ψ(u′,v′) denotes the maximum priority of the left intervals associated with the nodes u′ and v′ (see “Structure of large fan-out interval tree” section for details). For each such u′, we have a modified tournament tree T_u, such that every internal node stores the max and second-max priorities of the subtree. Note that this does not add asymptotic update overhead. We also modify the leaf tournament tree of T_u, in the same way. We query the subtree of T_u, rooted by the node corresponding to v′. If both max and second-max priorities are larger than x, we descend the tree, otherwise, we simply return the interval corresponding to max priority without descending the tree. This approach guards against unnecessary descending for paths that contain only one valid interval. Note that there are at most four nodes in all R_BST (v), H_v, and T_u, which are visited for every reported interval. Thus, for all v hanging right off the search path, the total query time is O(log n + k). It remains to search the leaf of the search path ∏_y and combine the results. A linear scan takes O(log n) time for O(log n) leaf nodes. Thus, the total query time for the right interval set S^r is O(log n + k).

Figure 6.

Search procedure on S^r for the o query given query interval s. R_BST(v) is the BST associated with a node v in S^r.

The query on S^l can be performed in a similar fashion, with a run time of O(log n + k). Therefore, the total query time on S is O(log n + k) for the o query given interval s.

For stabbing-interval queries on hard Allen relations, we now have a tool to reformulate them into a stabbing-max point queries. As presented in Table 2, of all Allen relations, three hard relations (o, oi, and d) can be reformulated into stabbing-max point queries.

Note that it may require building a new interval tree IT₂′ for each new query reformulation. This does not look too bad when we only need three query reformulations. Moreover, we can also pack the three secondary data structures into one interval tree IT₂′ and share the primary tree T_p. The stabbing-interval queries given interval s on the rest of Allen’s relations are relatively straightforward. For these relations, query procedures and (tight) time analysis are the same as in “Tight time complexity analysis on solving Allen’s algebra using basic interval tree” section.

Next, we show that the above logarithmic time complexities for the o, oi, and d queries are tight. We use query rewrite and proof by contradiction. For example, given a query point q, we can rewrite the stabbing-max query to the o query by stabbing s′:s = [–∞, q] o s′ and keeping track of s′ with max priority. Bookkeeping here takes O(k) time. When O(k) ≤ O(log n), stabbing-max query can be performed in less than O(log n) time, contradicting the fact that O(log n) is a tight bound on stabbing-max query given the IT₂′ data structure. We summarize the time complexity analysis of various interval trees examined so far in Table 3.

Table 3.

Comparison of operation time between multiple interval tree data structures.

	IT0	IT1	IT2	IT2′
Allen’s interval algebra queries	O(log2 n + k) for o, oi and d	NA	NA	O(log n + k)
Stabbing-max query	NA	O(log n)	O(log n)	NA
Insertion	O(log n)	O(log n)*	O(log n)*	O(log n)*
Deletion	O(log n)	O(log n log log n)*	O(log n)*	O(log n)*

Note:

^*Amortized time.

Generalize Into External Memory Structure and Higher Dimensions

Throughout the time complexity analysis in previous sections, we have followed the theoretic algorithm analysis convention in assuming an internal memory model where the cost of an algorithm depends on the total number of accesses to memory locations. However, in practice, one needs to take into account the memory hierarchy to better characterize different access speeds at different levels. External memory interval management is often used in database community, such as in spatial queries²⁷ and temporal aggregates,²⁸ for massive dataset. Arge and Vitter²² proposed an optimal data structure that performs stabbing-point query in O(log_B n + k/B) I/Os and update in O(log_B n) I/Os in worst case with a space requirement of O(n/B) disk blocks. With their proposed data structure, the IT₂ structure for stabbing-max query under internal model can be directly generalized to give an external memory logarithmic I/O structure for stabbing-max query, as pointed out by Agarwal et al.²⁴

It is conceivable that one needs to add more than one dimension to order the annotations. For example, one might need to store relation annotation between two or more medical concepts.²⁹ Stand-off annotation for relations can be indexed by multiple independent intervals. This exposes the necessity to generalize our algorithm to higher dimensions. Under internal memory model, generalization of the one-dimensional optimal structure to higher dimensions can be easily made by using segment trees.³⁰ This scales up the space, the update time, and the query time by a factor of O(log n) per dimension. Generalization under external memory model also has a scaling-up factor of O(log n) per dimension for space, update, and query time.³¹

Conclusion

Stand-off annotations are becoming ubiquitous for biomedical NLP, due to the advantages in computing and storing such annotations compared to in-line annotations. Stand-off annotations can be abstracted into interval representations. Efficient querying, updating, and storing stand-off annotations require carefully designed interval trees. The problem is even more challenging when we want to achieve theoretical lower bound on stabbing-interval query time for all possible relations in Allen’s interval algebra. We reviewed three types of interval trees (IT₀, IT₁, and IT₂) with increasingly complex secondary data structures. We modified and extended IT₂ into IT₂′ so that it can be used to attain desirable lower time bound for stabbing-interval queries with all Allen’s relations. At the same time, the update time is logarithmic and space complexity is linear, both at theoretical lower bound. Thus, IT₂′ is a generic and fundamental data structure and algorithmic tool that enables efficient queries, updates, and storage of stand-off annotations for NLP on EMRs.