Playing the role of weak clique property in link prediction: A friend recommendation model

Abstract

An important fact in studying link prediction is that the structural properties of networks have significant impacts on the performance of algorithms. Therefore, how to improve the performance of link prediction with the aid of structural properties of networks is an essential problem. By analyzing many real networks, we find a typical structural property: nodes are preferentially linked to the nodes with the weak clique structure (abbreviated as PWCS to simplify descriptions). Based on this PWCS phenomenon, we propose a local friend recommendation (FR) index to facilitate link prediction. Our experiments show that the performance of FR index is better than some famous local similarity indices, such as Common Neighbor (CN) index, Adamic-Adar (AA) index and Resource Allocation (RA) index. We then explain why PWCS can give rise to the better performance of FR index in link prediction. Finally, a mixed friend recommendation index (labelled MFR) is proposed by utilizing the PWCS phenomenon, which further improves the accuracy of link prediction.

The research of link prediction mainly focuses on forecasting potential relations between nonadjacent nodes, including the prediction of the unknown links or the further nodes¹. Owing to the wide range of applications of link prediction, such as recommending friends in online social networks², exploring protein-to-protein interactions³, reconstructing airline network⁴, and boosting e-commerce scales, study on link prediction has attracted much attention recently⁵,⁶,⁷,⁸. The probabilistic model and machine learning were mainly introduced in link prediction. The notion of probabilistic link prediction and path analysis using Markov chains method were first proposed and evaluated in ref. 9, and then Markov chains method was further studied in adaptive web sites¹⁰; in ref. 11, Popescul et al. studied the application of statistical relational learning to link prediction in the domain of scientific literature citations.

However, the mentioned methods for link prediction were mainly based on attributes of nodes. It is known that the structure of the network is easier to be obtained than the attributes of nodes, as a result, the network-structure-based link prediction have attracted increasing attention. Along this line, Liben-Nowell et al. developed approaches to link prediction based on measures for analyzing the “proximity” of nodes in a network¹². Since hierarchical structure commonly exists in the food webs, biochemical networks, social networks and so forth, a link prediction method based on the knowledge of hierarchical structure was investigated in ref. 13, and they found that such a method can provide an accurate performance. Zhou et al. proposed a local similarity index—Resource Allocation (RA) index to predict the missing links, and their findings indicate that RA index has the best performance of link prediction¹⁴. Given that many networks are sparse and very huge, Liu et al. presented a local random walk method to solve the problem of missing link prediction, and which can give competitively good prediction or even better prediction than other random-walk-based methods while has a lower computational complexity¹⁵. In view of the local community features in many networks, Cannistraci et al. proposed an efficient computational framework called local community paradigm to calculate the link similarity between pairs of nodes³. Liu et al. designed a parameter-free local blocking predictor to detect missing links in given networks via local link density calculations, which performs better than the traditional local indices with the same time complexity¹⁶.

Since the structural properties of networks have significant effects on the performance of algorithms in link predictions, some methods have been proposed by making use of the structural properties of networks. Such as the algorithms by playing the roles of hierarchical structure¹³, clustering¹⁷, weak ties⁵, local community paradigm³ or multiple structural features¹⁸. However, current advances in incorporating structural properties into link prediction are still not enough. In this paper, by investigating the local structural properties in many real networks, we find a typical phenomenon: nodes are preferentially linked to the nodes with weak clique structure (PWCS). Then based on the observed phenomenon, a friend recommendation (FR) index is proposed. In this method, when a node j introduces one of his friends to a node i, he does not introduce their common neighbors to node i. Our results show that the performance of FR index is significantly better than CN, AA and RA indices since FR index can make good use of the PWCS in networks. At last, to further play the role of PWCS, we define a mixed friend recommendation (MFR) method, leading to the better performance of link prediction.

Results

Typical PWCS phenomenon

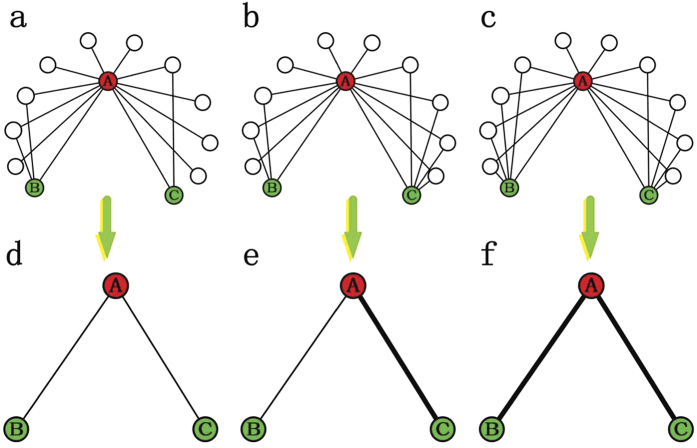
To check whether the PWCS phenomenon commonly exists in real networks, we divide all links into common links or strong-tie links by judging whether the number of common neighbors between the two endpoints is larger than a threshold β. Take Fig. 1 as an example, when we choose β = 3, the links {A, B} and {A, C} in Fig. 1(a–c) can be correspondingly degenerated to the sketches in Fig. 1(d–f), where common links and strong-tie links are marked by thin links and thick links, respectively.

Figure 1. Degenerating the upper sketches into the lower cases by judging whether two links {A, B} and {A, C} are strong-tie link or common link.

Here we assume that if the number of common neighbors between A and B (or A and C) is larger than β = 3, then the link is strong-tie link; otherwise, the link is common link in the opposite case. Thin lines and thick lines in (d–f) are the common links and the strong-tie links, respectively.

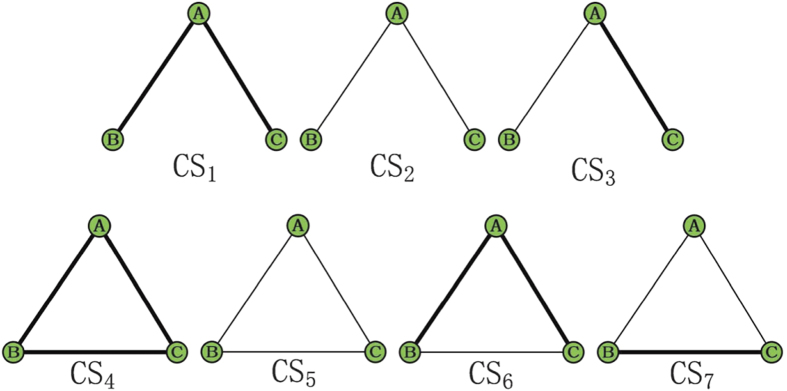
In this paper, the threshold β is chosen such that the number of common links and the number of strong-tie links are approximately equal in each network. Once the value of β is fixed, there are seven possible configurations for the connected subgraphs with 3 nodes (i.e., triples¹⁹), all the seven configurations are plotted in Fig. 2, where the thick links and thin lines denote strong-tie links and common links, respectively. Let N_i, i = 1, ···, 7 be the number of CS_i, i = 1, ···, 7 (each CS represents a configuration in Fig. 2) in networks. If {A, B} and {A, C} are strong-tie links, then the probability of node B connecting node C is defined as²⁰:

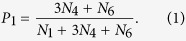Eq. (1) can be understood in the following ways: from Fig. 2, one can find that only CS₁, CS₄ and CS₆ have at least two strong-tie links, but CS₁ does not form a triangle. There are three possible combinations of two strong-tie links for CS₄, that is, {A, B} -{A, C}, {B, A}- {B, C} and {C, A}- {C, B}. However, there only exists one possible case ({A, B} -{A, C}) for CS₆. As a result, N₄ and N₆ in Eq. (1) are multiplied by 3 and 1, respectively. The following Eq. (2) and Eq. (3) can be explained in a similar way.

Figure 2. Seven possible configurations of connected subgraphs with three nodes.

Thin lines and thick lines are the common links and the strong-tie links, respectively.

If only one of links {A, B} or {A, C} is strong-tie link, then the probability of node B connecting node C is defined as:

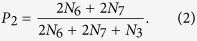If neither of them is strong-tie link, then the probability of node B connecting node C is:

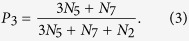We define a subgraph with n nodes be a weak clique if the number of links among the n nodes is rather dense, which is an extended definition of n-clique where all pairs of nodes are connected. Next, by calculating the probability of node B connecting C, we can judge whether the phenomenon that nodes are preferentially linked to the nodes with weak clique structure (i.e., PWCS phenomenon) commonly exists in a network. We say that the PWCS phenomenon exists in the network if P₁ > P₂ and P₁ > P₃. Moreover, we say that the PWCS phenomenon is significant if P₁ > P₂ > P₃, otherwise, the PWCS phenomenon is weak when P₁ > P₃ ≥ P₂.

Table 1 reports the values of P₁, P₂ and P₃ in the twelve real networks (labelled as RN) and the values on the corresponding null networks (labelled NN) are also comparatively shown. One can find that P₁ > P₂ and P₁ > P₃ in eleven networks except for Metabolic network (P₁ < P₃, emphasized by underlines). However, in the corresponding null networks, P₁ ≈ P₂ ≈ P₃. Also, for C. celegans, FWEW, FWFW, Power, Router and PB networks, where P₁ > P₂ > P₃. As a result, we can state that PWCS phenomenon is more significant in these six networks. Meanwhile, the values of P₁, P₂ and P₃ for other 15 real networks are summarized in table. S1 in Supplementary Information, and where P₁ > P₂ and P₁ > P₃ for all of these real networks, which again validates that PWCS is a typical phenomenon.

Table 1. The values of P ₁, P ₂ and P ₃ in 12 real networks (RN) and the corresponding null networks (NN) are reported.

Network	Network	P1	P2	P3
C. elegans	RN	0.2351	0.1654	0.1519
	NN	0.0483	0.0485	0.0487
NS	RN	0.9292	0.2392	0.5970
	NN	0	0.002	0.0022
FWEW	RN	0.5998	0.4832	0.2504
	NN	0.3691	0.3737	0.3761
FWFW	RN	0.4191	0.3532	0.1230
	NN	0.2545	0.2555	0.2554
USAir	RN	0.7008	0.1519	0.2355
	NN	0.0385	0.0387	0.0390
Jazz	RN	0.6902	0.3968	0.4503
	NN	0.14	0.1406	0.141
Tap	RN	0.7862	0.2969	0.3673
	NN	0.0069	0.0073	0.0073
Power	RN	0.2781	0.0854	0.0686
	NN	0	0	0
Metabolic	RN	0.1630	0.0760	0.1643
	NN	0.02	0.0198	0.0198
Yeast	RN	0.5945	0.1498	0.1530
	NN	0.0043	0.0042	0.0042
Router	RN	0.1992	0.0254	0.0022
	NN	0	0	0
PB	RN	0.3998	0.1247	0.0855
	NN	0.0224	0.0224	0.0224

Results in NN are marked in Italic. Results in networks with significant PWCS, i.e., P₁ > P₂ > P₃ are shown in blue color, and results in Metabolic are marked by red color due to its specificity.

Friend recommendation model

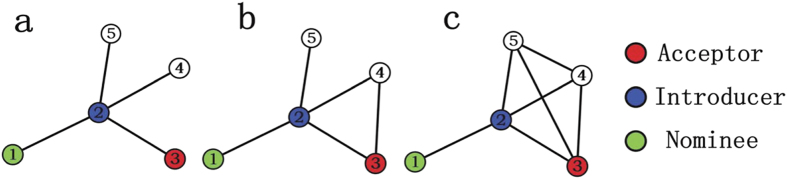
Given that PWCS phenomenon commonly exists in real networks, whether can we design an effective link prediction method based on this phenomenon. Considering the cases in Fig. 3, where node 3 asks its neighbor node 2 to introduce a friend to it. Since the number of common neighbors between node 2 and node 3 in Fig. 3(c) is larger than that of in Fig. 3(b) and is further larger than that of in Fig. 3(a), in other words, the strength of link {2, 3} in Fig. 3(c) is the strongest. According to PWCS phenomenon, the probability (labelled by f₁₂₃) of node 1 (call nominee, green color) being introduced to node 3 (call acceptor, red color) by node 2 (call introducer, blue color) in Fig. 3(c) should be larger than that of in Fig. 3(b), and then further larger than that of in Fig. 3(a). To reflect the mentioned fact, we define f_ilj be the probability of i being introduced to j by their common neighbor l, which is given as:

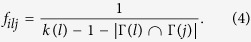Based on the definition in Eq. (4), the values of f₁₂₃ in Fig. 3(a–c) are 1/3, 1/2 and 1, respectively. That is to say, the probability f_ilj can reflect the PWCS phenomenon in real networks.

Figure 3. The role of PWCS on the probability of f₁₂₃.

Node 2 (blue color, call introducer) wants to introduce node 1 (green color, call nominee) to node 3 (red color, call acceptor). The number common neighbor between node 2 and node 3 in (a–c) is 0, 1 and 2, respectively. According to Eq. (4), one has (a) f₁₂₃ = 1/3; (b) f₁₂₃ = 1/2; (c) f₁₂₃ = 1. Namely, the probability of node 1 being introduced to node 3 in (c) is larger than (b) and is further larger than in (a).

More importantly, Eq. (4) addresses two important facts: first, since node l will not introduce node j to j, as a result, 1 is subtracted in denominator of Eq. (4); second, in social communication, when a friend introduces one of his friends to me, he should introduce his friends but excluding the common friends. Therefore, the common neighbors set between j and l (i.e., Γ(l) ∩ Γ(j)) should be subtracted in denominator of Eq. (4). For instance, in Fig. 3(c), node 2 will not introduce node 3 to node 3, and nodes 4 and 5 should not be introduced to node 3.

Let f_ij be the weight of node i being introduced to node j (we use weight rather than probability since f_ij may larger than 1), which is written as:

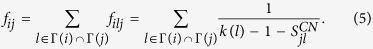Here the value of f_ij increases with the number of common neighbors, and 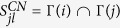is CN index between node j and node l [see the definition of CN index in Methods section].

With the above preparations, the similarity index 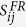for a pair of nodes i and j is defined as

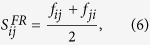which guarantees .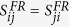

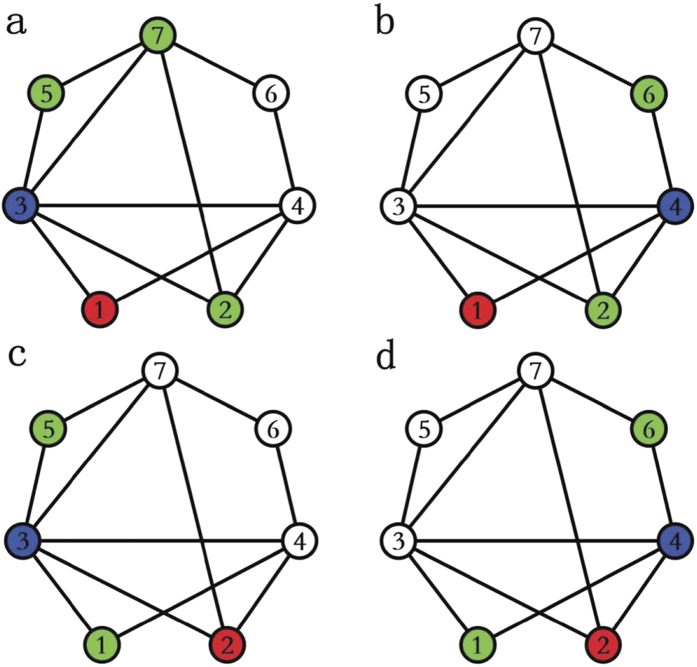
The sketches in Fig. 4 are given to show how to calculate the similarity between node 1 and node 2 based on the FR index. Also, the red, blue and green nodes denote the acceptors, introducers and nominees, respectively. Node 2 can be introduced to node 1 by node 3 (see Fig. 4(a)) or node 4 (see Fig. 4(b)). When node 3 is an introducer (see Fig. 4(a)), who will introduce nodes 2, 5 and 7 (green color) to node 1 with equal probability, but excludes node 4, i.e., f₂₃₁ = 1/3. Similarly, when node 4 is an introducer (see Fig. 1(b)), who just introduces nodes 2 and 6 (green color) to node 1 with equal probability, but excludes node 3, i.e., f₂₄₁ = 1/2. Therefore, the weight f₂₁ = 1/3 + 1/2 = 5/6. Likely, from Fig. 5(c,d), the value of f₁₂ = 1/2 + 1/2 = 1. Therefore, the FR similarity index is .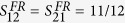

Figure 4. Calculation of the similarity.

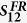between node 1 and node 2. Nodes 1 and 2 can be introduced by their common neighbors 3 and 4. (a) Node 3 introduces his friends to node 1. Only neighbor nodes 2, 5, 7 can be introduced to node 1 but excludes node 4, since node 4 has been a friend of node 1. Thus, the probability of node 3 introducing node 2 to node 1 is: f₂₃₁ = 1/3; (b) node 2 is introduced to node 1 by node 4, here only nodes 2 and 6 can be introduced to node 1. As a result, the probability f₂₄₁ = 1/2; (c) node 1 is introduced to node 2 by node 3, here only nodes 1 and 5 can be introduced to node 1. As a result, the probability f₁₃₂ = 1/2; (d) node 1 is introduced to node 2 by node 4, here only nodes 1 and 6 can be introduced to node 1. As a result, the probability f₁₄₂ = 1/2. We have f₂₁ = 1/3 + 1/2 by combing (a,b), and f₁₂ = 1/2 + 1/2 by combing (c,d). So the FR similarity index is .

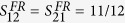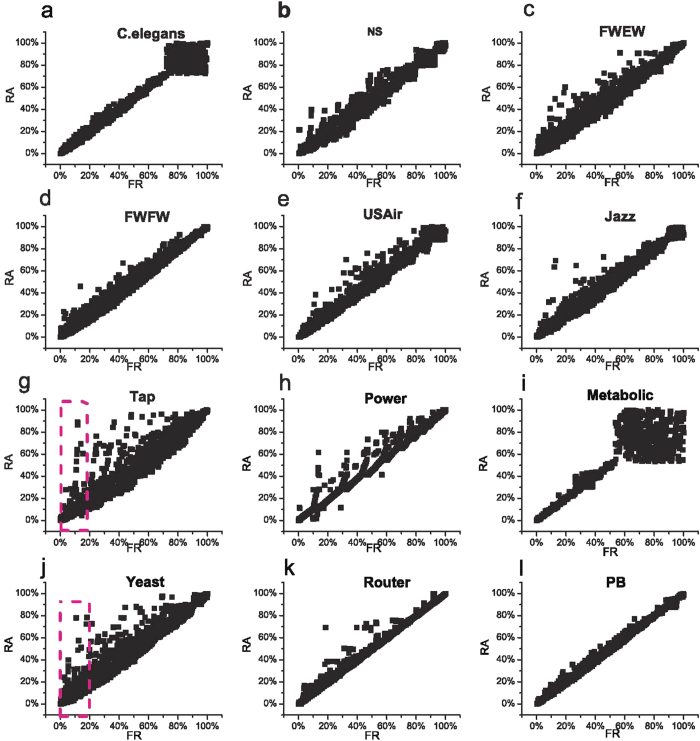
Figure 5. The correlation of ranking values between FR index and RA index based on Precision.

The percentage values in x-axis and y-axis are the top percentage ranking values of FR index and RA index, respectively. The regions marked by pink dash boundary in subfigures (g,j) correspond to the cases in which some links have higher FR ranking values but have lower RA ranking values.

Combing Eqs (4), (5) and (6), the advantages of FR index can be summarized as: (1) similar to many local similarity indices, the similarity between a pair of nodes increases with the number of common neighbors; (2) like AA index and RA index, FR index depresses the contribution of the high-degree common neighbors; (3) most importantly, FR index can make use of the PWCS phenomenon in many real networks; (4) FR index has higher resolution than other local similarity indices. For instance, the similarities 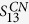, 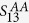[see the definition of Eq. (14) in Methods section] and 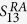[see the definition of Eq. (15) in Methods section] are the same in Fig. 3(a–c). Yet, the value of 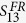in Fig. 3(c) is larger than Fig. 3(b), and is further larger than Fig. 3(a).

Performance of the FR model

The comparison of FR index with CN, AA and RA indices in twelve networks is summarized in Table 2. As shown in Table 2, FR index in general outperforms the other three indices in link prediction, regardless of AUC or Precision [see definitions in Methods section]. The highest accuracy in each line is emphasized in bold. Furthermore, Precision as a function of L in six networks is presented in Fig. S1 in Supplementary Information, which also confirms the good performance of FR index.

Table 2. Comparison of S ^FR with S ^CN , S ^AA and S ^RA in 12 networks, including AUC and Precision.

Network	Metric	CN	AA	RA	FR
C. elegans	AUC	0.8501	0.8663	0.8701	0.8756
	Precision	0.1306	0.1374	0.1315	0.1504
NS	AUC	0.9913	0.9916	0.9917	0.9916
	Precision	0.8707	0.9731	0.9712	0.9832
FWEW	AUC	0.6868	0.6939	0.7017	0.7595
	Precision	0.1415	0.1551	0.1664	0.2763
FWFW	AUC	0.6074	0.6097	0.6142	0.6623
	Precision	0.0837	0.0853	0.082	0.1798
USAir	AUC	0.9558	0.9676	0.9736	0.9752
	Precision	0.606	0.6218	0.6337	0.6586
Jazz	AUC	0.9563	0.963	0.9717	0.9714
	Precision	0.8247	0.8401	0.8192	0.8406
Tap	AUC	0.9538	0.9545	0.9548	0.955
	Precision	0.7594	0.78	0.7818	0.8659
Power	AUC	0.6249	0.6251	0.6245	0.6248
	Precision	0.1215	0.0952	0.0801	0.1275
Metabolic	AUC	0.9248	0.9565	0.9612	0.9623
	Precision	0.2026	0.2579	0.3219	0.3302
Yeast	AUC	0.9158	0.9161	0.9167	0.9172
	Precision	0.6821	0.6958	0.4988	0.8041
Router	AUC	0.6519	0.6523	0.652	0.6519
	Precision	0.1144	0.1104	0.0881	0.0592
PB	AUC	0.9239	0.9275	0.9286	0.9309
	Precision	0.4205	0.3782	0.2509	0.3454

The highest value in each row is marked in bold.

Moreover, the correlation of ranking values between FR index and RA index is given in Fig. 5, where the percentage values in x or y axis is the top percentage of ranking values based on Precision. As a result, a small percentage value means a higher ranking value. Figure 5 indicates that a high RA ranking value of links gives rise to a high FR ranking value. However, a high FR ranking value of links may induce a low RA ranking value of links. Take Tap and Yeast networks as examples, based on FR index, some links have higher ranking values, however their corresponding ranking values based on RA index may be very small (see the regions marked by pink dash boundary in Fig. 5(g,j)).

By analyzing a typical case in the Yeast network (see Fig. 6), where two nodes A and B are the neighbors of introducer C (in fact, there has a link connecting A and B in the Yeast network). Since links {A, C} and {B, C} are strong-tie links. When using FR index, the similarity 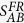is rather large, which can predict the existence of link {A, B}. However, for RA index, since the large degree value of introducer C, the similarity 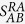is very small, such an existing link {A, B} cannot be accurately predicted by RA index.

Figure 6. A typical case in the Yeast network is considered to emphasize the difference between FR index and RA index, where nodes A, B and C are the node 1175, 421 and 205 in the Yeast network.

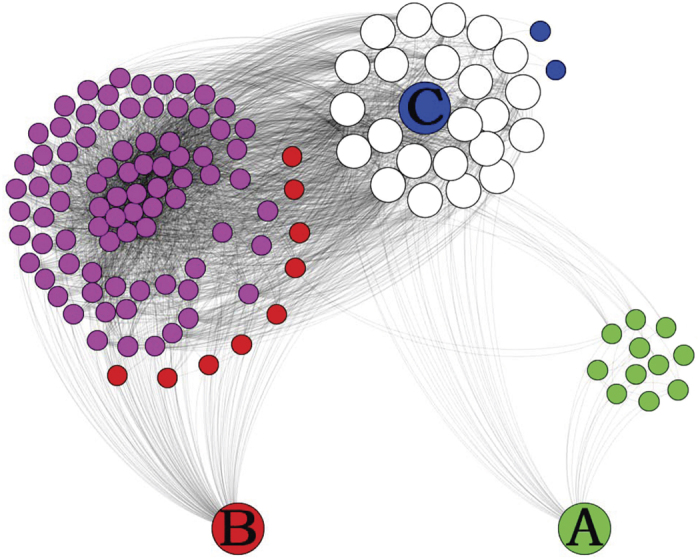
Two links {A, C} and {B, C} share a common endpoint C, and both of them are strong-tie links. Therefore, the similarity 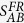is rather large. However, when using RA index, the ranking number of 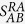is very low owing to the large degree value of node C, causing the failure of RA index in predicting such an existing link. Red nodes, green nodes and blue nodes are the neighbors of A, B and C (including themselves), respectively. Purple nodes are the common neighbors of A and C; white nodes are the common neighbors of A, B and C.

Role of PWCS

We have validated that the FR index based on PWCS phenomenon can improve the performance of link prediction, and the reasons were also analyzed. Here we want to know how the strength of PWCS affects the performance of link prediction. For this purpose, we propose a generalized friend recommendation (GFR) index, which is given as:

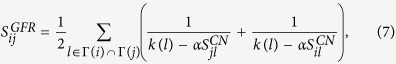where parameter 0 ≤ α ≤ 1 is used to uncover the role of PWCS in link prediction. As α = 0, Eq. (7) returns to RA index, that is, 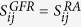. When α = 1, the difference between FR method and GFR method is the absence of 1 in the denominators of Eq. (7), therefore, we can simply view GFR index is the same as FR index when α = 1. As a result, with the increasing of α from zero to one, S^SFR index can comprehensively investigate the role of PWCS in the RA index and FR index.

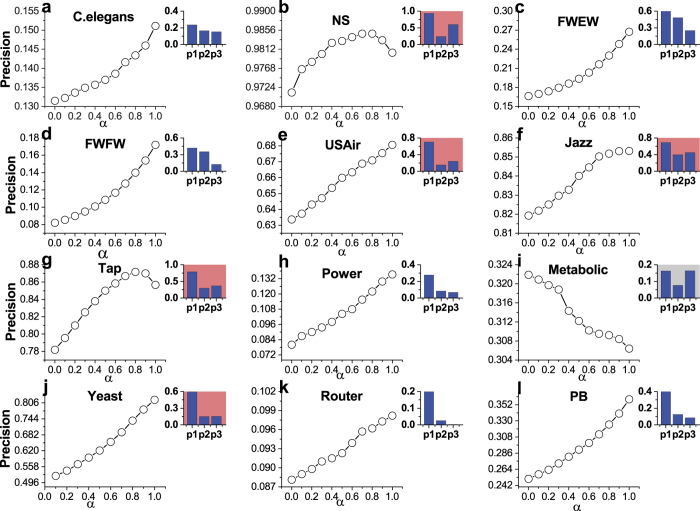
The effect of α on the Precision in all twelve networks is plotted in Fig. 7. As illustrated in Fig. 7, several interesting phenomena and meaningful conclusions can be summarized: First, except for Metabolic network, the Precision for the case of α > 0 is far larger than the case of α = 0 (i.e., RA index) in all other 11 networks. Since P₁ > P₂ and P₁ > P₃ in these 11 networks, which indicates that PWCS phenomenon in networks can ensure the higher accuracy of FR index (i.e., α = 1) in link prediction; Second, Metabolic network has non-PWCS phenomenon since P₁ > P₂ and P₂ < P₃, and Fig. 7(i) suggests that Precision decreases with the value of α. In other words, FR index is invalid in network with non-PWCS phenomenon, which again emphasizes the importance of PWCS in link prediction; At last, by systematically comparing the subfigures in Fig. 7, one can see that, when the networks with weak PWCS P₁ > P₃ ≥ P₂ (i.e., the insets are light red background, see Fig. 7(b,e–g,j)), Precision increases with α at first and then decreases when α is further increased (except Fig. 7(e)). However, when P₁ > P₂ > P₃ (i.e., networks with significant PWCS, the insets are white background, see Fig. 7(a,c,d,h,k,l)), Precision always increases with the value of α even when α = 1.0.

Figure 7. Effects of α in Eq. (8) on Precision are plotted in 12 networks.

Inset in each subfigure is to show the values of P₁, P₂ and P₃. The background of inset is white color when P₁ > P₂ > P₃; the background of inset is light red color when P₁ > P₃ ≥ P₂. Otherwise, the background of inset for Metabolic is gray color.

In view of this observation, we can conjecture the role of PWCS can be further explored when the PWCS phenomenon is significant. Unfortunately, the maximal value α in Eq. (7) is one, the denominator may be negative if α > 1. So we design a new index to further explore the role of significant PWCS.

Since Eq. (7) can be rewritten as

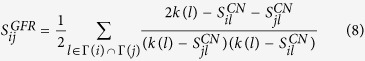when α = 1. To further play the role of PWCS, another similarity index, called strong friend recommendation (labelled as SFR) index, is given in following

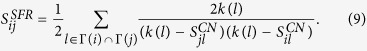Combing Eq. (8) with Eq. (9), we can find that two subtrahends 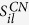and 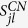in the numerator of Eq. (8) are removed. So Eq. (9) can better play the role of PWCS.

We conjecture that the performance of SFR index is better than GFR index when P₁ > P₂ > P₃ (i.e., significant PWCS), and worse than that of GFR index when P₁ < P₂ and P₁ < P₃ (i.e., non-PWCS). However, it is difficult to distinguish which one has better performance when P₁ > P₃ ≥ P₂ (i.e., weak PWCS). As presented in Table 3, Precision in 12 networks validates our conjecture.

Table 3. The comparison of Precision between SFR index and GFR index (α = 1) in 12 networks.

Index	P1 > P2 > P3
	C. elegans	FWEW	FWFW	Power	Router	PB
GFR (α = 1)	0.1511	0.2676	0.172	0.1354	0.0982	0.3595
SFR	0.1577	0.2912	0.2057	0.1658	0.112	0.4353
	P1 > P3 ≥ P2					P1 < P3, P2 < P3
Index	NS	USAir	Jazz	Tap	Yeast	Metabolic
GFR (α = 1)	0.9804	0.6807	0.8532	0.8568	0.8178	0.3064
SFR	0.9744	0.6866	0.8739	0.8485	0.8587	0.2912

The results suggest that the accuracy of link prediction can be further improved by SFR index when the networks have significant PWCS. The highest value in each case is marked as bold.

Synthesizing the above results, we can find that the ranking of P₁, P₂ and P₃ has a determinant effect on the performance of the proposed index. Inspired by this clue, we may design a universal indicator to do link prediction based on the values of P₁, P₂ and P₃ in different networks. To this end, we design a mixed friend recommendation (labelled MFR) index:

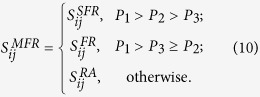Table 4 lists the results of MFR index and FR index in 7 networks (since MFR index is the same to FR index when P₁ > P₃ ≥ P₂, in this case, it is unnecessary to compare the two indices). The results in Table 4 indicate that, compared with FR index, MFR index can further improve the accuracy of link prediction.

Table 4. Comparison of Precision between FR index and MFR index in 7 networks.

Metric	Index	C.elegans	FWEW	FWFW	Power	Router	PB	Metabolic
AUC	FR	0.8756	0.7595	0.6623	0.6248	0.6519	0.9309	0.9623
	MFR	0.8771	0.7771	0.6878	0.6247	0.6516	0.9314	0.9612
Precision	FR	0.1504	0.2763	0.1798	0.1275	0.0592	0.3454	0.3302
	MFR	0.1577	0.2912	0.2057	0.1658	0.112	0.4353	0.3219

The highest value in each case is given in bold.

Conclusion

In summary, by analyzing the structural properties in real networks, we have found that there exists a typical phenomenon: nodes are preferentially linked to the nodes with weak clique structure. Then we have proposed a friend recommendation model to better predict the missing links based on the observed phenomenon. Through the detailed analysis and experimental results, we have shown that FR index has several typical characteristics: First, FR index is based on the information of common neighbors, which is a local similarity index. Thus, the algorithm is simple and has low complexity; Second, the common neighbors with small degrees have greater contributions than the common neighbors with larger degrees; Third, FR index can take full advantage of the PWCS phenomenon, and so forth.

Furthermore, we have also proposed an SFR index to further improve the accuracy of link prediction when networks have significant PWCS phenomenon. At last, by judging whether the networks have significant PWCS, weak PWCS or non-PWCS phenomenon, we have also proposed a mixed friend recommendation index which can increase the accuracy of link prediction in different networks. In this work, we mainly applied FR index to unweighed and undirected networks, and how to generalize our FR index to weighted²¹,²² or directed networks²³ is our further purpose.

Methods

Link prediction algorithm

Considering an undirected and unweighed network G(V, E), where V is the set of nodes and E is the set of links. The multiple links and self-connections are not allowed. For a network with size N, the universal set of all possible links, is denoted by U, consisting of 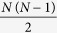pairs of links. For each pair of nodes, x, y ∈ V, we assign a score, S_xy, according to a defined similarity measure. Higher score means higher similarity between x and y, and vice versa. Since G is undirected, the score is supposed to be symmetry, that is S_xy = S_yx. All the nonexistent links are sorted in a descending order according to their scores, and the links at the top are most likely to exist¹⁴,¹⁵. To test the prediction accuracy of each index, we adopt the approach used in ref. 14. The link set E is randomly divided into two sets E = E^T ∪ E^P with E^T ∩ E^P = ∅. Where set E^T is the training set and is supposed to be known information, and E^P is the testing set for the purpose of testing and no information therein is allowed to be used for prediction. As in previous literatures, the training set E^T always contains 90% of links in this work, and the remaining 10% of links constitute the testing set.

Evaluation metrics

Two standard metrics are used to quantify the accuracy of prediction algorithms: area under the receiver operating characteristic curve (AUC) and Precision⁵.

Area under curve (AUC) can be interpreted as the probability that a randomly chosen missing link (a link in E^P) is given a higher score than a randomly chosen nonexistent link (a link in U − E^P). When implementing, among n independent comparisons, if there are n′ times the missing link having a higher score and n′′ times they are of the same score, AUC can be read as follow⁵:

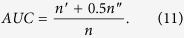If all the scores generated from independent and identical distribution, the accuracy should be about 0.5. Therefore, the degree to which the accuracy exceeds 0.5 indicates how much the algorithm performs better than pure chance.

Precision is the ratio of the number of missing links predicted correctly within those top-L ranked links to L, and L = 100 in this paper [Precision as a function of L is compared in Fig. S1 in Supplementary Information, which confirms that our FR index is better than other three indices for a large range of L]. If m links are correctly predicted, then Precision can be calculated as⁵:

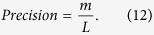Benchmarks

We mainly compare three local similarity indices for link prediction, including (1) Common Neighbors(CN)²⁴; (2) Adamic-Adar (AA) index²⁵; (3) Resource Allocation (RA) index¹⁴. Among which, CN index is the simplest index. AA index and RA index have the similar form, and they both depress the contribution of the high-degree common neighbors, however, Zhou et al. have shown that the performance of RA index is generally better than AA index.

Let Γ(i) be the neighbor set of node i, |.| be the cardinality of the set, and k(i) be the degree of node i. Then CN index, AA index and RA index are defined as

CN index

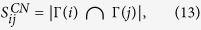AA index

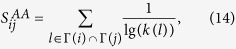RA index

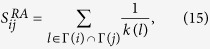respectively.

Data Set

In this paper, we choose twelve representative networks drawn from disparate fields: including: (1) C. elegans-The neural network of the nematode worm C. elegans²⁶; (2) NS-A coauthorship network of scientists working on network theory and experiment²⁷; (3) FWEW-A 66 component budget of the carbon exchanges occurring during the wet and dry seasons in the graminoid ecosystem of South Florid²⁸; (4) FWFW-A food web in Florida Bay during the rainy season²⁸; (5) USAir-The US Air transportation system⁵; (6) Jazz-A collaboration network of jazz musicians²⁹; (7) TAP-yeast protein-protein binding network generated by tandem affinity purification experiments³⁰; (8) Power-An electrical power grid of the western US²⁶; (9) Metabolic-A metabolic network of C. elegans³¹; (10) Yeast-A protein-protein interaction network in budding yeast³²; (11) Router-A symmetrized snapshot of the structure of the Internet at the level of autonomous systems³³; (12) PB-A network of the US political blogs³⁴. Topological features of these networks are summarized in Table 5.

Table 5. The basic topological features of twelve example networks.

Network	N	M	C	r	H
C. elegans	297	2148	0.308	−0.163	1.801
NS	1589	2742	0.791	0.462	2.011
FWEW	69	880	0.552	−0.298	1.275
FWFW	128	2075	0.335	−0.112	1.237
USAir	332	2126	0.749	−0.208	3.464
Jazz	198	2742	0.633	0.02	1.395
Tap	1373	6833	0.557	0.579	1.644
Power	4941	6594	0.107	0.003	1.45
Metabolic	453	2025	0.655	−0.226	4.485
Yeast	2375	11693	0.388	0.454	3,476
Router	5022	6258	0.033	−0.138	5.503
PB	1222	16724	0.36	−0.221	2.971

N and M are the total numbers of nodes and links, respectively. C and r are clustering coefficient and assortative coefficient, respectively. H is the degree heterogeneity, defined as 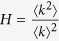, where 〈k〉 denotes the average degree¹⁹.

Additional Information

How to cite this article: Ma, C. et al. Playing the role of weak clique property in link prediction: A friend recommendation model. Sci. Rep. 6, 30098; doi: 10.1038/srep30098 (2016).