Abstract
Ion channels are the “building blocks” of the excitation process in excitable tissues. Despite advances in determining their molecular structure, understanding the relationship between channel protein structure and electrical excitation remains a challenge. The Kv7.1 potassium channel is an important determinant of the cardiac action potential and its adaptation to rate changes. It is subject to beta adrenergic regulation, and many mutations in the channel protein are associated with the arrhythmic long QT syndrome. In this theoretical study, we use a novel computational approach to simulate the conformational changes that Kv7.1 undergoes during activation gating and compute the resulting electrophysiologic function in terms of single-channel and macroscopic currents. We generated all possible conformations of the S4–S5 linker that couples the S3–S4 complex (voltage sensor domain, VSD) to the pore, and all associated conformations of VSD and the pore (S6). Analysis of these conformations revealed that VSD-to-pore mechanical coupling during activation gating involves outward translation of the voltage sensor, accompanied by a translation away from the pore and clockwise twist. These motions cause pore opening by moving the S4–S5 linker upward and away from the pore, providing space for the S6 tails to move away from each other. Single channel records, computed from the simulated motion trajectories during gating, have stochastic properties similar to experimentally recorded traces. Macroscopic current through an ensemble of channels displays two key properties of Kv7.1: an initial delay of activation and fast inactivation. The simulations suggest a molecular mechanism for fast inactivation; a large twist of the VSD following its outward translation results in movement of the base of the S4–S5 linker toward the pore, eliminating open pore conformations to cause inactivation.
Keywords: computational biology, ion-channel gating, mechanical coupling, cardiac electrophysiology, cardiac arrhythmia
1 Introduction
Membrane ion channels are the fundamental molecular “building blocks” of the excitation process in excitable tissues. In the cardiovascular system, ion-channels generate the heart rhythm and underlie synchronous cardiac contraction, control modulation of these processes by the autonomic nervous system, and play a central role in regulation of vascular tone and blood pressure. Much of cardiovascular pathology involves alterations in the molecular structure of ion-channels caused by mutations, remodeling by disease processes and/or environmental factors, or by unwanted effects of drugs. Ion channels are also potential targets for therapeutic interventions by drug binding or molecular modification. Therefore, understanding the relationship between the molecular structure of an ion-channel protein and electrical excitation is an objective of critical importance, which remains a difficult challenge. Of special interest in the context of this focused issue of Progress in Biophysics & Molecular Biology is the biophysical basis of cardiac ion-channel gating, which underlies the cardiac action potential and ultimately heart rhythm. Briefly, in response to changes in membrane voltage, the S3–S4 complex (voltage sensor domain, VSD) moves and its movement is transformed to pore opening or closing through mechanical coupling. Background information about voltage dependent channel gating is provided in Online Supplement 1. It is not possible to unveil the exact mechanism of mechanical coupling experimentally, as it is not possible to monitor the structural changes of the ion-channel protein during gating. However, experimental data have provided important information and insight about conformational changes of the ion-channel protein during gating that can provide the basis for simulating the gating movement. Previously, we developed a general computational-biology approach for simulating the structural dynamics of an ion channel protein during gating and the resulting function in terms of channel current (Nekouzadeh and Rudy, 2011a). This new method is based on physical principles and designed to simulate the large and gradual intra-molecular motions of macromolecules over the milliseconds time scale of gating and other biophysical processes that determine the multi-scale physiological system behavior (Gjuvsland et al., 2013). It differs from the conventional Molecular Dynamics (MD) computational approach, which simulates atomic-level motions over much shorter time scales. The current through ion-channels is controlled by the stochastic pattern of channel opening and closing (Nekouzadeh and Rudy, 2007a; Nekouzadeh and Rudy, 2007b), which is a consequence of conformational alterations within the ion-channel protein (Broomand and Elinder, 2008; Doyle, 2004; Gandhi et al., 2003; Gulbis and Doyle, 2004; Jiang et al., 2003; Long et al., 2005b; Nekouzadeh and Rudy, 2011a; Nishizawa and Nishizawa, 2009; Perozo, 2002; Perozo et al., 1999; Posson and Selvin, 2008; Ruta et al., 2005; Sansom and Weinstein, 2000; Silva et al., 2009; Tieleman et al., 2001).
The physiological function of an ion channel is determined by its large and gradual intramolecular motions, which occur on a time scale of milliseconds. The MD approach (Adcock and McCammon, 2006) simulates the small high frequency vibrations of all atoms in a molecule and therefore requires a very short time step (order of femto seconds) in simulations. Consequently, MD can simulate only several microseconds of protein motion. Large scale motions within an ion-channel protein require a coherent motion of a large group of atoms (a relatively rare event), which occurs over a much longer time scale (by several orders of magnitude) than the time scale of atomic vibrations. Additionally, MD simulates the motion trajectory for a randomly chosen initial state of the atoms, assuming one of infinite possibilities for their locations and velocities (the initial state) and simulating the subsequent state from their current state. Based on experimental recordings of single ion-channel currents, the large and gradual gating motions of an ion-channel protein are highly stochastic. Therefore, a single motion trajectory simulated by MD cannot be representative of all trajectories and conformational changes during ion-channel gating.
Traditionally, transmembrane ionic currents have been computed using the Hodgkin – Huxley (HH) formulation (Hodgkin and Huxley, 1952) or the Markovian approach (Clancy and Rudy, 1999; Rudy, 2012; Silva and Rudy, 2005). The HH approach computes the macroscopic current through a large ensemble of channels; it is phenomenological and does not relate function to structure. In the HH approach, relationships between gating processes (e.g., inactivation occurs only from an activated state) cannot be expressed because they are assumed independent of each other. Markov models specify channel states; however, these are abstract kinetic states, not representative of structural conformations of the ion channel protein. A Markov scheme is not a unique model of the channel function and different schemes that fit the same experimental data can be interpreted differently in terms of underlying mechanisms. The approach used here aims to overcome these limitations and relate explicitly molecular structure and channel function. It computes the ionic current directly from the dynamics of the ion-channel molecular structure, independent of an assumed Markov model.
We apply the computational approach to study gating aspects of the cardiac Kv7.1 potassium channel (also called KCNQ1). The choice of KCNQ1 (alpha subunit of cardiac IKs) is motivated by the important role of IKs in the cardiovascular system; in particular, its role in cardiac action potential repolarization and in cardiac arrhythmias. Specifically: 1. IKs plays a crucial role in action potential adaptation to rate changes (Bauer et al., 1999; Silva and Rudy, 2005; Viswanathan et al., 1999), 2. Mutations in KCNQ1 cause the most common arrhythmic long QT syndrome LQT1 (Aidery et al., 2012; Crotti et al., 2007; Splawski et al., 2000; Tsuji et al., 2007; Winbo et al., 2014) 3. IKs is subject to beta adrenergic regulation (Bosch et al., 2002; Kass and Moss, 2003; Sampson et al., 2008) and 4. Several mutations in IKs are associated with atrial fibrillation, the most common cardiac arrhythmia (Chen et al., 2003; Das et al., 2009; Hong et al., 2005). From a structural modeling perspective, KCNQ1 is highly homologous to Kv1.2 for which crystal structure is available (Silva et al., 2009). Starting from the simulated KCNQ1 molecular structure, we characterize the mechanical coupling between the VSD and pore domains during gating. We also compute the macroscopic current and suggest a novel molecular mechanism for its early inactivation.
2 Methods
The modeling method employed here is based on the governing equations we derived previously (Nekouzadeh and Rudy, 2011a). It is fundamentally different from the MD approach; the differences can be summarized as follows. The secondary structures of the protein (helices and beta sheets) are usually maintained during the large and gradual motions associated with channel gating (except for some low amplitude, high frequency atomic vibrations of their atoms). Therefore, we consider the elements of secondary structure as rigid bodies with 3 translational and 3 rotational degrees of freedom for both position and velocity. The limited number of degrees of freedom implies that only a limited number of energy terms vary during the motion and need to be computed. Consequently, the energy computation is faster by orders of magnitude than in the MD approach. Details of energy computation are provided in Online Supplement 2. For the chosen degrees of freedom we simulate the average molecular motion, defined as the motion averaged over a time window much larger than the time scale of the atomic vibrations, yet much smaller than the time scale of the large and gradual intra-molecular motions (Nekouzadeh and Rudy, 2011a). This removes the limitation of a very small time step (required in the MD approaches) and makes it possible to simulate the motion over much longer durations, as necessary for simulating ion-channel gating. In this approach, the high frequency vibrations of atoms are not simulated explicitly; however, their effect on the average motion is considered by including a stochastic term in the derivation of the governing equations for the motion of the rigid segments (Nekouzadeh and Rudy, 2011a). Unlike MD, which simulates a single motion trajectory, the approach used here simulates the temporal probability distribution of a protein in the entire configuration space of the chosen degrees of freedom. This makes it possible to relate macroscopic functional properties of the protein, such as the macroscopic current in the case of ion-channels, to its dynamic structure. Note that a macroscopic property of the protein is the average of that property over a large ensemble of proteins in different conformations. Obtaining the ensemble average requires knowing the probability distribution among all possible conformations and cannot be derived from one single motion trajectory.
The simulations presented here required further developments to the general approach in reference (Nekouzadeh and Rudy, 2011a). Instead of only 2 degrees of freedom (d.o.f.), we considered 20 d.o.f. that describe experimentally known large scale conformational changes of the Kv7.1 ion channel protein. We then examined all conformations within the entire configuration space of these d.o.f. For this purpose, computer codes were developed for simulating the conformational changes, closing intra-protein connecting loops, calculating energy, performing side chain repacking and determining steric clashes. The d.o.f. were sampled at a spatial resolution of 1 angstrom. The entire configuration space consisted of 9.3×1016 conformations, but the majority was eliminated due to steric clashes or other structural constraints, leaving about one million acceptable conformations. We developed a recursive algorithm that starts with one acceptable conformation and extracts all possible conformations within the entire configuration space by examining the neighboring conformations of the acceptable conformations; with this algorithm there is no need to examine all the conformations in the configuration space (9.3×1016 conformations) to determine all acceptable conformations. The set of acceptable conformations was used to study the voltage sensor motion and its mechanical coupling to the pore domain during ion-channel gating.
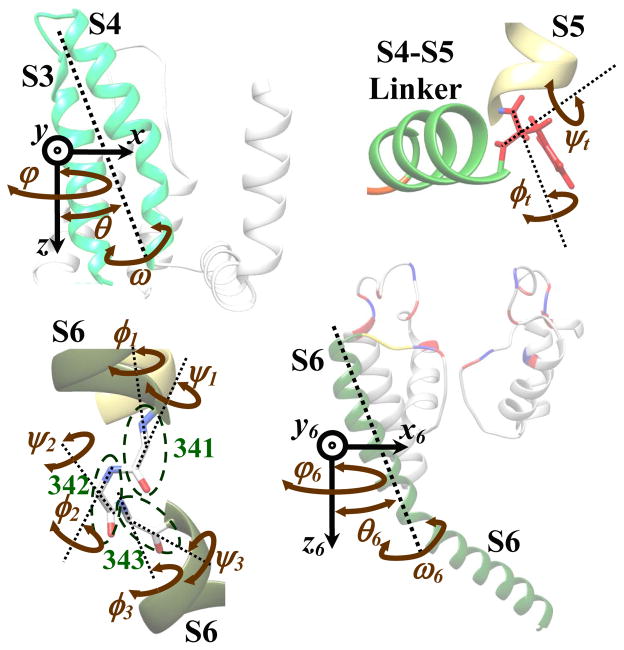
A 3D structure of the Kv7.1 channel (termed the initial structure in this paper) was derived previously(Silva et al., 2009) based on homology to Kv1.2 with a known crystal structure in the open state (Long et al., 2005a). We based our structural analysis on the assumption that the S4 motion is transferred to pore opening by moving the S4–S5 linker away from the pore region and providing space for the S6 tails to move away from each other (Broomand and Elinder, 2008; Doyle, 2004; Gandhi et al., 2003; Jiang et al., 2003; Labro et al., 2008; Long et al., 2005b; Nishizawa and Nishizawa, 2009; Perozo et al., 1999; Posson and Selvin, 2008; Seebohm et al., 2006; Tombola et al., 2005). We assumed that S3 moves with S4 (similar to Kv2.1 and KvAP; see Discussion). The motion of the S3–S4 complex was fully characterized by 3 translational and 3 rotational d.o.f. (Figure 1A). Backbone atoms of S1, S2, S5 and the P-Loop segments were assumed stationary during the gating process. Different S4–S5 linker conformations were generated by different probable combinations of φ and ψ angles (2 d.o.f.) of the residue that connects the S4–S5 linker to S5 (Figure 1B). S6 was allowed to bend along residues 341 to 343 with 6 d.o.f. (Figure 1C) and to move rigidly with 3 translational and 3 rotational d.o.f. (Figure 1D). These d.o.f. were chosen to be consistent with the experimentally determined conformational changes within the Kv7.1 and other potassium channels (Online Supplement 1). Including additional d.o.f., in particular for the rigid-body motion of the P-Loop, and the rotation and bending of S5, can reveal more details about the conformational changes during gating. However, this increases the size of the problem, and therefore of the simulation time, by several orders of magnitude. In the present simulations, we limited the d.o.f. to the known significant motions, thereby reaching an acceptable compromise between accuracy and simulation time. To reduce the complexity, the four S6 segments were assumed to be symmetric. The C-terminus (beyond Phe 364) was not considered in the simulations. To include any possible constraints imposed by the C-terminus on the S6 motion, the motion of Phe 364 was limited to 12 angstroms. The pore was considered closed if its minimum diameter was less than 8 Å (otherwise open). The moving segments of the structure were assumed to be connected to the stationary segments by 4 loops: a three residue loop (319–321) on top of S6, a one residue turn (258) between the S4–S5 linker and S5, a three residue loop (244–246) between the S4–S5 linker and S4 and a 22 residue loop (174–195) between S2 and S3. The last loop is sufficiently long that it can connect S2 and S3 for any conformation. The connection between the S4–S5 linker and S5 was maintained when generating various S4–S5 linker conformations. Closure of the two remaining loops was verified for each generated conformation using the previously developed approach (Nekouzadeh and Rudy, 2011b). A VSD conformation was considered an activated state if it could be connected to a number of open pore conformations via one or more S4–S5 linker positions. Channel opening was considered to be cooperative (pore opening requires all four VSDs to be activated). A side chain repacking algorithm was used to eliminate side chain clashes. In computing the energy of the conformations, we included only those terms which varied with the considered degrees of freedom. The electrostatic energy was calculated implicitly for any given membrane potential.
Figure 1.
The degrees of freedom (d.o.f.) used to simulate the large and gradual conformational changes within the Kv7.1 channel during gating. A) 3 translational and 3 rotational degrees of freedom for the rigid body motion of the VSD (S3–S4 complex). B) 2 dihedral angles for the conformational changes of the S4–S5 linker. C) 6 dihedral angles for the bending of the S6 segment. D) 3 translational and 3 rotational d.o.f. for the rigid body motion of S6.
Additional discussion of the methodology used in this study is provided in Online Supplement 2. Description of the general computational approach, the governing equations and mathematical derivations are provided in reference (Nekouzadeh and Rudy, 2011a).
3 Results
3.1 Probable Conformations and Mechanical Coupling
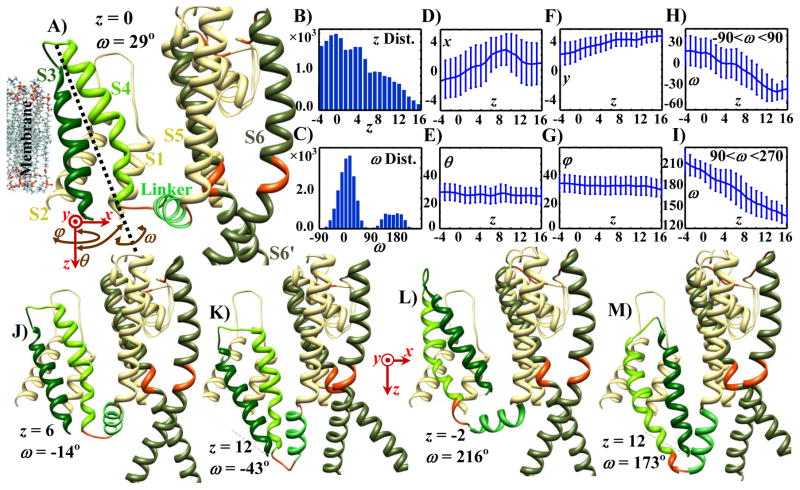
Figure 2A shows one VSD of the Kv7.1 structure together with two of its pore - domain S6 segments. The 3 translational (red arrows) and 3 rotational (brown arrows) degrees of freedom for the VSD are shown on the lower left. With a grid size of 1 Å, there are about 27,000 possible conformations of the VSD. The distribution of these possible conformations shows that the VSD can move inward (+z direction) for up to 16 Å (Figure 2B). The ω angle is distributed (normal distribution) about two central angles: 0° and 180° (Figure 2C), defining two conformational subgroups. The first group (group 1) is distributed about ω=0°, where S4 is facing the pore domain (Figures 2A, 2J and 2K). In the second group, about ω=180° (group 2), S3 is facing the pore domain (Figures 2L and 2M). Inward and outward z translations of S4 during gating have been verified experimentally by probing different residues from inside and outside of the cell (Ruta et al., 2005; Wu et al., 2010a). We used the generated pool of probable conformations to determine how other degrees of freedom vary during gating. The z translation was used as an indicator of the gating path and the distribution of other d.o.f was computed at every z along the path. Figures 2D to 2I show the average and standard deviation of the d.o.f among conformations with the same z. Figures 2D and 2F show that, on average, the inward motion of the VSD (+z translation) is accompanied by about 4 Å translation toward the pore (+x translation), and about 2 Å translation orthogonal to the z-x plane (+y translation). Throughout the z translation, the ω angle maintains a double distribution, though the number of conformations decreases more in group 1 compared with group 2 as the VSD moves inward (Supplement Figure S1). Figures 2H and 2I (and Supplement Figure S1) show that the inward motion of the VSD is accompanied by a significant counterclockwise rotation (viewed from the outside) of up to 60° within each group. Tilting (θ rotation) and revolving (φ rotation) vary over a limited range and, on average, do not show any significant change with respect to z translation (Figures 2E and 2G). In the initial structure, the VSD is in an outward position and the S4–S5 linker is positioned horizontally; the S6 tail is located under the S4–S5 linker (more inward). In this configuration the channel is considered open, because some possible S6 conformations are forming open pores. Hyperpolarizing the membrane potential applies an inward-directed electrostatic force on the VSD, which facilitates its inward translation. As shown in Figure 2, because of structural constraints this inward translation is accompanied by translation toward the pore domain and a counterclockwise twist. Figures 2A, 2J and 2K show locations of three randomly selected S3–S4 conformations (from group 1) at three z translations. The inward (+z) translation of the VSD causes an inward rotation of the S4–S5 linker (about its base, defined as its connecting point to S5); while the counterclockwise twist of the VSD causes a counterclockwise rotation of the S4–S5 linker (when viewed from the outside). Both rotations of the S4–S5 linker limit the space for the S6 tails (of the same and neighboring subunits) and eliminate S6 conformations that are farther from the center of the pore. This implies a reduction in the number of open pore conformations and consequently a reduced channel open probability. In conformations where VSD is twisted 180° with respect to the initial structure (group 2), the S4–S5 linker rotates about the z axis away from the pore domain and undergoes a counterclockwise twist about its main principal axis (Figures 2L and 2M). At a first glance, it seems that the rotation away from the pore should increase the number of open pore conformation. However, the counterclockwise twist of the S4–S5 linker moves its base toward the pore, thereby eliminating most of the open pore conformations regardless of the z translation of the VSD. It should be noted that of all the conformations that the ion-channel can assume during its activation or deactivation pathway, only those that are energetically favorable may be considered as closed or activated states.
Figure 2.
Distribution of the six degrees of freedom of the possible VSD (S3–S4 complex) conformations and sample conformations of Kv7.1. Ivory segments are assumed to be stationary (S1, S2, S5, and P-Loop); segments with rigid body motion are shown by different shades of green (S3 by green, S4 by lime green, S4–S5 linker by light green and S6 by dark green); deformable regions are shown in red. A) Initial structure of Kv7.1 showing one of the four subunits (S1 to S6 transmembrane segments) with S6 of an adjacent subunit (denoted S6’). The six degrees of freedom of the VSD are defined in the bottom left: three translations (red arrows) and three rotations (brown curved arrows). B) Distribution of the possible conformations in terms of their z translation across the membrane. The VSD can move inward up to 16 Å. C) Distribution of the possible conformations in terms of ω rotations. Conformations may be divided into two groups, around ω = 0 (group 1) and around ω = π (group 2). D–I) Mean and standard deviation of x, y, θ, φ and ω for the possible conformations at various z translations (for ω, calculations were performed in group 1 and group 2 separately). As the VSD moves inward (+z direction), on average it also moves toward the pore (+x direction), and slightly in the +y direction; it also twists counterclockwise (−ω direction) as viewed from the outside. J–M) Samples of possible conformations. Conformations in panels A, J and K belong to ω group 1, and conformations in panels L and M belong to ω group 2. In panel A the pore is open; in panels J–M the pore is closed. Translation values (x, y, z) are indicated in angstroms; rotations in degrees.
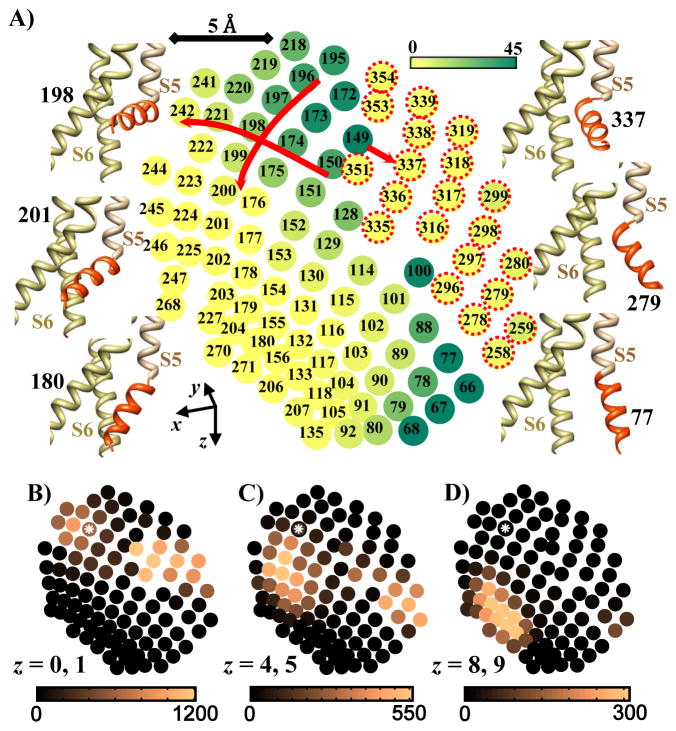
To provide a more quantitative analysis of how the z translation of the S3–S4 complex is associated with channel open probability (mechanical coupling), we computed the number of open pore conformations for each S4–S5 linker position. This determines the likelihood of channel opening at a given S4–S5 linker position. We then determined the distribution of the S4–S5 linkers that can be connected to S3–S4 conformations at different z translations. The intersection of these two requirements provides the likelihood of pore opening at different z translations of the voltage sensor during gating. Figure 3A shows the spatial location of the S4–S5 linker tip (Cα of T247, connection to S4) for the most probable S4–S5 linker conformations.
Figure 3.
S4–S5 linker conformations shown by mapping its tip (connection to S4) on the x-z′ plane. A) Density of open and closed pores associated with different S4–S5 linker conformations. Numbers identify S4–S5 linker conformations and color shades represent the number of possible open pore conformations at each S4–S5 linker position (increasing from yellow to dark green; scale is on top right). Samples of S4–S5 linker conformations are shown on both sides of the map (the S4–S5 linker is shown in red). 198 is the S4–S5 linker conformation in the initial structure. On the right side of the map (conformations 258 to 354) the base of the S4–S5 linker (connection to S5) is twisted toward the pore and the majority of the associated pores are in closed conformations. In the upper left region of the map there is significant number of open pores; the number of open pores decreases to zero as the S4–S5 linker tip moves downward in the map, except in conformations around 78. B–D) Density of S3–S4 (VSD) conformations associated with different S4–S5 linker positions (same map positions as in A; position 198 is marked with a white asterisk). Color shades (dark to light; scales under maps) indicate the number of VSD conformations that can connect to the S4–S5 linker at a given position. VSDs connect to S4–S5 linkers located on the upper left (open pore) or upper right (closed pore) of the map, if they are at their outward conformations (panel B, z = 0, 1). As the voltage sensors move inward by about 4 Å (panel C, z = 4, 5), very few can connect with S4–S5 linkers associated with open pore, and consequently the open probability drops significantly. Beyond 8 Angstrom inward motion (panel D, z = 8, 9) voltage sensors can connect only with S4–S5 linkers associated with closed pore and open probability is zero. Note that almost no voltage sensor conformation is associated with the region of open pore in the lower right of the map. z values are in Angstroms.
The left and right sides of the map correspond to conformations where the S4–S5 linker moved toward and away from the pore domain, respectively. The S4–S5 linker conformations for which the pore is open (green shades) are located in the upper left and lower right regions of the map. In both regions, motion of the S4–S5 linker tip in +x direction (toward the pore) and in +z direction (inward) reduces the number of open pore conformations. For example, the number of open conformations decreases gradually from 40 to zero when the S4–S5 linker moves toward the pore along the path 150 to 174 to 198 to 221 to 242, or inward along the path 196 to 197 to 198 to 199 to 200 (red arrows). These data confirm the intuitive prediction that both inward and toward the pore motion of the S4–S5 linker reduce the channel open probability. In contrast, there is a sharp decrease in the number of possible open pores as the S4–S5 linker moves away from the pore from conformation 149 to 337 (red arrow). In conformation 337, there is a displacement of the S4–S5 linker base (caused by a significant change in φ and ψ angles of His258) which eliminates almost all of the open pore conformations. Conformations on the upper right side of the map marked by red dotted circles (258 to 354) have a displaced S4–S5 linker base with no or very small open probability. It should be mentioned that many regions of this map can be reached by two different sets of φ and ψ angles of His258; one set causes a significant displacement in the S4–S5 linker base. These S4–S5 linker conformations are less stable (the average dihedral angle energy of the S4–S5 linkers with a displaced base is about 5kT higher than the S4–S5 linkers without a displaced base) and are associated with closed pore conformations; they are included in the map only for those locations that cannot be reached otherwise (i.e. conformations 258 to 354).
Figures 3B, 3C and 3D show the density of VSD conformations that can be connected to the S4–S5 linker at each position, at three different z translations. At outward positions of the VSD (Figure 3B) the S4–S5 linker in two distinct regions of the map can connect to the VSD: in the vicinity of position 198 and in the vicinity of position 337. The first region is mainly of open conformations, while the second region is mainly of closed conformations with a displaced base S4–S5 linker (Figure 3A). Considering that the S4–S5 linker energy in the second region is about 5kT higher than in the first region (supplement Figure S2), the channel has a significantly greater open probability at the outward positions of the VSD. As he VSD moves inward, both regions of possible S4–S5 linker connectivity move downward (in +z direction) in the map (Figure 3C). They are now in the vicinity of positions 201 and 279. These are S4–S5 linker conformations for which the pore is mostly closed and consequently the channel open probability is significantly reduced. Further inward motion of the VSD moves the possible linker positions farther down, in the vicinity of position 180 (Figure 3D), where all conformations are closed. Note that almost no VSD conformations can connect to S4–S5 linker positions associated with open pore in the vicinity of position 77.
The number of VSD conformations is significantly greater than the number of S4–S5 linker conformations and therefore several voltage sensor conformations are associated with each S4–S5 linker conformation. For any possible pair of S4–S5 linker and VSD conformations we determined the possible pore conformations. Analyzing the data revealed that there is greater similarity of pore conformations among pairs with the same S4–S5 linker conformation and different VSD conformations than among pairs with the same VSD conformation and different S4–S5 linker conformations. This supports the concept that motion of the VSD affects the open pore conformations mainly through altering the position of the S4–S5 linker.
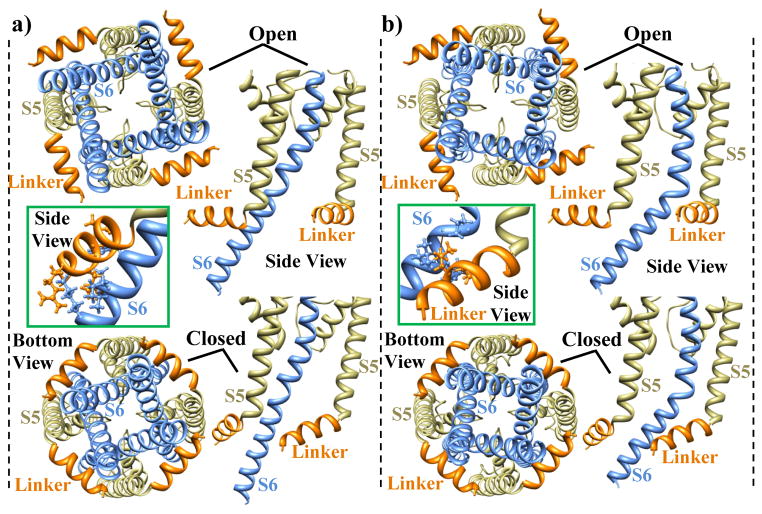
Examining the S6 conformations in the open pore revealed that the S6 tail may lean against the S4–S5 linker of its own subunit or the S4–S5 linker of an adjacent subunit. Figure 4 shows the two possibilities of the S6 to S4–S5 linker interaction and depicts the mechanical coupling in both cases. The S6 conformations that interact with the adjacent S4–S5 linker (panel B) have larger bending and revolution about the z axis than S6 conformations that interact with their own S4–S5 linker (panel A). To better understand mechanical coupling, we shifted the S4–S5 linker position inward and toward the pore, from 173 to 201. In the new position, the S4–S5 linker experiences steric clashes with the S6 tail in both cases (as shown in the framed insets). To prevent these clashes, the S6 tails must move toward the pore center, thereby decreasing the overall pore diameter. The S6 segments also undergo a small rotation (bottom views) when they are pushed together. Pore closure occurs when the diameter of the free space between gatekeeper residues on S6 (which delineate the smallest pore diameter) decreases below the open-pore threshold.
Figure 4.
Bottom and side views of the relative positions of the S4–S5 linker and S6 in open and closed pore conformations. A) S6 leans against the S4–S5 linker of its own subunit. B) S6 leans against the S4–S5 linker of an adjacent subunit. For open conformations the S4–S5 linker position is 173, and for closed conformations it is 201. When the S4–S5 linker moves from position 173 to position 201, its side chain atoms clash with the open pore S6 (insets). S6 moves toward the pore center to prevent the steric clashes and closes the channel (closed conformations).
3.2 Energy Considerations and Effect of Membrane Potential
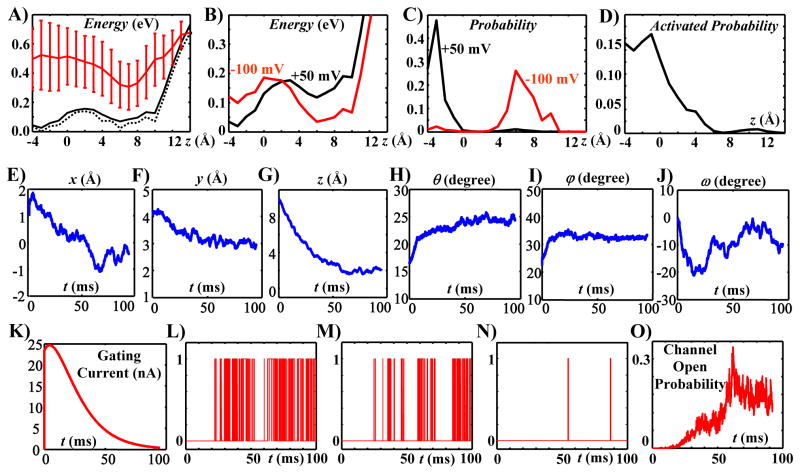
Not all possible conformations occur with the same likelihood. The energy of the protein at each conformation determines the probability distribution of the conformations and the dynamics of conformational changes. Figure 5A shows the mean energy and its standard deviation for Kv7.1 voltage sensor conformations at various z translations (in red); it compares it with the effective energy for the same conformations (solid black curve). The effective energy is defined in the Online Supplement 2; it represents the probability of S3–S4 complexes residing at different z translations. The effective energy is significantly different from the average energy, but closely follows the minimum energy (dashed black curve; also defined in online Supplement 2).
Figure 5.
A) Variation of the average (red curve), effective (solid black curve) and minimum (dashed black curve) energy with the z translation of the VSD. Membrane potential is zero. B) Effective energy at different VSD z translations for two membrane potentials of −100mV (red curve) and +50mV (black curve). Depolarizing the membrane stabilizes the outward positions and destabilizes the inward positions of the VSD. C) Probability distribution of the VSD conformations in terms of their z translations at two membrane potentials of −100mV and +50mV. D) Probability of an activated VSD conformation at different z translations (the channel can open when its VSDs are in activated conformations). E–J) Time variations of the six d.o.f. of the VSD averaged over 110 simulated motion trajectories during a voltage clamp test from −100mV to 50mV. K) Estimated gating current based on the average z translation of the VSD. LN) Three samples of simulated single channel records during the voltage clamp test. O) Channel open probability derived by averaging 1000 simulated single channels records. For the dynamics of conformational changes during activation gating see Supplement Movie File.
Therefore, among a group of conformations with the same z translation, the minimum energy conformation is an appropriate representative for studying the dynamics. Three local minima at z translations of −3, 6 and 10 are noticeable in both the effective and minimum energy curves. These z translations are consistent with the experimentally suggested displacement for the voltage sensor during activation (Posson and Selvin, 2008; Tombola et al., 2005). A significant energy barrier of about 5kT exists between the two minima at −3 and 6. Membrane potential (within the physiological range) can alter the effective energy; a +50mV membrane potential reduces the energy of the outward conformations with respect to the inward conformations, while a membrane potential of −100mV does the opposite (Figure 5B). As a result, as shown in Figure 5C, while at −100mV all voltage sensors are located at inward positions, membrane depolarization to +50mV moves those to outward positions. From a purely structural perspective, we showed that the open pore conformations are mostly associated with the outward positions of the S3–S4 complex and rarely with the inward positions (Figure 3). To verify that this holds when the energy-based probability distribution of the conformations is considered, we computed the average probability of activated voltage sensors at various z translations (Figure 5D). This computation takes into account the energy terms and the fraction of open pores associated with all possible S4–S5 linker positions for a given VSD conformation. A significant fraction of outward VSD conformations are activated at the outward position (−4<z<0). Starting at z = 0, the probability of having an activated voltage sensor conformation is reduced by about 80% within 3 Angstrom of inward motion of the S3–S4 complex; it diminishes completely within 6 Angstrom.
3.3 Structural Dynamics and Channel Current during Activation Gating
We simulated the dynamics of conformational changes during a voltage clamp test from −100 mV to +50 mV. Several trajectories of the Kv7.1 ion-channel conformational changes (averaged over a 1 μs time window) were generated by incorporating the conservative force field of the protein (associated with the chosen d.o.f) and the stochastic terms (of atomic vibrations) into the governing equation of motion derived previously (Nekouzadeh and Rudy, 2011a). The stochastic terms were determined for translational and rotational d.o.f of each rigid body segment (for an averaging time window of 1μs). Different trajectories were generated with different ensembles of the stochastic terms. The average time progressions of the VSD d.o.f. (over 110 simulated trajectories) are shown in Figures 5E to 5J. These computed dynamics are also visualized for a representative motion trajectory as continuous conformational changes in Supplement Movie File. There are three significant motions of the VSD during this activation trajectory: moving outward (Figure 5G), moving away from the pore (Figure 5E), and a clockwise twist when viewed from the outside (Figure 5J). Due to the stochastic nature of gating, motion trajectories vary in different simulation runs (Supplement Figure S3). However, these three motions are present in most trajectories and therefore in the average trajectory of 110 simulations (see also Supplement Figure S4). The VSD undergoes a rapid rotation (changes in θ, φ and ω) in the beginning of the simulation, followed by gradual rotation through the rest of the gating duration (Figures 5H, 5I, and 5J). Because all the trajectories are simulated starting from the same initial conformation, the initial rapid rotation of VSDs represents mostly the variability of VSD orientation among different conformations with an initial closed state (with insignificant energy barriers between them). Motion of charged residues on the VSD in the z direction produces a current across the cell membrane, known as gating current. Using the average motion of the VSD in the z direction (Figure 5G) the gating current was simulated and shown in Figure 5K. The simulated gating current displays a very fast rising phase, followed by a single exponential decay, consistent with the experimentally recorded gating currents from Kv7.4 potassium channels (Miceli et al., 2012). It should be noted that the simulated duration of gating current for Kv7.1 channels in this study (at 23°C) is ~50 ms, which is slightly longer than the experimentally recorded duration of ~30 ms for Kv7.4 channels at 28°C.
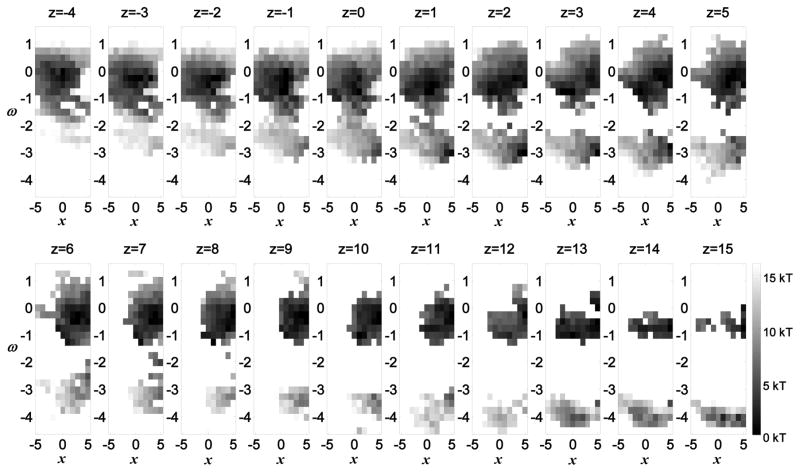
Representative records of single channel openings were simulated using four randomly selected motion trajectories of four voltage sensors and including a cooperative transition to the channel open state (Nekouzadeh et al., 2008). The morphology of single channel records varied from constant flickering between open and closed states to no openings (Figures 5L, 5M, 5N, and Supplemental Figure S5). The open probability was computed by averaging 1,000 simulated single channel records (Figure 5O). The simulated Kv7.1 open probability displays an inactivation characteristic; there is a decline in the open probability after it reaches its maximum at about 60 ms. The existence of inactivation in Kv7.1 channels is deduced from the presence of a hook in the macroscopic tail current during deactivation (Shalaby et al., 1997; Tapper and George, 2000; Wu et al., 2010a). However, in several experiments inactivation was also recorded early, following channel activation, while the membrane was still depolarized (Bendahhou et al., 2005; Schwake et al., 2003; Sesti and Goldstein, 1998; Yamagata et al., 2011). Seebohm et al. mapped the region of fast inactivation to transmembrane domain S5 and pore loop H5, distinct from N- or C-type inactivation (Seebohm et al., 2001). The simulations of this study suggest a new possible molecular mechanism, associated with the voltage sensor motion, which can account for the early inactivation following activation. By organizing the possible conformations in x–ω plane at different z translations and computing the associated energy landscapes (Figure 6) we observe that at the outward positions of the VSD, groups 1 (ω about 0°) and 2 (ω about 180°) of conformations are connected through a relatively low energy barrier, while at inward positions they are disconnected. Figure 6 presents the energy landscape when the membrane potential is zero. A negative membrane potential reduces the energy in proportion to the z position of the VSD, making the VSD inward positions (z > 5Å) more stable. Therefore, the majority of subunits are distributed among inward conformations. At inward positions (resting states), conformations in group 1 are energetically more stable than those in group 2 (Figure 6) and account for almost all the conformations. For z translations equal or greater than 5 Angstroms, the effective energy of conformations in group 1 is 4.03 kT, and the effective energy of conformations in group 2 is 10.67 kT. This implies that more than 99% of the channel conformations are in group 1. Upon depolarization of the membrane potential, the outward positions become more stable and the VSDs move outward, being redistributed mainly among outward positions (z < 5Å). At the outward positions, the VSD may overcome the low energy barrier between group 1 and group 2 and further twist −100 ° to −150° to enter group 2 of conformations. For z translations of 1 or 2 Angstroms (where the majority of VSDs reside at the depolarized state), the effective energy of the conformations of group 1 is 5.60 kT and the effective energy of the conformations of group 2 is 7.81 kT. This means that about 90% of the channel conformations are in group 1 and about 10% of the channel conformations are in group 2. For this 10% of channels, the base of the S4–S5 linker is shifted towards the pore. These S4–S5 linker conformations are associated only with closed pore conformations (S4–S5 linker conformations 258 to 354 in Figure 3A). The twist between group 1 and group 2 is slower than the upward motion (due to the energy barrier for the twist). Consequently, there is a temporary over occupancy of outward conformations in group 1, before the outward conformations in group 2 reach their steady state distribution. Because these final conformations are of closed pore, it follows that a large twist of the VSD, following its outward translation during activation, could provide a mechanism for early inactivation of Kv7.1 channels.
Figure 6.
Energy distribution of the VSD in the x−ω plane at different z translations for a zero membrane potential. At outward VSD positions (z = −4 Å) all possible conformations are distributed around the minimum energy at: x = 0 and ω = 0. As the VSD moves inward, a new set of possible conformations appears around ω = −π (ω = −3.14). This set of conformations separates from the conformations distributed around ω = 0 at z = 2 Å. Therefore, transitions between these two sets of conformations occur at the more outward positions of VSD. Energy levels are depicted in gray scale.
The average negative twist at the end of the activation phase (after about 70 ms) in Figure 5J represents this inactivating twist of the voltage sensor. It should be mentioned that based on the energy plots, less than 10% of voltage sensors are expected to pass through the barrier required for this −100 ° to −150° inactivating twist, and therefore the average magnitude of the twist (among all conformations) in Figure 5J is only about −12°. The time course of this inactivation process is similar to that of N-type inactivation of potassium channels, rather than C-type inactivation. We emphasize that this mechanism is suggested by the simulations as a model based hypothesis and should be tested experimentally. It does not overrule the other hypothesized inactivation mechanisms associated with the P-loop and S5 segments; it simply demonstrates that inactivation can also occur through voltage sensor movement. Cardiac IKs channels include the beta subunit KCNE1 and do not display inactivation. We are tempted to postulate that docking of KCNE1 can prevent inactivation by restricting the space and constraining the large twist of the VSD. Examination of this hypothesis will require future simulation studies that will incorporate KCNE1 in the channel protein structure.
4 Discussion
This work generated the first large pool of possible protein conformations that can occur during the large scale motions associated with ion channel gating. Analysis of these conformations determined that during activation, outward translation of the voltage sensor (−z) is accompanied by a translation away from the pore (−x) and a clockwise twist (ω). These motions cause pore opening by moving the S4–S5 linker upward and away from the pore, providing space for the S6 tails to move away from each other. Simulations of the voltage sensor motion during gating revealed that it is constantly moving within the configuration space (along different paths), rather than transitioning among few stable conformations. Therefore, the notion of stable conformations may refer to continuous regions in the configuration space where the voltage sensor can exist with high likelihood.
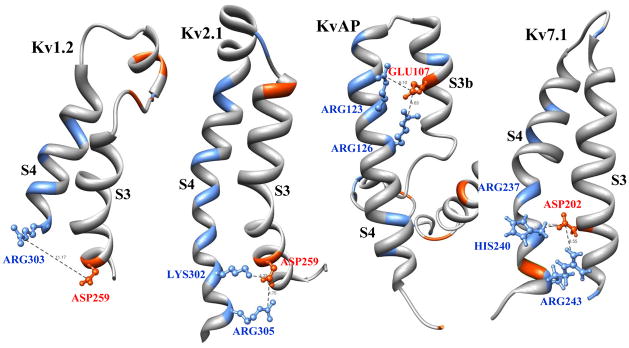
Although the initial structure of Kv7.1 is derived based on homology with Kv1.2, motion of S3 relative to S4 in Kv7.1 is restricted (similar to the S3 and S4 segments of Kv2.1 and KvAP) by a short interconnecting loop and strong electrostatic interactions between positive and negative residues on these segments (Figure 7). Assuming an average permittivity of 6 for proteins, a 3 Angstrom displacement of S4 with respect to S3 increases the energy of these electrostatic interactions (on the average) by approximately 0.5kT, 5kT, 8kT and 9kT in Kv1.2, Kv7.1, KvAP and Kv2.1, respectively. Change in the energy landscape caused by 100mV change in the membrane potential is about 2kT. Therefore, it is not likely that S4 moves with respect to S3 in the Kv7.1, KvAP and Kv2.1 channels. For Kv1.2, however, motion of S4 may not cause a significant motion of S3.
Figure 7.
VSD (S3–S4 complex) of four potassium channels. Crystal structures of Kv1.2, Kv2.1 and KvAP, and homology based structure of Kv7.1voltage sensors. S3 and S4 are connected by 12, 2, 2 and 5 residue loops in Kv1.2, Kv2.1, KvAP and Kv7.1, respectively. In Kv1.2 there is a relatively weak electrostatic interaction between ASP259 and ARG303 as they are ~11 Angstrom apart. In contrast, Kv2.1 has two strong electrostatic interactions: between ASP259 and LYS302 (~4 Angstrom apart) and between ASP259 and ARG305 (~5 Angstrom apart). KvAP also has two strong electrostatic interactions: between GLU107 and ARG123 (~6 Angstrom apart) and between GLU107 and ARG126 (~5 Angstrom apart). Kv7.1 has two relatively strong electrostatic interactions: between ASP202 and HIS240 (~6 Angstrom apart) and between ASP202 and ARG243 (~8 Angstrom apart). If the pH of solution is sufficiently high that HIS is not positively charged, the side chain of ARG237 repacks downward and makes a relatively strong electrostatic interaction with ASP202.
The simulations presented here employ simplifying assumptions that are based on specific properties of Kv7.1. Not considering a relative motion between S3 and S4 during VSD movement is an example, as is the assumption of symmetry between the four S6 segments. Simplifying assumptions can and should be made based on properties of the simulated protein, conditions during the simulated protocol and objective of the simulation. Such assumptions can shorten significantly the computing time and make the results more tractable and interpretable. The approach presented here is general; it provides a paradigm and an example from Kv7.1 for simulating the structure – function relationship of other ion channels. It could be used to study the functional consequences of mutations in the ion-channel protein and as a tool for the design and testing of drugs. Simplifying assumptions can be relaxed as dictated by a particular simulation, but at increased computational cost.
Direct validation of the simulated conformational changes is not possible, because direct measurement of these changes within an ion-channel protein is not possible. The gating current is a measurable ion-channel characteristic that is related closely to the dynamics of conformational changes during activation. This current is generated across the membrane by the translation of charged residues in the z direction. It is proportional to the average velocity of the charged residues on the VSD (the average velocity of the S3–S4 complex) in the z direction. The shape of the gating current simulated here (Figure 5K) is qualitatively very close to that of experimentally recorded gating currents (Miceli et al., 2012). This similarity indicates that the VSD velocity and its dynamics of motion in the z direction are simulated reliably throughout the gating process. Furthermore, the range of simulated motion of the VSD in the z direction (about 10 Angstroms) is consistent with experimental estimates. Additional, less direct validation is provided by the macroscopic current. The simulated macroscopic current (Figure 5O) displays the two signatures of recorded macroscopic Kv7.1 ionic currents: a short initial delay (5 to 10 ms) and early inactivation. Additionally, the activation duration is consistent with that of the experimentally recorded currents (Oliveras et al., 2014; Shamgar et al., 2008; Wu et al., 2010a; Wu et al., 2010b).
In conclusion, computational-biology provides a powerful approach for simulating the conformational changes that cardiac ion channels undergo during activation gating and for computing the resulting electrophysiologic function in terms of single-channel and macroscopic currents. In the context of this focused issue, future applications of this method could be used to link normal and abnormal heart rhythms to the biophysics of ion channels at the molecular scale.
Supplementary Material
Figure S1. Distribution of the ω angle.
Figure S2. Distribution of the gate keeper residue
Figure S3. The degrees of freedom of the S3–S4 complex along several simulated trajectories
Figure S4. Average Variations of the Voltage Sensor Degrees of Freedom
Figure S5. Simulated single channel records
Movie File. A Trajectory of Kv7.1 Ion Channel Structure during Activation.
Text 1. Background Information on Voltage Dependent Channel Gating
Text 2. Methodology Supplement.
Acknowledgments
Many thanks to Dr. Niloufar Ghoreishi, Dr. Ashwin Mohan, Jiajing Xu and Smiruthi Ramasubramanian for help, advice, and discussions. This research was supported by National Institutes of Health-National Heart, Lung and Blood Institute grants R01-HL049054 and R01-HL033343, and by a Leducq Foundation Award (to Y.R.). A.N. was supported in part by a Children’s Discovery Institute Fellowship No. CH-F-2008-121. Y.R. is the Fred Saigh Distinguished Professor at Washington University in St. Louis. Protein images and the supplemental movie were produced using the UCSF Chimera package (supported by NIH P41 RR-01081).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adcock SA, McCammon JA. Molecular dynamics: survey of methods for simulating the activity of proteins. Chem Rev. 2006;106:1589–615. doi: 10.1021/cr040426m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aidery P, Kisselbach J, Schweizer PA, Becker R, Katus HA, Thomas D. Impaired ion channel function related to a common KCNQ1 mutation - implications for risk stratification in long QT syndrome 1. Gene. 2012;511:26–33. doi: 10.1016/j.gene.2012.09.041. [DOI] [PubMed] [Google Scholar]
- Bauer A, Becker R, Freigang KD, Senges JC, Voss F, Hansen A, Muller M, Lang HJ, Gerlach U, Busch A, Kraft P, Kubler W, Schols W. Rate- and site-dependent effects of propafenone, dofetilide, and the new I(Ks)-blocking agent chromanol 293b on individual muscle layers of the intact canine heart. Circulation. 1999;100:2184–90. doi: 10.1161/01.cir.100.21.2184. [DOI] [PubMed] [Google Scholar]
- Bendahhou S, Marionneau C, Haurogne K, Larroque MM, Derand R, Szuts V, Escande D, Demolombe S, Barhanin J. In vitro molecular interactions and distribution of KCNE family with KCNQ1 in the human heart. Cardiovasc Res. 2005;67:529–38. doi: 10.1016/j.cardiores.2005.02.014. [DOI] [PubMed] [Google Scholar]
- Bosch RF, Schneck AC, Kiehn J, Zhang W, Hambrock A, Eigenberger BW, Rub N, Gogel J, Mewis C, Seipel L, Kuhlkamp V. beta3-Adrenergic regulation of an ion channel in the heart-inhibition of the slow delayed rectifier potassium current I(Ks) in guinea pig ventricular myocytes. Cardiovasc Res. 2002;56:393–403. doi: 10.1016/s0008-6363(02)00601-6. [DOI] [PubMed] [Google Scholar]
- Broomand A, Elinder F. Large-scale movement within the voltage-sensor paddle of a potassium channel-support for a helical-screw motion. Neuron. 2008;59:770–7. doi: 10.1016/j.neuron.2008.07.008. [DOI] [PubMed] [Google Scholar]
- Chen YH, Xu SJ, Bendahhou S, Wang XL, Wang Y, Xu WY, Jin HW, Sun H, Su XY, Zhuang QN, Yang YQ, Li YB, Liu Y, Xu HJ, Li XF, Ma N, Mou CP, Chen Z, Barhanin J, Huang W. KCNQ1 gain-of-function mutation in familial atrial fibrillation. Science. 2003;299:251–4. doi: 10.1126/science.1077771. [DOI] [PubMed] [Google Scholar]
- Clancy CE, Rudy Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature. 1999;400:566–9. doi: 10.1038/23034. [DOI] [PubMed] [Google Scholar]
- Crotti L, Spazzolini C, Schwartz PJ, Shimizu W, Denjoy I, Schulze-Bahr E, Zaklyazminskaya EV, Swan H, Ackerman MJ, Moss AJ, Wilde AA, Horie M, Brink PA, Insolia R, De Ferrari GM, Crimi G. The common long-QT syndrome mutation KCNQ1/A341V causes unusually severe clinical manifestations in patients with different ethnic backgrounds: toward a mutation-specific risk stratification. Circulation. 2007;116:2366–75. doi: 10.1161/CIRCULATIONAHA.107.726950. [DOI] [PubMed] [Google Scholar]
- Das S, Makino S, Melman YF, Shea MA, Goyal SB, Rosenzweig A, Macrae CA, Ellinor PT. Mutation in the S3 segment of KCNQ1 results in familial lone atrial fibrillation. Heart Rhythm. 2009;6:1146–53. doi: 10.1016/j.hrthm.2009.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyle DA. Structural changes during ion channel gating. Trends Neurosci. 2004;27:298–302. doi: 10.1016/j.tins.2004.04.004. [DOI] [PubMed] [Google Scholar]
- Gandhi CS, Clark E, Loots E, Pralle A, Isacoff EY. The orientation and molecular movement of a k(+) channel voltage-sensing domain. Neuron. 2003;40:515–25. doi: 10.1016/s0896-6273(03)00646-9. [DOI] [PubMed] [Google Scholar]
- Gjuvsland AB, Vik JO, Beard DA, Hunter PJ, Omholt SW. Bridging the genotype-phenotype gap: what does it take? J Physiol. 2013;591:2055–66. doi: 10.1113/jphysiol.2012.248864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulbis JM, Doyle DA. Potassium channel structures: do they conform? Curr Opin Struct Biol. 2004;14:440–6. doi: 10.1016/j.sbi.2004.06.008. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–44. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong K, Piper DR, Diaz-Valdecantos A, Brugada J, Oliva A, Burashnikov E, Santos-de-Soto J, Grueso-Montero J, Diaz-Enfante E, Brugada P, Sachse F, Sanguinetti MC, Brugada R. De novo KCNQ1 mutation responsible for atrial fibrillation and short QT syndrome in utero. Cardiovasc Res. 2005;68:433–40. doi: 10.1016/j.cardiores.2005.06.023. [DOI] [PubMed] [Google Scholar]
- Jiang Y, Ruta V, Chen J, Lee A, MacKinnon R. The principle of gating charge movement in a voltage-dependent K+ channel. Nature. 2003;423:42–8. doi: 10.1038/nature01581. [DOI] [PubMed] [Google Scholar]
- Kass RS, Moss AJ. Long QT syndrome: novel insights into the mechanisms of cardiac arrhythmias. J Clin Invest. 2003;112:810–5. doi: 10.1172/JCI19844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labro AJ, Raes AL, Grottesi A, Van Hoorick D, Sansom MS, Snyders DJ. Kv channel gating requires a compatible S4–S5 linker and bottom part of S6, constrained by non-interacting residues. J Gen Physiol. 2008;132:667–80. doi: 10.1085/jgp.200810048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long SB, Campbell EB, Mackinnon R. Crystal structure of a mammalian voltage-dependent Shaker family K+ channel. Science. 2005a;309:897–903. doi: 10.1126/science.1116269. [DOI] [PubMed] [Google Scholar]
- Long SB, Campbell EB, Mackinnon R. Voltage sensor of Kv1.2: structural basis of electromechanical coupling. Science. 2005b;309:903–8. doi: 10.1126/science.1116270. [DOI] [PubMed] [Google Scholar]
- Miceli F, Vargas E, Bezanilla F, Taglialatela M. Gating currents from Kv7 channels carrying neuronal hyperexcitability mutations in the voltage-sensing domain. Biophys J. 2012;102:1372–82. doi: 10.1016/j.bpj.2012.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nekouzadeh A, Rudy Y. Statistical properties of ion channel records. Part I: relationship to the macroscopic current. Math Biosci. 2007a;210:291–314. doi: 10.1016/j.mbs.2007.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nekouzadeh A, Rudy Y. Statistical properties of ion channel records. Part II: estimation from the macroscopic current. Math Biosci. 2007b;210:315–34. doi: 10.1016/j.mbs.2007.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nekouzadeh A, Rudy Y. Continuum molecular simulation of large conformational changes during ion-channel gating. PLoS One. 2011a;6:e20186. doi: 10.1371/journal.pone.0020186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nekouzadeh A, Rudy Y. Three-residue loop closure in proteins: a new kinematic method reveals a locus of connected loop conformations. J Comput Chem. 2011b;32:2515–25. doi: 10.1002/jcc.21812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nekouzadeh A, Silva JR, Rudy Y. Modeling subunit cooperativity in opening of tetrameric ion channels. Biophys J. 2008;95:3510–20. doi: 10.1529/biophysj.108.136721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishizawa M, Nishizawa K. Coupling of S4 helix translocation and S6 gating analyzed by molecular-dynamics simulations of mutated Kv channels. Biophys J. 2009;97:90–100. doi: 10.1016/j.bpj.2009.02.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliveras A, Roura-Ferrer M, Sole L, de la Cruz A, Prieto A, Etxebarria A, Manils J, Morales-Cano D, Condom E, Soler C, Cogolludo A, Valenzuela C, Villarroel A, Comes N, Felipe A. Functional assembly of Kv7.1/Kv7.5 channels with emerging properties on vascular muscle physiology. Arterioscler Thromb Vasc Biol. 2014;34:1522–30. doi: 10.1161/ATVBAHA.114.303801. [DOI] [PubMed] [Google Scholar]
- Perozo E. New structural perspectives on K(+) channel gating. Structure. 2002;10:1027–9. doi: 10.1016/s0969-2126(02)00812-2. [DOI] [PubMed] [Google Scholar]
- Perozo E, Cortes DM, Cuello LG. Structural rearrangements underlying K+-channel activation gating. Science. 1999;285:73–8. doi: 10.1126/science.285.5424.73. [DOI] [PubMed] [Google Scholar]
- Posson DJ, Selvin PR. Extent of voltage sensor movement during gating of shaker K+ channels. Neuron. 2008;59:98–109. doi: 10.1016/j.neuron.2008.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudy Y. Mathematical modeling of complex biological systems: From genes and molecules to organs and organisms: Heart. In: Egelman EH, Weinstein H, editors. Comprehensive Biophysics. Vol. 9, Simulation and Modeling. Academic Press; Oxford: 2012. pp. 268–327. [Google Scholar]
- Ruta V, Chen J, MacKinnon R. Calibrated measurement of gating-charge arginine displacement in the KvAP voltage-dependent K+ channel. Cell. 2005;123:463–75. doi: 10.1016/j.cell.2005.08.041. [DOI] [PubMed] [Google Scholar]
- Sampson KJ, Terrenoire C, Cervantes DO, Kaba RA, Peters NS, Kass RS. Adrenergic regulation of a key cardiac potassium channel can contribute to atrial fibrillation: evidence from an I Ks transgenic mouse. J Physiol. 2008;586:627–37. doi: 10.1113/jphysiol.2007.141333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sansom MS, Weinstein H. Hinges, swivels and switches: the role of prolines in signalling via transmembrane alpha-helices. Trends Pharmacol Sci. 2000;21:445–51. doi: 10.1016/s0165-6147(00)01553-4. [DOI] [PubMed] [Google Scholar]
- Schwake M, Jentsch TJ, Friedrich T. A carboxy-terminal domain determines the subunit specificity of KCNQ K+ channel assembly. EMBO Rep. 2003;4:76–81. doi: 10.1038/sj.embor.embor715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seebohm G, Scherer CR, Busch AE, Lerche C. Identification of specific pore residues mediating KCNQ1 inactivation. A novel mechanism for long QT syndrome. J Biol Chem. 2001;276:13600–5. doi: 10.1074/jbc.M008373200. [DOI] [PubMed] [Google Scholar]
- Seebohm G, Strutz-Seebohm N, Ureche ON, Baltaev R, Lampert A, Kornichuk G, Kamiya K, Wuttke TV, Lerche H, Sanguinetti MC, Lang F. Differential roles of S6 domain hinges in the gating of KCNQ potassium channels. Biophys J. 2006;90:2235–44. doi: 10.1529/biophysj.105.067165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sesti F, Goldstein SA. Single-channel characteristics of wild-type IKs channels and channels formed with two minK mutants that cause long QT syndrome. J Gen Physiol. 1998;112:651–63. doi: 10.1085/jgp.112.6.651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shalaby FY, Levesque PC, Yang WP, Little WA, Conder ML, Jenkins-West T, Blanar MA. Dominant-negative KvLQT1 mutations underlie the LQT1 form of long QT syndrome. Circulation. 1997;96:1733–6. doi: 10.1161/01.cir.96.6.1733. [DOI] [PubMed] [Google Scholar]
- Shamgar L, Haitin Y, Yisharel I, Malka E, Schottelndreier H, Peretz A, Paas Y, Attali B. KCNE1 constrains the voltage sensor of Kv7.1 K+ channels. PLoS One. 2008;3:e1943. doi: 10.1371/journal.pone.0001943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva J, Rudy Y. Subunit interaction determines IKs participation in cardiac repolarization and repolarization reserve. Circulation. 2005;112:1384–91. doi: 10.1161/CIRCULATIONAHA.105.543306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silva JR, Pan H, Wu D, Nekouzadeh A, Decker KF, Cui J, Baker NA, Sept D, Rudy Y. A multiscale model linking ion-channel molecular dynamics and electrostatics to the cardiac action potential. Proc Natl Acad Sci U S A. 2009;106:11102–6. doi: 10.1073/pnas.0904505106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Splawski I, Shen J, Timothy KW, Lehmann MH, Priori S, Robinson JL, Moss AJ, Schwartz PJ, Towbin JA, Vincent GM, Keating MT. Spectrum of mutations in long-QT syndrome genes. KVLQT1, HERG, SCN5A, KCNE1, and KCNE2. Circulation. 2000;102:1178–85. doi: 10.1161/01.cir.102.10.1178. [DOI] [PubMed] [Google Scholar]
- Tapper AR, George AL., Jr MinK subdomains that mediate modulation of and association with KvLQT1. J Gen Physiol. 2000;116:379–90. doi: 10.1085/jgp.116.3.379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tieleman DP, Shrivastava IH, Ulmschneider MR, Sansom MS. Proline-induced hinges in transmembrane helices: possible roles in ion channel gating. Proteins. 2001;44:63–72. doi: 10.1002/prot.1073. [DOI] [PubMed] [Google Scholar]
- Tombola F, Pathak MM, Isacoff EY. How far will you go to sense voltage? Neuron. 2005;48:719–25. doi: 10.1016/j.neuron.2005.11.024. [DOI] [PubMed] [Google Scholar]
- Tsuji K, Akao M, Ishii TM, Ohno S, Makiyama T, Takenaka K, Doi T, Haruna Y, Yoshida H, Nakashima T, Kita T, Horie M. Mechanistic basis for the pathogenesis of long QT syndrome associated with a common splicing mutation in KCNQ1 gene. J Mol Cell Cardiol. 2007;42:662–9. doi: 10.1016/j.yjmcc.2006.12.015. [DOI] [PubMed] [Google Scholar]
- Viswanathan PC, Shaw RM, Rudy Y. Effects of IKr and IKs heterogeneity on action potential duration and its rate dependence: a simulation study. Circulation. 1999;99:2466–74. doi: 10.1161/01.cir.99.18.2466. [DOI] [PubMed] [Google Scholar]
- Winbo A, Stattin EL, Nordin C, Diamant UB, Persson J, Jensen SM, Rydberg A. Phenotype, origin and estimated prevalence of a common long QT syndrome mutation: a clinical, genealogical and molecular genetics study including Swedish R518X/KCNQ1 families. BMC Cardiovasc Disord. 2014;14:22. doi: 10.1186/1471-2261-14-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu D, Delaloye K, Zaydman MA, Nekouzadeh A, Rudy Y, Cui J. State-dependent electrostatic interactions of S4 arginines with E1 in S2 during Kv7.1 activation. J Gen Physiol. 2010a;135:595–606. doi: 10.1085/jgp.201010408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu D, Pan H, Delaloye K, Cui J. KCNE1 remodels the voltage sensor of Kv7.1 to modulate channel function. Biophys J. 2010b;99:3599–608. doi: 10.1016/j.bpj.2010.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamagata K, Senokuchi T, Lu M, Takemoto M, Fazlul Karim M, Go C, Sato Y, Hatta M, Yoshizawa T, Araki E, Miyazaki J, Song WJ. Voltage-gated K+ channel KCNQ1 regulates insulin secretion in MIN6 beta-cell line. Biochem Biophys Res Commun. 2011;407:620–5. doi: 10.1016/j.bbrc.2011.03.083. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Distribution of the ω angle.
Figure S2. Distribution of the gate keeper residue
Figure S3. The degrees of freedom of the S3–S4 complex along several simulated trajectories
Figure S4. Average Variations of the Voltage Sensor Degrees of Freedom
Figure S5. Simulated single channel records
Movie File. A Trajectory of Kv7.1 Ion Channel Structure during Activation.
Text 1. Background Information on Voltage Dependent Channel Gating
Text 2. Methodology Supplement.