Abstract
Finite element (FE) models built from quantitative computed tomography (QCT) scans can provide patient-specific estimates of bone strength and fracture risk in the spine. While prior studies demonstrate accurate QCT-based FE predictions of vertebral stiffness and strength, the accuracy of the predicted failure patterns, i.e., the locations where failure occurs within the vertebra and the way in which the vertebra deforms as failure progresses, is less clear. This study used digital volume correlation (DVC) analyses of time-lapse micro-computed tomography (µCT) images acquired during mechanical testing (compression and anterior flexion) of thoracic spine segments (T7–T9, n = 28) to measure displacements occurring throughout the T8 vertebral body at the ultimate point. These displacements were compared to those simulated by QCT-based FE analyses of T8. We hypothesized that the FE predictions would be more accurate when the boundary conditions are based on measurements of pressure distributions within intervertebral discs of similar level of disc degeneration vs. boundary conditions representing rigid platens. The FE simulations captured some of the general, qualitative features of the failure patterns; however, displacement errors ranged 12–279%. Contrary to our hypothesis, no differences in displacement errors were found when using boundary conditions representing measurements of disc pressure vs. rigid platens. The smallest displacement errors were obtained using boundary conditions that were measured directly by DVC at the T8 endplates. These findings indicate that further work is needed to develop methods of identifying physiological loading conditions for the vertebral body, for the purpose of achieving robust, patient-specific FE analyses of failure mechanisms.
Keywords: Vertebral fracture, Digital volume correlation, Intervertebral disc, Quantitative computed tomography, Finite element analysis
1. Introduction
Vertebral fractures are the most common type of osteoporotic fracture (Burge et al., 2007) and are associated with increased morbidity and excess mortality. Prevalent vertebral fracture increases the risk of subsequent vertebral and hip fracture two- to three-fold (Black et al., 1999; Cauley et al., 2007; Klotzbuecher et al., 2000), and there is a 20% increased risk of death five years following clinical vertebral fracture (Cooper et al., 1993). Current methods of estimating fracture risk in the spine are based on measurements of bone mineral density (BMD) by dual-energy x-ray absorptiometry (DXA). However, BMD explains only approximately 60% of the variation in vertebral strength (Cheng et al., 1997), and almost half of patients with vertebral fracture do not exhibit osteoporotic values of BMD (Kanis et al., 2002). Finite element analysis (FEA) of quantitative computed tomography (QCT) scans of the vertebra has long been proposed as an improved method (Faulkner et al., 1993; Keaveny, 2010; Zysset et al., 2013). Given the use of QCT-based FEA for evaluating osteoporosis therapies and other drug treatments (Gluer et al., 2013; Keaveny et al., 2007), sex-related differences in bone strength (Christiansen et al., 2011), and implant designs (Polikeit et al., 2003), the accuracy of this method must be fully established.
Prior studies have found that QCT-based FEA can provide good predictions of vertebral stiffness and strength, yet the evidence regarding predictions of failure patterns, i.e., the locations where failure occurs within the vertebra and the way in which the vertebra deforms as failure progresses, is less clear. Compressive stiffness and strength computed by QCT-based FEA are highly correlated with values measured in laboratory tests (Bozic et al., 1994; Buckley et al., 2007b; Crawford et al., 2003; Dall'Ara et al., 2012; Imai et al., 2006; Wang et al., 2012). QCT-based FE estimates of vertebral strength under compressive loading are also associated with fracture even after adjusting for BMD (Kopperdahl et al., 2014; Wang et al., 2012) and discriminate between fracture and non-fracture cohorts better than BMD (Imai et al., 2006). However, QCT-based FEA has not performed as well for anterior flexion (Buckley et al., 2007a; Dall'Ara et al., 2010). Studies also suggest that FEA predictions of vertebral failure patterns can be inaccurate because of the highly non-uniform loading applied across the vertebral endplates by the adjacent intervertebral discs (IVDs) (Adams and Roughley, 2006; Clouthier et al., 2015; Hussein et al., 2013b; Jones and Wilcox, 2008; Maquer et al., 2015; Maquer et al., 2014). Moreover, the impact of the choice of material properties for bone tissue, and in particular the yield criterion, on the accuracy of the FEA predictions of failure patterns has not been addressed.
The goal of this study was to assess the accuracy of QCT-based FEA in predicting vertebral failure patterns. QCT-based FEA calculations of displacements throughout the vertebral body were compared to those measured via digital volume correlation (DVC) analyses of micro-computed tomography (µCT) images acquired as the vertebrae were loaded to the ultimate point. The specific objectives were to evaluate the accuracy of the FEA-computed displacements: (1) for different boundary conditions, representing either rigid platens or IVDs; (2) in two different loading modes (axial compression, axial compression combined with anterior flexion); and (3) for different yield criteria. We hypothesized that boundary conditions based on specimen-specific data on IVD degeneration would improve the FEA predictions, for both loading modes and both yield criteria.
2. Materials and methods
2.1. Specimen Preparation
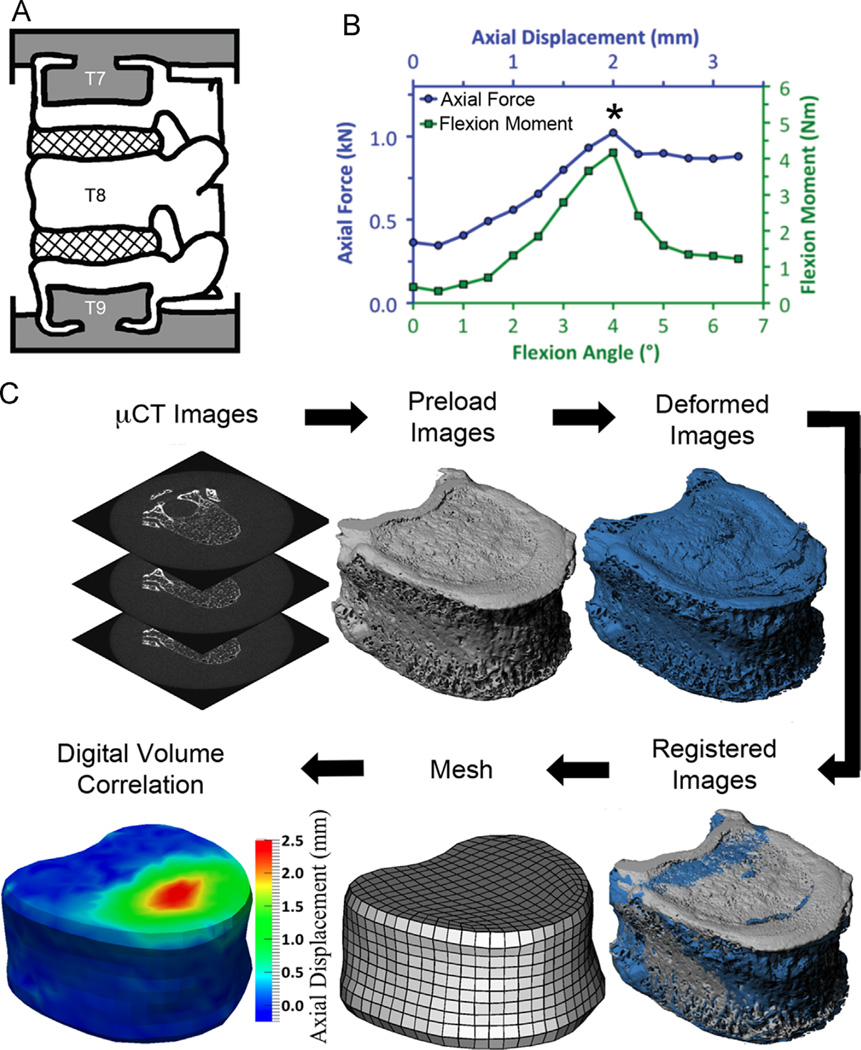
Twenty-eight T7–T9 spine segments were dissected from fresh-frozen human spines (age: 35–91 years; mean ± stdev: 71.2 ± 14.2 years; 16 male, 12 female) and were potted in polymethyl methacrylate (PMMA) (Fig. 1A). Specimens were kept hydrated at all times and, when not in use, wrapped in saline-soaked gauze, sealed in plastic bags, and stored at −20 °C.
Fig. 1.
(A) Preparation of the T7–T9 spine segments (grey = PMMA; cross-hatch = IVD; white = bone); (B) Mechanical testing involved stepwise loading with a µCT scan performed at each loading step; the asterisk denotes the peak of loading, which was the loading step used for comparison of the measured and FE-computed displacements; (C) Experimental procedure for image processing in preparation for digital volume correlation; The output of the digital volume correlation are the displacements occurring throughout the T8 vertebral body, though only the axial displacements on the surface of T8 are depicted in the figure.
2.2. Mechanical testing and imaging
The spine segments were randomly assigned for testing under axial compression (“compression”, n = 14) or axial compression with anterior flexion (“flexion”, n = 14). Each segment was first imaged with QCT (GE Lightspeed VCT; GE Health-care, Milwaukee, WI; 0.3125 × 0.3125 × 0.625 mm3/voxel) and then placed in a radiolucent device for mechanical testing. Testing involved stepwise loading (0.5 mm per step at 0.25 mm/s for compression; 0.25 mm and 0.5° per step, at 0.25 mm/s and 0.5°/s, for flexion) applied via screws within the device (Jackman et al., 2015) (Fig. 1B; Supplemental material). A µCT scan (µCT 80; Scanco Medical, Brüttisellen, Switzerland; 37 µm/voxel; 70 kVp, 114 mA, 300 ms) was performed at each step. The device was temporarily removed from the µCT scanner following each scan, to avoid damaging the scanner when turning the loading screws. Stepwise loading continued to failure, identified by visible deformation in the T8 vertebral body in lateral scout views acquired prior to each µCT scan.
For flexion, the compressive force and flexion moment experienced by the spine segment were obtained using a calibration layer as a low-profile multiaxial load cell (Supplemental material) (Jackman et al., 2015). For compression, a load cell (LLB450, Futek Advanced Sensor Technology, Irvine, CA) measured the axial force.
2.3. Experimental measurement of failure patterns using digital volume correlation (DVC)
The displacements occurring through the T8 vertebral body at the peak of loading (defined as the ultimate point on the moment-angle curve and force–displacement curve for flexion and compression loading, respectively (Fig. 1B)) were quantified using a previously established method of DVC applied to the time-lapsed µCT images (Hussein et al., 2012). Briefly, image registration (IPL; Scanco Medical) was used to align the series of images, and then the T8 vertebral body was virtually subdivided into hexahedral with ~1.9 mm side lengths (Fig. 1C). This hexahedral mesh was constructed by mapping a cubic mesh onto the irregular geometry of the vertebral body (IA-FEMesh; MIMX, The University of Iowa, Iowa City, IA). The displacement of each node in the hexahedral mesh was estimated using a custom optimization approach (Liu and Morgan, 2007; Richards, 2007). Any displacements in the pedicles and posterior elements were not analyzed, although these parts of the vertebra were present and intact during the mechanical testing.
2.4. Measurement of pressure within IVDs
The pressure distributions within IVDs were measured for the purpose of estimating the loading that the IVD exerts across the vertebral endplates. These measurements were performed in a separate cohort of spine segments (eight T9–T11 and 18 T10–T12 from 26 donors aged 35–86 years; mean ± stdev: 68 ± 16 years; 16 male, 10 female) (DelMonaco et al., 2015). The segments were dissected and prepared for testing in the identical manner as used for the spine segments tested to failure. Following QCT imaging (0.3125 × 0.3125 × 0.625 mm3 or 0.3906 × 0.3906 × 0.625 mm3), the specimens were affixed in a commercial test frame (Instron 8875, Canton, MA) and subjected to a compressive preload of 300 N for 30 min (Adams et al., 2000; McNally and Adams, 1992) followed by a 500 N, axial compressive load in either an anteriorly flexed (5° flexion; n = 14) or an erect (0° flexion; n = 12) posture. A 1.3-mm-diameter, needle-tip pressure transducer (4F HP, Gaeltec Ltd., Dunvegan, Isle of Skye, UK) was inserted entirely through the disc and then retracted at approximately 1 mm/s while the gauge pressure and position within the IVD were recorded digitally. Measurements were performed along mid-sagittal and mid-coronal lines for both IVDs of the segment, producing a “pressure profile” along each midline (Adams et al., 1996). Pressure was not measured in the superior IVD in one specimen because bridging osteophytes prevented insertion of the transducer. Specimens were kept hydrated throughout testing by a wrapping of PBS-soaked gauze.
2.5. Non-invasive assessment of IVD degeneration
Using the QCT image of a mid-transverse cross-section of each IVD in both cohorts, a trained observer assigned each IVD an “apparent loss of disc integrity” (ALDI) score (Hussein et al., 2013a). Clear demarcation between the presumptive nucleus pulposus and annulus fibrosus indicates a healthy IVD, while a loss of discernibility of the nucleus pulposus indicates degenerative changes.
2.6. QCT-Based FEA
Voxel-based FE models of T8, including the entire vertebral body and posterior elements, were generated from QCT images by converting each voxel into a hexahedral element of 0.625 mm side length. The mesh for each FE model consisted of approximately 90,000 elements and the run-time ranged 5–10 h (2.6 GHz, Intel Xeon E5-2670 processor with 128 GB shared RAM).
Linear elastic material properties and uniaxial yield strength (σy, MPa) were assigned based on local bone mineral density (ρQCT, mg/cc), averaged for each finite element. The elastic modulus along the axial direction (Ezz, MPa) and σy were computed as (Kopperdahl et al., 2002):
| (1) |
| (2) |
Any negative moduli obtained from Eq. (1) for elements with low ρQCT caused, for example by air bubbles were assigned an elastic modulus of 0.1 kPa. Both Ezz and σy were scaled by a factor of 1.28 to account for side-artifact errors (Bevill et al., 2007).
Two yield criteria were used: a crushable foam (CF) plasticity model and the von Mises (VM) criterion (Abaqus FEA 6.12, Dassault Systèmes, Vèlizy-Villacoublay, France). In the former, the yield surface is a function of the hydrostatic pressure (p) and von Mises stress (q). This function describes an ellipse in the p–q plane and is completely defined by σy and the ratios
| (3) |
| (4) |
where pc,y and pt,y are the vertices of the ellipse along the p-axis and, in this study, were assigned values of 1.181 and 0.540, respectively (Kinzl et al., 2013) (Supplemental material). Use of the CF criterion required isotropic elastic properties (Dassault Systèmes, 2012). The elastic modulus was assigned according to Eq. (1), and the Poisson's ratio was set to 0.381. For the VM yield criterion, transversely isotropic elastic properties were assigned (Unnikrishnan et al., 2013). For both CF and VM criteria, the post-yield behavior was perfectly plastic.
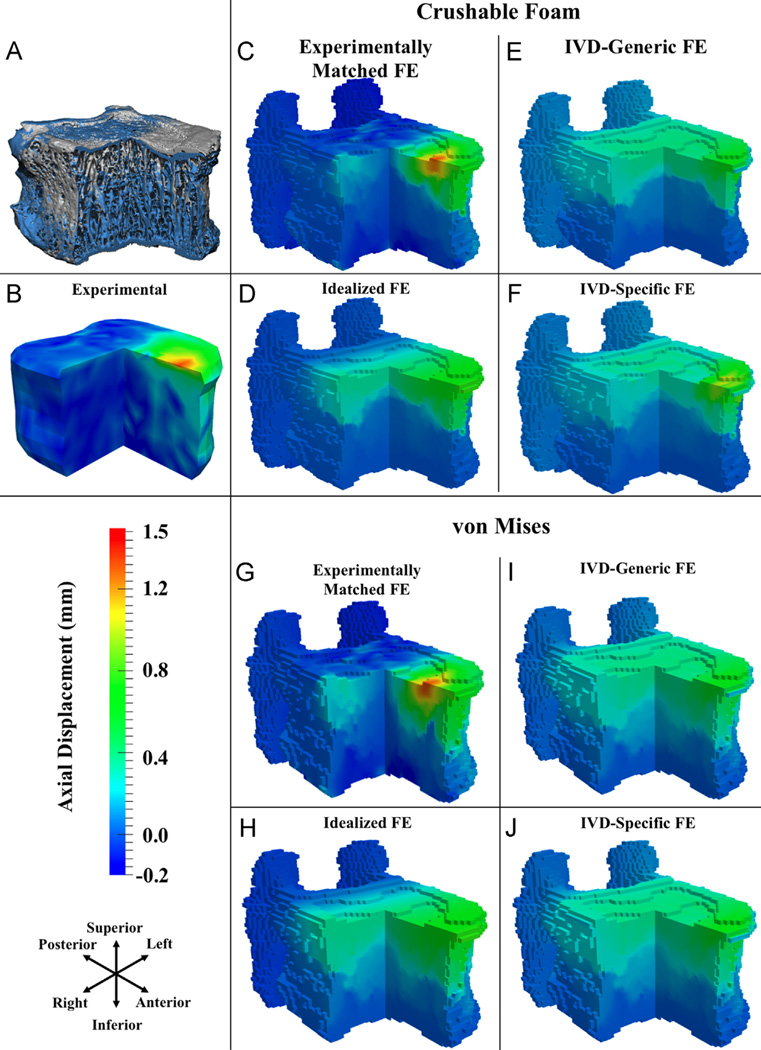
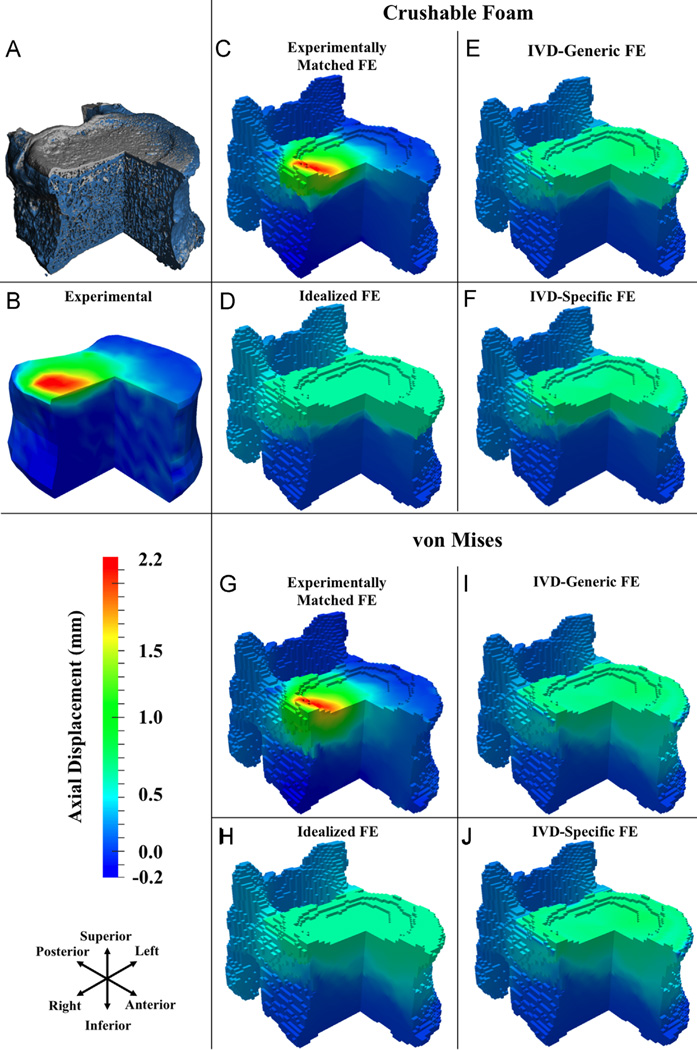
For each T8 FE model, four different boundary conditions, representing different types of endplate loading, were applied (Fig. 2). The first, “Experimentally Matched”, were the displacements measured by DVC at the superior and inferior endplates for that vertebra. This type of boundary condition would not be available clinically, but it provides a best-case scenario for the accuracy of the FEA predictions. The second type, “Idealized”, represents loading between rigid platens: for flexion, a uniform compressive displacement combined with a uniform angular displacement was applied to the superior endplate; for compression, a uniform compressive displacement was applied. To allow comparisons between the Idealized and Experimentally Matched simulations, the magnitudes of the uniform displacements used in the Idealized loading were set as equal to the respective specimen-specific averages of the Experimentally Matched displacements across the endplate.
Fig. 2.
(Left) Measured mid-sagittal pressure profiles averaged for moderately healthy (ALDI = 0–1), degenerated (ALDI = 2), and all (ALDI = 0–2) IVDs loaded under (A) flexion and (F) compression; (Right) Color maps of the distributed load across the superior endplate for (B) Experimentally Matched, (C) Idealized, (D) IVD-Generic, and (E) IVD-Specific boundary conditions for flexion and (G) Experimentally Matched, (H) Idealized, (I) IVD-Generic, and (J) IVD-Specific boundary conditions for compression.
The third and fourth types of boundary conditions, “IVD-Generic” and “IVD-Specific”, were created using the IVD pressures measured in the separate cohort of specimens. The pressure profiles were resampled at fixed percentages of the width of the IVD, and then were normalized by a scaling factor such that the area underneath the profile was the same for every IVD of each loading mode. These normalized profiles were averaged for ALDI scores of 0–1, for scores of 2, and across all IVDs to obtain average pressure profiles for each loading mode (i.e., flexion and compression) for moderately healthy, degenerated, and all IVDs, respectively. The last of these averaged profiles was used for the IVD-Generic boundary condition, and one of the first two profiles was used for the IVD-Specific condition, depending on the ALDI score of the IVD adjacent to the endplate in the vertebra being modeled. Mid-coronal profiles were modeled as an isosceles trapezoid based on pressure profiles observed experimentally and in FE simulations (Jacobs et al., 2014). The mid-coronal and mid-sagittal profiles were interpolated in the transverse plane of the IVD to produce an applied distributed load on the superior endplate. The distributed load was scaled uniformly such that the total applied force matched the force developed across the endplate when Experimentally Matched boundary conditions were applied.
For 24 specimens, only small displacements (<0.2 mm) were observed at the inferior T8 endplate, thus this endplate was fixed in the Idealized, IVD-Generic, and IVD-Specific boundary conditions. The remaining four specimens (all compression) experienced failure in the inferior endplate, and only small displacements (<0.2 mm) were observed in the superior endplate. For the FE models of these four, the superior endplate was fixed and the loading was applied to the inferior endplate.
The element size (0.625 mm) was half that used in a prior study that used similar material properties when simulating vertebral failure (Kinzl et al., 2013). Ancillary analyses demonstrated that decreasing the element size by two-fold did not change the results of the comparisons of DVC-measured vs. FE-computed displacements.
2.7. Statistical analyses
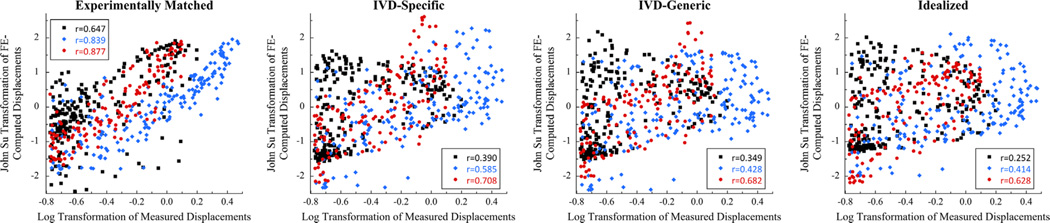
Pearson correlation analyses were used to assess correlations between the experimentally measured displacements throughout the interior of T8 and the corresponding FE-computed displacements (Matlab R2014a, Mathworks, Natick, MA). One correlation analysis was run separately for each specimen, boundary condition, and yield criterion (Fig. 3). For these correlations, the nodal FE displacements were averaged over 2 mm regions to match the spatial resolution of the DVC measurements. Points with measured displacements lower than the DVC detection limit (three times the standard deviation of the DVC displacement error (0.0556 mm)) were excluded (Ghosh et al., 2012), as were the displacements along the endplates because these were used as input when constructing the Experimentally Matched boundary conditions. The correlation coefficients were compared among boundary conditions and yield criteria in a pairwise fashion (Steiger, 1980) with Bonferroni correction to account for the multiple comparisons. As a measure of accuracy, the median percent error between measured and FE-computed values of displacements was computed for each specimen. This error was analyzed using a repeated-measures ANOVA with boundary condition and yield criterion as the within-subjects factors and loading mode as the between-subjects factor (JMP 11, SAS Institute, Cary, NC). Paired t-tests with Bonferroni correction were used as post-hoc tests. The significance level for all statistical analyses was 0.05.
Fig. 3.
Scatter plot of FE-computed and measured displacements for each of the four boundary conditions and the CF yield criterion, for three representative specimens loaded in flexion: prior to computing the Pearson correlation coefficient, the measured and FE-computed displacements were transformed to fit a log-normal and a Johnson SU distribution, respectively, to achieve approximately Gaussian distributions of the data.
3. Results
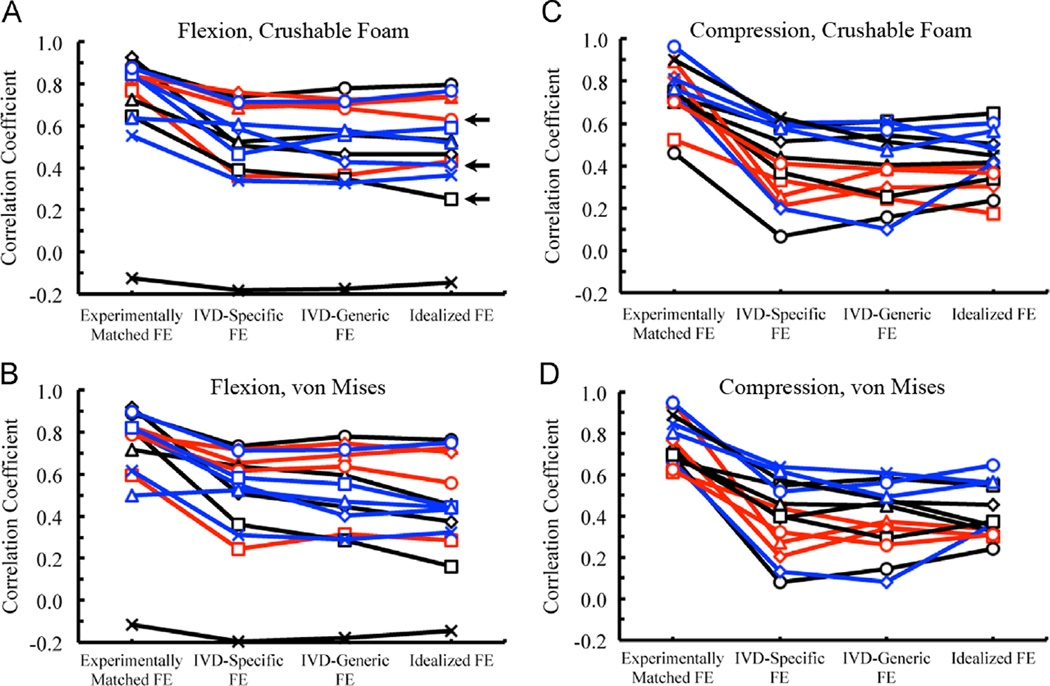
For flexion loading, the FE simulations captured some of the general, qualitative features of the deformation experienced by the T8 vertebra; however, the Idealized, IVD-Specific, and IVD-Generic models did not predict the localized deformation occurring superiorly (Fig. 4). Poor qualitative match was also observed for these three boundary conditions in compression loading (Fig. 5). For ten of the flexion specimens and 11 of the compression specimens, the correlation coefficients for FE-computed vs. measured displacements were higher (p < 0.001) for the Experimentally Matched boundary conditions as compared to the other three boundary conditions, for each yield criterion (Fig. 6). Among the remaining four specimens, no consistent differences in correlation coefficients were found between the Experimentally Matched boundary condition and any one of the other boundary conditions. Similarly, among all 28 specimens, no consistent differences in correlation coefficients were found among IVD-Specific, IVD-Generic, and Idealized boundary conditions, or between yield criteria. For one flexion specimen, displacements measured throughout the vertebral body remained small (≤ 0.3 mm) for the duration of loading, and poor agreement between measured and FE-computed displacements was observed for all boundary conditions and yield criteria (r < 0.17, Fig. 6).
Fig. 4.
For flexion: (A) three-quarter section view of a representative T8 vertebral body before loading (gray) and at the load increment following peak of loading (blue); (B–J) three-quarter section views of measured and FE-computed axial displacements (positive values are downward displacements) at the load increment following peak of loading, for CF (C–F) and VM (G–J) yield criteria. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 5.
For compression: (A) three-quarter section view of a representative T8 vertebral body before loading (gray) and at the load increment following peak of loading (blue); (B–J) three-quarter section views of measured and FE-computed axial displacements (positive values are downward displacements) at the load increment following peak of loading, for CF (C–F) and VM (G–J) yield criteria. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 6.
Pearson correlation coefficients for the correlations between FE-computed and measured displacements for all four boundary conditions using CF and VM yield criteria, for both flexion and compression loading; in all four plots, the line color corresponds to the ALDI score of the T7/8 IVD (blue = 0, black = 1, red = 2), and for a given ALDI score each specimen is indicated with a different symbol. The three specimens used for the scatterplots in Fig. 3 are denoted with a horizontal black arrow. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
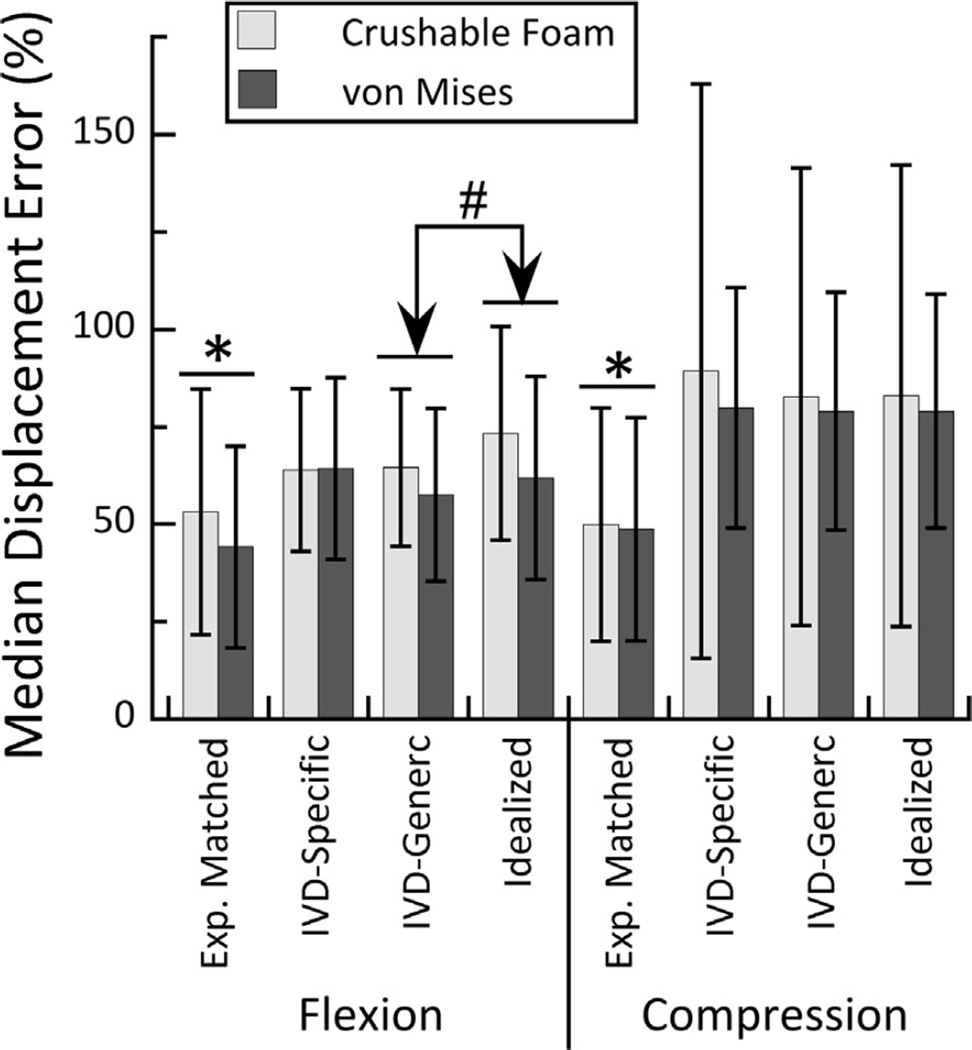
The accuracy of the FE-computed displacement fields was higher in flexion compared to compression (p = 0.009) and differed among boundary conditions (p < 0.001) in a manner that depended on loading mode (interaction effect: p = 0.009) (Fig. 7). For both loading modes, the median displacement errors were lower for Experimentally Matched vs. all other boundary conditions; however, in flexion loading, the errors were lower for also lower for IVD Generic vs. Idealized boundary conditions. Over all simulations, the median displacement error ranged 12–279%. The displacement errors did not depend on yield criterion (p = 0.416) or the interaction between yield criterion and any of the other factors (p > 0.073).
Fig. 7.
Median percent error for FE-computed axial displacements compared to the measured displacements, for the CF and VM yield criteria and both loading modes. For both loading modes and both yield criteria, the median percent errors were lower for the Experimental Matched vs. all other boundary conditions (* p < 0.001). For flexion loading and both yield criteria, the errors were lower for the IVD-Generic vs. Idealized boundary condition (# p = 0.004).
4. Discussion
The goal of this study was to assess the accuracy of QCT-based FEA in predicting vertebral failure patterns. Four different types of boundary conditions were investigated, to test the hypothesis that boundary conditions that incorporate specimen-specific data on disc degeneration would provide more accurate predictions. The results did not support our hypothesis. Simulations using boundary conditions based on pressure profiles from IVDs of comparable health were no more accurate than those using boundary conditions derived from generic pressure profiles. Moreover, neither IVD-based boundary condition produced smaller displacement errors than the platen boundary condition. The accuracy of the predicted failure patterns was better when using boundary conditions based on displacements measured at the vertebral endplates. These results emphasize that assumptions regarding boundary conditions can negatively impact the fidelity of the FE results. Further work is needed to develop methods of identifying physiological loading conditions for the vertebral body, for the purpose of achieving robust, patient-specific FEA of failure mechanisms.
The primary strength of this study is the quantitative measurement of vertebral failure patterns and IVD pressure profiles. These measurements enabled direct evaluation of the accuracy of the failure patterns predicted by a clinically feasible, QCT-based method for constructing a patient-specific FE model of the vertebra, complete with patient-specific estimates of boundary conditions. The comparison among boundary conditions that ranged from highly idealized to experimentally matched revealed the magnitude of the impact of each level of simplification.
This study also has limitations. First, the FE and DVC meshes differed from each other in spatial resolution and node locations. These differences arose from constraints imposed by the minimum region size required for sufficient accuracy in the DVC calculations, convergence requirements for the FEA, and the desire to use voxel-based meshes (as opposed to meshes that conform to the surfaces of the vertebral body) because of their frequent use in QCT-based FEA. Despite region-averaging of the FE displacements, the differences in meshes likely introduced some imprecision in comparing DVC and FE displacements, particularly in regions of large displacement gradients. Second, the IVD-based boundary conditions were constructed from pressures measured at different spinal levels and, due to the upper limit of the pressure transducer, at a lower applied force (500 N) than those occurring at the loading step modeled in the FEA (760–3880 N in compression). Although linearity between applied load and IVD pressure has been demonstrated (Pollintine et al., 2004), the shape of the pressure profile may change at the brink of vertebral failure. It is also possible that the ALDI scoring is not sufficiently sensitive for assignment of IVD-based boundary conditions. This may explain why the IVD-Specific simulations were no more accurate that the IVD-Generic ones. Another category of limitations pertains to some non-physiologic aspects of the experiments. The partial filling of T7 and T9 with PMMA may have affected the load distribution transmitted to T8. Also, each loading step involved a hold period because the duration of each µCT scan was 3–4 h. The exudation of fluid from IVDs during the sustained loading could dampen differences in vertebral loading between healthy vs. degenerated IVDs (McMillan et al., 1996). However, creep loading is widely believed to contribute to vertebral fractures in the elderly, and hence the long duration of loading may be very relevant to fractures in this population. Finally, although the axial force and anterior flexion moment that developed during mechanical testing were measured, these quantities are the loads applied to the entire segment, not specifically to the T8 vertebral body (Supplemental data). Hence, we could not perform a direct assessment of the accuracy of the FE-computed values of vertebral strength.
Progress in IVD imaging may provide a path towards defining patient-specific vertebral loading. For example, endplate boundary conditions obtained from magnetic resonance imaging (MRI)-based FE modeling of IVDs have aided predictions of failure patterns made with high-resolution peripheral QCT (HR-pQCT)-based FE models (Maquer et al., 2015). MRI protocols that resolve the condition of the IVD and, separately, the cartilaginous endplate (Bae et al., 2013; Fields et al., 2015), may be particularly advantageous for estimating load transfer between IVD and vertebra.
Yet our results also indicate that boundary conditions are not the only salient source of error in the FE predictions. Even for the Experimentally Matched simulations, the median displacement error was greater than 50% for many specimens. Some of this error may be due to errors in the DVC measurements, though excluding points below the DVC error threshold reduced this possibility. Large errors in FE predictions were found for both sets of material properties, which differed in elastic anisotropy and yield criterion but not post-yield constitutive behavior. Recent studies have shown good qualitative correspondence between patterns of frank vertebral collapse observed at very large applied displacements vs. patterns predicted by FE analyses using a damage-plastic constitutive model (Clouthier et al., 2015; Hosseini et al., 2014). In contrast, further refinements to the modeling of elastic anisotropy have only a minor effect on FE predictions of vertebral deformation (Unnikrishnan et al., 2013). Thus, while the present study focused on the ultimate point as opposed to the ensuing frank collapse, improved modeling of the yield and post-yield behavior of bone tissue may increase the fidelity of the FE results.
In summary, the findings presented here indicate that QCT-based FEA does not perform well in predicting vertebral failure patterns. Despite ample evidence that this FEA approach can accurately predict the compressive stiffness and strength of the vertebra, our findings emphasize that prediction of stiffness and strength is not the same as prediction of whole bone structural behavior. Further development of QCT-based FEA is required to allow broad applicability of this approach in modeling failure mechanisms in the spine.
Supplementary Material
Acknowledgments
Funding was provided by National Institutes of Health R01 AR054620. The authors also thank Paul Barbone, Ginu Unnikrishnan, Alexander Adams, Kamil Makhnejia, Greg Janese, and Paul Fein for their contributions to this study.
Footnotes
Conflict of interest statement
The authors of this manuscript have no conflicts of interest to disclose.
Appendix A. Supplementary material
Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.jbiomech.2015.12.004.
References
- Adams MA, Freeman BJ, Morrison HP, Nelson IW, Dolan P. Mechanical initiation of intervertebral disc degeneration. Spine. 2000;25:1625–1636. doi: 10.1097/00007632-200007010-00005. [DOI] [PubMed] [Google Scholar]
- Adams MA, McNally DS, Dolan P. 'Stress' distributions inside inter-vertebral discs. The effects of age and degeneration. J. Bone Jt. Surg. Br. 1996;78:965–972. doi: 10.1302/0301-620x78b6.1287. [DOI] [PubMed] [Google Scholar]
- Adams MA, Roughley PJ. What is intervertebral disc degeneration, and what causes it? Spine (Phila. Pa. 1976) 2006;31:2151–2161. doi: 10.1097/01.brs.0000231761.73859.2c. [DOI] [PubMed] [Google Scholar]
- Bae WC, Statum S, Zhang Z, Yamaguchi T, Wolfson T, Gamst AC, Du J, Bydder GM, Masuda K, Chung CB. Morphology of the cartilaginous endplates in human intervertebral disks with ultrashort echo time MR imaging. Radiology. 2013;266:564–574. doi: 10.1148/radiol.12121181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bevill G, Easley SK, Keaveny TM. Side-artifact errors in yield strength and elastic modulus for human trabecular bone and their dependence on bone volume fraction and anatomic site. J. Biomech. 2007;40:3381–3388. doi: 10.1016/j.jbiomech.2007.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Black DM, Palermo L, Nevitt MC, Genant HK, Christensen L, Cummings SR. Defining incident vertebral deformity: a prospective comparison of several approaches. The study of osteoporotic fractures research group. J. Bone Min. Res. 1999;14:90–101. doi: 10.1359/jbmr.1999.14.1.90. [DOI] [PubMed] [Google Scholar]
- Bozic KJ, Keyak JH, Skinner HB, Bueff HU, Bradford DS. Three-dimensional finite element modeling of a cervical vertebra: an investigation of burst fracture mechanism. J. Spinal Disord. 1994;7:102–110. doi: 10.1097/00002517-199407020-00002. [DOI] [PubMed] [Google Scholar]
- Buckley JM, Cheng L, Loo K, Slyfield C, Xu Z. Quantitative computed tomography-based predictions of vertebral strength in anterior bending. Spine. 2007a;32:1019–1027. doi: 10.1097/01.brs.0000260979.98101.9c. [DOI] [PubMed] [Google Scholar]
- Buckley JM, Loo K, Motherway J. Comparison of quantitative computed tomography-based measures in predicting vertebral compressive strength. Bone. 2007b;40:767–774. doi: 10.1016/j.bone.2006.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burge R, Dawson-Hughes B, Solomon DH, Wong JB, King A, Tosteson A. Incidence and economic burden of osteoporosis-related fractures in the United States, 2005–2025. J. Bone Min. Res. 2007;22:465–475. doi: 10.1359/jbmr.061113. [DOI] [PubMed] [Google Scholar]
- Cauley JA, Hochberg MC, Lui LY, Palermo L, Ensrud KE, Hillier TA, Nevitt MC, Cummings SR. Long-term risk of incident vertebral fractures. J. Am. Med. Assoc. 2007;298:2761–2767. doi: 10.1001/jama.298.23.2761. [DOI] [PubMed] [Google Scholar]
- Cheng XG, Nicholson PH, Boonen S, Lowet G, Brys P, Aerssens J, Van der Perre G, Dequeker J. Prediction of vertebral strength in vitro by spinal bone densitometry and calcaneal ultrasound. J. Bone Min. Res. 1997;12:1721–1728. doi: 10.1359/jbmr.1997.12.10.1721. [DOI] [PubMed] [Google Scholar]
- Christiansen BA, Kopperdahl DL, Kiel DP, Keaveny TM, Bouxsein ML. Mechanical contributions of the cortical and trabecular compartments contribute to differences in age-related changes in vertebral body strength in men and women assessed by QCT-based finite element analysis. J. Bone Min. Res. 2011;26:974–983. doi: 10.1002/jbmr.287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clouthier AL, Hosseini HS, Maquer G, Zysset PK. Finite element analysis predicts experimental failure patterns in vertebral bodies loaded via inter-vertebral discs up to large deformation. Med. Eng. Phys. 2015;37:599–604. doi: 10.1016/j.medengphy.2015.03.007. [DOI] [PubMed] [Google Scholar]
- Cooper C, Atkinson EJ, Jacobsen SJ, O'Fallon WM, Melton LJ., 3rd Population-based study of survival after osteoporotic fractures. Am. J. Epidemiol. 1993;137:1001–1005. doi: 10.1093/oxfordjournals.aje.a116756. [DOI] [PubMed] [Google Scholar]
- Crawford RP, Cann CE, Keaveny TM. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone. 2003;33:744–750. doi: 10.1016/s8756-3282(03)00210-2. [DOI] [PubMed] [Google Scholar]
- Dall'Ara E, Pahr D, Varga P, Kainberger F, Zysset P. QCT-based finite element models predict human vertebral strength in vitro significantly better than simulated DEXA. Osteoporos. Int. 2012;23:563–572. doi: 10.1007/s00198-011-1568-3. [DOI] [PubMed] [Google Scholar]
- Dall'Ara E, Schmidt R, Pahr D, Varga P, Chevalier Y, Patsch J, Kainberger F, Zysset P. A nonlinear finite element model validation study based on a novel experimental technique for inducing anterior wedge-shape fractures in human vertebral bodies in vitro. J. Biomech. 2010;43:2374–2380. doi: 10.1016/j.jbiomech.2010.04.023. [DOI] [PubMed] [Google Scholar]
- Dassault Systèmes. Abaqus Keywords Reference Manual. Providence, RI: 2012. [Google Scholar]
- DelMonaco AM, Jackman TM, Fein PM, Adams AM, Makhneija KK, Morgan EF. Quantifying the Spatial Distribution of Intradiscal Pressure and its Assessment via Non-Invasive Estimates of Intervertebral Disc Degeneration. Proceedings of the 61st Annual Meeting of the Orthopaedic Research Society. 2015 [Google Scholar]
- Faulkner K, Cummings S, Black D, Palmero L, Gluer C, Genant H. Simple measurement of femoral geometry predicts hip fracture: the study of osteo-porotic fractures. J. Bone Miner. Res. 1993;8:1211–1217. doi: 10.1002/jbmr.5650081008. [DOI] [PubMed] [Google Scholar]
- Fields AJ, Han M, Krug R, Lotz JC. Cartilaginous end plates: quantitative MR imaging with very short echo times-orientation dependence and correlation with biochemical composition. Radiology. 2015;274:482–489. doi: 10.1148/radiol.14141082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh R, Gupta S, Dickinson A, Browne M. Experimental validation of finite element models of intact and implanted composite hemipelvises using digital image correlation. J. Biomech. Eng. 2012;134:081003. doi: 10.1115/1.4007173. [DOI] [PubMed] [Google Scholar]
- Gluer CC, Marin F, Ringe JD, Hawkins F, Moricke R, Papaioannu N, Farahmand P, Minisola S, Martinez G, Nolla JM, Niedhart C, Guanabens N, Nuti R, Martin-Mola E, Thomasius F, Kapetanos G, Pena J, Graeff C, Petto H, Sanz B, Reisinger A, Zysset PK. Comparative effects of teriparatide and risedronate in glucocorticoid-induced osteoporosis in men: 18-month results of the EuroGIOPs trial. J. Bone Min. Res. 2013;28:1355–1368. doi: 10.1002/jbmr.1870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosseini HS, Clouthier AL, Zysset PK. Experimental validation of finite element analysis of human vertebral collapse under large compressive strains. J. Biomech. Eng. 2014;136 doi: 10.1115/1.4026409. [DOI] [PubMed] [Google Scholar]
- Hussein AI, Barbone PE, Morgan EF. Digital volume correlation for study of the mechanics of whole bones. Procedia IUTAM. 2012;4:116–125. doi: 10.1016/j.piutam.2012.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussein AI, Jackman TM, Morgan SR, Barest GD, Morgan EF. The intravertebral distribution of bone density: correspondence to intervertebral disc health and implications for vertebral strength. Osteoporos. Int. 2013a;24:3021–3030. doi: 10.1007/s00198-013-2417-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hussein AI, Unnikrishnan GU, Barest GD, Morgan EF. Accuracy of QCT-based finite element models of the vertebra. Proceedings of the Annual Meeting of the American Society for Bone and Mineral Research. 2013b [Google Scholar]
- Imai K, Ohnishi I, Bessho M, Nakamura K. Nonlinear finite element model predicts vertebral bone strength and fracture site. Spine. 2006;31:1789–1794. doi: 10.1097/01.brs.0000225993.57349.df. [DOI] [PubMed] [Google Scholar]
- Jackman TM, Hussein AI, Anderson C, De Barros L, Curtiss C, Morgan EF. Quantitative, 3-D visualization of the inititiation and progression of thoracic vertebral fracture under compression and anterior flexion. J. Bone Min. Res. 2015 Nov 21; http://dx.doi.org/10.1002/jbmr.2749. [Epub ahead of print] [Google Scholar]
- Jacobs NT, Cortes DH, Peloquin JM, Vresilovic EJ, Elliott DM. Validation and application of an intervertebral disc finite element model utilizing independently constructed tissue-level constitutive formulations that are nonlinear, anisotropic, and time-dependent. J. Biomech. 2014;47:2540–2546. doi: 10.1016/j.jbiomech.2014.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones AC, Wilcox RK. Finite element analysis of the spine: towards a framework of verification, validation and sensitivity analysis. Med. Eng. Phys. 2008;30:1287–1304. doi: 10.1016/j.medengphy.2008.09.006. [DOI] [PubMed] [Google Scholar]
- Kanis JA, Johnell O, Oden A, De Laet C, Jonsson B, Dawson A. Ten-year risk of osteoporotic fracture and the effect of risk factors on screening strategies. Bone. 2002;30:251–258. doi: 10.1016/s8756-3282(01)00653-6. [DOI] [PubMed] [Google Scholar]
- Keaveny TM. Biomechanical computed tomography-noninvasive bone strength analysis using clinical computed tomography scans. Ann. N Y. Acad. Sci. 2010;1192:57–65. doi: 10.1111/j.1749-6632.2009.05348.x. [DOI] [PubMed] [Google Scholar]
- Keaveny TM, Donley DW, Hoffmann PF, Mitlak BH, Glass EV, San Martin JA. Effects of teriparatide and alendronate on vertebral strength as assessed by finite element modeling of QCT scans in women with osteoporosis. J. Bone Min. Res. 2007;22:149–157. doi: 10.1359/jbmr.061011. [DOI] [PubMed] [Google Scholar]
- Kinzl M, Wolfram U, Pahr DH. Identification of a crushable foam material model and application to strength and damage prediction of human femur and vertebral body. J. Mech. Behav. Biomed. Mater. 2013;26:136–147. doi: 10.1016/j.jmbbm.2013.04.026. [DOI] [PubMed] [Google Scholar]
- Klotzbuecher CM, Ross PD, Landsman PB, Abbott TA, 3rd, Berger M. Patients with prior fractures have an increased risk of future fractures: a summary of the literature and statistical synthesis. J. Bone Min. Res. 2000;15:721–739. doi: 10.1359/jbmr.2000.15.4.721. [DOI] [PubMed] [Google Scholar]
- Kopperdahl DL, Aspelund T, Hoffmann PF, Sigurdsson S, Siggeirsdottir K, Harris TB, Gudnason V, Keaveny TM. Assessment of incident spine and hip fractures in women and men using finite element analysis of CT scans. J. Bone Min. Res. 2014;29:570–580. doi: 10.1002/jbmr.2069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopperdahl DL, Morgan EF, Keaveny TM. Quantitative computed tomography estimates of the mechanical properties of human vertebral trabecular bone. J. Orthop. Res. 2002;20:801–805. doi: 10.1016/S0736-0266(01)00185-1. [DOI] [PubMed] [Google Scholar]
- Liu L, Morgan EF. Accuracy and precision of digital volume correlation in quantifying displacements and strains in trabecular bone. J. Biomech. 2007;40:3516–3520. doi: 10.1016/j.jbiomech.2007.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maquer G, Schwiedrzik J, Huber G, Morlock MM, Zysset PK. Compressive strength of elderly vertebrae is reduced by disc degeneration and additional flexion. J. Mech. Behav. Biomed. Mater. 2015;42:54–66. doi: 10.1016/j.jmbbm.2014.10.016. [DOI] [PubMed] [Google Scholar]
- Maquer G, Schwiedrzik J, Zysset PK. Embedding of human vertebral bodies leads to higher ultimate load and altered damage localisation under axial compression. Comput. Methods Biomech. Biomed. Eng. 2014;17:1311–1322. doi: 10.1080/10255842.2012.744400. [DOI] [PubMed] [Google Scholar]
- McMillan DW, Garbutt G, Adams MA. Effect of sustained loading on the water content of intervertebral discs: implications for disc metabolism. Ann. Rheum. Dis. 1996;55:880–887. doi: 10.1136/ard.55.12.880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNally DS, Adams MA. Internal intervertebral disc mechanics as revealed by stress profilometry. Spine. 1992;17:66–73. doi: 10.1097/00007632-199201000-00011. [DOI] [PubMed] [Google Scholar]
- Polikeit A, Ferguson SJ, Nolte LP, Orr TE. Factors influencing stresses in the lumbar spine after the insertion of intervertebral cages: finite element analysis. Eur. Spine. J. 2003;12:413–420. doi: 10.1007/s00586-002-0505-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollintine P, Przybyla AS, Dolan P, Adams MA. Neural arch load-bearing in old and degenerated spines. J. Biomech. 2004;37:197–204. doi: 10.1016/s0021-9290(03)00308-7. [DOI] [PubMed] [Google Scholar]
- Richards MS. Quantitative Three Dimensional Elasticity Imaging (Unpublished doctoral dissertation) Boston University: United States; 2007. [Google Scholar]
- Steiger JH. Tests for comparing elements of a correlation matrix. Psychol. Bull. 1980;87:245–251. [Google Scholar]
- Unnikrishnan GU, Barest GD, Berry DB, Hussein AI, Morgan EF. Effect of specimen-specific anisotropic material models the QCT-based finite element analysis of vertebra. J. Biomech. Eng. 2013;135:101007. doi: 10.1115/1.4025179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Sanyal A, Cawthon PM, Palermo L, Jekir M, Christensen J, Ensrud KE, Cummings SR, Orwoll E, Black DM, Keaveny TM. Prediction of new clinical vertebral fractures in elderly men using finite element analysis of CT scans. J. Bone Miner. Res. 2012;27:808–816. doi: 10.1002/jbmr.1539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zysset PK, Dall'ara E, Varga P, Pahr DH. Finite element analysis for prediction of bone strength (Bonekey Report) 2013;2:386. doi: 10.1038/bonekey.2013.120. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.