Abstract
Objective
In this work we propose a probabilistic graphical model framework that uses language priors at the level of words as a mechanism to increase the performance of P300-based spellers.
Approach
This paper is concerned with brain-computer interfaces based on P300 spellers. Motivated by P300 spelling scenarios involving communication based on a limited vocabulary, we propose a probabilistic graphical model framework and an associated classification algorithm that uses learned statistical models of language at the level of words. Exploiting such high-level contextual information helps reduce the error rate of the speller.
Main results
Our experimental results demonstrate that the proposed approach offers several advantages over existing methods. Most importantly, it increases the classification accuracy while reducing the number of times the letters need to be flashed, increasing the communication rate of the system.
Significance
The proposed approach models all the variables in the P300 speller in a unified framework and has the capability to correct errors in previous letters in a word, given the data for the current one. The structure of the model we propose allows the use of efficient inference algorithms, which in turn makes it possible to use this approach in real-time applications.
Keywords: brain computer interfaces, probabilistic graphical models, language models, P300 speller, inference algorithms
1. Introduction
The P300 speller is one of the most successful applications of electroencephalography (EEG) based brain-computer interfaces (BCIs) [1–4]. The P300 speller is based on the detection of P300 potentials, which can be described as a positive deflection of the EEG amplitude 300 ms after an non-common event is observed by a subject. In the last 10 years a great amount of work has been done in two different constitutive areas of the P300 systems: (1). Signal processing methods that underlie reliable detection of P300 potentials (see [5] for a survey of signal processing methods in P300 based BCIs) and (2). Classification methods for differentiating between segments of EEG signals containing P300 potentials from those that do not. (See [6] and [7] for comparison of different classification algorithms used in P300 based BCIs.) Although not a new idea [4], recently there has been growing interest in the incorporation of language models into the P300 speller with the intention to increase its performance [8–10]. Methods following this line of thought make use of language statistics as a prior, making it less likely for the system to declare sequences of letters that are unlikely in the language. With this perspective, a dictionary-based method was proposed in [11]. This speller auto-completes the words based on prior information obtained from a newspaper corpus. This method effectively increases the performance of the P300 speller by reducing the number of letters that the subject must type. However, it assumes that the first letters of the words are decoded correctly, and in case of error, the whole word will be decoded incorrectly. In [12] a solution to this problem has been presented. This method classifies the EEG signal and outputs a word that is compared to the words in a custom dictionary. The word in the dictionary that is closest to the classifier’s output is then declared. This method assumes that the maximum number of misclassified letters in a word is 50% in an attempt to reduce the number of possible matches in the dictionary. The employed dictionary makes use of a small subset of 942 words, all words with a length of four letters, which is restrictive. Recently, a natural language processing (NLP) approach has been presented in [13]. In this approach each letter receives a score based on the output of the step wise linear discriminant analysis (SWLDA). The scores obtained by SWLDA are transformed into probabilities by assuming a Gaussian distribution. These probabilities are combined with language priors based on frequency statistics of the language. These statistics are simplified by assuming a second order hidden Markov model (HMM) structure in order to calculate 3 g. One limiting factor in this work is that greedy decisions are made about letters, i.e., once a letter is declared it is not possible to modify it based on new information obtained by new letters spelled by the subject. Given the dependence between letters in a word, if an error is made by the classifier, the error will propagate in the remaining letters of the word. Following the work in [13], in [14] a work using models of different orders shows that a 4 g model provides the best results. In [14] it is also proposed that after the initials letters of a word have been predicted, it is possible to decrease the number of times that a letter should be flashed, without compromising performance. In this method as in [13], a letter that has been declared cannot be changed. This issue was resolved in [15] where two generative methods are combined. In this approach, first a Bayesian LDA classifier for P300 signal detection is utilized and then the scores of each letter produced by that classifier are turned into probabilities to be combined with the language model for Bayesian inference. This allows to make inference in different ways. In particular, the use of the forward–backward algorithm for inference allows the method proposed in [15] to correct previously declared letters if current information supports that change. A recent work [16] also makes use of HMMs for modeling the language. The key difference between the work in [15] and [16] is that the former uses as input to the HMM the scores for each letter obtained by means of the Bayesian LDA, while the latter directly uses the EEG signals as input for the HMM.
In this work, we propose taking one further step incorporating higher-level language models into P300 spellers. To the best knowledge of the authors, this is the first fully probabilistic approach for incorporation of word-level language models in the context of BCI. Our motivation comes from BCI applications that involve typing based on a limited vocabulary. In a particular context, if it is known that a user is likely to type words from a dictionary of, say, a few thousand words, that provides very valuable prior information that can potentially be exploited to improve the performance of the BCI system. Based on this perspective, we propose a discriminative graphical model-based framework for the P300 speller with a language model at the level of words. The proposed model integrates all the elements of the BCI system from the input brain signals to the spelled word in a probabilistic framework in which classification and language modeling are integrated in a single model. Moreover, the structure of the graph allows efficient inference methods, making the system suitable for online applications. Results show that the proposed method provides significant improvement in the performance of the P300 speller by increasing the classification accuracy while reducing the number of flash repetitions.
2. Proposed method
2.1. Overview of the proposed graphical model
The proposed model is shown in figure 1. The model represents a hierarchical structure in which different aspects of the P300 speller system are integrated. The bottom layer (first layer) represents the EEG signal. The variables xi,j represent the EEG signal recorded during the intensification of each row and column (a total of twelve variables for each spelled letter). The index i is used to identify the number of the letter being spelled and the index j represents a row or column (j = {1, …, 6} for rows and j = {7, …, 12} for columns). The second layer contains a set of twelve variables ci,j indicating the presence or absence of the P300 potential for a particular flash. Each ci,j is a binary variable taking values form the set C ∈ {0, 1}. The sub-graph formed by the nodes ci,j and xi,j and the edges between them encode conditional dependence that can be expressed as:
| (1) |
where F1,j is a probability density function (pdf4) with parameters θ1. Note that the structure of the graph allows the possibility of having a different set of parameters for each pdf associated with each row–column combination. This feature of the model could be beneficial if there is evidence that the characteristics of the P300 vary with the spatial position of the row or column that is highlighted. Otherwise, the parameters can be shared between the nodes ci,j, which would allow learning a single set of parameters making use of all available data and then to use those parameters for all the conditional densities in (1). This is the approach we follow in our experiments.
Figure 1.
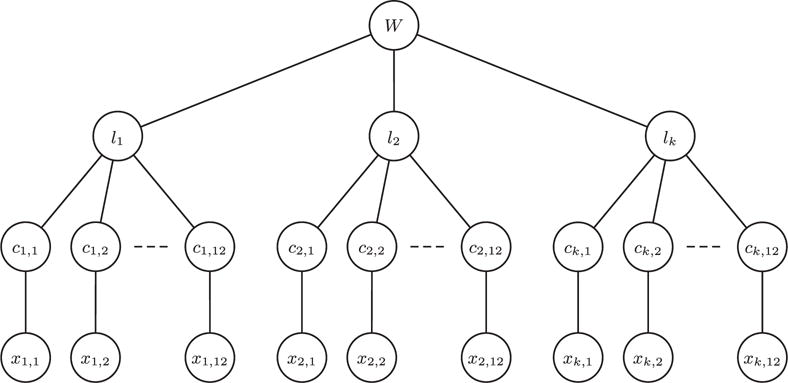
Proposed graphical model framework for the P300 speller. The bottom layer represents the brains signals, the second layer represents the presence or absence of P300 in each row or column of the speller matrix, the third layer represents the spelled letter and the top layer represent the word that the subject intends to communicate.
The third layer contains variables li representing the letter being spelled. The variables li are related to the variables ci,j in the same fashion as in traditional P300 speller systems: the presence of a P300 potential in a particular row–column pair encodes one letter. However, given that the detection of P300 potentials is not perfect (false detection or miss-detection of P300 potentials), a probabilistic approach is taken:
| (2) |
where F2 is a probability density function with parameters θ2.
The fourth layer contains the variable w which represents valid words in the English language. The learned distribution of this variable is used as a language prior. The conditional dependence between w and li can be expressed as:
| (3) |
where F3 is a probability density function with parameters θ3. At the level of the variable w the system predicts the target word based on the current number of letters spelled while at the level of the variables li the variable w imposes a prior on the sequence of letters which has the potential to reduce the error rate by forcing the sequence of letters to be a valid sequence in the language. Furthermore, the system does not make greedy assignments which implies that when a new letter is spelled by the subject, this information can be used to update the belief about the previously spelled letters.
2.2. Detailed description of the proposed model
The distributions of the variables (w, l = {l1, …, lk }, c = {c1,1:12, …, ck,1:12}) given the observations (x = {x1,1:12, …, xk,1:12}) can be written as a product of factors over all the nodes and edges in the graph:
| (4) |
where Ψ4 is the potential function for node w, Ψ3 is the potential function for the edge connecting node w with node li, Ψ2 is the potential function for the edge connecting node li with node ci,j, Ψ1 is the potential function for node ci,j, and Z is the partition function, which is a normalization factor. The potential functions in equation (4) are defined as follows:
| (5) |
| (6) |
| (7) |
| (8) |
where d is the dimensionality of the data. The parameter θ4 is a vector of weights of length equal to the number of states of the node w (i.e., the number of words in the dictionary). The element wise product θ4f4 (w) models a prior for the probability of a word in the language with the feature function f4 (w) = 1{w}, where 1{w} is a vector of length equal to the number of words in the dictionary, with a single nonzero entry of value 1 at the location corresponding to the argument of f4.
The element wise multiplication measures the compatibility between a word and a letter li appearing in the ith position of that word. The feature function we use here is . Where is a matrix of size equal to the number of states in the node li (i.e., letters in the spelling matrix) by the number of states in the node w. This matrix has a non-zero entry in the position li, w. The weights have the same size as f3 (i, w, li), and are binary valued, with non-zero entries where, based on the language statistics, lm,i = wk(i), where m indexes a particular letter in the ith position of each word wk. Note that is a different matrix for each value of i.
The element wise multiplication measures the compatibility between the variable ci,j and the variable li with the feature function The term is a matrix of size equal to the number of states in the node ci, j by the number of states in the node l, with non-zeros entries in the position {ci,j, li}. The term is a matrix of the same size as f2 (j, li, ci,j), with non-zero entries in positions according to a code-book that maps the intersections of rows and columns in the spelling matrix to letters. For instance, the entry for A in the code-book assuming a spelling matrix containing A on its top left corner would be CB(A, 1: 12) = {100000100000}.
The product is a measure of the compatibility of the mth element of the EEG signals xi,j ∈ Rd with the variable ci,j. Here we use the feature function . Where is a real number and is a vector of size one by the number of states in the node ci,j with a non-zero entry in the position ci,j. The term has the same size as and the values for each one of its elements are learned in the way explained below, in the section model selection.
Learning in the model corresponds to finding the set of parameters Θ = {θ4, θ3, θ2, θ1} that maximizes the log-likelihood of the conditional probability density function described in equation (4). Given that the structure of the model does not involve loops, inference in the model can be made using the belief propagation algorithm which can efficiently provide the marginals of interest:
| (9) |
| (10) |
Such marginals can be used respectively to declare the word or letter that the subject intends to communicate. In this model, a word is declared according to:
| (11) |
and in the same fashion letters are declared according to:
| (12) |
Note that although the word level inference has to produce words existing in our dictionary, it is in principle possible for the letter-level inference to produce sequences of letters that constitute words that are not in the specific dictionary used to train the model.
3. Description of experiments and methods
3.1. Problem and data set description
In a typical P300 spelling session, the subject sits upright in front of a screen observing a matrix of letters. The task involves focusing attention on a specific letter of the matrix and counting the number of times the character is intensified. The EEG signals were recorded using a cap embedded with 64 electrodes according to the modified 10–20 system of Sharbrough et al [17]. All electrodes were referenced to the right earlobe and grounded to the right mastoid. All aspects of the data collection and experimental control were controlled by the BCI2000 system [18]. From the total set of electrodes a subset of 16 electrodes in positions F3, Fz, F4, FCz, C3, Cz, C4, CPz, P3, Pz, P4, PO7, PO8, O1, O2, Oz were selected, motivated by the study presented in [6]. The classification problem is to declare one letter out of 26 possible letters in the alphabet. In total, each subject spelled 32 letters (nine words). Each subject participated in training and testing sessions held on different days.
Two kinds of experiments were executed by the subjects. First, eight subjects were instructed to spell words, one by one. In this scenario (which we call screening) the number of letters that form the word that the subjects should spell is known a priori. In the second scenario (which we call continuous decoding), seven subjects were requested to write words in a continuous fashion, using the character ‘−’ as a mark for end-of-word.
3.2. Signal pre-processing
The EEG signals were sampled at 240 Hz. Segments of 600ms following the intensification of each row or column were selected. For each segment and each electrode, the EEG signal was initially de-trended by removing a linear fit from the signal. The de-trended signals were then filtered between 0.5 and 20 Hz using a zero-phase IIR filter of order 8 and decimated at 40 Hz. Signals from all electrodes were concatenated and used as the inputs for the classifier during training. For testing, the segments were averaged across repetitions (up to 15 repetitions) and fed to the classifier. This allows to determine the performance as a function of the number of repetitions.
3.3. Model selection
Referring to section 2.2, the set of parameters in equations (5)–(7) are independent of the brain signals and can be learned before the recording of the brain signals. The language-dependent set of parameters θ4 are learned by calculating the relative frequency of each word in the language. The parameters are binary valued matrices with its entries taking values of one or zero depending of the presence or absence of a letter in the ith position of a word. The statistics involve in the determination of θ4 and can be learned from a text corpus. However, the structure of the model allows to select a dictionary based on the specific application of the BCI system. This means that the number of words in the dictionary can be adjusted to satisfy particular requirements of the application. In this work, the statistics about the language were calculated using the Corpus of Contemporary American English [19] which contains 450 million words. The dictionary was then built using the 5000 words most frequently used in the English language. Note that further reducing the number of words has a positive impact on the performance of the BCI system, as long as the limited dictionary captures the diversity of words in the intended application domain. The node w in figure 1 contains 5000 states, one for each word in the dictionary. As described previously, the parameters represent a matrix that encode how each state of the variable ci,j is related to each letter li. Note that the parameters θ2 do not depend on i, the position of a letter in a word.
The parameters θ1 are the set of parameters that maximize the potential function Ψ1 (j, ci,j, xi,j) in equation (8) for each class (i.e., P300 versus not P300). In order to obtain a robust estimation of the parameters θ1, the parameters are shared across nodes. This assumes that the generation of the P300 is independent of the position of the letter in the matrix. Therefore, the parameters are the same for any value of j. For learning, we use a nonlinear optimization method based on the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm.
3.4. Classification Problem
In the screening experiments, eight subjects are requested to spell a number of words one by one with pauses between words. The end of the spelling of a word is determined by the system, therefore the number of letters forming each word is known a priori. Each word is then classified by restricting the dictionary to words that match the length of the current spelled word. It is expected that this information will increase the classification performance.
The experiments with continuous decoding match the conditions of real life operation of the P300 speller system. In this scenario, the number of letters that form a word are not known to the system and the subject uses the character ‘−’ as an indicator of end-of-word. The algorithm proposed works as follows: given n spelled letters l1, …, ln, the algorithm computes the most likely word with l1, …, ln as initial letters to provide online feedback. If the most likely sequence of letters ends with the character ‘−’ the word is declared and the next spelled letter is assumed to be the first letter of the next word. The number of subjects for the continuous decoding experiment was 7.
In both scenarios (screening and continuous decoding), the classification performance is calculated by counting the correct number of letters spelled by the subjects rather than words, in order to provide a fair comparison with methods that do not use word-level language modeling.
4. Results
The proposed method is compared to a letter-level language model-based BCI approach using 3 g for modeling letter sequences. The classification of P300 potentials is left unchanged and the modeling of the language is made based on a 3 g method that makes use of statistics on sequences of 3 letters in the language. The graphical model for the 3 g method is presented in figure 2. Also for reference, results based on a common method used in the context of P300, the SWLDA [20], are also shown. Classification results are presented in figure 3 for the average accuracy across subjects and in figures 4 and 5 for the screening scenario and continuous coding scenario respectively. The proposed method produces an average accuracy of 99% across all subjects for the screening scenario and 96% in the continuous decoding scenario, with as few as 8 repetitions. In order to verify the results of correct classification accuracy, a statistical test was performed. For the screening scenario, a repeated measures ANOVA on the performance results reveals significant difference (F (2, 14) = 15.05, ɛ = 0.56, p = 0.0041, non-sphericity correction [21]) between the three compared methods. Using a post hoc Tukey–Kramer test, the proposed method performs significantly better (p < 0.01) than the 3 g based method and than SWLDA (p < 0.01). The 3 g based method (as expected) performs significantly better (p < 0.01) than SWLDA. For the continuous decoding scenario the results are similar: repeated measures ANOVA reveals significant difference (F (2, 12) = 9.15, ɛ = 0.69, p = 0.01150, non-sphericity correction) between the compared methods. Using a post hoc Tukey–Kramer test, the proposed method performs significantly better (p < 0.01) than the 3 g based method and than SWLDA, and the 3 g based method performs significantly better (p < 0.01) than SWLDA.
Figure 2.
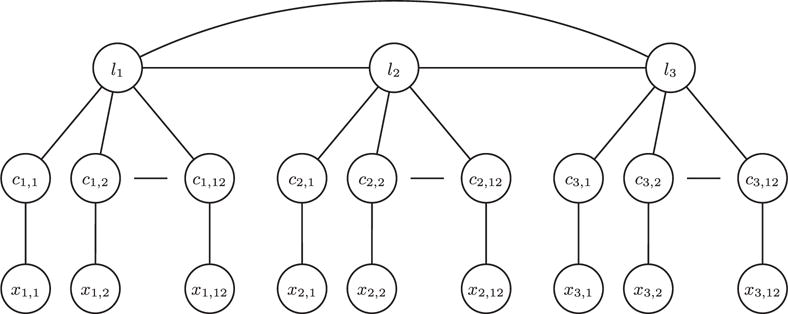
Example of a 3 g model for a 3 letter word. Note that this graph models the language to the level of letters.
Figure 3.
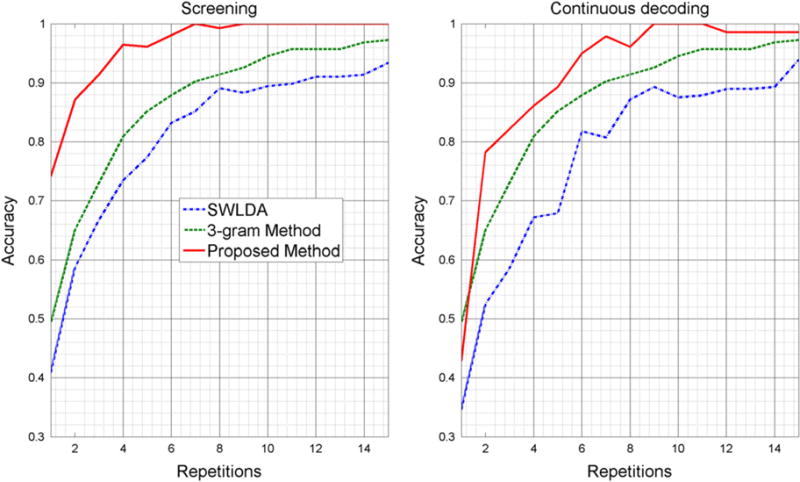
Average classification accuracy across subjects.
Figure 4.
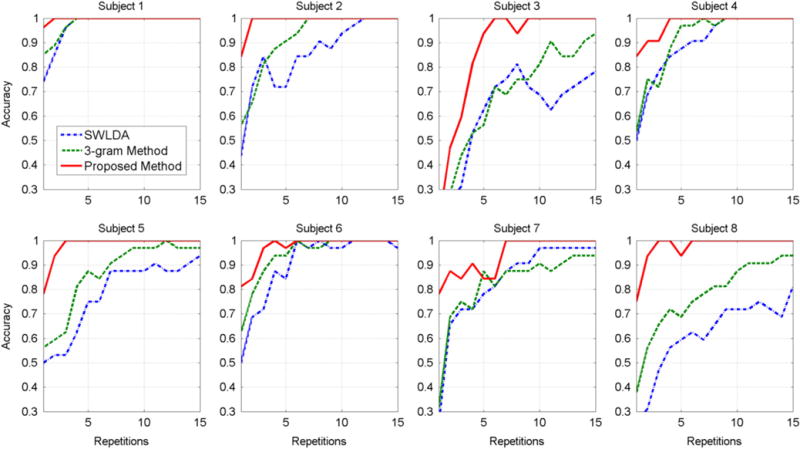
Accuracy as a function of the number of repetitions, for all subjects, in the screening scenario.
Figure 5.
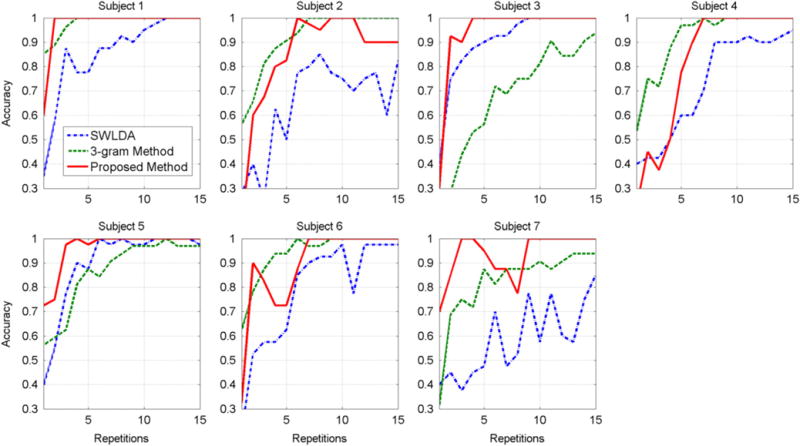
Accuracy as a function of the number of repetitions, for all subjects, in the continuous decoding scenario.
5. Discussion
The proposed method attempts to solve several problems of the P300-based BCI speller systems by integrating in a probabilistic model all variables in the P300 system from brain signals to the words spelled by the subject. This framework would allow one to build up any language model in a consistent way. The 3 g method in figure 2 makes use of a probabilistic framework as well. The 3 g method is presented for comparison given the popularity of the language models based on n g [10, 13, 15]. Note that methods based on n g found in the literature need to incorporate separated modules for classification of the P300 and language modeling which is not the case with the proposed method.
The construction of the proposed method enables the learning of the parameters of different parts of the model in an independent fashion, which reduces the complexity of the learning process. The main differences with other methods that include language modeling by means of n g (i.e. 3 g) are (1) probabilities of all previously spelled letters are used to predict the word. This implies that the method does not fix the final estimate of the letters before the whole word is declared. This allows to correct misspelt letters in the past, based on current letters. That is, the decoding of the currently spelled letter by the subject could provide strong evidence that all or some of the letters spelled by the subject in the past were incorrect, (2) the language can be adapted to the subject or the task by limiting the vocabulary. As a result the performance of the system is increased while the the number of repetitions needed to achieve a level of practical usability of the system is reduced.
It is also worth noting that the structure of the model has been carefully designed to avoid loops, therefore, efficient inference algorithms such as belief propagation can be used without compromising the use of the model in online applications. Furthermore, the features used in the proposed model are not limited to the particular choices we made in our experiments: different approaches can be incorporated by redefining the feature function in equation (8) to incorporate any state-of-the-art signal processing methods into our word-level language model-based P300 spelling framework.
A practical implementation of this method, should take into consideration that although not very often, the language model could incorrectly replace the word that the subject intends to communicate. If this is a concern, we suggest that the user interface should display both, the sequence of letters decoded solely by the P300 potentials and the sequence of letters decoded using the prior information provided by the language model as well. This would be useful for the person reading the message as it would be easy to determine if the corrections performed by the system make sense given the context of the conversation.
6. Conclusion
We present a probabilistic framework, as well as an inference approach for P300-based spelling that exploits learned prior models of words. While language models at the level of letters have already been proposed for BCI, word-level statistical language modeling is, to the best knowledge of the authors, new. The structure of the model that we propose enables the use of efficient inference algorithms, making it possible to use our approach in real-time applications. While our approach can in principle be used with word prior models learned from any corpus, we expect it to be of great interest for applications involving the use of a limited vocabulary in a specific context. Note that although reducing the vocabulary could restrict the flexibility of the system, the increase in reliability could prove to be more significant. Furthermore, the proposed method can be extended by modeling the relationships between consecutive words, which could enable the system to correct entire sentences.
Acknowledgments
This work was partially supported by Universidad del Norte (Colombia), by the Scientific and Technological Research Council of Turkey under Grant 111E056, by Sabanci University under Grant IACF-11-00889, and by NIH grant EB00085605 (NIBIB).
Footnotes
Note that we use the term probability density function, rather than probability mass function for discrete random variables as well.
References
- 1.Wang M, Daly I, Allison B, Jin J, Zhang Y, Chen L, Wang X. A new hybrid {BCI} paradigm based on {P300} and {SSVEP} J Neurosci Methods. 2014 doi: 10.1016/j.jneumeth.2014.06.003. in press. [DOI] [PubMed] [Google Scholar]
- 2.Jin J, Allison B, Sellers E, Brunner C, Horki P, Wang X, Neuper C. An adaptive P300-based control system. J Neural Eng. 2011;8:036006. doi: 10.1088/1741-2560/8/3/036006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhou Z, Yin E, Liu Y, Jiang J, Hu D. A novel task-oriented optimal design for P300-based brain-computer interfaces. J Neural Eng. 2014;11:056003. doi: 10.1088/1741-2560/11/5/056003. [DOI] [PubMed] [Google Scholar]
- 4.Donchin E, Spencer K, Wijesinghe R. The mental prosthesis: assessing the speed of a P300-based brain-computer interface. IEEE Trans Rehabil Eng. 2000;8:174–9. doi: 10.1109/86.847808. [DOI] [PubMed] [Google Scholar]
- 5.Bashashati A, Fatourechi M, Ward R, Birch G. A survey of signal processing algorithms in brain-computer interfaces based on electrical brain signals. J Neural Eng. 2007;4:R32. doi: 10.1088/1741-2560/4/2/R03. [DOI] [PubMed] [Google Scholar]
- 6.Krusienski D, Sellers E, McFarland D, Vaughan T, Wolpaw J. Toward enhanced P300 speller performance. J Neurosci Methods. 2008;167:15–21. doi: 10.1016/j.jneumeth.2007.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Manyakov N, Chumerin N, Combaz A, Marc HVM. Comparison of classification methods for P300 brain-computer interface on disabled subjects. Intell Neurosci. 2011;2011:2–1. doi: 10.1155/2011/519868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kindermans P, Verschore H, Verstraeten D, Schrauwen B. A P300 BCI for the masses: prior information enables instant unsupervised spelling. Adv Neural Inf Process Syst. 2012;25:9. [Google Scholar]
- 9.Speier W, Arnold C, Pouratian N. Evaluating true bci communication rate through mutual information and language models. PLoS One. 2013;8:e78432. doi: 10.1371/journal.pone.0078432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Orhan U, Erdogmus D, Roark B, Purwar S, Hild KE, Oken B, Nezamfar H, Fried-Oken M. Fusion with language models improves spelling accuracy for erp-based brain computer interface spellers. EMBC Ann Int Conf IEEE (Boston, MA) 2011:5774–7. doi: 10.1109/IEMBS.2011.6091429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mathis T, Spohr D. Corpus-driven enhancement of a bci spelling component. Int Conf on Recent Advances in Natural Language Processing (Borovets, Bulgaria) 2007 [Google Scholar]
- 12.Ahi ST, Kambara H, Koike Y. A dictionary-driven P300 speller with a modified interface. IEEE Trans Neural Syst Rehabil Eng. 2011;19:6–14. doi: 10.1109/TNSRE.2010.2049373. [DOI] [PubMed] [Google Scholar]
- 13.Speier W, Arnold C, Lu J, Taira R, Pouratian N. Natural language processing with dynamic classification improves P300 speller accuracy and bit rate. J Neural Eng. 2012;9:016004. doi: 10.1088/1741-2560/9/1/016004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Orhan U, Erdogmus D, Roark B, Oken B, Fried-Oken M. Offline analysis of context contribution to erp-based typing bci performance. J Neural Eng. 2013;10:066003. doi: 10.1088/1741-2560/10/6/066003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ulas C, Cetin M. Incorporation of a language model into a brain computer interface based speller through HMMs. IEEE Int Conf on Acoustics Speech and Signal Processing (Vancouver, Canada) 2013:1138–42. [Google Scholar]
- 16.Speier W, Arnold C, Lu J, Deshpande A, Pouratian N. Integrating language information with a hidden Markov model to improve communication rate in the P300 speller. IEEE Trans Neural Syst Rehabil Eng. 2014;22:1–1. doi: 10.1109/TNSRE.2014.2300091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sharbrough F, Chatrian GE, Lesser RP, Lüders H, Nuwer M, Picton TW. American electroencephalographic society guidelines for standard electrode position nomenclature. J Clin Neurophysiol. 1991;8:200–2. [PubMed] [Google Scholar]
- 18.Schalk G, McFarland D, Hinterberger T, Birbaumer N, Wolpaw J. BCI2000: a general-purpose brain-computer interface (BCI) system. IEEE Trans Biomed Eng. 2004;51:1034–43. doi: 10.1109/TBME.2004.827072. [DOI] [PubMed] [Google Scholar]
- 19.University Brigham-Young. Corpus of Contemporary American English. 2012 www.corpus.byu.edu/coca.
- 20.Krusienski D, Sellers E, Cabestaing F, Bayoudh S, McFarland D, Vaughan T, Wolpaw J. A comparison of classification techniques for the P300 speller. J Neural Eng. 2006;3:299. doi: 10.1088/1741-2560/3/4/007. [DOI] [PubMed] [Google Scholar]
- 21.Howell D. Statistical Methods for Psychology (International edition) 7th. Belmont: Wadsworth Publishing; 2009. [Google Scholar]


