Accelerating the weighted histogram analysis method by direct inversion in the iterative subspace

Abstract

The weighted histogram analysis method (WHAM) for free energy calculations is a valuable tool to produce free energy differences with the minimal errors. Given multiple simulations, WHAM obtains from the distribution overlaps the optimal statistical estimator of the density of states, from which the free energy differences can be computed. The WHAM equations are often solved by an iterative procedure. In this work, we use a well-known linear algebra algorithm which allows for more rapid convergence to the solution. We find that the computational complexity of the iterative solution to WHAM and the closely-related multiple Bennett acceptance ratio (MBAR) method can be improved by using the method of direct inversion in the iterative subspace. We give examples from a lattice model, a simple liquid and an aqueous protein solution.

1. Introduction

An important problem in computational physics and chemistry is to obtain the best estimate of a quantity of interest from a given set of data[1]. For free energy calculations, the multiple histogram method[2–5] or its generalisation, the weighted histogram analysis method (WHAM)[1, 6–17], is an effective tool for addressing such a problem. WHAM is statistically efficient in using the data acquired from molecular simulations, and it has become a standard free energy analysis tool, particularly popular for enhanced-sampling simulations, such as umbrella sampling[18, 19], and simulated[20, 21] and parallel[22–26] tempering.

Given several distributions collected at different thermodynamic states, WHAM obtains the optimal estimate of the free energies of the states. This problem arises in the calculation of potentials of mean force and a variety of free energy difference methods. The central idea of WHAM is to find an optimal estimate of the density of states, or the unbiased distribution, which then allows the free energies to be evaluated as weighted integrals. The optimal density of states is computed from a weighted average of the reweighted energy histograms (hence the name of the method) from different distribution realisations or trajectories. The weights, however, depend on the free energies, so that the free energies and the density of states must be determined self-consistently.

WHAM can be reformulated[1, 17] in the limit of zero histogram bin width as an extension of the Bennett acceptance ratio (BAR) method[27]. This form, adopted by the multistate BAR (MBAR) method[1], avoids the histogram dependency[1, 6, 12].

The straightforward implementation of WHAM or MBAR, in which the equations regarding the free energies are solved by direct iteration, can suffer from slow convergence in the later stages[14, 16, 28]. Several remedies have been proposed[1, 14, 16, 28, 29]. For example, one may use the Newton-Raphson method, which involves a Hessian-like matrix, although the approach sometimes can be unstable[1]. Other more advanced techniques include the trust region and Broyden-Fletcher-Goldfarb-Shanno (BFGS) methods[16].

An elegant non-iterative alternative is the statistical-temperature WHAM (ST-WHAM)[28, 29], which determines the density of states through its logarithmic derivative, or the statistical temperature. In this way, the method estimates the density of states non-iteratively with minimal approximation. ST-WHAM can be regarded as a refinement of the more approximate umbrella integration method (UIM)[30, 31]. However, the extension to multidimensional ensembles, e.g., the isothermal-isobaric ensemble, can be numerically challenging[28].

Here, we discuss a numerical improvement of the implementation of WHAM and MBAR using the method of direct inversion in the iterative subspace (DIIS)[32–36]. DIIS shares characteristics with other optimisation techniques which use a limited (non-spanning) basis of vectors which produce the most gain towards the optimum. Although still iterative in nature, this implementation can often improve the rate of convergence significantly in difficult cases.

2. Method

2.1. WHAM

WHAM is a method of estimating the free energies of multiple thermodynamic states with different parameters, such as temperatures, pressures, etc. Below, we shall first review WHAM in the particular case of a temperature scan, since it permits simpler mathematics without much abstraction. Generalisations to umbrella sampling and other ensembles are discussed afterwards.

Consider K temperatures, labelled by β = 1/(k_BT), as β₁, …, β_K. Suppose we have performed the respective canonical (NVT) ensemble simulations at the K temperatures, and we wish to estimate the free energies at those temperatures.

In WHAM, we first estimate the density of states, g(E) = ∫ δ(ℰ(x) − E) dx, as the number density of configurations, x, with energy E, from

$$g(E)=\frac{{\sum }_{k=1}^K{n}_k(E)}{{\sum }_{k=1}^K{N}_k\text{exp}(-{\beta }_{k}E)/Z_k},$$ (1)

where n_k(E) is the unnormalised energy distribution observed from trajectory k, which is usually estimated from the energy histogram as the number of independent trajectory frames whose energies fall in the interval (E − ΔE/2, E + ΔE/2) divided by ΔE (we shall omit “independent” below for simplicity); thus, n_k(E)/N_k is the normalised distribution with N_k being the total number of trajectory frames from simulation k; and finally,

$$\text{exp}(-f_k)=Z_k=\int g(E)\text{ exp}(-{\beta }_{k}E)dE,$$ (2)

with f_k and Z_k being the dimensionless free energy and partition function, respectively.

To understand Eq. (1), we first observe from the definition the single histogram estimate

$$g(E)=\frac{n_k(E)}{d_k(E)}\text{ for }k=1,\dots ,K,$$ (3)

where d_k(E) ≡ N_k exp(−β_kE + f_k). That is, the observed distribution, n_k(E)/N_k, should roughly match the exact one, g(E) w_k(E), where w_k(E) ≡ exp(−β_kE + f_k) is the normalised weight of the canonical ensemble. The values of Eq. (3) from different k can be combined to improve the precision, and Eq. (1) is the optimal combination[4, 5, 7, 12, 13]. To see this, recall that in an optimal combination, the relative weight is inversely proportional to the variance. Assuming a Poisson distribution so that var(n_k ΔE) ≈ 〈n_k〉 ΔE, we have $\text{var}(n_k\mathrm{\Delta }E/d_k)\approx \langle n_k\rangle \mathrm{\Delta }E/d_k^2\propto 1/d_k$ (here, 〈⋯〉 means an ensemble average). Averaging the values from Eq. (3) using (1/d_k)⁻¹ as the relative weight yields Eq. (1).¹ Since for a fixed E, d_k(E) is proportional to 〈n_k(E)〉, several variants of WHAM may be derived by using n_k(E) in place of d_k(E) as the relative weight for g(E)[37] or related quantities[7, 28–31, 38, 39].

From Eqs. (1) and (2), we find that f_i satisfies

$$f_i=-\text{log}\int \frac{{\sum }_{k=1}^K{n}_k(E)\text{ exp}(-{\beta }_{i}E)}{{\sum }_{k=1}^K{N}_k\text{ exp}(-{\beta }_{k}E+f_k)}dE\equiv -\text{log }{𝒵}_i(\mathbf{f}),$$ (4)

where 𝒵_i(f) denotes the integral on the right-hand side as a function of f = (f₁, …, f_K). Once all f_i and g(E) are determined, the free energy at a temperature not simulated, β, can be found from Eq. (2) by substituting β for β_k.

Histogram-free form

The histogram dependency of WHAM [in using n_k(E)] can be avoided by noticing from definition that[12]

$$n_k(E)=\sum _{\mathbf{x}}^{(k)}\delta (ℰ(\mathbf{x})-E),$$ (5)

where, ℰ(x) is the energy function, and ${\sum }_{\mathbf{x}}^{(k)}$ denotes a sum over trajectory frames of simulation k. Using Eq. (5) in Eq. (4) yields the histogram-free, or the MBAR, form[1, 6, 12, 17]:

$$f_i=-\text{log}\sum _{j=1}^K\sum _{\mathbf{x}}^{(j)}\frac{q_i(\mathbf{x})}{{\sum }_{k=1}^K{N}_k{q}_k(\mathbf{x})\text{exp}(f_k)}.$$ (6)

where q_i(x) ≡ exp[−β_i ℰ(x)]. The K = 2 case is the BAR result[27], and Eq. (6) also holds for a general setting, which permits, e.g., a nonlinear parameter dependence (see Appendix A for derivation). In this sense, MBAR is not only the zero-bin-width limit of WHAM[1, 17], but also a generalisation[1]. As we shall see, the structural similarity of Eqs. (4) and (6) allows our acceleration technique to be applicable to both cases. Since both Eqs. (4) and (6) are invariant under f_i → f_i + c for all i and an arbitrary c, f_i are determined only up to a constant shift.

Extensions to umbrella sampling

We briefly mention a few extensions. First, for a general Hamiltonian with a linear bias

$$\mathscr{H}(\mathbf{x};{\lambda }_i)={\mathscr{H}}_0(\mathbf{x})+{\lambda }_i𝒲(\mathbf{x}),$$

such that q_i(x) = exp [−ℋ(x; λ_i)], we can show, by inserting 1 = ∫ δ(𝒲(x) − W) dW into Eq. (6), that

$$f_i=-\text{log}\int \frac{{\sum }_{k=1}^K{n}_k(W)\text{ exp}(-{\lambda }_{i}W)}{{\sum }_{k=1}^K{N}_k\text{ exp}(-{\lambda }_{k}W+f_k)}dW,$$

where $n_k(W)\equiv {\sum }_{\mathbf{x}}^{(k)}\delta (𝒲(\mathbf{x})-W)$ is understood to be the unnormalised distribution of the bias 𝒲(x). Equation (4) is the special case of ℋ₀(x) = 0, 𝒲(x) = ℰ(x), and λ_i = β_i. Another common example is a system under a quadratic restraint (umbrella) ${ℰ}_i={ℰ}_0+\frac{1}{2}A{(\xi -{\lambda }_i)}^2$ for some reaction coordinate ξ ≡ ξ(x). In this case, ${\mathscr{H}}_0(\mathbf{x})=\beta ({ℰ}_0+\frac{1}{2}A{\xi }^2)$, and 𝒲(x) = −βAξ. The configuration independent term, $\frac{1}{2}\beta A{\lambda }_i^2$, can be added back to f_i after the analysis.

Extensions to other ensembles

Further, λ_i and W can be generalised to vectors as λ_i and W, respectively. For example, for simulations on multiple isothermal-isobaric (NpT) ensembles with different temperatures and pressures, we set λ_i = (β_i, β_ip_i) and W = (E, V) with p_i and V being the pressure and volume, respectively. However, if the vector dimension is high, or if the Hamiltonian ℋ(x; λ_i) depends nonlinearly on λ_i, the histogram-free form, Eq. (6), is more convenient[1]. Besides, the factor exp(−β_i E) can be replaced by a non-Boltzmann (e.g., the multicanonical[40–42], Tsallis[43], microcanonical[44, 45]) weight for multiple non-canonical simulations[28].

Solution by iteration

Numerically, the f_i are most often determined by treating Eq. (4) as an iterative equation,

$$f_i^{(\text{new})}=-\text{log }{𝒵}_i\left({\mathbf{f}}^{(\text{old})}\right).$$

However, this approach, referred to as direct WHAM below, can take thousands of iterations to finish[14, 16, 28] (cf. Appendix B). In Secs. 2.3 and 2.4, we give a numerical technique to accelerate the solution of Eq. (4) or (6).

2.2. ST-WHAM and UIM

For comparison, we briefly discuss two non-iterative alternatives, ST-WHAM[28, 29] and UIM[30, 31]. By taking the logarithmic derivative of the denominator of Eq. (1), we get,

$$\frac{d}{dE}\text{log}\sum _{k=1}^K{d}_k(E)=-\frac{{\sum }_{k=1}^K{d}_k(E){\beta }_k}{{\sum }_{k=1}^K{d}_k(E)}=-\frac{{\sum }_{k=1}^K{n}_k(E){\beta }_k}{{\sum }_{k=1}^K{n}_k(E)},$$

where we have used Eq. (3) to make the final expression independent of d_k(E), hence f_k. So

$$g(E)=[\sum _{k=1}^K{n}_k(E)]\text{ exp }[{\int }^E\frac{{\sum }_{k=1}^K{n}_k(E\prime ){\beta }_k}{{\sum }_{k=1}^K{n}_k(E\prime )}dE\prime ].$$

This is the ST-WHAM result. In evaluating the integral, we may encounter an empty bin with ${\sum }_{k=1}^K{n}_k(E\prime )\mathrm{\Delta }E=0$, which leaves the integrand indeterminate. An expedient fix is to let the integrand borrow the value from the nearest non-empty bin [note, however, setting the integrand to zero would cause a larger error in g(E)]. ST-WHAM is most convenient in one dimension, and its results usually differ only slightly from those of WHAM[28]. In UIM[30, 31], the distribution n_k(E) is further approximated as a Gaussian. We note that ST-WHAM is difficult when we have more thermodynamic variables in the ensemble of interest. Below we show that WHAM with the DIIS method can handle such a case for the Lennard-Jones (LJ) fluid, readily.

2.3. DIIS

DIIS is a technique useful for solving equations[32–36], and we use it to solve Eq. (4) here. A schematic illustration is shown in Fig. 1. We first represent an approximate solution by a trial vector, f = (f₁, …, f_K), which is, in our case, the vector of the dimensionless free energies. The target equations can be written as

$$R_i(\mathbf{f})=0\text{ for }i=1,\dots ,K,$$ (7)

which is −log 𝒵_i (f) − f_i in our case. The left-hand side of Eq. (7) also forms a K-dimensional vector, R = (R₁, …, R_K), which is referred to as the residual vector. The magnitude ‖R‖ represents the error, and R(f) should optimally point in a direction that reduces the error of f.

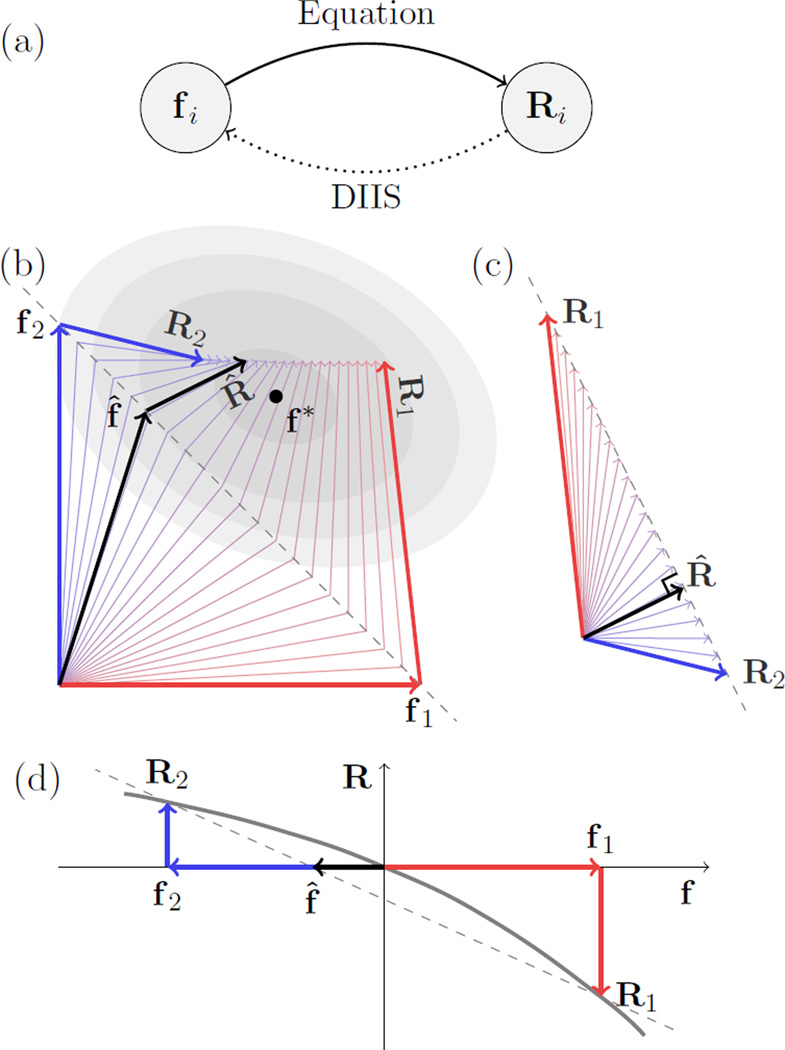
Figure 1.

Schematic illustrations of the method of direct inversion of the iterative subspace (DIIS). (a) As an iterative method, DIIS solves the equation, R(f) = 0, by a feedback loop. When the equation is applied to a trial solution, represented by vector f_i, we get a residual vector R_i ≡ R(f_i), whose magnitude indicates the error. Ideally, if f_i were the true solution, R_i would be zero. In the feedback step, we correct f_i using R_i. The task of DIIS is to construct from a few previous vectors accumulated during the iteration an optimal trial vector f̂ with hopefully the smallest error ‖R̂‖ to help the next round of iteration. (b) and (c) Given a basis of M (two here) trial vectors, DIIS seeks the combination $\hat{\mathbf{R}}={\sum }_{i=1}^M{c}_i{\mathbf{R}}_i$ that minimises the magnitude ‖R̂‖ under the constraint ${\sum }_{i=1}^M{c}_i=1$ [panel (c)]. The corresponding combination of the trial vectors, $\hat{\mathbf{f}}={\sum }_{i=1}^M{c}_i{\mathbf{f}}_i$, is expected to be close to true solution, f*. Then, we construct the new trial vector as f⁽ⁿ⁾ = f̂ + R̂ and use it to update the basis for the next round of iteration. (d) If the vectors are one-dimensional (i.e., scalars), it is possible to find a vanishing R̂, and DIIS is equivalent to the secant method.

If Eq. (7) is solved by direct iteration, f is replaced by f + R(f) in each time. This can be a slow process because the residual vector R does not always have the proper direction and/or magnitude to bring f close to the true solution f*. The magnitude of R, however, can be used as a reliable measure of the error of f. Thus, in DIIS, we try to find a vector f̂ with minimal error ‖R(f̂)‖, which would be more suitable for direct iteration.

Suppose now we have a basis of M trial vectors f₁, … f_M (where M can be much less than K), and the residual vectors are R₁, … R_M [where R_j ≡ R(f_j) for j = 1, …, M], respectively. We wish to construct a vector f̂ with minimal error from a linear combination of the trial vectors.

To do so, we first find the combination of the residual vectors $\hat{\mathbf{R}}={\sum }_{i=1}^M{c}_i{\mathbf{R}}_i$, that minimises the error ‖R̂‖ under the constraint

$$\sum _{i=1}^M{c}_i=1.$$ (8)

Mathematically, this means that we solve for the c_i simultaneously from Eq. (8) and

$$\sum _{j=1}^M({\mathbf{R}}_i·{\mathbf{R}}_j)c_j=\lambda ,$$ (9)

for all i, with λ being an unknown Lagrange multiplier that is to be determined from along with c_i. Now the corresponding combination of the trial vectors, $\hat{\mathbf{f}}={\sum }_{i=1}^M{c}_i{\mathbf{f}}_i$, should be close to the desired minimal-error vector. This is because around the true solution f*, Eq. (7) should be nearly linear; so the residual vector

$$\mathbf{R}(\hat{\mathbf{f}})=\mathbf{R}\left(\sum _{i=1}^M{c}_i{\mathbf{f}}_i\right)\approx \sum _{i=1}^M{c}_i\mathbf{R}({\mathbf{f}}_i)=\hat{\mathbf{R}},$$

has the minimal magnitude. In other words, f̂, among all linear combinations of {f_i}, is the closest to the true solution, under the linear approximation. Thus, an iteration based on f̂ should be efficient.

With M = K + 1 independent bases, one can show that it is possible to find a combination with zero R̂, which means that f̂ would be the true solution if the equations were linear. A particularly instructive case is that of two vectors (M = 2) in one dimension (K = 1)². We then recover the secant method[46], as shown in Fig. 1(d). The number of bases, M, however, should not exceed K + 1 (or, in our case, K because of the arbitrary shift constant of f_i) to keep Eqs. (9) independent, although this restriction may be relaxed by using certain numerical techniques[46].

We now construct a new trial vector f⁽ⁿ⁾ as

$${\mathbf{f}}^{(n)}=\hat{\mathbf{f}}+\alpha \hat{\mathbf{R}}(\hat{\mathbf{f}}),$$

where the factor α is 1.0 in this study (although a smaller value is recommended for other applications[35, 36]). The new vector f⁽ⁿ⁾ is used to update the basis as shown next.

2.4. Basis updating

In each iteration of DIIS, the basis is updated by the new trial vector f⁽ⁿ⁾ from the above step. Initially, the basis contains a single vector. As we add more vectors into the basis in subsequent iterations, some old vectors may be removed to maintain a convenient and efficient maximal size of M.

A simple updating scheme[35] is to treat the basis as a queue: we add f⁽ⁿ⁾ to the basis, if the latter contains fewer than M vectors, or substitute f⁽ⁿ⁾ for the earliest vector in the basis. If, however, f⁽ⁿ⁾ produces an error greater than K_r times the error of f_min, the least erroneous vector in the basis, we rebuild the basis from f_min. Here, the error of a vector f is defined as ‖R(f)‖, and K_r = 10.0 is recommended[35].

We used the following modification in this study. First, we find the most erroneous vector, f_max, from the basis. If the new vector, f⁽ⁿ⁾, produces an error less than f_max, we add f⁽ⁿ⁾ into the basis or, if the basis is full, substitute f⁽ⁿ⁾ for f_max. Otherwise, we remove f_max from the basis, and if this empties the basis, we rebuild the basis from f⁽ⁿ⁾.

Since the DIIS process is reduced to the direct iteration if M = 1, the method is effective only if multiple basis vectors are used.

3. Results

We tested DIIS WHAM and MBAR on three systems: Ising model, LJ fluid, and the villin headpiece (a small protein) in aqueous solution (see Secs. 3.2, 3.3, and 3.4, respectively, for details). We tuned the parameters such that direct WHAM and MBAR would take thousands of iterations to finish.

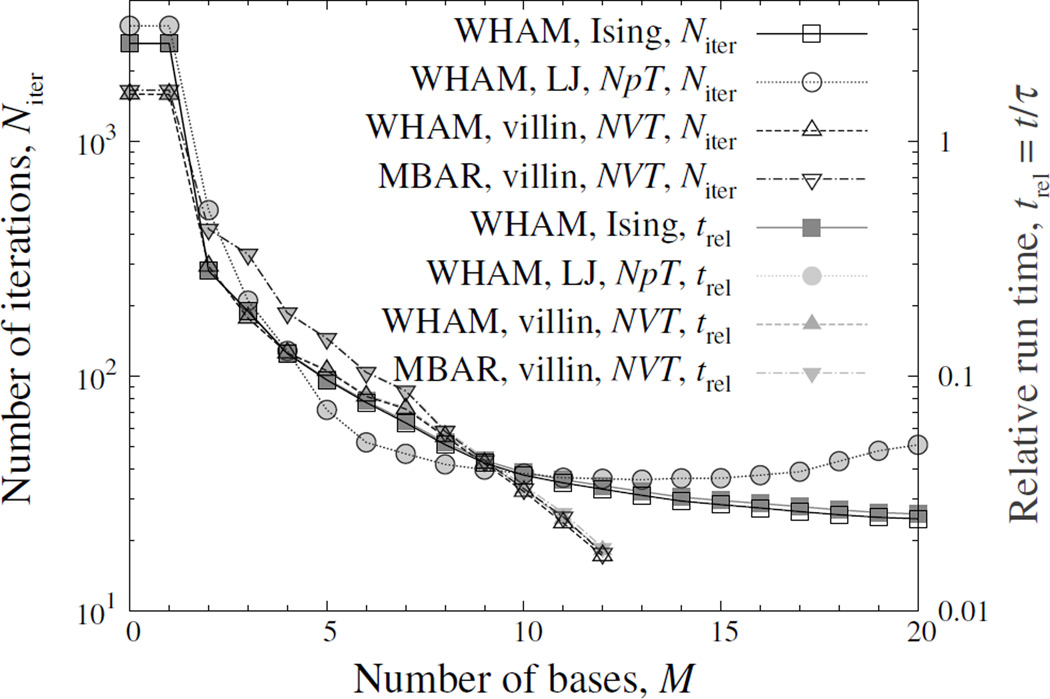
The main results are summarised in Fig. 2, from which one can see that DIIS can speed up WHAM and MBAR dramatically in these cases. The real run time roughly matched the number of iterations, suggesting a negligible overhead for using DIIS. This is unsurprising, for it is often much more expensive to compute the right-hand side of Eq. (4) or (6).

Figure 2.

Number of iterations and run time versus the number of bases, M, in DIIS. The four test cases are (1) WHAM on the Ising model, (2) WHAM on the LJ fluid in the NpT ensemble, (3) WHAM on the mini-protein villin headpiece in the NVT ensemble (with the bin width of energy histograms being 1.0), and (4) MBAR on the same protein system. The M = 0 points represent direct WHAM. The run times are inversely scaled by a factor τ for better alignment with the numbers of iterations. The scaling factors τ for cases 1–4 are 12.5, 1.87 × 10³, 14.3, and 260 seconds, respectively. The results were averaged over independent samples for the Ising model and LJ fluid. For the villin headpiece, the results were averaged over bootstrap[4, 15, 47] samples for WHAM, or over random subsamples with about 1% of the trajectory frames for MBAR. To mimic the correlation in the trajectories, each data point in the bootstrap sample is either randomly drawn from the trajectory, or the same as the previous one (if any) with probability exp(−Δt_MD/t_act), where Δt_MD and t_act are the time step of molecular dynamics and the autocorrelation time of the potential energy, respectively. Here, the error tolerance max{|R_i|} is 10⁻⁸. The lines are a guide for the eyes.

3.1. Set-up

For simplicity, we assumed equal autocorrelation times from different temperatures (and pressures). The approximation should not affect the convergence behaviour of the methods.

In testing WHAM and MBAR, the initial free energies were obtained from the single histogram method:

$$\mathrm{\Delta }{f}_i=\text{log}{\langle \text{exp}(\mathrm{\Delta }{\beta }_{i}E)\rangle }_{i+1},$$

where ΔA_i ≡ A_i+1 − A_i, for any quantity A, and 〈…〉_i+1 denotes an average over trajectory i + 1. Then, $f_i=f_1+{\sum }_{j=1}^{i-1}\mathrm{\Delta }{f}_j$. Iterations are continued until all |R_i| are reduced below a certain value.

For comparison, we also computed f_i from three approximate formulae. The first is[16, 48]

$$\mathrm{\Delta }{f}_i\approx {\overline{\langle E\rangle }}_i\mathrm{\Delta }{\beta }_i,$$ (10)

where Ā_i ≡ (A_i+1 + A_i)/2. The second is an improvement by the Euler-Maclaurin expansion[49–52]:

$$\mathrm{\Delta }{f}_i\approx {\overline{\langle E\rangle }}_i\mathrm{\Delta }{\beta }_i+({\langle \delta E^2\rangle }_{i+1}-{\langle \delta E^2\rangle }_i)\frac{\mathrm{\Delta }{\beta }_i^2}{12},$$ (11)

where 〈δE²〉_k ≡ 〈(E − 〈E〉_k)²〉_k for k = i and i + 1. The third formula is derived from the same expansion but using E instead of β as the independent variable (after integration by parts, ∫ E dβ = E β − ∫ β dE):

$$\mathrm{\Delta }{f}_i\approx {\overline{\langle E\rangle }}_i\mathrm{\Delta }{\beta }_i-({\langle \delta E^2\rangle }_{i+1}^{-1}-{\langle \delta E^2\rangle }_i^{-1})\frac{{(\mathrm{\Delta }{\langle E\rangle }_i)}^2}{12}.$$ (12)

3.2. Ising model

The first system is a 64 × 64 Ising model. We used parallel tempering[22–26] Monte Carlo (MC) for eighty temperatures: T = 1.5, 1.52, …, 3.08,

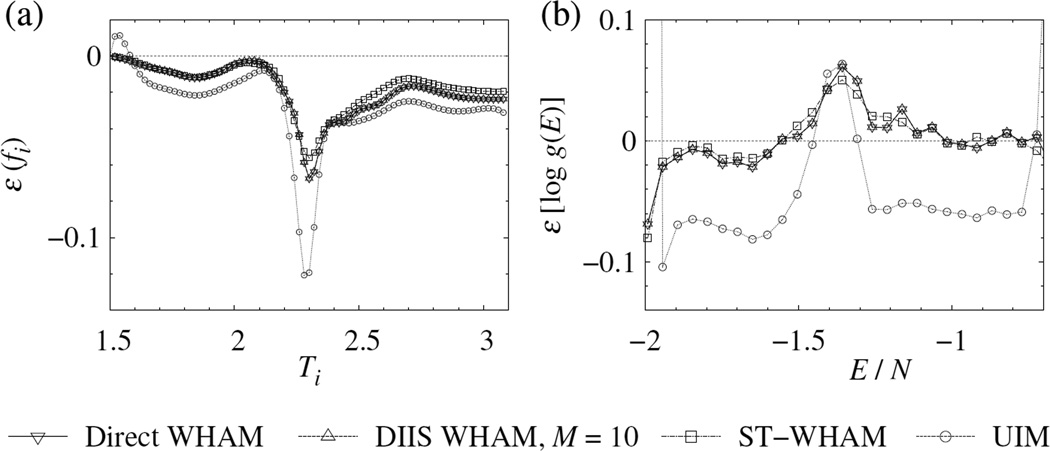
To study the accuracy, we generated a large sample with 10⁹ single-site MC steps for each temperature. Figure 3 shows that DIIS and direct WHAMs produced identical dimensionless free energies. The differences between the ST-WHAM and WHAM results were subtle, whereas the approximate UIM produced more deviation in the results, especially around the critical region.

Figure 3.

Errors of (a) the dimensionless free energies, f_i, and (b) the logarithmic density of states, log g(E), for the N = 64 × 64 two-dimensional Ising model (plotted with an energy spacing of 200). Here, ε(a) ≡ a − a^ref, and the reference values for f_i and g(E) were computed using the methods in Refs. [53] and [54], respectively. The bin size of the energy histograms is Δ E = 4. Lines are a guide for the eyes.

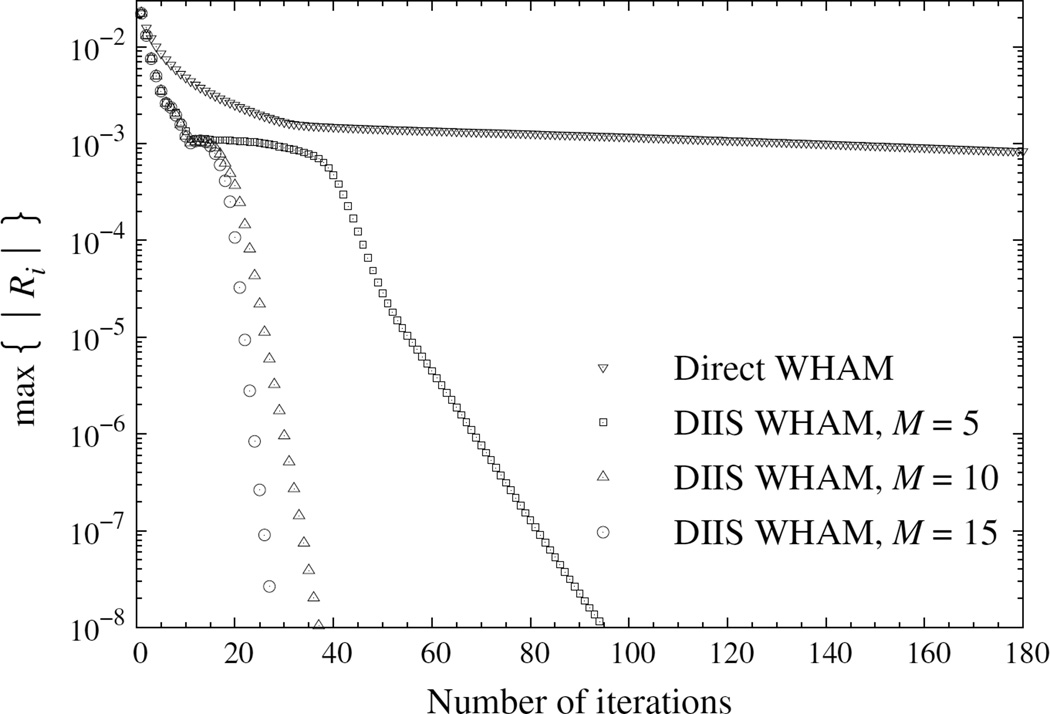
To study the rate of convergence, we generated independent samples with 10⁷ MC steps at each temperature. Figure 4 shows a faster decay of the error in DIIS WHAM than in direct WHAM.

Figure 4.

Convergence error, max{|R_i|}, versus the number of iterations in direct and DIIS WHAMs for the 64 × 64 two-dimensional Ising model. Results were geometrically averaged over independent samples.

3.3. LJ fluid

We tested the DIIS method on the 256-particle LJ fluid in the isothermal-isobaric (NpT) ensemble. This is a case for the two-dimensional (p and T) WHAM, which can be difficult for ST-WHAM[28]. The potential interaction between particles was cutoff at half the box size. We simulated the system using parallel tempering MC. We considered the system at N_T × N_p = 6 × 3 conditions, with temperatures T = 1.2, 1.3, …, 1.7, and pressures p = 0.1, 0.15, 0.2. The bin sizes for energy and volume were 1.0 and 2.0, respectively.

As shown in Fig. 2, DIIS WHAM effectively reduced the run time, although the efficiency of DIIS does not always increase with the number of basis set members, M.

3.4. Villin headpiece

We tested the methods on a small protein, the villin headpiece (PDB ID: 1VII), in aqueous solution. This is a well-known test system[55]. The protein was immersed in a dodecahedron box with 1898 TIP3P water molecules and two chloride ions. The force field was AMBER99SB[56, 57] with the side-chain modifications[58]. Molecular dynamics (MD) simulations were performed using GROMACS 5.0[59–65], with a time step of 2 fs. Velocity rescaling[66] was used as the thermostat with the time constant being 0.1 ps. The electronic interaction was handled by the particle mesh Ewald method[67]. The constraints were handled by the LINCS method[68] for hydrogen-related chemical bonds on the protein and by the SETTLE method[69] for water molecules.

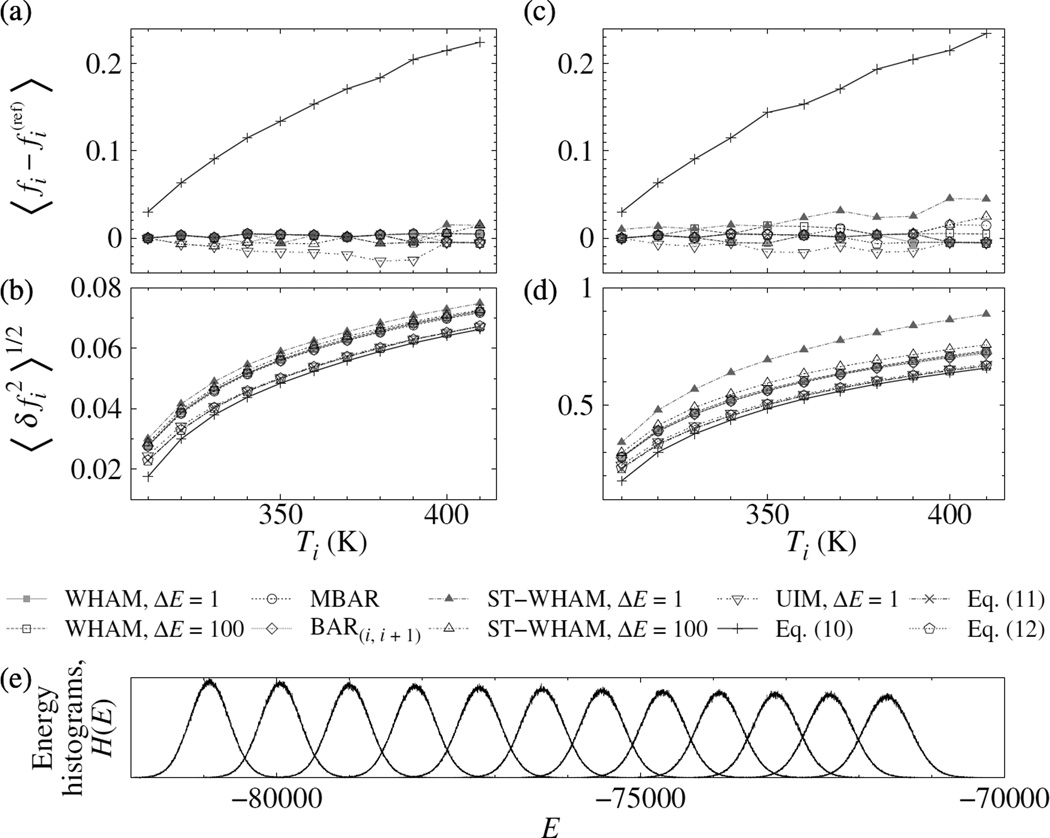
We simulated the system at 12 temperatures T = 300 K, 310 K, …, 410 K, each for approximately 200 ns. The energy distributions were properly overlapped, as shown in Fig. 5(e). The energies of individual trajectory frames were saved every 0.1 ps, so that there were about 2 million frames for analysis at each temperature.

Figure 5.

Accuracy [(a) and (c)] and precision [(b) and (d)] of the dimensionless free energies, f_i, from WHAM, BAR, ST-WHAM, UIM, and approximate formulae for the villin headpiece in solution. Two types of samples were used. A large sample [(a) and (b)] and a small sample [(c) and (d)] contain roughly 1% and 0.01% of all trajectory frames, respectively. The results were averaged over random samples. The MBAR results computed from all trajectory frames were used as the reference. f_i at T = 300 K is fixed at zero. The lines are a guide for the eyes. (e) Energy histograms collected with bin width ΔE = 1.0.

As shown in Fig. 2, direct WHAM suffered from slow convergence, while the DIIS methodology again delivered a speed-up of two orders of magnitude, in the number of iterations or in real time. The MBAR case was similar, although MBAR was slower than WHAM as it did not use histogram to aggregate data.

To compare the errors of the methods, we prepared two types of samples of different sizes. A larger sample was randomly selected from roughly r = 1% of all trajectory frames from every temperature. In a smaller one, r was reduced to 0.01%. The reference values of f_i were computed from all trajectory frames using MBAR, which is the zero-bin-width limit of WHAM[1, 17]. In terms of accuracy [Figs. 5(a) and 5(c)], WHAM, MBAR, BAR, ST-WHAM, Eqs. (11) and (12) were comparably good; UIM was slightly inferior for the larger sample; Eq. (10) was the worst. The accuracy was largely independent of the sample size. In terms of precision [Figs. 5(b) and 5(d)], the differences were small. Generally, WHAM was insensitive to the bin size, whereas ST-WHAM was slightly affected by a small bin size for the smaller samples.

4. Conclusions

In this work, we showed that the DIIS technique can often significantly accelerate WHAM and MBAR to produce free energy difference. The technique achieves rapid convergence by an optimal combination of the approximate solutions obtained during iteration. DIIS does not require computing the Hessian-like matrix, −∂R(f)/∂f, and is numerically stable with minimal run time overhead. Compared to other advanced techniques[1, 16], DIIS is relatively simple and easy to implement. However, methods based on Hessian matrices may further accelerate the solution process for final stages. Other related free energy methods[7, 37–39] may also benefit from this technique.

There are some non-iterative alternatives to WHAM, although they may be less general and/or accurate in some aspect. The use of DIIS makes scanning more than one thermodynamic state variable or a nonlinear variable computationally convenient. This was demonstrated here in the NpT LJ fluid case. Problems with only one thermodynamic variable to scan, such as temperature, are amenable to the non-iterative ST-WHAM, or the more approximate UIM.

Appendix A

Probabilistic derivations of Eq. (6)

Here we give some derivations of Eq. (6). First, we show that Eq. (6) is a generalisation of Eq. (4) from the energy space to the configuration space. We follow the probabilistic argument[8–11, 16, 17] for simplicity. We assume that the system is subject to an unknown underlying configuration-space field, g(y), such that the distribution of state k is w_k(y) ≡ g(y) q_k(y)/Z_k[g], with

$$Z_k[g]=\int g(\mathbf{y})q_k(\mathbf{y})d\mathbf{y}.$$ (A1)

We now seek the most probable g(y) from the observed trajectory. Given a certain g(y), the probability of observing the trajectories, {x}, is given by

$$p(\{\mathbf{x}\}|g)\propto \prod _{k=1}^K\prod _{\mathbf{x}}^{(k)}\frac{g(\mathbf{x})q_k(\mathbf{x})}{Z_k[g]}.$$

This is also the likelihood of g given the observed trajectory, {x}. Thus, to find the most probable g(y), we only need to maximise log p ({x}|g) by taking the functional derivative with respect to g(y) and setting it to zero, which yields

$$g(\mathbf{y})=\frac{{\sum }_{j=1}^K{\sum }_{\mathbf{x}}^{(j)}\delta (\mathbf{x}-\mathbf{y})}{{\sum }_{k=1}^K{N}_k{q}_k(\mathbf{y})/Z_k[g]},$$ (A2)

where we have used δ log g(x)/δg(y) = δ(x − y)/g(y), and δZ_k[g]/δg(y) = q_k(y).³ Using Eq. (A2) in Eq. (A1), and then setting g to 1.0 yields Eq. (6).

We can also show Eq. (6) without introducing the configuration-space field [thus, g(x) = 1 below]. Instead, we now assume that each trajectory frame x is free to choose the state i according to the Bayes' rule[70, 71]: since the prior probability of state i is N_i/N_tot, and the conditional probability of observing x in state i is w_i(x) ≡ q_i(x)/Z_i, the posterior probability of x being in state i is given by[11]

$$p(i|\mathbf{x})=\frac{(N_i/N_{\text{tot}})w_i(\mathbf{x})}{{\sum }_{k=1}^K(N_k/N_{\text{tot}})w_k(\mathbf{x})}.$$

Summing this over all trajectory frames x (no matter the original state j) yields the expected population of state i,

$${\hat{N}}_i=\sum _{\mathbf{x}}p(i|\mathbf{x})=\sum _{\mathbf{x}}\frac{N_i{w}_i(\mathbf{x})}{{\sum }_{k=1}^K{N}_k{w}_k(\mathbf{x})},$$ (A3)

where ${\sum }_{\mathbf{x}}\equiv {\sum }_{j=1}^K{\sum }_{\mathbf{x}}^{(j)}$. If we demand N̂_i to be equal to the N_i, Eq. (6) is recovered. Alternatively, by following the argument used in the expectation-maximisation algorithm[11, 71–74], we can view Eq. (A3) as the result of maximising the probability of observing the trajectory {x},

$$p(\{\mathbf{x}\}|N_1,\dots ,N_K)\propto \prod _{\mathbf{x}}\sum _{k=1}^K(N_k/N_{\text{tot}})w_k(\mathbf{x}),$$

with respect to variations of N_i under the constraint ${\sum }_{i=1}^K{N}_i=N_{\text{tot}}$.

Appendix B

Models for the convergence of direct WHAM

Here, we use simple models to study the convergence of direct WHAM. We shall show that slow convergence is associated to a wide temperature range, especially with a large spacing.

B.1. Linearised WHAM equation

Consider K distributions, ρ_i(E), at different temperatures, β_i (i = 1, …, K), normalised as ∫ ρ_i(E) dE = 1. For simplicity, we assume equal sample sizes, N_i. Then, Eq. (4), can be written in the iterative form as

$$f_i^{(\text{new})}=-\text{log}\int \frac{{\sum }_{k=1}^K{\rho }_k(E)\text{ exp}(-{\beta }_{i}E)}{{\sum }_{k=1}^K\text{exp}(-{\beta }_{k}E+f_k^{(\text{old})})}dE.$$ (B1)

Around the true solution, ${\mathbf{f}}^{*}=(f_1^{*},\dots ,f_K^{*})$, the equation can be linearised as

$$\delta f_i^{(\text{new})}=\sum _{j=1}^K{A}_{ij}\delta f_j^{(\text{old})},$$

where $\delta f_i^{(\text{new}/\text{old})}\equiv f_i^{(\text{new}/\text{old})}-f_i^{*}$, and

$$A_{ij}=\int \frac{{\sum }_{k=1}^K{\rho }_k(E)e^{-({\beta }_i+{\beta }_j)E+f_i^{*}+f_j^{*}}}{D^2(E;{\mathbf{f}}^{*})}dE.$$ (B2)

with $D(E;{\mathbf{f}}^{*})={\sum }_{k=1}^K{e}^{-{\beta }_{k}E+f_k}$. In matrix form, we have δf^(new) = A δf^(old).

The elements of matrix A are positive, i.e., A_ij > 0, and normalised, i.e.,

$$\sum _{i=1}^K{A}_{ij}=1.$$ (B3)

The latter can be seen from Eq. (B1) with $f_i^{(\text{new}/\text{old})}\to f_i^{*}$. Besides, A is symmetric:

$$A_{ij}=A_{ji}.$$ (B4)

Thus, A can be regarded as a transition matrix[4]. Each left eigenvector c = (c₁, …, c_K) of A is associated to a mode of δf and the eigenvalue λ gives the rate of error reduction during iteration. That is, ${\sum }_{i=1}^K{c}_i\delta f_i$ decays as λⁿ asymptotically with the number of iterations, n.

The largest eigenvalue is λ₀ = 1.0, and its eigenvector c = (1, …, 1) corresponds to a uniform shift of all δf_i, which is unaffected by the iteration, i.e., ${\sum }_{i=1}^K\delta f_i^{(\text{new})}={\sum }_{i=1}^K\delta f_i^{(\text{old})}$, as a consequence of Eq. (B3). The next largest eigenvalue, λ₁, determines the rate of convergence of the slowest mode, and a larger value of 1 − λ₁ means faster convergence. Below, we determine λ₁ in a few solvable cases.

B.2. Exact distribution approximation (EDA)

To proceed, we assume that the observed distributions are exact, and thus the solution, $(f_1^{*},\dots ,f_K^{*})$, is also exact. Then, for any k, we have

$${\rho }_k(E)=g(E)e^{-{\beta }_{k}E+f_k^{*}},$$ (B5)

with g(E) being the density of states. This simplifies Eq. (B2) as

$$A_{ij}=\int \frac{g(E)e^{-({\beta }_i+{\beta }_j)E+f_i^{*}+f_j^{*}}}{D(E;{\mathbf{f}}^{*})}dE.$$ (B6)

B.3. Gaussian density of states

Further, we approximate g(E) as a Gaussian[14]. With a proper choice of the multiplicative constant of g(E), we have,

$$g(E)=\sqrt{\frac{\alpha }{2\pi }}\text{exp }[-\frac{1}{2}\alpha {(E-E_c)}^2].$$ (B7)

It follows

$$f_i=-\text{log}\int g(E)\text{ exp}(-{\beta }_{i}E)dE={\beta }_i{E}_c-\frac{{\beta }_i^2}{2a},$$ (B8)

and

$${\rho }_i=\sqrt{\frac{a}{2\pi }}\text{exp }[-\frac{1}{2}a{(E-E_c+\frac{{\beta }_i}{a})}^2].$$

Thus, the distribution at any temperature is a Gaussian of the same width ${\sigma }_E=1/\sqrt{a}$. The inverse temperature β_i affects the energy distributions only as a linear shift to the distribution centre. It follows that both the origin of β and that of E, represented by E_c, can be set to any values that help calculation, without affecting the value of A_ij.

B.4. Two-temperature case

For the two-temperature case, the matrix A has only one free variable because of Eqs. (B3) and (B4), and it can be written as

$$\mathbf{A}=\left(\begin{array}{cc}\hfill 1-A_{12}\hfill & \hfill A_{12}\hfill \\ \hfill A_{12}\hfill & \hfill 1-A_{12}\hfill \end{array}\right).$$

Thus, the second largest eigenvalue is λ₁ = 1 − 2 A₁₂.

Under EDA, we have, from Eqs. (B5) and (B6),

$$A_{12}=\int \frac{{\rho }_1(E){\rho }_2(E)}{{\rho }_1(E)+{\rho }_2(E)}dE\le \int \frac{{\rho }_1(E)+{\rho }_2(E)}{4}dE=\frac{1}{2},$$

where the equality is achieved only for identical distributions. Geometrically, A₁₂ represents the degree of overlap of the distributions, as shown in Fig. B1(a), and it decreases with the separation of the two distributions, from the maximal value, 1/2, achieved at β₁ = β₂.

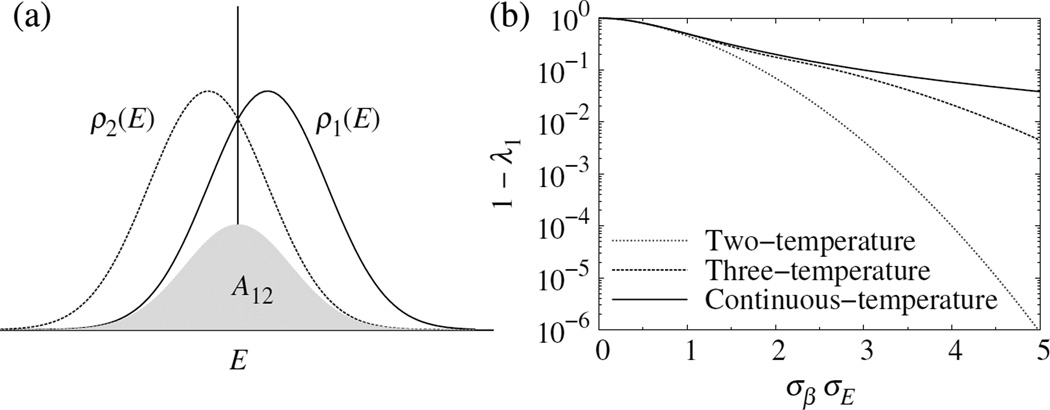
Figure B1. (a) A₁₂, which determines the rate of convergence in the two-temperature case, as a measure of overlap of the two energy distributions. (b) Comparison of the rates of convergence in the two-, three-, and continuous-temperature cases, Eqs. (B9), (B10), and (B12), respectively. Here, σ_β is the standard deviation of the β distribution; σ_E is that of the energy distribution at any temperature. A larger value of 1 − λ₁ means faster convergence.

By further assuming a Gaussian density of states, we can, without loss of generality, set β₁ = − σ_β, β₂ = σ_β, and E_c = 0. Then, from Eqs. (B6), (B7) and (B8), we have

$$1-{\lambda }_1=2A_{12}=\sqrt{\frac{a}{2\pi }}\int \frac{\text{exp }[-a{E}^2/2-{\sigma }_{\beta }^2/(2a)]}{\text{cos}\mathrm{h}({\sigma }_{\beta }E)}dE\approx \frac{e^{-{\sigma }_{\beta }^2{\sigma }_E^2/2}}{\sqrt{1+{\sigma }_{\beta }^2{\sigma }_E^2}}[1+\frac{{\sigma }_{\beta }^4{\sigma }_E^4}{4{(1+{\sigma }_{\beta }^2{\sigma }_E^2)}^2}],$$ (B9)

where ${\sigma }_E=1/\sqrt{a}$, and we have used 1/cosh x ≈ exp(−x²/2)(1 + x⁴/12). This model shows a rapid decrease in the rate of convergence of direct WHAM with the temperature separation.

B.5. Three-temperature case

Similarly, for three evenly-spaced temperatures, we can, without loss of generality, set β₁ = −Δβ, β₂ = 0, and β₃ = Δ β, with $\mathrm{\Delta }\beta =\sqrt{\frac{3}{2}}{\sigma }_{\beta }$. Then,⁴

$$1-{\lambda }_1=A_{12}+2A_{13}\approx 𝒜(\sqrt{\frac{3}{8}}{\sigma }_{\beta }{\sigma }_E,-\frac{5}{2})+2𝒜(\sqrt{\frac{3}{2}}{\sigma }_{\beta }{\sigma }_E,\frac{1}{2}),$$ (B10)

where

$$𝒜(b,t)=\frac{e^{-b^2/2}/(1+\frac{1}{2}{e}^{t{b}^2})}{2\sqrt{1+b^2/(1+\frac{1}{2}{e}^{t{b}^2})}}[1+\frac{(2-\frac{1}{2}{e}^{t{b}^2})b^4/8}{{(1+b^2+\frac{1}{2}{e}^{t{b}^2})}^2}].$$

B.6. Continuous-temperature case

If there are a large number K of temperatures in a finite range, we can approximate them by a continuous distribution, w(β). In this case, the sum over temperatures can be replaced by an integral: ${\sum }_{k=1}^K\to K\int d\beta w(\beta )$.

The eigenvalue λ_l and eigenvector c_l(β) are now determined from the integral equation

$$K\int w(\beta \prime )c_l(\beta \prime )A(\beta ,\beta \prime )d\beta \prime ={\lambda }_l{c}_l(\beta ),$$ (B11)

where A(β, β′) is A_ij with β_i → β and β_j → β′.

Equation (B11) can be solved in a special case, in which we assume EDA, Eq. (B6), a Gaussian density of states, Eq. (B7), and a Gaussian β distribution:

$$\omega (\beta )=\frac{1}{\sqrt{2\pi a\prime }}\text{exp }[-\frac{{(\beta -{\beta }_c)}^2}{2a\prime }],$$

with width ${\sigma }_{\beta }=\sqrt{a\prime }$. The physical solution is

$${\lambda }_l={\left(\frac{a\prime }{a+a\prime }\right)}^l,$$

$$c_l(\beta )=H_l\left(\frac{\beta -{\beta }_c}{\sqrt{2a\prime }}\right),$$

where H_l(x) is the Hermite polynomial[49–51], generated as $e^{-t^2+2xt}={\sum }_{l=0}^{\infty }{H}_l(x)t^l/l!$. Thus, for the second largest eigenvector, we have

$$1-{\lambda }_1=\frac{1}{1+{\sigma }_{\beta }^2{\sigma }_E^2},$$ (B12)

which decreases with increasing temperature range, σ_β, albeit more slowly than the two- and three-temperature values, as shown in Fig. B1(b). Thus, Eq. (B12) only gives a upper bound, and nonzero spacing between temperatures can further slow down the convergence. Besides, sampling error, which is ignored in the above calculation, may also slow down the convergence.