Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Sep 1.
Published in final edited form as: J Mech Behav Biomed Mater. 2016 Apr 23;62:24–32. doi: 10.1016/j.jmbbm.2016.04.025

The concentration of stress at the rotator cuff tendon-to-bone attachment site is conserved across species

Fatemeh Saadat 1, Alix C Deymier 2, Victor Birman 3, Stavros Thomopoulos 4,*, Guy M Genin 5,*
PMCID: PMC4955721  NIHMSID: NIHMS785082  PMID: 27161959

Abstract

The tendon-to-bone attachment site integrates two distinct tissues via a gradual transition in composition, mechanical properties, and structure. Outcomes of surgical repair are poor, in part because surgical repair does not recreate the natural attachment, and in part because the mechanical features that are most critical to mechanical and physiological function have not been identified. We employed allometric analysis to resolve a paradox about how the architecture of the rotator cuff contributes to load transfer: whereas published data suggest that the mean muscle stresses expected at the tendon-to-bone attachment are conserved across species, data also show that the relative dimensions of key anatomical features vary dramatically, suggesting that the amplification of stresses at the interface between tendon and bone should also vary widely. However, a mechanical model that enabled a sensitivity analysis revealed that the degree of stress concentration was in fact highly conserved across species: the factors that most affected stress amplification were most highly conserved across species, while those that had a lower effect showed broad variation across a range of relative insensitivity. Results highlight how micromechanical factors can influence structure-function relationships and cross-species scaling over several orders of magnitude in animal size, and provide guidance on physiological features to emphasize in surgical and tissue engineered repair of the rotator cuff.

Keywords: tendon-to-bone attachment, allometry, stress concentration, functionally graded attachment

1. Introduction

The tendon-to-bone attachment connects two very different materials: compliant tendon and stiff bone. As an interface between such dissimilar materials, it is prone to stress concentrations and increased risk of failure (Munz and Yang, 1992; Thomopoulos et al., 2012). In healthy tissue, the attachment site exhibits a number of structures which serve to attenuate stress concentration (Thomopoulos et al., 2003b; Liu et al., 2011; Schwartz et al., 2012). However, after healing or surgical repair, these structures are not recovered in adults. Post-surgical failures, which can occur in 94% of elderly patients with massive tears (Galatz et al., 2004; Cummins and Murrell, 2003; Zumstein et al., 2008; Thomopoulos et al., 2010), tend to occur at the interface and constitute a major clinical challenge in orthopedic surgery (Paxton et al., 2013). These high failure rates point to the importance of identifying and reconstituting the interfacial structures most important to maintaining the structural integrity of the attachment. Understanding the mechanisms of load transfer at the tendon-to-bone attachment and characterizing this transitional tissue may uncover strategies to create stronger and more resilient interfaces in both engineering and medical applications.

The focus in this study is a gradient region from tendon to bone showing gradual increases in mineral content and collagen misalignment (Qu et al., 2013; Thomopoulos et al., 2006; Wopenka et al., 2008; Schwartz et al., 2012). With the goal of providing guidance for surgical repair and healing strategies, we quantified how anatomic features of the attachment site, including relative dimensions and anisotropy, affect load tendon-to-bone transfer across species ranging in size from 30 g mice to 45 kg pigs.

The efficient binding of dissimilar materials has been studied widely, as have engineered material systems that exhibit analogous spatial gradations in material properties, termed functional grading (Liu et al., 2011; Birman, 2014; Apalak, 2014). The mechanics of load transfer at isotropic functionally graded interfaces is well understood (Birman et al., 2013; Byrd and Birman, 2007). However, the tendon to-bone attachment exhibits a 10 fold change in tissue anisotropy between strongly anisotropic tendon and nearly isotropic bone. This latter effect has not been well studied, and results from the existing mechanics literature cannot provide guidance for the problem of interest (Birman et al., 2013; Byrd and Birman, 2007; Genin and Birman, 2009). We therefore approached our problem with an anisotropic generalization of an approach that has been applied previously to study isotropic attachments.

The cross-species approach we adopted falls under the rubric of allometry (cf. Huxley et al. (1932); Thompson et al. (1942); Huxley and Teissier (1936)). The allometric scaling of rotator cuff anatomy with body size was pursued both to gain insight into the sizing and mechanical function of the tendon-to-bone attachment site and to address the challenge of relating research on small animal models to human health. A specific question of interest is whether experiments on the mineral gradient at the tendon-to-bone attachment of the rat can inform human surgeries through the principle of similarity (Schmidt-Nielsen, 1984; Wopenka et al., 2008). We studied the scaling via the Huxley and Teissier (1936) power-law expression for the relationship between the size of a body part and the size of the body as a whole:

Y=bMα (1)

where Y is a biological variable, M is a measure of body size, and α and b are fitting parameters (Gayon, 2000). This has proven effective in describing scaling of morphological traits (e.g., brain versus body size among adult humans), physiological traits (e.g., metabolic rate versus body size among mammals) and ecological traits (e.g., wing size versus flight performance in birds) (West and Brown, 2005; Smith, 1984; Huxley et al., 1932; Gould, 1966, 1977; Klingenberg and McIntyre, 1998). The range of animals considered stretched from small rodents to pigs, with the mass of pigs approaching the lower end of the normal range for humans.

The current study follows recent investigations of the scaling of the supraspinatus muscle and the force it applies in relation to the geometry of the insertion into the humeral head (Mathewson et al., 2013; Deymier-Black et al., 2015). Volume and physiological cross-sectional area (PCSA) of the muscle scale geometrically across species, and the area of attachment at the humeral head scales to maintain constant nominal stress at the interface. However, paradoxically, the microscale mineral gradient length changes minimally across species: given that the mean muscle stresses are conserved across species, why would this factor, known to affect the amplification of stress at the bi-material interface, show such broad variation? The answer that emerged from a simple model is that cross-species variation was substantial only in a range of parameters for which the effect on stress amplification was relatively low: the design of the rotator cuff attachment and cross-species variation appear intertwined in a way that conserves stress concentrations across species.

In the current study, we first adapted a mathematical idealization of the rotator cuff attachment site to identify the effects of anisotropy on load transfer. Special attention was devoted to finding a smooth spatial scaling of material properties between tendon and bone that did not violate thermodynamic bounds at any point between the two tissues. Then, the concept of allometry was employed to test the hypothesis that, despite the unusual scaling of the size of the mineral gradient, stress concentration is conserved across species.

2. Methods

2.1. Stress analyses

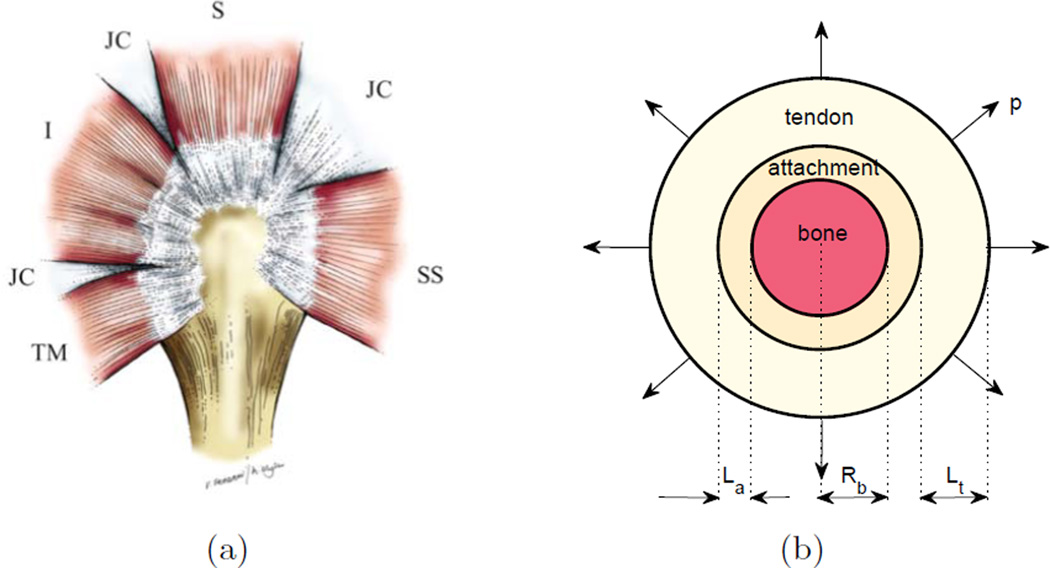
The mechanical consequences of mineral gradation allometry were studied through an adaptation of a previously published idealized mathematical model of the rotator cuff attachment site (Fig.1b) (Liu et al., 2012). The mathematical model is an axisymmetric, orthotropic linear elastic idealization of the anatomy of the rotator cuff viewed in the sagittal plane (Fig.1a). In this model, the tendon-to-bone attachment was idealized as three concentric layers including: (1) a central core of bone with a radius of Rb, (2) a graded attachment band in the middle with a length La, and (3) an outer sheath of tendon with length Lt (Fig.1b). Stresses were estimated by idealizing the attachment as a series of N axisymmetric concentric cylinders. The tendon was loaded with a uniform radial stress p, which is a reasonable first order approximation of loading that might occur physiologically (Liu et al., 2012). Using the plane stress solution presented in Liu et al. (2012) and the radial distribution of orthotropic material properties described below, we estimated the radial and tangential stresses in each band and then computed the maximum principal stress in the attachment site. A sufficient number of bands (typically N > 500) was used to ensure that subsequent refinement would not change the estimated peak stress by more than 1%. Hence, this discrete solution approximated the continuous solution.

Figure 1.

Figure 1

Open in a new tab

(a) The model used was based upon a lateral view of the rotator cuff of the humeral head (from Liu et al. (2012), used with permission). JC: joint capsules that interconnect with muscles (red). Tendons (white) connect the humeral head (bone, tan) to muscles. SS: subscapularies tendon; S: supraspinatus tendon; I: infraspinatus tendon; TM: teres minor tendon. (b) The plane stress, axisymmetric model for the rotator cuff tendon-to-bone attachment contained a bone core, a concentric graded attachment layer, and a concentric tendon layer. The latter was loaded with a uniform radial traction of magnitude p.

The stress concentration arising at the tendon-to-bone attachment was studied as a function of tendon length, attachment length, and bone radius. Because linear elasticity solutions are independent of length scale, the stress concentrations could be described in terms of two dimensionless variables: the normalized attachment length La/Rb, and the normalized tendon length, Lt/Rb.

The effects of the normalized attachment length on stress concentration were studied over a broad range that encompassed the physiological range (0.001 < La/Rb < 0.02) observed in adult animals ranging from mice (0.03 kg) to pigs (40 kg) (Deymier-Black et al., 2015). In these studies, the normalized tendon length was held constant, with the value of Lt/Rb = 20 chosen as a baseline; this value represents the approximate ratio of the Achilles tendon length and calcaneus radius over a broad range of animals (Gàlvez-López and Casinos, 2012). In other studies focusing on the effects of tendon length, the normalized attachment length was held constant at La/Rb = 0.0120, the value for mice, while the normalized tendon length was varied over a range encompassing the physiological range (0.0001 < Lt/Rb < 100).

Finally, the data of Deymier-Black et al. (2015) were input into the model to estimate how stress concentration varied across species (Table I). In the absence of data for the ratio of the length of the supraspinatus tendon to the radius of the humeral head, a scaling was used based upon the cross-species scaling relationship of Pollock and Shadwick (1994) for the Achilles tendon length and body mass, m:

Lta=63.7m0.34, (2)

where Lta is in mm and m is in kg, and that of Gàlvez-López and Casinos (2012) for calcaneus radius and body mass:

Rbc=5.45m0.36, (3)

where Rbc is in mm and m is in kg. These relationships indicated that the ratio Lt/Rb is nearly independent of body mass. However, La/Rb scaled strongly with animal mass, m (Deymier-Black et al., 2015):

m=6.91×10−8(LaRb)3.23 (4)

where m is in kg. This relationship enabled the establishment of a trend relating stress concentration to animal mass.

Table 1.

Cross-species morphometric data.

species body mass,
m (kg)		 humeral head
radius, Rb (mm)		 attachment length,
La (µm)		 normalized attachment
length, La=Rb
mouse 0.03* 2.4** 14.7 ± 4.31 0.0120 ± 0.0036
rat 0.30 ± 0.01 5.16 ± 0.24 29.0 ± 4.0 0.010 ± 0.001
rabbit 4.24 ± 0.23 12.3 ± 0.4 26.2 ± 2.7 0.0042 ± 0.0003
dog 21.7 ± 2.4 31.4 ± 1.0 39.3 ± 9.0 0.0025 ± 0.0006
pig 43.3 ± 2.3 40.0 ± 2.4 43.6 ± 16.4 0.0022 ± 0.0008
Open in a new tab

Data from Deymier-Black et al. (2015), Pollock and Shadwick (1994), and Gàlvez-López and Casinos (2012). In computing the variances of ratios, attachment lengths were assumed to be independent of humeral head radius.

Notes:

*

average mass,

**

average diameter

2.2. Material properties

In the above analyses, the mechanical properties of bone were modeled as isotropic, while those of tendon were modeled as cylindrically orthotropic (Fung and Cowin, 1994). The two material constants used for bone were elastic modulus Ebone = 20 GPa and Poisson’s ratio νbone = 0.3. For tendon, three elastic constants were required. Following Liu et al. (2014b), the radial elastic modulus was Er = 450 MPa, the tangential elastic modulus was Eθ = 45 MPa, and the Poisson’s ratio for tangential contraction arising from radial tension was νrθ = 3. While these latter values are for ligaments rather than tendons, they represent the best data available. Despite morphological and compositional variations unique to the rotator cuff, the mechanical properties of rotator cuff tendons are expected to be of the same order as those of other tendons and ligaments of the body.

Little information is available in the literature about the material properties of the graded attachment site. Its structure and composition vary smoothly from tendon (unmineralized and compliant) to bone (mineralized and stiff) (Thomopoulos et al., 2003a), and the mechanical properties appear to vary smoothly as well (Genin et al., 2009).

Our primary model involved a linear gradation in the tangential elastic modulus Eθ(r) over the attachment site (Fig. 2c), and a linear gradation in the ratio of tangential to radial elastic modulus Eθ(r)/Er(r) (Fig. 2a). This required a parabolic gradation in the radial modulus Er(r) (Fig. 2d). The interpolation of the Poisson’s ratio νrθ(r) between tendon and bone required special care to stay below the thermodynamic bound (cf. (Liu et al., 2014b)):

υrθ(r)≤Eθ(r)Er(r). (5)

A cubic interpolation between νbone and νrθ was the simplest implementation that stayed (just) beneath the thermodynamic bound for Eθ/Er ≤ 10 for the moduli interpolations used (Fig. 2b). This was thus adopted in our analyses. The other Poisson ratio, νθr, could be computed from the three independent moduli using the relation (cf. (Liu et al., 2014b)):

υθr(r)=Eθ(r)Er(r)υrθ(r) (6)

This resulted in a function that was continuous and was equal to 0.3 at the interfaces of the attachment site with tendon and bone (Fig. 2).

Figure 2.

Figure 2

Open in a new tab

The simplified distribution of mechanical properties considered for tendon, bone, and the graded attachment site. Bone was modeled as isotropic; tendon and the attachment site were modeled as cylindrically orthotropic, and mechanical properties were required to be continuous. (a) Within the graded attachment site, the anisotropy ratio was modeled as linear. (b) This required a cubic interpolation of the Poisson ratio νrθ(r); this relationship lay below the upper bound on νrθ(r) for an anisotropy ratio less than 10. (c) The tangential modulus Eθ(r) was modeled as varying linearly. (d) The radial modulus was thus required to follow a parabolic interpolation. (e) The resulting interpolation of νθr(r) was non-monotonic but continuous, smooth, and positive.

Beyond this baseline model, we explored the effects of the degree of tendon anisotropy and Poisson’s ratio on the stress field. To avoid complications associated with the thermodynamic bound (Eq. 5), the effects of tendon anisotropy were first studied using a fictional attachment site, bone, and tendon with Poisson’s ratios all set to zero. In other analyses, the Poisson ratios of tendon, bone, and each point within the graded attachment site were set to the upper bound at that point (cf. Eq. 5). We note that although several studies show a non-monotonic variation in Er(r) within the graded attachment (Thomopoulos et al., 2003a; Genin et al., 2009), the monotonic gradient adopted here serves as a first order representation to estimate how the relative size of the graded attachment site affects stress concentrations.

3. Results

3.1. The model is not sensitive to assumptions made about material properties

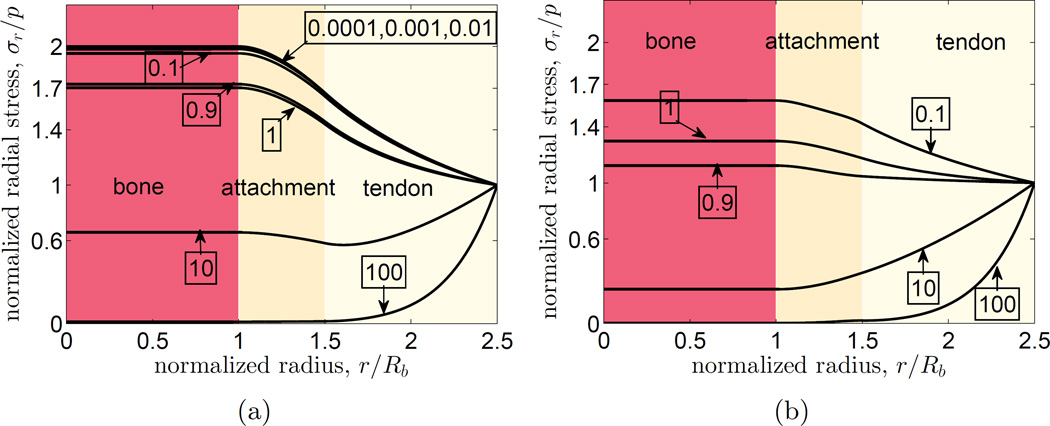
We began by studying the nature of the stress field in our model to determine how the assumed material properties affected the peak stresses. The first variable studied was the degree of anisotropy of the tendon, Eθ/Er. In these first studies, Poisson’s ratio was set to zero throughout the attachment site (Fig.3a). In cases for which tendon was taken as stiffer along its axis than transverse to its axis (Eθ/Er < 1), as occurs in the physiological case, the peak radial stress σrmax occurred at the outer boundary of the bone. The stress distribution did not change substantially for Eθ/Er ≤ 0.1. For the isotropic case (Eθ/Er=1), the peak radial stress occurred at the bone-attachment boundary with a maximum radial stress of ~ 1.7. For all (non-physiological) cases of Eθ/Er > 1, the peak radial stress occurred at the outermost boundary. As a comparison, the normalized radial stress field for a completely isotropic and homogeneous system would be uniform, with a magnitude of σr(r)/p = 1.

Figure 3.

Figure 3

Open in a new tab

The effect of anisotropy ratio Eθ/Er in the tendon (numbers in boxes) on the radial stress distribution at the tendon-to-bone attachment. (a) With Poisson’s ratio of the tendon, bone, and the attachment site considered to be zero, all models of tendon with radial modulus exceeding tangential modulus showed monotonically increasing radial stress from tendon-to-bone. For anisotropy ratio ≤ 0.1, the stress distributions reached a peak value of approximately 2. A tendon ring that was stiffer in the transverse than radial direction would shield the attachment site from radial stresses. Note that experimentally measured anisotropy ratio for tendon is in the range of 0.1 – 0.01. (b) Trends were similar with Poisson’s ratio set close to the upper bound, with the exception of the case of anisotropy ratio equal to 1 (see note in text).

When Poisson’s ratio was varied according to upper limit of Eq.(5), the peak stress concentrations were all reduced and the trends of Fig. 3a were retained (Fig.3b). The one exception was the isotropic case (Eθ/Er = 1), which had a higher stress concentration due to irregularities that arose with the interpolation scheme: the peak allowable Poisson ratio for an isotropic material is 0.5 due to an additional thermodynamic constraint that differs from Eq. 5, which allows a Poisson ratio of 1. Trends were similar for several additional, non-linear, radial distributions tested for the degree of anisotropy, Eθ/Er(r) (data not shown). From this, we concluded that the trends arising from the model were sufficiently insensitive to the choice of material parameters around the baseline model of Eθ/Er = 0.1 that we could proceed to use it to assess qualitative trends associated with allometry.

3.2. The stress concentration is insensitive to the length of the graded attachment site over the physiological range, but highly sensitive beyond the physiological range

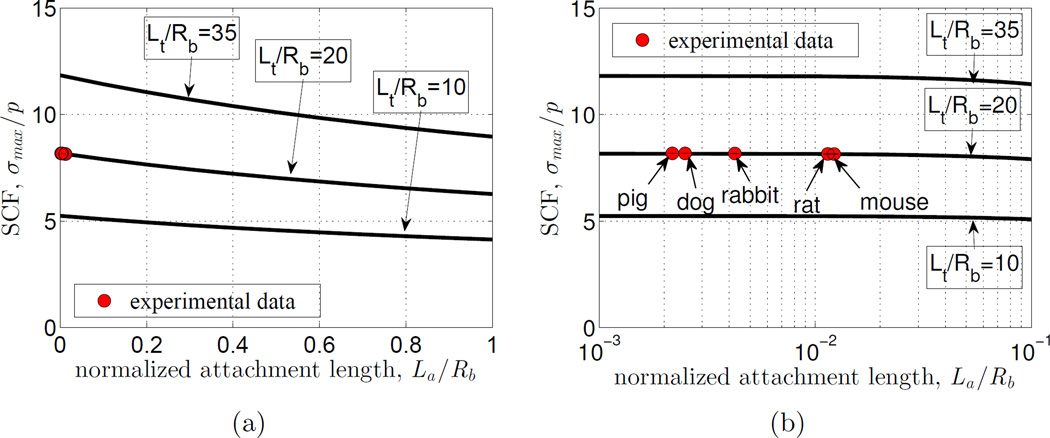
We next studied the degree to which stress concentrations were affected by variations in the normalized graded attachment length (Fig.4a) when the normalized tendon length was held constant (Lt/Rb = 20). Decreasing the normalized attachment length (La/Rb) an order of magnitude, from 1 to 10−1, increased the SCF by 1/3. Note that, We also examined the effect of the normalized tendon length for two other constants (Lt/Rb = 10, 35) which resulted in a similar trend as Lt/Rb = 20. The physiological range is very broad, extending over two orders of magnitude. However, the SCF was almost invariant over the two decades of the physiological range (Fig. 4b).

Figure 4.

Figure 4

Open in a new tab

(a) The stress concentration factor (SCF) varied substantially with the normalized gradient size (La/Rb) for all various ratio of Lt/Rb = 10, 20, 35. (b) However, in the two decades of the physiological range, this variation was only a few percent. In both figures, Red circles are data for animals ranging from mice to pigs at a constant normalized tendon length Lt/Rb = 20. Note that error bars are too narrow to be seen relative to the red circles.

3.3. The stress concentration is highly sensitive to the normalized tendon length

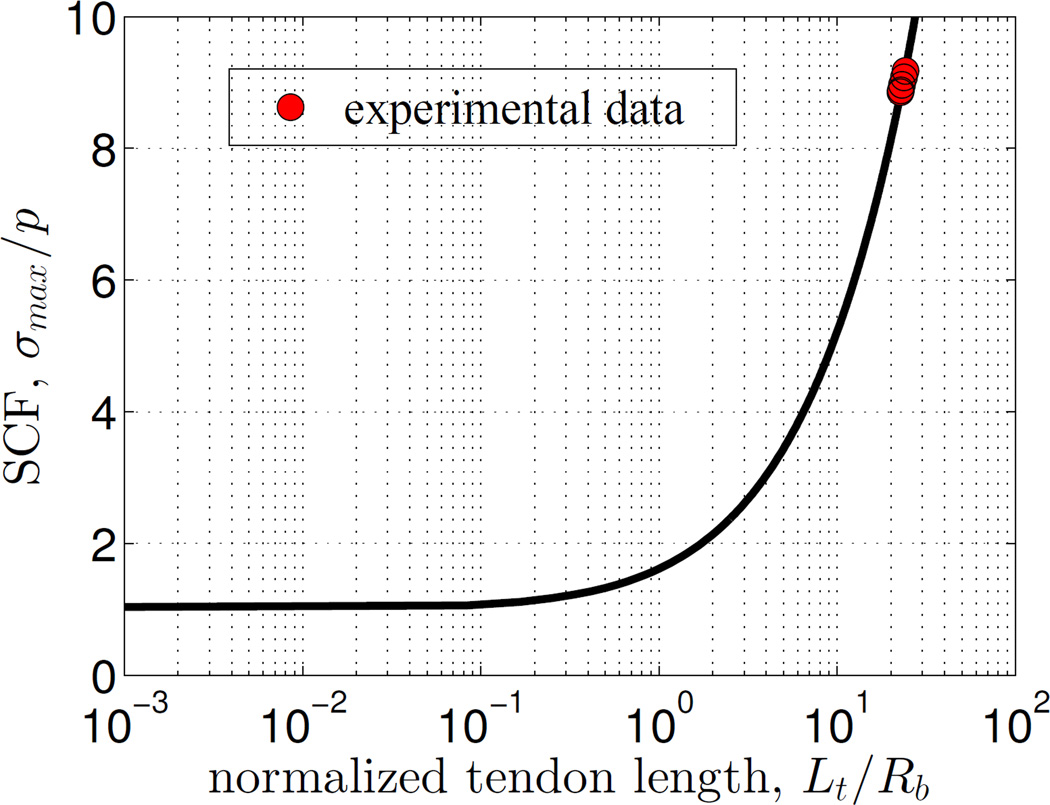
The normalized tendon length (Lt/Rb) had a significant effect on the SCF over a range that encompassed the physiological range (Fig.5). This sensitivity was lost for Lt/Rb < 1. However, above this range the SCF increased ~ 25 fold over two decades of (Lt/Rb). The physiological range lay within the region of high sensitivity, but was limited a relatively narrow portion of this region.

Figure 5.

Figure 5

Open in a new tab

The stress concentration factor (SCF) was highly sensitive to tendon length over the physiological range (red circle corresponding to Lt/Rb = 20).

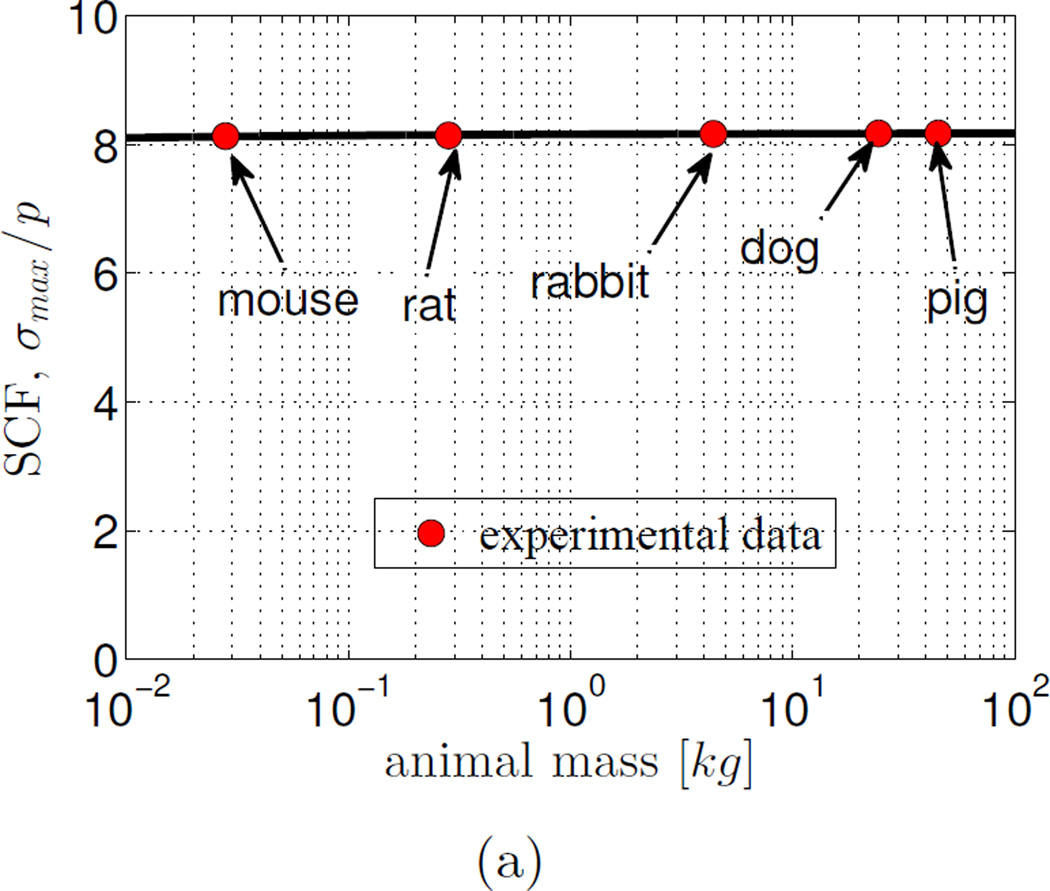
3.4. The stress concentration does not vary significantly across animals whose mass varies over three orders of magnitude

Combining these effects, SCF was seen to be nearly invariant with respect to animal body mass for all animals studied (Fig. 6). SCF reduced only a few percent between mice and pigs.

Figure 6.

Figure 6

Open in a new tab

The stress concentration factor (SCF) was invariant across species for animals ranging from 0.03 kg (mice) to 50 kg (pigs). Lt/Rb = 20; red circles: physiological data.

4. Discussion

We studied the mechanical function of the tendon-to-bone attachment across species using a mathematical model, with the aim of gaining insight into strategies for surgical and tissue engineered repair of the rotator cuff. A hypothesis in the literature is that the attachment site is optimized to minimize stress concentration (Liu et al., 2012).

However, data from a broad range of species, when interpreted through our models, suggest that this is not the case. The model shows that SCF decreases with increasing normalized attachment length, La/Rb (Fig. 4a), and with decreasing normalized tendon length, Lt/Rb (Fig. 5). The SCF can clearly be reduced by eliminating the tendon altogether and replacing it with a long graded attachment site. Even minor changes to the normalized tendon length would reduce the SCF. The morphometrics of the animals considered were clearly not optimized to minimize the SCF.

Instead, results supported a hypothesis that SCF is conserved across species. This was evident when predictions were plotted as a function of animal body mass (Fig. 6), and was further supported by the amount of variance across species in the normalized length of the attachment and tendon. The normalized attachment length La/Rb has a physiological range over which the sensitivity of the SCF is low. La/Rb ranged over more than two orders of magnitude (0.001 < La/Rb < 0.02) across the species studied, but this two-decade variance corresponded to less than 4% change in SCF. This variance within a region of relative insensitivity is consistent with a design that conserves stress concentration across species. The normalized tendon length, on the other hand, has a physiological range over which the sensitivity of the SCF is very high. Although a plateau region exists (Fig. 5), the physiological range is far from it. From the perspective of our hypothesis, the relatively small cross-species variance in normalized tendon length conserves SCF across species.

As the animal mass increases, one might expect the size of the gradient region to also increase to accommodate the higher applied loads. However, Deymier-Black et al. (2015) showed that the mean muscle stress at the rotator cuff attachment site, analogous to the applied load p in our model, is highly conserved across species. Our results demonstrate that the SCF ≡ σmax/p is also conserved across species. Taken together, these data suggest that the peak stress level at the attachment site is also highly conserved. This suggests that the tendon-to-bone attachment site is tailored to ensure a homeostatic range of stresses that is conserved across species.

Why would such a homoeostatic stress target be optimal for tendon-to-bone attachment sites across species? Mechanical loading is well known to play an essential role in musculoskeletal growth and development (Robling and Turner, 2009; Ehrlich and Lanyon, 2002; Klein-Nulend et al., 2005). Inadequate mechanical stimulation reduces bone mineral content, retards bone formation, and increases bone resorption, and increased mechanical stimulation leads to increased bone formation and decreased bone resorption (Morey and Baylink, 1978). Numerous studies have highlighted the interplay between mechanical, structural and biochemical signals that cells use to adapt and respond to the local stain/stress environments (Benjamin and Ralphs, 1998), and the tendon-to-bone attachment site does not develop a proper fibrocartilaginous transition or cell population in the absence of physiological loading (Schwartz et al., 2013, 2015). Indeed, the challenge during development might be to amplify low stresses generated by small muscles to homeostatic levels sufficient to promote and sustain bone mineralization (Liu et al., 2014a; Schwartz et al., 2012). Given the well known mechanical adaption of cells and its dependence upon the magnitude, duration, and rate of the applied loads (Duncan and Turner, 1995; Liedert et al., 2005; Nekouzadeh et al., 2008; Thomopoulos et al., 2011; Lee et al., 2012; Elson and Genin, 2013), and given that the machinery used to transduce loads is highly conserved across mammals, the existence of a highly conserved target stress range is logical.

These results have ramifications for the broad sets of literature on tendon-to-bone healing, development, and tissue engineering (Lu and Thomopoulos, 2013; Smith et al., 2012; Kolluru et al., 2013; Lipner et al., 2014; Thomopoulos et al., 2010). Results suggest that a preferred range of target stresses is desirable within the tendon-to-bone attachment in animals across a three order of magnitude range of body mass, and motivate further study to determine whether extrapolation to humans is possible. In these animals, factors such as the length of tendon are critically important to the stress distribution. The size of the graded attachment site can vary over several orders of magnitude without affecting the stress concentration substantially, but would have a significant effect outside of that range.

5. Conclusions

Using data from a number of mammals and a simplified mechanical model, we found support for a hypothesis that the structures of the tendon-to-bone complex combine to conserve stress concentrations across species. The results indicate that the stress concentration factor arising at the attachment of tendon to bone is insensitive to the variation of the normalized graded attachment length over the physiological range. The stress concentration is sensitive to the normalized tendon length, but little variation exists across species. As a result, within the range of body masses studied, mammals all maintain a constant peak stress at the attachment of tendon to bone. This observation motivates further study of stress concentration in human rotator cuffs. Furthermore, this highly conserved range of stresses, and the structures that support it, are potential targets for improved surgical and tissue engineered repair of the rotator cuff tendon-to-bone attachment.

Acknowledgments

This work was supported in part by the National Science Foundation and the National Institutes of Health through grant U01EB016422, and by the Chinese Ministry of Education through at Changjiang Scholar Award to GMG.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Contributor Information

Fatemeh Saadat, Department of Mechanical Engineering & Materials Science Washington University, St. Louis, MO 63130, USA.

Alix C. Deymier, Department of Orthopaedic Surgery Columbia University, New York, NY 10032, USA

Victor Birman, Missouri S&T Global – St. Louis Missouri University of Science and Technology, St. Louis, MO 63131, USA.

Stavros Thomopoulos, Department of Orthopaedic Surgery Department of Biomedical Engineering Columbia University, New York, NY 10032, USA.

Guy M. Genin, Department of Mechanical Engineering & Materials Science Washington University, St. Louis, MO 63130, USA.

References

  1. Apalak MK. Functionally graded adhesively bonded joints. Reviews of Adhesion and Adhesives. 2014;2(1):56–84. [Google Scholar]
  2. Benjamin M, Ralphs J. Fibrocartilage in tendons and ligamentsan adaptation to compressive load. Journal of Anatomy. 1998;193(04):481–494. doi: 10.1046/j.1469-7580.1998.19340481.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Birman V. Encyclopedia of Thermal Stresses. Springer; 2014. Functionally graded materials and structures; pp. 1858–1865. [Google Scholar]
  4. Birman V, Keil T, Hosder S. Structural Interfaces and Attachments in Biology. Springer; 2013. Functionally graded materials in engineering; pp. 19–41. [Google Scholar]
  5. Byrd LW, Birman V. Modeling and analysis of functionally graded materials and structures. Applied Mechanics Reviews. 2007;60:195–216. [Google Scholar]
  6. Cummins CA, Murrell GA. Mode of failure for rotator cuff repair with suture anchors identified at revision surgery. Journal of shoulder and elbow surgery. 2003;12(2):128–133. doi: 10.1067/mse.2003.21. [DOI] [PubMed] [Google Scholar]
  7. Deymier-Black AC, Pasteris JD, Genin GM, Thomopoulos S. Allometry of the tendon enthesis: mechanisms of load transfer between tendon and bone. ASME Journal of Biomechanical Engineering. 2015 doi: 10.1115/1.4031571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Duncan R, Turner C. Mechanotransduction and the functional response of bone to mechanical strain. Calcified tissue international. 1995;57(5):344–358. doi: 10.1007/BF00302070. [DOI] [PubMed] [Google Scholar]
  9. Ehrlich P, Lanyon L. Mechanical strain and bone cell function: a review. Osteoporosis International. 2002;13(9):688–700. doi: 10.1007/s001980200095. [DOI] [PubMed] [Google Scholar]
  10. Elson E, Genin G. The role of mechanics in actin stress fiber kinetics. Experimental cell research. 2013;319(16):2490–2500. doi: 10.1016/j.yexcr.2013.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fung Y, Cowin S. Biomechanics: mechanical properties of living tissues. Journal of Applied Mechanics. 1994;61:1007. [Google Scholar]
  12. Galatz LM, Ball CM, Teefey SA, Middleton WD, Yamaguchi K. The outcome and repair integrity of completely arthroscopically repaired large and massive rotator cuff tears. The Journal of Bone & Joint Surgery. 2004;86(2):219–224. doi: 10.2106/00004623-200402000-00002. [DOI] [PubMed] [Google Scholar]
  13. Gàlvez-López E, Casinos A. Scaling and mechanics of the felid calcaneus: geometric similarity without differential allometric scaling. Journal of anatomy. 2012;220(6):555–563. doi: 10.1111/j.1469-7580.2012.01502.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gayon J. History of the concept of allometry. American Zoologist. 2000;40(5):748–758. [Google Scholar]
  15. Genin GM, Birman V. Micromechanics and structural response of functionally graded, particulate-matrix, fiber-reinforced composites. International journal of solids and structures. 2009;46(10):2136–2150. doi: 10.1016/j.ijsolstr.2008.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Genin GM, Kent A, Birman V, Wopenka B, Pasteris JD, Marquez PJ, Thomopoulos S. Functional grading of mineral and collagen in the attachment of tendon to bone. Biophysical journal. 2009;97(4):976–985. doi: 10.1016/j.bpj.2009.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gould SJ. Allometry and size in ontogeny and phylogeny. Biological Reviews. 1966;41(4):587–638. doi: 10.1111/j.1469-185x.1966.tb01624.x. [DOI] [PubMed] [Google Scholar]
  18. Gould SJ. Ontogeny and phylogeny. Harvard University Press; 1977. [Google Scholar]
  19. Huxley J, Strauss RE, Churchill FB. Problems of relative growth. London: Methuen; 1932. [Google Scholar]
  20. Huxley JS, Teissier G. Terminology of relative growth. Nature. 1936;137(3471):780–781. [Google Scholar]
  21. Klein-Nulend J, Bacabac R, Mullender M. Mechanobiology of bone tissue. Pathologie biologie. 2005;53(10):576–580. doi: 10.1016/j.patbio.2004.12.005. [DOI] [PubMed] [Google Scholar]
  22. Klingenberg CP, McIntyre GS. Geometric morphometrics of developmental instability: analyzing patterns of uctuating asymmetry with procrustes methods. Evolution. 1998:1363–1375. doi: 10.1111/j.1558-5646.1998.tb02018.x. [DOI] [PubMed] [Google Scholar]
  23. Kolluru PV, Lipner J, Liu W, Xia Y, Thomopoulos S, Genin GM, Chasiotis I. Strong and tough mineralized plga nanofibers for tendon-to-bone scaffolds. Acta biomaterialia. 2013;9(12):9442–9450. doi: 10.1016/j.actbio.2013.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lee S-L, Nekouzadeh A, Butler B, Pryse KM, McConnaughey WB, Nathan AC, Legant WR, Schaefer PM, Pless RB, Elson EL, et al. Physically-induced cytoskeleton remodeling of cells in three-dimensional culture. PloS one. 2012;7(12):e45512. doi: 10.1371/journal.pone.0045512. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Liedert A, Kaspar D, Augat P, Ignatius A, Claes L. Mechanobiology of bone tissue and bone cells. In: Kamkin A, Kiseleva I, editors. Mechanosensitivity in Cells and Tissues. Moscow: Academia; 2005. [PubMed] [Google Scholar]
  26. Lipner J, Liu W, Liu Y, Boyle J, Genin G, Xia Y, Thomopoulos S. The mechanics of plga nanofiber scaffolds with biomimetic gradients in mineral for tendon-to-bone repair. Journal of the mechanical behavior of biomedical materials. 2014;40:59–68. doi: 10.1016/j.jmbbm.2014.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Liu Y, Birman V, Chen C, Thomopoulos S, Genin GM. Mechanisms of bimaterial attachment at the interface of tendon to bone. Journal of engineering materials and technology. 2011;133(1):011006. doi: 10.1115/1.4002641. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Liu Y, Schwartz AG, Birman V, Thomopoulos S, Genin GM. Stress amplification during development of the tendon-to-bone attachment. Biomechanics and modeling in mechanobiology. 2014a;13(5):973–983. doi: 10.1007/s10237-013-0548-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Liu Y, Thomopoulos S, Birman V, Li J-S, Genin GM. Bimaterial attachment through a compliant interfacial system at the tendon-to-bone insertion site. Mechanics of Materials. 2012;44:83–92. doi: 10.1016/j.mechmat.2011.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Liu Y, Thomopoulos S, Chen C, Birman V, Buehler MJ, Genin GM. Modelling the mechanics of partially mineralized collagen fibrils, fibres and tissue. Journal of The Royal Society Interface. 2014b;11(92):20130835. doi: 10.1098/rsif.2013.0835. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lu HH, Thomopoulos S. Functional attachment of soft tissues to bone: development, healing, and tissue engineering. Annual review of biomedical engineering. 2013;15:201. doi: 10.1146/annurev-bioeng-071910-124656. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Mathewson MA, Kwan A, Eng CM, Lieber RL, Ward SR. Comparison of rotator cuff muscle architecture among humans and selected vertebrate species. The Journal of experimental biology, jeb–083923. 2013 doi: 10.1242/jeb.083923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Morey ER, Baylink DJ. Inhibition of bone formation during space flight. Science. 1978;201(4361):1138–1141. doi: 10.1126/science.150643. [DOI] [PubMed] [Google Scholar]
  34. Munz D, Yang Y. Stress singularities at the interface in bonded dissimilar materials under mechanical and thermal loading. Journal of Applied Mechanics. 1992;59(4):857–861. [Google Scholar]
  35. Nekouzadeh A, Pryse KM, Elson EL, Genin GM. Stretch-activated force shedding, force recovery, and cytoskeletal remodeling in contractile fibroblasts. Journal of biomechanics. 2008;41(14):2964–2971. doi: 10.1016/j.jbiomech.2008.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Paxton ES, Teefey SA, Dahiya N, Keener JD, Yamaguchi K, Galatz LM. Clinical and radiographic outcomes of failed repairs of large or massive rotator cuff tearsminimum ten-year follow-up. The Journal of Bone & Joint Surgery. 2013;95(7):627–632. doi: 10.2106/JBJS.L.00255. [DOI] [PubMed] [Google Scholar]
  37. Pollock CM, Shadwick RE. Allometry of muscle, tendon, and elastic energy storage capacity in mammals. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology. 1994;266(3):R1022–R1031. doi: 10.1152/ajpregu.1994.266.3.R1022. [DOI] [PubMed] [Google Scholar]
  38. Qu J, Thoreson AR, Chen Q, An K-N, Amadio PC, Zhao C. Tendon gradient mineralization for tendon to bone interface integration. Journal of Orthopaedic Research. 2013;31(11):1713–1719. doi: 10.1002/jor.22412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Robling AG, Turner CH. Mechanical signaling for bone modeling and remodeling. Critical reviews in eukaryotic gene expression. 2009;19(4):319. doi: 10.1615/critreveukargeneexpr.v19.i4.50. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Schmidt-Nielsen K. Scaling: why is animal size so important? Cambridge University Press; 1984. [Google Scholar]
  41. Schwartz A, Lipner J, Pasteris J, Genin G, Thomopoulos S. Muscle loading is necessary for the formation of a functional tendon enthesis. Bone. 2013;55(1):44–51. doi: 10.1016/j.bone.2013.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Schwartz AG, Long F, Thomopoulos S. Enthesis fibrocartilage cells originate from a population of hedgehog-responsive cells modulated by the loading environment. Development. 2015;142(1):196–206. doi: 10.1242/dev.112714. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Schwartz AG, Pasteris JD, Genin GM, Daulton TL, Thomopoulos S. Mineral distributions at the developing tendon enthesis. PLoS one. 2012;7(11):e48630. doi: 10.1371/journal.pone.0048630. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Smith L, Xia Y, Galatz LM, Genin GM, Thomopoulos S. Tissue-engineering strategies for the tendon/ligament-to-bone insertion. Connective tissue research. 2012;53(2):95–105. doi: 10.3109/03008207.2011.650804. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Smith RJ. Allometric scaling in comparative biology: problems of concept and method. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology. 1984;246(2):R152–R160. doi: 10.1152/ajpregu.1984.246.2.R152. [DOI] [PubMed] [Google Scholar]
  46. Thomopoulos S, Birman V, Genin GM. Structural interfaces and attachments in biology. Springer Science & Business Media; 2012. [Google Scholar]
  47. Thomopoulos S, Das R, Birman V, Smith L, Ku K, Elson EL, Pryse KM, Marquez JP, Genin GM. Fibrocartilage tissue engineering: the role of the stress environment on cell morphology and matrix expression. Tissue Engineering Part A. 2011;17(7–8):1039–1053. doi: 10.1089/ten.tea.2009.0499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Thomopoulos S, Genin GM, Galatz LM. The development and morphogenesis of the tendon-to-bone insertion what development can teach us about healing. Journal of musculoskeletal & neuronal interactions. 2010;10(1):35. [PMC free article] [PubMed] [Google Scholar]
  49. Thomopoulos S, Marquez JP, Weinberger B, Birman V, Genin GM. Collagen fiber orientation at the tendon to bone insertion and its influence on stress concentrations. Journal of biomechanics. 2006;39(10):1842–1851. doi: 10.1016/j.jbiomech.2005.05.021. [DOI] [PubMed] [Google Scholar]
  50. Thomopoulos S, Williams G, Soslowsky L. Tendon to bone healing: differences in biomechanical, structural, and compositional properties due to a range of activity levels. Journal of biomechanical engineering. 2003a;125(1):106–113. doi: 10.1115/1.1536660. [DOI] [PubMed] [Google Scholar]
  51. Thomopoulos S, Williams GR, Gimbel JA, Favata M, Soslowsky LJ. Variation of biomechanical, structural, and compositional properties along the tendon to bone insertion site. Journal of Orthopaedic Research. 2003b;21(3):413–419. doi: 10.1016/S0736-0266(03)00057-3. [DOI] [PubMed] [Google Scholar]
  52. Thompson DW, et al. On growth and form. On growth and form. 1942 [Google Scholar]
  53. West GB, Brown JH. The origin of allometric scaling laws in biology from genomes to ecosystems: towards a quantitative unifying theory of biological structure and organization. Journal of Experimental Biology. 2005;208(9):1575–1592. doi: 10.1242/jeb.01589. [DOI] [PubMed] [Google Scholar]
  54. Wopenka B, Kent A, Pasteris JD, Yoon Y, Thomopoulos S. The tendon-to-bone transition of the rotator cuff: a preliminary raman spectroscopic study documenting the gradual mineralization across the insertion in rat tissue samples. Applied spectroscopy. 2008;62(12):1285–1294. doi: 10.1366/000370208786822179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Zumstein MA, Jost B, Hempel J, Hodler J, Gerber C. The clinical and structural long-term results of open repair of massive tears of the rotator cuff. The Journal of Bone & Joint Surgery. 2008;90(11):2423–2431. doi: 10.2106/JBJS.G.00677. [DOI] [PubMed] [Google Scholar]

RESOURCES