Abstract
A novel concept for ion spatial peak compression is described, and discussed primarily in the context of ion mobility spectrometry (IMS). Using theoretical and numerical methods, the effects of using non-constant (e.g., linearly varying) electric fields on ion distributions (e.g., an ion mobility peak) is evaluated both in the physical and temporal domains. The application of linearly decreasing electric field in conjunction with conventional drift field arrangements is shown to lead to a reduction in IMS physical peak width. When multiple ion packets (i.e. peaks) in a selected mobility window are simultaneously subjected to such fields, there is ion packet compression, i.e., a reduction in peak widths for all species. This peak compression occurs with only a modest reduction of resolution, and which can be quickly recovered as ions drift in a constant field after the compression event. Compression also yields a significant increase in peak intensities. Ion mobility peak compression can be particularly useful for mitigating diffusion driven peak spreading over very long path length separations (e.g., in cyclic multi-pass arrangements), and for achieving higher S/N and IMS resolution over a selected mobility range.
INTRODUCTION
Ion mobility based separation techniques [1-3], combined with mass spectrometry (MS), have broad analytical applications [4-6], with higher throughput measurements due to the high speed of IMS accompanied by its orthogonal dimension of structure related information (i.e., collision cross sections) [7-12]. Ions introduced as a packet (e.g., generated by MALDI or ESI [13, 14]) separate on a milliseconds timescale due to differences in their ionic mobilities while drifting under the influence of a weak electric field. At low E/N ratio (E is electric field; N is number density) the resolving power achievable for an infinitesimally small initial ion packet size is dependent on the applied electric field and the distance or time over which this field is applied [11]. For packets of finite initial thickness, the ion mobility resolving powers are lower. These losses can be somewhat recovered by using non-linear voltages for ion injection into drift cell [15]. Detailed studies of ion motion in arbitrary drift fields help elucidate the factors involved in mobility separations [16, 17]. In addition to traditional constant drift field based IMS, approaches that use dynamic fields to separate ions have been developed, e.g., differential mobility spectrometry [18, 19], travelling wave [20, 21], and overtone mobility spectrometry [22, 23]. IMS measurements in cyclic path devices [8, 24] have been demonstrated to extend resolving powers, by switching voltages to maintain ions in a field gradient [8, 24, 25].
Unlike effects due to scattering in a reflectron of a TOF MS (which are addressed by some form of signal recombination) [26], and where peak broadening occurs purely due to kinetic energy, in the ion mobility realm random Brownian motion of ions or thermal diffusion is the limiting factor for the maximum achievable resolution. With an initially compressed injection packet diffusional broadening quickly becomes predominant. This effect becomes increasingly limiting for IMS separations using e.g. multi-pass/cyclical separation devices. The number of cycles that ion packets can execute is ultimately limited by the IMS peak diffusional broadening, ultimately reaching a point where even a single peak exceeds the range that can be studied in a single separation. This issue is further aggravated by the decreased signal intensities as a function of number of cycles due to the effective diffusion driven peak dilution. Even with the ability to losslessly manipulate ions, e.g. using SLIM devices [27-32], the reduced peak intensities and mobility range with increasing numbers of passes presents significant challenges. We have recently described travelling wave-based SLIM devices that can potentially provide very high mobility resolution using long drift paths [33] over a much greater range of mobilities, including much longer multi-pass designs, but diffusional broadening for greatly extended drift lengths would remain problematic.
In this work we describe a new approach that would counter the diffusional broadening in IMS by spatially compressing individual ion mobility packets with a minimal loss of resolution between different ion packets. The present approach is different from previous works on resolution enhancement e.g. by modulating injection packet widths or controlling gate effects (which aim at approaching the diffusion limited resolving power) [15], in that it proposes a dynamic peak width manipulation concept that can overcome the effects of diffusional peak broadening occurring during the separation and which can be applied at an arbitrary time. The new approach relies on the dynamic application of a non-constant drift field to compress ion packets. As opposed to the linear potential profiles (i.e., constant drift fields) generally used in IMS, we use electric fields having a decreasing magnitude in the direction of ion motion to spatially compress ion packets. Ions located at the ‘trailing’ high field portion of the potential profile drift faster than ions located at the ‘leading’ low field portion of the potential profile. By applying such a field profile for a short period of time, ion packets can be compressed, and then resume motion in a conventional uniform drift field. Any reduction in the resolution during the compression event can be recovered after traversing a modest additional drift length. By performing such compression periodically, the ion packet widths can potentially be restricted to some minimal value, providing much greater peak intensities. IMS peak compression thus can enable very high resolving power separations in very long drift path devices. Where peak broadening is limiting (e.g. ion mobility cyclic multi-pass devices), peak compression can potentially enable much greater resolution measurements that are in principle not limited by diffusion or drift path length. In this manuscript we theoretically evaluate the compression of ion packets that momentarily experience a nonlinear field, the effect of peak compression on IMS resolution under different operating conditions.
METHODS
The velocity (vi) of an ion drifting in a buffer gas under the influence of a weak electric field (E, V/cm) is determined by its mobility Ki as: vi=KiE. At low E/N, under the conditions of a constant electric field this ion motion results in constant ion velocity. If the electric field is not constant, the ions move with different velocities at different positions. For example, as in the case considered here, if the electric field E(x) is varying linearly with a slope B (V/m2) then the field and ion velocity conditions at a point x(m) are described as follows.
| (1) |
| (2) |
| (3) |
If xi>0 is the initial mean position of the ion packet within the non-constant field, xfi < E0/B is the final mean position of ion packet, t is the time for which the non-constant field is applied, then Equation 4 gives the value of xfi after evaluating the integral in Equation 3.
| (4) |
If we assume that ions drift and separate for a fixed time (t0) prior to being subjected to the non-constant electric field, then the peak dispersion in physical space at a time just before the non-constant field is applied is given by Var(xi)=2Dit0. Here, is the diffusion constant, kB is Boltzmann constant, T is temperature, and q is the ion charge in Coulombs. From Equation 4, the spatial variance of an ion packet after passing through the non-constant field for time t can be calculated as Var(x)=Var(xi) e−2KiBt, and is dependent on the initial plume width Var(xi), the steepness/slope of the electric field B (V/m2), and the time t for which the non-constant field is applied. During application of the non-constant field, diffusional broadening has an additional contribution to the variance of the peak that can be expressed as: 2Dit. Thus, when non-constant fields are experienced by the ion packet for time t, the spatial variance of an ion packet with prior drift in a constant field for a time t0, is given as:
| (5) |
Equation 5 assumes preservation of the symmetric (Gaussian) distribution during ion motion through the non-constant profile. This assumption is further supported through the computation of ion number density n (m−3) distributions for ions with ion mobility Ki (m2/Vs) and diffusion coefficient Di (m2/s), with flight through a non-constant electric field E(x). The ion number density can be calculated using the drift-diffusion equation [34, 35], shown below.
| (6) |
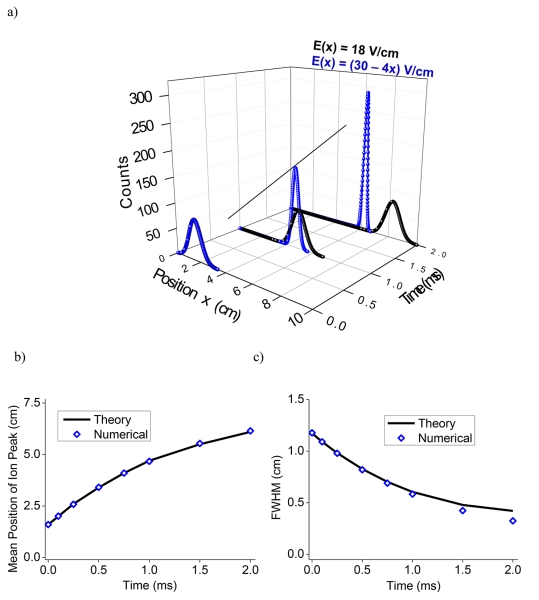
Solving Equation 6 computationally using first order explicit time differencing and second order space differencing using the finite difference method[36] yielded final ion packet distributions after time t in the nonlinear compression field. Figure 1a shows the evolution of the ion plume distributions along the direction of the ion motion and in the time domain, based upon the numerical solution using Equation 6. The peak distributions obtained when ions were subjected to a constant field (black) and a decreasing (blue) electric field (30 to 0 V/cm over 7.5 cm) are shown in Figure 1a. With a linearly decreasing electric field, the width of the ion distribution decreases with time. The numerical calculations of the ion peak position and width (from Equation 6) are in agreement with theoretical estimates from Equations 4 and 5 (Figure 1b and 1c), validating our theoretical and computational approach.
Figure 1.
a) Comparison of ion packet evolution in a drift field with a constant (black, 18 V/cm) and varying (blue, (30-4x) V/cm) electric fields. b) Mean position of the peak distribution as a function of compression time calculated from theoretical and numerical methods. c) FWHM in physical space as a function of compression time calculated from theoretical and numerical methods.
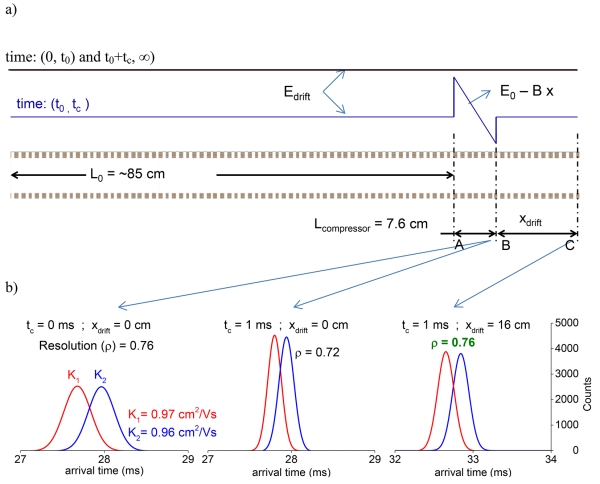
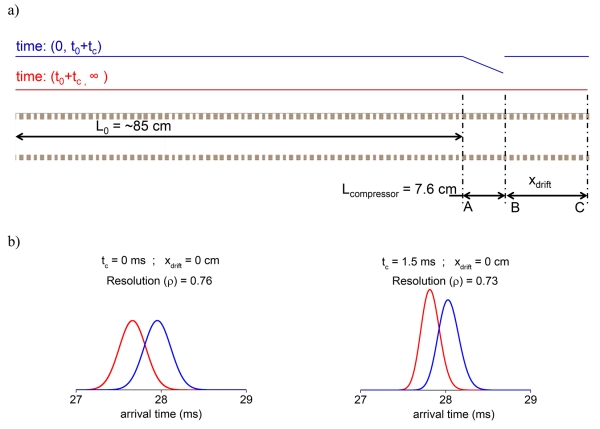
After application of the non-constant field for time t, the drift field was changed back to the original constant field of Edrift. The ion plume drifts for the remaining path and ion arrival time statistics were collected. The non-constant field was applied for a short time (t) as shown in the timing diagram (Figure 2a). Also, the varying electric field was applied over a small section Lcompressor of the overall drift device (Figure 2a).
Figure 2.
a) Electric field profile timing diagram, t0 (time for which the constant field is applied) is the time it takes to drift 85 cm and reach compression region (a-B) and tc is the time for which compressor field (E0-Bx) is applied. b) Ion arrival time distributions for two ion packets having the indicated mobilities under different compressor conditions: Left) normal drift conditions at 18 V/cm and ion statistics collected at point B, middle) 1 ms compression in the Lcompressor (A-B) region with ion statistics collected at point B; right) 1 ms compression in Lcompressor, with ion statistics collected at point C (using xdrift = 16 cm). The simulations show a small loss of resolution after compression. This is offset by an additional drift time of ~ 5 ms in the constant electric field over an additional drift length of 16 cm in region B-C.
The initial drift time t0 determined the mobility range (Ki) within the compression region (Lcompressor), t is the time for which the compression field is applied, and the final ion position after time t0+t is xfi. The final mean arrival time tfi (Equation 7) for a given mobility to reach the end of the compression region (point B in Figure 2a) and the temporal full width at half maximum δti (Equation 8) are shown below.
| (7) |
| (8) |
Using Equations 7 and 8, the arrival time distributions for mobilities were compared and the peak characteristics without peak compression and with peak compression were evaluated under different conditions.
RESULTS AND DISCUSSION
In this work IMS separations of two singly-charged species having 1% difference in their mobility (reduced mobilities of 0.97 and 0.96 cm2/Vs) were used to theoretically and computationally explore the utility of ion packet compression. Most calculations assumed the ion packets were separated over an initial drift time of t0 = 0.026 s, prior to application of (i.e. switching to) the ion compression voltage profile. The initial drift paths were Lo = 86.2 cm and 84.5 cm for K01 and K02 species, respectively, for Edrift = 18 V/cm in nitrogen at a pressure (p) of 4 Torr (typical for the uniform drift field IMS devices in our laboratory [37-40]). In the compression approach, the field is ‘switched’ (i.e., to non-constant values) for a short time period t, and then switched back to constant Edrift = 18 V/cm to e.g., to continue the separation, or transport ions to the detector. We note that rather than switching the non-constant field ‘on’ at a specific time (when the selected mobility window is fully within the compressor region); ions can alternatively drift into a region of non-constant field that is then switched to a constant field at a specified time (as discussed below in conjunction with Figure 5). In this work we also investigated the use of an additional drift length of xdrift after the compression event, with particular interest in the additional xdrift required to recover any loss of resolution during compression. Also some of the effects of peak distortion that may occur when only a part of the peak is within the compressor region when switching to compression profiles, is discussed.
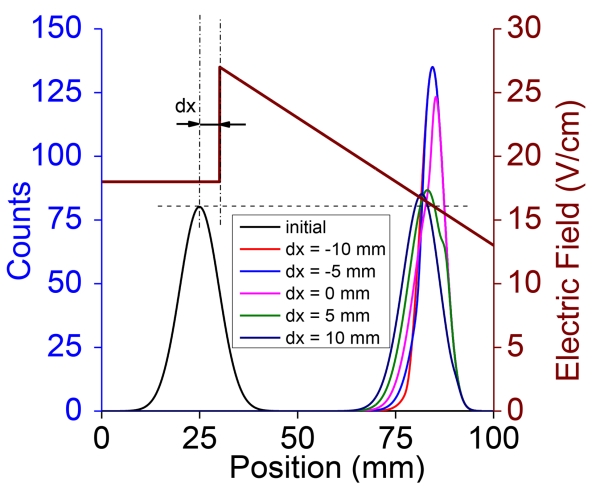
Figure 5.
Final peak shapes with peak compression being switched on when a portion of the selected mobility window is outside the compressor region.
Ion statistics were recorded, either at point B or point C during separations (Figure 2a), to determine the ion distribution in the packet (i.e. peak shape). If ion losses are avoided, effective peak compression should result in final peak intensities (after an additional xdrift) that are higher than the peak intensity in normal drift IMS (i.e. at point B), with resolution comparable (at point C) to that obtained without compression at point B.
Figure 2b shows the peak characteristics of two ionic species with and without compression; and the recovery of the ‘lost’ resolution using an additional drift length. Ions drift through a total path length comprising of an initial drift length, the length of compression region (7.6 cm), and a final variable drift length xdrift. Figure 2b (left panel) shows the calculated drift spectrum for t = 0, i.e., with no compression field applied. In this case the ions drifted through 92 cm to point B, an average full width at half maximum (<FWHM>) of 366 μs and a resolution for the selected mobilities of 0.76 (Δt/<FWHM>) is obtained without compression. If the compression field is applied for 1 ms (Figure 2b, center), peak heights at point B are 1.9-fold greater, <FWHM> is 195 μs and their resolution is 0.72 (~5% lower). If ions drift for an additional 16 cm the resolution is recovered (0.76), the final <FWHM> is 245 μs and the final peak height is 1.5-fold greater (Figure 2b, right). In the context of applying such compression in a multi-pass separation, additional drift length can be obtained without any geometry or ion loss related limitations (particularly in the context of lossless ion manipulation devices [28, 29]). Further, for clarity, it can be noted that the temporal width of the peaks being compressed are largely independent of the compression operation time, as there is essentially instantaneous switching of compression fields over the total physical area spanned by the peaks, and this compression field is active for a certain period of time. Such precise mobility selection and switching of voltages has been demonstrated previously [28, 30]. Of course, the physical location of a peak vis-à-vis the geometry of the device where compression fields are active is quite important, lest there be peaks that are partially outside the compression region when the compression fields are switched on. These effects are discussed later, though experimental implementation would aim to avoid such events by preselecting mobility windows.
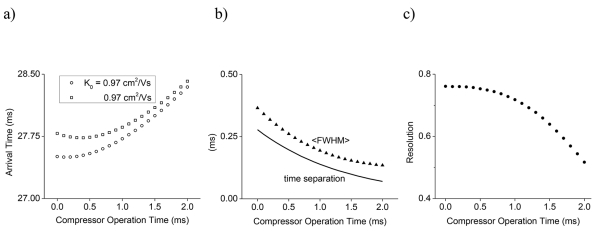
The effects of compression time t on the peak characteristics at point B (i.e., xdrift = 0) are shown in Figure 3. Ion arrival times increase with increasing compression time, as the ions spend more time in the low field portion of the compression region. Peak widths (FWHM) decrease and peak intensities increase, and a modest loss in peak resolution is observed. We note that the steepness of the field profile is also an important factor, and that the compression fields are ultimately constrained by practical issues associated with the highest field region (typically limited by field heating of ions or electrical breakdown). Imperfections in the applied field profile, due to e.g., electrode arrangements or imperfections of the field due to variances in applied voltages, may also degrade compression performance. However, when compression is applied multiple times the net gain in the performance can be significant, even if a single compression event might not provide very high gain in separation performance due to field imperfections. Also, confining ions far away from electrode surfaces where fields are smoother, and e.g., power supplies enabling fast switching and precise voltage profiles across arrays of electrodes, can also help reduce field imperfections. Also, confining ions far away from electrode surfaces where fields are smoother, and e.g., power supplies enabling fast switching and precise voltage profiles across arrays of electrodes may also help reduce field imperfections. Also, in the context of performing cyclical separations, several design geometry related challenges have been discussed previously. As ions cycle, diffusional broadening and the ‘lapping’ of faster peaks by slower ones, largely defines the maximum number of cycles that are practical. The number of passes that can be executed in a cyclical separation without peak lapping is determined by the mobility difference, the effective path length and the applied fields in the specific implementation. However, diffusional broadening is an additional factor, wherein peaks broaden to such a degree that they cover a significant portion of the effective path length of the separation device. For use of a multi-pass separator over a targeted mobility range, periodically applied peak compression can help offset diffusional broadening and provide advantage to significantly higher pass numbers.
Figure 3.
a) Arrival time (open symbols), b) <FWHM> (solid triangles), time separation (solid line) and c) peak resolution (solid circles,) as a function of the time for which the compression field is applied.
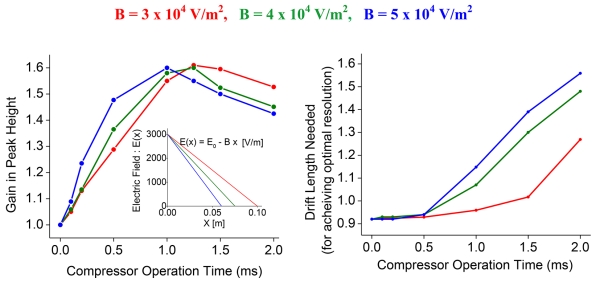
Figure 4 shows the gain in peak intensities for different compression times and for different field steepness/slope. In all cases the resolution achieved at point C was held constant at 0.76 (as for normal drift at point B) by adjusting the distance after compression xdrift. For the steepest electric field considered (E(x)=3 × 103−5×104x), the gain in peak height is greater at longer compression times. However, beyond a certain compression time, the total drift length needed is higher for steeper profiles due to greater loss in resolution during compression. Also at longer compression times, the final gain in peak height decreases due to the increase in additional drift distance needed to maintain the resolution. This additional drift distance contributes to diffusional broadening, ultimately limiting the maximum peak compressibility.
Figure 4.
Left panel shows the increase in peak height in non-constant fields of different slopes. Right panel shows the effect of additional drift length needed to achieve same peak resolution as obtained in a constant field (18 V/cm).
Theoretical arrival time distributions (Equations 7 and 8) and results shown in Figures 1-4 were based upon three sequential steps in order to compress ion packets. The first step involves conventional drift in a constant field, followed by time-synchronized change to the non-constant electric field used for compression, and finally switching back to the (typically initial) constant field to continue the separation. One of the issues in the implementation of this approach experimentally is the need to time the switching so that the totality of the selected mobility range is within the compressor region, particularly when there is a complex mixture involved. If a part of a peak, for example, is outside the compressor region when there is switching to the non-linear profile, the leading portion of the peak experiences varying velocity and the trailing portion is still in the uniform velocity condition, and potentially leading to peak distortion (Figure 5). Figure 5 shows such a case, where the spatial distribution of peaks after 1 ms of compression with varying initial peak starting positions outside the compressor region. While there is a potential for some peak distortion, experimental implementation would involve switching to the compressor field profiles for a pre-selected ion mobility window, and in which case such occurrences can be eliminated. In addition to timed switching of selected mobilities, approaches that can ‘filter out’ undesirable mobilities (for example by using overtone mobility [41], or other forms of mobility based filters) can potentially address issues with complex mixture analysis while using peak compression.
Also, an alternative approach for achieving peak compression involves ions drifting into a region of non-constant field (e.g. cases corresponding to dx > 10 mm in Figure 5) that is then switched to a constant field at a specified time. For clarity, it is to be noted here that ions drift into a region with a different field, and as such this field profile can be created while maintaining a decreasing voltage profile, albeit a non-linear one. We briefly investigated this two-step approach numerically (by solving Equation 6). In this approach, the first step constituted ion motion through a field profile shown in Figure 6a (blue), i.e. ions drift from a constant field region into the decreasing field region. After time t, the decreasing field is switched into a constant field condition (Figure 6a, red) to continue the separation. This ion transport process was simulated by defining the two electric field conditions in the device and switching between them at the chosen compression time (tc = 1.5ms). The computed gain in peak intensity using this approach (Figure 6b) is similar to the three step approach (Figure 2b), but with the need to switch voltages only once instead of twice.
Figure 6.
a) A timing diagram for a compression approach where field switching occurs once. Ions are allowed to drift into a region of decreasing field gradient where compression occurs (blue), instead of switching to the decreasing field once the selected mobility range is within the region. After ions spend some time in compression region the field is switched to constant value (red line). b) Left panel shows drift through constant field and arrival time distribution at point B; right panel shows arrival time distribution at point B with the compression field applied for 1.5 ms.
We envision the ion peak compression process to occur over selected windows of ion mobilities. The analogy of ion isolation in mass spectrometry is relevant in this context. After obtaining an MS spectrum, many MS allow a selected mass range to be isolated and fragmented to obtain MS/MS with better selectivity and better sensitivity. Similarly, in an ion mobility separation a targeted mobility range may be chosen for ion compression to enable long path length separations for that particular mobility range, such as we expect to be feasible using SLIM-based devices [28, 30]. By selecting a mobility range and performing peak compression, the limitations of diffusional broadening can be overcome. Periodic peak compression during a multi-pass separation can potentially provide means to achieve previously unmatched separation capabilities; i.e. significantly larger gains in peak resolution over the selected mobility range can potentially be achieved. We also note that this capability would have advantages in conjunction with techniques such as overtone mobility spectrometry [23, 41, 42], multipass separations [8], differential mobility, FAIMS [43, 44], mobility based filters or devices where mobility windows are selected or transmitted [45], and where compression fields would allow for compacting the chosen mobility windows and improved peak intensities.
CONCLUSIONS
In this work we have shown that ion peak compression can be used to overcome the limitations of diffusional broadening in IMS. When a decreasing electric field profile is applied to an ion packet, the ions downstream of the profile drift slowly; thus allowing the upstream ions to catch up. The concept for ion packet compression was evaluated for two peaks of close mobility (difference of 1%) moving simultaneously in the non-constant field, where we have theoretically and computationally demonstrated the ability to e.g., achieve greater peak intensities with the use of a modest increase in drift length to maintain the resolution. The implementation of peak compression concept effectively requires the prior selection of a separation region, making it a targeted approach. Such targeted mobility selection has recently been demonstrated in devices that allow flexible ion manipulation (such as using SLIM) [28, 30]. IMS peak compression can be used over any range of ion mobilities, and here we have focused on its application over a relatively narrow selected range, such as might be relevant to a smaller multi-pass cyclic IMS design. Periodic peak compression during multi-pass separations can potentially provide means for achieving practically unlimited separation power. This mobility based selection capability and multi-pass separations are facilitated using SLIM, and we anticipate that SLIM will also facilitate the development of practical IMS peak compression designs. Finally, peak compression has broader applications beyond IMS and utility in all cases where ion separations are of interest, and more intense spatially distinct ion populations in gases are advantageous.
ACKNOWLEDGEMENTS
Portions of this research were supported by the Department of Energy Office of Biological and Environmental Research Genome Sciences Program under the Pan-Omics Program, and by the National Institutes of Health (NIH) NIGMS grant P41 GM103493. Work was performed in the Environmental Molecular Sciences Laboratory (EMSL), a DOE national scientific user facility at the Pacific Northwest National Laboratory (PNNL) in Richland WA. PNNL is operated by Battelle for the DOE under Contract DE-AC05-76RL0 1830.
REFERENCES
- 1.Hoaglund CS, Valentine SJ, Sporleder CR, Reilly JP, Clemmer DE. Three-Dimensional Ion Mobility/TOFMS Analysis of Electrosprayed Biomolecules. Anal Chem. 1998;70:2236–2242. doi: 10.1021/ac980059c. [DOI] [PubMed] [Google Scholar]
- 2.Collins DC, Xiang Y, Lee ML. Comprehensive ultra-high pressure capillary liquid chromatography/ion mobility spectrometry. Chromatographia. 2002;55:123–128. [Google Scholar]
- 3.Eckers C, Laures AMF, Giles K, Major H, Pringle S. Evaluating the utility of ion mobility separation in combination with high-pressure liquid chromatography/mass spectrometry to facilitate detection of trace impurities in formulated drug products. Rapid Commun Mass Sp. 2007;21:1255–1263. doi: 10.1002/rcm.2938. [DOI] [PubMed] [Google Scholar]
- 4.Bronsema KJ, Bischoff R, van de Merbel NC. High-Sensitivity LC-MS/MS Quantification of Peptides and Proteins in Complex Biological Samples: The Impact of Enzymatic Digestion and Internal Standard Selection on Method Performance. Anal Chem. 2013;85:9528–9535. doi: 10.1021/ac4015116. [DOI] [PubMed] [Google Scholar]
- 5.Baker ES, Livesay EA, Orton DJ, Moore RJ, Danielson WF, 3rd, Prior DC, et al. An LC-IMS-MS platform providing increased dynamic range for high-throughput proteomic studies. J Proteome Res. 2010;9:997–1006. doi: 10.1021/pr900888b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bohrer BC, Mererbloom SI, Koeniger SL, Hilderbrand AE, Clemmer DE. Biomolecule Analysis by Ion Mobility Spectrometry. Annual Reviews, Palo Alto. 2008 doi: 10.1146/annurev.anchem.1.031207.113001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kemper PR, Dupuis NF, Bowers MT. A new, higher resolution, ion mobility mass spectrometer. Int J Mass Spectrom. 2009;287:46–57. [Google Scholar]
- 8.Merenbloom SI, Glaskin RS, Henson ZB, Clemmer DE. High-Resolution Ion Cyclotron Mobility Spectrometry. Anal Chem. 2009;81:1482–1487. doi: 10.1021/ac801880a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Baker ES, Clowers BH, Li FM, Tang K, Tolmachev AV, Prior DC, et al. Ion mobility spectrometry-mass spectrometry performance using electrodynamic ion funnels and elevated drift gas pressures. J Am Soc Mass Spectr. 2007;18:1176–1187. doi: 10.1016/j.jasms.2007.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Belov ME, Buschbach MA, Prior DC, Tang KQ, Smith RD. Multiplexed ion mobility spectrometry-orthogonal time-of-flight mass spectrometry. Anal Chem. 2007;79:2451–2462. doi: 10.1021/ac0617316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Davis EJ, Dwivedi P, Tam M, Siems WF, Hill HH. High-Pressure Ion Mobility Spectrometry. Anal Chem. 2009;81:3270–3275. doi: 10.1021/ac802431q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shvartsburg AA, Smith RD. Accelerated High-Resolution Differential Ion Mobility Separations Using Hydrogen. Anal Chem. 2011;83:9159–9166. doi: 10.1021/ac202386w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bhardwaj C, Hanley L. Ion sources for mass spectrometric identification and imaging of molecular species. Natural Product Reports. 2014;31:756–767. doi: 10.1039/c3np70094a. [DOI] [PubMed] [Google Scholar]
- 14.Covey TR, Thomson BA, Schneider BB. Atmospheric Pressure Ion Sources. Mass Spectrom Rev. 2009;28:870–897. doi: 10.1002/mas.20246. [DOI] [PubMed] [Google Scholar]
- 15.Du YZ, Wang WG, Li HY. Resolution Enhancement of Ion Mobility Spectrometry by Improving the Three-Zone Properties of the Bradbury-Nielsen Gate. Anal Chem. 2012;84:1725–1731. doi: 10.1021/ac203013u. [DOI] [PubMed] [Google Scholar]
- 16.Mason EA, E.W. M. Wiley-VCH Verlag; 1988. [Google Scholar]
- 17.Verbeck GF, Ruotolo BT, Gillig KJ, Russell DH. Resolution equations for high-field ion mobility. J Am Soc Mass Spectr. 2004;15:1320–1324. doi: 10.1016/j.jasms.2004.06.005. [DOI] [PubMed] [Google Scholar]
- 18.Shvartsburg AA, Smith RD. Protein Analyses Using Differential Ion Mobility Microchips with Mass Spectrometry. Anal Chem. 2012;84:7297–7300. doi: 10.1021/ac3018636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shvartsburg AA, Tang KQ, Smith RD. FAIMS operation for realistic gas flow profile and asymmetric waveforms including electronic noise and ripple. J Am Soc Mass Spectr. 2005;16:1447–1455. doi: 10.1016/j.jasms.2005.04.003. [DOI] [PubMed] [Google Scholar]
- 20.Scarff CA, Thalassinos K, Hilton GR, Scrivens JH. Travelling wave ion mobility mass spectrometry studies of protein structure: biological significance and comparison with X-ray crystallography and nuclear magnetic resonance spectroscopy measurements. Rapid Commun Mass Sp. 2008;22:3297–3304. doi: 10.1002/rcm.3737. [DOI] [PubMed] [Google Scholar]
- 21.Shvartsburg AA, Smith RD. Fundamentals of Traveling Wave Ion Mobility Spectrometry. Anal Chem. 2008;80:9689–9699. doi: 10.1021/ac8016295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Valentine SJ, Stokes ST, Kurulugama RT, Nachtigall FM, Clemmer DE. Overtone Mobility Spectrometry: Part 2. Theoretical Considerations of Resolving Power. J Am Soc Mass Spectr. 2009;20:738–750. doi: 10.1016/j.jasms.2009.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kurulugama RT, Nachtigall FM, Lee S, Valentine SJ, Clemmer DE. Overtone Mobility Spectrometry: Part 1. Experimental Observations. J Am Soc Mass Spectr. 2009;20:729–737. doi: 10.1016/j.jasms.2008.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Glaskin RS, Valentine SJ, Clemmer DE. A Scanning Frequency Mode for Ion Cyclotron Mobility Spectrometry. Anal Chem. 2010;82:8266–8271. doi: 10.1021/ac1017474. [DOI] [PubMed] [Google Scholar]
- 25.Glaskin RS, Ewing MA, Clemmer DE. Ion Trapping for Ion Mobility Spectrometry Measurements in a Cyclical Drift Tube. Anal Chem. 2013;85:7003–7008. doi: 10.1021/ac4015066. [DOI] [PubMed] [Google Scholar]
- 26.Moskovets EV. Line-Shape of Mass Peaks in a Reflectron with Plane Metal Grids. Appl Phys B-Photo. 1993;57:397–403. [Google Scholar]
- 27.Zhang XY, Garimella SVB, Prost SA, Webb IK, Chen TC, Tang KQ, et al. Ion Trapping, Storage, and Ejection in Structures for Lossless Ion Manipulations. Anal Chem. 2015;87:6010–6016. doi: 10.1021/acs.analchem.5b00214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Garimella SVB, Ibrahim YM, Webb IK, Ipsen AB, Chen TC, Tolmachev AV, et al. Ion manipulations in structures for lossless ion manipulations (SLIM): computational evaluation of a 90 degrees turn and a switch. Analyst. 2015;14:6845–6852. doi: 10.1039/c5an00844a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Webb IK, Garimella SVB, Tolmachev AV, Chen TC, Zhang XY, Norheim RV, et al. Experimental Evaluation and Optimization of Structures for Loss less Ion Manipulations for Ion Mobility Spectrometry with Time-of-Flight Mass Spectrometry. Anal Chem. 2014;86:9169–9176. doi: 10.1021/ac502055e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Webb IK, Garimella SVB, Tolmachev AV, Chen TC, Zhang XY, Cox JT, et al. Mobility-Resolved Ion Selection in Uniform Drift Field Ion Mobility Spectrometry/Mass Spectrometry: Dynamic Switching in Structures for Lossless Ion Manipulations. Anal Chem. 2014;86:9632–9637. doi: 10.1021/ac502139e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tolmachev AV, Webb IK, Ibrahim YM, Garimella SVB, Zhang XY, Anderson GA, et al. Characterization of Ion Dynamics in Structures for Lossless Ion Manipulations. Anal Chem. 2014;86:9162–9168. doi: 10.1021/ac502054p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Garimella SVB, Ibrahim YM, Webb IK, Tolmachev AV, Zhang XY, Prost SA, et al. Simulation of Electric Potentials and Ion Motion in Planar Electrode Structures for Lossless Ion Manipulations (SLIM) J Am Soc Mass Spectr. 2014;25:1890–1896. doi: 10.1007/s13361-014-0976-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hamid AM, Ibrahim YM, Garimella SVB, Webb IK, Deng L, Chen T-C, et al. Characterization of Traveling Wave Ion Mobility Separations in Structures for Lossless Ion Manipulations. Anal Chem. 2015;87:11301–11308. doi: 10.1021/acs.analchem.5b02481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Laiko VV. Orthogonal extraction ion mobility spectrometry. J Am Soc Mass Spectr. 2006;17:500–507. doi: 10.1016/j.jasms.2005.12.009. [DOI] [PubMed] [Google Scholar]
- 35.Garimella S, Xu W, Huang GM, Harper JD, Cooks RG, Ouyang Z. Gas-flow assisted ion transfer for mass spectrometry. J Mass Spectrom. 2012;47:201–207. doi: 10.1002/jms.2955. [DOI] [PubMed] [Google Scholar]
- 36.Tannehill JC, Anderson DA, Pletcher RH. Taylor and Francis; Philadelphia,PA: 1997. [Google Scholar]
- 37.Ibrahim Y, Tang K, Tolmachev AV, Shvartsburg AA, Smith RD. Improving mass spectrometer sensitivity using a high-pressure electrodynamic ion funnel interface. J Am Soc Mass Spectrom. 2006;17:1299–1305. doi: 10.1016/j.jasms.2006.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ibrahim Y, Belov ME, Tolmachev AV, Prior DC, Smith RD. Ion funnel trap interface for orthogonal time-of-flight mass spectrometry. Anal Chem. 2007;79:7845–7852. doi: 10.1021/ac071091m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ibrahim YM, Prior DC, Baker ES, Smith RD, Belov ME. Characterization of an Ion Mobility-Multiplexed Collision Induced Dissociation-Tandem Time-of-Flight Mass Spectrometry Approach. Int J Mass Spectrom. 2010;293:34–44. doi: 10.1016/j.ijms.2010.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ibrahim YM, Shvartsburg AA, Smith RD, Belov ME. Ultrasensitive identification of localization variants of modified peptides using ion mobility spectrometry. Anal Chem. 2011;83:5617–5623. doi: 10.1021/ac200719n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ewing MA, Zucker SM, Valentine SJ, Clemmer DE. Overtone Mobility Spectrometry: Part 5. Simulations and Analytical Expressions Describing Overtone Limits. J Am Soc Mass Spectr. 2013;24:615–621. doi: 10.1007/s13361-012-0559-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ewing MA, Conant CRP, Zucker SM, Griffith KJ, Clemmer DE. Selected Overtone Mobility Spectrometry. Anal Chem. 2015;87:5132–5138. doi: 10.1021/ac504555u. [DOI] [PubMed] [Google Scholar]
- 43.Prasad S, Tang K, Manura D, Papanastasiou D, Smith RD. Simulation of Ion Motion in FAIMS through Combined Use of SIMION and Modified SDS. Anal Chem. 2009;81:8749–8757. doi: 10.1021/ac900880v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shvartsburg AA, Smith RD. Optimum waveforms for differential ion mobility spectrometry (FAIMS) J Am Soc Mass Spectr. 2008;19:1286–1295. doi: 10.1016/j.jasms.2008.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.May JC, McLean JA. Ion Mobility-Mass Spectrometry: Time-Dispersive Instrumentation. Anal Chem. 2015;87:1422–1436. doi: 10.1021/ac504720m. [DOI] [PMC free article] [PubMed] [Google Scholar]