National Institute of Standards and Technology measurement service of the optical properties of biomedical phantoms: Current status

Abstract

The National Institute of Standards and Technology (NIST) has maintained scales for reflectance and transmittance over several decades. The scales are primarily intended for regular transmittance, mirrors, and solid surface scattering diffusers. The rapidly growing area of optical medical imaging needs a scale for volume scattering of diffuse materials that are used to mimic the optical properties of tissue. Such materials are used as phantoms to evaluate and validate instruments under development intended for clinical use. To address this need, a double-integrating sphere based instrument has been installed to measure the optical properties of tissue-mimicking phantoms. The basic system and methods have been described in previous papers. An important attribute in establishing a viable calibration service is the estimation of measurement uncertainties. The use of custom models and comparisons with other established scales enabled uncertainty measurements. Here, we describe the continuation of those efforts to advance the understanding of the uncertainties through two independent measurements: the bidirectional reflectance distribution function and the bidirectional transmittance distribution function of a commercially available solid biomedical phantom. A Monte Carlo-based model is used and the resulting optical properties are compared to the values provided by the phantom manufacturer.

1. INTRODUCTION

The National Institute of Standards and Technology (NIST) is currently developing a service for the measurement of the optical properties of biomedical phantoms. Such artifacts are used to simulate the optical properties of tissues for the purpose of calibration and validation of biomedical instruments. The validation of measurement accuracy of these optical properties can be tested by comparing measurements using different techniques. In previous work, we presented the measurements of the optical properties of solid biomedical phantoms manufactured by the Institut National d'Optique (Biomimic, INO Inc., Quebec, Canada) (1) using the NIST double-integrating sphere instrument and a modified inversion routine of the adding-doubling algorithm (2-4) for measuring the optical properties of biomedical phantoms. The values were compared to the measurement obtained by INO using a time-domain instrument. As a further step toward developing inter-comparison studies inside and outside of NIST, we present in this study the measurements of the bidirectional reflectance distribution function (BRDF) and the bidirectional transmittance distribution function (BTDF) of a similar INO phantom using a goniometric reflectometer, and we compare the absorption coefficient, μ_a, and the reduced scattering coefficient, μ′_s, measured by INO at λ = 805 nm to the results obtained from an inversion procedure based on the Monte Carlo in Multi-Layered tissue (MCML) algorithm (5).

2. MATERIALS AND METHODS

2.1 Experimental setup

Measurements of the BRDF and BTDF were performed using the NIST spectral tri-function automated reflectometer (STARR), which serves as the standard reference instrument for spectral reflectance measurements. The design of the instrument also enables the measurement of spectral BTDF measurements. The STARR is described extensively in Ref. (6). A schematic of the instrument and its major components are depicted in Figure 1.

Figure 1.

Top-down schematic view of STARR's bidirectional measurement system with major components labeled.

The radiant flux from the source (quartz-tungsten-halogen lamp) is focused through an order-sorting filter and a shutter onto the entrance slit of a single-grating monochromator. The beam exits the monochromator, passes through an iris to provide a circular incident beam, and is collimated by an off-axis paraboloid mirror. It then passes through a Glan-Taylor polarizer before passing through the sample goniometer. The beam is collected by the detector aperture, and is focused by a lens onto the detector (ultraviolet-enhanced silicon photodiode), which produces a signal proportional to the radiant flux.

The translation and rotation stages of the goniometer enable the acquisition of both reflected or transmitted and incident signals. The sample is positioned in the holder so that it is normal to the incident beam. The detector rotates around the sample to collect the reflected or transmitted signals at various viewing angles, which are in the same plane as the sample normal and the incident beam. The incident radiant flux is measured by positioning the detector in the beam path of the incident light with the sample translated out of the beam path.

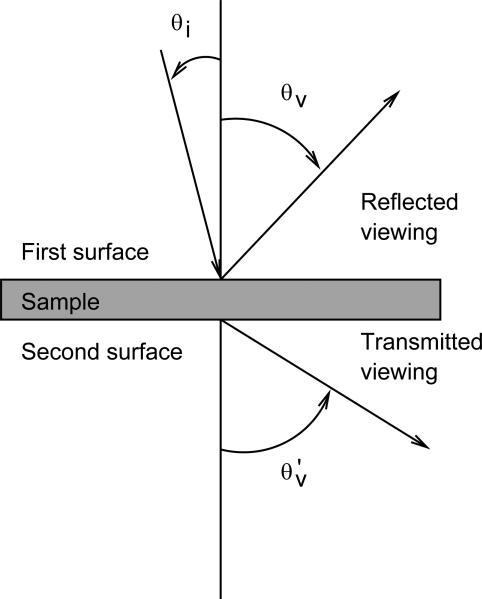
Figure 2 describes the geometry of the BRDF and BTDF measurements. The incident and viewing angles, θ_i and θ_v, respectively, are defined with respect to the normal of the sample.

Figure 2.

Top-down view of the incident and viewing angles, θ_i and θ_v, respectively. Viewing angles for BRDF measurements are 0° ≤ θ_v ≤ +90° defined with respect to the normal of the first surface of the sample, while viewing angles for BTDF are defined 0° ≤ θ′_v ≤ +90° defined with respect to the normal of the second surface of the sample.

2.2 Sample

The solid phantoms are manufactured by INO and are made of a polyurethane-based material mixed with titanium dioxide and carbon black to adjust the scattering and absorption properties, respectively. The nominal values of these properties as determined by INO are μ_a = 0.01 mm^–1 and μ′_s = 1 mm^–1 at λ = 805 nm, where λ is the wavelength of the light. The sample has a nominal thickness of d = 5 mm and lateral dimensions of about 100 mm each.

2.3 Measurements

The BRDF at each wavelength, polarization, and viewing angle is calculated using

$$BRDF=\frac{D^2}{A\cos {\theta }_v}\frac{S_v}{S_i}\eta ,$$ (1)

where D (669.8 mm) is the distance between the first surface of the sample and the aperture of the detector, A (796.7 mm²), θ_v is the viewing angle of the reflected radiant flux, S_v is the net signal at the viewing angle due to the reflected radiant flux, and S_i is the net signal at the incident angle due to the incident radiant flux, such that both signals are corrected for the dark current. η is the gain factor correction between the two signals. Similarly, the BTDF is expressed as

$$BTDF=\frac{D^{\prime 2}}{A\cos {{\theta }_v}^{\prime }}\frac{S_v}{S_i}\eta ,$$ (2)

where D′ is the distance from the second surface of the sample to the aperture of the detector and θ_v′ is the viewing angle of the transmitted radiant flux, which is dependent on D, θ_v and the thickness of the sample.

For the BRDF measurements as a function of wavelength, the geometry of measurement was set with an incident angle of 0° and discrete viewing angles, increasing from 5° to 85° at 5° steps. For the BTDF measurements as a function of wavelength, the geometry of measurement was set likewise. The sample was measured at a wavelength λ = 805 nm at a polarization state either parallel (p polarization) or perpendicular (s polarization) to the plane of incidence. The average polarization refers to an unpolarized measurement.

For each wavelength and polarization, the following signals were collected: incident signal, dark signal in the incident position, reflected or transmitted signal, dark signal in the sample position, incident signal, and dark signal in the incident position. The dark signals were obtained by closing the shutter on the monochromator and were used to correct the background signal attributed to the dark current of the detector. The average net signal due to the incident radiant flux, acquired before and after each measurement of the reflected or transmitted signal, was used to minimize the effects of source drift and fluctuations on the time scale of a single BRDF or BTDF measurement.

2.4 Data analysis

The MCML program (5) calculates, through Monte Carlo simulation, the proportion of incoherent scattered light leaving a sample at given angles before and after the sample. The principal physical inputs are μ_a, μ_s, and g, as well as the refractive indices of a number of layers. Here, we have a single layer with a known index of refraction, n. In practice, the result depends almost entirely on the reduced scattering coefficient, μ′_s = μ_s(1 – g). We treat the scattering anisotropy, g, as a known constant since variation in g by 20 %, several times its uncertainty, has negligible effect on μ′_s.

Estimation of (μ_a, μ′_s) proceeds by maximum likelihood. Likely values of (μ_a, μ′_s) are those for which the predictions from MCML provide a good match to the measurements. The degree to which the measurements match the predictions is assessed by assuming the measurements to be independent Gaussian deviates with a mean equal to the prediction from MCML. The likelihood is thus the product of Gaussian distributions, and the (μ_a, μ′_s) that maximizes the product is the estimate. Most of the computation time is occupied by the MCML runs for various sets of (μ_a, μ′_s). To choose a computationally economical parameter space of (μ_a, μ′_s), our algorithm proceeds as follows: because the results depend more strongly on μ′_s than on μ_a, we pick a preliminary value for μ_a, and vary μ′_s over the full allowed range specified by the user. We find that the integrated BRDF is a monotonic function of (μ′_s), so we make a preliminary estimate of μ′_s, which best simulates the experimental angle-integrated BRDF. Given this value, we search a region that includes the full range of μ_a and is a factor of 2 smaller in the range of μ′_s. We then estimate the likelihood using 25,000 Monte Carlo samples per point on a 4×4 grid. A most likely coordinate in (μ_a, μ′_s) is found from a quadratic fit to the logarithm of the likelihood. The search range is recentered about this coordinate and the range is reduced by half in both μ_a and μ′_s, and the likelihood is found again on a new 4×4 grid using 100,000 Monte Carlo samples. The uncertainty of the location is determined by an F statistic (7). (For readers unfamiliar with the F statistic, we consider the case of finding the location of the minimum of a 1D quadratic function ax² + bx + c =0 which occurs at x₀=–b/(2a). If b and a are both given by Gaussian distributions, then x₀ follows the F distribution). The reason the initial fit is to a different function, namely the integrated BRDF, is that the quadratic surface is not a sufficiently good approximation over the full range.

Looking forward, we must consider more sources of uncertainty, including g, n, the observational geometry, departures of the sample and measurement geometries from their ideal values, sample inhomogeneities, and uncertainties in the measurements. The confidence regions below are for the stationary point of the final fitted quadratic surface (7), and may undersestimate a more refined region that carefully includes the aforementioned components.

3. RESULTS

The phantoms are cut from a block of material to provide both the 2 cm-thick sample needed for characterization by INO using a time domain instrument and the sample at the required thickness and lateral dimensions. Hence, typical phantoms are machined, and both faces of the sample are non-specular. The BRDF measurement of the sample (INO batch B0430; thickness d = 5.15 mm) resulted in a polarization dependent signature at detection angles greater than 30°. This polarization dependence is attributed to the surface scattering effect that is incompatible with the MCML model to be used for analyzing the data (Figure 3-a, 0°-incident angle). In transmittance measurements, the light was completely depolarized due to multiple-scattering events as expected. For the purpose of the experiment, a sample with both faces specular would have been ideal but this was not available from INO. However, INO was able to produce a sample with similar optical properties cut to the required thickness with one face specular and the other non-specular (INO batch B0436; μ_a = 0.0109 mm^–1, μ′_s = 1.03mm^–1 at λ = 805 nm; thickness d = 4.81 mm). Figure 3-b shows the BRDF and BTDF results for a 0°-incident angle with the beam incident on either the specular or the non-specular face of the sample. While the polarization dependency of the BDRF signal is preserved when the beam is incident on the non-specular face, flipping the sample to have the beam incident on the specular face results in a BRDF signal with no polarization dependence. In this case, the detected photons are subjected to multiple-scattering events in the volume of the material, which conforms to the MCML model. The BTDF measurements are comparable with the beam incident on either the specular or the non-specular face.

Figure 3.

BRDF and BTDF at λ=805 nm of: (a) INO sample batch B0430 with both faces non-specular and (b) INO sample batch B0436 with one face specular and the other non-specular. When the beam is incident on the non-specular face the polarization signature of the BDRF is preserved at high detection angles whereas when the beam is incident on the specular face there is no polarization dependence. From (b) the BTDF measurements are comparable in both cases.

Figure 4-a presents the unpolarized BRDF and BTDF measurements at λ=805 nm with the beam incident on the specular face along with the best fit from the MCML simulations. The corresponding values, μ_a = 0.00638 mm^–1 and μ′_s = 1.024 mm^–1 are presented in Figure 4-b along with confidence regions for the stationary point of a fitted quadratic surface (7). Monte Carlo counting statistics are the major source of uncertainty accounted for by these regions. Our estimate of μ_s′ is consistent with the one from INO (μ′_s = 1.03 mm^–1), but there is a discrepancy on the μ_a value (μ_a = 0.0109 mm^–1 for INO).

Figure 4.

Results at λ=805 nm of: (a) the measured BRDF and BTDF (*) with the beam incident on the specular face along with the fitted MCML simulation (red line) and (b), the corresponding μ_a and μ_s′ values (+) with the confidence region for the location of a stationary point based on an F statistic (7).

CONCLUSION

In this paper, we presented measurements of the optical properties of solid biomedical phantoms at λ = 805 nm using BRDF and BTDF measurements fitted with an inversion routine based on the MCML model. Phantom material from INO was cut to the desired dimensions and the faces were made non-specular in the process. Preliminary BRDF measurements showed that the surface roughness significantly affects the signal, but this is not taken into account in the MCML model. However, samples with one specular face and one non-specular were available. Such a sample was measured with the beam incident to the specular face to allow only for the detection of the volume scattering component of the BRDF compatible with the model. The BTDF was only sensitive to the surface roughness of the non-specular face of the sample at high detection angles. There is an agreement between the value of μ′_s obtained with our experiment and the one provided by INO at the same wavelength λ = 805 nm. However, our value of μ_a is significantly lower than the one from INO. Future work will include the computation of an uncertainty budget for our experiment and the measurements of the phantom presented in this paper of at λ=543.5 nm and λ=632.8 nm in order compare the results from the BRDF and BTDF measurements to the results obtained by the NIST instrument for the measurement of optical properties of biomedical phantoms.