Abstract
This paper describes a phase-resolved ferromagnetic resonance (FMR) measurement using a heterodyne method. Spin precession is driven by microwave fields and detected by 1550 nm laser light that is modulated at a frequency slightly shifted with respected to the FMR driving frequency. The evolving phase difference between the spin precession and the modulated light produces a slowly oscillating Kerr rotation signal with a phase equal to the precession phase plus a phase due to the path length difference between the excitation microwave signal and the optical signal. We estimate the accuracy of the precession phase measurement to be 0.1 rad. This heterodyne FMR detection method eliminates the need for field modulation and allows a stronger detection signal at higher intermediate frequency where the 1/f noise floor is reduced.
I. Introduction
In recent years, demands for increased speed and capacity of information storage have directed a large amount of attention to the use of spin torques to control magnetization [1–4]. A wide variety of spin torque effects and mechanisms have been investigated and observed. For instance, spin currents are carried parallel to charge currents in ferromagnetic materials, and spin currents can also be generated perpendicular to charge currents via the spin Hall effect in heavy metals [5–10]. Additionally, interfacial mechanisms giving rise to Rashba-like effects also contribute to spin currents and spin torques [11,12]. In addition to these novel effects, classical magnetic fields from charge currents also exert torques on the magnetization, and these torques can be difficult to separate from the spin-transfer torques. This rich phenomenology of torques presents a challenge to the experimenter not only to measure the torques but also to interpret them in terms of different mechanisms.
Phase-resolved ferromagnetic resonance (FMR) measurements are attractive for characterization of current driven torques including spin-transfer torques for high-speed applications. Conceptually, by resolving the phase of FMR, one can deduce the direction of the torques [13,14]. A simple phase-sensitive method involves mixing AC current with magnetoresistance oscillations to generate a DC signal, and this self-rectification scheme has been used in a number of significant papers [5,8,13–17]. A review article [18] covers much of the literature. In these self-rectification measurements, the detected voltage is sensitive to the phase of the magnetization with respect to the phase of the current. In addition to spin-transfer torques, the magnetic field due to the microwave current, i.e., the Oersted field, also exerts torque on the magnetization. Often the Oersted fields are estimated by straightforward application of Ampere’s Law. However the field torque phase can differ significantly from the phase of the nearby driving current due to propagation delays in the metal layers [19–21] and eddy currents in substrates [21]. These phase effects can be significant despite the fact that the layers are much thinner than the skin depth.
Stroboscopic methods have been used frequently to make phase-resolved FMR measurements. A microwave source is synchronized with a fast-pulsed light source, and the light measures or images the magnetization via a magneto-optical effect such as Kerr rotation or x-ray magnetic circular dichroism [22–32]. An interesting variation on the stroboscopic method is an electrical measurement of the Nernst voltage under microwave excitation and pulsed laser heating [33–35]. Previously, we reported a phase-sensitive, magneto-optical FMR detection method using a stroboscopic method with light modulated at the resonance frequency [36].
In this paper, we focus on phase-resolved detection of FMR by magneto-optical Kerr effect using a heterodyne technique. Recently, an optical heterodyne method for FMR detection was developed to increase the signal-to-noise ratio of the dynamic magneto-optical Kerr signal [37]. In that paper, the heterodyne effect was created from two stable lasers with optical frequencies offset by a microwave frequency. In the present paper, the heterodyne effect is created from frequency-offset microwave signals, one driving magnetization dynamics and the other modulating the light used for detecting the dynamics. The benefits of this method include strong signals and high measurement frequencies to avoid 1/f noise without field modulation. In Sec. II, we describe the experimental setup, and in Sec. III we describe calibration methods, testing the determination of phase from FMR line shape and accounting for instrumental phase offsets. Finally, in Sec. IV, we demonstrate imaging of FMR using precession phase contrast.
II. Experimental
The principle of the measurement hinges on the use of amplitude-modulated light to measure the magnetization precession. For simplicity, first consider the case where the light modulation frequency and the precession frequency are identical, and the light arrives in short pulses. In this case the sample will be illuminated (and measured) repeatedly at a particular point in the precession cycle. That point can be selected by changing the phase of the arriving light pulses relative to the excitation microwaves. This situation describes homodyne detection. For heterodyne detection, we arrange for the light pulses to arrive at a slightly lower frequency than the excitation. In this case, each light pulse arrives slightly later in the precession cycle, so that over time, the Kerr response traces out complete precession cycles. A final detail is that the light pulses may be replaced by a sinusoidal power modulation since the higher harmonics will not produce slowly varying signals.
The experimental setup illustrated in Fig. 1 contains two main signal paths, a microwave excitation path and an optical detection path. Signals on these paths are derived from the split output of a single microwave signal generator (SG: Fig. 1) that operates at a frequency, fRF = ωRF/2π. The microwave signal is divided with part driving spin dynamics in a microwave branch and part driving light modulation in an optical branch for detection of the magnetization dynamics. In the microwave branch, spin precession is driven by frequency-shifted microwaves. To shift the frequency, an arbitrary waveform generator (AWG: Fig. 1) provides two sinusoidal signals at an intermediate frequency (IF), fIF = ωIF/2π = 100 kHz, with a constant phase difference of 90°. These in-phase and quadrature signals drive the I and Q inputs of an IQ mixer to generate a single sideband signal at the sum frequency, fRF + fIF = fPump. The mixer also produces output in other sidebands surrounding the microwave carrier frequency, including the image side band at fRF − fIF. Though tuning of the relative I and Q signal amplitudes, DC offsets and a 90° phase difference, the sum frequency is made dominant, and all other frequency components are suppressed by more than ≈20 dB. This single sideband signal is then launched into a coplanar waveguide (CPW) where magnetic samples may be excited electrically and/or inductively, depending on the sample design.
FIG 1.
(a) Schematic of the heterodyne ferromagnetic resonance detection method. The SG feeds RF current to the IQ mixer and the EOM. The AWG provides 100 kHz in-phase and quadrature signals to the I and Q inputs of the IQ mixer to produce a frequency-shifted excitation microwave to the CPW. In the reflected light, the spin precession and the linearly polarized and modulated light produce a slowly oscillating Kerr rotation signal component with a phase conveniently equal to the spin precession plus a phase caused by the path length difference between the microwave and the optical signal. This signal is then demodulated by the lock-in amplifier for analysis. (b) Illustration of field-modulation and heterodyne methods showing the advantage in signal strength afforded by the heterodyne method.
The optical path of the setup performs phase-sensitive detection of magnetization dynamics. The output of a telecommunications fiber laser at 1550 nm wavelength is fully modulated by controlling the microwave amplitude and the DC offset in the electro-optical intensity modulator (EOM) driver. Following the modulation, the pulsed laser is launched into free space, linearly polarized and focused onto the sample with an objective lens. The spot size is 15 µm. Upon reflection from the sample surface, the magneto-optical polar Kerr effect [38] rotates the polarization by an angle proportional to the surface-normal component of the magnetization, and reflected light is collected through the objective lens for polarization analysis and for reflectivity monitoring. With the sample mounted on an x-y stage, the reflectivity allows imaging of the different sample structures to be positioned in the focus of the objective lens.
To describe the heterodyne detection of the dynamics, we begin by considering a film-normal component of the magnetization (m0) that oscillates as a result of pumping at angular frequency ωRF + ωIF and also oscillates with smaller relative amplitude a at the image sideband frequency ωRF and ωRF−ωIF from the IQ mixer,
| (1) |
The phase of the precession (ϕm) and the arbitrary phase of the image sideband (ψ) are given relative to the phase at the microwave splitter where the two branches of the setup have a common phase.
The magnetization is measured through the Kerr-effect polarization rotation of reflected light, and the instantaneous Kerr angle is directly proportional to mz(t). However, the measured Kerr rotation comes from time-averaged light intensity where the averaging is slow compared to radio frequencies (RFs), but fast compared to the IF. The measured Kerr rotation is therefore given by the time-averaged product of the Kerr angle, which is proportional to mz(t) and the light intensity. We model the light intensity incident on the sample as
| (2) |
where ϕL describes the accumulated phase for the signal propagation from the splitter to the sample. The detector output voltage is then proportional to the measured Kerr rotation, which oscillates at frequency ωIF,
| (3) |
Finally, the detector voltage is demodulated by the lock-in amplifier using an IF reference signal from the AWG, yielding in-phase (X) and quadrature signals (Y),
| (4) |
We develop a model for the magnetization phase (ϕm), which includes the components due to propagation of the microwaves from the splitter to the waveguide current (ϕMW), a possible phase delay (ϕh) between waveguide current and effective driving field (h0) and the phase of the magnetic response to the field (ϕχ),
| (5) |
Note that the phase difference ϕL − ϕm appearing in the lock-in output includes the difference ϕL − ϕMW ≡ ϕPL, which describes only path length effects.
With these definitions, Eq. (4) can be rewritten as
| (6) |
Here we have made substitutions m0 cos(ϕχ) = h0χ′ and m0 sin(ϕχ) = h0χ″, where the off-diagonal component of the magnetic susceptibility χzy has real () and imaginary () parts. In the derivation of (6) we have used only the off-diagonal component of the susceptibility. Omission of the diagonal component χzz apparently neglects the response to out-of-plane effective fields, but there is little loss of generality. At least near resonance, the effects of an out-of-plane field can be recast as a phase-advanced in-plane field.
Typical spectra are shown in Fig. 2, where output of the heterodyne setup is compared with the output from a homodyne, stroboscopic method described in Ref. [39]. The sample is a Ta (3 nm)/Ni80Fe20 (10 nm)/Ta (3 nm) thin film, deposited on a thin glass cover slip (150 µm thick), placed face-up on the CPW for easy optical access and for electrical isolation from the waveguide. In the strobed (homodyne) measurement, the light modulation and magnetization driving frequencies are identical, so the detected phase remains constant for constant frequency and field. To distinguish the magnetic resonance signal from DC offsets, the applied field was modulated at 12.6 kHz with an amplitude of 0.9 mT and the Kerr signal was then demodulated by the lock-in amplifier. Comparison of the heterodyne spectra in Fig. 2(a) and the strobed (homodyne) spectra in Fig. 2(b) shows similar noise levels but larger signals for the heterodyne method. The spectral density of the noise in our setup is approximately flat above 5 kHz, so similar noise levels at 12.6 kHz (homodyne, field modulation frequency) and 100 kHz (heterodyne, IF frequency) are expected. With similar noise levels, larger FMR signals were obtained using the heterodyne method [see Fig. 1(b)]. The heterodyne signal fully oscillates between positive and negative values, +|θK| and −|θK|, while the field modulation only allows relatively small Kerr signal oscillations.
FIG 2.
The FMR spectra of (a) heterodyne and (b) homodyne FMR detection method (dots). The lines in the figures are the fits for the ferromagnetic resonance line shapes. Microwave power and optical power are the same for both sets. The signals are plotted on the same scale for comparison. The heterodyne detection method produces a stronger signal even at higher frequencies. The spectra are 20 µV offset vertically for clarity.
Figure 3 plots the resonance field and the half-line width values measured for of heterodyne, strobed (homodyne), and field-modulated microwave transmission methods as a function of frequency. For the heterodyne method, the spectra were fit to symmetric and antisymmetric Lorentzian line shapes, as described in more detail below, yielding values of the resonance field, HRes and the half-linewidth, δH. For the homodyne and transmission spectra, similar fits were made to the field-derivative line shapes appropriate for field-modulated spectra. Error bars and uncertainty values in this paper indicate one standard deviation of fit parameters. Comparing the results, the resonance field values are in reasonable agreement between the three methods, but there are significant differences between the linewidth values. The two methods using field modulation (strobed and waveguide transmission) yield line widths that are larger than the values from the heterodyne method. We speculate that the larger line width values may have been artificially broadened by excessive modulation field. We fit the resonance field data to the Kittel equation,
| (7) |
to obtain µ0Ms (γ and Hp held fixed) and we fit the half-width data to
| (8) |
yielding the damping constant α and the inhomogeneous broadening δH0. Best fit values and their uncertainties are presented in Fig. 3. The Ms and α values are in reasonable agreement with permalloy properties from other studies.
FIG 3.
(a) The resonance field and the half-line width (inset) variation of heterodyne, homodyne, and microwave transmission FMR detection method as a function of the resonance frequency The dashed lines represent the fits for the saturation magnetization and damping constant of the heterodyne detection data. The fitting results of saturation magnetization (Ms) damping constant (α), and half-width (δH0) are shown in Figs. 3(b), 3(c), and 3(d), respectively. Error bars are one-sigma uncertainties of the fit values.
III. Calibration
Having demonstrated the general measurement scheme, we now turn to calibration of the phase measurement. Instrumental artifacts appearing in (6) include the path length phase and the amplitude and phase (a and ψ, respectively) of the image sideband. We address these artifacts in this section beginning with a test our phase measurements using known phase changes followed by calibration of ϕPL. We will assume that the magnetization dynamics in this film are well described by the Landau-Lifshitz-Gilbert equations of motion for a macrospin [40], which yields the following expressions for the susceptibility [39]:
| (9a) |
| (9b) |
Here HRes is the resonance field for excitation at angular frequency ωPump, and δH is the half-width of the resonance curve. Note that is symmetric about H = HRes, and is antisymmetric. We therefore define symmetric and antisymmetric Lorentzian functions
| (10a) |
| (10b) |
With the definitions given in (7) and (8), the lock-in outputs given by (6) become
| (11a) |
| (11b) |
Fitting involves four fitting parameters for each peak, the resonance field (HRes), the half-linewidth (δH), and the amplitude coefficients of S(H) and A(H). The amplitude coefficients, which correspond to the terms in square brackets in Eq. (11), are complicated by the amplitude a and phase ψ of the image sideband. If we can neglect the image sideband effects, the phase can be obtained straightforwardly from the amplitude coefficients. In the following subsection, we test whether the image sideband can be neglected.
A. Phase measurement
To test the procedure of determining phase by fitting line shapes, we use an optical delay to vary ϕPL by known amounts. The in-phase FMR spectra [VX(H), black dots] with symmetric and antisymmetric fitting results (green lines) are shown in Fig. 4(a), for optical path length changes ranging from 0 mm to 80 mm which produce precise shifts in ϕPL at 4.5 GHz. The phases, obtained by fitting the line shapes, are plotted in Fig. 4(b) and change linearly with increasing optical delay. The estimated slope from the fitting, (−0.094 ±0.003) rad/mm, corresponds well to the expected value of 0.0943 rad/mm using the optical wavelength of 66.622 mm at 4.500 GHz. The residuals from the curve fitting are also shown in Fig. 4(c), where the standard deviations determined from the line shape fits are shown by small error bars. These error bars are clearly smaller than the root-mean-square of the residuals, 0.08 rad, suggesting that our phase uncertainty will be limited by systematic effects rather than by measurement noise.
FIG 4.
The phase ϕPL is evaluated by introducing an optical delay. (a) The FMR spectra [lock-in output X(H), black dots] with fits (green line), as the optical delay is changed from 0 mm to 80 mm. (b) The estimated ϕPL varies linearly with increasing optical delay. The linear fit shows a slope of (−0.094 ± 0.003) rad/mm, corresponding to the optical wave length at the driving frequency, 4.5 GHz. The small error bars represent the standard deviation from the line shape fits. (c) The residuals of the fits.
B. Path length phase
In this section, we address an instrumental phase that stems from differences in the effective path lengths of the optical and microwave branches of the measurement setup. The effective measured phase is ϕeff = ϕPL + ϕh, where ϕPL is an experimental artifact due to different path lengths of the microwave and optical branches. We concentrate on ϕPL in order to either account for it or eliminate it, keeping in mind that ϕh can be very important for studies of spin-transfer torques and spin orbit torques because it encodes the direction of the effective field. With propagation delays τL and τMW in the optical and microwave branches, respectively, the net path length phase is
| (12) |
The ωIFτMW term here is small, constant and negligible, (of order 0.001 rad in our setup), but the leading term is proportional to frequency; we use this frequency dependence to calibrate ϕPL. We also cast the path length phase in the form ϕPL = (2πf/c)ΔLeff, where c is the speed of light and ΔLeff is an effective path length difference that incorporates physical path length differences as well as propagation speeds through optical fibers and microwave cables. To evaluate the path length phase ϕPL, we need a known sample where the effective phase ϕh between the CPW current and the effective field can be neglected.
For the sample described above, the 10 nm thick permalloy film is separated from the CPW by a 150 µm glass cover slip, so spin torque effects are not expected. In using this sample as a phase reference, we are also assuming that the phase delay ϕh between the current and the field is negligible, i.e. that there is no propagation delay between the current in the waveguide and the torque exerted on the magnetization and that the effects of eddy currents are negligible. Using the material parameters from the Kittel and linewidth fits, we estimate a maximum relative permeability of approximately 1000 at 3 GHz. With resistivity of 20 µΩ cm, the estimated skin depth is 130 nm, which is much greater than the 10 nm film thickness.
FMR spectra are shown in Fig. 5(a) for a set of frequencies varying from 4.001 GHz to 4.030 GHz. Each ϕPL is estimated from the symmetric-antisymmetric Lorentzian fitting described above. Further phase values are measured over the range from 3.001 GHz to 6.085 GHz. The details of the ϕPL variation are shown in Fig. 5(b), where the frequency increased from 4.981 GHz to 5.199 GHz in increments of 2 MHz. Due to a large variation of the phase depending on the frequency, we expand the phase shift by ±2πn at the periodicity; gaps in the data reflect a compromise between a desire to cover a broad frequency range and the need to ensure that the phase expansion is consistent over the data set. The linear behavior of ϕPL as a function of the resonance frequency are shown in Fig. 5(c). The effective path length difference of 8.485 m ± 0.006 m is determined by the fit slope of (177.828 ± 0.013) rad/GHz from the linear fit.
FIG 5.
(a) The FMR spectra [lock-in X(H), black dots], as the resonance frequency changes from 4.001 GHz to 4.030 GHz. The symmetric and antisymmetric Lorentzian fits (red lines) provides the ϕPL variation as a function of the resonance frequency. (b) The details of linear ϕPL variation over the frequency range from 4.981 GHz to 5.199 GHz. (c) The periodic phase modification produces a linear fit, corresponding to an effective path length difference of 8.485 m ± 0.006 m. The residuals of the fit indicate systematic errors.
While the linear frequency dependence of the phase can be determined with precision, our knowledge of the path length phase is limited by systematic error revealed in the residual plot. The root-mean-square residual value of 0.1153 rad represents an angle uncertainty due to systematic effects that are especially apparent in the fit residual near 5.0 GHz.
IV. Spatial Imaging
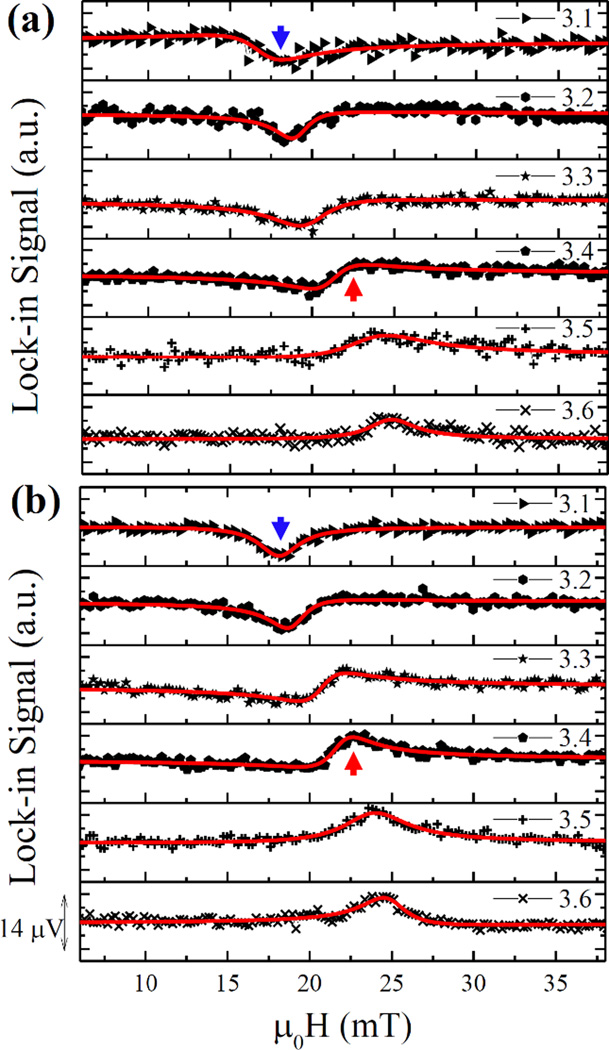
Finally, we demonstrate spatial FMR imaging in patterned samples. Two permalloy samples (700 µm × 600 µm) are fabricated on the CPW chip, and the sample is imaged by scanning the sample position under the focal spot of the objective lens. See Fig. 6. By selecting the applied field, frequency and detection phase, the images can be made sensitive to precession amplitude [Fig. 6(b)] or to precession phase [Fig. 6(c)]. We also recorded FMR spectra at the center of the left (L) and right (R) samples as a function of frequency. The in-phase [VX(H)] FMR spectra of L and R samples are shown in Fig. 7, when the frequency changes from 3.1 GHz to 3.6 GHz. A difference in phase between the spectra can be seen, for example, L and R samples show similar negative peaks relative to the background offset with the magnetic field 18 mT at 3.1 GHz. On the other hand, the R sample shows a larger lock-in signal than the L sample, when the magnetic field is 23 mT with 3.4 GHz. The phase difference between the two samples is consistent with an estimated propagation phase delay of 0.17 rad based on the calculated propagation velocity in our CPW structure and the 2.3 mm separation between the sample centers. These results suggest that this spatial phase-sensitive FMR imaging provides a method of tracking propagation phase in magnetoelectronic circuits.
FIG 6.
(a) Reflection image for the left (L) and right (R) samples on the CPW chip. (b), (c) The FMR intensity images taken under constant resonance frequency and magnetic field. (b) Similar lock-in intensities for L and R samples are observed at 3.1 GHz with 18 mT applied field. (c) On the other hand, L and R samples show different FMR intensity at 3.4 GHz with 23 mT applied.
FIG 7.
The FMR spectra of left (L) and right (R) samples as a function of the magnetic field, when the resonance frequency changed from 3.1 GHz to 3.6 GHz. The FMR spectra of the left and right samples show different phase due to the microwave propagation along the coplanar waveguide. The blue and red arrows indicate the magnetic field for the FMR images shown in Figs. 6(b) and 6(c), respectively.
V. Discussion
The magneto-optical microwave spectrometer presented here is a low-cost alternative to time-resolved magneto-optical Kerr effect (TRMOKE) or other techniques involving pulsed lasers. In particular, the fiber coupled laser chip light source and modulator are relatively inexpensive. The frequency range of our setup is limited to 10 GHz by the fiber modulator, but modulators are commercially available up to 40 GHz. The most promising avenue for future development is in eliminating the systematic errors that are found in extracting phase from line shapes. In our analysis, we included effects of image sidebands and showed how they complicated the fitting. As a cautionary note, we expect that additional small signals at the pumping frequency, such as from reflections in the waveguide and cabling, may cause similar difficulties for both heterodyne and homodyne detection.
Despite the effects that limit the phase accuracy, we found that the heterodyne technique produced better signal-to-noise than a comparable homodyne method. Phase uncertainties from individual line shape fits were routinely on the order of 0.01 rad and this phase precision allowed imaging of the phase difference between two samples placed 2.3 mm apart on a waveguide.
In summary, we have developed a new FMR detection method using heterodyning. We use an excitation microwave frequency that is shifted slightly from the laser modulation. The continuously varying phase between the magnetization precession and the light modulation produces an oscillating Kerr rotation signal with a phase equal to the spin precession plus a phase (ϕPL) due to the path length difference between the microwave excitation and the optical signal. This slow signal is conveniently converted to the in-phase and the quadrature signals in the lock in amplifier. The intrinsic parameters of the ferromagnet and ϕPL are estimated by the symmetric and antisymmetric Lorentzian fitting. The phase precision is evaluated and determined using the optical delay and the FMR spectra as a function of the resonance frequency, respectively. We also demonstrate the capability of the FMR detection depending on the sample position in the patterned substrate. This detection method provides the stronger FMR signal at a higher frequency where the 1/f noise floor is reduced and a possibility to verify the phase of the spin precession in the ferromagnets.
Acknowledgments
S.Y. acknowledges support under the Cooperative Research Agreement between the University of Maryland and the National Institute of Standards and Technology Center for Nanoscale Science and Technology, Award No. 70NANB10H193, through the University of Maryland.
References
- 1.Krause S, Berbil-Bautista L, Herzog G, Bode M, Wiesendanger R. Science. 2007;317:1537. doi: 10.1126/science.1145336. [DOI] [PubMed] [Google Scholar]
- 2.Chureemart P, Evans RFL, Chantrell RW. Phys. Rev. B. 2011;83:184416. [Google Scholar]
- 3.Parkin SSP, Hayashi M, Thomas L. Science. 2008;320:190. doi: 10.1126/science.1145799. [DOI] [PubMed] [Google Scholar]
- 4.Stiles MD, Saslow WM, Donahue MJ, Zangwill A. Phys. Rev. B. 2007;75:214423. [Google Scholar]
- 5.Mosendz O, Pearson JE, Fradin FY, Bauer GEW, Bader SD, Hoffmann A. Phys. Rev. Lett. 2010;104:046601. doi: 10.1103/PhysRevLett.104.046601. [DOI] [PubMed] [Google Scholar]
- 6.Mosendz O, Vlaminck V, Pearson JE, Fradin FY, Bauer GEW, Bader SD, Hoffmann A. Phys. Rev. B. 2010;82:214403. doi: 10.1103/PhysRevLett.104.046601. [DOI] [PubMed] [Google Scholar]
- 7.Weiler M, Althammer M, Schreier M, Lotze J, Pernpeintner M, Meyer S, Huebl H, Gross R, Kamra A, Xiao J, Chen Y-T, Jiao HJ, Bauer GEW, Goennenwein STB. Phys. Rev. Lett. 2013;111:176601. doi: 10.1103/PhysRevLett.111.176601. [DOI] [PubMed] [Google Scholar]
- 8.Liu L, Moriyama T, Ralph DC, Buhrman RA. Phys. Rev. Lett. 2011;106:036601. doi: 10.1103/PhysRevLett.106.036601. [DOI] [PubMed] [Google Scholar]
- 9.Liu L, Pai C-F, Li Y, Tseng HW, Ralph DC, Buhrman RA. Science. 2012;336:555. doi: 10.1126/science.1218197. [DOI] [PubMed] [Google Scholar]
- 10.Demidov VE, Urazhdin S, Edwards ERJ, Stiles MD, McMichael RD, Demokritov SO. Phys. Rev. Lett. 2011;107:107204. doi: 10.1103/PhysRevLett.107.107204. [DOI] [PubMed] [Google Scholar]
- 11.Mihai Miron I, Gaudin G, Auffret S, Rodmacq B, Schuhl A, Pizzini S, Vogel J, Gambardella P. Nat. Mater. 2010;9:230. doi: 10.1038/nmat2613. [DOI] [PubMed] [Google Scholar]
- 12.Chernyshov A, Overby M, Liu X, Furdyna JK, Lyanda-Geller Y, Rokhinson LP. Nat. Phys. 2009;5:656. [Google Scholar]
- 13.Sankey JC, Cui Y-T, Sun JZ, Slonczewski JC, Buhrman RA, Ralph DC. Nat. Phys. 2008;4:67. [Google Scholar]
- 14.Kubota H, Fukushima A, Yakushiji K, Nagahama T, Yuasa S, Ando K, Maehara H, Nagamine Y, Tsunekawa K, Djayaprawira DD, Watanabe N, Suzuki Y. Nat. Phys. 2008;4:37. [Google Scholar]
- 15.Ganguly A, Kondou K, Sukegawa H, Mitani S, Kasai S, Niimi Y, Otani Y, Barman A. Appl. Phys. Lett. 2014;104:072405. [Google Scholar]
- 16.Harder M, Cao ZX, Gui YS, Fan XL, Hu C-M. Phys. Rev. B. 2011;84:054423. [Google Scholar]
- 17.Weiler M, Shaw JM, Nembach HT, Silva TJ. Phys. Rev. Lett. 2014;113:157204. doi: 10.1103/PhysRevLett.113.157204. [DOI] [PubMed] [Google Scholar]
- 18.Sinova J, Valenzuela SO, Wunderlich J, Back CH, Jungwirth T. Rev. Mod. Phys. 2015;87:1213. [Google Scholar]
- 19.Kostylev M. J. Appl. Phys. 2012;112:093901. [Google Scholar]
- 20.Kostylev M. J. Appl. Phys. 2009;106:043903. [Google Scholar]
- 21.Bailey WE, Cheng C, Knut R, Karis O, Auffret S, Zohar S, Keavney D, Warnicke P, Lee J-S, Arena DA. Nat. Commun. 2013;4:2025. doi: 10.1038/ncomms3025. [DOI] [PubMed] [Google Scholar]
- 22.Choe S-B, Acremann A, Scholl A, Bauer A, Doran A, Stöhr J, Padmore HA. Science. 2004;304:420. doi: 10.1126/science.1095068. [DOI] [PubMed] [Google Scholar]
- 23.Raabe J, Quitmann C, Back CH, Nolting F, Johnson S, Buehler C. Phys. Rev. Lett. 2005;94:217204. doi: 10.1103/PhysRevLett.94.217204. [DOI] [PubMed] [Google Scholar]
- 24.Guslienko KY, Han XF, Keavney DJ, Divan R, Bader SD. Phys. Rev. Lett. 2006;96:067205. doi: 10.1103/PhysRevLett.96.067205. [DOI] [PubMed] [Google Scholar]
- 25.Van Waeyenberge B, Puzic A, Stoll H, Chou KW, Tyliszczak T, Hertel R, Fähnle M, Brückl H, Rott K, Reiss G, Neudecker I, Weiss D, Back CH, Schütz G. Nature. 2006;444:461. doi: 10.1038/nature05240. [DOI] [PubMed] [Google Scholar]
- 26.Bolte M, Meier G, Krüger B, Drews A, Eiselt R, Bocklage L, Bohlens S, Tyliszczak T, Vansteenkiste A, Van Waeyenberge B, Chou KW, Puzic A, Stoll H. Phys. Rev. Lett. 2008;100:176601. doi: 10.1103/PhysRevLett.100.176601. [DOI] [PubMed] [Google Scholar]
- 27.Curcic M, VanWaeyenberge B, Vansteenkiste A, Weigand M, Sackmann V, Stoll H, Fähnle M, Tyliszczak T, Woltersdorf G, Back CH, Schütz G. Phys. Rev. Lett. 2008;101:197204. doi: 10.1103/PhysRevLett.101.197204. [DOI] [PubMed] [Google Scholar]
- 28.Vansteenkiste A, Chou KW, Weigand M, Curcic M, Sackmann V, Stoll H, Tyliszczak T, Woltersdorf G, Back CH, Schütz G, Van Waeyenberge B. Nat. Phys. 2009;5:332. [Google Scholar]
- 29.Klaer P, Hoffmann F, Woltersdorf G, Jorge EA, Jourdan M, Back CH, Elmers HJ. J. Phys. Appl. Phys. 2011;44:425004. [Google Scholar]
- 30.Martin T, Woltersdorf G, Stamm C, Dürr HA, Mattheis R, Back CH, Bayreuther G. J. Appl. Phys. 2008;103:07B112. [Google Scholar]
- 31.Arena DA, Vescovo E, Kao C-C, Guan Y, Bailey WE. Phys. Rev. B. 2006;74:064409. [Google Scholar]
- 32.Bailey WE, Cheng L, Keavney DJ, Kao C-C, Vescovo E, Arena DA. Phys. Rev. B. 2004;70:172403. [Google Scholar]
- 33.Bartell JM, Ngai DH, Leng Z, Fuchs GD. Nat. Commun. 2015;6:8460. doi: 10.1038/ncomms9460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Guo F, Bartell JM, Ngai DH, Fuchs GD. Phys. Rev. Appl. 2015;4:044004. [Google Scholar]
- 35.Guo F, Bartell JM, Fuchs GD. Phys. Rev. B. 2016;93:144415. [Google Scholar]
- 36.Yoon S, Jang Y, Kim K-J, Moon K-W, Kim J, Nam C, Choe S-B, Cho BK. J. Appl. Phys. 2012;111:07B910. [Google Scholar]
- 37.Nembach HT, Shaw JM, Boone CT, Silva TJ. Phys. Rev. Lett. 2013;110:117201. doi: 10.1103/PhysRevLett.110.117201. [DOI] [PubMed] [Google Scholar]
- 38.Qiu ZQ, Bader SD. Rev. Sci. Instrum. 2000;71:1243. [Google Scholar]
- 39.Moriyama T, Yoon S, McMichael RD. J. Appl. Phys. 2015;117:213908. [Google Scholar]
- 40.Kittel C. J. Phys. Radium. 1951;12:291. [Google Scholar]