The free energy cost of reducing noise while maintaining a high sensitivity

Abstract

Living systems need to be highly responsive, and also to keep fluctuations low. These goals are incompatible in equilibrium systems due to the Fluctuation Dissipation Theorem (FDT). Here, we show that biological sensory systems, driven far from equilibrium by free energy consumption, can reduce their intrinsic fluctuations while maintaining high responsiveness. By developing a continuum theory of the E. coli chemotaxis pathway, we demonstrate that adaptation can be understood as a non-equilibrium phase transition controlled by free energy dissipation, and it is characterized by a breaking of the FDT. We show that the maximum response at short time is enhanced by free energy dissipation. At the same time, the low frequency fluctuations and the adaptation error decrease with the free energy dissipation algebraically and exponentially, respectively.

Living organisms need to respond to external signals with high sensitivity, and at the same time, they also need to control their internal fluctuations in the absence of signal. In equilibrium systems, the fluctuation dissipation theorem (FDT) dictates that these two desirable properties, high sensitivity and low fluctuation, can not be satisfied simultaneously. Most sensory and regulatory functions in biology are carried out by biochemical networks that operate out of equilibrium – metabolic energy is spent to drive the dynamics of the network [1–4]. Thus, in principle they are not constrained by the FDT [5]. How fluctuations, energy dissipation, and sensitivity are related for such systems remains not well understood. Here, we address this question by studying a negative feedback network responsible for adaptation in the bacterial chemosensory system [6–9].

A typical adaptive behavior in a small system such as a single cell is shown in Fig. 1A [10]. In response to a change of the signal S, the output y of the sensory system first changes quickly with a fast time scale τ_y. After the fast response, the output slowly adapts back towards its pre-stimulus level a_ad with an adaptation time τ_ad ≫ τ_y. The new steady state (adapted) output may differ from the pre-stimulus value, and the difference is quantified by the adaptation error ε. In our previous work [11], we showed that the negative feedback network responsible for adaptation operates out of equilibrium with a finite free energy dissipation rate Ẇ. The average adaptation error 〈ε〉 was found to decrease exponentially with τ_ad Ẇ. However, how the variance ${\sigma }_{\epsilon }^2$ of the error behaves in an adaptive system still remains unknown. This is an important question as adaptive feedback systems are intrinsically noisy due to the slow adaptation dynamics [12].

FIG. 1. Noisy response of feedback adaptation.

A) Adaptive output response to a step input signal increase at time 0. After a sharp decrease in a time τ_y, the output y recovers back in a time τ_ad to its adapted value a_ad. The adaptation error is characterized by its average 〈ε〉, as well as its variance σ_ε. B) Schematic of the feedback adaptation model. Transitions between the active and inactive memory energy landscapes, f₁ and f₀, are mediated via equilibrium activity transitions with rates ω₀ and ω₁. An external chemical energy input μ is used to drive the memory variable uphill in both the active and inactive states. The result is a dissipative loop of probability flow around the adapted memory state m_ad, which ensures the output to be near a_ad.

In the linear response regime, the output response of a system to an input signal S(t) is given by $R(t)=R(0)+{\int }_0^t\chi (t-t^{\prime })S(t^{\prime })\mathrm{d}{t}^{\prime }$, where χ is the response function. For equilibrium systems, under the general assumption that response and signal are conjugate variables, the FDT establishes that χ(t) = −β∂_tC_R(t)Θ(t), where C_R(t) ≡ 〈R(t)R(0)〉 − 〈R〉² is the auto-correlation function, Θ(t) is the Heaviside function, and β = (k_BT)⁻¹ is the inverse thermal energy set to unity hereafter. For a small step stimulus S(t) = S₀Θ(t), integration of the FDT leads to a relation between the response and its correlation: R(t) = R(0) − S₀(C_R(t) − C_R(0)). Since for equilibrium systems C_R(t) is a monotonically decreasing function of time [13], the response R(t) is also monotonic in time, and thus no adaptation dynamics is possible. Furthermore, the long time response ΔR ≡ R(t = ∞) − R(0) is linearly proportional to the variance ${\sigma }_R^2=C_R(0)$, i.e., $\mathrm{\Delta }R=S_0{\sigma }_R^2$.

In this paper, we show that in a non-equilibrium adaptive system both the average adaptation error 〈ε〉 (analogous to ΔR) and its variance ${\sigma }_{\epsilon }^2$ (analogous to ${\sigma }_R^2$) are suppressed by the free energy dissipation of the system but in different ways, which results to a nonlinear (log2 arithmic) relationship between them. More importantly, violation of the FDT allows suppression of noise without compromising the strength of the short time response.

The continuous model of feedback adaptation

We start by introducing a discrete adaptation model motivated by the E. coli chemotaxis pathway. The system is characterized by its binary receptor activity A = 0, 1, its output y, and an internal control variable M = 0, 1, … , N, that corresponds to the chemoreceptor’s methylation level in E. coli chemotaxis [9]. For a given external input signal S, the free energy of the system can be written as:

$$F_A(M,S)=-(A-1/2)[(M-M_{\mathrm{r}})E-(S-S_{\mathrm{r}})],$$ (1)

where S_r is a reference signal at a methylation level M_r, and E(> 0) sets the methylation energy scale. For E. coli chemotaxis, the signal S depends on the ligand attractant concentration logarithmically [14].

The dynamics of the system is characterized by the transitions among the 2 × (N + 1) states in the A × M phase space. The receptor activity switches at a time scale τ_a, which is much shorter than the adaptation time scale τ_ad at which the internal variable M is controlled. The activity A determines the output y of the signaling pathway. In the case of E. coli chemotaxis, this is carried out by the phosphorylation and dephosphorylation reactions of the response regulator CheY with an intermediate time scale τ_y: τ_ad ≫ τ_y ≫ τ_a. To account for this, we express y by $y(t)={\tau }_y^{-1}{\int }_{-\infty }^t{\mathrm{e}}^{(t^{\prime }-t)/{\tau }_y}A(t^{\prime })\mathrm{d}{t}^{\prime }$, which averages the fast binary activity A over the time scale τ_y.

According to Eq. (1), a larger signal S favors the inactive state A = 0. Thus, an increase in S quickly reduces the system’s average activity, at time scale ~ τ_a, and output, at time scale ~ τ_y, as represented in Fig. 1A. After this sudden initial response, the system slowly adapts by adjusting its internal variable M to balance the effect of the increased signal. Due to its slow time scale, M effectively serves as a memory of the system. This adaptation process restores activity and output to a level near their pre-stimulus value 〈A〉 = 〈y〉 ≈ a_ad. Although highly precise, adaptation is imperfect, and its inaccuracies are quantified by the adaptation error ε, which we define as

$$\epsilon =\frac{y-a_{\text{ad}}}{a_{\text{ad}}}.$$ (2)

For E. coli chemotaxis, the adaptive machinery consists of chemical reactions that increase M in the inactive state and decrease it in the active state. Note from Eq. (1) that such regulatory reactions are energetically unfavorable, and thus require a chemical driving force μ, see Fig. 1B.

To gain analytical insights about dynamics and energetics of adaptation, we consider the limit where N → ∞ and m = M/N ∈ [0, 1] becomes a continuous variable [15]. Note that free energy and bare rates need to be rescaled for the continuum limit to converge (see Supplementary Information, SI, for details). Proceeding in this way we obtain two coupled Fokker-Planck equations that describe the chemotaxis pathway dynamics:

$$\begin{array}{l}{\partial }_t{p}_1=p_0{\omega }_0-p_1{\omega }_1-{\partial }_m{J}_1\\ {\partial }_t{p}_0=p_1{\omega }_1-p_0{\omega }_0-{\partial }_m{J}_0,\end{array}$$ (3)

where p₁(m, t) and p₀(m, t) are the probabilities of m for the active and inactive states, respectively. The probability currents are given by

$$J_A=D_A((-{\partial }_m{f}_A-\mu )p_A-{\partial }_m{p}_A),A=0,1,$$ (4)

where f_A(m) = − (A − 1/2)[(m − m_r)e − (S − S_r)] is the continuum limit of Eq. (1) characterized by the rescaled energy parameter e = NE. The fast transition rates between the active and inactive states, ω₀ and ω₁, satisfy detailed balance ω₀/ω₁ = exp(f₀−f₁). The diffusion-like constants D₁ and D₀ set the time scale of m changes for active and inactive states, and thus the adaptation time goes as ${\tau }_{\text{ad}}~D_A^{-1}$, see SI for details. Our model is analogous to that of an isothermal ratchet [16], where a chemical driving fuels directed motion. Whereas in ratchets μ drives directed motion, here it fuels currents up the energy landscapes f₀ and f₁ to achieve adaptation.

In the absence of external driving, i.e. μ = 0, the system relaxes to a state of thermal equilibrium with no phase-space fluxes J₀ = J₁ = 0. In this regime adaptation is impossible. The chemical driving μ > 0 breaks detailed balance and creates currents that increase m in the inactive state and decrease it in the active state. For large enough μ, the memory variable m can be stabilized (trapped) in a cycle around its adapted state m_ad, which ensures 〈y〉 ≈ a_ad as illustrated in Fig. 1B. The free energy dissipation rate Ẇ can be computed, and is given by Ẇ ≈ C|μ|/τ_ad, with C a system specific constant set to unity by our parameter choice, see SI. In the following, we will use the chemical driving μ ≈ τ_ad Ẇ to characterize the system’s energy dissipation.

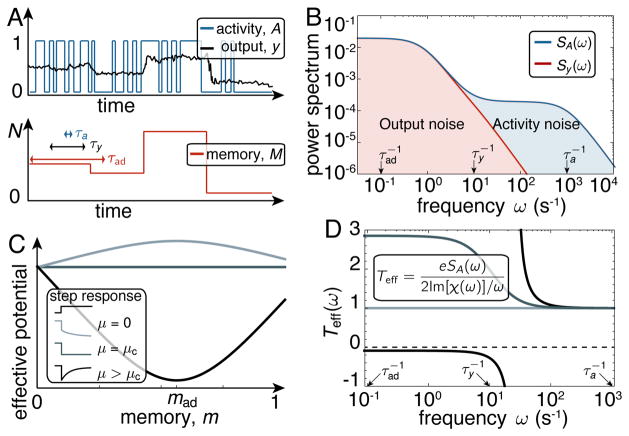
The dynamics of A, y, and m are illustrated in Fig. 2A. The power spectra of A and y, given in Fig. 2B, show that the high frequency fluctuation of y is suppressed with respect to that of A by time-averaging. However, the low frequency fluctuations of y, which are caused by the slow fluctuations of m, are not affected. These low frequency noise can be suppressed by free energy dissipation, as we show later in this paper.

FIG. 2. Adaptation as a non-equilibrium transition.

A) Schematic time traces of the binary activity A (blue), the output y (black), and the memory M (red) in steady state. The slow M variations induce large fluctuations in the output y, while the fast A switching for a fixed M only produces small fluctuations in y. B) Power spectra of the activity S_A and output S_y. The output noise is filtered (reduced) in the high frequency range ${\tau }_y^{-1}<\omega <{\tau }_a^{-1}$; but it remains unfiltered in the range ${\tau }_{\text{ad}}^{-1}<\omega <{\tau }_y^{-1}$. C) Effective memory potential in Eq. 5 for three values of the chemical driving μ (due to the choice D₁ = D₀ taken here, m_ad = m_*). At equilibrium, μ = 0, the adapted memory state m_ad is unstable. At the value μ = μ_c the system becomes critical. In the region μ > μ_c the adapted state m_ad is stable, and the system adapts output and activity to a(m_ad). Inset: Activity response to step signal increase for corresponding values of μ. D) Effective temperature T_eff for three different values of the chemical driving μ. After the onset of adaptation a region with “negative friction” develops, at the end of which the effective temperature diverges. Values of μ from lighter to darker blue are μ = 0, μ = 0.65μ_c, and μ = 20μ_c (the same as in panel C). The other parameters are from [17], see SI.

Adaptation as a non-equilibrium phase transition

Given the separation of time scales τ_a ≪ τ_ad, we can solve Eqs. (3) by using the adiabatic approximation [13, 17]: p₁(m) = a(m)p(m), and p₀(m) = (1 − a(m))p(m), with a(m) = (1+e^{f₁(m)−f₀(m)})⁻¹ the average equilibrated activity for a fixed value of m. The distribution of m can be written as p(m) = e^−h(m,S)/Z with h the effective potential and Z a normalization constant. We have determined the effective potential h analytically (see SI for 3 derivation):

$$h(m,S)=\frac{\mu }{{\mu }_c}ln[D_0{e}^{-(m-m_{\ast })e/2}+D_1{e}^{(m-m_{\ast })e/2}]-ln[e^{-(m-m_{\ast })e/2}+e^{(m-m_{\ast })e/2}],$$ (5)

where we have defined the critical chemical driving as μ_c = e/2, and m_* = m_r + (S − S_r)/e.

The analytical form of the effective potential is one of the main results of this paper. The effect of energy dissipation and the onset of adaptation can be understood intuitively with h(m, S), which contains two terms with similar shapes, see Fig. 2C. The first term (proportional to μ/μ_c) in the right hand side of Eq. (5) comes from chemical driving (non-equilibrium effect) and has a stable free energy minimum. The second term is the equilibrium potential in the absence of driving, and has a maximum at m_*. At equilibrium the only critical point m_* is unstable, so the system tends to go to the boundaries without adapting. As μ increases the first part of the potential starts to dominate. For μ > μ_c, the system develops a stable fixed point at m_ad indicating the onset of adaptive behaviors towards a(m_ad) [18]. As μ grows further this fixed point becomes increasingly stable, and adaptation accuracy improves. The transition of a feedback system to adaptation can thus be loosely understood as a continuous phase transition (see SI for details). Since the control parameter is the free energy dissipation, the transition to adaptation occurs far from equilibrium and a breaking of FDT is to be expected.

Breakdown of Fluctuation Dissipation Theorem

In our feedback model, the observable conjugate to the signal is eA = −∂_Sf_A, for feedforward models this is not true [19–21]. At equilibrium the FDT leads to χ(t) = e∂_tC_A(t), where χ is the activity response function and C_A the monotonic correlation function. In an adaptive system the integral of χ, which is just the response to a step stimulus, is non-monotonic, therefore FDT is broken and adaptation occurs out of equilibrium.

To quantify the departure from equilibrium, we define an effective temperature T_eff using the formulation of the FDT in frequency space [5, 22], see inset in Fig. 2D. The frequency-dependence of T_eff for μ > 0 implies a breakdown of FDT. As shown in Fig. 2D, while for any value μ ≠= 0 we have T_eff ≠= 1, after the transition to the adaptive regime μ ≥ μ_c a divergence occurs. This corresponds to the appearance of a frequency region where Im[χ(ω)] < 0. A negative effective viscosity indicates the dominance of the active effects that drive a net current to flow against the gradients of the equilibrium energy landscapes (f_A), which was also observed in other biological systems such as collections of motors [23] or the inner ear hair bundle [5]. The breakdown of FDT means that there is no a priori connection among fluctuations ${\sigma }_{\epsilon }^2$, chemical driving μ (dissipation), and long-time response 〈ε〉. In the following we derive relations linking these three quantities in the adaptive feedback system studied here.

The free energy cost of suppressing fluctuations

As evident from the effective potential, increasing the chemical driving μ stabilizes the adapted state. In the limit μ → ∞, the system thus goes to its perfectly adapted state with average activity and output a_ad = D₀/(D₀ + D₁), that is a(m_ad) → a_ad. For finite μ, the output differs from a_ad, which can be characterized by the average error 〈ε〉 and its variance ${\sigma }_{\epsilon }^2$.

The average adaptation error is 〈ε〉 = (〈y〉 − a_ad)/a_ad. Summing and integrating Eqs. (3) at the steady state, we have

$$\langle \epsilon \rangle =\frac{D_1{p}_1(1)+D_0{p}_0(1)}{D_0(e/2-\mu )}-\frac{D_1{p}_1(0)+D_0{p}_0(0)}{D_0(e/2-\mu )}.$$ (6)

Thus to obtain the adaptation error we only need to evaluate the probability at the boundaries. In the limit of μ ≫ μ_c, we have:

$$\langle \epsilon \rangle \approx {\epsilon }_{\mathrm{c}}{\mathrm{e}}^{-k\mu {\mu }_c},$$ (7)

where k and ε_c are constants with only weak dependence on μ (see SI for derivation). This shows explicitly that the adaptation error goes down exponentially with energy dissipation, as found numerically in our previous work for the discrete model [11]. Here, we show this relationship analytically in the continuum limit, which is consistent with direct simulations of the discrete model, see Fig. 3A.

FIG. 3. Free energy cost of reducing error and noise.

A). Dependence of average error with chemical driving for several system sizes. The decay is exponential, in agreement with the infinite size limit (dashed red). Saturation of the decay for finite N is due to finite size effects. B) Adaptation noise as a function of chemical driving for several system sizes, together with the analytical estimate in dashed red. At very large driving the noise saturates to its minimum σ_ym dictated by the intrinsic activity fluctuations. Note that at the critical driving μ_c the analytical estimate diverges. This divergence is smoothed for finite N.

Besides stabilizing the adapted state, Eq. (5) shows that increasing μ also reduces the m–fluctuations by making the effective potential sharper. The reduction in these fluctuations implies a decrease in the variance of the error ${\sigma }_{\epsilon }^2$. Taking into account the separation of time scales, the variance of the output y can be approximated as the sum of two variances ${\sigma }_{ym}^2$ and ${\sigma }_a^2$. They respectively correspond to variation of y at time scale ~ τ_y around its average a(m) for a fixed m, and the variation of a(m) due to variation of m at the adaptation time ~ τ_ad, see Fig. 2A. We thus have

$${\sigma }_{\epsilon }^2\approx ({\sigma }_{ym}^2+{\sigma }_a^2)/a_{\text{ad}}^2.$$ (8)

The variance ${\sigma }_{ym}^2$ of y is caused by the fast fluctuations of the binary variable A at timescale ~ τ_a averaged over the output timescale τ_y ≫ τ_a (see SI for derivation):

$${\sigma }_{ym}^2=(a_{\text{ad}}-a_{\text{ad}}^2){\tau }_a/({\tau }_y+{\tau }_a),$$

which clearly shows that ${\sigma }_{ym}^2\propto {\tau }_a/{\tau }_y$ is reduced by time-averaging [12, 24].

The variance ${\sigma }_a^2={\langle a\rangle }^2-\langle a^2\rangle$, where $\langle a^n\rangle ={\int }_0^1{a}^n(m)p(m)\mathrm{d}m$ for n = 1, 2, is caused by the slow variation of m, and can not be reduced by time average. To obtain an analytical expression for ${\sigma }_a^2$ we approximate p(m) by a Gaussian, valid for μ ≫ μ_c. This results in ${\sigma }_a^2\approx {({\partial }_m{a}_{\text{ad}})}^2{\sigma }_m^2/a_{\text{ad}}^2$. The variance ${\sigma }_m^2={\langle m\rangle }^2-\langle m^2\rangle$ within the same Gaussian approximation of p(m) is given by ${\sigma }_m^2\approx {(\mu {\mu }_{\mathrm{c}})}^{-1}$. Defining now a characteristic variance as ${\sigma }_{\mathrm{c}}^2=4{(1-a_{\text{ad}})}^2{a}_{\text{ad}}^2$, we finally have:

$${\sigma }_a^2\approx {\sigma }_{\mathrm{c}}^2{\mu }_{\mathrm{c}}/\mu ,$$ (9)

which vanishes when μ → ∞. This is a main result of the paper, which shows that energy dissipation is used to reduce error noise by suppressing slow activity fluctuations. This result is verified by direct simulations of the discrete models with increasing N, see Fig. 3B.

Discussion

Biochemical networks are non-equilibrium systems fueled by free energy dissipation to achieve their biological functions. Energy dissipation liberates the networks from constraints such as the Fluctuation Dissipation Theorem and Detailed Balance. Here, we show in a negative feedback network that the long-time output response Δ〈y〉= a_ad〈ε〉 decreases with the free energy dissipation μ ≈ τ_ad Ẇ exponentially, and its fluctuation ${\sigma }_y^2=a_{\text{ad}}^2{\sigma }_{\epsilon }^2$ decreases as μ⁻¹. Both these effects, especially the slower decay of ${\sigma }_y^2$ with μ, contribute to enhance the short time response 〈y〉_max, see Fig. 4.

FIG. 4. Response and correlations in systems out of equilibrium.

A) (top panel) Average output response to a signal decrease for several values of the chemical driving beyond μ_c, see the color-code for μ in panel B. As the chemical driving μ increases, the maximal transient response 〈y〉_max increases, but the long time response Δ〈y〉= a_ad〈ε〉 decreases. (bottom panel) The correlation function also decreases as the system is driven further away from equilibrium. B) The dependence of 〈y〉_max, Δ〈y〉, and 〈y〉_max on the chemical driving μ. The long-time response (adaptation error) Δ〈y〉 decreases quickly with μ. The decrease of the output fluctuation (noise) σ_y with μ is more gradual, and controls the increase in the maximal response 〈y〉_max for large μ. In this figure N = 15, and S = S_r.

Even though FDT is broken in the adaptive system studied here, fluctuations and long-time response of the output are linked via a non-linear relation: ${\sigma }_y^2\approx d{\mu }_{\mathrm{c}}/log(y_{\mathrm{c}}/\mathrm{\Delta }\langle y\rangle )+{\sigma }_{ym}^2$, where $d=k{\sigma }_{\mathrm{c}}^2$ and y_c = a_ad〈ε〉. Unlike the linear non-equilibrium FDT derived by a change of observables [25–27], our non-linear relation links observables that are conjugate at equilibrium, making it particularly appealing. Another approach is taken in [28], where near equilibrium linear response is used to show that the dispersion of variables can be reduced by dissipation. Adaptation however is a far from equilibrium phenomenon which requires a critical finite amount of free energy dissipation. As a result, the energy scale is set by the intrinsic energy μ_c instead of the thermal energy k_BT in [28]. It remains a challenging question whether these approaches can be combined to obtain a general relationship among response, fluctuation, and energy dissipation for systems far from equilibrium.