Electrostatic effects on the folding stability of FKBP12

Abstract

The roles of electrostatic interactions in protein folding stability have been a matter of debate, largely due to the complexity in the theoretical treatment of these interactions. We have developed computational methods for calculating electrostatic effects on protein folding stability. To rigorously test and further refine these methods, here we carried out experimental studies into electrostatic effects on the folding stability of the human 12-kD FK506 binding protein (FKBP12). This protein has a close homologue, FKBP12.6, with amino acid substitutions in only 18 of their 107 residues. Of the 18 substitutions, 8 involve charged residues. Upon mutating FKBP12 residues at these 8 positions individually into the counterparts in FKBP12.6, the unfolding free energy (ΔG_u) of FKBP12 changed by −0.3 to 0.7 kcal/mol. Accumulating stabilizing substitutions resulted in a mutant with a 0.9 kcal/mol increase in stability. Additional charge mutations were grafted from a thermophilic homologue, MtFKBP17, which aligns to FKBP12 with 31% sequence identity over 89 positions. Eleven such charge mutations were studied, with ΔΔG_u varying from −2.9 to 0.1 kcal/mol. The predicted electrostatic effects by our computational methods with refinements herein had a root-mean-square deviation of 0.9 kcal/mol from the experimental ΔΔG_u values on 16 single mutations of FKBP12. The difference in ΔΔG_u between mutations grafted from FKBP12.6 and those from MtFKBP17 suggests that more distant homologues are less able to provide guidance for enhancing folding stability.

Introduction

Protein folding is governed by intra-protein interactions and interactions with the solvent. The contributions of hydrophobic interactions to folding stability are universally accepted (Kauzmann, 1959; Dill, 1990; Makhatadze and Privalov, 1995; Baldwin, 2007; Pace et al., 2014). In contrast, the roles of electrostatic interactions in folding stability have been a matter of debate (Hendsch and Tidor, 1994; Xiao and Honig, 1999; Sanchez-Ruiz and Makhatadze, 2001; Vijayakumar and Zhou, 2001; Pace et al., 2014) due to the experimental technical complication in isolating electrostatic effects and the complexity in the theoretical treatment of these effects. Electrostatic interactions of proteins occur in a heterogeneous dielectric environment. In addition, mobile ions in the solvent modulate these interactions. We have developed computational methods for predicting electrostatic effects on protein folding stability (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002; Zhou, 2002a, 2005; Zhou and Dong, 2003). To rigorously test and further refine these methods, here we carried out experimental studies into electrostatic effects on the folding stability of the human 12-kD FK506 binding protein (FKBP12).

FKBP12 has been established to be a two-state reversible folder (Egan et al., 1993; Main et al., 1998, 1999; Korepanova et al., 2001; Fulton et al., 2003; Russo et al., 2003; Spencer et al., 2005). A single tryptophan residue, Trp59, allows for the measurement of the unfolding free energy by monitoring tryptophan fluorescence as a function of denaturant concentration. Previously, we have measured the effects of pH and salt concentration on the folding stability of FKBP12 (Spencer et al., 2005), and the results were found to be in quantitative agreement with theoretical predictions (Zhou, 2002a, 2005). The focus of the present study is the electrostatic contributions of individual residues.

FKBP12 belongs to a family of proteins which vary in size from 12 to 54 kDa and play diverse functional roles, including as peptidyl prolyl cis–trans isomerases, as protein folding chaperones, as targets of immunosuppressant drugs, and as modulators of ryanodine receptors (which are Ca²⁺-releasing channels) (Kang et al., 2008). A close homologue of FKBP12 is FKBP12.6. These two proteins differ in only 18 of their 107 amino acids, and their structures are very similar (Van Duyne et al., 1991; Deivanayagam et al., 2000) (Supplementary Fig. S1). Eight of the 18 substitutions between FKBP12 and FKBP12.6 involve charged residues. Here, we replaced FKBP12 residues in these 8 positions by the counterparts in FKBP12.6, either individually or in combinations, and studied the consequences on the folding free energy. The two proteins have a conserved salt bridge, formed between Asp37 and Arg42. To investigate its contribution to the folding stability, we studied mutations of this salt bridge. A remote homologue of human FKBP12 is a 17-kDa protein in Methanococcus thermolithotrophicus, referred to as MtFKBP17 (Furutani et al., 1998; Suzuki et al., 2003). These two proteins have 31% sequence identity over 89 positions, with MtFKBP17 featuring an additional domain inserted into a flap (Supplementary Fig. S2). Again, substitutions for FKBP12 residues by their MtFKBP17 counterparts, when the corresponding residues in either or both proteins are charged, were studied to assess electrostatic effects on folding stability.

The substitutions that we made here were modeled after homologues of FKBP12. A similar approach was taken by Fersht and coworkers (Serrano et al., 1993) to analyze substitutions between barnase and a close homologue binase. Other strategies of introducing charged (or polar) mutations for probing electrostatic contributions to folding stability have also been taken. For example, Pace and coworkers (Myers and Pace, 1996; Pace, 2001; Takano et al., 2003) used mutations to introduce or remove polar groups in order to study the effects of hydrogen bonds and buried polar groups on folding stability. Raleigh and coworkers (Spector et al., 2000; Luisi et al., 2003) focused on charged residues and salt bridges, which were suggested by computations to be particularly destabilizing or stabilizing. Makhatadze and coworkers (Loladze et al., 1999; Sanchez-Ruiz and Makhatadze, 2001; Makhatadze et al., 2003; Makhatadze et al., 2004; Strickler et al., 2006; Gribenko and Makhatadze, 2007; Gribenko et al., 2009; Tzul et al., 2015) focused on optimizing surface charge–charge interactions, as guided by computations. Charge mutation studies by Wong and coworkers (Lee et al., 2005; Chan et al., 2011) on a thermophilic protein have demonstrated that salt bridges contribute to thermostability through both electrostatic stabilization and reduction in the unfolding heat capacity, in agreement with theoretical prediction (Zhou, 2002d). In related work, Garcia-Moreno and coworkers (Fitch et al., 2002; Karp et al., 2007; Isom et al., 2010, 2011; Robinson et al., 2014) determined pK_as of ionizable groups introduced into buried positions in order to probe electrostatic interactions in the native state.

The effects of many mutations involving charged or polar groups on protein folding stability have been calculated using a continuum treatment of electrostatic interactions (Hendsch and Tidor, 1994; Xiao and Honig, 1999; Sanchez-Ruiz and Makhatadze, 2001; Vijayakumar and Zhou, 2001; Dong and Zhou, 2002; Zhou and Dong, 2003; Tan and Luo, 2008). A protein molecule solvated in a buffer is modeled as a set of point charges embedded in a ‘solute’ dielectric, which in turn is surrounded by an infinite ‘solvent’ dielectric. Mobile ions in the solvent are accounted for by the Poisson–Boltzmann equation. The precise boundary between the solute and solvent dielectrics has been a matter of debate. Most continuum electrostatic calculations have used Richards’ molecular surface as the dielectric boundary, but through systematic studies on the effects of charged and polar mutations on protein folding (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002) and binding (Dong et al., 2003; Dong and Zhou, 2006; Qin and Zhou, 2007) stability and on the protein–protein and protein–RNA absolute binding rate constants (Alsallaq and Zhou, 2008; Qin and Zhou, 2008), we have concluded that a dielectric boundary specified as the protein van der Waals surface provides a more physical description and superior match with experimental results. Alexov and coworkers have explored other options, including the use of a smooth Gaussian-based dielectric function in treating the dielectric boundary (Li et al., 2013, 2014) and the use of amino acid-specific dielectric constants (Wang et al., 2013). Instead of a continuum treatment, Horii et al. (Horii et al., 2001) have used molecular dynamics (MD) simulations in explicit solvent to calculate mutational effects on the unfolding free energy (ΔΔG_u) using an improvised scheme.

The denatured state of a protein has generally been modeled as the individual residues separately solvated and not interacting with each other. A large number of experimental studies have demonstrated significant charge–charge interactions in the denatured state (Oliveberg et al., 1995; Kuhlman et al., 1999; Pace et al., 2000; Whitten and Garcia-Moreno, 2000; Tollinger et al., 2003), prompting the development of theoretical models for the denatured state (Elcock, 1999; Zhou, 2002a). A model that assumes Gaussian statistics for inter-residue distances has been used to rationalize experimental data on many proteins (Zhou, 2002a, b, c, 2003, 2004; Spencer et al., 2005). Here, we applied the Gaussian chain model to account for residual charge–charge interactions. We also introduced two refinements to our basic model (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002; Zhou and Dong, 2003) for calculating the electrostatic contribution to ΔΔG_u. Previously in treating the denatured state, we carved out the single residue under mutation from the native structure and solvated it in isolation (with subsequent account of residual charge–charge interactions via the Gaussian chain model); here, we explored a variation of this protocol by carving out a triplet of residues, consisting of the residue under mutation plus the preceding and following nearest neighbors (Tan and Luo, 2008; Zhang et al., 2012). In many previous continuum electrostatic calculations of mutational effects, a single protein conformation was used, due to the computational cost of solving the Poisson–Boltzmann equation. We have developed a fast generalized Born model that accurately reproduces the Poisson–Boltzmann results (Tjong and Zhou, 2007, 2008). Here, we took advantage of this method and introduced conformational sampling in our electrostatic calculations of mutational effects.

Results and discussion

Along with wild-type FKBP12 and FKBP12.6, the unfolding free energies of 25 FKBP12 mutants were measured. Of these mutants, 13 were based on FKBP12.6 and 12 were grafted from MtFKBP17. There were 16 mutants with single substitutions, 4 with double substitutions, 2 mutants with triple substitutions, 1 each with quadruple substitutions and with quintuple substitutions, and finally a mutant with a 13-residue insertion plus quintuple substitutions. These diverse data provided a stringent test of our methods for computing electrostatic effects on protein folding stability (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002; Zhou, 2002a; Zhou and Dong, 2003) and spurred new refinements of these methods.

FKBP12 mutations based on FKBP12.6

These two close homologues differ in 18 of their 107 amino acids, and 8 of these substitutions involve charged residues (Supplementary Fig. S1). Five of the latter substitutions are very conservative, between cationic arginine and cationic lysine or between carboxyl-bearing aspartate and glutamate and amide-bearing asparagine and glutamine. The structures of the two proteins are also very similar, with Cα atoms of the 107 amino acids superimposing to a root-mean-square deviation (RMSD) of 0.5 Å (Van Duyne et al., 1991; Deivanayagam et al., 2000). All the 8 substitutions involving charged residues are highly exposed to solvent. Other than the sequentially neighboring residues 31 and 32, the 8 substituted residues are well disbursed on the protein surface.

Our strategy here was to mutate these eight amino acids in FKBP12 individually into the corresponding ones in FKBP12.6, identify the stabilizing substitutions and combine the stabilizing substitutions into a hyper-stable variant. A similar strategy was employed by Jiang et al. (Jiang et al., 2001) to increase the folding stability of the WW domain, though in departure from the present study these authors explored both core and surface positions and both nonpolar and polar/charged amino acids. In theory, the effects of individual substitutions may not be additive. Therefore, we used double-mutant cycles (Carter et al., 1984) to investigate (anti-)cooperative effects, in particular on the pair, between residues 31 and 32, where such effects are most likely to be prominent. The interaction between two residues, A and B, can be captured by the coupling energy measured when these residues are individually and simultaneously mutated into A′ and B′:

$$\begin{array}{c}\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{int}}=\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{u}}(\text{A}\to {\mathrm{A}}^{\mathrm{\prime }};\text{B}\to {\mathrm{B}}^{\mathrm{\prime }})-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{u}}(\text{A}\to {\mathrm{A}}^{\mathrm{\prime }})-\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{u}}(\text{B}\to {\mathrm{B}}^{\mathrm{\prime }})\end{array}$$ (1)

The mutations should be designed to eliminate the interaction in question. For example, charge neutralization is likely to eliminate charge–charge attraction or repulsion. A positive $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{int}}$ could mean stronger attraction in the folded state than in the denatured state, or it could mean stronger repulsion in the denatured state than in the folded state.

FKBP12 and FKBP12.6 have a conserved, semi-buried salt bridge formed by D37 and R42 (Supplementary Fig. S1). We were also interested in the contribution of this salt bridge to the folding stability. This was investigated by introducing mutations where these residues were replaced by neutral amino acids (serine and alanine, respectively).

Unfolding free energies of FKBP12.6-based mutants

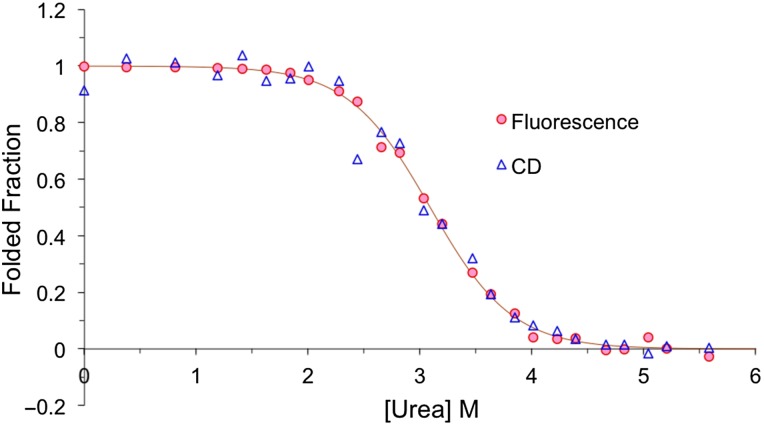
The unfolding free energy, ΔG_u, was measured by monitoring the fraction of folded protein as a function of urea concentration. For most FKBP12 variants, the monitoring was done by tryptophan fluorescence. For a few variants, including wild-type FKBP12 and the D37S/R42A mutant, monitoring was also done by circular dichroism (CD) spectroscopy to confirm the two-state folding behavior. The denaturation of FKBP12.6, which lacks Trp59, was monitored only by CD spectroscopy. The procedure was described in our previous study (Spencer et al., 2005) and is briefly summarized under the Materials and methods section. The denaturation curves of the D37S/R42A double mutant monitored by tryptophan fluorescence and CD are shown in Fig. 1 as a representative.

Fig. 1.

The denaturation curves of the D37S/R42A double mutant monitored by tryptophan fluorescence and CD. The curve is a fit to the fluorescence data; a fit to the CD data yields identical results (not shown).

Of the 13 FKBP12.6-based mutations, 10 involved single substitutions, two involved double substitutions, and the remaining one involved triple substitutions (Table I). Relative to FKBP12, even though FKBP12.6 was less stable by 1.22 kcal/mol, all but 2 of the 8 single substitutions grafted from the latter protein were stabilizing. The stabilizing effects of the 6 single substitutions ranged from marginal (0.03 kcal/mol for E31Q) to appreciable (0.66 kcal/mol for H94N), whereas the two destabilizing substitutions, Q3E and R57K, each reduced ΔG_u by 0.3 kcal/mol. These results demonstrate that stabilizing substitutions can be grafted from homologues that have less overall stability.

Table I.

Unfolding free energies of FKBP12 and 14 FKBP12.6-based variants

Variant	ΔGu (kcal/mol)a	ΔΔGu (kcal/mol)b
Wild-type FKBP12	5.07 ± 0.02
Wild-type FKBP12.6	3.85c	−1.22
Q3E	4.73 ± 0.10	−0.34
R18K	5.27 ± 0.13	0.20
E31Q	5.10 ± 0.13	0.03
D32N	5.15 ± 0.13	0.08
E31Q/D32N	5.53 ± 0.10	0.46
D37S	4.63 ± 0.10	−0.44
R42A	4.43 ± 0.10	−0.64
D37S/R42A	4.89 ± 0.01	−0.18
M49R	5.21 ± 0.20	0.14
R57K	4.77c	−0.30
H94N	5.73 ± 0.10	0.66
K105N	5.21 ± 0.10	0.14
E31Q/D32N/H94N	5.94 ± 0.18	0.87

^aData are reported as mean plus/minus standard error of measurement.

^bChange in unfolding free energy relative to wild-type FKBP12.

^cData from a single measurement. Since these were destabilizing variants, more precise determination of ΔG_u was not pursued.

To probe possible interaction between E31 and D32, we introduced the double mutation E31Q/D32N. Individually, the substitutions only marginally increased the stability (with ΔΔG_u at 0.03 and 0.08 kcal/mol), but upon combining these substitutions, the stabilizing effect, at 0.46 kcal/mol, became appreciable. A double-mutant cycle analysis led to a coupling energy of 0.35 kcal/mol. As noted above, a positive $\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{int}}$ can be explained either by stronger attraction in the folded state than in the denatured state or by stronger repulsion in the denatured state than in the folded state. Given that E31 and D32 have like charges, the latter explanation seems more plausible.

We further combined the E31Q/D32N double substitutions with the most stabilizing single substitution, H94N. The stability of the resulting triple mutant was higher than that of wild-type FKBP12 by 0.87 kcal/mol. This increase in stability is higher than both that by the E31Q/D32N double substitutions and that by the H94N, but lower than expected from additivity. The apparent coupling energy was −0.25 kcal/mol. There does not appear to be any single dominant factor that explains the interference between the E31Q/D32N and H94N substitutions.

We also investigated the contribution of the conserved salt bridge formed by D37 and R42 to the folding stability of FKBP12. When either partner was neutralized (by the D37S or R42A mutation), the destabilizing effect was considerable (at 0.44 or 0.64 kcal/mol). However, when both mutations were made, the destabilizing effect, at 0.18 kcal/mol, became modest. For charges in semi-buried (and buried) positions, two prominent and likely opposing contributions to folding stability are the unfavorable desolvation cost and the (often) favorable interactions with neighboring charged or polar groups in the folded state, as in the case of a salt bridge. Relative to the D37S/R42A double mutant, the contribution of the favorable interactions between D37 and R42 as well as between these two charges and more distant polar and charged groups apparently is slightly higher than the desolvation cost of the two charges, leading to a modestly higher ΔG_u for the wild-type protein. The coupling energy between the two charges is 0.9 kcal/mol by a double-mutant cycle analysis.

In short, our strategy of designing a more stable FKBP12 mutant by accumulating stabilizing substitutions grafted from FKBP12.6 was successful, with the triple mutant E31Q/D32N/H94N increasing stability by ∼0.9 kcal/mol. Our study provides strong support to the conclusion of others that electrostatic interactions can make significant contributions to protein folding stability (Gribenko et al., 2009; Pace et al., 2014). However, the results presented here also highlight the complexity of characterizing electrostatic effects. In particular, while E31Q and D32N individually had marginal effects, their combination resulted in considerable stabilization. In contrast, while D37S and R42A individually had appreciable destabilizing effects, their combination had only very modest destabilization. Overall, accumulating stabilizing substitutions from close homologues can be an effective alternative to consensus-based design (Porebski et al., 2015).

Grafting substitutions from MtFKBP17

MtFKBP17 is a remote homologue of human FKBP12 (Furutani et al., 1998; Suzuki et al., 2003). When structurally aligned over 89 positions, the Cα RMSD is as high as 1.7 Å, and the sequence identity of these aligned positions is 31% (Supplementary Fig. S2). Compared with FKBP12, MtFKBP17 has a 14-residue deletion at the N-terminus, a 13-residue insertion in a region known as bulge, and a 44-residue insertion in a region known as flap. The 13-residue insertion is unique to thermophilic archaea (Furutani et al., 1998). The 44-resiude insertion forms a domain (called IF, or the insertion in the flap) that has chaperone activity (Furutani et al., 1998; Suzuki et al., 2003). Engineering of an IF domain into FKBP12 endowed the protein with chaperone activity, while decreasing the folding stability by 1.1 kcal/mol (Knappe et al., 2007).

We made 12 FKBP12 mutants based on MtFKBP17 (Table II). One contained the 13-residue insertion along with double substitutions R40I/D41E at the N-terminal side and triple substitutions R42E/N43Y/K44E at the C-terminal side of the insertion. These flanking substitutions ensured that at least three residues on each side of the insertion were the same as in the MtFKBP17 parent. We also characterized two intermediate mutants before the insertion was made: the R40I/D41E double mutant and the K44E single mutant.

Table II.

Unfolding free energies of FKBP12 mutants grafted from MtFKBP17

Variant	ΔGu (kcal/mol)a	ΔΔGu (kcal/mol)b
R40I/D41E	3.60 ± 0.12	−1.47
K44E	5.20 ± 0.02	0.13
R40I/D41E-13res-R42E/N43Y/K44E	3.18c	–1.89
I91E/A95K	2.71 ± 0.02	–2.36
T21K	3.80 ± 0.10	–1.27
T21K/V23K/K47E	2.19c	–2.88
T21K/V23K/K47E/K52E	2.31c	–2.76
T21K/V23K/K47E/K52E/K105E	3.22c	–1.85
T96D	2.15 ± 0.20	–2.92
K17D	3.16c	–1.91
S67E	3.52 ± 0.06	–1.55
Q70D	2.40 ± 0.10	–2.67

^aData are reported as mean plus/minus standard error of measurement.

^bChange in unfolding free energy relative to wild-type FKBP12.

^cData from a single measurement.

A double mutant I91E/A95K aimed to introduce a salt bridge formed by the corresponding residues, E137 and K141, in MtFKBP17. A quintuple mutant, T21K/V23K/K47E/K52E/K105E, was made to graft an ionic network from MtFKBP17. Three intermediate mutants, the single mutant T21K, the triple mutant T21K/V23K/K47E and the quadruple mutant T21K/V23K/K47E/K52E, were also characterized.

One single mutant, T96D, concerned a small ionic cluster formed by the corresponding MtFKBP17 residue, D142, with K77 and E20. E20 corresponds to an identical residue (i.e. E31) in FKBP12, but K77 is substituted into T75. The three remaining single mutants, K17D, S67E and Q70D, were chosen as examples of isolated charges, although the latter two residues in MtFKBP17 appear to form a hydrogen bond (E69 Oϵ1 and D72 Oδ2 distance at 2.7 Å).

Unfolding free energies of MtFKBP17-based mutants

The unfolding free energies of the 12 MtFKBP17-based mutants are listed in Table II. Relative to those based on FKBP12.6, these mutations here were much less successful in achieving stabilization. Except for one (K44E) that resulted in a marginal increase in stability, all the mutations produced decreases in stability, from 1.27 kcal/mol by the T21K mutation to 2.92 kcal/mol by the T96D mutation.

There are two likely important reasons for the failure in achieving significant stabilization by grafting substitutions from MtFKBP17. First, the structures of FKBP12 and MtFKBP17 superimpose poorly. Therefore, the local environments of corresponding residues can be quite different. Second, the corresponding residues in MtFKBP17 mostly contribute to the latter's stability by being part of an ionic cluster. For example, the MtFKBP17 counterpart of FKBP12 T21 is part of a five-residue ionic network, and the MtFKBP17 counterpart of FKBP12 T96 is part of a three-residue ionic cluster. To achieve the precise interatomic distances in these ionic clusters, especially in a background with poor structural similarity to the parent protein, is extremely challenging. The challenge of grafting complementarity determining regions (CDRs) for stabilization from distantly related antibody frameworks was discussed by Ewert et al. (Ewert et al., 2004), who suggested that it was important to identify and co-graft key residues that directly and indirectly interact with the grafted CDRs.

Test of electrostatic calculations

The diverse data presented above for the effects of charge mutations on the folding stability of FKBP12 afforded an opportunity to rigorously test our methods for computational electrostatic contributions (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002; Zhou, 2002a; Zhou and Dong, 2003). Admittedly, predicting mutational effects on folding stability is a daunting task and our methods have a number of limitations. First, for charge mutations like the ones studied here, it is not always clear that electrostatic contribution dominates over non-electrostatic effects. Second, there is significant uncertainty in modeling the denatured state. Although our Gaussian chain model has shown potential in treating pH dependence of folding stability (Zhou, 2002a, b, c, 2003, 2004; Spencer et al., 2005), the effects of individual mutations in the denatured state may be far more delicate to model. Third, a protein may respond to a mutation in compensatory ways, e.g. via local or even global conformational relaxation. In our previous studies, we did not allow any residues, even the immediate neighbors, to adjust their conformations after introducing a mutation.

In view of the latter two limitations, here we refined our methods in two ways. Firstly, we previously modeled the denatured state as individually solvated residues and corrected for residual charge–charge interactions by the Gaussian chain model. Here, we assumed that, in the denatured state, the residue under mutation and its immediate preceding and following neighbors along the sequence preserved their conformation in the folded state, and only accounted for the more distant charge–charge interactions by the Gaussian chain model. This refinement was expected to moderate the effect of mutation due to the inheritance of the local folded conformation by the denatured state. Both Tan and Luo (Tan and Luo, 2008) and Zhang et al. (Zhang et al., 2012) have previously found the three-residue model to be optimal (relative to one-residue and five-residue models) for treating local electrostatic effects in the denatured state.

Secondly and more importantly, instead of using a single protein conformation for electrostatic calculations, we used an ensemble of conformations sampled from MD simulations. These conformation-averaged electrostatic calculations were made possible by our fast generalized Born model that accurately reproduces the Poisson–Boltzmann results (Tjong and Zhou, 2007, 2008). For each sampled conformation, mutation was still modeled by fixing all other residues. The conformational averaging was expected to produce two positive effects. The first was to reduce the chance of spurious results arising from the inadequate modeling of mutation; outliers were removed by clustering the results for mutational effects predicted on the sampled conformations, and the mean of the largest cluster was taken as the final prediction. The second was that the sampled conformations provided more varieties for the mutated residue to select for a suitable environment.

Our refined method bears similarity to that proposed by Zhang et al. (Zhang et al., 2012) in carrying out conformational averaging and in using a generalized Born model to account for solvation effects. However, here we focused on charge mutations and also did not empirically tune weighting factors of various terms in the calculated mutational effects. We further note that double and higher mutations were modeled by sequentially accumulating single mutations. Hence, the deficiencies in modeling mutations are compounded for higher mutants. For this reason, below we report the performance of our computational methods both on the 24 mutants overall and on the 16 single mutants separately.

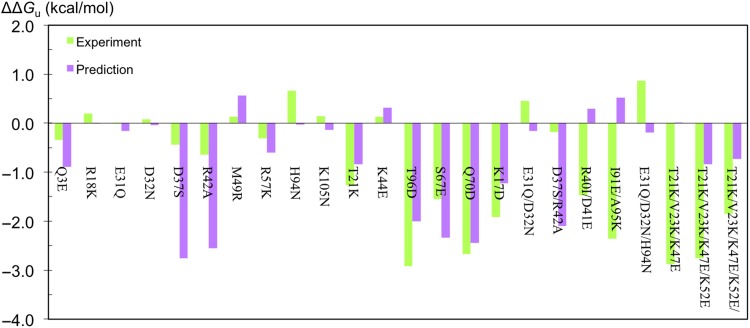
Using our previous protocol based on a one-residue model for the denatured state and a single protein conformation (i.e. the crystal structure) for electrostatic calculations, the RMSDs of predicted mutational effects from the experimental ΔΔG_u were 1.8 kcal/mol for the 24 mutants overall and 1.3 kcal/mol for the 16 single mutants. Using a three-residue model for the denatured state along with conformational averaging and clustering of calculated mutational effects, these RMSDs were reduced to 1.3 and 0.9 kcal/mol, respectively (Fig. 2). Among the single mutants, the destabilizing effects of D37S and R42A were significantly overestimated. The clustering had a modest contribution to the improved performance, as without it the RMSDs were 1.4 kcal/mol for the 24 mutants overall and 1.0 kcal/mol for the 16 single mutants.

Fig. 2.

Comparison of experimental and computational results for the effects of 24 charge mutations on the folding free energy of FKBP12. The experimental results are listed in Tables I and II. The computational results were obtained using a three-residue model for the denatured state along with conformational averaging and clustering.

Conclusion

We have carried out a joint experimental and computational study to investigate the effects of charged residues on the folding stability of FKBP12 and its homologues. Our results suggest that it is relatively easy to accumulate stabilizing substitutions on a protein from a close homologue, even when that homologue has lower overall stability. On the other hand, achieving stabilization by grafting substitutions from a more distant homologue, especially when the corresponding residues form an interaction network in the latter protein, is very challenging. We have also attained a measure of success in predicting mutational effects on folding stability through judicious methodological improvements. However, there is much more to be desired from computation, including accounting for non-electrostatic effects and for conformational relaxation upon mutations, especially those involving multiple residues.

Materials and methods

Protein expression and purification

Wild-type FKBP12 has a single cysteine, Cys22. Like in most previous studies of folding stability (Egan et al., 1993; Main et al., 1998, 1999; Korepanova et al., 2001; Fulton et al., 2003; Russo et al., 2003; Spencer et al., 2005), this cysteine was mutated to an alanine to avoid potential disulfide cross-linking. Hereafter, FKBP12 bearing the C22A mutation was simply referred to as the wild-type protein. The generation of mutations and the expression and purification of FKBP12 variants were described previously (Spencer et al., 2005). Briefly, a pET expression vector containing the wild-type or mutant FKBP12 cDNA was used to transfect the BL21 strain of Escherichia coli cells for protein overexpression. Cells were harvested by centrifugation for 15 min at 6000 rpm. The pellet was resuspended in a lysis buffer [50 mM Tris (pH 7.5), 25 mM NaCl, 1 mM EDTA, 0.04% (w/v) sodium azide], and lysed using Microfluidizer-110L, with phenylmethanesulfonyl fluoride (at 1 mM) added to limit protease degradation. The lysate was centrifuged using a Beckman JA25.5 rotor for 15 min at 10 000 rpm. The supernatant was loaded onto a DE52 anion exchange column (Whatman), which was pre-equilibrated with the lysis buffer for at least 30 min. Fractions containing FKBP12 were collected in an elution buffer [50 mM Tris (pH 7.5) and 500 mM NaCl], and concentrated by an Amicon stirred cell unit (Millipore) with membranes of 5000 NMWL. The concentrated fractions were then loaded onto a Q-Sepharose anion exchange column (Sigma) and eluted [load buffer: 20 mM Tris (pH 8) and 25 mM NaCl; elution buffer: 20 mM Tris (pH 8.0) and 700 mM NaCl]. Finally, the FKBP12 fractions were concentrated and loaded onto a 2.5 × 75 cm column containing S-200 size exclusion media (Amersham Biosciences), and collected [load buffer and elution buffer: 20 mM Tris (pH 8)].

The FKBP12.6 plasmid was a gift from Dr Hong-Bo Xin (Cornell University). The expression and purification of FKBP12.6 were as described above, except that dithiothreitol was added to all buffers as a reducing agent, because FKBP12.6 contains two cysteine residues, Cys22 and Cys76.

Measurement of unfolding free energy

Tryptophan fluorescence spectroscopy of urea-denatured protein samples and data analysis were described previously (Spencer et al., 2005). Briefly, 31 samples containing the same protein concentration but increasing urea concentrations were prepared. The standard buffer was 50 mM potassium phosphate (pH 6.5) and 100 mM KCl. Stock urea concentrations were determined by measuring the refractive index as described by Pace (Pace, 1986). Tryptophan fluorescence intensities at 356 nm were measured on a Varian Cary Eclipse spectrofluorometer with an excitation wavelength of 294 nm (with 2.5-nm band pass filter for both excitation and emission). Each sample, thermostated at 21.5°C, was allowed to equilibrate for 5 min. Data were analyzed by the linear extrapolation method (Greene and Pace, 1974; Santoro and Bolen, 1998) using gnuplot. That is, the fluorescence intensity (F) as a function of urea concentration ([U]) was fitted to

$$F=\frac{F_{\mathrm{N}}([U])+F_{\mathrm{D}}([U])\exp (-(\mathrm{\Delta }{G}_{\mathrm{u}}-m[U])/k_{\mathrm{B}}T)}{1+\exp (-(\mathrm{\Delta }{G}_{\mathrm{u}}-m[U]/k_{\mathrm{B}}T))}$$ (2)

where m is the slope in the linear extrapolation of the unfolding free energy to zero urea concentration; k_B is Boltzmann's constant; T is the absolute temperature; and F_s([U]), s = N or D, is the fluorescence intensity of the native state or denatured state at a urea concentration [U]. The dependence of F_s on [U] was assumed to be linear: F_s = F_0s + s_s[U]. Measurements for each FKBP12 variant were done two to six times, and the data were globally analyzed to determine ΔG_u and individually analyzed to determine the standard error of measurement. The value of m was fixed at 1.6 kcal/mol/M to facilitate the calculation of changes in ΔG_u by mutations. This m value was determined in our previous study (Spencer et al., 2005). When m was allowed to vary in the fitting, the fitted values for different FKBP12 variants showed small fluctuations around 1.6 kcal/mol/M. With the fixed m value, the fitting errors in ΔG_u were 0.02–0.06 kcal/mol.

Urea denaturation of several FKBP12 variants, including the wild-type protein, the D37S/R42A double mutant and the FKBP12.6 protein, was monitored on an Aviv-202 CD spectrometer. Samples were placed in a 1-mm path length rectangular quartz cuvette (VWR) and thermostated at 21.5°C. CD signals in the range of 212–232 nm were recorded with a 1-nm bandwidth, sampling every 0.5 nm. A minimum of six scans were taken, and the spectra were averaged and smoothed. The resulting signal at 222 nm as a function of urea concentration was analyzed according to Equation (2), in which F now represented the CD signal.

Calculation of ΔΔG_u due to charge mutations: basic model

The basic model for calculating the electrostatic contribution to the change in unfolding free energy by a point mutation has been established in our previous studies (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002; Zhou and Dong, 2003); here, a brief description is given. We use E to denote the electrostatic free energy of a protein in the native (N) or denatured (D) state. The change in E upon denaturation is ΔE_u = E_D – E_N, and the difference in ΔE_u between the wild-type (wt) protein and a mutant (mt) is ΔΔE_u = ΔE_u(mt) – ΔE_u(wt). The electrostatic free energy was obtained from a continuum treatment, with

$$E=E_{\mathrm{Coul}}+E_{\mathrm{Solv}}$$ (3)

where the first term denotes the Coulomb interaction energy between charges in the protein, and the second term denotes the electrostatic solvation free energy. The latter was obtained by solving the Poisson–Boltzmann equation using the UHBD program (Madura et al., 1995), with the dielectric boundary set to the protein van der Waals surface. In the calculations, the temperature was 294.5 K, and the ionic strength was 150 mM, to match with the experimental conditions.

The denatured state was treated as the individual residues separately solvated. In this treatment, residues other than the one under mutation make the same contributions to E_D(wt) and E_D(mt). Therefore, for the purpose of calculating ΔΔE_u, we can replace E_D by E_res, the electrostatic free energy of the residue under mutation. The conformation of this residue was carved out from the native structure. Including the charge–charge interaction energy E_int in the denatured state [as predicted by the Gaussian chain model (Zhou, 2002a)], we have

$$\mathrm{\Delta }{E}_{\mathrm{u}}=E_{\mathrm{res}}+E_{\mathrm{int}}-E_{\mathrm{N}}=-(E_{\mathrm{N}}-E_{\mathrm{res}})+E_{\mathrm{int}}=-\mathrm{\Delta }{E}_{\mathrm{N}}+E_{\mathrm{int}}$$ (4)

Calculation of ΔΔG_u due to charge mutations: further refinements

In this study, we introduced two refinements to our basic model for calculating ΔΔE_u, which denotes the electrostatic contribution to ΔΔG_u. One is conformational averaging. By allowing the protein molecule to experience conformational fluctuations, the results of ΔΔE_u is expected to be more robust. This is especially true given the relatively simple way in which we modeled mutations (see below).

We sampled protein conformations by running MD simulations. The protocol was as follows. Starting with the Protein Data Bank (PDB) entry 1FKB, we added hydrogen atoms and then placed the protein molecule in a simulation box with 5350 of TIP3P water molecules and a single Cl^– ion for charge neutralization, using the LEAP program of the Amber package (Case et al., 2006). To start the MD simulations, which used the ff99SB force field (Hornak et al., 2006), the solvent molecules were energy minimized for 200 cycles and equilibrated for 100 ps under constant pressure, while the protein molecule was fixed. The whole system was then energy minimized for 2500 cycles, with harmonic constraints on the protein molecule gradually reducing from 50 kcal/mol/Ų to 0. Subsequently, the system was heated to room temperature and equilibrated under constant volume for 40 ps. Finally, the simulations were run under constant temperature and constant pressure, with 200 snapshots during 1–3 ns of the trajectory sampled for electrostatic calculations.

The inclusion of conformational averaging in the electrostatic calculations was afforded by a fast method called scaled GBr⁶ (Tjong and Zhou, 2008). Briefly, out of the 200 protein conformations, 5 were selected (based on variations of raw GBr⁶ results for ΔE_Solv) to do the Poisson–Boltzmann calculations for ΔE_Solv). The GBr⁶ results were then scaled to optimally match the Poisson–Boltzmann counterparts. The scaling factor was finally applied to all the other protein conformations. This scaling procedure was separately applied to the wild-type protein and to the mutant.

The ΔΔE_u results from the 200 protein conformations allowed us to remove spurious data arising from inadequate modeling of mutations. To this end, we clustered the 200 ΔΔE_u results using a cutoff of 1 kcal/mol for the standard deviation of each cluster. The mean ΔΔE_u of the largest cluster was taken as the final calculation result.

The other refinement here was the use of a triplet of residues, consisting of the residue under mutation plus the preceding and following nearest neighbors, in representing the denatured state (Tan and Luo, 2008; Zhang et al., 2012). This triplet was again carved out from the native structure. To avoid double counting, the charge–charge interaction of the residue under mutation with its nearest neighbors was removed in calculating E_int.

Mutations were modeled as follows. For each mutant with a single substitution, the side chain under mutation was deleted and rebuilt with the mutant side chain, using the LEAP program. The new side chain alone (the original one-residue model) or the triplet of residues (the three-residue model) was energy minimized in vacuum for a maximum of 50 000 cycles, with the rest of the protein molecule fixed. A double mutant was connected to the wild-type protein with a single mutant as the intermediary, such that each step involved a single mutation. Similarly, triple and higher mutants were modeled by sequentially accumulating single mutations.

Supplementary data

Supplementary data are available at PEDS online.

Funding

This work was supported by National Institutes of Health Grants GM058187 and GM118091.