Role of Cytosolic Calcium Diffusion in Murine Cardiac Purkinje Cells

Abstract

Cardiac Purkinje cells (PCs) are morphologically and electrophysiologically different from ventricular myocytes and, importantly, exhibit distinct calcium (Ca²⁺) homeostasis. Recent studies suggest that PCs are more susceptible to action potential (AP) abnormalities than ventricular myocytes; however, the exact mechanisms are poorly understood. In this study, we utilized a detailed biophysical mathematical model of a murine PC to systematically examine the role of cytosolic Ca²⁺ diffusion in shaping the AP in PCs. A biphasic spatiotemporal Ca²⁺ diffusion process, as recorded experimentally, was implemented in the model. In this study, we investigated the role of cytosolic Ca²⁺ dynamics on AP and ionic current properties by varying the effective Ca²⁺ diffusion rate. It was observed that AP morphology, specifically the plateau, was affected due to changes in the intracellular Ca²⁺ dynamics. Elevated Ca²⁺ concentration in the sarcolemmal region activated inward sodium–Ca²⁺ exchanger (NCX) current, resulting in a prolongation of the AP plateau at faster diffusion rates. Artificially clamping the NCX current to control values completely reversed the alterations in the AP plateau, thus confirming the role of NCX in modifying the AP morphology. Our results demonstrate that cytosolic Ca²⁺ diffusion waves play a significant role in shaping APs of PCs and could provide mechanistic insights in the increased arrhythmogeneity of PCs.

Introduction

The cardiac Purkinje system forms a specialized electrical conduction system in the ventricles and is crucial for synchronized contraction of ventricles to maintain proper heart rhythm. The Purkinje system has been suggested to play a pivotal role in initiation and maintenance of life-threatening ventricular arrhythmias.^1–3 Recent experimental studies in transgenic mice carrying ryanodine receptor (RyR₂) mutations, typically observed in the catecholaminergic polymorphic ventricular tachycardia patients,⁴ have shown that the His-Purkinje system is a major source of focal activations that initiated arrhythmia.^5,6 Experimental studies firmly suggest that action potential (AP) abnormalities in the form of early and delayed afterdepolarizations (EADs and DADs, respectively) are a more common occurrence in Purkinje cells (PCs) than in ventricular myocytes (VMs).⁷ However, the exact mechanisms underlying the increased propensity to AP abnormalities in PCs are not well understood.

PCs are morphologically and electrophysiologically distinct from VMs. Specifically, T-tubules are absent in most PCs,^8,9 which results in a unique calcium (Ca²⁺) homeostasis in PCs.^10,11 Ca²⁺ ions entering PCs via sarcolemmal (SL) channels diffuse through the cytosol to reach the sarcoplasmic reticulum (SR), before triggering Ca²⁺-induced -Ca²⁺-release (CICR).¹² PCs also express T-type Ca²⁺ current (I_CaT), absent in VMs and activating at more negative potentials than the L-type Ca²⁺ current (I_CaL).^13,14 As such, Ca²⁺ dynamics in PCs differs significantly from that in VMs, which may explain their increased arrhythmogeneity. Electrical excitation induces a biphasic Ca²⁺ transient in Purkinje fiber strands¹⁵ and in isolated PCs,¹² which consists of (i) Ca²⁺ diffusion wavelets from the subsarcolemmal (subSL) region toward the central core of the cell and (ii) a focally arising Ca²⁺ wave that propagates throughout the cell.^12,16 Altered Ca²⁺ handling contributes to triggered activity,¹⁷ and moreover, the spontaneous Ca²⁺ waves have been thought to play a role in initiating membrane depolarizations, but the mechanisms by which cytosolic Ca²⁺ diffusion alters AP morphology and potentially promotes afterdepolarizations are not well studied.

In this study, we utilized a detailed biophysical mathematical model of a murine PC to study the significant role of cytosolic Ca²⁺ diffusion waves in shaping the APs of PCs that might elucidate the mechanisms for initiating arrhythmia. The unique behavior of cytosolic Ca²⁺ diffusion in PC, as recorded in recent experiments,¹⁶ was implemented in our model and its implications on the increased propensity of arrhythmia in PCs were investigated.

Methods

Biophysical model of a PC

In this study, the murine PC model described in the study by Vaidyanathan et al.¹⁸ was modified to include geometrical details of a PC, described below, and extended by adding the late Na⁺ current (I_NaL) as described in the study by Li and Rudy.¹⁹ It has been demonstrated that I_NaL inactivation is a critical contributing factor in AP duration shortening in PCs during short-paced cycle lengths and alterations in I_NaL may contribute to EAD generation in PCs.²⁰

A schematic of our PC model, including all ionic current components, buffers, and fluxes, is shown in Figure 1. The cell is assumed to be cylindrical in shape with 129 μm length and 8 μm width, based on experimentally measured dimensions of 129 ± 7 μm and 8 ± 0.3 μm, respectively.¹⁸ Figure 1B shows the intracellular compartmentalization of the model, which is assumed to be symmetric along the length. SL currents are uniformly distributed along the length, and the SR is assumed to be in the core of the cell. RyR₂ receptors are also uniformly distributed throughout the cell.¹⁶ The membrane currents are collected in a subSL region of 0.1 μm depth, immediately below the SL. The SR consists of two compartments: (1) a release compartment called the junctional SR (JSR), which is responsible for the release of Ca²⁺ from the SR into the cytosol (blue arrow in Fig. 1B), and (2) an uptake compartment called network SR (NSR), which is responsible for the uptake of Ca²⁺ from the cytosol into the SR (red arrow in Fig. 1B). Similar to SL, the fluxes to and from the SR are collected in a subsarcoplasmic reticulum (subSR) region of 0.1 μm depth, surrounding the SR. The radius of the SR is 2 μm and the total width of the cytosolic region is 2 μm, surrounding the SR.

Figure 1.

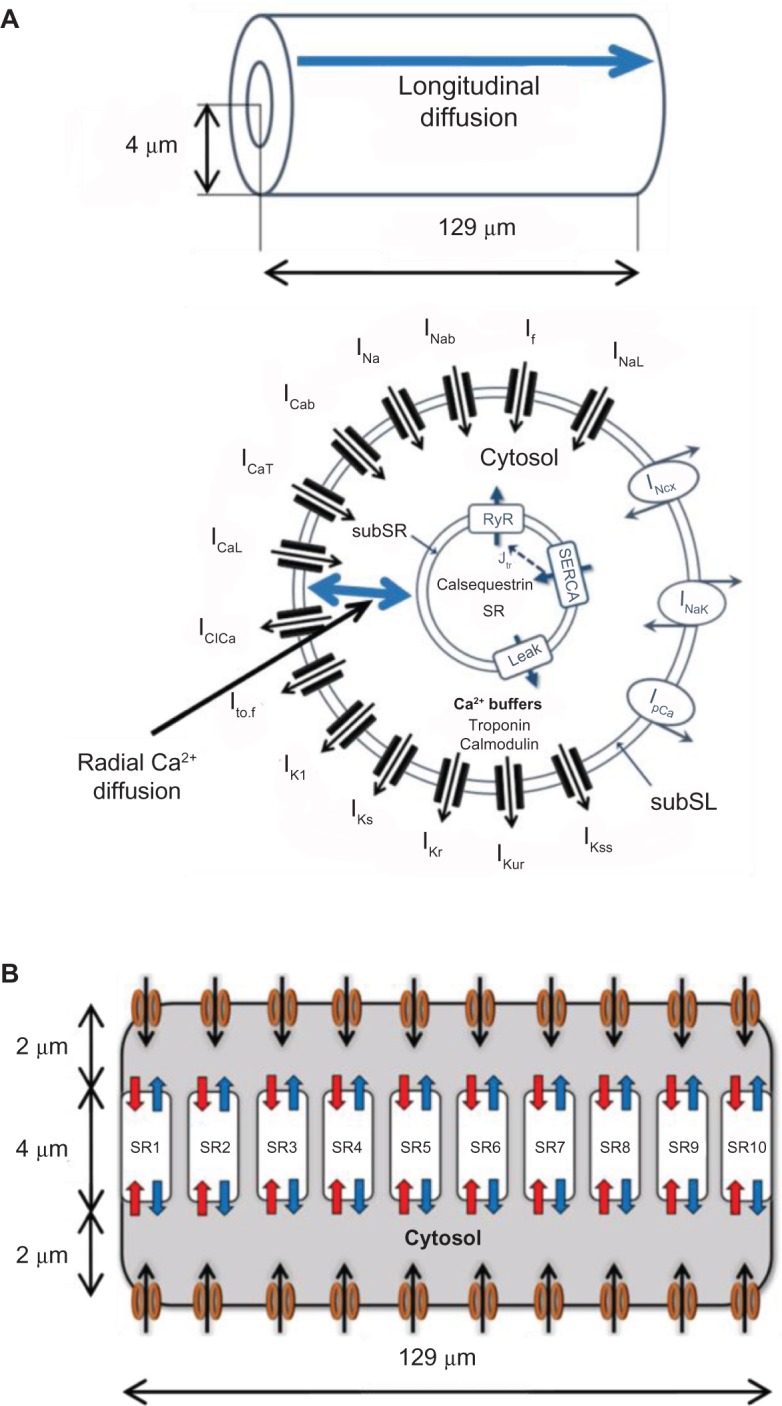
(A) Schematic showing various ionic currents and the two components of Ca2+ diffusion (radial and longitudinal) in the PC biophysical model. (B) The SR is divided into 10 discrete subcompartments (SR1–SR10) along the cell length each having its own Ca²⁺ release/uptake machinery.

Figure 2.

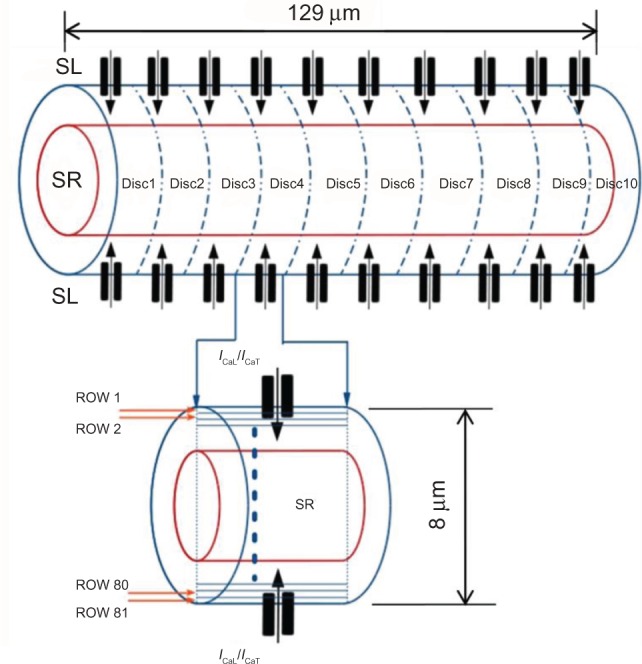
Implementation of spatiotemporal diffusion in the PC model. The cell is divided into 10 disks, each consisting of 81 concentric layers.

Cytosolic Ca²⁺ diffusion process

A two-component cytosolic Ca²⁺ diffusion process, as observed experimentally,^12,16 was implemented in our model as follows: (1) radial diffusion of Ca²⁺ entering the cell via SL Ca²⁺ channels (I_CaL and I_CaT) propagating toward the central core (SR), referred to as wavelets, and (2) cell-wide longitudinal Ca²⁺ diffusion wave (CWW) initiated as a result of local CICRs propagating along the length of the cell. The length of the cell was divided into 10 discrete disks, with each disk possessing L- and T-type SL Ca²⁺ channels and an SR compartment, and the width of the cell was divided into 81 concentric layers, as shown in Figure 2. Cellular volume discretization enabled the simulation of longitudinal and radial Ca²⁺ diffusion processes, with a reasonable computational cost, without the necessity of representing individual Ca²⁺ release sites. The number of SR disks was constrained to 10 to minimize the computational load, while maintaining an adequate spatiotemporal Ca²⁺ resolution.

A three-dimensional diffusion equation in cylindrical coordinates was used to model the cytosolic Ca²⁺ diffusion process as follows.^21,22

$$\frac{\partial c}{\partial t}={\beta }_i\left(c\right)\cdot \left[D_{\text{Car}}\frac{{\partial }^{2}c}{\partial r^2}+D_{\text{Cal}}\frac{{\partial }^{2}c}{\partial x^2}+J_{\text{Ca}}\right]$$ (1)

where c is the intracellular Ca²⁺ concentration, $D_{\text{Car}}\frac{{\partial }^{2}c}{\partial r^2}$ term represents the radial diffusion and $D_{\text{Cal}}\frac{{\partial }^{2}c}{\partial x^2}$ represents longitudinal diffusion. Here, D_Cal and D_Car represent the longitudinal and radial diffusion coefficients, respectively. Considering similar diffusion velocity in radial and longitudinal directions in the model, these coefficients are assumed to be equal and will be referred to as D_Ca (D_Ca = D_Cal = D_Car). J_Ca is the Ca²⁺ flux from SL or SR in cytosol and β_i(c) accounts for rapid cytosolic Ca²⁺ buffering. Finite-difference time-domain (FDTD) solution²³ was used to produce a finite and linear discretization of Equation (1) as follows:

$$\begin{array}{l}\frac{d{c}_{\left(n,k,t\right)}}{dt}={\beta }_i\left(c_{\left(n,k,t\right)}\right)\\ \left\{\frac{D_{\text{Car}}}{j_n{\left(\mathrm{\Delta }r\right)}^2}\left[\left(1+j_n\right)c_{\left(n+1,k,t\right)}-2j_n{c}_{\left(n,k,t\right)}+\left(j_n-1\right)c_{\left(n-1,k,t\right)}\right]+\frac{D_{\text{Cal}}}{{\left(\mathrm{\Delta }x\right)}^2}\left[c_{\left(n,k+1,t\right)}-2c_{\left(n,k,t\right)}+c_{\left(n,k-1,t\right)}\right]+J_{\text{Ca}\left(n,k,t\right)}\right\}\end{array}$$ (2)

where c_(n,k,t) represents intracellular Ca²⁺ concentration at a discrete node (n,k) at a time instance t. Here, n represents the number of rows used in the model, k represents the number of columns used in the model, Δr is a small increment in the width of the model, Δx is a small increment in the length of the model, and j_nΔr represents the spatial coordinate for concentration c_n along radial axis of cylindrical model. The flux term J_Ca(n,k,t) at node (n,k) at a time instance t, is defined as J_CaSR/V_subSR for the subSR compartment, J_CaSL/V_subSL for the subSL compartment, and zero elsewhere.

Ca²⁺ releases from the JSR compartment in the form of a RyR flux (J_RyR) is described as

$$J_{\text{RyR}}=k_{\text{RyR}}\cdot P_{\text{open}}\cdot \left({\left[{\text{Ca}}^{2+}\right]}_{\text{JSR}}-{\left[{\text{Ca}}^{2+}\right]}_{\text{subSR}}\right),$$ (3)

and NSR Ca²⁺ uptakes via the SR Ca²⁺ ATPase (SERCA) pump (J_SERCA),

$$J_{\text{SERCA}}=k_{\text{SERCA}}\cdot \frac{V_{\max ,f}{\left({\left[{\text{Ca}}^{2+}\right]}_{\text{subSR}}/K_{mf}\right)}^H-V_{\max ,r}{\left({\left[{\text{Ca}}^{2+}\right]}_{\text{NSR}}/K_{mr}\right)}^H}{1+{\left({\left[{\text{Ca}}^{2+}\right]}_{\text{subSR}}/K_{mf}\right)}^H+{\left({\left[{\text{Ca}}^{2+}\right]}_{\text{NSR}}/K_{mr}\right)}^H}$$ (4)

where [Ca²⁺]_x is the Ca²⁺ concentration in the x compartment, P_open is the RyR channel opening probability, k_y is the rate for flux J_y, and K_mf and K_mr are half-saturation parameters for forward and reverse SERCA, respectively. H = 2 is the Hill coefficient for the SERCA pump.

A two-state Markov model of RyR gating was used in our model, consisting of an open and a closed state, with opening and closing of rates k_open and k_close, respectively, formulated as in the study by Korhonen et al.²² The half-saturation concentration for the RyR channel, K_m,RyR, has sigmoidal dependence with [Ca²⁺]_JSR as given in Equation (5),

$$K_{m\text{,RyR}}=3.51{\left\{1+\exp \left(\left({\left[{\text{Ca}}^{2+}\right]}_{\text{JSR}}-530)/200\right)\right)\right\}}^{-1}+0.25$$ (5)

such that the RyR channel open probability (P_open) dynamics, governed by [Ca²⁺]_subSR, are described as in Equation (6),

$$\frac{d{P}_{\text{open}}}{dt}=P_{\text{closed}}{k}_{\text{open}}{\left[1+{\left(K_{m\text{,RyR}}/{\left[{\text{Ca}}^{2+}\right]}_{\text{subSR}}\right)}^4\right]}^{-1}-k_{\text{close}}{P}_{\text{open}}$$ (6)

To initiate a CWW at one cell end, a [Ca²⁺]_subSR threshold for SR Ca²⁺ release was defined for each SR compartment, such that the SR1 threshold ([Ca²⁺]_subSR > 0.5 μM) is less than the threshold for other compartments SR2–SR10 (0.6 μM). In a given subSR compartment, when [Ca²⁺]_subSR exceeded threshold, P_open was increased to 0.6 for a single time step (dt = 1 μs), triggering SR Ca²⁺ release and a rapid rise in the subSR Ca²⁺ concentration. For all other numerical integration steps, P_open was governed by Equation (6). The PC ionic model was paced at 1 Hz throughout the cell with stimulus current of amplitude −80 μA/μF with duration of 0.5 ms for five minutes to attain a steady state. Model parameters and values are provided in Table 1.

Table 1.

Parameters of the model.

PARAMETER	DEFINITION	VALUE
rSR	Radius to the surface of SR	2 μm
rSL	Radius to the surface of cell	4 μm
Acap	Capacitive membrane area	7.99 × 10–5 cm2
Cm	Specific membrane capacitance	1.0 μF/cm2
F	Faradays constant	96.5 C/mmol
T	Temperature	308 K
R	Ideal gas constant	8.314 J/(mol K)
VsubSR	Volume of subSR compartment	0.082794 μL
VsubSL	Volume of subSL compartment	0.247012 μL

Results

Action potential morphology

Figure 3 shows the AP morphology obtained in our model (Fig. 3B) compared to the experimentally recorded AP (Fig. 3A) in murine PCs.¹⁸ Our model successfully reproduced the AP durations at 70% and 90% of repolarization (APD₇₀ and APD₉₀, respectively), as well as the maximum dV/dt values obtained in the experiments (summarized in Table 2).¹⁸ The peculiar low-voltage plateau in the mouse PC AP is apparent in the figure and was observed to be sensitive to T-type Ca²⁺ current (I_CaT), which is active at membrane potentials between −40 and −60 mV.^13,14 Increasing I_CaT magnitude resulted in more pronounced plateau (not shown), demonstrating that the I_CaT was responsible for the characteristic AP plateau in murine PC, in agreement with the recent findings.¹⁸

Figure 3.

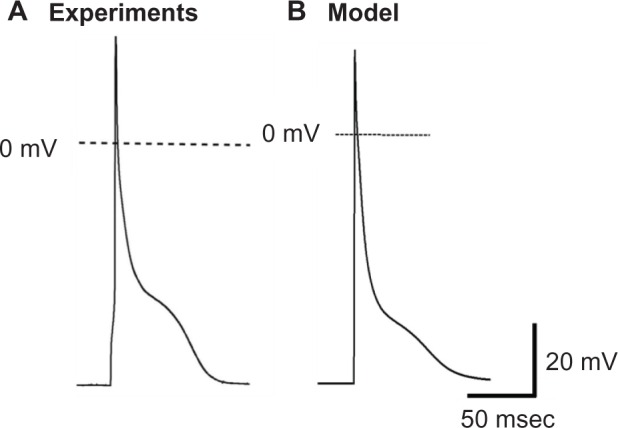
AP morphology (A) as experimentally recorded in mouse PCs¹⁸ and (B) that obtained from our PC model.

Table 2.

Comparison of the AP parameters recorded in experiments with those obtained in the PC model.

PARAMETER	EXPERIMENTS	MODEL
		SLOWER DCa = 5 µm2/ms	CONTROL DCa = 7 µm2/ms	FASTER DCa = 10 µm2/ms	FASTER DCa = 15 µm2/ms
dV/dtmax (mV/ms)	212 ± 15	211.34	211.39	211.43	211.44
APD50 (ms)	4.7 ± 0.3	7.7	7.7	7.7	7.6
APD70 (ms)	14.4 ± 1.6	15.6	15.5	15.7	16.4
APD90 (ms)	68.6 ± 5	52.99	67.29	76.39	83.69

Intracellular Ca²⁺ diffusion

Figure 4 shows the radial and longitudinal Ca²⁺ transients observed in the PC model, clearly illustrating the biphasic nature of the Ca²⁺ transients, resulting from the two diffusion processes components. Ca²⁺ enters the cell through the SL channels (I_CaL and I_CaT) and diffuse radially toward the core of the cell where the SR is located (Fig. 4A). These radial wavelets, upon reaching the SR, trigger a CWW traveling along the length of the cell, as shown in Figure 4B. The CWWs are much higher in amplitude than the wavelets. The parameters of the average Ca²⁺ transient obtained in the model were adjusted to match the experimentally observed values reported in the study by Vaidyanathan et al.¹⁸ Table 3 lists the characteristics of the average Ca²⁺ transients of the PC model, compared to the experimental values. The time required to attain the peak magnitude was 25 ms, and the Ca²⁺ transient decay time was 210 ms, both within the experimental ranges.

Figure 4.

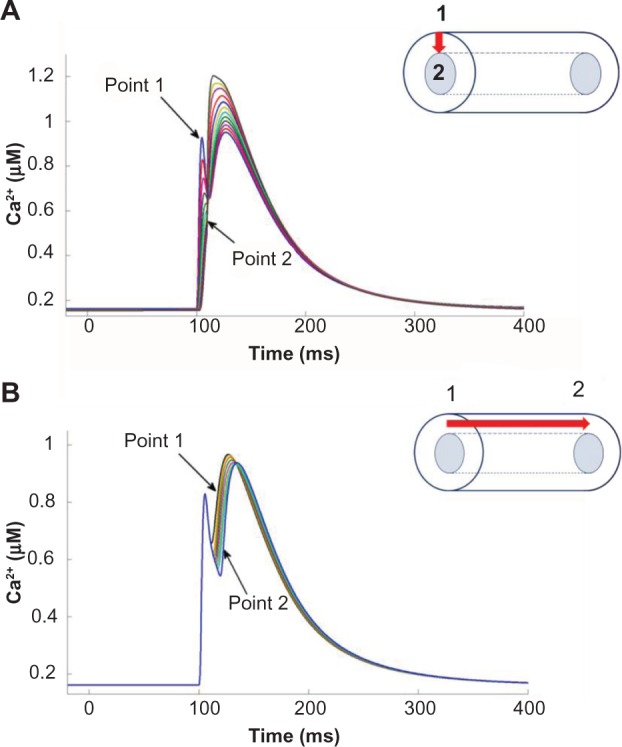
Cytosolic Ca²⁺ transients observed in the model representing (A) diffusion of radial wavelets and (B) longitudinal diffusion of CWW. The locations of Point 1 and Point 2 are shown on the right. The red arrow represents the component of Ca²⁺ diffusion shown.

Table 3.

The parameters of average calcium transients recorded in the experiments and obtained in the model.

PARAMETER	EXPERIMENTS18	MODEL
Peak Amplitude	31.193 ± 0.91 AU	1.03 μM
Time to Peak	18.8 ± 13.2 ms	25 ms
Decay time	261 ± 69.18 ms	210 ms

Note: The experimental values are obtained from the study by Vaidyanathan et al.¹⁸

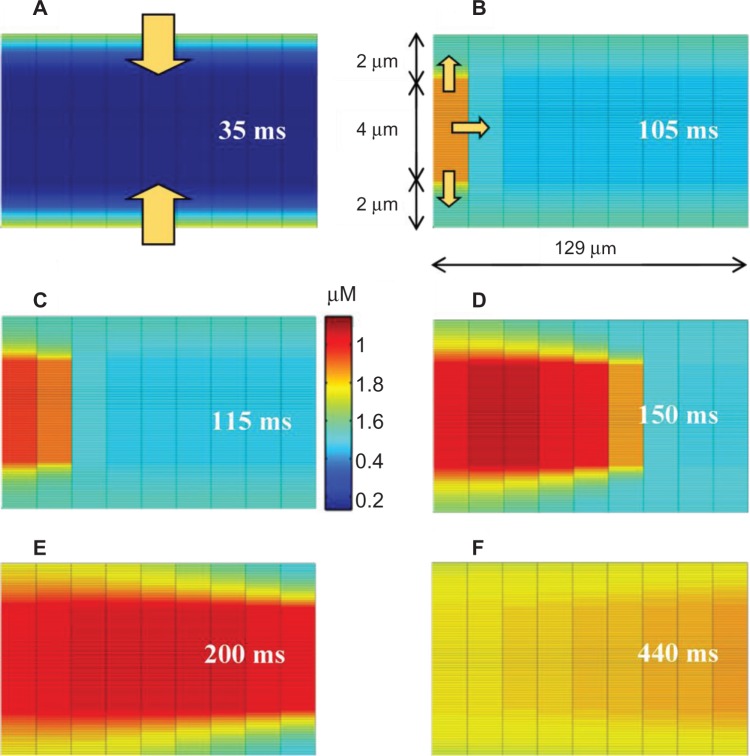
Experimental studies have suggested that a small increase in subSL Ca²⁺ can initiate the wavelets, but relatively higher Ca²⁺ threshold is needed to trigger the CWWs.¹⁶ Figure 5 shows that Ca²⁺ diffusion waves elicited during 1 Hz pacing stimulus. During Phase 2 of the AP, Ca²⁺ enters the cell via SL channels initiating radial wavelets (arrows in Fig. 5A). When the concentration of the Ca²⁺ wavelets arriving at SR1 exceeded threshold, Ca²⁺ was released from the junctional SR1 via CICR, leading to a larger Ca²⁺ wave propagating largely in longitudinal direction from SR1 toward SR2 (Fig. 5B). The Ca²⁺ concentration at SR2 was thus elevated from both radial wavelets and the longitudinal Ca²⁺ wave initiated at SR1. Ca²⁺ release from junctional SR2 was triggered when the subSR Ca²⁺ concentration exceeded threshold, slightly larger than the SR1 threshold, which in turn supplements the CWW. This process was continued in subsequent SR compartments, as shown in Figure 5C–F. The magnitude of the CWW increased monotonically as it propagated from one end of the cell to the other due to contributions from the successive local CICRs.

Figure 5.

Propagation of Ca²⁺ transients in the PC model. (A) Simultaneous propagation of wavelets from SL to SR. (B) Initiation of CWW at SR1. (C), (D), (E), and (F) Propagation of CWW along the cell length. The arrows inside figures show direction of Ca²⁺ propagation. The time lapsed just after Ca²⁺ entered into the cell from external is also given.

Effects of Ca²⁺ diffusion on AP

In order to assess the effects of Ca²⁺ diffusion on the AP morphology, we studied the individual effects of Ca²⁺ wavelets and CWWs in our model. Ca²⁺ wavelets were produced by the SL Ca²⁺ currents (I_CaL and I_CaT), without which (when both blocked) the Ca²⁺ transients were not observed. Moreover, when the CWWs were inhibited, wavelets alone were not able to produce the AP plateau (Fig. 6A). Thus, both components of Ca²⁺ diffusion process were necessary to establish the biphasic Ca²⁺ transients and reproduce the AP morphology observed in the PCs.

Figure 6.

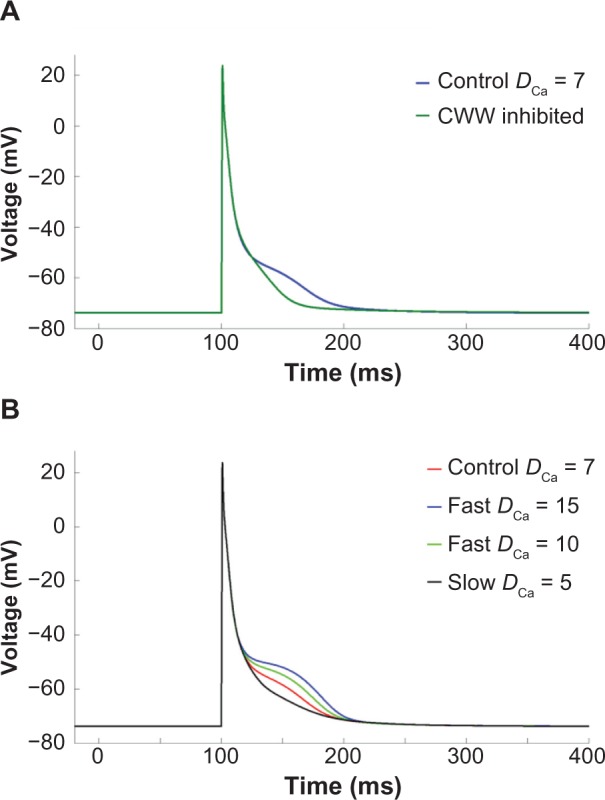
Ca²⁺ diffusion effect on AP. (A) AP plateau is disappeared when CWW is disabled. (B) Effect of Ca²⁺ diffusion coefficient (D_Ca) on AP morphology. Increasing the diffusion velocity (D_Ca = 10 μm²/ms and 15 μm²/ms) resulted in more pronounced plateau while slowing it (D_Ca = 5 μm²/ms) suppressed the plateau.

We next examined the influence of the effective diffusion coefficient, D_Ca, on AP morphology. By varying D_Ca we could alter the speed of the propagating Ca²⁺ transients. The baseline value of D_Ca in our model was chosen to be 7 μm²/ms to reproduce experimentally observed Ca²⁺ transients. This value was referenced from the study by Korhonen et al.²², where D_Ca was fitted to get single effective diffusion coefficient parameter based on cytosolic Ca²⁺ propagation velocity. This value represents an effective Ca²⁺ diffusion coefficient that accounts for the influence of intracellular Ca²⁺ binding proteins or buffers, which can greatly reduce effective diffusion relative to free Ca²⁺.²⁴ We found that increasing D_Ca produced a more pronounced plateau and significantly increased APD₉₀, and while reducing D_Ca to 5 μm²/ms reduced the AP plateau duration (Fig. 6B). Thus, faster Ca²⁺ transients were counterintuitively associated with more pronounced AP plateau, prompting a further investigation in the mechanisms of AP prolongation.

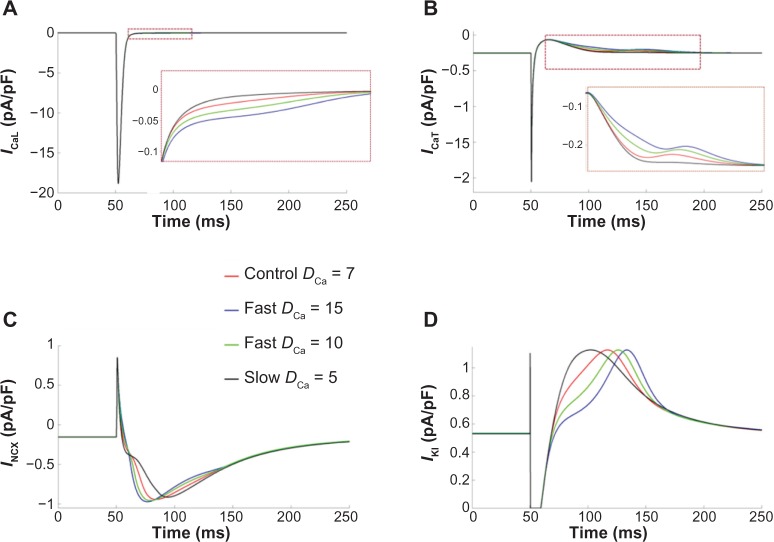
The average cytosolic Ca²⁺ concentration for different values of D_Ca is shown in Figure 7A. We found that faster Ca²⁺ transients produced larger Ca²⁺ transient amplitudes. More notable average Ca²⁺ variations were observed in the subSL compartment, which exhibited biphasic transients (Fig. 7B). The subSL Ca²⁺ concentration is mainly contributed by L-type Ca²⁺ channels, such that slower diffusion results in slower wavelet propagation, and thus large Ca²⁺ accumulation and a larger initial peak in the subSL Ca²⁺ concentration. Faster diffusion resulted in faster CICRs from each SR, ie, a smaller temporal delay between CICR events at each SR, which subsequently led to larger subSL Ca²⁺ accumulation and higher magnitude transients, observed in the second peak in the subSL Ca²⁺ concentration. These variations in cytosolic Ca²⁺ resulted in alterations in the membrane potential and various SL current magnitudes. Among the SL currents, I_NCX, I_CaT, and I_K1 were significantly affected (Fig. 8).

Figure 7.

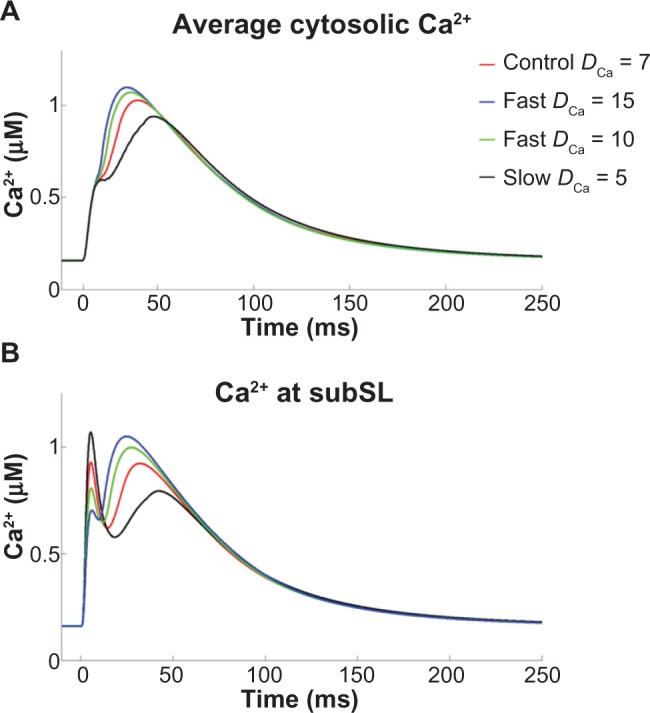
(A) Average cytosolic Ca²⁺ concentration, and (B) Ca²⁺ amount reaching subSL region for different values of D_Ca.

Figure 8.

Ionic currents with notable variations for different D_Ca: (A) I_CaL – L-type Ca²⁺ current, (B) I_CaT – T-type calcium current, (C) I_NCX – sodium–Ca²⁺ exchanger current, and (D) I_K1 – inward rectifier current. Insets show zoomed regions highlighted by rectangles.

We next investigated if the changes in the SL ionic currents were indeed due to variations in the subSL Ca²⁺ for different values of D_Ca. The subSL Ca²⁺ concentration was artificially maintained at normal levels (control case) while varying the D_Ca values as before. We found that the alterations in the current magnitudes as observed previously for varying D_Ca (Fig. 8) disappeared completely. More importantly, the variations in AP plateau were also reversed, suggesting that the variations in subSL Ca²⁺ concentration due to faster diffusion were responsible for the pronounced AP plateau.

Individual contributions of I_CaT, I_CaL, and I_NCX in prolongation of AP plateau

We further analyzed the individual contributions of I_CaT, I_CaL, and I_NCX in prolongation of the AP plateau at higher values of D_Ca. In each case, the ionic current under consideration was artificially clamped to its normal time-dependent values as in control case (D_Ca = 7 μm²/ms), while varying D_Ca (Fig. 9). It was observed that when I_CaT and I_CaL were individually clamped to the control values, the prolongation of the AP plateau at higher D_Ca persisted (Fig. 9A and B), indicating insignificant contribution of these two currents in the AP prolongation. In contrast, when NCX was clamped to its control magnitude, the alterations in the AP plateau were almost reversed completely (Fig. 9C), confirming that the alterations in NCX were responsible for the prolongation of AP plateau at faster Ca²⁺ diffusion.

Figure 9.

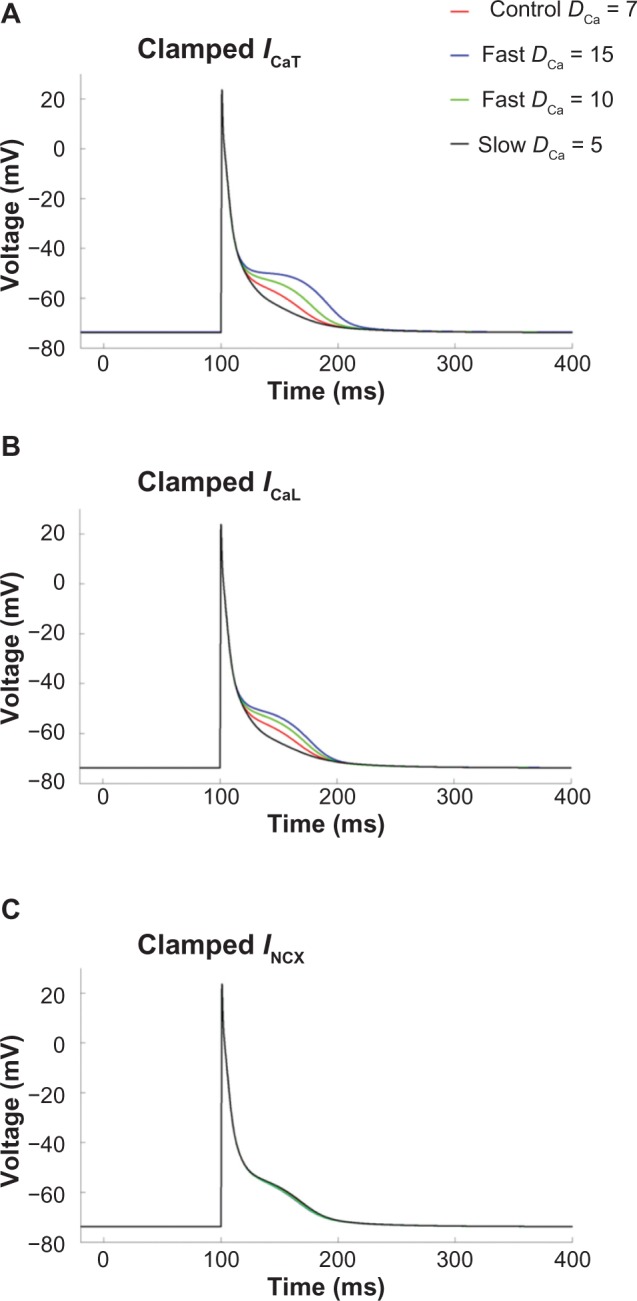
APs when (A) I_CaT, (B) I_CaL, and (C) I_NCX were individually clamped to control values during varying D_Ca. Note that the AP prolongation was completely reversed in (C).

Discussion

In this study, we employed a detailed mouse PC model to gain understanding of Ca²⁺ propagation inside the cell and the consequences of fast and slow cytosolic Ca²⁺ transients. The spatiotemporal implementation of realistic cytosolic Ca²⁺ diffusion waves in our PC model, the first of its kind to our knowledge, provided us a unique capability to investigate the individual and combined contributions of various ionic components of a PC AP. Our main findings were: (1) during an AP, Ca²⁺ diffusion produced biphasic cytosolic Ca²⁺ transients, namely, radial wavelets and longitudinal CWWs, (2) AP plateau was specifically affected by the changes in subSL Ca²⁺ levels, (3) faster Ca²⁺ transients produced dramatic changes in subSL Ca²⁺, which resulted in significant prolongation of the AP plateau, and (4) the prolongation of the AP plateau during faster diffusion was mediated through the inward NCX current. The low-voltage plateau phase observed in murine PCs is similarly observed in many species, including canine,²⁵ rabbit,²⁶ and human,²⁷ suggesting that the influence of subcellular Ca²⁺ dynamics on the plateau phase, and repolarization more generally, may be significant in other species as well.

Extensive experimental studies have demonstrated the presence of the distinct types of Ca²⁺ waves in PCs.^11,12 Stuyvers et al.¹⁶ reported two types of Ca²⁺ transients in canine PCs: (1) Ca²⁺ transients originating directly under the sarcolemma, mostly due to influx through Ca²⁺ channels, initiating small Ca²⁺ wavelets in a region between a depth of ∼6 μm under the sarcolemma and the SR, and (2) when the amplitude of these wavelets is greater than a threshold, they trigger cell-wide large Ca²⁺ waves that travel across the cell length and have much lower velocity. These Ca²⁺ waves travel at a constant velocity and with constant amplitude throughout the cell, which suggests a mechanism of Ca²⁺ diffusion boosted by local CICRs.^11,16 Our implementation of Ca²⁺ diffusion through subcellular compartmentalization satisfies these experimental observations. Because the magnitude of wavelets is lower than CWW, the possibility of wavelets alone triggering CWW is small.¹² Our mouse PC model satisfies this condition by incorporating distinct threshold values for the SR at one cell end and the remaining SR compartments. Since the SR threshold at one cell end is slightly lower, CICR is triggered by the wavelets, and the cumulative accumulation of Ca²⁺ from wavelets and the Ca²⁺ released are sufficient to subsequently trigger CICR in adjacent SR compartments. Thus, CICRs in successive compartments are triggered as the CWW propagates through the cell. The wavelets, on the other hand, propagate via diffusion between the cell periphery and the core of the cell. Spontaneous Ca²⁺ release from the SR can propagate in the reverse direction toward the membrane and may increase the local Ca²⁺ concentration in the subSL region, thereby causing membrane depolarizations through transient inward currents.^28,29

Our results show that faster Ca²⁺ diffusion resulted in prolongation of AP plateau. When Ca²⁺ concentration in subSL region was elevated, it activated NCX to extrude Ca²⁺ ions, thus causing a net inward current. This inward I_NCX resulted in prolongation of the plateau. We confirmed the contribution of NCX by artificially clamping the current magnitude to its control case and observing its effect on AP plateau for various Ca²⁺ diffusion velocities. Recent experiments in isoproterenol-stimulated murine VMs with RyR₂ mutations showed that random bursts of prolonged Ca²⁺ release activated NCX, which triggered low-plateau voltage EADs, with plateau voltages comparable to murine PCs.³⁰ Furthermore, experiments conducted using selective NCX inhibitors ORM-10103 and SEA0400 have reported successful suppression of EADs and DADs, in canine VMs and PCs.^31,32 Our results are in agreement with these experimental studies and provide further insights in the role of NCX in EAD- or DAD-induced arrhythmias originated in PCs.

Limitations

Our model assumes that the SR is situated symmetrically at the center of the cell and is uniformly divided into 10 subcompartments. The exact location and distribution of the SR in PCs is largely unknown and warrants further experimental evidence to faithfully implement it. Further, our model does not differentiate between the Ca²⁺ release mechanisms of IP₃ receptors and ryanodine (RyR₂ and RyR₃) receptors as suggested in the study by Stuyvers et al.¹⁶ Instead, a basic two-dimensional spatiotemporal diffusion was implemented in our model to study the effects of collective cytosolic Ca²⁺ diffusion. Finally, our model does not account for the influence of stochasticity in RyR gating and fluctuations driven by stochastic Ca²⁺ release.^33–37 As highlighted in the studies by Stuyvers et al.¹⁶ and Boyden et al.¹², the biphasic nature of Ca²⁺ transients involves both spatial aspects of Ca²⁺ diffusion and spontaneous SR Ca²⁺ release. In order to avoid the complexity and variability of a stochastic model, we artificially triggered SR Ca²⁺ release from one cell end, such that we could focus on the regulatory role of Ca²⁺ diffusion in Ca²⁺ dynamics and subsequent influence on electrophysiology. Future work will investigate these issues by incorporating a stochastic RyR gating model for SR Ca²⁺ release. Notwithstanding these limitations, the model was able to reproduce the experimental observations and provided significant insights in the role of Ca²⁺ diffusion in shaping the AP of PCs.

Conclusions

The study used a morphologically detailed numerical model of murine PC integrated with a spatiotemporal cytosolic Ca²⁺ diffusion process to study a possible mechanism of AP abnormalities, which could lead to arrhythmia. The PC model successfully reproduced the distinct Ca²⁺ dynamics and the AP morphology reported in experiments. It was observed that cytosolic Ca²⁺ diffusion waves in PCs characterized their peculiar AP morphology. The faster Ca²⁺ diffusion produced biphasic transients in the subSL region, which led to the prolongation of the AP plateau. Detailed analysis revealed that the AP prolongation at faster diffusion was mediated via inward NCX current. Our simulation results provide valuable insights in the mechanisms of increased propensity to AP abnormalities in cardiac PCs when compared to VMs.