A Flexible Analysis Tool for the Quantitative Acoustic Assessment of Infant Cry

Abstract

Purpose

In this article, the authors describe and validate the performance of a modern acoustic analyzer specifically designed for infant cry analysis.

Method

Utilizing known algorithms, the authors developed a method to extract acoustic parameters describing infant cries from standard digital audio files. They used a frame rate of 25 ms with a frame advance of 12.5 ms. Cepstral-based acoustic analysis proceeded in 2 phases, computing frame-level data and then organizing and summarizing this information within cry utterances. Using signal detection methods, the authors evaluated the accuracy of the automated system to determine voicing and to detect fundamental frequency (F₀) as compared to voiced segments and pitch periods manually coded from spectrogram displays.

Results

The system detected F₀ with 88% to 95% accuracy, depending on tolerances set at 10 to 20 Hz. Receiver operating characteristic analyses demonstrated very high accuracy at detecting voicing characteristics in the cry samples.

Conclusions

This article describes an automated infant cry analyzer with high accuracy to detect important acoustic features of cry. A unique and important aspect of this work is the rigorous testing of the system’s accuracy as compared to ground-truth manual coding. The resulting system has implications for basic and applied research on infant cry development.

Acoustic analysis of infant cry has been a focus of clinical and developmental research for a number of decades. A variety of approaches to cry analysis have been employed, but each has its drawbacks. Over time, advances in computing have allowed for increased power and flexibility in acoustic analysis, including the ability to utilize robust techniques for the accurate estimation of fundamental frequency and other acoustic features of cry vocalizations. This article describes the development and validation of a modern tool for the acoustic analysis of infant cry.

Applied and clinical studies of infant cry have examined features of cry production that may discriminate babies with specific conditions or medical risks. For example, there has been considerable interest in utilizing infant cry analysis as a measure of developmental status in babies with pre- and peri-natal risk factors, such as prenatal substance exposure (e.g., Lester et al., 2002) or premature birth (e.g., Goberman & Robb, 1999). There has also been interest in utilizing infant cry to identify babies at risk for developmental or medical conditions including hearing impairment (Várallyay, Benyó, Illényi, Farkas, & Kovács, 2004) and, recently, autism spectrum disorders (Esposito & Venuti, 2010; Sheinkopf, Iverson, Rinaldi, & Lester, 2012).

Early studies in this area relied on visual inspection of sound spectrograms in order to describe acoustic features of the cry in specific clinical populations (e.g., Karelitz & Fisichelli, 1962; Lind, Vuorenkoski, Rosberg, Partanen, & Wasz-Hockert, 1970; Prechtl, Theorell, Gramsbergen, & Lind, 1969; Vuorenkoski et al., 1966). Manual inspection of spectrograms has been seen as a gold-standard method for detecting acoustic features in cry sounds, including the timing and onset of cry vocalizations and the fundamental frequency (F₀) of cry. Such visual inspection has also been used to describe melodic variations in F₀ across an utterance, and voicing or periodicity in the cry utterance. However, although these manual approaches have the advantage of being able to robustly detect F₀, the trade-off is that the process is slow, limiting the amount of data that can be analyzed in any one study.

More recent approaches have utilized computer-assisted methods or commercially available speech analysis software packages to code acoustic aspects of infant cry. For example, one approach uses a computer cursor that is moved along a digitally displayed sound spectrogram to quantify aspects of cry duration and selects locations on the spectrogram for acoustic analysis (Goberman & Robb, 1999; Grau, Robb, & Cacace, 1995; Wermke & Robb, 2010; Zeskind & Barr, 1997). In this way, resulting portions of the cry can be subjected to a fast Fourier transform (FFT) to yield information from the power spectrum in the cry (e.g., maximum/minimum F₀). As we noted previously, abstracting quantitative data from spectrograms by this method is time consuming (LaGasse, Neal, & Lester, 2005). In addition, these approaches utilize speech analysis tools that were designed to extract acoustic information from adult speech. Given the anatomical differences in the vocal tract of infants, there is a need for tools designed to track and extract the F₀ and other acoustic features from infant cries specifically. Finally, advances in computing capacity now allow researchers to utilize methods for quantifying aspects of the sound spectrum that can be expected to yield more accurate estimates of F₀ and related parameters.

Automated approaches have the advantage of fast analysis of very large data sets, objective assessment, the ability to quantify multiple data points, and the flexibility to yield derivative measures (e.g., jitter, pitch contours, etc.), which have the potential to increase the applied value and clinical utility of cry assessment. These advantages notwithstanding, past automated approaches have also suffered from weaknesses due to limits in computing power. This has resulted in, for example, difficulties in signal detection and in not being able to pinpoint important cues when multiple analyses are required to do so. Automated detection of the F₀ of infant cry is a difficult challenge, and the accuracy of F₀ detection has not been fully reported in many approaches.

There are multiple challenges to the design of an automated acoustic analysis of infant cry. Past researchers have developed automated analysis systems intended for the quantification of cry acoustics in larger samples of babies and with a method that minimizes the need for visual inspection or manual processing of data. For example, researchers have utilized automated application of FFTs to detect F₀ in cry utterances or across whole cry episodes (Branco, Fekete, Rugolo, & Rehder, 2007; Corwin et al., 1992; Lester et al., 1991). In this general approach, digitized and filtered samples are subjected to an FFT in order to compute the log magnitude spectrum for analysis blocks of specific lengths (e.g., 25 ms). Summary variables for each analysis block can then be aggregated to yield summary statistics for a cry episode and for the individual cry utterances (a single expiratory period) within cry episodes (a series of expiratory periods).

Alternative automated approaches have also been recently described. Manfredi and colleagues (Manfredi, Bocchi, Orlandi, Spaccaterra, & Donzelli, 2009; Manfredi, Tocchioni, & Bocchi, 2006) have described a method that utilizes simple inverse filter tracking (SIFT) of short, fixed-length analysis frames followed by adaptive estimation of F₀ using 5- to 15-ms frames, varied in proportion to the changing F₀ of the signal. Várallyay et al. (2004) used what they termed a “smoothed spectrum method” to detect F₀ for the purpose of identifying infants with possible hearing loss.

These automated approaches have the potential to speed scientific inquiry, allowing for the study of large numbers of infants with efficient and rapid analyses. In addition, they bypass the need for manual inspection of spectrograms and do not require the time-consuming task of cursor placement and frame selection used in some computer-assisted methods. In this way, automated approaches allow for more rapid analysis that is less prone to observer bias or coding errors. Also, because these systems were developed specifically for the study of infant cry, there is the assumption that these algorithms accurately track F₀ and differentiate voiced from unvoiced utterances. However, with the exception of a study of the efficiency of F₀ detection by Várallyay et al. (2004), formal studies of the actual accuracy of measurement have not been conducted. Moreover, the automated approaches described above often utilize older signal processing approaches (FFT, SIFT). More modern approaches may now be employed given advances in computing power.

In this article, we describe the development and validation of a cry analysis tool that utilizes robust methods for voicing determination along with a cepstral analysis for the detection and tracking of F₀. Investigating the validity of automated acoustic assessment of cry can be thought of as studying the sensitivity and specificity of an automated method of detecting the signal periodicity that constitutes F₀. We have developed a new, robust tool for extracting acoustic information from digitally recorded infant cries, and we evaluated its validity by describing the sensitivity and specificity of the automated system to detect F₀ (pitch periods) in comparison to the pitch periods manually coded by a trained observer from a sound spectrogram (oscilloscope view). In addition, we describe a method for categorizing voiced versus typically short, unvoiced utterances, or segments of utterances that are unvoiced. This includes a quantification of the confidence of the voicing determination, which can be adapted by researchers depending on the scientific questions being addressed. Finally, we describe the detailed output from this system that can be easily subjected to statistical analysis for hypothesis testing. This system is detailed and flexible enough to allow researchers to describe infant cries at the utterance level while also producing detailed frame-by-frame acoustic output.

Method

In developing our analysis tool, we began by defining the range of measures or outputs that we wanted to examine, basing this list on prior cry analysis work. These included parameters to characterize F₀, amplitude or energy of cry, timing variables (latency, onset, duration, interutterance interval, etc.), and formants (while acknowledging difficulty in measurement). In addition to the kinds of variables used in prior automated analyses, we also had the aim of using the F₀ tracking to model the shape or contour of F₀ across each cry utterance in a cry episode. This would be similar to the studies of cry melody in some past research, such as Wermke, Leising, and Stellzig-Eisenhauer (2007), in which F₀ was characterized as rising then falling, or having other contours across a cry utterance.

Acoustic characteristics of infant crying are determined by the complex interplay of neural, physiological, and anatomical factors manifested in the properties of the driving function of the cry (Newman, 1988). Notably, periodicity of the glottal motions determines properties such as the pitch or the amount of voicing/excited turbulence in a cry. The shape of the vocal tract determines the resonant frequencies (formants) of the spectrum of the cry at a given instant. Important acoustic properties of infant cry include F₀, defined as the fundamental frequency of the glottal excitation (vibrations of the vocal folds), and the formant frequencies, defined as resonances of the vocal tract. Non-vocal-fold driven turbulences need also to be detected and categorized in a suitable analysis system.

Our system is run as two sequential programs: Phase I analyzes the digitized data to produce a set of parameters for each consecutive 12.5-ms frame. Phase II takes the Phase I output as input and produces an output record for each consecutive group of frames that has similar properties. The analysis tool is currently implemented in MATLAB, but it is easily adaptable for any embedded processor. The analyzer assumes the input is a .wav file, sampled at 48 ks/s with 16 bits per sample (768 kbits/s). Using these high sampling and quantization parameters ensures that all cues are captured and that there is sufficient headroom for dynamic range differences. In this study, we recorded cry samples using an Olympus DM-520 digital voice recorder (Olympus Imaging America, Inc., Center Valley, PA). This standardized input format can easily be replicated in other studies.

Phase I takes the .wav files and produces a comma-separated value (CSV) file that is readable not only by the Phase II program but also by programs such as Microsoft Excel. In the first phase of the analysis system, all outputs relate to the unit of a fixed-length, fixed-advance frame described by 22 numerical parameters. Thus, because each number has a 32-bit representation, this implies a data rate of only 56.32 kbits/s, a significant reduction. The first two lines of each Phase I output file are headers. The fields for the header record are defined in Table 1. We needed to address the fact that there are many useful (older) infant cry samples that have been recorded on analog tape. However, the recording quality of these tapes may vary. Thus, a preliminary automatic scan of a digitized recording has been designed to ascertain a recording’s quality based on background noise—usually hum and signal-to-noise ratio (SNR; as determined by an average amplitude for high-energy events to the amplitude of easily identifiable “silence” regions)—and a detection of saturation at some phase of the recording process. The mean value of the recording, an estimate of the dynamic range, and a classification of the quality of the file (high quality, noisy, low level, analog saturated, digital saturated) are all put into the header file for the Phase I system. The rest of the output file consists of fixed-length records, one record per frame, as defined in Table 2.

Table 1.

Initial header record definitions.

Field	Definition
1	Phase I or Phase II (text)
2	Subject (text)
3	Subject description (text)
4	Number of zero frames
5	Mean value of recording [0, 32767]
6	1% dynamic range (dB)
7	1% dynamic range [0, 32767]
8	5% dynamic range (dB)
9	5% dynamic range [0, 32767]
10	10% dynamic range [0, 32767]
11	10% dynamic range [0, 32767]
12	Quality class

Table 2.

Phase I: Definition of fields of per frame record.

Frame record	Field
1	Frame number
2	Time (ms)
3	F0 (Hz)
4	F0 amplitude (dB)
5	F0 confidence [0, 1]
6	Hyper-pitch (Hz) ([1, 5] kHz range)
7	Hyper-pitch amplitude (dB)
8	Hyper-pitch confidence [0,1]
9	Peak pitch amplitude (dB)
10	Overall amplitude (dB)
11	Amplitude [0.5, 10] kHz (dB)
12	Amplitude [0, 0.5] kHz (dB)
13	Amplitude [0, 5, 1] kHz (dB)
14	Amplitude [1, 2.5] kHz (dB)
15	Amplitude [2.5, 5] kHz (dB)
16	Amplitude [5, 10] kHz (dB)
17	F1 (Hz)
18	Amplitude of F1 (dB)
19	F2 (Hz)
20	Amplitude of F2 (dB)
21	F3 (Hz)
22	Amplitude of F3 (dB)

We use a fixed-frame rate of 1,200 samples (25 ms) with a frame advance of 600 samples (12.5 ms) to keep reasonably high resolution in both time and frequency. Given today’s technology, the analysis system was designed to be liberal with its use of computation so as to reflect resultant parameters more accurately. Thus, three discrete Fourier transforms are computed for each 1,200-point frame. The middle 768 points are transformed for the F₀ estimate as explained below. The full frame (1,200 points) is transformed for amplitude computations, and an interpolated transform of 4,096 points (1,448 zeros, the 1,200 point frame, and 1,448 zeros) is used to detect F₀ above 1 kHz (what we term hyper-pitch).

The Phase II program takes the Phase I data as input and reduces the data further, separating them into groups of frames having similar properties, which we call sound segments. The CSV output has a record for each of these groups of frames. The concatenated groups of frames are labeled to be one of the following classes:

1. silence

2. short utterances (length < 0.5 s, relatively high energy)

3. long utterances (length > 0.5 s, high energy)

The output from Phase II contains information summarizing utterance-level characteristics of infant cries, and thus the Phase II output is expected to be most useful for studies of crying in various infant populations. Phase I accuracy has been carefully tested for this article because it is upon this phase that the validity of the summary output rests.

Phase I System

There are several approaches that can be used for pitch detection, and the more common of these methods are based on (a) time-event rate detection (Ananthapadmanabha & Yegnanarayana, 1975; Rader, 1964; Smith, 1954, 1957), (b) autocorrelation methods (Dubnowski, Schafer, & Rabiner, 1976; Gill, 1959; Rabiner, 1977; Stone & White, 1963), and (c) frequency domain methods. Time-event rate detection methods are based on the fact that if an event is periodic, then there are extractable time-repeating events that can be counted and the number of these events per second is inversely related to the frequency. Autocorrelation methods are used as a measure of the consistency or sameness of a signal with itself at different time delays; the peak of the time-delay value is returned as the pitch period. Finally, frequency domain approaches include methods such as comb filters (filters in which a signal is subtracted from itself at different time-delay values; Martin, 1981), tunable infinite impulse response (IIR) filters (Baronin & Kushtuev, 1971), and cepstrum analysis (Bogert, Healy, & Tukey, 1963; Noll, 1967).

The time-event rate detection methods are extremely simple and easy to implement. However, they have immense difficulties dealing with spectrally complex signals such as human speech or a baby’s cry. The autocorrelation and the first two frequency domain methods are also more suitable for cleaner signals (e.g., sounds produced by musical instruments). Perhaps the method most widely used for obtaining F₀ for adult speech is cepstrum analysis. When applied correctly, it has proven to be a robust method for describing acoustic properties of noninfant vocalizations, and it should be suitable for the complex vocalic signals of infant cry. The resulting cepstral coefficients are the standard features for speech recognition algorithms. Accordingly, we have selected cepstrum analysis to develop the cry analysis algorithm in this project.

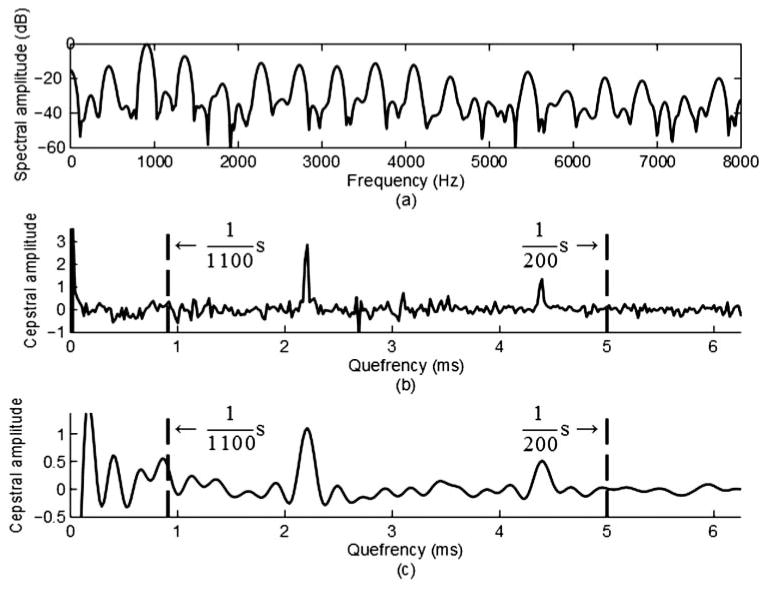
It is accepted that a normal infant cry F₀ range is 200 Hz to 1 kHz, or a pitch-period range of 5 ms to 1 ms. Because pitch-period estimates are obtained using a modified version of the cepstrum method (Noll, 1967), several pitch periods are required within each frame to make the short time frame appear periodic. Thus, to get a minimum of three pitch periods (and a “nice” number for an FFT), we selected a fixed frame of 768 points (or 16 ms for 48 kHz sampling) of each 1,200-point frame and a 768-point Hamming window. A larger window will cause the cepstral pitch peak to broaden for the higher F₀ values, and a smaller window will not have as good cepstral peaks for low values of F_0. The Hamming window will broaden the harmonic peaks but eliminate most the effects due to sidelobe accumulations. This analysis strategy was decided upon in order to capture four to eight pitch periods per frame. Given the nature of infant cry, greater frame lengths would decrease the reliability of pitch-period estimation. Thus, we had to modify the basic technique in order to compensate for the unique characteristics of infant cry. The first change was to apply a frequency window W[r], effectively limiting the band to be considered to be from 200 Hz to 2200 Hz to the log-spectrum before computing the inverse discrete Fourier transform (IDFT). Because energy in voiced speech naturally falls off after 4 kHz, the spectral harmonic structure is amplitude modulated by the roll-off function, which can cause multiple peaks in the cepstrum when the sampling rate exceeds 8 kHz. Applying a frequency window smoothes the cepstrum, eliminating these modulation effects. The window also deemphasizes low- and high-frequency noise. The effects of the frequency window are depicted in Figure 1, specifically in Panel (c), in which the pitch period is easy to identify, although a second rahmonic is also evident (the term rahmonic refers to harmonics in the cepstral domain).

Figure 1.

Panel (a): An example of a voiced infant cry spectrum. Panel (b): Nonwindowed cepstrum of same frame showing range for inspecting for rahmonics. Panel (c): Windowed cepstrum showing range for inspecting rahmonics.

It is noted that infants generally do not double or halve their pitch frequency nearly instantaneously during voiced portions of a cry vocalization. Thus, by considering multiple frames at once, many F₀ doubling and halving estimation errors can be eliminated. We consider halving and doubling errors to be those that occur for one or two frames, which would imply very rapid changes in pitch frequency. It is these that we try to eliminate, not the longer doubling or halving regions that appear when even or odd harmonics disappear in the spectrogram. A dynamic-programming smoother is a reasonable mechanism to ensure continuity in the F₀ estimates at transitions and many other anomalies. This is not a new idea (Secrest & Doddington, 1982), although our implementation is specifically set up for infant cries. In our implementation, 50-frame blocks (0.625 s) are run through the dynamic-programming algorithm after determining F₀ and a confidence measure for independent frames. The last 50 frames of the recorded cry constitute the last block. As the number of frames is not likely to be divisible by 50, there is some special processing due to overlap for the last block. All negative cepstral values are truncated to zero, and the accumulated path metric is simply the sum of the 50 cepstral values built in the normal forward part of the dynamic-programming algorithm. The pitch period is allowed to change no more than plus or minus 20 cepstral points (0.416 ms) per frame. The backtracked path is used for the initial estimates for F₀. Following the dynamic programming, some further outliers (typically at utterance transitions) are eliminated using a standard five-point median filter. The result is pitch-period estimate q₀[i] for Frame i, and pitch frequency (Data Element 3 as in Table 2) is simply F₀ [i] = f_s /q₀[i], where f_s is the sampling frequency. Data Element 4, pitch energy, is the cepstral value of q₀[i], C[q₀[i], i].

Instead of using amplitude alone, the pitch-estimation system is also well suited for making voicing decisions for each frame. Data Element 5 in Table 2 is a pseudoprobability for voicing based on the cepstral analysis. For cepstrum C[q, i] and pitch-period estimate q₀[i], the traditional cepstrum method uses C[q₀[i]] as a measure of voicing. This measure has been found to fluctuate under different noise conditions, making it difficult to find a reliable threshold for a multi-environment system. Instead, we use an SNR-like measure to make a voicing decision. This measure is based on the height of the cepstral peak with respect to the cepstrum noise level. The window W [r] effectively smoothes the cepstrum of length N by a factor of D, where

$$D\equiv \frac{N}{{\sum }_{r=0}^{N-1}W[r]}.$$ (1)

This smoothing causes peaks in the cepstrum to have a width of approximately D + 1 samples. This information is used to compute the voicing confidence measure V, which is a function of C[q₀[i], i] and its surrounding. The cepstrum method searches for evidence of periodicity within a finite pitch-period range based on knowledge of human F₀ production. In this method, q_min and q_max are the minimum and maximum pitch- period (quefrency) indices in the search region. These are fixed and do not vary with the frame index i. The voicing-detection algorithm begins by zeroing out all negative C[q] values and all values outside the region q∈ [q_min, q_max] in the cepstrum C[q, i]. This nonnegative cepstrum is denoted as Ĉ [q, i], and let D̂ = ⌠D⌡. Pitch-period estimate q₀[i] is chosen to correspond to the maximum value of Ĉ [q, i], as is done in the traditional method. Then, the voicing confidence V [q₀[i], i] is defined as

$$V[q_0[i],i]=\frac{{\sum }_{r=1}^R{\sum }_{i=-\widehat{D}}^{\widehat{D}}(\widehat{C}{[r·q_0[i],i)}^2}{{\sum }_{j=q_{min}}^{q_{max}}{(\widehat{C}[j,i])}^2},$$ (2)

where R is the number of rahmonics to include. It was found that R = 3 was sufficient, because larger rahmonics were often insignificantly small.

V [q₀[i], i] is a number between 0 and 1. Values of V [q₀[i], i] corresponding to high-quefrency (low-frequency) pitch-period estimates tend to have smaller magnitudes because fewer rahmonics fall within the search interval [q_min, q_max]. The decision threshold, α [q₀[i]], depends linearly (from 0.7 at q_min to 0.5 at q_max) on the index of the current pitch-period estimate q₀[i]. In the Phase II program, a frame would be labeled as voiced if V [q₀[i], i] ≥ α[q₀] perhaps along with some amplitude criteria.

$$\alpha [q_0]\equiv \frac{0.2}{q_{max}-q_{min}}(q_{min}-q_0)+0.7$$ (3)

In addition to being more robust to different noise conditions, V [q₀[i], i] also protects against doubling errors by including the magnitude of cepstral content away from the peak. Although doubling errors will not be corrected by using this method, it was ultimately found that ignoring such difficult frames by labeling them unvoiced was sufficient for the task at hand.

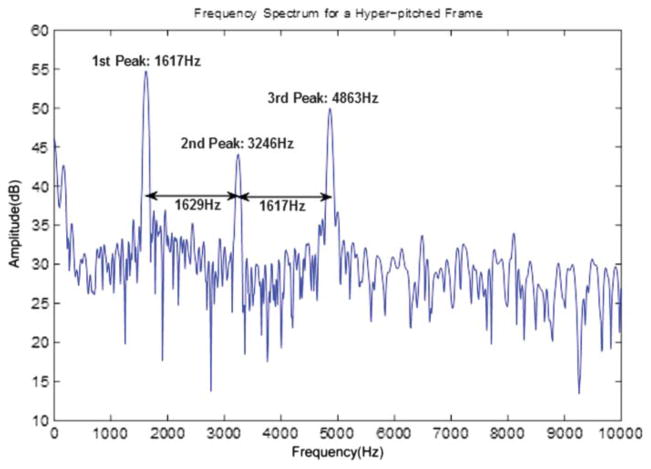
There is a mode in an infant’s cry when the fundamental frequency is above 1000 Hz, which we call hyper-pitch (Golub, 1989; LaGasse et al., 2005). Thus we attempt to determine a set of hyper-pitch values for each frame. We use a Hamming-windowed 4,096-point DFT with the full 1,200-point frame data in the center of inserted zeros to compute an interpolated spectrum and search its log magnitude for peaks in the range of 1000 Hz to 5000 Hz. The highest peak P[1] in the range is found first, and, because the lowest hyper-pitch is 1000 Hz, the spectrum is masked from max[1000, P[1, i] – 1000] to min[5000, P[1, i] + 1000] and searched for another peak. This process is repeated until three such peaks have been found P[k, i], where k denotes the individual elements of the set of three peaks (kε [1, 3]). The set is then reordered to be left to right as P̂ [k, i]. It is hypothesized that the three peaks form some harmonic set, and the frequency differences are taken, yielding a hyper-pitch value Fhp[i] = 0.5(P̂ [3, i] – –P̂ [1, i]). If only two peaks can be found, then F_hp[i] = P̂ [2, i] – –P̂ [1, i]. There is a special case when the hyper-pitch is about 1000 Hz and the odd harmonics dominate. In this case, the minimum difference between peaks is taken as the hyper-pitch frequency. An example of a spectrum for a frame driven by hyper-pitch is shown in Figure 2.

Figure 2.

An example of the spectrum of a hyper-pitch-excited frame and the cues from the peaks.

The hyper-pitch energy (seventh value in the record) is simply taken as the average of the fundamental hyper-pitch value and two of its harmonics. It is not necessarily that of the average of the peaks. The hyper-pitch confidence (eighth value in the record) is determined in a similar fashion to that of the confidence in the normal pitch range. It is a number between 0 and 1 that correlates well with the validity of the hyper-pitch condition being active in the frame. For this result the power, A, not the log power, is accumulated for the range 1000 Hz–5000 Hz, and the power in the detected peaks, B (up to four in the range), is also accumulated. The power for a given peak is accumulated over about 30 interpolated points or about 360 Hz about the peak. The ratio B/A is the confidence measure.

Fields 10 to 16 of the record give the amplitudes in dB for the entire band and for the six subbands listed above. The full Hamming-windowed 1,200-point DFT output is used to accumulate the power in each prescribed band (and overall). Those values are directly converted to dB without any normalization. Thus no information is lost, but differences in recording levels, distance from the microphone, and other aspects of sound acquisition will also affect these data. However, keeping nonnormalized data allows the Phase II system to consider the recording conditions when making its decisions.

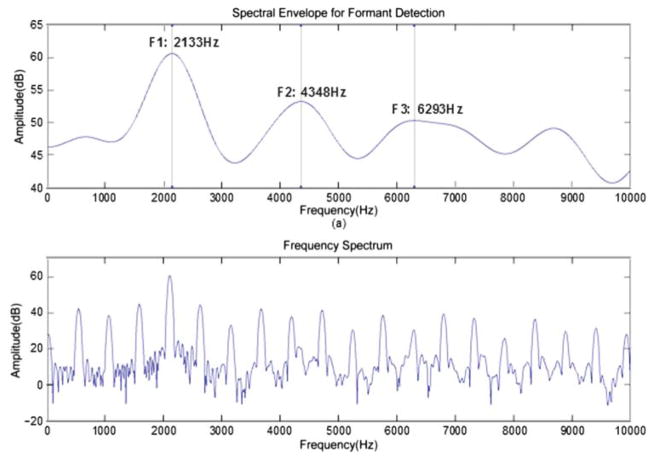
As has been stated, the determination of formants is a very difficult problem for analyzing infant cries because of the high pitch of the cries and thus the sparse harmonics. Formant positions can be estimated, but their precise central values, if somewhat distant from a pitch harmonic, may be hard to obtain. To estimate formants as accurately as possible, we use the interpolated 4,096-point DFT data. After obtaining the log-magnitude spectral data, we apply a low-pass “lifter” to the data, whose parameters depend upon the pitch value. Then substantial peaks in the smoothed data are taken for the formant positions and the heights of the peaks are taken for the magnitudes. Figure 3 shows a typical voiced frame. In Panel (a) the smoothed spectrum is shown, whereas in Panel (b) the unsmoothed spectrum is given. The formant positions and their magnitudes take up the last six positions in each record. One should note that the third formant is more arbitrary than the first two and for this reason has really not been used yet in our follow-up work.

Figure 3.

An example of the smoothed function for the determination of formant positions; there is strong influence from the harmonics of F₀.

Phase II

Because this article is meant to describe the Phase I part of the analyzer and validate this first extraction of infant cry data, the Phase II analyzer is only described somewhat briefly. Phase II output starts with two header records, the first being the same one as the Phase I header with the first field changed to read “Phase II.” The second contains the 81 Phase II column headings. (Specific definitions of the fields are given in the supplementary material at www.lems.brown.edu/array/download.htm.) The first step in the Phase II processing utilizes the recording quality classification that is contained in the header information from the Phase I prescan. When running Phase II, the user defines which quality classes should be used, and Phase II processing is then performed only on recordings with quality classifications that have been entered by the user. The Phase II data output consists of records, each of which describes a sound segment, where a sound segment is a group of consecutive frames that are similar. The Phase II analyzer takes in the Phase I data and produces an output .csv file with sound segment records of size 81 and an average rate of about 3 sound segments per second. Thus the data rate, using 32-bit numbers, is reduced by a factor of about 7 to 7,776 bits per second. In Phase II, the user makes decisions, the most fundamental of which have to do with the partitioning into these utterances.

The output contains one 81-element record for each of the three sound segment types that were defined previously, long utterance, short utterance, and silence. (The specific field definitions are available in the supplementary material; see above.) All 81 fields are filled for long utterances, and appropriate fields are filled for the other types. The 81 fields quantify file ID and five various classifier outputs, eight timing parameters, six F₀ parameters, five hyper-pitch parameters, 13 formant parameters, 15 parameters from fitting a polynomial to the pitch contour, and 28 parameters for amplitudes from several octave frequency bands. The segmentation is obtained by K-means clustering the 500-Hz to 10-kHz amplitude (dB) data into three classes in a prescan of the whole recording and using the results to classify each frame as one of three classes: 1 = low energy, 2 = transition energy, and 3 = high energy. The important long utterances consist of a contiguous sequence of frames that each has a 500-Hz to 10-kHz amplitude (dB) classified as in the high-energy cluster with a high F₀ confidence. Using these frame labels, the change in energy to help with the boundaries, and some extension rules, the partitioning is determined. If a contiguous sequence of high-energy frames is longer than 0.5 s (40 frames), a long utterance is created. If only the length criterion is not met, then that sequence is classified as a short utterance, and if the sequence is of low energy, then the sequence is called a silence. The operational definition of a long utterance is consistent with prior research on infant crying (LaGasse et al., 2005) and allows for analyses of utterances produced in different types of cries (e.g., initial utterances of pain-induced cries can be expected to be longer than 0.5 s, but cry utterances produced in different contexts may be shorter). In our work with sound files of adequate quality, there has been virtually no mis-labeling of low-energy cry information as silence.

Many infant cries are very intensive, with a large amount of frication in the high-energy long utterances. This can be found in our system by seeing if there is very high energy for a frame but low F₀ confidence; the extra frication-sounding energy for this frame tends to mask the cepstral detector. We call this phenomenon voiced frication and extract pertinent information about it for the Phase II output. Also, many infants exhibit a short air-intake noise—audible inspiration that typically follows a long cry and/or one produced by an infant under duress—immediately after a long utterance. If sufficiently close (in time) to the end of a long utterance, this period is included in the long utterance but specifically noted as a classifier for the long utterance. An audible inspiration of this type is likely to be perceived as a part of the cry utterance. The use of this classifier retains the full length of the utterance while also allowing for the user to examine utterances with this classifier separately. Although the third formant is very suspect, it has been included. Because the contours of the F₀ data within an utterance are important, we approximate these contours by a polynomial fit. Using an information-theoretic criterion, we estimate the best order to use for this model. This number is often large, approaching 20 or more. We then restrict the fit to be of order five or fewer, and the best fit is often of the third or fourth order. All the polynomial fitting is done on the F₀ data. The class field is a number (1 to 10) descriptor of the shape of the fit: rising, falling, flat, double peak, and so forth. The final 28 fields contain information on the amplitudes. Again, these values have not been normalized in any way. Each of the sound segment–level statistics has been calculated by going back to the power domain, accumulating properly over the frames of an utterance, and then transforming back to dB.

Validation of Pitch-Estimation and Frame Voicing-Decision Algorithms

Interpreted results from older analysis systems most often indicate that timing—lengths and spacing of utterances—F₀, and voicing are highly informative features of infant cry production. Moreover, other features of infant cry, such as the contours of F₀ across utterances, are dependent on the accuracy of F₀ estimation. Therefore, an experiment was conducted to evaluate the performance of the voicing-detection and pitch-estimation algorithm. We identified cry recordings recorded previously in an ongoing longitudinal study (Lester et al., 2002). Cries were elicited and recorded using procedures approved by the hospital institutional review board (IRB). The IRB also approved access to these archival recordings for the purpose of the analyses reported in this paper. Recordings were made of cries elicited by standard methods (LaGasse et al., 2005) from typically developing infants at 1 month of age. Cries were elicited by a specially designed device that applied a painful stimulus (analogous to a rubberband snap) to the sole of the right foot while babies lay supine in a stroller with a unidirectional microphone suspended at a standardized distance above the baby (5 inches). Cry samples were selected from an existing longitudinal data set. A total of 15 cries from 15 individual babies were evaluated, each sample containing between 36 and 42 s of cry data. We coded and analyzed only cries characterized by intense, loud, rhythmic, and sustained vocalizations that were differentiated from brief cries and fusses characteristic of lower states of arousal.

These cries were selected on the basis of the infants being the products of full-term normal pregnancies and receiving scores within normal limits on later assessments of developmental functioning (e.g., Bayley Scales of Infant and Toddler Development [Bayley, 2005] at 24 months of age). Recordings were made in a quiet and controlled setting at a hospital-based developmental assessment center, and thus the recording quality was high and background noise was minimal. Recordings were sampled at 48 kHz with the Olympus direct PCM recorder described above.

Establishing ground truth

Ground truth was established for both the presence of voicing and the corresponding F₀ by hand-labeling each cry. Pitch-frequency labels were obtained by hand-marking pitch-period intervals from the time-domain plot of the cry waveform. For this purpose we utilized a software program developed in our lab that conveniently displays both time and frequency plots from .wav files (Silverman, 2011). All labels were affixed by a single person trained to affix time markers at the high-energy peaks that generally allow the denotation of a pitch frequency. Pitch-period labels were affixed for regions of each cry recording determined to be clearly voiced.

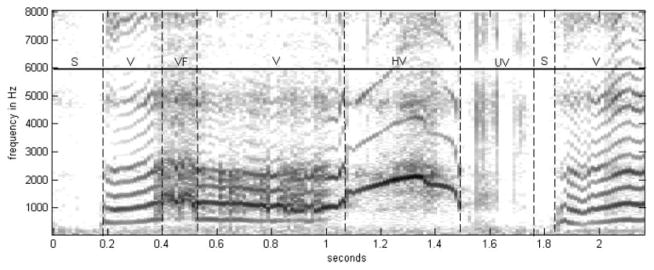
The intervals of voicing were also hand labeled using a spectrogram plot, as shown in Figure 4. Intervals were first marked at the frame level, indicating that the region about that particular 12.5-ms frame advance was voiced. Then, the regions indicated by the labels on the frames as voiced were fine-tuned to indicate specific interval types at the resolution of the sampling time by viewing the corresponding time-domain plot. Five different interval types were defined: voiced (V), unvoiced (UV), silence (S), voiced frication (VF), and high voicing (HV). An interval was labeled as V if the spectrogram showed a well-defined harmonic structure, indicating periodicity. An interval was labeled as UV if the spectrogram showed significant energy without the presence of harmonics. S intervals showed very low signal energy. The VF label was assigned when an interval exhibited a harmonic structure in addition to turbulent (frication) noise at nonharmonic frequencies. VFs were given a separate label because it is unclear whether such frames should be labeled as V or UV. Finally, the HV label was assigned to intervals with a very sparse harmonic structure, indicating a very high fundamental frequency (greater than 1 kHz), which we have called hyper-pitch–excited frames.

Figure 4.

Ground truth for voicing type was established by hand labeling a spectrogram plot. Intervals were labeled as voiced (V), unvoiced (UV), silence (S), voiced frication (VF), or high voicing (HV).

Table 3 shows the number of frames in the data set corresponding to each of the five voicing classes. The infant cries in this data set consisted mainly of voiced speech. Examples of the HV and UV classes occurred quite infrequently.

Table 3.

Number of frames in the data set, labeled with each of the five voicing classes.

Voicing class	# of frames
Voiced (V)	27,745
High voiced (HV)	92
Unvoiced (UV)	3,155
Voiced frication (VF)	560
Silence (S)	13,638

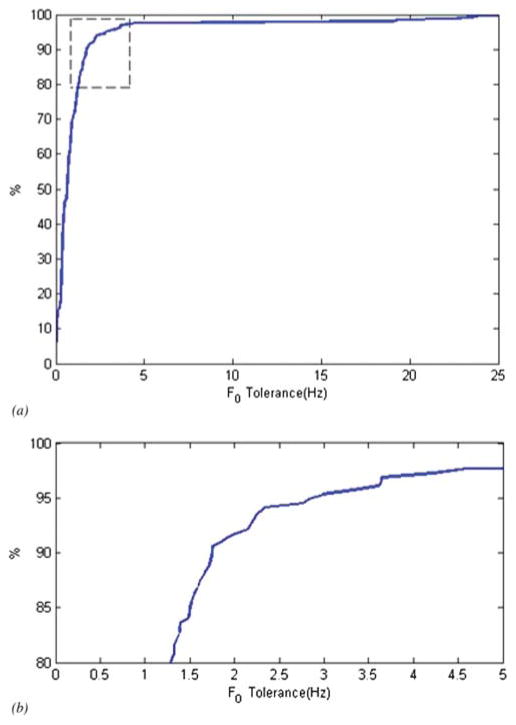
The labeling was conducted by a research assistant who was first trained to understand the kinds of patterns that should be labeled and then trained to criterion level of accuracy by the first author. Once the labeler’s accuracy was confirmed on a series of training samples, she then hand coded the cry samples as described above. It was these hand-coded cry samples that were used as the gold standard or ground truth for subsequent analyses of the accuracy of the automated system. Each frame required the careful labeling of 4 to 15 (or more if hyper-pitch) F₀ onsets, and some 2,915 frames were hand labeled. To cross-validate the hand-labeled ground truth, the author (X. L.) used the same criterion to hand label a little less than 10% of the frames (256). The receiver operating characteristic (ROC) curve and an expansion of the “knee” part of the curve are shown in Figure 5. It may be seen in this figure that about 92% of the ground-truth data agree with the data labeled by X. L. within a 2-Hz tolerance and that there is 98% agreement within a 5-Hz tolerance. We are thus quite confident in our ground-truth data.

Figure 5.

Panel (a): Receiver operating characteristic (ROC) curve showing agreement between ground-truth hand labeling and author X. L. hand labeling of about 10% of data used in the validation. Panel (b): Expanded graph of the dotted area of Panel (a).

Fundamental frequency

The results presented here demonstrate the accuracy of the F₀ estimation algorithm. The ground-truth labels were placed at sample indices of consistent peaks bracketing each pitch period during clearly voiced cries. There are clearly multiple pitch periods in each voiced frame. The sample indices were compared with the frame boundaries used by the analysis system to find all frames that were 100% covered by the pitch-period labels. The subset of frames for which hand-marked pitch-period labels were available is represented as v₀. The same set of cry recordings were processed by the analysis system, which output the set of estimated voiced frames v. The following analysis was carried out on v ∩ v0, the set of all frames for which the automatic voicing labels, v, and the ground-truth voicing labels, v0, agreed. The set v ∩ v0 contained a total of 2,915 voiced frames.

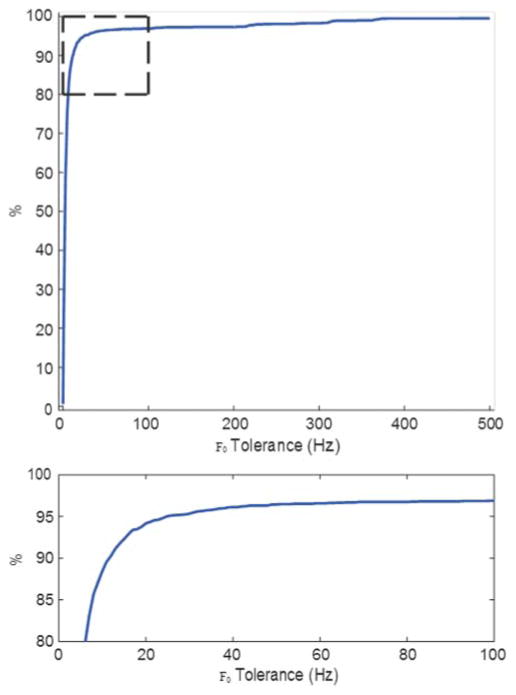
For each voiced frame in v ∩ v0, the magnitude of the error between the estimated pitch frequency, f, and the ground-truth pitch frequency, F₀, was computed. The pitch frequency estimate was considered to be correct if |f – F₀| ≤ T for some tolerance T in Hz. One should note that the quantization tolerance in the cepstral domain varies from about 1 Hz at F₀ = 200 Hz to about 5 Hz at F₀ = 1 kHz. Figure 6 shows the percentage of frames with correct pitch-frequency estimates corresponding to each pitch-frequency tolerance, T. Several operating points are also shown in Table 4. As can be seen, the automated F₀ detection had an accuracy of about 90% at a tolerance of 10 Hz and nearly 95% at a tolerance of 20 Hz. We did not see evidence for any systematic disagreement between the hand-coded and automated F₀ detection.

Figure 6.

Percentage of the 2,915 voiced frames with correct pitch-frequency estimates (|f – F₀| ≤ T ) for several error tolerances (T in Hz).

Table 4.

Percentage of the 2,915 voiced frames with correct pitch-frequency estimates (|f – f₀| ≤ T) for several error tolerances (T in Hz).

T (Hz)	% Correct frames
10	88.44
20	94.17
30	95.33
40	96.12
50	96.43

Voicing

A separate analysis was carried out to evaluate voicing-detection capabilities of the system. This analysis was formulated as a simple two-category classification problem, and Figures 7 and 8 give standard ROC curves showing the results. The two figures differ in that Figure 7 includes S frames, whereas Figure 8 does not.

Figure 7.

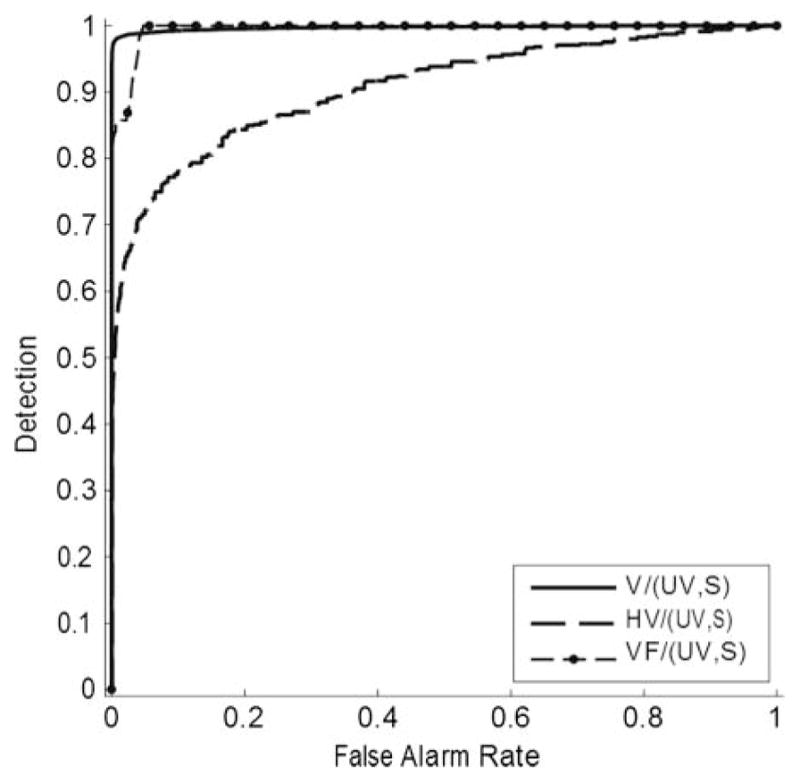
ROC curves giving the voicing-detection performance of the system. V, VF, and HV frames were separately considered to be positives. In each case, both UV and S frames were considered to be negatives. Area under the curve (Az) values were as follows: V/(UV,S) = .997; HV/(UV,S) = .907; VF/(UV,S) = .995.

Figure 8.

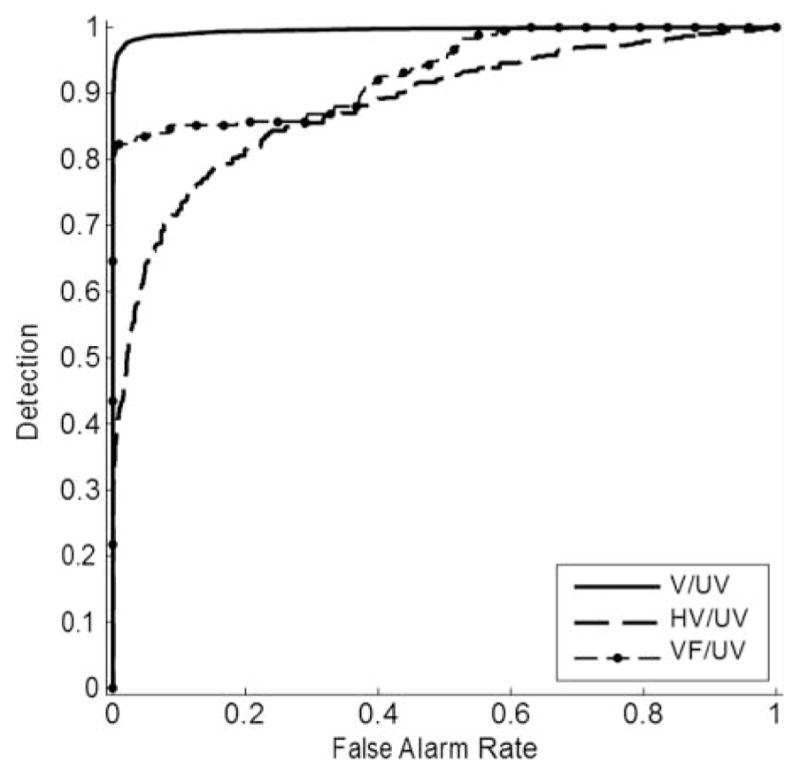
ROC curves giving the voicing-detection performance of the system. V, VF, and HV frames were separately considered to be positives. Only UV frames were considered to be negatives. Az values were: V/(UV) = .995; HV/(UV) = .883; VF/(UV) = .934.

Figures 7 and 8 show that the system is very effective in distinguishing V frames from UV and S frames. As expected, the system achieves much higher error rates when attempting to detect VF, which by definition is a mixture of voicing and turbulent signals. The HV frames were also more difficult to detect, although they occurred infrequently in this data set. Figures 7 and 8 include area under the curve (Az) values demonstrating accurate detection of V sound segments. Az values ranged from .907 to .997 for the analysis that included frames with S and .883 to .995 for frames that did not include S.

Conclusions

We have presented the details of a modern infant cry analyzer that can be run in near real time on a normal PC platform or could be run in real time on many of today’s embedded processors. The design is the result of 2 years of collaborative effort between hospital-based and engineering-based faculty at Brown University. The intent of this collaboration was to produce a system that would have utility for both basic and applied research on infant cry production. This system extends and builds upon recent approaches to quantifying acoustic features of infant cry (e.g., Branco et al., 2007; LaGasse et al., 2005; Lester et al., 1991; Manfredi et al., 2009; Várallyay et al., 2004). This automated system is described in detail in order to provide the reader and potential users with a clear understanding of the approach that we used to develop this system. In addition, and quite uniquely, we conducted stringent tests of the accuracy of this automated system as compared to hand-labeled cry spectrograms.

The analysis system has two levels of output. Phase I segments the sound into analysis frames with an advance of 12.5 ms. Each frame is summarized by the system for features that include timing, voicing, F₀, amplitude, and formant information. Phase II operates on the Phase I data, making decisions with regard to classifying portions of the sample as cry utterances or silence, which could be a portion of the recording prior to cry onset or could represent time periods between cry utterances. This timing information allows researchers to utilize measures such as latency to cry, which is of interest for researchers utilizing standard methods to elicit infant cries (LaGasse et al., 2005), and interutterance intervals, which may be useful for classifying different types of infant cries (e.g., pain vs. nonpain cries). In addition to this timing information, the Phase II output yields summary descriptors of cry utterances, including measures of F₀, amplitude of cry in various frequency bands, and estimates of formant location. This Phase II output also yields measures of the voiced proportion of each cry utterance. A unique aspect of this output is that it includes a confidence estimate for the voicing decision. This is based on an SNR analysis and allows the researcher both full information on how the voicing decision was made and the ability to modify this decision, should the research question call for a more- or less-stringent definition of voicing.

An additional unique feature of the Phase II output is an automated approach to describing F₀ contours across a cry utterance. Some past research has made use of this variation in F₀ across utterances to describe “melodic” aspects of cries, but it has accomplished this task by hand classification of F₀ contours from spectrograms (Mampe, Friederici, & Wermke, 2009; Wermke, Mende, Manfredi, & Bruscaglioni, 2002). The system described here utilizes a polynomial fit method to classify F₀ contours. Initially, the system classifies these contours into one of 10 categories. This output may be used to identify cry utterances with more or less prototypical contours, to characterize the complexity of such F₀ variation, or to explore differences in F₀ contours related to development or population differences. The validity of an automated acoustic analysis is dependent on its performance accuracy. Therefore, we conducted a substantial experiment that indicates the accuracy of both the voicing and the fundamental frequency detectors. The features that were selected, F₀ and voicing, are the ones that have proven to be most discriminating of clinical populations in past literature.

As depicted in Figure 6, about 90% of the automatic estimates were within a F₀ tolerance of 10 Hz. The best the estimator does is 96.4% when the tolerance is opened up a bit to 50 Hz. Virtually all errors occur at the boundaries of voiced utterances. Equal-error rates for voiced (vs. unvoiced or silence) frame detection is nearly 99%. Much more difficult to detect hyper-pitch frames are identified with an equal-error rate of about 80%. Past research utilizing automated analyses of infant cry has generally not reported this type of performance analysis. Furthermore, other computer-assisted methods have utilized analyzers designed for adult speech. Validation of a system specifically designed to summarize the acoustic features of infant cry is therefore an advance in the field and a unique strength of the study reported here. The results of our experiments revealed high accuracy of the automatic detectors of F₀ and voicing decisions in comparison to gold- standard hand coding from spectrogram displays.

Our careful experiment demonstrates that the analysis system yields an excellent reduced data representation of the desired acoustic features of babies’ cries. However, there are some areas of analysis that are a significant challenge for infant cry analysis. In particular, the accurate automatic detection of formants is quite difficult given the high pitch and wide harmonic structure of infant cry (Robb & Cacace, 1995). In adult speech, the shape of the vocal tract determines the resonant frequencies, which are described as formants. For our purposes, we applied a low-pass “lifter” to the data in order to assist in estimating the location and magnitude of formants in the infant cry. We have described this approach, but we acknowledge that the problem of both the measurement and interpretation of formants in infant cry remains to be fully resolved. An additional challenge is to reliably determine voicing in conditions that we refer to as voiced frication or high voicing portions of a cry utterance. These issues are a reflection of some of the conceptual and methodological challenges to infant cry analysis more generally. Thus, these issues notwithstanding, our interpretation is that this study reports a level of performance accuracy that is quite sufficient for both human and automatic interpretation of cries for various phenomena. For example, the automated nature of this analysis system makes possible rapid analysis for large data sets and thus studies of substantial numbers of subjects, allowing for more powerful studies of differences in infant cry associated with various medical or developmental conditions or populations. A highly unique aspect of this system is that it allows researchers to summarize broad characteristics of cry utterances using the Phase II output while also preserving detailed microanalytic data in the Phase I output that would allow for precise characterization of within-utterance variations in cry production.

A number of future directions for this research are possible: It can be applied to questions pertaining to possible individual or group differences in cry production that may help to screen for infants at risk for various developmental disorders, or it may find use in medical applications, such as identifying infants at risk for poor developmental outcomes. Thus, a validated cry analyzer will be useful for continued research on developmental outcomes in at-risk infants, including investigations of neurobehavioral outcomes associated with prenatal environmental risk factors. Moreover, the complex nature of infant cry acoustics has the potential to yield feature patterns that can be used to identify infants at elevated risk for poor developmental outcomes or specific developmental disorders such as autism spectrum disorders. More basic research may also utilize this system in order to study normative aspects of infant cry production with larger samples than has been possible in the past. To this end, we intend to make the MATLAB version available online at www.brown.edu/Departments/Children_at_Risk, so that the general community will have access to a high-quality infant cry analyzer. Future efforts will involve refining the analysis and output of this system, as well as developing a more user-friendly interface to enhance its accessibility for a variety of researchers.