A practical Bayesian stepped wedge design for community-based cluster-randomized clinical trials: the British Columbia Telehealth Trial

Abstract

Background

Many clinical trial designs are impractical for community-based clinical intervention trials. Stepped wedge trial designs provide practical advantages, but few descriptions exist of their clinical implementational features, statistical design efficiencies, and limitations.

Objectives

Enhance efficiency of stepped wedge trial designs by evaluating the impact of design characteristics on statistical power for the British Columbia Telehealth Trial.

Methods

The British Columbia Telehealth Trial is a community-based, cluster-randomized, controlled clinical trial in rural and urban British Columbia. To determine the effect of an internet-based telehealth intervention on health care utilization, 1000 subjects with an existing diagnosis of congestive heart failure or type 2 diabetes will be enrolled from 50 clinical practices. Hospital utilization is measured using a composite of disease-specific hospital admissions and emergency visits. The intervention comprises of online telehealth data collection and counseling provided to support a disease-specific action plan developed by the primary care provider. The planned intervention is sequentially introduced across all participating practices. We adopt a fully Bayesian, Markov chain Monte Carlo-driven statistical approach wherein we use simulation to determine the effect of cluster size, sample size, and crossover interval choice on Type I error and power to evaluate differences in hospital utilization.

Results

For our Bayesian stepped wedge trial design, simulations suggest moderate decreases in power when cross-over intervals from control to intervention are reduced from every three weeks to two weeks, and dramatic decreases in power as the numbers of clusters decrease. Power and Type I error performance were not notably affected by the addition of nonzero cluster effects or a temporal trend in hospitalization intensity.

Conclusions/Limitations

Stepped wedge trial designs that intervene in small clusters across longer periods can provide enhanced power to evaluate comparative effectiveness, while offering practical implementation advantages in geographic stratification, temporal change, use of existing data, and resource distribution. Current population estimates were used; however, models may not reflect actual event rates during the trial. In addition, temporal or spatial heterogeneity can bias treatment effect estimates.

Introduction

Although randomized controlled trials (RCTs) have long been recognized as the gold standard for evaluating clinical interventions, the availability of high quality RCT evidence on clinical outcomes from community-based interventions remains limited.¹ Practical community-based clinical trials provide important information for dissemination, and are essential for ensuring high quality evidence for health policy.² Translational research can be categorized into 3 types: Type 1 evaluates the controlled application of a hypothesis on humans, Type 2 evaluates the hypothesis in a controlled clinical setting, and Type 3 evaluates implementation across a representative community setting.³ Clinical RCTs have historically focused on Type 2 research, determining whether an intervention provides any beneficial effect when selectively applied. Health policy and community practice, however, is better informed by Type 3 translational research that focuses on the effectiveness of an intervention compared with existing approaches or alternative treatments applied under conditions that are more typical of the settings where most people receive care.⁴ Although Type 2 RCTs maximize internal validity by assuring rigorous control of all variables other than the intervention, Type 3 translational RCTs maximize external validity, helping to ensure that similar results can be expected when the intervention is generalized to a more diverse and less controlled world.⁵ Practical considerations such as competing clinical demands, availability of resources, common comorbidities, community expectations, and impact on work flow or costs can alter clinical outcomes in surprising and unexpected ways.^6,7 Barriers to community adoption that remain unidentified will inhibit dissemination and contribute to the 17-year estimated average lag for new scientific discoveries to enter day-to-day clinical practice, or to the 86 percent of discoveries never adopted.³

Practice-based research networks, involving over 70,000 primary care providers throughout the U.S., offer a valuable infrastructure for addressing the science of community-based implementation and dissemination research.⁸ Practical limitations of existing RCT methodologies, however, inhibit the ability of large networks of practices (over which the simultaneous introduction of the intervention is infeasible) to implement rigorous community-based trials. This has contributed to a demand for new trial methodologies, such as the “stepped wedge” design, to facilitate pragmatic or practical clinical trials characterized by inclusion of (1) clinically relevant alternative interventions, (2) a diverse population, (3) heterogeneous practice settings, and (4) a broad range of health outcomes.² A stepped wedge design is a form of crossover study where one practice cluster crosses over from the control arm to the intervention arm at every time period (“step”); no clusters ever “cross back” from intervention to control. Kotz et al.^9,10 give a set of arguments that seem to suggest stepped wedge designs are of little use compared to the RCT. Mdege et al.^11,12 respond to these criticisms, advocating a stepped wedge design for certain situations. However, none of these papers consider the implementation of a stepped wedge design for a community based clinical intervention trial, perhaps its most natural setting. Several authors offer more recent implementations of the stepped wedge design in various applications,^13–16 such as quality improvement,¹⁷ colorectal cancer,¹⁸ and Ebola vaccine trials.¹⁹ Handley et al.²⁰ discuss the clinical advantages of a stepped wedge design, while Hemming et al.²¹ offer an extensive review and power analysis for several stepped wedge design variations. However, all of these papers consider the stepped wedge design only from a classical, frequentist statistical paradigm; more modern and flexible Bayesian statistical approaches²² are not considered. More recently, multiple papers^23–25 provide critical reviews of published stepped wedge trials. Copas et al.²⁶ discuss in detail three main categories of stepped wedge designs, such as our design using a closed cohort, in which all participants are identified from the onset of the trial until completion without any changes between clusters. Baio et al.²⁷ validate using a simulation-based approach for sample size calculations by comparing with analytical methods; furthermore, they perform a sample size/power analysis for continuous and binary outcomes in closed cohort designs for cross-sectional data. In this paper, we propose and perform a sample size/power analysis for a novel Bayesian stepped wedge, closed cohort design for count outcomes.

Investigators planning practical community-based RCTs are challenged to balance internal and external validity, while accommodating high production environments typical of community-based health care delivery. Principal outcomes are commonly population-based clinical measures aggregated from patient-level observations. Since the broad spectrum of care provided by an individual’s primary care provider outside of a trial protocol can compromise the independence of clinical outcomes achieved across multiple subjects sharing one provider, patient-level repeated measures are most appropriately nested within provider. In addition, practical considerations, such as shared resources, potential for contamination bias, cost, or ethical considerations, often drive investigators to randomize experimental interventions at the level of the practice instead of at the level of the patient or provider. In addition, some interventions such as educational programs or new resources, once introduced into a practice, may be difficult or impossible to withdraw, preventing the application of standard crossover designs. Community participation is inhibited when using parallel designs with “usual care” controls, since practices randomized to control perceive less benefit in continuing study participation than practices receiving support for a new approach or intervention. This has led some investigators to offer study interventions to all control practices at the conclusion of a trial, introducing an additional expense with little research benefit.²⁸ Finally, practical limitations exist for implementing complex interventions across geographically dispersed practices, since practice randomization influences the cost and convenience of distributing necessary resources and training.

Methods

Design overview of the British Columbia Telehealth Trial (BCTT)

The BCTT is a pragmatic, cluster-randomized controlled clinical trial using an stepped wedge design to evaluate the effect of internet-based telehealth support to improve the percent of patients achieving compliance with recommended disease-specific action plans on hospital and emergency room utilization. The study evaluates compliance with recommended disease-specific care guidelines for individuals with chronic heart failure or diabetes mellitus to determine the effect on disease-specific utilization, quality of care, and clinical outcomes over 12 months, as measured by the reduction in emergency room visits and hospitalizations. The study compares telehealth support with usual care in 50 primary care practices. Practice clusters are the unit of randomization, and patient outcomes are the unit of observation. Each cluster of 2 practices contributes provider-selected subjects to the observation cohort for a total of 1000 subjects. Specifically, at each practice, the physicians will enroll and follow the the first N_ijpatients they see who consent, have access to the internet, can speak English, and who the physicians feel can most benefit from the treatment. Clusters within a geographically defined block are randomized to a time allocation using a stepped wedge design. Clusters move to the intervention group at a selected time interval continuously over the study period. All practices enrolled are recruited from the British Columbia Health Authority. Recruitment and randomization is divided into five geographical regions or blocks as shown in Figure 1. Also in Figure 1, we give an example of a block configuration of the Northern Health region to display the cluster and practice units. We illustrate our block randomization scheme with the following example. Consider the randomization order: 3, 5, 1, 2, 4, for Block 1 in Figure 1. Then Practices E and F would crossover from control to intervention at the first step/time period and so forth. This randomization scheme provides contiguous geographic regions for convenient distribution of resources, controlling staff travel time around the province; a standard randomization schedule could have trial staff working simultaneously, or consecutively, in practices located hundreds of miles apart. Block order, that is the order in which Block 1, Block 2, etc. are randomized, might be randomized as well.

Figure 1.

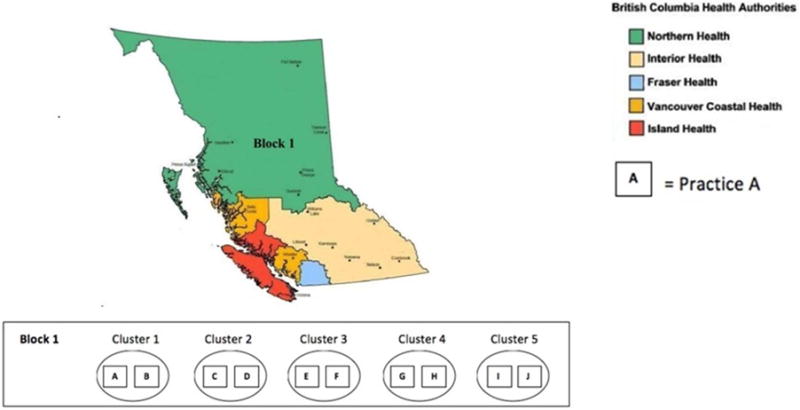
Geographic stratification for the British Columbia Telehealth Trial, with example Block 1 configuration in Northern Health region.

The practice intervention is estimated to take two weeks per practice. Randomization to periods of time less than two weeks would increase the overlap that occurred between practices undergoing sequential implementation; furthermore, it would provide diminishing value for defining a more precise implementation time and date. Since the implementation time is two weeks and the initial study period is 12 months, two practices are assigned to each two-week randomized cluster.

Settings and participants

Based on practical recruitment considerations, 10 subjects at least 45 years old with a history of chronic heart failure and 10 subjects at least 18 years old with Type 2 diabetes mellitus will be recruited from each of 50 primary care practices. Eligible subjects will have access to an online telehealth intervention providing disease-specific support for individual action plans developed in cooperation with the providers.

Intervention

The study intervention provides home monitoring, self-management education, and telehealth support for a disease-specific action plan using a team of allied healthcare professionals. Chronic heart failure subjects are provided with scales and blood pressure cuffs, while diabetes patients are provided with glucose meters. Each device uploads data into an electronic personal health record to facilitate support. Subjects are provided with an average of 150 minutes of support over the course of the trial. Data and results of the consultations are provided to the primary care provider to facilitate provider-directed care management. The control arm provides “usual care” reflecting the range of clinical services for chronic disease management commonly available in general practice sites in the British Columbia Health Authority, excluding telehealth care.

Outcomes

The primary outcome measure for the BCTT is the control-intervention difference in disease-specific health care utilization (emergency room visits and hospitalizations) over the 12-month intervention period. Health care utilization is measured using a composite of five Prevention Quality Indicators developed by the Agency for Healthcare Research and Quality identifying chronic heart failure and diabetes related hospitalization.²⁹ Prevention Quality Indicators are standardized national measures that are used to estimate the number of hospitalizations for a particular disease that could be preventable through better clinical management or utilization of clinical services. Our endpoint is the subset of emergency room visits and hospitalizations that meet one of the 5 Prevention Quality Indicators, i.e., emergency room visits or hospitalizations that can be thought of as “preventable” in this context. Diabetes-related admissions include: diabetes short-term and long-term complications, uncontrolled diabetes, and lower-extremity amputation among patients with diabetes. Power estimates were based on data from the Agency for Health Research and Quality Healthcare Cost and Utilization Project (the largest collection of longitudinal hospital care data in the United States), and the National Health Interview Survey.^30–32 During the current planning phase of the study, we evaluate the effect of modifying trial design characteristics in order to provide the optimal power to detect a primary outcome change while addressing practical implementation issues.

Statistical model and inference

The study will evaluate the number of events, defined as either an emergency room visit or any hospitalization, among all subjects (both diabetes mellitus and chronic heart failure) in each of the M = 25 clusters (each containing 2 practices) over T time intervals. Let Y_ijk be the number of events for patient k = 1,…, N_ij within a given time interval j = 1,…, T in cluster i = 1,…, M, and let Y_ij be the cluster-level outcome aggregated over the N_ij patients in cluster i and time interval j.

If we assume the Y_ij are independent Poisson(λ_ij) random variables, we can define the mean function as λ_ij = E_ij exp(μ_ij) where

$${\mu }_{\mathit{ij}}={\alpha }_i+{\beta }_j+\theta X_{\mathit{ij}}$$

Here E_ij is the expected number of events for cluster i during time period j and μ_ij is the log Poisson rate parameter for cluster i at time period j, so that μ_ij greater than 0 means more cases in cluster-time interval ij than expected, and μ_ij less than 0 means fewer than expected. Regarding the components of μ_ij, α_i is a random effect for cluster i, β_j is a fixed effect for time period j, X_ij is an indicator variable, taking value 1 for intervention and 0 for standard of care, and thus θ is the log-relative risk of either an emergency room visit or hospitalization for treatment versus control. Here, E_ij is a function of N_ij, the number of patients at risk in each cluster, and may be obtained using either a table of sex- and age-specific hospitalization rates appropriate for our population, or via crude standardization as N_ij times the overall expected hospitalization and emergency room visit rate across all times and clusters; see our Simulations and Power Calculations section below for full details.

For a conventional statistical analysis, we could use generalized linear mixed models or generalized estimating equations to compute mean and variance estimates for our fixed and random effects. An attractive alternate approach is to use a Bayesian analysis, since it facilitates straightforward estimation of population probabilities of interest, yet its use does not appear to have been explored to date in the stepped wedge context. We therefore explore a Bayesian approach, basing inference on Markov chain Monte Carlo sampling from the posterior distribution using the Gibbs sampler.³³ In our setting, Gibbs sampling was carried out in JAGS 3.1.0, as called from the R software using rjags.³⁴ We can summarize our Gibbs samples to determine the posterior probability of a significant reduction in the log-relative risk of being hospitalized for intervention versus control, i.e., to see if $\mathrm{Pr}\left(\theta <0|\overrightarrow{y}\right)>0.95$, where here we condition on all data observed in the trial. Using our Gibbs samples, we can calculate 90% equal-tail Bayesian credible intervals to quickly check the significance of the treatment effect. We evaluate the design’s Type I error and power performance in our simulations below. For our simulation study, we used relatively flat prior distributions for our fixed and random effects. To improve estimates and increase power, we could also incorporate professional expertise or historical knowledge from existing community provider records to inform a more realistic prior for such parameters.

Our model permits an unbalanced design, having N_ij patients in cluster i at time j. However, since practitioners will be trained to select N patients from their set of all diabetes mellitus and chronic heart failure patients, we implemented a balanced design (i.e., one setting N_ij= N for all i and j), which in any case offered higher power.

The intracluster correlation coefficient is a commonly used descriptive statistic in cluster-randomized trials to capture the ratio of the between-cluster variance and total variance. Following the work of Clark and Bachmann,³⁵ we use the following definition for the intracluster correlation coefficient for count data (using a relative rate model), ${\rho }_j=\frac{\left(\exp \left({\sigma }_{\alpha }^2\right)-1\right)A_j}{1+\left(\exp \left({\sigma }_{\alpha }^2\right)-1\right)A_j}$, where $A_j\equiv E\left({\lambda }_{\mathit{ij}}\right)=\exp \left({\beta }_j+0.5{\sigma }_{\alpha }^2\right)$ is the mean of the log-Normal distribution defined for λ_ij (see Appendix A in reference ³⁵ for further details) and ${\sigma }_{\alpha }^2$ is the variance of the random cluster effects. With this definition for ρ_j, as the between-cluster variance increases the intracluster correlation coefficient tends towards one; and when there is no between-cluster variance, i.e., ${\sigma }_{\alpha }^2=0$, the intracluster correlation coefficient is zero. We calculate the time-averaged intracluster correlation coefficient by averaging over ρ_j for all j = 1, …, T.

The presented stepped wedge design is non-adaptive and will complete regardless of the observed treatment effect over time. This is appropriate for our intervention, as we want to see how the on-line intervention affects utilization over time. For other interventions, it may be important to incorporate adaptive early stopping rules to guide the safety monitoring board if the intervention displays a large superiority or inferiority in the treatment effect.

Prior distributions

Since we want to implement a Bayesian framework, we must specify prior distributions for our parameters of interest and nuisance parameters. First, we need to define some notation. Let Normal(a,b) refer to a Normal distribution with mean a and precision b, where precision is defined as the reciprocal of the variance. For our cluster random effects, we assume a non-informative prior over a relatively large (on the log scale) range, ${\alpha }_i~\mathit{Normal}\left(0,{\tau }_{\alpha }^2\right)$ (independent and identically distributed for all i) where we let ${\tau }_{\alpha }^2~\mathit{Gamma}\left(0.1,1\right)$ (with corresponding mean and variance 0.1). This specification means a majority of α_i’s prior mass is contained within the interval (−6,6). Similarly for our fixed effects capturing time trends, we set β_j ~ Normal(0,0.1) (independent and identically distributed for all j), so that approximately 95% of each β_j’s prior density is also within (−6,6). Lastly, for our treatment effect we assume a prior distribution with mass defined over potential clinical values for the log-relative risk of either an emergency room visit or hospitalization for intervention vs. control, corresponding to θ ~ Normal(0,10). Then a majority of θ’s prior density is within (−0.63,0.63), or (0.53,1.9) on the relative risk scale centered around the prior mean of 1 (with value 1 corresponding to no difference between intervention and control, and 0.5 to a 50% reduction in relative risk). Note the only conditionally conjugate prior is the Gamma prior for ${\tau }_{\alpha }^2$. A conjugate prior has the same distributional form as the corresponding posterior, and allows for quicker computations. The posteriors of θ, α_i, and β_j are non-conjugate, so Gibbs sampling in JAGS is done using slice sampling.³⁶

Design parameters

A stepped wedge design sequentially adds an additional cluster to the intervention arm at each time point. For our implementation of the simulation study below, we randomize a new cluster to the intervention arm every two weeks, and use the data observed in the study up to the present time period j as our control measurements. In our power calculations, for comparison we also consider randomizing a new cluster to the intervention arm every three weeks. Here, our blocking factor is geographical region (see Figure 1). Using a block size of five clusters (assuming 25 clusters), we randomize the (unidirectional) crossover order for each cluster within a block. To reduce systematic bias, clusters within a block are blinded to their randomization order. A display of our stepped wedge design for the first five time periods (ten weeks) is in Figure 2. In our BCTT design and simulation, we allow for one cluster made up of two clinical practices to be randomized to the intervention arm at each step.

Figure 2.

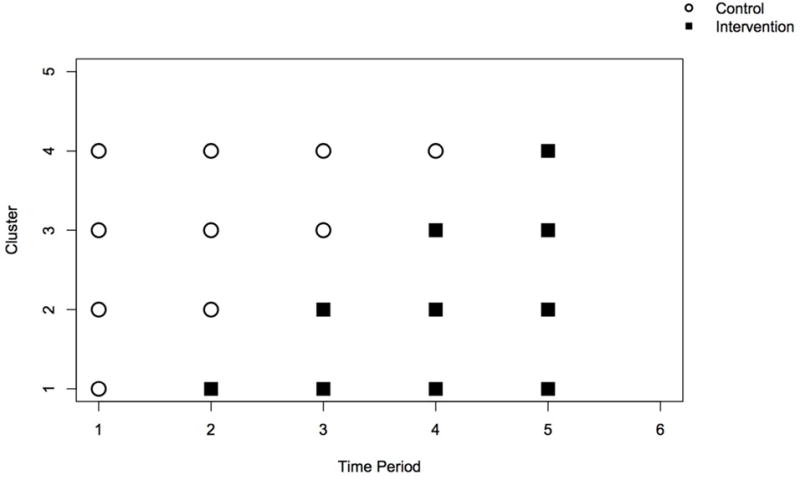
A display of the first five time periods of our stepped wedge design, assuming a cluster is added to the intervention group every time period, or every two/three weeks.

Simulations and power calculations

To examine the power and Type I error performance of our design, we ran a simulation study. Initially, we assume no time trends (β_j = 0, for j = 1,…, T) and no cluster effects (α_i = 0, for i = 1,…, M). To check sensitivity to these assumptions, we first assume a cluster effect exists and sample each α_i from a Normal(0,4) for i = 1,…, M. Thus, the mean function λ_ij varies by cluster with a multiplicative adjustment to the average number of emergency room visits or hospitalizations ranging from exp(−1.5) = 0.22 to exp(1.5) = 4.48 days, by taking three standard deviations from 0. Next, we instead assume there is a linear time trend (on the log scale) by setting β_j = log(j) − log (T/2) for j = 1,…, T; corresponding to a multiplicative increase of exp(log(T/(T/2)) = 2 days for the mean function λ_ij by the last time period, T. Lastly, we run a simulation where the mean function λ_ij varies across both clusters and time periods. The true time-averaged intracluster correlation coefficient varies from 0 to 0.25 across all scenarios. For simplicity, we assume the expected number of events within each cluster is fixed and does not change over time (E_ij = E_i for all i and j). If we expect 83.5 chronic heart failure and 280 diabetes events per 1000 subjects per year, then we estimate a total of 363.5 events.^31,37

Assuming N_ij= N patients per cluster, and using simple crude standardization, the expected number of events during any given week in cluster i is E_i = N*(0.3635 events per year)/(52 weeks) for all i = 1,…, M. We can recalculate E_i in the various settings under consideration, using the appropriate N and time interval length values, such as 2 E_i when a cluster is randomized from the control arm to the intervention arm every two weeks. All simulations were completed in R version 2.15.0. We simulated 1000 trials for each of five true reductions in the relative risk of being hospitalized during any time period: 30%, 20%, 15%, 10%, and 0%, with the fifth being the null scenario of no treatment effect. Within each trial, 5000 Markov chain Monte Carlo iterations were kept for inference following 2000 iterations for burn-in. We include our JAGS and R code in the online Supplementary Material for reference.

Estimated power curves for different treatment effects, varying the number of clusters M, patients N within each cluster (with the constraint of 1000 patients total), and time interval length between the unidirectional crossovers, are displayed in Figure 3. Type I error values are those corresponding to the right side of the plots in Figure 3 (i.e., when the true treatment effect θ is zero). The top left plot gives the results assuming no time or cluster effects, the top right plot assumes an underlying cluster effect, the bottom left plot assumes an underlying linear time trend, and the bottom right plot assumes both time and cluster effects. We consider M = 50 clusters and N = 20 patients, corresponding to a 2- or 3-year study for two- or three-week time intervals, respectively. When we have M = 25 clusters with N = 40 patients, the trial duration is either 1 or 1.5 years for two- or three-week time intervals, respectively. The last configuration of 1000 patients we consider is M = 10 clusters with N = 100 patients, which corresponds to a 22-or a 33- week long study for two- or three-week time intervals, respectively. Recall a cluster is comprised of two practices, so this last setting would enroll 20 practices with 50 patients in each practice.

Figure 3.

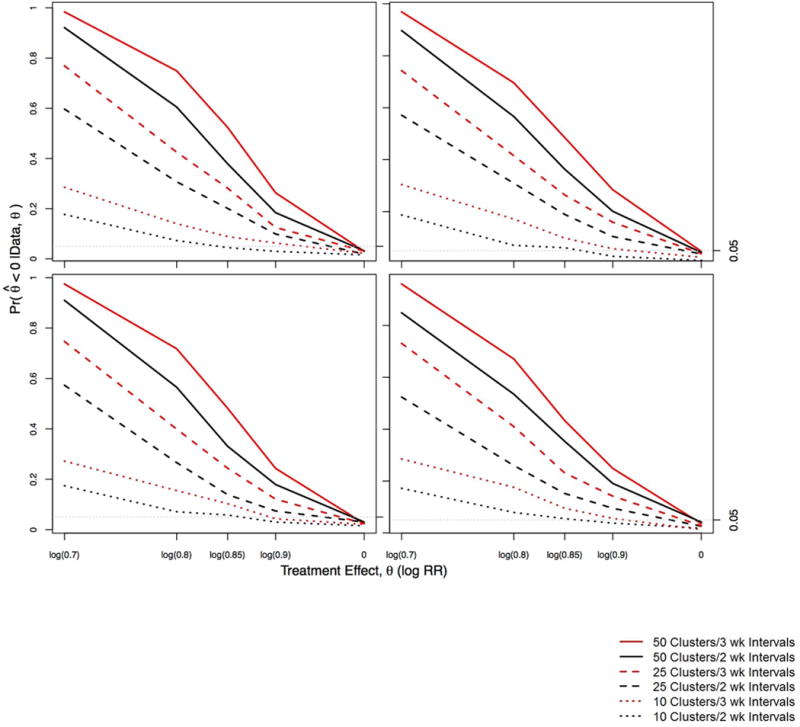
Estimated power curves for 1000 patients divided among 50 clusters with 20 patients each, 25 clusters with 40 patients each, or 10 clusters with 100 patients each. The black lines assume a cluster is randomized to the intervention arm every 2 weeks, whereas the red lines assume a cluster is randomized every 3 weeks. Top left, no time or cluster effects; top right, nonzero underlying cluster effects; bottom left, underlying time trend; bottom right, both nonzero cluster effects and underlying time trend.

In Figure 3, we see assuming M = 50 clusters with N = 20 patients within each cluster and a three-week time interval between crossovers displays the highest power for detecting a reduction in θ, and the Type 1 error when θ = 0 (0.03) is neglibly smaller than that for two-week intervals (0.032). If we assume a cluster crosses over to the intervention arm every two weeks, the study is shortened by 1 year (33% decrease). Although the study may be faster and cheaper, our power decreases by 6–15%.

While we see a slight decrease in power when we use the shorter time interval, the treatment effects’ point estimates and Bayesian credible intervals from 1000 simulations are consistent with the true values. (We also acknowledge the “unfairness” of directly comparing the 2- and 3-week interval trials, since they do not have the same total duration.) Assuming M = 50 clusters with N = 20 patients within each cluster for exp(θ) = 0.7 (30% relative risk reduction) with two-week time intervals, the mean relative risk (95% Bayesian credible interval) is 0.73 (0.61,0.88), whereas for three week time intervals it is 0.73 (0.62,0.85). In our simulations, recall we initially set α_i = 0 for all i and β_j = 0 for all j, so there are no underlying cluster or time effects, and we set a flat prior for these parameters. Given the flat prior on the random effects, we observe a slight overestimate of the treatment effect toward 1, but underestimation of the time effects. This suggests a small negative correlation (between −0.1 and −0.3) between the treatment effect and the time effect; recall the prior standard deviation for our time effect is 0.1. We note that we observe less than the nominal 5% Type 1 error rate of incorrectly identifying a significant treatment when one in fact does not exist.

Turning to our sensitivity analyses, we see the appearance of our power curves is rather robust across all four sets of assumptions in Figure 3. We see a slight decrease in power when an underlying cluster effect is present, and the expected shrinkage of the estimated time effects toward the true value of 0. We see a slight decrease in power when an underlying time trend is present; and an underestimation of the cluster effects (again toward the true value of 0) is also present. When both time and cluster effects exist, we see a decrease in power, slight overestimation of the treatment effect, and widened treatment effect 95% Bayesian credible intervals. For example, M = 50 clusters with N = 20, we have 85% power (assuming two-week time intervals) or 96% power (assuming three-week time intervals) to detect a true treatment effect of exp(θ) = 0.7 (30% relative risk reduction), compared to 92% power (assuming two-week time intervals) or 98% power (assuming three-week time intervals) when α_i = 0 for all i and β_j = 0 for all j. Also when both time and cluster effects exist, the mean relative risk (95% Bayesian credible interval) is 0.75 (0.62, 0.9) with two-week time intervals, and 0.73 (0.62, 0.86) for three-week time intervals.

As previously discussed, we calculate the time-averaged intracluster correlation coefficient for each setting. In our simulations, we found only a modest correlation present, with $\widehat{\rho }$ ranging from 0.1 to 0.35 across all simulations, except when we consider M = 10 clusters. For M = 10 clusters, we have 100 patients per cluster and we can expect the between-cluster variation to increase, since we have greatly reduced the number of clusters. In this setting, we see $\widehat{\rho }$ ranging from 0.32 to 0.56 across all simulations.

Limitations

With this design, there are some limitations and concerns over potential sources of bias. First, it is important to ensure a fair comparison of data collected before and after the crossover. Data collection methods and instruments should be consistent over time, allowing a “like with like” comparison among data collected over time. Second, while the randomization order is blinded, treatment status is not blinded. Since health care providers and patients are aware of cluster assignment, it is important to consider the potential for bias due to un-blinded treatment status. For example, patients in an intervention cluster may be more likely to be sent home prematurely from the hospital in “local” attempts to show improvement. Other potential sources of bias include selection bias, which could arise if the clusters enrolled are systematically different than those refusing enrollment or those not recruited (though in this case we have little interest in the effect of the intervention to persons who the physicians feel are unlikely to benefit). To avoid systematic bias due to training improvement over time, we assume no “training learning effect” should exist; that is, the trainers should not improve in their ability to teach the intervention to providers over the course of the study.

Another limitation is that a single crossover stepped wedge design does not allow order effects to be distinguished. That is, since every patient receives the intervention second, if there is a tendency for patients to prefer the second treatment, the stepped wedge design cannot distinguish this order effect from the treatment effect. This may be less of a consideration in community-based trials that compare a single intervention to the provision of “usual care”. Also, since the composite outcome includes both diabetes mellitus and chronic heart failure patient events, care should be taken not to misinterpret results. Event rates for diabetes mellitus and chronic heart failure may respond differently in the intervention arm. Observable treatment effects do not necessarily represent events expected for either disease independently. Events were modeled to equate one emergency room visit or one hospitalization. Modeling “events” meant three emergency room visits and three one-day hospitalizations were three events, while a three-day hospitalization was one event. Although hospitalization may require greater resources, we were hesitant to give hospitalizations more weight in the outcome, since the intervention could impact either emergency room visits or hospitalizations. In addition, long hospitalizations would become problematic, and make it difficult to interpret whether the findings represented an overall reduction in emergency room visits or hospital days. Finally, while our statistical model does not assume the availability of individual counts Y_ijk, were they available, we could contemplate a model that included individual-level random effects. However it is not clear if the likelihood for this model should remain as a Poisson, switch to Bernoulli (i.e., assume each patient can have at most one event per time period j), or something in between – say, a zero-inflated Poisson model.

Discussion

Commonly, a parallel design for a two-arm study randomizes K independent clusters to each study arm at a single time point, for a total of 2K independent clusters. A crossover design typically requires fewer clusters than a parallel design, but a longer trial duration since each cluster serves as its own control. In standard crossover designs, a “washout” period is often included during the crossover period between one intervention and the next, in an effort to remove any residual effect of the previous intervention. The washout period lengthens trial duration, but is generally necessary only for drug interventions. The stepped wedge trial duration can be even longer than a standard crossover design, since only a fraction of the clusters are added to the experimental arm during any given time period. However, additional temporal information can be gained by the sequential roll-out of the intervention, potentially improving estimation and power.³⁸ The stepped wedge design also allows researchers to investigate potential time trends in the treatment effect, though not an order effect, since clusters only cross in one direction (from control to intervention).

Stepped wedge designs offer advantages when an intervention can only be initiated at a limited number of sites at one time, whence an intervention must be staged or stepped. It also avoids potential ethical concerns and retainment issues that arise from withholding an intervention from subsets of patients or practices since all participants receive the intervention at some time during the study.³⁹ It has been suggested that stepped wedge designs are burdensome because repeated measurements are necessary, or are potentially more dangerous since the intervention is administered to all clusters.^9,10 In practical community trials, however, repeated measures on individual subjects are commonly necessary for the ongoing provision of care. When one arm is usual care, administration of the intervention to all clusters generally enhances recruitment and retainment by ensuring each practice has an opportunity to participate in the experimental intervention. Finally, in pragmatic community trials, patients have often been seen at a community-based clinic for many years, potentially providing rich historical data. In this case, as each practice cluster enters the trial, retrospective control arm data can be captured from the medical record for previous time points.

Another obstacle for community-based trials is efficient implementation across geographically dispersed practices. It is often impractical to travel large distances between scattered clinics dictated by the randomization order of a parallel RCT. In addition, recruitment efforts across large regions with diverse populations may be costly, less focused, and less well received. A practical solution with the stepped wedge design is to block by geographic location and randomize the order in which clinics cross from the control arm to the treatment arm within each block; block order might be at least partially randomized as well. In this case, the blocks contain practice clusters located closer to one another. This allows focused recruitment efforts in smaller geographic regions, decreases the impact of proximity problems on training resources, and diminishes issues of contamination, attrition, and the impact of changes in population characteristics among clusters enrolled later in the trial. This can be particularly valuable for large studies with national site distribution.

Finally, as in any study, patient dropout and possible consequent loss to follow-up is a concern in stepped wedge trials. In our BCTT setting, we expect only between 1 and 5% dropout over the course of our 12-month study, so we do not expect it to be a major source of bias. See Little et al.⁴⁰ for a summary of a report by a blue-ribbon National Research Council panel on minimizing missing data in clinical trials.

Conclusions

Traditional controlled clinical trial designs present practical barriers to community-based trials that potentially compromise the likelihood of finding important treatment effects. The stepped wedge design is a practical alternative that resolves several issues while maintaining a rigorous clinical trial methodology. While stepped wedge designs should be expected to require a longer trial duration than parallel designs, the resources required for implementation are evenly distributed over time and can be focused geographically to conserve resources. Stepped wedge trials have the added capability of providing valuable temporal information for discerning secular trends from intervention effects. The stepped wedge design appears to provide particular benefit in community-based practical trials by potentially allowing investigators to include previously collected historical information on subjects. Examining stepped wedge trial data under a Bayesian framework allows a full posterior inference for the treatment effect, time trends, and cluster random effects, and readily accommodates other generalized models. For reference or to adapt for a sample size/power analysis in a particular setting, we include our R and JAGS code in the online Supplementary Material.