Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jul 22;6:30324. doi: 10.1038/srep30324

The influence of porosity and structural parameters on different kinds of gas hydrate dissociation

S Y Misyura 1,a
PMCID: PMC4957226  PMID: 27445113

Abstract

Methane hydrate dissociation at negative temperatures was studied experimentally for different artificial and natural samples, differing by macro- and micro-structural parameters. Four characteristic dissociation types are discussed in the paper. The internal kinetics of artificial granule gas hydrates and clathrate hydrates in coal is dependent on the porosity, defectiveness and gas filtration rate. The density of pores distribution in the crust of formed ice decreases by the several orders of magnitude and this change significantly the rate of decay. Existing models for describing dissociation at negative temperatures do not take into account the structural parameters of samples. The dissociation is regulated by internal physical processes that must be considered in the simulation. Non-isothermal dissociation with constant external heat flux was simulated numerically. The dissociation is simulated with consideration of heat and mass transfer, kinetics of phase transformation and gas filtering through a porous medium of granules for the negative temperatures. It is shown that the gas hydrate dissociation in the presence of mainly microporous structures is fundamentally different from the disintegration of gas hydrates containing meso and macropores.

Gas hydrate deposits contain huge reserves of natural gas, and their intensive development will be started in the next decade1,2. Safety and environmental issues becomes one of the most challenging area in the world energy industry3,4. Now, not only the questions about the cost of conventional technologies of natural gas production, including shale gas, become urgent, but also the environmental problems play the primary role. The studies of gas hydrates are closely connected with the problem of global warming. The release of methane from the permafrost leads to the climate changes5. Alternative energy technologies can effectively solve the environmental problems6. Among such alternative technologies, there are production and storage of natural and artificial methane hydrates and burning of combustible gas hydrates. Many efforts are spent not only for improving the efficiency of technologies of gas hydrate production, but also the fight against hydrate plugs in the pipelines. These plugs grow rapidly, leading to a sharp increase in hydraulic resistance and stop of the oil and gas flows. In this regard, a large class of hydrate inhibitors is applied. A new class of hydrophobic amino acids kinetic inhibitors can effectively fight hydrate formation7. Pectin (kinetic hydrate inhibitor) also has the unique properties8. Much attention is paid to the problems, related to transportation and storage of raw materials in large containers9,10,11,12,13,14. Pelleted methane hydrate can be stored for a long time due to the phenomenon of self-preservation at the annealing temperatures and the lowest rate of methane hydrate dissociation is achieved at the temperatures of 265–267 K15. The effectiveness of the above technologies depends on the depth of understanding the dissociation mechanisms, boundaries of phase stability and metastable state. It is important to understand the fundamental difference between disintegration of gas hydrates at positive temperatures and dissociation at temperatures below the freezing point. At positive temperatures, gas diffusion occurs through the film or layer of water and it is described by the well-known dependencies. The kinetic equation satisfactorily describes the experiment and determined kinetic constants are used for a wide range of problems16,17,18. At dissociation in a porous media, Darcy’s law and Corey’s model for permeability19 are used in addition to the kinetic equations. Since gas hydrate collapse is accompanied by cooling, it is necessary to take into account heat exchange with the environment20,21. The rate of gas hydrate formation and decomposition is limited by thermal inertia of the medium and the rate of gas diffusion in liquid and solid. The influence of environmental heat transfer on the mechanism of gas hydrate decay is considered in refs 22, 23, 24, 25. Both kinetics and heat transfer should be taken into account26. The effect of heat transfer during crystal growth and decay is particularly important for highly nonequilibrium systems27,28.

The physical pattern of gas hydrate disintegration at negative temperatures is much more complex, and to date there are no accurate models, describing this dissociation. The problem is that in this case we are faced with a variety of structures and morphologies of crystal surface. In this case, it has no sense to choose the kinetic constants, describing the decay, since the value of the dissociation rate in the temperature range from 190 K to 273 K is changed by five orders, and it depends on the external pressure, type of hydrate, and ice morphiology29. The surfaces of hydrated rocks of marine hydrate deposits, mined in various places (Dongsha Area of the South China Sea, Pearl River Mouth Basin), have different morphology (laminated, nodular, vein, disseminated) with different grain sizes30. In literature, a lot of attention is paid to the study of ice structures in application to gas hydrate dissociation. Gas and ice are formed at decay of gas hydrates. There are three main structures of gas hydrates: cubic structure (sI); cubic structure (sII); and hexagonal structure (sH). Natural gas hydrates have usually structures sI and sII. When gas hydrates dissociate at temperatures below zero, there is the variety of ice structures and surface morphologies. Today, more than 15 crystalline phases have been discovered for ice; each of them has a characteristic metastable area31,32. The most common structure of ice in the range of low negative temperatures is hexagonal ice Ih. The crystal structure of cubic ice Ic, obtained at very low temperatures, is less stable and with increasing temperature, it turns to hexagonal ice. It is characteristic that for the external pressure of 1 bar and temperatures below 230 K, near the melting point ice has a branched pore structure. At the annealing temperatures, there is an abnormally low rate of gas hydrate decomposition (the phenomenon of self-preservation) and the ice surface is covered by a solid ice crust. At that, the surface ice structures have complex and differing morphology (disseminated, ramified, domed), which depends on the pressure, temperature and type of gas hydrate. Often in literature, abnormally low dissociation is associated with the morphology of the surface ice structures33. When dissociating at the annealing temperatures, a thin and very strong ice crust is formed on the granule surface. There is high internal pressure under the ice crust and it prevents further decay of gas hydrate. It turned out that the ultimate strength of this crust is many times higher than that of coarse-grained polycrystalline ice and its grain size is about 10 μm34. The structural characteristics of the surface envelope are investigated in refs 15 and 34, 35, 36, 37. The effect of key factors on the mechanism of self-preservation and the metastable state is considered in papers15,29,36,37,38. Self-preservation for hydrate dissociation in water + diesel oil dispersion systems is presented by ref. 39. The behavior of combined hydrates at the annealing temperature is considered in paper40. The effect of the thickness of gas hydrate layer and pellet diameter on the rate of decay is shown in refs 41 and 42. At gas hydrate combustion, not only the ice crust is formed on the surface of granules layer, but a water film; at that, the velocity of flame propagation depends on the velocity of the forced air flow43. Self-preservation at methane hydrate combustion leads to a multiple decrease in the fuel flow. As a result, the injection parameter and stoichiometric ratio, affecting the rate of chemical reaction at combustion, change44.

The porosity can be formed at both destruction and formation of gas hydrates. Kuhs et al. in detail investigated the formation of meso- and macro-pores of gas hydrates using scanning electron microscopy45,46. The porous structures were also detected and studied in a small growing hydrate layer at the liquid-liquid interface47. Natural gas hydrates, formed both from the continental and seafloor, are also indicate the presence of microporous structures48. The occurrence of porosity is associated with an excess of gas molecules at the time of gas hydrate formation49. Porous gas hydrates themselves in nature are formed in the pore space of a hard rock50,51. Coal moisture in porous leads to the formation of methane clathrate hydrates52. The formation of methane hydrates in coals increases the capacity of the coal to store gas. Methane storage capacity in gas hydrates is up to 2 orders of magnitude greater than the gas storage capacity of the coal by adsorption53. Formation and dissociation of gas hydrates in a porous medium are considered in refs 54 and 55. Mathematical models for reacting porous particles are widely used in problems of chemical engineering and combustion theory. Chemical transformations for porous particles in catalytic processes are considered in refs 56, 57, 58, 59. The effect of porous structures on chemical reactions at pyrolysis and solid fuels combustion are presented in refs 60, 61, 62, 63, 64, 65, 66, 67.

Currently, simulation (for negative temperatures) does not consider the diffusion and the filtration during dissociation and does not account structural parameters and as a result there is only a qualitative analysis. To model gas hydrate at negative temperatures, the following data are required: size distribution of granules; size distribution of pores, change in the ice crust thickness and pore density with time; heat flux value, as well as the values of pressure and temperature. For most experimental data obtained by now, only some of the mentioned parameters were measured. At that, the experiments are usually carried out under the quasi-isothermal conditions at a given temperature. The main purposes of the current study: to obtain the experimental data on methane hydrate dissociation in the presence of non-isothermal heat transfer and continuous change in the sample temperature (∆Т = const in the framework of one experiment and alteration of ∆Т in different experiments); to model dissociation using a new approach with consideration of heat transfer, dissociation kinetics and gas diffusion through the porous structures of samples; investigations of the influence of the pore size on the dissociation of methane hydrate granules and the decay of methane clathrate formed in the pores of coal; investigation of differences in the dissociation of gas hydrates in the presence of various pores (microporosity, meso and macroporosity).

Experimental Data and Discussion

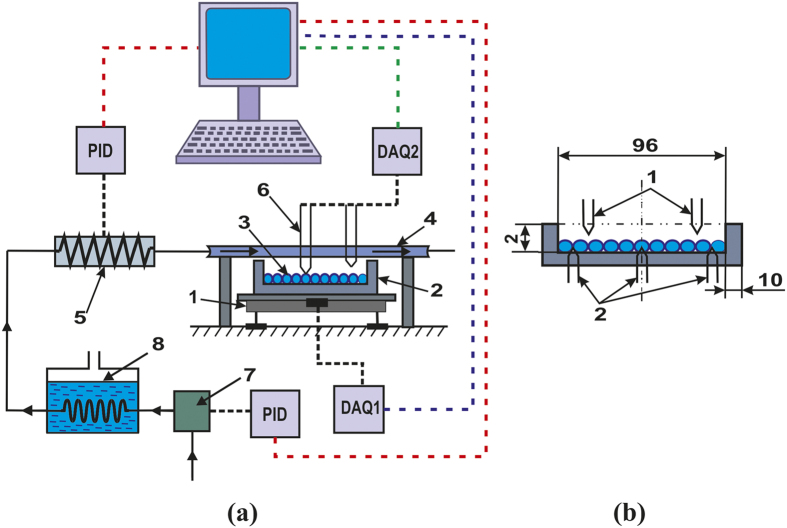
The scheme of setup and experimental section are shown in Fig. 1(a,b)).

Figure 1.

Figure 1

Open in a new tab

(a) Scheme of setup; (b) container with methane hydrate powder.

When the pressure and temperature deviate from the equilibrium, dissociation of gas hydrate starts and methane escapes from the powder. A decrease in the sample mass is registered by digital scales 1. The powder of methane hydrate 3 in the form of one granules layer of a fixed size is located in container 2. Compressed air of the given temperature is fed via metal heat exchanger 4 from heater 5. Air from the compressor 7 is fed into a Dewar 8 for cooling. Thermocouples 6 measure the temperature of powder surface and gas above the sample. Thermocouples 1 (Fig. 1(b)) are between the heat exchanger and powder, and they measure the gas (methane) temperature T0. Before the experiment, above the working section there was air under the pressure of 1 bar. During the experiment, the pressure inside the working setup was kept constant (1 bar), using a pressure regulator. Thermocouples 2 (Fig. 1 (b)), measuring the powder temperature, were located in the sample layer on the axis and near the lateral walls and allowed determination of the average sample temperature. The total error of temperature measurements, taking into account the adjustment error, varied within 0.5–0.9 °C. Diameter of the cylindrical container 2 (a) was 96 mm, container height (b) h = 2 mm and the wall thickness of the tank (b) was 10 mm. The tank was manufactured from insulating material. The temperature difference between the gaseous environment above the powder and the sample (ΔT) was kept constant automatically. Methane hydrate granules were produced by the cooled autoclave. Fine crushed powder of ice was placed in this autoclave. Methane was fed into the autoclave and methane pressure 5–5.5 MPa was set (T = 0.5–1 °C). The granules, whose diameter varied in the range of d = 0.9–1.2 mm were used in experiments. During the experiment, the powder was presented by a single layer of granules. The reservoir with methane hydrate powder was stored in the Dewar vessel. The initial gas temperature above the reservoir was T = 220 K and pressure was 0.6 MPa. When the initial temperature was stabilized the reservoir pressure was reduced to 1 atm. At heating the powder emitted gas and the sample mass changed; this was registered by the digital balance. The total mass of remote gas corresponded to mass concentration of methane. Initial methane mass concentration was 12.41%. The structure of methane hydrate corresponded to sI with the elementary cell formula 2D·6T·46H2O (2(512) + 6(51262)). The cell consists of 46 water molecules, six large and two small cavities. Porous characteristics are measured by the scanning electron microscopy. The average pore diameter was 0.8 μm. The size of ice grains was 10–50 μm. The density of open pores distribution before self-preservation was about 5·1011–7·1011 m-2 and 1·108–1·109 m−2 with partial self-preservation. The test coal had parameters: density (kg/m3) was 1490; coal moisture (wt %) was 29.5. Coal powder was produced by crushing and sieving (the average particles diameter was 1–1,5 mm). Powder X-ray Diffraction profiles show formation of methane hydrate (type sI) at 165 K. Low-pressure nitrogen and carbon dioxide adsorption used to determine pore size distribution. Large pores had the average diameter of about 50 nm.

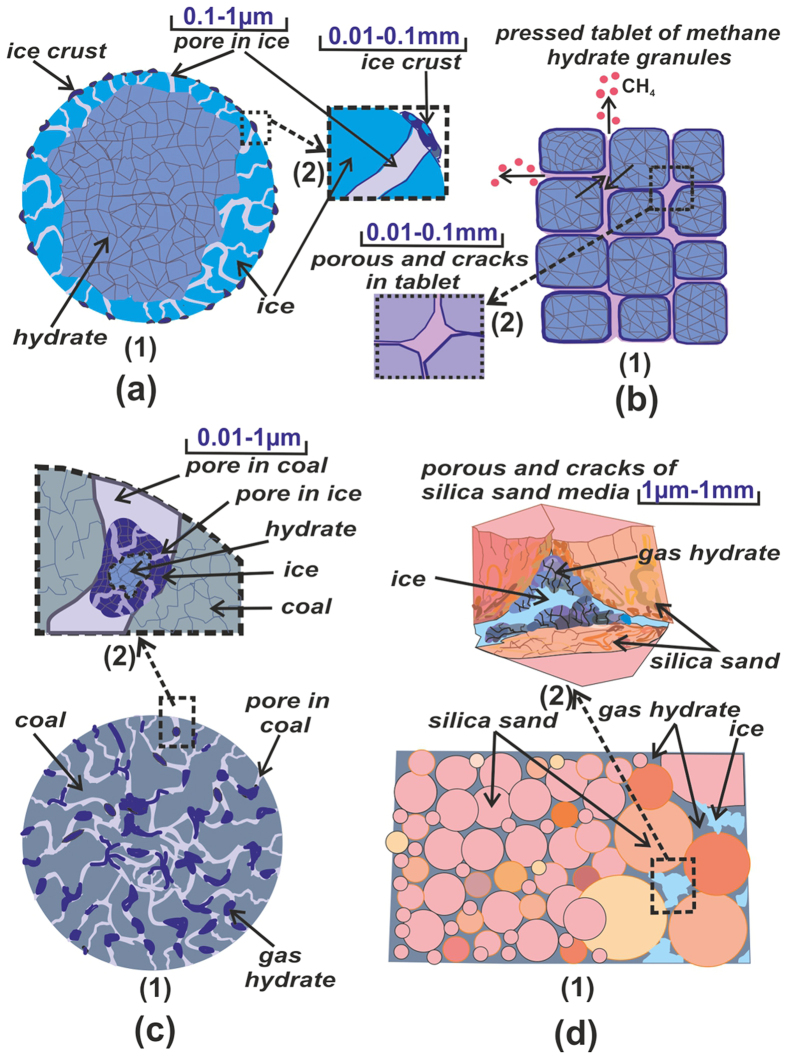
A wide range of problems in relation to gas hydrates is indicated in the Introduction. At sub-zero collapse temperatures, we have to deal with different types of gas clathrates and crystals with different morphologies. Depending on the characteristic scales of medium, porous matrix, hydrate particles and pores, different decomposition mechanisms can occur. Several specific types of gas hydrates with different physical scales, which should be considered at simulation, are shown in Fig. 2.

Figure 2.

Figure 2

Open in a new tab

Scheme of gas hydrate dissociation at negative temperatures: (a) for granule; (b) for pressed tablet; (c) gas hydrate dissociation within coal pores; (d) dissociation within porous silica sand.

The sizes of natural and synthetic granules (Fig. 2(a)), used in process applications, usually vary from 50 μm to 5 mm. At the very beginning of decay, the granule surface is coated with open pores with the sizes from 0.1 to 1 μm. At the annealing temperatures, the pores surface and granules are covered with a thin ice shell with the thickness of 0.01–0.1 mm. With time, the thickness of the ice cover increases and the predominant part of pores becomes closed. Methane diffuses through the ice cover via the closed pores, and gas is removed through the open pores by filtration. The cellular structures (grains) with the size of about 10–50 μm are formed on the ice surface. Such microcellular ice cover has great strength, keeps the methane in the pores at high equilibrium pressure and inhibits rapid decomposition of gas hydrate. For large granules in the presence of external forced flow of gas and external heat transfer, it is also necessary to solve the equations of energy and thermal conductivity. Heat transfer should take into account the size of external environment, for instance, the thickness of the boundary gas layer. Pelleted gas hydrate (Fig. 2(b)) is obtained by pressing the individual granules. In this case, at dissociation filtration of two types should be modeled: inside the porous spaces of a granule and porosity of the tablet (pellet) itself. Both filtration rate and thermal conductivity inside the pellet will depend on porosity. The sizes of tablet pores are several orders larger than the granule porosity, but at a large height of the pellet, filtration resistance and thermal inertia should be also taken into account. In recent years, the increased attention is paid to gas hydrates, formed on the moisture inside the coal pores (Fig. 2(c)). Dimensions of coal pores vary in an extremely wide range of 1–1000 nm53. However, in very small pores of coal water drops cannot form due to the high capillary pressure. Therefore, not all pores contain gas hydrate. The amount of methane in the form of gas hydrate can be many times greater than the amount of gas adsorbed in the pores. This fact should be considered not only for the technological purposes, but also for safety reasons. It is necessary to calculate the dissociation rate to evaluate sudden methane emissions from mines, evaluate the risks of critical methane concentration in the air and possibility of its explosion. When modeling this type of dissociation, it is also necessary to consider the porosity of a hydrated particle, as well as coal porosity. A wide range of problems is associated with the hydrate porous medium in the following forms: porous medium of silica sand (d); huge amount of natural gas hydrates on the deep ocean floor and as permafrost. The heat transfer rate in such a matrix depends not only on the porosity of hydrate and entire matrix, but also on the contact area between hydrate and silica sand particles. Reduction in the area of permafrost on the Earth could significantly accelerate global warming due to the release of huge amounts of methane. Thus, kinetics of natural gas hydrate decay will vary greatly at ice formation in the porous matrix and in the event of self-preservation.

Dissociation at positive temperatures T > 0 °С occurs on the granule surface without pore formation and it depends on activation energy, pressure and temperature differences (system deviation from the equilibrium) and powder area16. The dissociation rate is quasi-constant for the most period of decay. Decay of gas hydrates at negative temperatures T < 0 °С is different, and its simulation is much more complex and currently there are no reliable calculation methods. At that, the temperature region is divided into three typical physical ranges. In this paper, we consider non-isothermal decay of methane hydrate, when the powder temperature changes from the temperature of liquid nitrogen to the melting point of ice under the external pressure of 1 bar. At that, temperature difference ∆T (∆T = T0 − Ts, T0 is the ambient gas temperature, Ts is the powder temperature) is kept constant in each experiment. ∆T changes in different experiments. In this case for gas hydrate granules, we pass several heat regimes. We performed numerical simulation using filtration-kinetic model of dissociation. We used only one powder layer with the granule diameter d = 0.9–1.2 mm. Therefore, the powder behavior is determined as the total behavior of independent particles. Then, in the dimensionless form m/m0 (m is the initial mass of powder, m0 is the final mass of powder after gas hydrate decay) the behavior of a separate particle and powder layer will be the same. For the gas mass flow it is necessary to multiply the mass of a single particle to a value that the initial powder mass and the particles mass in the simulation will be equal. Dissociation occurs under the external atmospheric pressure of 1 bar. The calculations also used the following data. The average diameter of a particle (granule) is d = 1.05 mm. Initial methane concentration in a particle is 12.41%. The average granule pores diameter is 0.8 μm and for coal pores d = 50 nm, and the pore density changes from 6·1011 m−2 for the first regime (T < 228 K) to 1·108 m−2 for the second annealing regime and then increases again up to 6·1011 (the third regime corresponds to creep, when 270 K < T < 273 K). The heat transfer coefficient αe = 5.2 W/m2K was determined using the expression for the effective heat transfer coefficient for the layer (excluding radiation)68. Heat transfer between the gas medium and granule is determined by heat transfer coefficient αe and temperature difference ∆T. The filtration mechanism inside the granule is described by Darcy relationship. The expression for heat balance of a separate particle (an ideal spherical granule) with the diameter of 1.05 mm will take form (1)

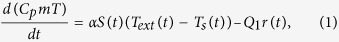graphic file with name srep30324-m1.jpg

where cp is average specific heat capacity (J/(kgK)) (an average value for ice and hydrate), m is the mass of particle (kg), T is average temperature of particle (K), Ts is particle surface temperature, T0 is ambient temperature (∆T = T0 − Ts = const), t is time (s), S is the area of granule surface (m2), αe is heat transfer coefficient (W/(m2K)), Q1 (Q1 = 1020 kJ/kg)69,70 is heat of phase transformation at methane hydrate dissociation, r is the phase transformation rate of gas hydrate into methane and ice (kg/s). The equation for mass balance is written as (2)

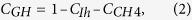graphic file with name srep30324-m2.jpg

where CGH, CIh, CCH4 are mass concentrations of methane hydrate, ice and methane. For the dissociation kinetics without filtration (no pores), we use (3)16,17,18

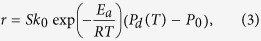graphic file with name srep30324-m3.jpg

Pd(T) is dissociation pressure of CH4 gas at temperature T; P0 is pressure of CH4 gas in the surrounding atmosphere, S is the surface area, k0 (k0 = 3.6·1010 mol/(m2·MPa·s))16 is pre-exponential factor, Ea (Ea = 78,4 kJ/mole)16 is activation energy at phase transformation. The equilibrium pressure depends on the temperature in the form of (4)71,72,73.

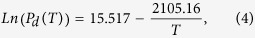graphic file with name srep30324-m4.jpg

where Pd(T), kPa, the temperature corresponds to range 148.8–262.3 К. For the higher temperatures, relationship (5) was used69.

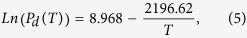graphic file with name srep30324-m5.jpg

the temperature corresponds to range 260–273 К. Methane is filtered through the ice pores of the granule by the Darcy law (6)

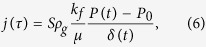graphic file with name srep30324-m6.jpg

where j is the gas mass flow from the particle surface (kg/s), S(t) is the area of filtration (surface of granule, m2), ρg(T) is density of gas (kg/m3), P(t) is pressure inside the pore (Pa), δ is the ice crust thickness (m), kf is permeability coefficient, dynamic viscosity μ was determined by relationship in ref. 74. The permeability coefficient depends on pore diameter dp and pore density σp, according to ref. (7)68

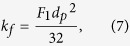graphic file with name srep30324-m7.jpg

F1 is a part of the surface occupied by open pores, it is expressed by surface pore density σp (number of pores per 1 square meter (m−2)) by (8)

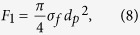graphic file with name srep30324-m8.jpg

The simplified scheme of dissociation is used for simulation, when ice crust thickness δ is distributed uniformly over the circumference of a cylindrical granule. Simulation data on mi/m0 with self-preservation for the second region and without self-preservation for the first and third regions are shown in Fig. 3. There are four specific time intervals from the experiment: (1) high rate of decay due to high pore density, (2) the region of self-preservation; (3) high rates of decay and less noticeable effect of self-preservation, (4) a significant decrease in the rate of decay at the end of decomposition.

Figure 3.

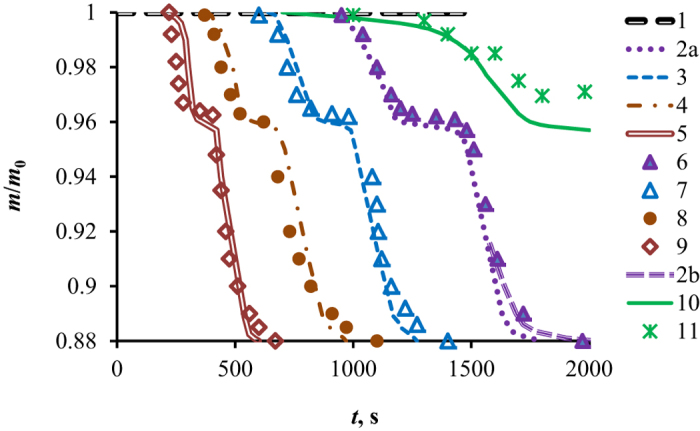
Figure 3

Open in a new tab

Dimensionless mass of methane hydrate (mi/m0) vs. time with self-preservation (1–9 for the artificial gas hydrate; 10–11 for the coal particles): simulation 1–5; 1 – ∆T = 5 °C; 2a–10 °C (1 self-preservation section); 2b–10 °C (2 self-preservation section); 3–15 °C; 4–25 °C; 5–40 °C; experiment 6–9: 6 – ∆T = 10 °C; 7–15 °C; 8–25 °C; 9–40 °C; 10 – simulation for coal (∆T = 15 °C); 11–experiment for coal (∆T = 15 °C).

At ∆T = 10 °C, simulation was performed for one region of self-preservation (curve 2a). Simulation for two regions of self-preservation is presented by curve 2b. Experimental data correspond better to curve 2b, and this proves a significant decrease in the pore density at the end of the third region of dissociation (excluding the zone of ice creep near the melting point). A noticeable deviation of experimental data from calculation is observed near m/m0 = 1. The calculation curve has the value of derivative for curve dm/dt is much smaller than the experimental curve. Perhaps, this is due to a higher rate of gas filtration through the pores, when the thickness of the ice crust tends to 0. It is obvious that for this case, the Darcy equation can be non-linear. A significant deviation of experiment from simulation for coal (curve 10) is also quite logical. To date, there are no reliable data on how water or hydrates are distributed in the pores of different sizes. It is necessary to know gas hydrate distribution over the volume of coal particle. However, it can be clearly seen that the dissociation rate for coal particles is significantly lower than for the granules consisting only of gas hydrate. The lower dissociation rate is certainly connected with a small size of pores in coal and with high thickness of the ice within the coal pore. A similar result can be obtained at dissociation of a porous hydrated matrix (Fig. 2d) at T < 0 °C and with self-preservation. A particularly low rate of decay will be observed for not broken unified rock with great height and small size of cracks in the rock. To simulate this process, it is necessary to know not only the porosity and rock composition, but also size distribution of pores and cracks.

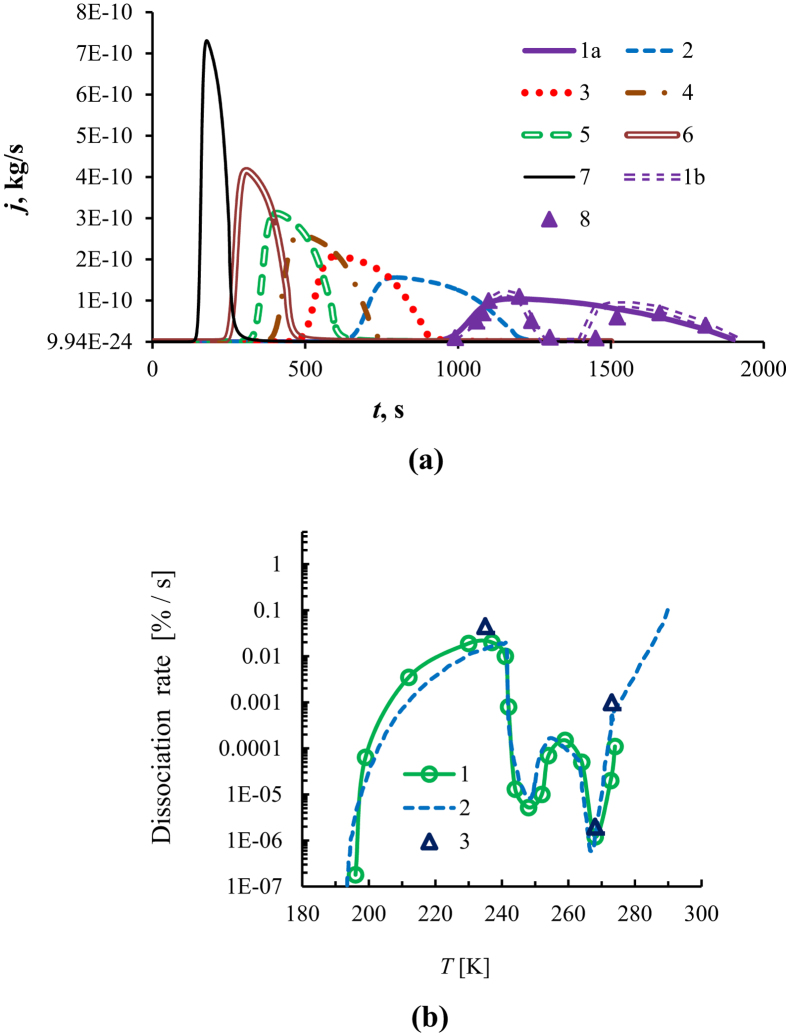
The calculated curves and experimental points for dissociation rate J are shown in Fig. 4a. It is evident that J has strongly non-linear character vs. time: it increases first, reaches the maximum and then decreases. At the final stage of dissociation, the derivative dJ/dt tends to zero, and this is associated with the spherical shape of a granule. When approaching the dissociation front to the center, the mass of emitted methane tends to 022. This non-linear character of dissociation rate was obtained for the first time by simulation and it is in good agreement with the experimental data with consideration of self-preservation (points 8). The similar non-linear character vs. time and temperature was observed in experiments on gas hydrate combustion75,76.

Figure 4.

Figure 4

Open in a new tab

(a) Methane mass flux vs. time: simulation 1–7: 1a – ∆T = 10 °C (without self-preservation); 1b – ∆T = 10 °C (with self-preservation); 2–15 °C; 3–20 °C; 4–25 °C; 5–30 °C; 6–40 °C; 7–70 °C; experiment 8 – ∆T = 10 °C. (b) Dissociation of methane hydrate: Curve 1(experiment from presented paper); Curve 2 (experiment from refs 15 and 77); 3 – simulation.

According to simulation, dissociation rate depends on the pellet diameter, porosity and self-preservation temperature. In the annealing zone, the pore density depends strongly on the sample temperature and changes by several orders of magnitude, which leads to a change in the dissociation rate by 4–5 orders. Figure 4b shows the overall methane hydrate dissociation curves at the atmospheric pressure of 1 bar. Each point of the curve corresponds to a given constant temperature and it was obtained at loss of 50% of methane (i.e., the rate of 50% of methane loss per a certain time). Curve 1 corresponds to the experimental data of this study. Curve 2 corresponds to the experiment of refs 15 and 77.

Experimental points for (1) are obtained as an average value in several repeated experiments. The difference of the average dissociation rate (%/s) for each constant temperature (Ti) on the average value (for the same fixed Ti) is within (8–15%). At that, an error in determination of the dissociation rate is within 3–6%. The difference between the repeated experiments is determined by the fact that it is difficult to maintain the uniform size distribution of granules and that the geometric parameters of porosity vary. Even a slight change in the granule diameter (about 10%) affects significantly the dissociation rate because it is related nonlinearly to the initial diameter of a particle78. Some difference between the experimental values and simulation results can be caused by a slight change in the sample temperature at dissociation and inaccurate data on the value of pore density.

Conclusion

To simulate the dissociation of gas hydrates, it is necessary to take into account heat transfer for both the quasi-isothermal case (while decaying the sample is cooled and heat supply is required) and non-isothermal conditions. For this, it is important to know the temperature difference between the sample and external environment and the heat transfer coefficient. Non-isothermal dissociation in a powder layer of gas hydrate at negative temperatures has four characteristic time regimes: (1) high rate of decay due to high pore density; (2) the region of self-preservation at the annealing temperature and the low rate of decomposition; (3) high rates of decay due to the growth of pore density; (4) a significant decrease in the rate of decay because of an increasing role of self-preservation. Dissociation at low temperatures is fundamentally different from dissociation at temperatures above zero due to formation of porosity and filtering mechanism. The dissociation processes differ significantly at a change in morphology of the surface structures and characteristic sizes of a porous medium. In this regard, kinetics of dissociation of natural gas hydrate for one granule, compressed pellet, coal and various sedimentary rocks, and porous media will differ significantly. Low coal pore diameter (10–100 nm) leads to the significant decrease in the rate of dissociation and in release rate of methane from the sample. The real natural and technical processes are nonstationary and non-uniform, and this should be taken into account at simulation of gas hydrate dissociation. Gas hydrate kinetics dissociation is determined not only by the dissociation front motion, but also by the pore density and their size distribution over the whole volume of the granules. When modeling non-isothermal dissociation for the negative temperatures, it is necessary to take into account heat transfer, kinetics of phase transformation and gas filtering through a porous media. More accurate simulation of the dissociation kinetics is required to improve the technology of long-term storage and transportation of gas hydrate. It will allow us to reduce the cost of technology. Storage efficiency is increased while maintaining the strength of the ice crust at a temperature maximally close to the ice melting point. The presented model assumes quasi-stationary thermal conditions, i.e., a slow change in the powder temperature versus time. At high rates of heating or cooling and a thick layer of powder or porous rock, it is necessary to solve the heat conductivity equation for the solid and gas phases, and this is the subject of further research. To improve simulation accuracy, additional experimental studies are required to determine pore distribution and derive experimental dependence of pore density on temperature at self-preservation, as well as when approaching the melting point. This modeling approach is important for solving the problems of storage and transport of gas hydrates and improving technological efficiency. It is also important for the assessment of the risk of explosion at transportation of raw materials in tankers and sudden release of methane in coal mines as well as for the development of the global warming models.

Additional Information

How to cite this article: Misyura, S. Y. The influence of porosity and structural parameters on different kinds of gas hydrate dissociation. Sci. Rep. 6, 30324; doi: 10.1038/srep30324 (2016).

Acknowledgments

This work was carried out at the Kutateladze Institute of Thermophysics SB RAS and financially supported by the Russian Science Foundation (project number 15-19-10025).

Footnotes

Author Contributions S.Y. Misyura received experimental data, analyzed the results and wrote the manuscript text.

References

  1. Rehder G. et al. Methane hydrate pellet transport using the self-preservation effect: A techno-economic analysis. Energies 5, 2499–2523 (2012). [Google Scholar]
  2. Chon Z. R., Yang S. H. B., Babu P., Linga P. & Li X.-S. Review of natural gas hydrates as an energy resource: Prospects and challenges. Applied Energy 162, 1633–1652 (2016). [Google Scholar]
  3. Sloan E. D. Fundamental principles and applications of natural gas hydrates. Nature 426, 353–359 (2003). [DOI] [PubMed] [Google Scholar]
  4. Howarth R. W., Ingraffea A. & Engelder T. Natural gas: Should fracking stop? Nature 477, 271–275 (2011). [DOI] [PubMed] [Google Scholar]
  5. Kennedy M., David Mrofka D. & Chris von der Borch Snowball Earth termination by destabilization of equatorial permafrost methane clathrate. Nature 453, 642–645 (2008). [DOI] [PubMed] [Google Scholar]
  6. Dresselhaus M. S. & Thomas I. L. Alternative energy technologies. Nature 414, 332–337 (2001). [DOI] [PubMed] [Google Scholar]
  7. Sa J.-H. et al. Hydrophobic amino acids as a new class of kinetic inhibitors for gas hydrate formation. Scientific Report 3(2428), 1–7 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Xu S. et al. Pectin as an extraordinary natural kinetic hydrate inhibitor. Scientific Report 6(23220), 1–6 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Xie Y. et al. Experimental study on a small scale of gas hydrate cold storage apparatus. Appl Energy 87, 3340–3346 (2010). [Google Scholar]
  10. Khokhar A. A., Gudmundsson J. S. & Sloan E. D. Gas storage in structure H hydrates. Fluid Phase Equilibria 150–151, 383–392 (1998). [Google Scholar]
  11. Javanmardi J., Nasrifar K., Najibi S. H. & Moshfeghian M. Economic evaluation of natural gas hydrate as an alternative for natural gas transportation. Appl Therm Eng 25, 1708–1723 (2005). [Google Scholar]
  12. Kim N. J. & Kim C. B. Study on gas hydrates for the solid transportation of natural gas. KSME Int. J 18, 699–708 (2004). [Google Scholar]
  13. Mimachi H. et al. Effect of long-term storage and thermal history on the gas content of natural gas hydrate. Energy and Fuels 29, 4827–4834 (2015). [Google Scholar]
  14. Rehder G. et al. Methane hydrate pellet transport using the self-preservation effect: a techno-economic analysis. Energies 5, 2499–2523 (2012). [Google Scholar]
  15. Kuhs W. F., Genov G., Staykova D. K. & Hansen T. Ice perfection and onset of anomalous preservation of gas hydrates. Phys.Chem.Chem.Phys. 6, 4917–4920 (2004). [Google Scholar]
  16. Kim H. C., Bishnoi P. R., Heidemann R. A. & Rizvi S. S. H. Kinetics of methane hydrate decomposition. Chemical Engineering Science 42, 1645–1653 (1987). [Google Scholar]
  17. Clarke M. & Bishnoi P. R. Determination of the intrinsic rate of ethane gas hydrate decomposition. Chem Eng Sci 55, 4869–4883 (2000). [Google Scholar]
  18. Clarke M. & Bishnoi P. R. Determination of the active energy and the intrinsic rate constant of methane gas hydrate decomposition. Can J Chem Eng 79, 143–147 (2001). [Google Scholar]
  19. Liang H., Song Y. & Chen Y. Numerical simulation for laboratory-scale methane hydrate dissociation by depressurization. Energy Convers Manage 51, 1883–1890 (2010). [Google Scholar]
  20. Selim M. C. & Sloan E. D. Hydrate dissociation in sediment. SPE Reserv Eng 5, 245–251 (1990). [Google Scholar]
  21. Hong H., Pooladi-Darvish M. & Bishnoi P. R. Analytical modeling of gas production from hydrates in porous media. J Can Pet Technol 42, 45–46 (2003). [Google Scholar]
  22. Misyura S. Y. Effect of heat transfer on the kinetics of methane hydrate dissociation. Chemical Physics Letters 583, 34–37 (2013). [Google Scholar]
  23. Song Y., Wang J., Liu Y. & Zhao J. Analysis of heat transfer influences on gas production from methane hydrates using a combined method. Int. J. Heat MassTransfer 92, 766–773 (2016). [Google Scholar]
  24. Nakoryakov V. E., Misyura S. Y. & Elistratov S. L. Methane combustion in hydrate systems: water-hydrate and water-hydrate-isopropanol, Journal of Engineering Thermophysics 22, 169–173 (2013). [Google Scholar]
  25. Nakoryakov V. E., Misyura S. Y. & Elistratov S. L. Combustion of methane hydrates, Journal of Engineering Thermophysics 22, 87–92 (2013). [Google Scholar]
  26. Kowalsky M. B. & Moridis G. J. Comparison of kinetic and equilibrium reaction in simulation gas hydrate behavior in porous media. Energy Convers Manage 48, 1850–1863 (2007). [Google Scholar]
  27. Chernov A. A. & Pil’nik A. A. Mechanism of growth of a crystalline nucleus in a supercooled melt at large deviations from equilibrium, J. Exp. Theor. Phys. Letters. 102, 526–529 (2015). [Google Scholar]
  28. Chernov A. A. Theory of volumetric crystallization of the undercooled melt, Int. J. Heat Mass Transfer. 52, 3290–3296 (2009). [Google Scholar]
  29. Stern L. A., Circone S., Kirby S. H. & Durham W. B. Anomalous preservation of pure methane hydrate at 1 atm. J. Phys. Chem. B 105, 1756–1762 (2001). [Google Scholar]
  30. Wang Y. Evaluation of gas production from marine hydrate deposits at the GMGS2-Site 8, Pearl river Mouth Basin, South China Sea. Energies 9, 222 (2016). [Google Scholar]
  31. Lobban C., Finney J. L. & Kuhs W. F. The structure of a new phase of ice. Nature 391, 268–270 (1998). [Google Scholar]
  32. Falenty A., Hansen T. C. & Kuhs W. F. Formation and properties of ice XVI obtained by emptying a type sII clathrate hydrate. Nature 516, 231–233 (2014). [DOI] [PubMed] [Google Scholar]
  33. Shimada W. et al. Texture change of ice on anomalously preserved methane clathrate hydrate. J. Phys. Chem. B 109, 5802–5807 (2005). [DOI] [PubMed] [Google Scholar]
  34. Zhang G. & Rogers R. E. Ultra-stability of gas hydrates at 1 atm and 268,2K. Chemical Engineering Science 63, 2066–2074 (2008). [Google Scholar]
  35. Nguyen A. H., Koc M. A., Shepherd T. D. & Molinero V. Structure of the ice-clathrate interface. Journal of Physical Chemistry C 119, 4104–4117 (2015). [Google Scholar]
  36. Falenty A. & Kuhs W. F. “Self-preservation of CO2 gas hydrates-surface microstructure and ice perfection. J. Phys. Chem. B 113, 15975–15988 (2009). [DOI] [PubMed] [Google Scholar]
  37. Takeya S. & Ripmeester J. A. Anomalous preservation of CH4 hydrate and its dependence on the morphology of ice. ChemPhysChem 11, 70–73 (2010). [DOI] [PubMed] [Google Scholar]
  38. Madygulov M. S. et al. Study of gas hydrate metastability and its decay for hydrate samples containing unreacted supercooled liquid water below the ice melting point using pulse NMR. Chemical Engineering Science 137, 287–292 (2015). [Google Scholar]
  39. Yi-Ning Lv. et al. Self-Preservation effect for hydrate dissociation in water + diesel oil dispersion systems. Energy Fuels 29, 5563–5572 (2015). [Google Scholar]
  40. Prasad P. S. R. & Chari V. D. Preservation of methane gas in the form of hydrates: Use of mixed hydrates. Journal of Natural Gas Science and Engineering 25, 10–14 (2015). [Google Scholar]
  41. Takeya S. et al. Particle size effect of CH4 hydrate for self-preservation. Chemical Engineering Science 60, 1383–1387 (2005). [Google Scholar]
  42. Mimachi H. et al. Natural gas storage and transportation within gas hydrate of smaller particle: Size dependence of self-preservation phenomenon of natural gas hydrate. Chem. Eng. Sci. 118, 208–213 (2014). [Google Scholar]
  43. Nakamura Y. et al. Combustion characteristics of methane hydrate in a laminar boundary layer. Energy and Fuels 23, 1445–1449 (2009). [Google Scholar]
  44. Misyura S. Y. Efficiency of methane hydrate combustion for different types of oxidizer flow. Energy 103, 430–439 (2016). [Google Scholar]
  45. Kuhs W. F., Klapproth A. & Gotthardt F. The formation of meso- and macroporus gas hydrates. Geophys. Res. Lett. 27, 2929–2932 (2000). [Google Scholar]
  46. Kuhs W. F. et al. The impact of porous microstructures of gas hydrates on their macroscopic properties. International Journal of Offshore and Polar Engineering 14, 305–309 (2004). [Google Scholar]
  47. Kobayashi I., Ito Y. & Mori Y. H. Microscopic observation of clathrate-hydrate films formed at liquid/liquid interfaces, I. Morphology of hydrate films. Chemical Engineering Science 56, 4331–4338 (2001). [Google Scholar]
  48. Boetius A. & Suess E. Hydrate ridge: a natural laboratory for the study of microbial life fueled by methane from near-surface gas hydrates. Chemical Geology 205, 291–310 (2004). [Google Scholar]
  49. Staykova D. K., Kuhs W. F., Salamatin A. N. & Hansen T. “Formation of porous gas hydrates from ice powders: diffraction experiments and multi-stage model”. J Phys Chem B 107, 10299–10311 (2003). [Google Scholar]
  50. Dai J., Snyder X. H. F. & Dutta N. Detection and estimation of gas hydrates using rock physics and seismic inversion: Examples from the northern deepwater Gulf of Mexico: Detection and estimation of gas hydrates using rock physics and seismic inversion: Examples from the northern deepwater Gulf of Mexico. The Leading Edge 23, 60–66 (2004). [Google Scholar]
  51. Dvorkin J., Nur A., Uden R. & Taner T. Rock physics of a gas hydrate reservoir: The Leading Edge 22, 842–847 (2003). [Google Scholar]
  52. Allardice D. J. et al. The characterization of different forms of water in low rank coals and some hydrothermally dried products. Fuel 82, 661–667 (2003). [Google Scholar]
  53. Bustin A. M. M., Bustin R. M., Moudrakovskim I. L., Takeya S. & Ripmeester J. A. Formation of methane clathrate hydrates in coal moisture: implications for coalbed methane resources and reservoir pressures. Energy and Fuels 30, 88–97 (2016). [Google Scholar]
  54. Yang M. et al. A temperature mapping method for THF hydrate formation in porous media. Experimental Heat Transfer: A Journal of Thermal Energy Generation, Transport, Storage, and Conversion. doi: 10.1080/08916152.2014.973977 (2015). [DOI] [Google Scholar]
  55. Zhao J. et al. In-situ visual observation for the formation and dissociation of methane hydrates in porous media by magnetic resonance imaging. Magnetic Resonance Imaging 33, 485–490 (2015). [DOI] [PubMed] [Google Scholar]
  56. Bhatia S. K. & Perlmutter D. D. A random pore model for fluid-solid reactions: I. Isothermal, kinetic control. AIChE Journal 26, 379–386 (1980). [Google Scholar]
  57. Zeldovich Y. B. To the Theory of Reaction on a Porous and Powder-Like Materials. Zhurnal Fizicheskoy Khimii 13, 161–168 (1939). [Google Scholar]
  58. Aris R. Analysis of Processes in Chemical Reactors book. (Leningrad, Khimiya Press, 1967). [Google Scholar]
  59. Slin’ko M. G., Kirillov V. A., Mikhailova I. A. & Fadeev S. I. Mathematical model of the catalytical process on a porous grain in the three-phase system gas-liquid-solid body. Doklady Physical Chemistry 376, 219–223 (2001). [Google Scholar]
  60. Phuoc T. X. & Durbetaki P. Heat and mass transfer analysis of a coal particle undergoing pyrolysis. Int. J. Heat Mass Transfer 30, 2331–2339 (1987). [Google Scholar]
  61. Morell J. I., Amundson N. R. & Park S. K. Dynamics of a single particle during char gasification. Chem. Eng. Sci. 45, 387–401 (1990). [Google Scholar]
  62. Mitchell R. E., Ma L. & Kim B. On the burning behaviour of pulverized coal chars. Combustion and Flame 151, 426–436 (2007). [Google Scholar]
  63. Lu H. et al. Effects of particle shape and size on devolatilization of biomass particle. Fuel 89, 1156–1168 (2010). [Google Scholar]
  64. Nikrityuk P. A. & Meyer B. Gasification processes. Modeling and simulation. (Wiley-VCH, 2014). [Google Scholar]
  65. Jovanovic R., Marek E., Maletic S., Cvetinovic D. & Markovic Z. Lattice Monte Carlo simulation of single coal char particle combustion under oxy-fuel conditions. Fuel 151, 172–181 (2015). [Google Scholar]
  66. Karlstrom O., Brink A. & Hupa M. Desorption kinetics of CO in char oxidation and gasification in O2, CO2 and H2O. Combustion and Flame 162, 788–796 (2015). [Google Scholar]
  67. Simons G. A. Char gasification: Part I. Transport model, Combustion Science and Technology 20, 107–116 (1979). [Google Scholar]
  68. Aerov M. E., Todes O. M. & Narinsky D. A. Apparatuses with the Steady Grain Layer: Hydraulic and Thermal Fundamentals of Operation book. (Leningrad, Khimiya Press, 1979). [Google Scholar]
  69. Istomin V. A. & Yakushev V. S. Gas hydrates in nature book. (Moscow, Nedra Press, 1992). [Google Scholar]
  70. Handa Y. P. Compositions, enthalpies of dissociation, and heat capacities in the range 85 to 270 K for clathrate hydrates of methane, ethane, and propane, and enthalpy of dissociation of isobutane hydrate, as determined by a heat-flow calorimeter. J. Chem. Thermodynamics 18, 915–921 (1986). [Google Scholar]
  71. Takeya S., Ebinuma T., Tsutomu U., Nagao J. & Narita H. Self-preservation effect and dissociation rates of CH4 hydrate. Journal of Crystal Growth 237–239, 379–382 (2002). [Google Scholar]
  72. Makogon T. Y. & Sloan E. D. Phase equilibrium for methane hydrate from 190 to 262 K. J. Chem. Eng. Data 39, 351 (1994). [Google Scholar]
  73. Falabella B. J. A study of natural gas hydrates, Dissertation, University of Massachusetts, University of Microfilms, No. 76–5849, Ann Arbor, MI (1975).
  74. Tables of Physical Units. Hand-Book. Edit. By Kikoin I. K. (Moscow, Atomizdat Press, 1976). [Google Scholar]
  75. Misyura S. Y. & Nakoryakov V. E. Nonstationary combustion of methane with gas hydrate dissociation, Energy and Fuels 27, 7089–7097 (2013). [Google Scholar]
  76. Maruyama Y. et al. Experimental investigation of flame spreading over pure methane hydrate in a laminar boundary layer. Proceedings of the Combustion Institute 34, 2131–2138 (2013). [Google Scholar]
  77. Circone S., Stern L. A. & Kirby S. H. The effect of elevated methane pressure on methane hydrate dissociation. American Mineralogist 89, 1192–1201 (2004). [Google Scholar]
  78. Misyura S. Y. & Donskoy I. G. Dissociation of natural and artificial gas hydrate, Chemical Engineering Science 148, 65–77 (2016). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES