Formation of morphogen gradients: Local accumulation time

Abstract

Spatial regulation of cell differentiation in embryos can be provided by morphogen gradients, which are defined as the concentration fields of molecules that control gene expression. For example, a cell can use its surface receptors to measure the local concentration of an extracellular ligand and convert this information into a corresponding change in its transcriptional state. We characterize the time needed to establish a steady-state gradient in problems with diffusion and degradation of locally produced chemical signals. A relaxation function is introduced to describe how the morphogen concentration profile approaches its steady state. This function is used to obtain a local accumulation time that provides a time scale that characterizes relaxation to steady state at an arbitrary position within the patterned field. To illustrate the approach we derive local accumulation times for a number of commonly used models of morphogen gradient formation.

I. INTRODUCTION

A remarkable transformation of a fertilized egg into an organism with multiple tissues and organs depends on spatial control of cell differentiation [1]. This important function can be provided by concentration fields of molecules that act as dose-dependent regulators of gene expression. Known as morphogen gradients, such concentration fields can be established by reaction-diffusion mechanisms. For example, a locally secreted ligand can diffuse through the tissue and be degraded by cells or extracellular enzymes. Cells located at different distances from the source of signal production are exposed to different levels of this signal and, as a consequence, express different genes that determine whether a cell dies, divides, or differentiates [2].

A morphogen gradient was a purely theoretical concept for a better part of the 20th century [3,4]. At the end of 1980’s, the first morphogen gradients were identified in fruit fly development. Shortly thereafter, morphogens were discovered in other organisms, including vertebrates. Today morphogen gradients are studied in a large number of systems [5–7]. Candidate morphogens are identified by genetic approaches, purified biochemically, and their distributions in tissues are visualized by multiple imaging tools. As the experimental analysis of morphogen gradients becomes increasingly quantitative, it is important to develop a theoretical framework that can address the dynamics of morphogen gradients and its interaction with the patterned tissue.

In the simplest case, morphogens act locally. A cell can use its surface receptors to measure the local value of the extracellular morphogen concentration and translate this information into a corresponding change in the activation of its signaling pathways and gene expression [8,9]. The question arises of whether or not the time of the morphogen gradient formation is small compared to the time of the cell differentiation. If so, then the cell fate is determined by the steady-state value of the local morphogen concentration. If not, then the cell reads the local morphogen concentration that changes with time. This question was first posed by Francis Crick [10] who recognized its importance more than 40 years ago.

In analyzing the question, one faces a conceptual problem of how to characterize the local time required to establish the gradient at a given point of the patterned field. To the best of our knowledge, a systematic framework for addressing this question is still lacking. In this paper, we fill in this gap and provide such a framework for the simplest models of morphogen gradient formation. We illustrate its application by analyzing a number of reaction-diffusion models. Some of the results derived in the present paper have been reported in our recent short communication [11], where the consideration is formulated in terms of the concentrations. Here we derive the results using the Green function formalism, which is the most natural approach to the problem.

The outline of the paper is as follows. The general formalism is developed in the next section. In Sec. III the formalism is used to find the local accumulation time for four models of increasing complexity. The simplest situation when a localized source of diffusing particles is located at the boundary of a semi-infinite interval is considered in Sec. IIIA. The result obtained is then generalized to the cases of a distributed source of the particles and a finite interval in Secs. IIIB and IIIC, respectively. A two-state model when diffusing particles can reversibly bind to immobile traps and are degraded in both mobile and immobile states with different rates is considered in Sec. IIID. One can skip the technical details and find the expressions for the local accumulation time for the four models in Eqs. (3.14),(3.20), (3.26), (3.38), and (3.39). These expressions show how the local accumulation times depend on the parameters of the models. These dependencies are illustrated in Figs. 2 and 3. We illustrate the application of our results to a real morphogen gradient in Sec. IV where we calculate the local accumulation time for the gradient formed by Decapentaplegic (Dpp), which is a bone morphogenetic protein ligand that controls pattern formation and growth in the wing imaginal disk in Drosophila.

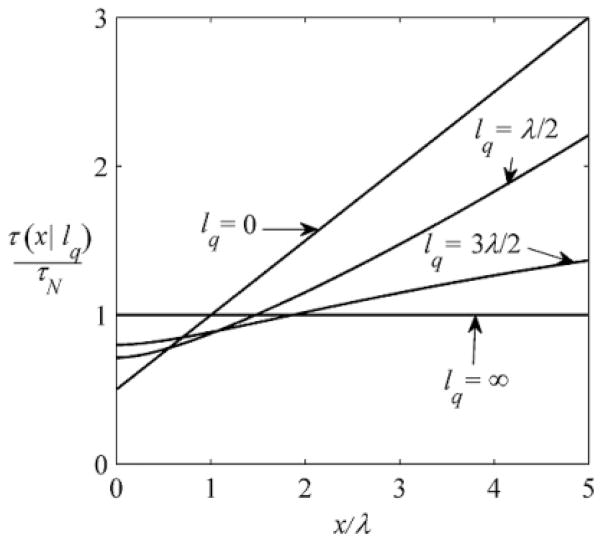
FIG. 2.

Local accumulation time τ (x|l_q) given in Eq. (3.20), for several values of the injection length, l_q = 0, λ/2, 3λ/2 , ∞.

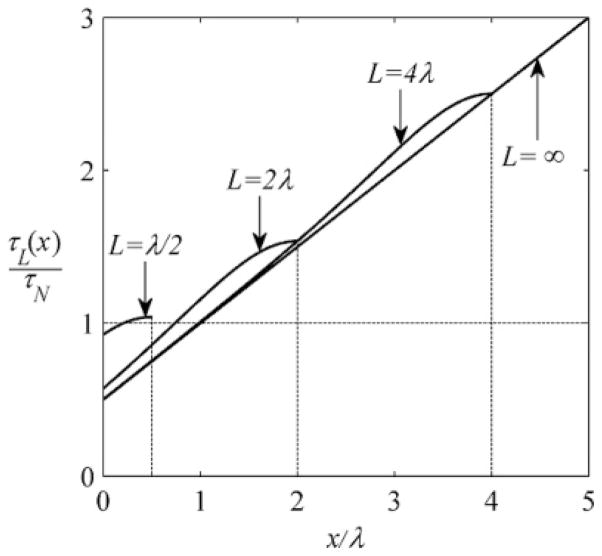
FIG. 3.

Local accumulation time τ_L(x) given in Eq. (3.26), for intervals of different length L = λ/2, 2λ, 4λ, ∞.

II. LOCAL ACCUMULATION TIME

Consider particles injected into an interval of length L (0 < x < L) with reflecting boundaries. The particles diffuse with diffusivity D and are degraded with the rate constant k. The source of the particles, q(x), is independent of time. It is characterized by the total injection rate Q:

$$Q={\int }_0^{L}q(x)dx,$$ (2.1)

and the normalized injection density p_q (x):

$$q(x)=Q{p}_q(x),{\int }_0^L{p}_q(x)dx=1.$$ (2.2)

The interval is free from particles when injection begins at t = 0. The particle concentration c(x,t ) at point x and time t satisfies

$$\frac{\partial c}{\partial t}=D\frac{{\partial }^{2}c}{\partial x^2}-kc+q(x),0<x<L,$$ (2.3)

with initial and boundary conditions

$$c(x,0)=0,{\frac{\partial c(x,t)}{\partial x}|}_{x=0,L}=0.$$ (2.4)

As t →∞, c(x,t ) approaches its steady-state (ss) value c_ss (x):

$$c_{ss}(x)=\underset{t\to \infty }{lim}c(x,t).$$ (2.5)

Our goal is to characterize the kinetics of this process at an arbitrary observation point x.

To begin with, we introduce the local relaxation function R(t |x) defined as

$$R(t\mid x)=\frac{c(x,t)-c_{ss}(x)}{c(x,0)-c_{ss}(x)}=1-\frac{c(x,t)}{c_{ss}(x)}.$$ (2.6)

The ratio c(x,t )/c_ss (x) is the fraction of the steady-state concentration of the particles accumulated at point x by time t . Denoting this fraction by W(t |x), we can write

$$R(t\mid x)=1-W(t\mid x),W(t\mid x)=\frac{c(x,t)}{c_{ss}(x)}.$$ (2.7)

As time increases from zero to infinity, W(t |x) increases from zero to unity while the relaxation function decreases from unity to zero.

We can use W(t |x) or R(t |x) to introduce the function φ(t |x) defined by

$$\phi (t\mid x)=\frac{\partial W(t\mid x)}{\partial t}=-\frac{\partial R(t\mid x)}{\partial t}.$$ (2.8)

This function can be interpreted as the local probability density of time associated with the formation of the steady-state concentration profile at point x. Then the mean time τ (x) is

$$\tau (x)={\int }_0^{\infty }t\phi (t\mid x)dt={\int }_0^{\infty }R(t\mid x)dt,$$ (2.9)

which is the local accumulation time that characterizes the process at point x.

For linear models of morphogen gradient formation, the local accumulation time can be found analytically, based on the relation between the local accumulation time and the particle propagator or the Green’s function G(x,t |x₀). The latter is the probability density of finding the particle at point x at time t conditional on the particle being at x₀ at t = 0. The propagator satisfies

$$\frac{\partial G}{\partial t}=\frac{{\partial }^{2}G}{\partial x^2}-kG,0<x<L,$$ (2.10)

with initial and boundary conditions

$$G(x,0\mid x_0)=\delta (x-x_0),{\frac{\partial G(x,t\mid x_0)}{\partial x}|}_{x=0,L}=0.$$ (2.11)

Using the propagator, the particle concentration profile at time t can be written as

$$c(x,t)={\int }_0^{t}d{t}^{\prime }{\int }_0^{L}G(x,t-t^{\prime }\mid x_0)q(x_0)d{x}_0.$$ (2.12)

Substituting here q(x₀) = Qp_q (x₀) [Eq. (2.2)], we arrive at

$$c(x,t)=Q{\int }_0^t{\langle G(x,t-t^{\prime }\mid x_0)\rangle }_{q}d{t}^{\prime },$$ (2.13)

where 〈G(x,t |x₀)〉_q is the propagator G(x,t |x₀) averaged over the particle starting point x₀ with the normalized injection density p_q (x₀):

$${\langle G(x,t\mid x_0)\rangle }_q={\int }_0^{L}G(x,t\mid x_0)p_q(x_0)d{x}_0.$$ (2.14)

The Laplace transform of c(x,t) [Eq. (2.13)] is

$$\widehat{c}(x,s)={\int }_0^{\infty }c(x,t)e^{-st}dt=\frac{Q}{s}\langle \widehat{G}{(x,s\mid x_0\rangle }_q,$$ (2.15)

where 〈Ĝ(x,s|x₀)〉_q is the Laplace transform of the averaged propagator. The steady-state concentration c_ss (x) can be expressed in terms of this Laplace transform at s = 0:

$$c_{ss}(x)=\underset{s\to 0}{lim}s\widehat{c}(x,s)=Q{\langle \widehat{G}(x,0\mid x_0)\rangle }_q.$$ (2.16)

We use Eqs. (2.15) and (2.16) to present the Laplace transform of the relaxation function, Eq. (2.6), in terms of the Laplace transform of the averaged propagator:

$$\widehat{R}(s\mid x)=\frac{1}{s}\left[1-\frac{{\langle \widehat{G}(x,s\mid x_0)\rangle }_q}{{\langle \widehat{G}(x,0\mid x_0)\rangle }_q}\right].$$ (2.17)

According to the definition of τ (x) [Eq. (2.9)], the local accumulation time is the Laplace transform of the relaxation function at s = 0:

$$\tau (x)=\underset{s\to 0}{lim}\widehat{R}(s\mid x).$$ (2.18)

Substituting here R̂ (s|x) given in Eq. (2.17) and using L’Hospital’s rule we obtain

$$\begin{array}{l}\tau (x)={-\frac{1}{{\langle \widehat{G}(x,0\mid x_0)\rangle }_q}\frac{d{\langle \widehat{G}(x,s\mid x_0)\rangle }_q}{ds}|}_{s=0}\\ ={-\frac{dln{\langle \widehat{G}(x,s\mid x_0)\rangle }_q}{ds}|}_{s=0}.\end{array}$$ (2.19)

This formula, which is one of the main results of the present paper, establishes the relation between the local accumulation time and the particle propagator. Below we use this result to characterize the dynamics of gradients in several commonly used reaction-diffusion models.

III. ILLUSTRATIVE EXAMPLES

As an introduction to specific examples, we consider the relaxation to the steady state of the total number of particles, N(t ), accumulated in the system by time t :

$$N(t)={\int }_0^{L}c(x,t)dx.$$ (3.1)

The kinetic equation describing the dynamics of N(t ) can be obtained by integrating Eq. (2.3) with respect to x from zero to L. The result is

$$\frac{dN(t)}{dt}=-kN(t)+Q.$$ (3.2)

Solving this equation with the initial condition N(0) = 0 we obtain

$$N(t)=N_{ss}(1-e^{-kt}),$$ (3.3)

where N_ss = Q/k is the total number of particles in the system at steady state.

The relaxation function of the total number of particles, R_N(t ), is defined as

$$R_N(t)=\frac{N(t)-N_{ss}}{N(0)-N_{ss}}=1-\frac{N(t)}{N_{ss}}.$$ (3.4)

Substituting here N(t ), given in Eq. (3.3), we arrive at

$$R_N(t)=e^{-kt}.$$ (3.5)

The accumulation time τ_N that characterizes accumulation of the particles in the system is

$${\tau }_N={\int }_0^{\infty }{R}_N(t)dt=\widehat{R}(s){\mid }_{s=0}=k^{-1},$$ (3.6)

as might be expected for the kinetics described by the rate equation in Eq. (3.2).

A. Localized source, semi-infinite interval

As a first application of the general formalism, consider the case of a semi-infinite interval, L→∞, with the particle source localized on its reflecting boundary at x = 0. This model is commonly used as the first step in the analysis of morphogen gradient dynamics [12–15]. In this case,

$$p_q(x)=\delta (x),$$ (3.7)

and the averaged propagator takes the form

$${\langle G(x,t\mid x_0)\rangle }_q=G(x,t\mid 0)=\frac{1}{\sqrt{\pi Dt}}{e}^{-\frac{x^2}{4Dt}-kt},$$ (3.8)

where we have used the solution for the propagator G(x,t |0), which can be readily obtained.

The Laplace transform of this propagator is given by

$$\widehat{G}(x,s\mid 0)=\frac{1}{\lambda \sqrt{1+s/k}}{e}^{-(x/\lambda )\sqrt{1+s/k}},$$ (3.9)

where $\lambda =\sqrt{D/k}$ is a characteristic length. This length specifies the steady-state concentration profile, which in this case is given by

$$c_{ss}(x)=\frac{N_{ss}}{\lambda }{e}^{-x/\lambda }.$$ (3.10)

The length λ has a simple physical interpretation. To illustrate this we use the fact that the product kĜ(x,0|0) is the probability density of distance x from the origin to the point where the particle was degraded. The mean value of this distance is

$${\int }_0^{\infty }x[k\widehat{G}(x,0\mid 0)]dx=\sqrt{D/k}=\lambda ,$$ (3.11)

where we have used the formula in Eq. (3.9). Thus, λ is the mean distance traveled by the particle to its degradation point.

Substituting the Laplace transform of the propagator, Eq. (3.9), into Eq. (2.17), we find the Laplace transform of the relaxation function:

$$\begin{array}{l}\widehat{R}(s\mid x)=\frac{1}{s}\left[1-\frac{\widehat{G}(x,s\mid 0)}{\widehat{G}(x,0\mid 0)}\right]\\ =\frac{1}{s}\left[1-\frac{1}{\sqrt{1+s/k}}{e}^{-(x/\lambda )(\sqrt{1+s/k}-1)}\right].\end{array}$$ (3.12)

Inverting this Laplace transform we obtain

$$R(t\mid x)=\frac{1}{2}\left[\mathit{erfc}\left(\sqrt{kt}-\frac{x/\lambda }{2\sqrt{kt}}\right)+e^{2x/\lambda }\mathit{erfc}\left(\sqrt{kt}+\frac{x/\lambda }{2\sqrt{kt}}\right)\right],$$ (3.13)

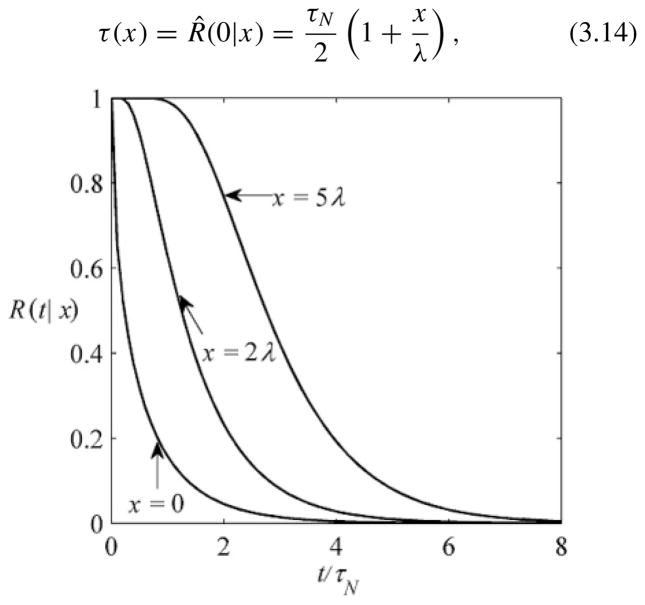
where erf c(z) is the complementary error function [16]. As might be expected, the larger the distance from the origin to the observation point x, the slower the relaxation function approaches zero (Fig. 1). The local accumulation time can be found using R̂ (s|x) in Eq. (3.12):

$$\tau (x)=\widehat{R}(0\mid x)=\frac{{\tau }_N}{2}\left(1+\frac{x}{\lambda }\right),$$ (3.14)

where τ_N = 1/k [Eq. (3.6)]. For x ≪ λ, τ (x) ≈ τ_N/2, whereas for x ≫ λ, $\tau (x)\approx (1/2)\sqrt{{\tau }_N{\tau }_D(x)}$, where τ_D(x) = x²/D is the characteristic time of diffusive passage of distance x. The linear dependence of the relaxation time on x is counterintuitive. Based on general arguments, one might expect that the relaxation time is determined by the largest of the two characteristic times τ_N and τ_D(x). While this is true for x ≪ λ, the general arguments fail for x ≫ λ.

FIG. 1.

Time dependencies of the local relaxation functionR(t |x) given in Eq. (3.13) at several observation points: x = 0 , 2λ , 5λ.

Note that the relaxation function in Eq. (3.13) can be obtained by substituting the solution for c(x,t ) obtained in [17] into the definition of R(t |x) [Eq. (2.6)]. The authors of this work suggested the following phenomenological approximation for the time-dependent concentration profile: c(x,t ) = c(0,t) exp[– (x/λ(t ))^{p(t )}], where λ(t ) is a time-dependent length scale and p(t ) is the exponent that monotonically decreases with time. The approximation is constructed so that c(x,t ) has the same structure as c_ss (x) [Eq. (3.10)]; namely, the concentration is scaled by its value at x = 0 and its dependence on x is exponential. As t →∞, the length scale approaches its steady-state value, $\lambda =\sqrt{D/k}$, while the exponent approaches unity. As a result, the distribution approaches the steady-state exponential profile, Eq. (3.10). The structure of the phenomenological approximation is qualitatively different from that used in our approach, in which the time-dependent concentration at point x is scaled by its steady-state value. According to the definition of the relaxation function, Eq. (2.6), we have c(x,t ) = [1 – R(t |x)]c_ss (x).

B. Distributed source, semi-infinite interval

Our second example ismotivated by the recent experiments in the early Drosophila embryo, where it has been proposed that the length scale of the patterning gradient is controlled by the spatial distribution of the source of signal production [18]. Consider the case of a distributed source of the particles injected into a semi-infinite interval, x > 0, terminated by a reflecting boundary at x = 0. We assume that the normalized injection density is

$$p_q(x)=\frac{1}{l_q}{e}^{-x/l_q},$$ (3.15)

where l_q in the mean injection length:

$$l_q={\int }_0^{\infty }x{p}_q(x)dx.$$ (3.16)

As l_q → 0, p_q (x) tends to δ(x) and we recover the situation discussed in Sec. IIIA.

Using the method of images, we find the propagator of a particle injected at x₀, x₀ > 0, at t = 0:

$$G(x,t\mid x_0)=G(x+x_0,t\mid 0)+G(x-x_0,t\mid 0).$$ (3.17)

The Laplace transform of this propagator is

$$\widehat{G}(x,s\mid x_0)=\widehat{G}(x+x_0,s\mid 0)+\widehat{G}(x-x_0,s\mid 0).$$ (3.18)

Averaging this propagator over x₀ with the normalized injection density given in Eq. (3.15), we obtain

$${\langle \widehat{G}(x,s\mid x_0)\rangle }_q=\frac{\lambda e^{-(x/\lambda )\sqrt{1+s/k}}-l_q\sqrt{1+s/k}{e}^{-x/l_q}}{k\sqrt{1+s/k}[{\lambda }^2-l_q^2(1+s/k)]},$$ (3.19)

where we have used the formula for the Laplace transform of the propagator given in Eq. (3.9).

Substituting the averaged propagator [Eq. (3.19)] into Eq. (2.19), we find the accumulation time at point x for an arbitrary value of the injection length, τ (x|l_q ):

$$\tau (x\mid l_q)=\frac{{\tau }_N}{2}\left[\left(1+\frac{x}{\lambda }\right)\frac{\lambda e^{-x/\lambda }}{\lambda e^{-x/\lambda }-l_q{e}^{-x/l_q}}+\frac{2l_q^2}{l_q^2-{\lambda }^2}\right].$$ (3.20)

As l_q → 0, this reduces to τ (x) given in Eq. (3.14). At l_q = λ, the result simplifies:

$$\tau (x\mid l_q=\lambda )=\frac{{\tau }_N}{4}\left(3+\frac{x^2}{\lambda (x+\lambda )}\right).$$ (3.21)

As illustrated in Fig. 2, in our model the delocalization of the source slows down the formation of the steady-state concentration profile at small x and accelerates this process at large x. As follows from Eq. (3.20), τ (0|l_q ) is always larger than τ (0|0):

$$\tau (0\mid l_q)=\tau (0\mid 0)\left(1+\frac{l_q}{\lambda +l_q}\right).$$ (3.22)

Large-x asymptotic behavior of τ (x|l_q ) depends on whether l_q is smaller or larger than λ:

$$\tau (x\mid l_q)\underset{x\to \infty }{\to }\{\begin{array}{cc}\tau (x\mid 0),& l_q<\lambda \\ \tau (0\mid 0)\frac{2l_q^2}{l_q^2-{\lambda }^2},& \lambda <l_q.\end{array}$$ (3.23)

As l_q →∞(uniform injection of particles), τ (x|l_q ) becomes independent of x and takes its asymptotic value τ (x|∞) = 2τ (0|0) = τ_N = 1/k.

C. Localized source, finite interval

We now discuss how a finite length L of the interval affects the kinetics of the formation of the steady-state concentration profile. In addition to problems with morphogen gradients, this case is also relevant for the analysis of intracellular concentration profiles; a number of examples can be found in recent publications [19–24]. Consider the case when the source of the particles is localized near the reflecting boundary at x = 0, and the normalized injection density is given by Eq. (3.7). In this case, the averaged propagator, Eq. (2.14), is identical to the propagator of a particle that starts from the left boundary of the interval:

$${\langle G_L(x,t\mid x_0)\rangle }_q=G_L(x,t\mid 0),$$ (3.24)

where the subscript L is used to indicate the length of the interval. The Laplace transform of G_L(x,t|0) is given by the following expression:

$${\widehat{G}}_L(x,t\mid 0)=\frac{cosh[(L-x)\sqrt{(s+k)/D}]}{\sqrt{(s+k)D}sinh[L\sqrt{(s+k)/D}]}.$$ (3.25)

Using this result, one can find the local accumulation time from Eq. (2.19):

$${\tau }_L(x)=\frac{{\tau }_N}{2}\left[1+\frac{L}{\lambda }coth\left(\frac{L}{\lambda }\right)-\frac{L-x}{\lambda }tanh\left(\frac{L-x}{\lambda }\right)\right].$$ (3.26)

As L → ∞, τ_L(x) reduces to τ(x) derived for the problem with a semi-infinite interval. When L ≪ λ, the accumulation time is independent of x and is identical to τ_N = 1/k. In the opposite limiting case, L ≫ λ, τ(x) is larger than τ_∞(x) inside the interval and close to τ_∞(0) and τ_∞(L) at its ends. This is illustrated in Fig. 3.

D. Two-state problem

Finally, we consider the case where diffusing particles can reversibly bind to immobile traps and are degraded, with different rates, in both mobile and immobile states [25,26]. This two-state model is used for gradients that are formed by locally secreted proteins that diffuse through the extracellular medium and bind to cell surface receptors, which both transduce the signal and limit its spatial range by mediating ligand degradation [27–30]. To analyze this case, we use a two-state model in which injected particles can be in mobile (m) and immobile (im) states. Transitions between these states are described by the rate constants α and β. In each state, particles are degraded with the rate constants k_m and k_im, respectively. We assume that particles are injected into the mobile state by a localized source located near the reflecting boundary at x = 0 of a semi-infinite interval, x > 0.

The particle propagator has two components, G_m(x,t) and G_im(x,t), which satisfy

$$\frac{\partial G_m}{\partial t}=D\frac{{\partial }^2{G}_m}{\partial x^2}-(k_m+\alpha )G_m+\beta G_{im},$$ (3.27)

$$\frac{\partial G_{im}}{\partial t}=\alpha G_m-(k_{im}+\beta )G_{im},$$ (3.28)

with the initial and boundary conditions

$$G_m(x,0)=\delta (x),G_{im}(x,0)=0,{\frac{\partial G_m(x,t)}{\partial x}|}_{x=0}=0.$$ (3.29)

The problem can be readily solved in Laplace space. The result is

$${\widehat{G}}_m(x,s)=\frac{1}{\sqrt{D\sigma }}{e}^{-x\sqrt{\sigma /D}},$$ (3.30)

$${\widehat{G}}_{im}(x,s)=\frac{\alpha }{k_{im}+\beta +s}{\widehat{G}}_m(x,s),$$ (3.31)

where

$$\sigma =k_m+\alpha +s-\frac{\alpha \beta }{k_{im}+\beta +s}.$$ (3.32)

We use the two components of the propagator to describe time-dependent concentration profiles of mobile and immobile particles, c_m(x,t) and c_im(x,t), respectively:

$$c_m(x,t)=Q{\int }_0^t{G}_m(x,t^{\prime })d{t}^{\prime },c_{im}(x,t)=Q{\int }_0^t{G}_{im}(x,t^{\prime })d{t}^{\prime }.$$ (3.33)

As t → ∞ the concentration profiles approach their steady states,

$$\begin{array}{c}{c}_{m,ss}(x)=Q{\int }_0^{\infty }{G}_m(x,t)dt=Q{\widehat{G}}_m(x,0),\\ c_{im,ss}(x)=Q{\int }_0^{\infty }{G}_{im}(x,t)dt=Q{\widehat{G}}_{im}(x,0).\end{array}$$ (3.34)

We introduce a two-component local relaxation function with the components R_m(t|x) and R_im(t|x) defined as

$$\begin{array}{c}{R}_m(t\mid x)=\frac{c_m(x,t)-c_{m,ss}(x)}{c_m(x,0)-c_{m,ss}(x)}=1-\frac{c_m(x,t)}{c_{m,ss}(x)},\\ R_{im}(t\mid x)=\frac{c_{im}(x,t)-c_{im,ss}(x)}{c_{im}(x,0)-c_{im,ss}(x)}=1-\frac{c_{im}(x,t)}{c_{im,ss}(x)}.\end{array}$$ (3.35)

We use these functions to define local accumulation times τ_m(x) and τ_im(x):

$$\begin{array}{c}{\tau }_m(x)={\int }_0^{\infty }{R}_m(t\mid x)dt={\widehat{R}}_m(s\mid x){\mid }_{s=0}=-\frac{dln{\widehat{G}}_m(x,s)}{ds}{\mid }_{s=0},\\ {\tau }_{im}(x)={\int }_0^{\infty }{R}_{im}(t\mid x)dt={\widehat{R}}_{im}(s\mid x){\mid }_{s=0}=-\frac{dln{\widehat{G}}_{im}(x,s)}{ds}{\mid }_{s=0},\end{array}$$ (3.36)

where R̂_m(s|x) and R̂_im(s|x) are the Laplace transforms of the relaxation function components.

It is convenient to introduce a renormalized degradation rate constant in the mobile state, $k_m^{\#}$, defined by

$$k_m^{\#}=k_m+\frac{\alpha k_{im}}{k_{im}+\beta },$$ (3.37)

and the length scale λ^# defined in terms of $k_m^{\#}:{\lambda }^{\#}=\sqrt{D/k_m^{\#}}$. Using these quantities, the two local accumulation times can be written as

$${\tau }_m(x)=\frac{1}{2k_m^{\#}}\left[1+\frac{\alpha \beta }{{(k_{im}+\beta )}^2}\right]\left(1+\frac{x}{{\lambda }^{\#}}\right),$$ (3.38)

$${\tau }_{im}(x)={\tau }_m(x)+\frac{1}{k_{im}+\beta }.$$ (3.39)

The fact that τ_im(x) > τ_m(x) is not surprising since the particles are injected into the mobile state. As expected, τ_m(x) in Eq. (3.38) reduces to the accumulation time τ(x) in Eq. (3.14) as β → ∞.

IV. CONCLUDING REMARKS

We have developed a general approach for characterizing the local kinetics of the morphogen gradient formation. The approach is based on consideration of the relaxation function, which describes relaxation of the concentration to its steady-state value at an arbitrary location within the patterned field. This function is used to introduce the local accumulation time that provides a time scale characterizing local accumulation of themorphogen. Our approach is illustrated by consideration of a number of commonly used models that account for diffusion and degradation of locally produced chemical signals.

To illustrate the application of our results to real morphogen gradients, we calculate the local accumulation time for the gradient formed by Decapentaplegic (Dpp), a bone morphogenetic protein ligand that controls pattern formation and growth in the wing imaginal disk in Drosophila [31]. Dpp was one of the first discovered morphogen gradients and is one of the few gradients for which there are quantitative measurements of diffusivity, degradation time, and positions of the gene expression boundaries established by the gradient [32,33]. Dpp is secreted from the anteroposterior compartment boundary in the wing disk, diffuses in the extracellular space, and is degraded as a consequence of its binding to cell surface receptors. Based on the fluorescence recovery after photobleaching (FRAP) experiments, the Gonzalez-Gaitan group reported that Dpp has a lifetime of ~66 minutes and an effective diffusivity of 0.01 μm²/sec, which leads to $\lambda =\sqrt{D/k}=20\mu \mathrm{m}$. The most distant gene expression boundary controlled by the Dpp gradient is located 40 μm from the site of Dpp production. Substituting these values into Eq. (3.14), we get the local accumulation time of 99 min. This estimate can be compared to the time scale of cell divisions in the wing disk, which is always greater than 3 hours. Based on this analysis we can conclude that the relaxation time of the Dpp gradient is smaller than the characteristic time of tissue growth. We emphasize that this analysis is based on the simplest model of the Dpp gradient. In the future, it can be extended to more complex models [30].

We have shown that both the relaxation function and the local accumulation time are independent of the total injection rate. Moreover, the local accumulation time can be expressed in terms of the propagator that describes the fate of a single particle. This is a consequence of the linearity of the considered models. Linear models are applicable when the morphogen concentration is not too high. When the concentration is high enough, such models fail and nonlinearity of the degradation process must be taken into account [34].