Growth and splitting of neural sequences in songbird vocal development

Abstract

Neural sequences are a fundamental feature of brain dynamics underlying diverse behaviors, but the mechanisms by which they develop during learning remain unknown. Songbirds learn vocalizations composed of syllables; in adult birds, each syllable is produced by a different sequence of action potential bursts in the premotor cortical area HVC. Here we carried out recordings of large populations of HVC neurons in singing juvenile birds throughout learning to examine the emergence of neural sequences. Early in vocal development, HVC neurons begin producing rhythmic bursts, temporally locked to a ‘prototype’ syllable. Different neurons are active at different latencies relative to syllable onset to form a continuous sequence. Through development, as new syllables emerge from the prototype syllable, initially highly overlapping burst sequences become increasingly distinct. We propose a mechanistic model in which multiple neural sequences can emerge from the growth and splitting of a common precursor sequence.

Introduction

Sequences of neural activity have been observed during various behaviors, including navigation^1–4, short-term memory^5–7, decision making^8,9, and complex movements^10,11, suggesting that neural sequences are a fundamental form of brain dynamics^12,13. However, the circuit mechanisms underlying the generation of neural sequences and their development during learning are not well understood.

The songbird is a good model system to address such questions because the song produced by adults is learned during development^14–18. Furthermore, adult song is associated with neural sequences in nucleus HVC (used as a proper name)^19–24, a premotor cortical area necessary for the production of stereotyped adult song^25–30. Most projection neurons in HVC generate a brief burst of spikes at one specific time in the song motif and different neurons are active at different times in the song^19–24,30; thus, distinct syllable types are produced by largely non-overlapping neural sequences in HVC. Here we ask how these different neural sequences are constructed during vocal development.

Zebra finches acquire their stereotyped song through a gradual learning process^14,31. Young birds initially produce a highly variable ‘subsong’³¹, akin to human babbling¹⁵. Birds then enter the protosyllable stage as they begin to incorporate syllables of a characteristic ~100 ms duration^32–35. This is followed by the gradual emergence of multiple syllable types^32,33,36, and a final ‘motif’ stage in which syllables are produced in a reliable sequence. While HVC activity is not required for subsong^27,34,35, it is required for song components in all later stages, including protosyllables, emerging syllable types, and adult song^{25–28,34,35}.

Developmental progression of HVC activity

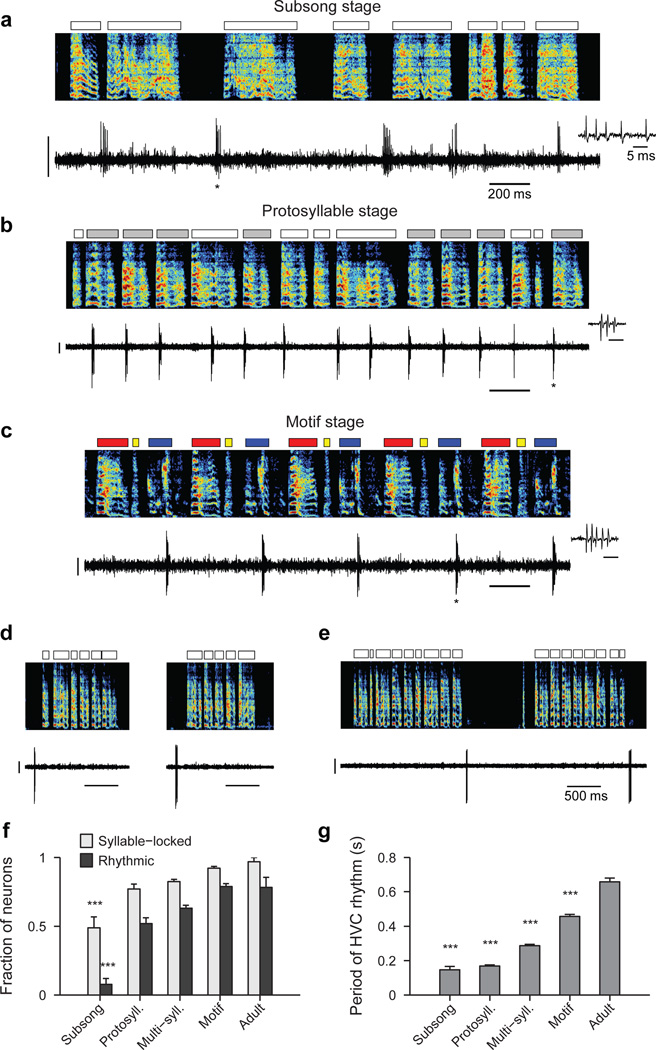
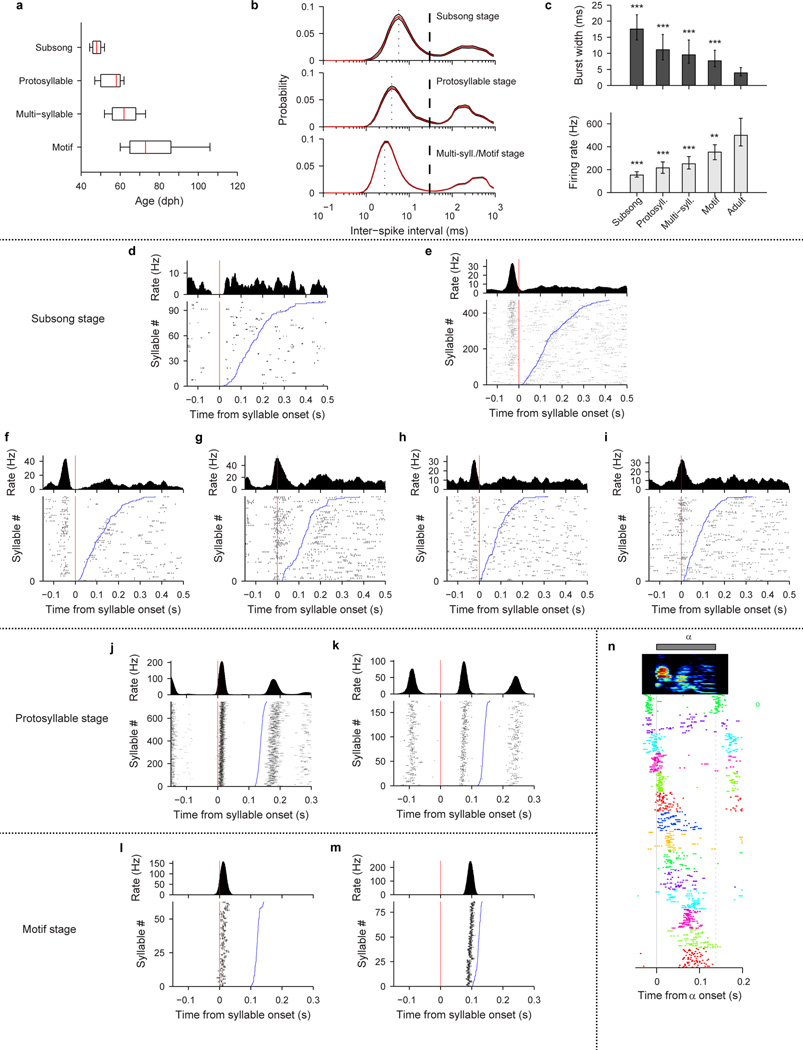
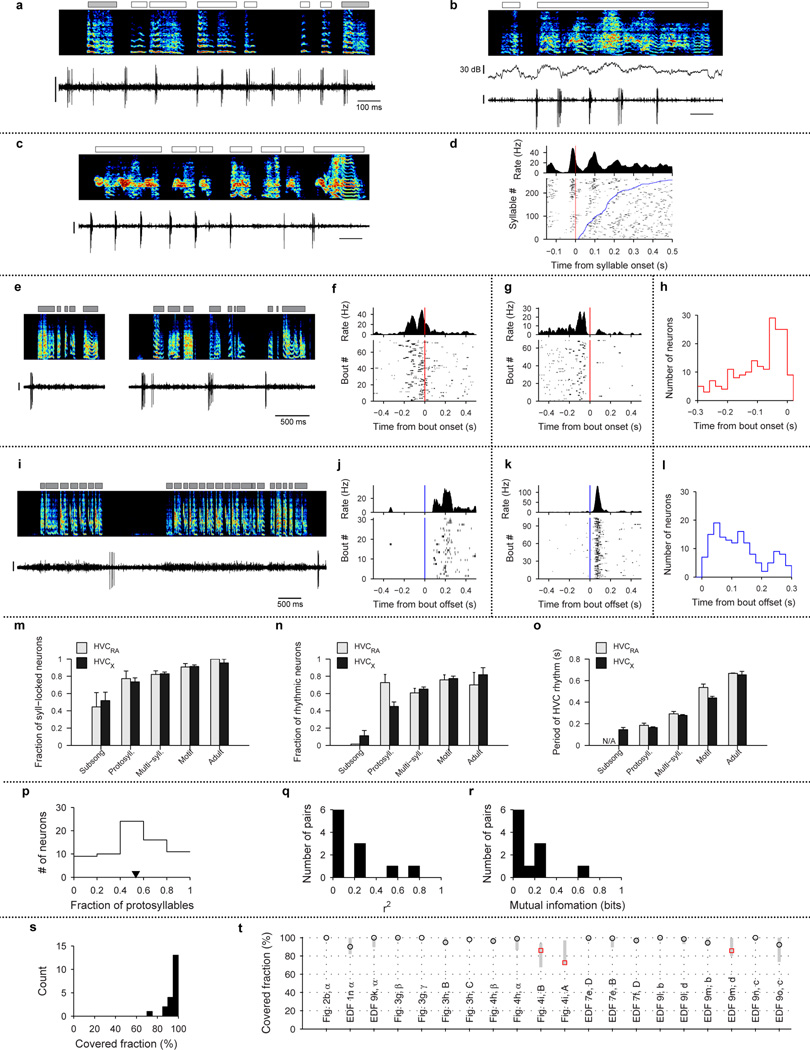
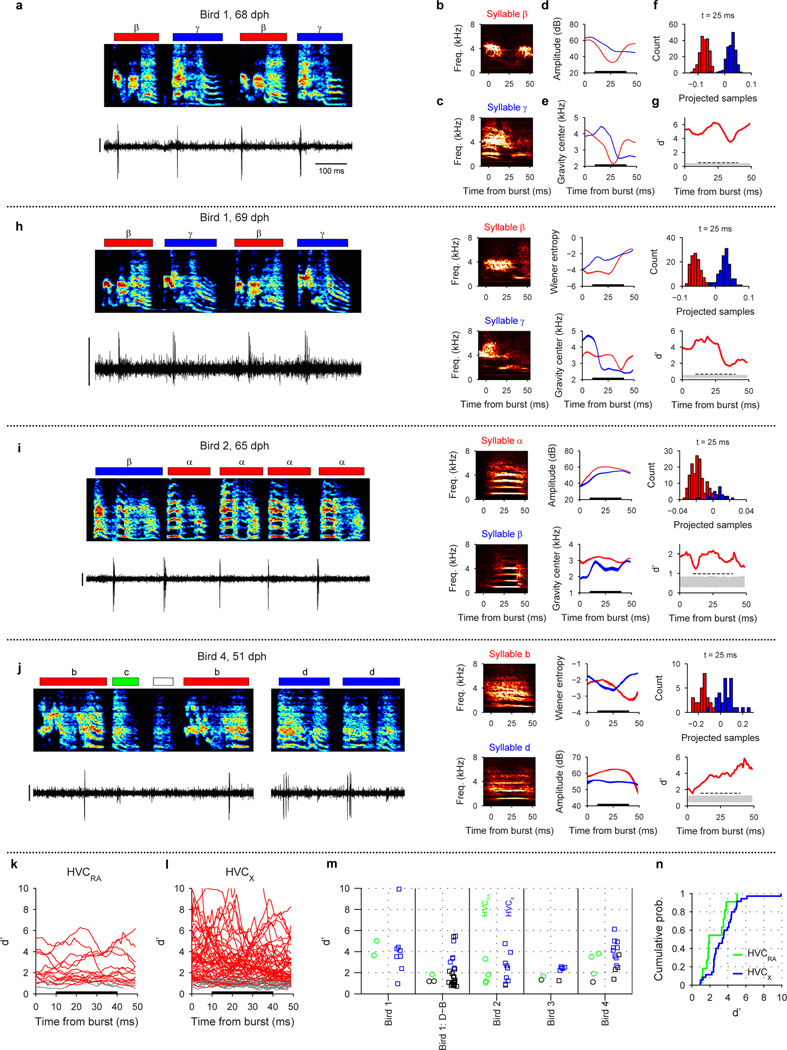
To elucidate the mechanisms by which neural sequences in HVC develop, we recorded from populations of HVC projection neurons in juvenile and adult birds (n=1,150 neurons, 35 birds; Extended Data Fig. 1a). At all stages of vocal development, HVC projection neurons generated brief bursts of spikes during singing (Fig. 1a–c, Extended Data Fig. 1b–c). In the subsong stage (n=12 birds; defined by exponential distribution of syllable durations, prior to the emergence of protosyllables) roughly half of neurons generated bursts not temporally locked to syllable onsets (Extended Data Fig. 1d), while the other half produced bursts that tended to occur at a particular latency relative to subsong syllable onsets (Fig. 1a, Extended Data Fig. 1e–i; 19/39 neurons exhibited syllable locking). The fraction of neurons locked to syllable onsets exhibited a gradual and significant increase throughout vocal development (Fig. 1f; correlation with song stage: r=0.22, P<10⁻¹⁰; see Methods) until, in adult birds, virtually every projection neuron generated bursts precisely locked to syllables, as previously described^19–24.

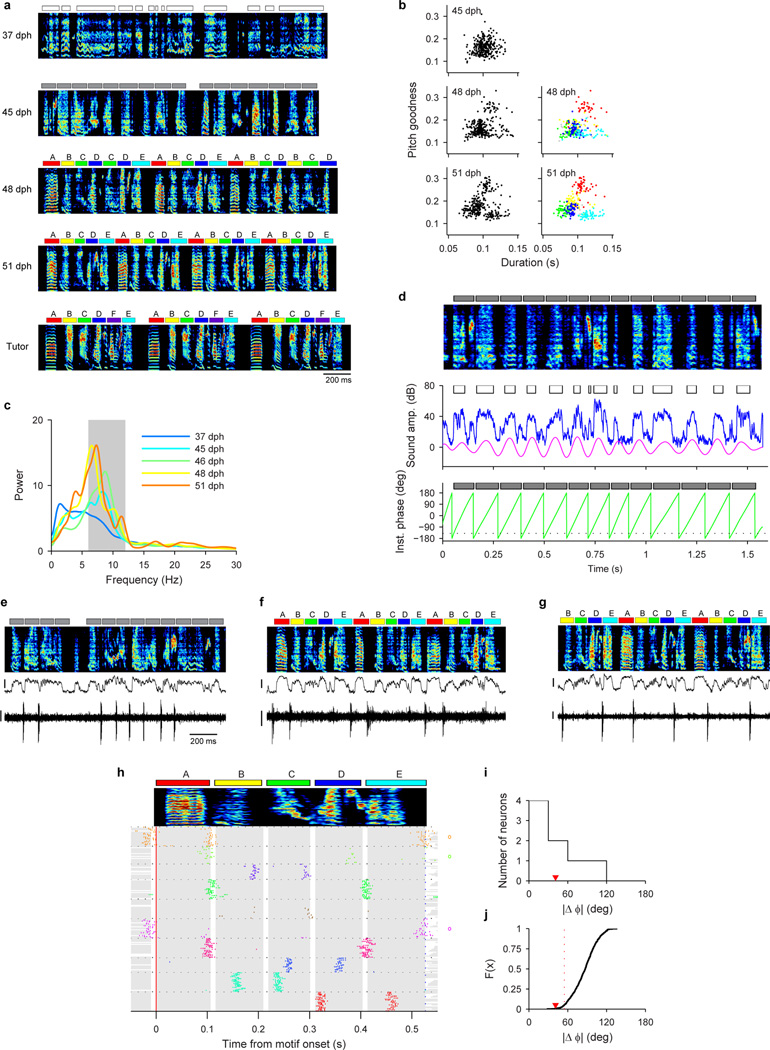
Figure 1. Singing-related firing patterns of HVC projection neurons in juvenile birds.

a, Neuron recorded in the subsong stage, prior to the formation of protosyllables (HVC_RA; 51 dph; Bird 7). Top: song spectrogram with syllables indicated above. Bottom: extracellular voltage trace. b, Neuron recorded in the protosyllable stage (HVC_RA; 62 dph; Bird 2). Protosyllables indicated (gray bars). c, Neuron recorded after motif formation (HVC_RA; 68 dph; Bird 8). d, Neuron bursting exclusively at bout onset (HVC_X; 61 dph; Bird 2). e, Neuron bursting exclusively at bout offset (HVC_RA; 65 dph; Bird 2). f, Developmental change in the fraction of neurons locked to syllable onsets (gray) and fraction of neurons with rhythmic bursting (black) (mean ± s.e.m; n=39, 135, 566, 378, 32 neurons, respectively). g, Mean period of the HVC rhythmicity as a function of song stage (n=3, 70, 357, 298, 25 neurons, respectively). ***P<0.001, post-hoc comparison with the adult stage. Spectrogram vertical axis 500–8000 Hz. Scale bars: (a–c) 0.5 mV, 200 ms; (d–e) 1 mV, 500 ms. Inset in (a–c) shows zoom of bursts indicated by asterisk; scale bar: 5 ms.

Song development is characterized by a gradual change in song rhythm^33,37,38. The subsong stage, with little evidence of rhythmic song structure, ends with the emergence of a rhythmically produced protosyllable (5–10 Hz)^32–35. This is followed by a subsequent increase in the period between repetitions of the same sound, attributable to the addition of new song syllables³³. HVC exhibited parallel changes in rhythmicity. In the subsong stage, most projection neurons did not burst rhythmically (Fig. 1a, f; 3/39 neurons were rhythmic). In the protosyllable stage, roughly half of the projection neurons generated rhythmic bursts (5–10 Hz) (Fig. 1b,f; 70/135 neurons were rhythmic; period 169 ± 6.4 ms, mean ± s.e.m.). Such bursts were typically locked to rhythmic protosyllables, but were also commonly observed during less rhythmic portions of the song, particularly early in the protosyllable stage (Extended Data Fig. 2a–d). On average, both the fraction of rhythmic HVC neurons, and the period of the HVC burst rhythm gradually increased during the emergence of new syllable types and the formation of the song motif (Fig. 1f,g; correlation between song stage and fraction of rhythmic neurons: r=0.28, P<10⁻¹⁰; correlation between song stage and period of burst rhythm: r=0.57, P<10⁻¹⁰).

A significant fraction of projection neurons (285/1118 neurons) in juvenile birds generated bursts related to song bouts—defined as epochs of continuous singing bounded by periods of silence (see Methods). Bout-related neurons generated brief bursts of spikes immediately prior to bout onset (‘bout-onset’ neurons; 137/285 neurons) or after bout offset (98/285 neurons) (Fig. 1d,e, Extended Data Fig. 2e–l; an additional 50/285 neurons were active both before and after bouts).

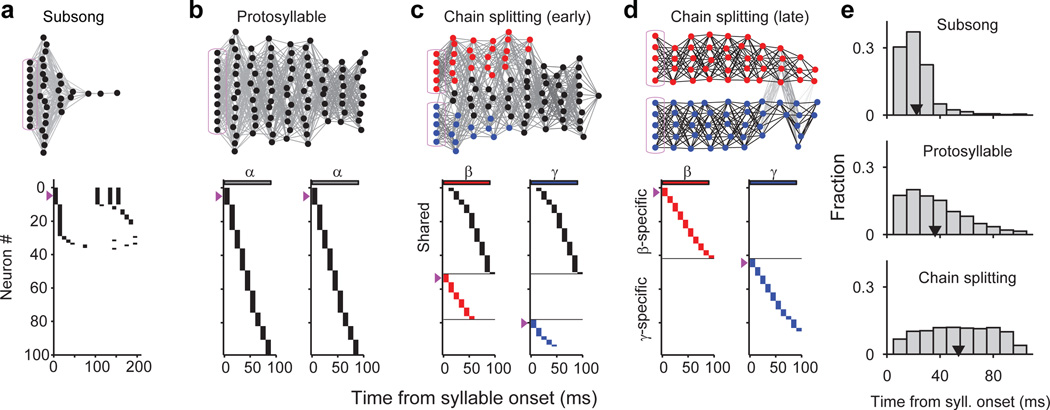
Growth of a neural protosequence

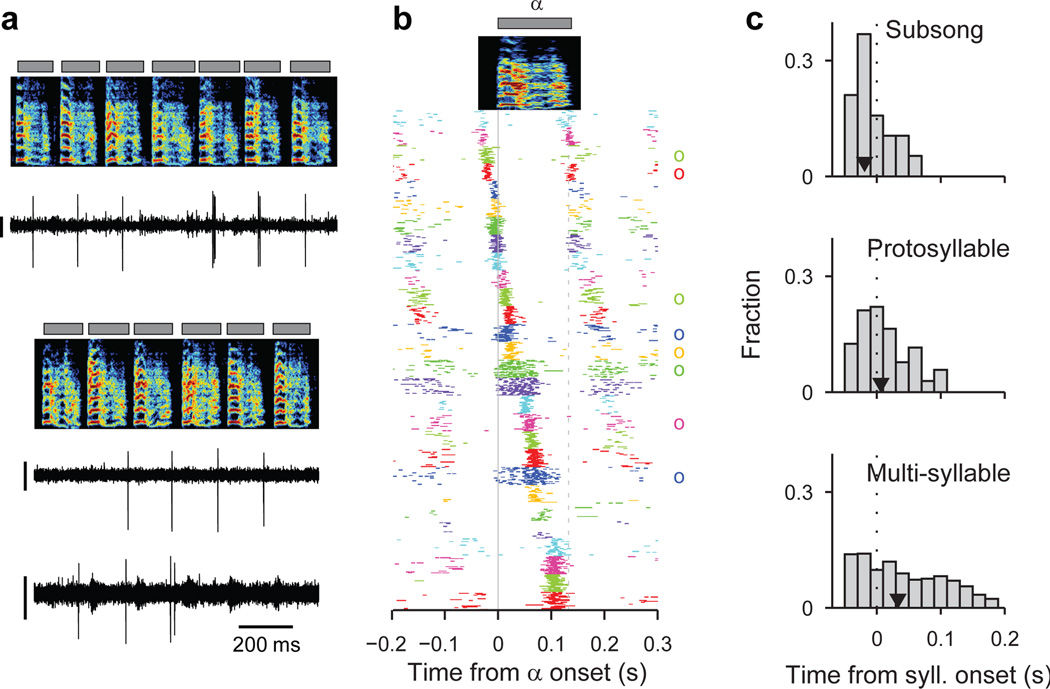
We next wondered how the activity of HVC projection neurons is coordinated across the neural population during protosyllables. Multiple recordings in the same bird revealed that different neurons were active at different times with respect to protosyllable onsets (Fig. 2a,b; Extended Data Fig. 1n, 9k; n=3 birds, 54 neurons), with latencies spanning the duration of the protosyllable and the intervening gap (>90% burst coverage; Extended Data Fig. 2t). These findings suggest that protosyllables are generated by a rhythmic protosequence—a repeating motor program comprised of a continuous sequence of bursts in HVC.

Figure 2. Rhythmic sequences in HVC during the protosyllable stage.

a, Three neurons recorded from Bird 2 during protosyllable stage (top: HVC_X; 63 dph; bottom: simultaneous recording two neurons; both HVC_X; 64 dph; scale bar 0.5 mV). b, Raster plot of 28 HVC projection neurons aligned to protosyllable onsets (sorted by latency; 57–64 dph, Bird 2). Antidromically identified HVC_RA neurons indicated by circles at right. c, Distribution of burst latencies relative to syllable onset in subsong stage (top), protosyllable stage (middle), and multi-syllable/motif stages (bottom), across all birds (n=19, 104, 814 neurons, respectively). Black triangle: median burst times.

We next examined the developmental emergence of this rhythmic protosequence. In the subsong stage (Fig. 2c; n=19 neurons, 12 birds), bursts had a significantly earlier distribution of latencies compared to the broader distribution of burst latencies in the protosyllable stage (n=104 neurons, 13 birds; P=0.02; 63% vs. 43% of bursts prior to syllable onset in subsong stage and protosyllable stage, respectively). Even though the range of latencies was narrower in subsong birds, different neurons recorded in the same bird were locked to syllable onsets at different latencies (Extended Data Fig. 1f–i). This suggests the existence of transient sequential activity, initiated just prior to syllable onset, but decaying within a few tens of milliseconds. This sequential activity appears to grow during the protosyllable stage to form longer sequences that can persist for more than a hundred milliseconds, throughout the duration of the protosyllable (Fig. 2b,c).

Sequence splitting during syllable formation

We next wondered how distinct sequences in HVC, each corresponding to a distinct adult syllable type, emerge during vocal learning. Here we hypothesize that new syllable types can emerge by the gradual splitting of a single protosequence. In this view, we imagine that the neural sequences underlying newly emerging syllable types would initially be largely overlapping, with neurons shared across the emerging syllables. Splitting would be associated with an increasing number of neurons selective for a particular emerging syllable type, and a decreasing fraction of shared neurons.

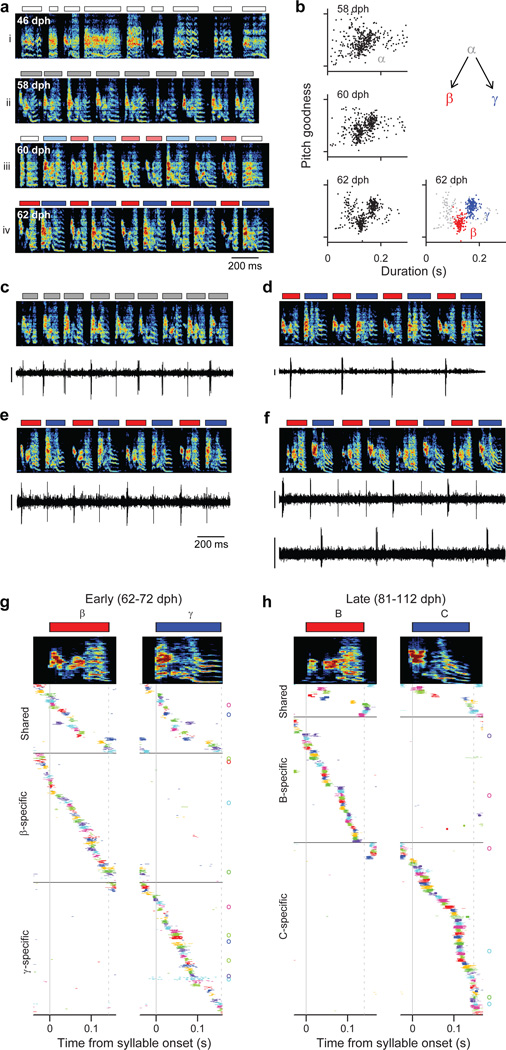
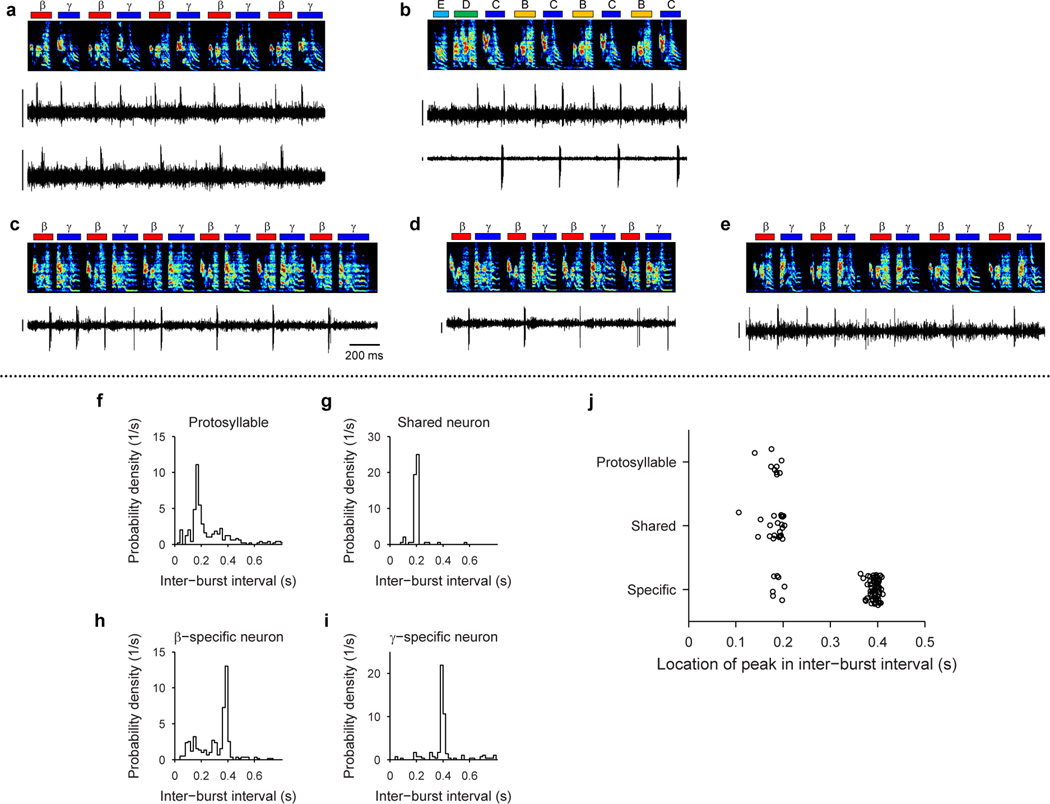
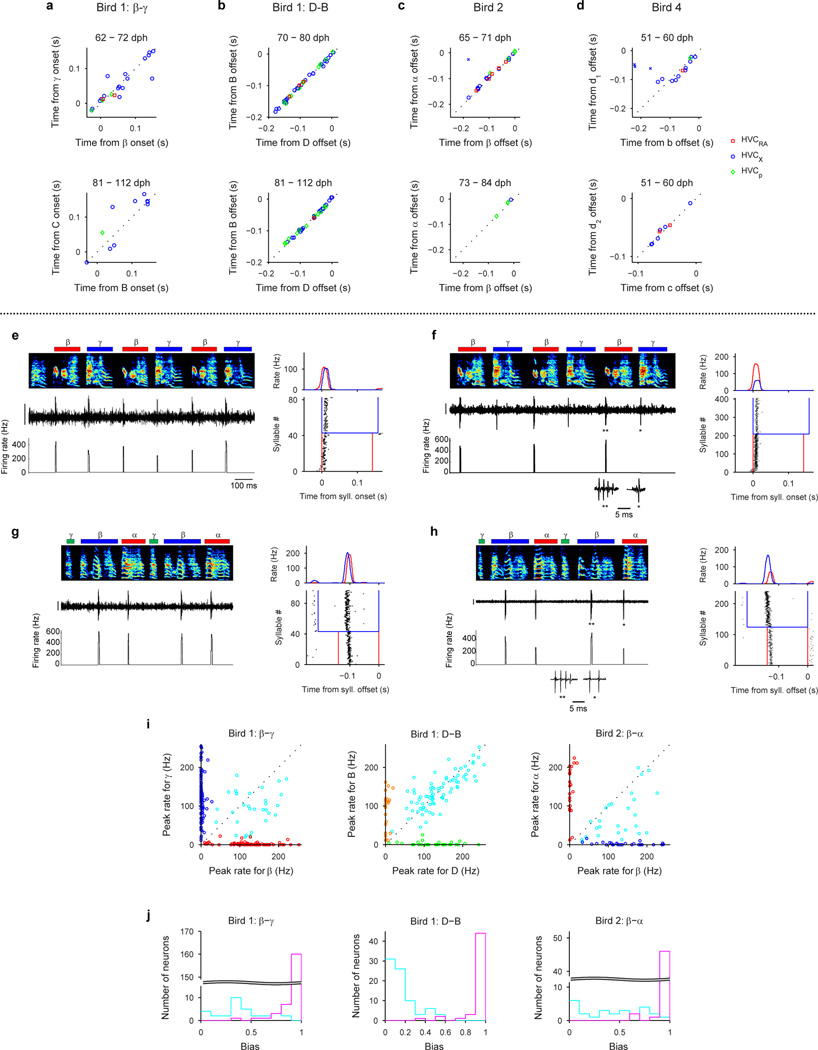
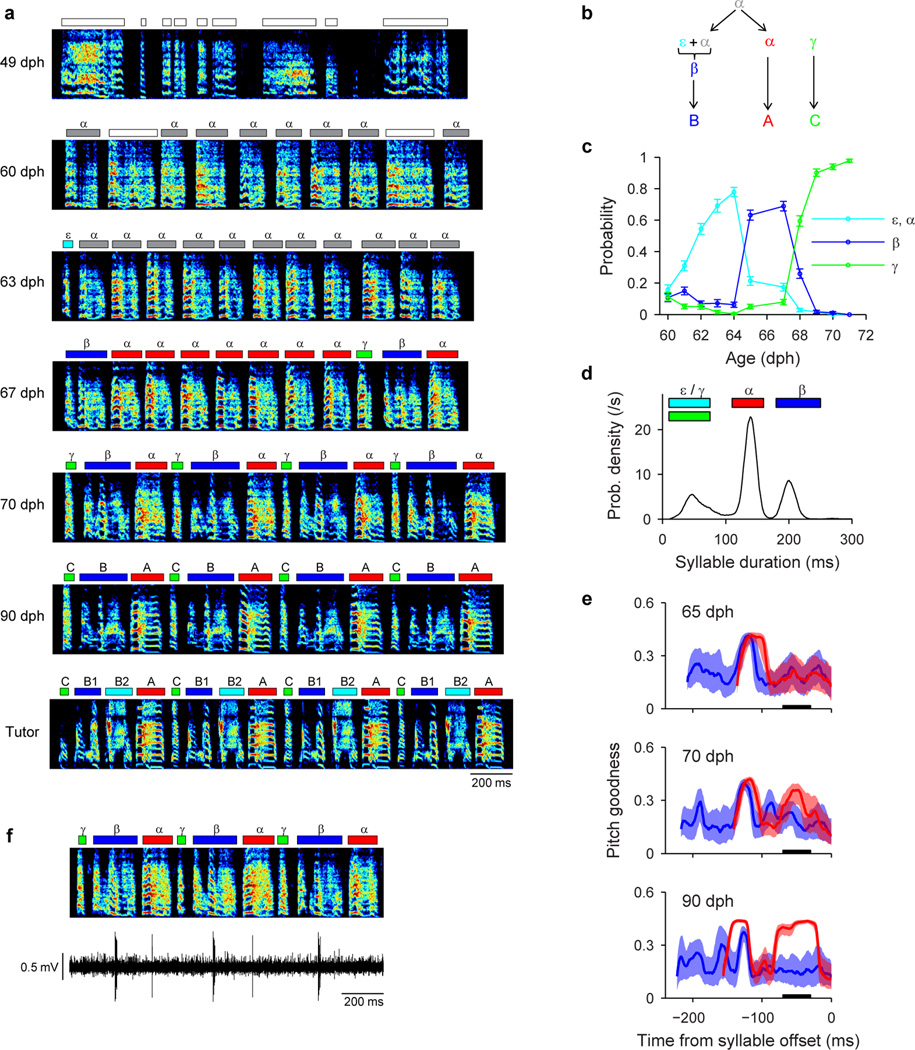
To test this hypothesis, we recorded from HVC projection neurons (n=769) in 6 juvenile birds while they acquired multiple syllable types. As a first example, we will describe changes in the HVC population activity in a bird (n=375 projection neurons; Bird 1) that developed two acoustically distinct syllable types (labeled β and γ) over the course of several days (Fig. 3a,b; β and γ eventually form adult syllables B and C, respectively). During the protosyllable stage (56–59 dph), the majority of projection neurons participated in a rhythmic protosequence (Extended Data Fig. 1n; n=14/16 neurons; e.g. Fig. 3c). After the emergence of syllable types β and γ (62–72 dph), many neurons were selectively active only during β or during γ, but not both (Fig. 3d,f; of 105 neurons active during either β or γ, 41 were β-specific and 42 were γ-specific). The bursts of these syllable-specific neurons exhibited a wide range of latencies, with spiking activity of neurons in each group spanning the entire duration of each syllable (Fig. 3g). Notably, we also observed a substantial population of neurons that were significantly active during both β and γ (n=22 ‘shared’ neurons; Fig. 3e–g). Simultaneous recordings revealed the co-occurrence, in different neurons, of shared and specific firing patterns (Fig. 3f, Extended Data Fig. 3a,b).

Figure 3. Shared and specific sequences during the emergence of multiple syllable types.

All data from Bird 1. a, Song examples during the emergence of syllables β (red) and γ (blue). Panels i: subsong stage (46 dph); ii: rhythmic repetition of protosyllable α (grey bars; 58 dph); iii: rhythmic repetition of variants of the protosyllable (β and γ; 60 dph); iv: further acoustic differentiation of β and γ (red and blue bars; 62 dph). b, Scatter plot of syllable duration versus mean pitch goodness (each dot is one syllable rendition; n=400 syllables per day; unclassified syllables gray). c, Neuron recorded during protosyllable stage (HVC_X; 56 dph). d, β-specific neuron (HVC_X; 64 dph). e, Shared neuron active during both β and γ (HVC_RA; 68 dph). f, Simultaneously-recorded pair of HVC_X neurons: shared neuron (top) and γ-specific neuron (bottom; 71 dph). g, Raster of 105 projection neurons early in syllable differentiation showing shared and specific sequences. HVC_RA neurons indicated by circles at right. h, Same as panel g but for 100 neurons recorded after differentiation of β and γ into adult syllables B and C. Scale bars: (c–f) 0.5 mV, same time scale.

Shared neurons exhibited a number of striking characteristics. These neurons burst rhythmically with the same inter-burst interval as neurons recorded in the protosyllable stage (Fig. 3e, f; Extended Data Fig. 3f–j). Shared neurons were active, as a population, at a wide range of latencies within emerging syllables (Fig. 3g), and crucially, for a given shared neuron, the bursts during β occurred at a similar latency as the bursts during γ (Fig. 3g, Extended Data Fig. 4a–d). Thus, shared neurons generated the same continuous burst sequence during both β and γ. This shared sequence occurred even at times when there was a significant acoustic difference between the shared syllables (Extended Data Fig. 5). We also found that the fraction of shared neurons later in development (81–112 dph) was significantly lower compared to the earlier recordings (Fig. 3h; 10 shared and 90 specific neurons; P=0.03). Thus, the refinement of β and γ into the adult syllables B and C coincides with a decrease in the fraction of shared neurons, producing a gradual splitting of these representations into increasingly non-overlapping ‘daughter’ neural sequences.

The tendency of the song in Bird 1 to alternate between syllables β and γ means that syllable-specific neurons had an inter-burst interval, and thus a period, that was twice as long as that observed in the earlier protosyllable stage (Fig. 3c–f, Extended Data Fig. 3f–j). Therefore, the increase in the period of neural activity through skipping or alternating cycles of an underlying rhythm appears to be a basis of the increase in song period during vocal learning³³.

Although our key findings are described above for Bird 1, a similar pattern of HVC coding by shared and specific neurons was seen in a total of 6 birds for which recordings were made during the emergence of multiple syllable types (Birds 1–6; 185 shared neurons and 496 specific neurons for 8 syllable pairs analyzed). Across three birds in which neurons were also recorded in later song stages, there was a significant decrease in the fraction of shared neurons during syllable development (n=5 syllable pairs; P=3×10⁻⁶; Birds 1, 2, 4). Neurons exhibiting an increased burst period by skipping cycles of an underlying rhythm were observed in 4 of the 6 birds (Birds 1, 3, 4, 6).

Splitting in other learning strategies

Behavioral studies have shown that new syllable types can emerge using several distinct developmental strategies^{32,33,36,39,40}. The bird described above (Bird 1) used the ‘serial repetition’ strategy³² and ‘sound differentiation in situ’³³ to develop two new syllables by alternating increasingly different variants of the protosyllable. Alternatively, birds can acquire multiple syllables simultaneously to form an entire motif (‘motif strategy’)³², or form new syllables at bout edges (onset or offset)^39,40. We wondered if the splitting of neural sequences underlies these other strategies.

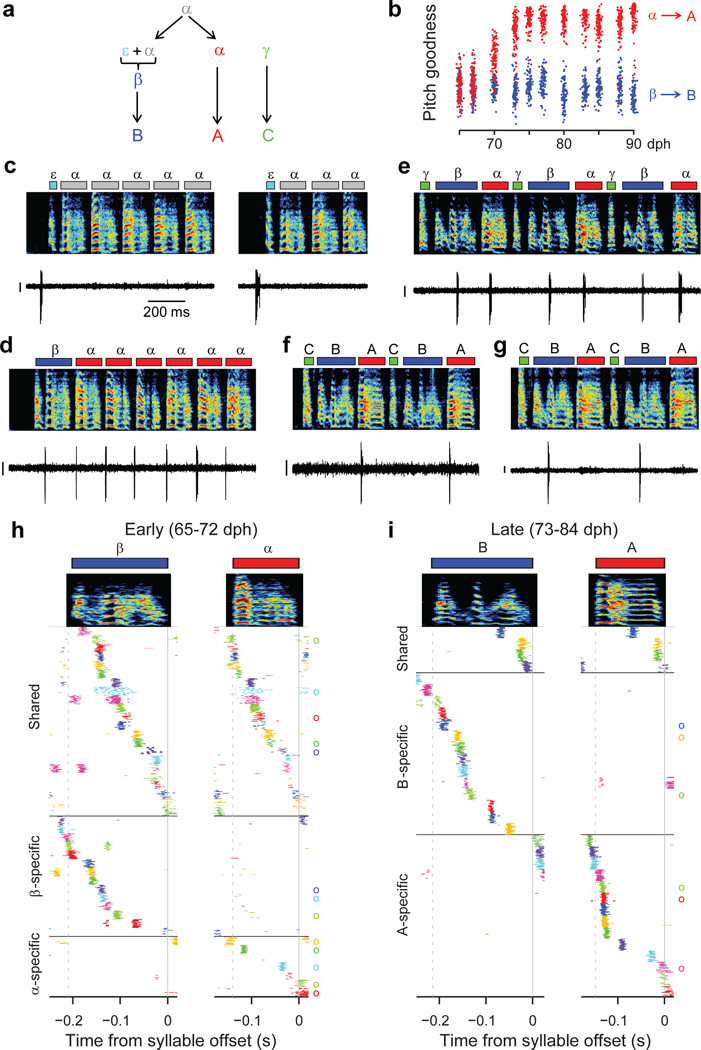
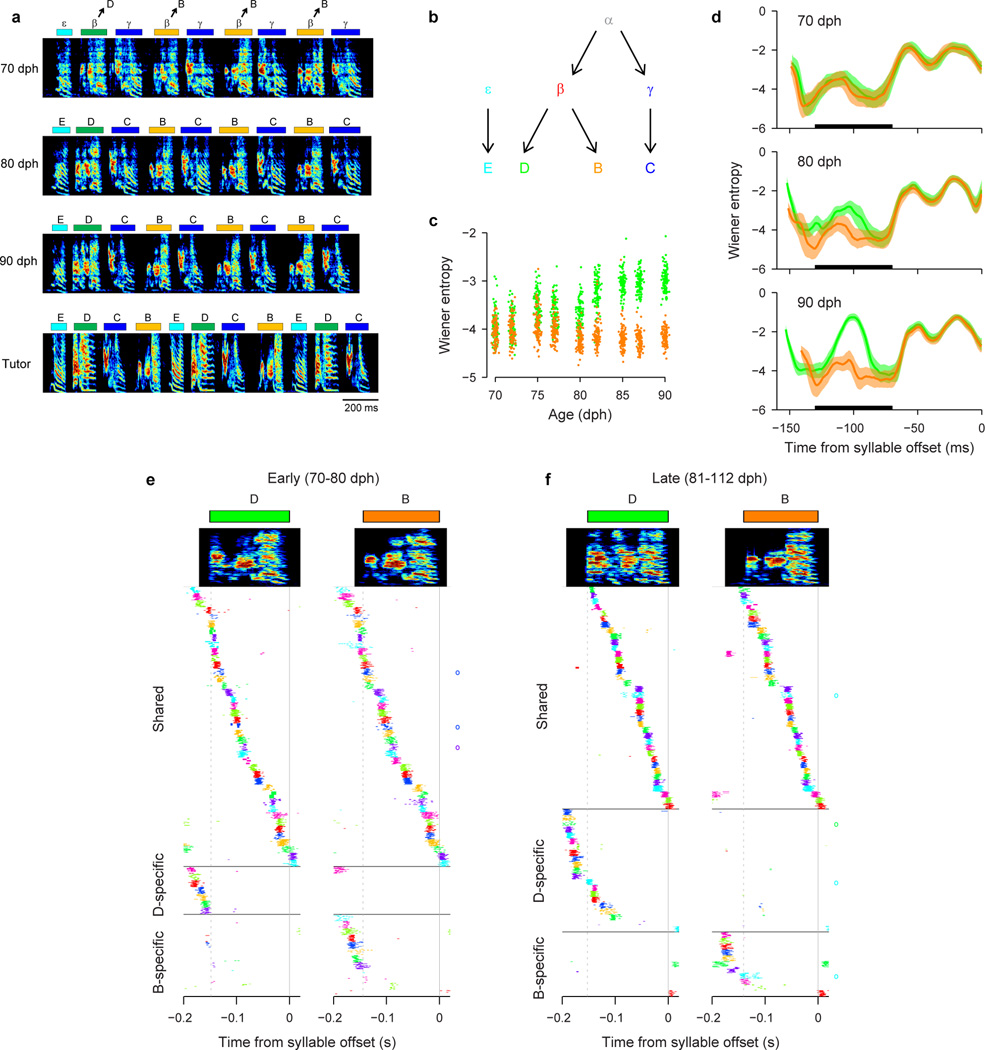
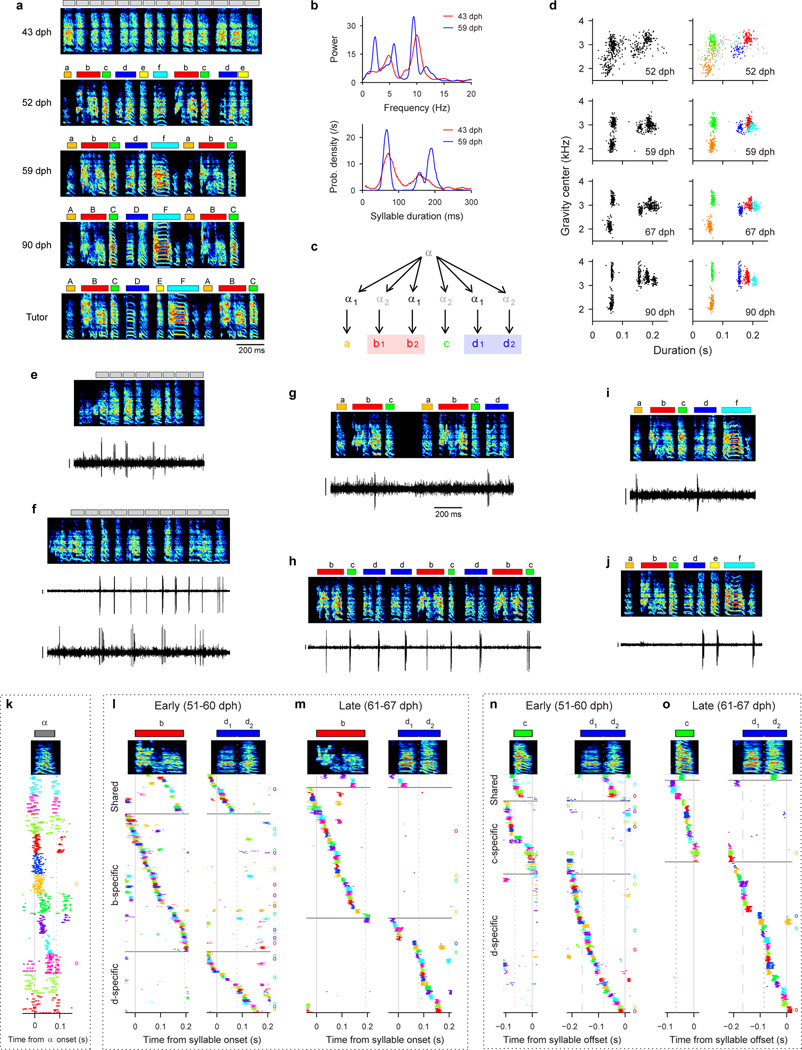
Neural recordings were obtained in three birds (Birds 1, 2, 5) that exhibited bout-onset syllable formation. We focus here on Bird 2 in which projection neurons were recorded throughout song development (57–84 dph). Tracking of syllable structure (Extended Data Fig. 6) revealed that syllables A and B of the adult song derived from a common, rhythmically repeated protosyllable (labeled α; Fig 4a,b), and that syllable B arose from the first repetition of α at bout onset (Fig. 4c,d). This bout-onset syllable emerged as a distinct syllable type (labeled β) by fusion of this first α with a brief vocal element ε at bout onset (Fig. 4c,d).

Figure 4. Shared and specific sequences during the emergence of a new syllable at bout onset.

All data from Bird 2. a, Schematic of syllable formation. b, Scatter plot of mean pitch goodness of syllables α (red) and β (blue) through development (n=100 syllables per day; horizontal jitter added to improve data visibility). c, Bout-onset neuron active before element ε (HVC_RA; 64 dph). d, New syllable β formed by fusion of ε and α. Neuron shared between α and β (HVC_RA; 65 dph). e, Neuron shared between α and β (HVC_X; 70 dph). f, A-specific neuron (HVC_RA; 80 dph). g, B–specific neuron (HVC_RA; 73 dph). h, Population raster plot of 43 projection neurons recorded early in the emergence of syllable β showing shared and specific sequences. l, Raster plot of 32 neurons recorded after differentiation of β and α into adult syllables B and A. Scale bars: (c–g) 0.5 mV, same time scale.

To examine the neural mechanisms underlying the emergence of the new syllable β at bout onsets, we analyzed the firing patterns of 125 HVC projection neurons. Before the emergence of syllable β, the majority of recorded projection neurons participated in a rhythmic protosequence (Fig. 2b; n=28/35 neurons; 57–64 dph,). A different subset of neurons was active at bout onsets (Fig. 4c; 4 of 35 neurons). After the emergence of β at bout onsets, roughly half of projection neurons generated bursts during both syllables α and β (65–72 dph; Fig. 4d,e; n=22 ‘shared’ neurons; 21 ‘specific’ neurons). These shared neurons produced nearly identical sequences during these two syllables (Fig. 4h, Extended Data Fig. 4c). Later in song development (73–84 dph), we observed a larger fraction of syllable-specific neurons (Fig. 4f,g,i; n=28 ‘specific’ neurons), and a correspondingly smaller fraction of shared neurons (4 ‘shared’ neurons; P=5×10⁻⁴), consistent with a gradual splitting of the protosequence into increasingly non-overlapping ‘daughter’ sequences. Evidence for sequence splitting during bout-onset differentiation was also observed in Birds 1 and 5 (Extended Data Fig. 7).

Note that the bout-onset differentiation in Bird 1 occurred after the earlier emergence of the syllables β and γ (Fig. 3), suggesting that new syllables may emerge in a hierarchical process—that is, by the splitting of sequences that are themselves the daughters of an earlier splitting process (Extended Data Fig. 7).

We were able to examine the question of whether neural sequence splitting also underlies the ‘motif strategy’ of song learning in two birds (Birds 3, 4; Extended Data Fig. 8, 9). In both birds, neural recordings showed the existence of rhythmically bursting neurons in the protosyllable stage (Extended Data Fig. 8e, 9e,f). After the emergence of multiple syllable types, every syllable in the emerging motifs had at least one neuron that was shared with another syllable at similar latencies (Extended Data Fig. 8f–j, 9g-o), consistent with the view that all of these syllables arose from the simultaneous splitting of a common protosequence.

Mechanistic Model and Discussion

Here, we propose a mechanistic model of learning in the HVC network to describe how sequences emerge during song development. This model is based on the idea that sequential bursting results from the propagation of activity through a continuous synaptically-connected chain of neurons within HVC^21,41–47. It also captures non-uniformities such as increased burst density at syllable onsets, formulated in a perspective of HVC function emphasizing vocal gestures²².

Modeling studies have shown that a combination of two synaptic plasticity rules—spike-timing dependent plasticity (STDP) and heterosynaptic competition—can transform a randomly connected network into a feedforward synaptically-connected chain that generates sparse sequential activity^43,44. We hypothesize that the same mechanisms can lead to the formation of a single chain that generates a rhythmic protosyllable, followed by the splitting of this chain into multiple daughter chains for different syllable types. To test this hypothesis, we constructed a simple network of binary units representing HVC projection neurons⁴⁴.

The model neurons are initially connected with random excitatory weights, representing the subsong stage. We hypothesize that a subset of HVC neurons receives an external input at syllable onsets and serves as a seed from which chains grow during later learning stages^43,45. Before learning, activation of these seed neurons produced a transiently propagating sequence of network activity that decayed rapidly (within tens of milliseconds; Fig. 5a).

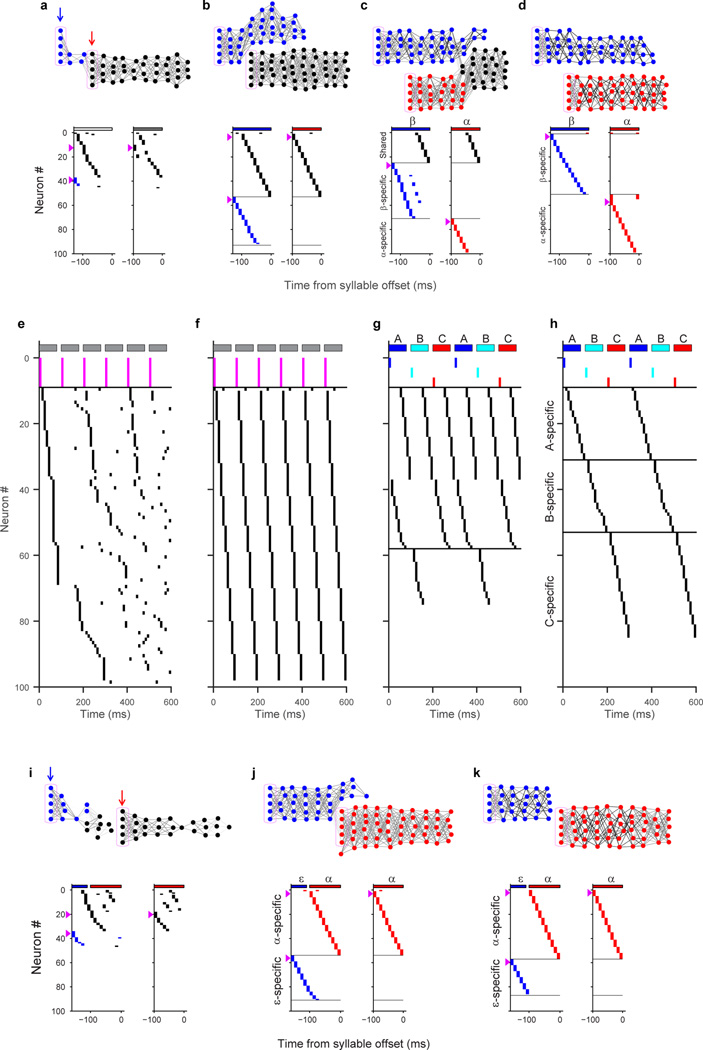
Figure 5. A neural model of sequence formation and splitting in HVC.

a–d, Top: network diagrams of participating neurons (darker lines indicate stronger connections; magenta boxes indicate seed neurons). Bottom: raster plot of neurons showing shared and specific sequences. Neurons sorted by relative latency. Magenta arrows indicate groups of seed neurons. a, Subsong stage: activation of seed neurons produces a rapidly-decaying burst of sequential activity. b, Protosyllable stage: rhythmic activation of seed neurons induces formation of a protosyllable chain. c, Alternating activation of red and blue seed neurons and synaptic competition drives the network to split into two chains (specific neurons: red and blue; shared neurons: black). d, Network after chain splitting. e, Distribution of model burst latencies during subsong, protosyllable stage, and chain splitting stage (early and late combined).

In the next stage, the network is trained to produce a single protosyllable by activating seed neurons rhythmically (100 ms period). The connections are modified according to the learning rules described above^43,44. As a result, connections were strengthened along the population of neurons sequentially activated after syllable onsets, resulting in the growth of a feedforward synaptically-connected chain that supported stable propagation of activity (Fig. 5b).

We found that this single chain could be induced to split into two daughter chains by dividing the seed neurons into two groups activated on alternate cycles of the rhythm (Fig. 5c,d, Supplementary Video 1). Local inhibition⁴⁸ and synaptic competition were also increased (see Methods). During the splitting process, we observed neurons specific to each of the emerging syllable types, as well as shared neurons that were active at the same latencies in both syllable types (Fig. 5c). Just as observed in our data, the distribution of burst latencies in the model continued to broaden (Fig. 5e), and the fraction of shared neurons decreased during development (Fig. 5c,d). The average period of rhythmic bursting in model neurons increased during chain splitting as neurons became ‘specific’ for one emerging syllable type and began to participate only on alternate cycles of the protosyllable rhythm (Fig. 5d, Extended Data Fig. 10g,h).

Other strategies for syllable formation

Our model can reproduce other strategies by which birds learn new syllable types. We implemented bout-onset differentiation in the model by also including a population of seed neurons activated at bout onsets (cf. Fig. 1d, 4c; Extended Data Fig. 10a). This caused the protosyllable chain to split in such a way that one daughter chain was reliably activated only at bout onsets, while the other daughter chain was active only on subsequent syllables (Extended Data Fig. 10a–d, Supplementary Video 2). Our model was also able to simulate the simultaneous emergence of a three-syllable motif (‘motif strategy’) by dividing the seed neurons into three subpopulations (Extended Data Fig. 10e–h).

Our data and modeling support the possibility of syllable formation by mechanisms other than sequence splitting. For example, in several birds, a short vocal element emerged at bout onsets that did not appear to differentiate acoustically from the protosyllable (and thus was not bout-onset differentiation; e.g. ‘E’ in Bird 1, Extended Data Fig. 7a; or ‘C’ in Bird 2, Extended Data Fig. 6a,b). We found that by using different learning parameters, our model allows bout-onset seed neurons to induce the formation of a new syllable chain at bout onset, rather than inducing bout-onset differentiation (Extended Data Fig. 10i–k).

In summary, our model of learning in a simple sequence-generating network captures transformations that underlie the formation of new syllable types via a diverse set of learning strategies.

Why sequence splitting?

The process of splitting a prototype neural sequence allows learned components of a prototype motor program to be reused in each of the daughter motor programs. For example, one of the earliest aspects of vocal learning is the coordination between singing and breathing³⁵, specifically, the alternation between vocalized expiration and non-vocalized inspiration typical of adult song⁴⁹. The protosequence in HVC would allow the bird to learn the appropriate coordination of respiratory and vocal musculature. Duplication of the protosequence through splitting would result in two ‘functional’ daughter sequences, each already capable of proper vocal/respiratory coordination, and each suitable as a substrate for rapid learning of a new syllable type.

This proposed mechanism resembles a process thought to underlie the evolution of novel gene functions: gene duplication followed by divergence through independent mutations⁵⁰. Similarly, for the acquisition of complex behaviors, the duplication of neural sequences by splitting, followed by independent differentiation through learning, may provide a mechanism for constructing complex motor programs.

Full Methods

Animals

We used juvenile male zebra finches (Taeniopygia guttata) 44–112 days post hatch (dph) singing undirected song (n=32 birds). Animals were not divided into experimental groups; thus, randomization and blinding were not necessary. No statistical methods were used to predetermine sample size. Birds were obtained from the Massachusetts Institute of Technology zebra finch breeding facility (Cambridge, Massachusetts). The care and experimental manipulation of the animals were carried out in accordance with guidelines of the National Institutes of Health and were reviewed and approved by the Massachusetts Institute of Technology Committee on Animal Care.

All the juvenile birds were raised by their parents in individual breeding cages until 38 ± 5.2 dph (mean ± s.d.) when they were removed and were singly housed in custom-made sound isolation chambers (maintained on a 12:12 hour day-night schedule). In a subset of the birds (Bird 1, 2, 4), additional tutoring was carried out after removal from the breeding cages to facilitate song imitation. This was done by playback of the tutor song through a speaker (20 bouts per day). Additional tutoring was done for 12 days for Bird 1, 7 days for Bird 2, and 18 days for Bird 4. Bird identification key: Bird 1, to3965; Bird 2, to3779; Bird 3, to3017; Bird 4, to5640; Bird 5, to3396; Bird 6, to2309; Bird 7, to3412; Bird 8, to3567; Bird 9, to2462; Bird 10, to2331; Bird 11, to2427; Bird 12, to3352.

To compare the activity of HVC projection neurons in juvenile birds with that of adult birds, we also included neurons recorded in adults (>120 dph, n=3 birds) which included a reanalysis of previously published HVC recordings performed in adult male zebra finches singing directed song²⁰.

Song recordings

Songs were recorded with Sound Analysis Pro⁵¹ or a custom-written MATLAB software (A. Andalman), which was configured to ensure triggering of recordings on all quiet vocalizations of juvenile birds²⁷. The vertical axis range for all spectrograms is 500–8000 Hz.

Classification of song stages

We classified each day of juvenile singing into four song stages: subsong stage, protosyllable stage, multi-syllable stage, and motif stage (Extended Data Fig. 1a). Subsong stage (48 ± 4 dph, median ± inter-quartile range) is defined as having a syllable duration distribution well-fit by an exponential distribution^34,35, with an upper limit for the Lilliefors goodness-of-fit statistic of 6. Following the subsong stage, birds enter the protosyllable stage (58 ± 10 dph, median ± i.q.r.) characterized by the presence of syllables with consistent timing reflected in a peak in the distribution of syllable durations^32–35. The onset of the protosyllable stage was defined here as the first day in which the syllable duration distribution deviated from an exponential distribution (Lilliefors goodness-of-fit statistic greater than 6). Following the protosyllable stage, birds transition to the multi-syllable stage (62 ± 12 dph, median ± i.q.r.) in which multiple distinct syllable types are visible in the song spectrogram and as multiple clusters in a scatter plot of syllable features⁵² (e.g. Fig. 3a, b; 62 dph). The motif stage (73 ± 21 dph, median ± i.q.r.) was defined by the production of a sequence of syllables in a relatively fixed order³¹. Finally, songs recorded in birds older than 120 dph were assigned as adult stage. A slightly older cutoff than the typical definition of adulthood in zebra finches (~90 dph)¹⁴ was used, because some of our birds in the 90–120 dph continued to undergo some small developmental changes, as has been reported³¹.

Syllable segmentation and bout extraction

Syllable segmentation of the juvenile song was done based on the song power in a spectral band between 1–4 kHz, as described previously^27,34,35. In a few cases, cutoff frequencies of the band-pass filters were adjusted to avoid the inclusion of high-frequency inspiratory sounds^35,53. Introductory notes were removed manually to avoid including HVC neurons that are rhythmically active during these elements⁵⁴. Song bouts were defined as a sequence of syllables separated by gaps less than 300 ms³⁵. Bout onset was defined as the onset of the first syllable in the bout, and bout offset was defined as the offset of the last syllable in the bout.

Syllable segmentation based on the song rhythmicity (‘phase segmentation’)

For Bird 3 (‘motif strategy’), it was difficult to segment syllables consistently using previous methods based on setting a threshold on the sound amplitude^27,34,35. To overcome this limitation, we segmented syllables based on the phase of the rhythmicity in the song (‘phase segmentation’). The peak of the song rhythm, defined as the spectrum of the sound amplitude during singing³⁸, exhibited a peak around 9 Hz (Extended Data Fig. 8c). To estimate the instantaneous phase of this rhythm, we first band-pass filtered the sound amplitude (Extended Data Fig. 8c, d; second-order IIR resonator filter with peak at 9 Hz and −3 dB half-bandwidth of 3 Hz; MATLAB command iirpeak). The band-pass filtered signal was then processed using the Hilbert transform (MATLAB command hilbert) to compute the instantaneous amplitude and phase (Extended Data Fig. 8d). Next, we set a threshold on this instantaneous amplitude to find the rhythmic part of the song. Finally, within this rhythmic part, song was segmented by detecting threshold crossings of the instantaneous phase (Extended Data Fig. 8d, bottom). Phase segments that contain no sounds or calls were manually removed. Similarly, phase segmentation (band-pass filter with peak at 10 Hz and half-bandwidth of 3 Hz) was used to segment the song during the protosyllable stage for Bird 4 (Extended Data Fig. 9a, e, f). Note that this method is best suited for segmenting songs that are rhythmic, but in which syllable boundaries are not strongly rhythmic. This appeared to be typical of birds employing the ‘motif strategy’³².

Syllable classification and labeling

Protosyllables were defined by their characteristic durations as has been described previously^34,35. In short, to identify the protosyllables, we first subtracted the best-fit exponential distribution (using 200–400 ms) from the syllable duration distribution, and fitted a Gaussian distribution to this residual. Protosyllables were defined as syllables having durations within two standard deviations from the mean of this Gaussian distribution. We labeled protosyllables using the Greek letter ‘α’ in all our birds for consistency.

To label the emerging syllables in the juvenile song, we used the Greek letters β, γ, δ, and ε. In contrast, to label the syllables in the adult motif, we used the capital letters of the Latin alphabet A, B, C, etc. For birds in which the song learning trajectory was tracked developmentally, we labeled the syllables such that the correspondence between the juvenile syllables and adult syllables is straightforward: for example, α becomes A, β becomes B, γ becomes C, δ becomes D, and ε becomes E. Note that this labeling scheme leads to a slightly unconventional labeling of adult song in the sense that a motif can have letters in a reverse order (e.g. CBA in Fig. 4f, g; Extended Data Fig. 6a), or a motif might not have a syllable A (e.g. EDCB in Extended Data Fig. 7a).

Syllable labeling was done manually by visual inspection of the song spectrogram; this was done blind with respect to the neural activity. The existence of multiple distinct syllable types were confirmed by calculating the syllable duration and acoustic features commonly used to analyze birdsong syllables^51,55, and visualizing the clusters for each syllables in a two-dimensional space⁵² (Fig. 3b, Extended Data Fig. 8b, 9d). In some cases, syllable order was used as an additional indicator of syllable identity (e.g. Extended Data Fig. 7a, 70 dph; Extended Data Fig. 8a, 51 dph; Extended Data Fig. 9a, 59 dph).

In Bird 1, syllables β and γ were labeled manually by the visual inspection of the song spectrogram (Fig. 3a). Since characterizing shared neurons and specific neurons depends on the reliable labeling of syllables, we took a conservative approach and only labeled syllables that were clearly identifiable and did not label the syllables that were ambiguous (fraction of syllables labeled as β or γ during 62–66 dph: 70 ± 5.5%, mean ± s.d.). We then estimated the error rate of our labeling procedure by plotting the labeled syllables (n=200 syllables per type on each day) in a two-dimensional space of syllable duration and mean pitch goodness (Fig. 3b), and obtained a decision boundary using linear discriminant analysis. We used mismatch between manual labeling and feature-based labeling to estimate the error rate for syllable β and γ. The error rate during the first five days of syllable differentiation (62–66 dph), when the labeling was most difficult, was only 1.1 % on average (range: 0.25–3.0%).

For the second round of differentiation in Bird 1, syllable order was used to assist in the labeling of syllables in early stages when syllables ‘B’ and ‘D’ were not easily distinguishable based on acoustic differences. Because these syllables underwent bout-onset differentiation, the first β after bout onset was labeled ‘D’; later renditions of β in the bout were labeled ‘B’ (Extended Data Fig. 7a).

In Bird 2, several emerging syllables could be easily distinguished based on syllable durations (Extended Data Fig. 6d). Specifically, syllables whose durations were 110–160 ms, and 180–250 ms were defined as α and β, respectively. Syllables that were 10–75 ms in duration were labeled γ if they were followed by a β, and labeled ε otherwise.

Chronic neural recordings

Single-unit recordings of HVC projection neurons during singing were carried out using a motorized microdrive described previously^56,57. Single-units were confirmed by the existence of the refractory period in the inter-spike interval (ISI) distribution (Extended Data Fig. 1b). Neurons that were active only during distance calls and not during singing²⁰ were excluded from the analysis. In addition, neurons recorded for less than 5 seconds of singing were excluded since the short recording duration did not allow us to reliably quantify the activity pattern of these neurons.

Antidromic identification of HVC projection neurons was carried out with a bipolar stimulating electrode implanted in RA and Area X (single pulse of 200 µs every 1 second; current amplitude: 50–500 µA)^{19,20,57–59}. A subset of antidromically-identified projection neurons was further validated with collision testing^{19,20,57–59}. A subset of single units were identified as putative projection neurons based on sparse bursting, but could not be antidromically identified because they did not respond to antidromic stimulation or were lost before antidromic identification could be carried out (211/1150 neurons). These neurons were included in the data set as unidentified HVC projection neurons (HVC_p).

Analysis of neural activity

Spikes were sorted offline using a custom MATLAB software (D. Aronov).

Definition of bursts

HVC projection neurons exhibited bursts of action potentials during singing (Fig. 1a–c). The bursting nature of these neurons was evident in the inter-spike interval (ISI) distribution during singing, which exhibited two peaks with an inter-peak minimum near 30 ms. ISIs shorter than 30 ms correspond to ISIs within bursts, and ISIs longer than 30 ms correspond to ISIs between bursts (Extended Data Fig. 1b). We defined a ‘burst’ as a continuous group of spikes separated by intervals of 30 ms or less. Thus, by definition, bursts are separated from other spikes by intervals greater than 30 ms. Note that single spikes separated by more than 30 ms from both the preceding spike and the following spikes were also counted as a burst. Burst time was defined as the center of mass of all the spikes within the burst. Burst width was defined as the interval between the first and the last spike in a burst (Extended Data Fig. 1c, top). Firing rate during burst was defined as a reciprocal of the mean inter-spike interval in a burst (Extended Data Fig. 1c, bottom). For the calculation of burst width and firing rate during bursts, bursts composed of a single spike were excluded.

Syllable-related neural activity

To analyze the temporal relation between neural activity and song syllables, we aligned the spike times to syllable onsets and constructed a rate histogram (1 ms bin, smoothed over 20 bins; range: ±0.5 s from syllable onsets). Peak in this rate histogram was found between 50 ms before syllable onset and 200 ms after syllable onset. To test the significance of this peak, surrogate histograms were created by adding different random time shifts to the spike times on each trial⁶⁰. Random time shifts were drawn from a uniform distribution over ±0.5 s. The peak of this surrogate histogram was recorded, and this shuffling procedure was repeated 1,000 times; P-values were obtained by analyzing the frequency with which the peaks of surrogate data were larger than that of the real data, and P<0.05 was considered significant⁶⁰. To visualize the population activity associated with protosyllables, we constructed a population raster plot by choosing 20 protosyllable renditions for which each neuron was most active, and by plotting different neurons in different colors (Fig. 2b, Extended Data Fig. 1n, 9k). For all the other population raster plots associated with identified syllables, 20 random renditions were chosen for display. For all the population raster plots, syllable duration from each rendition was linearly time-warped to the mean duration of the syllable. Spike times were warped by the same factor.

Bout-related neural activity

A subset of HVC projection neurons exhibited bout-related activity: bursting before bout onsets and/or after bout offsets (Fig. 1d, e, Extended Data Fig. 2e–l). To quantify the pre-bout activity, we generated histograms aligned to bout onsets (Extended Data Fig. 2f, g) and found a peak in the histogram in a 300 ms window prior to bout onset. We considered a neuron to be exhibiting ‘pre-bout activity’ if the size of this peak was significant (P<0.05) compared to peaks obtained from the surrogate histograms (identical to the procedure described above in Syllable-related neural activity). To eliminate the possibility of including syllable-related activity as bout-related activity, we did not consider a neuron to be exhibiting pre-bout activity if the neuron showed a peak in the bout-onset aligned histogram and a peak at a similar latency (less than 25 ms apart) for the syllable-onset aligned histogram. We considered a neuron to be exhibiting ‘post-bout activity’ if there was a significant peak in the bout-offset aligned histogram (Extended Data Fig. 2j,k) in a 300 ms window after bout-offset.

Quantification of the rhythmic neural activity

To quantify the rhythmic neural activity of HVC projection neurons, we used four different methods: inter-burst interval, spike-train autocorrelation, spectrum of the spike train, and cepstrum of the spike train. Only spikes that were produced during singing (i.e. between the onset of the first syllable and the offset of the last syllable in the bout) were used for the calculation of these measures. (1) Inter-burst interval. Intervals between burst times were calculated and the peak between 80–1000 ms was found. (2) Spike-train autocorrelation. To quantify the second-order statistics of the firing pattern of HVC neurons, spike-train autocorrelation, expressed as a conditional firing rate⁶¹, was calculated, and the peak between 80–1000 ms was found. The width of the center peak indicates the width of bursts, and multiple side lobes with regular intervals indicate rhythmic bursting. (3) Spectrum of the spike train. Rhythmicity of the single-unit activity was also quantified in the frequency domain using the multi-taper spectral analysis of spike trains treated as point processes⁶². We used the Chronux software to calculate spectrum for the spike trains^63,64. First, bouts of singing were segmented into non-overlapping analysis windows of 1.5 second long, and then spectrum for each window was calculated using the multi-taper spectral analysis with time-bandwidth product NW = 3/2 and the number of tapers K=2. To obtain the mean spectrum for a given neuron, spectra calculated from all the analysis windows were averaged. Finally, we found the peak in the mean spectrum within the range 2–15 Hz. (4) Cepstrum of the spike train. HVC projection neurons often exhibited rhythmic bursts with precise inter-burst intervals (Fig. 1b, c). Thus, the spectrum of the spike train tended to have multiple peaks at the multiples of the fundamental frequency. To represent these burst trains that have regular intervals in a more compact way, we calculated the cepstrum (a technique commonly used in speech processing to extract the period of glottal pulses) of the spike train, defined as the inverse Fourier transform of the log spectrum⁶⁵, and found the peak in the cepstrum between 80–1000 ms.

To assess the significance of the peaks in these four measures, we compared the distribution of peak amplitude obtained from the real data with that of the surrogate data obtained by shuffling the bursts times. For this shuffling procedure, we first identified all the bursts during a bout of singing as described above. We then randomly placed bursts sequentially in an interval that has the same duration as the song bout; when spikes from two bursts were closer than 30 ms, we repeated the random placement until they were spaced by more than 30 ms. Note that this randomization procedure only shuffles the burst times and preserves both the number of bursts and the ISIs within bursts. Then, all four metrics listed above were calculated by applying the same method to this surrogate spike trains. This shuffling was repeated (1,000 times for the IBI and auto-correlation, 100 times for the spectrum and cepstrum) and the P-values of the peak were calculated by analyzing the frequency at which the peaks from the surrogate spike trains were larger than the peak obtained from real data. A neuron was considered to exhibit ‘rhythmic’ bursting if it had significant peaks in at least two of the four metrics. The period of the rhythm was defined as the location of the largest peak of spike-train autocorrelation between 80–1000 ms.

Quantification of the probabilistic neural activity during the protosyllable stage (Extended Data Fig. 2p)

Although many HVC projection neurons recorded in the juvenile bird exhibited rhythmic bursts, these bursts did not occur reliably on every cycle of the rhythm, but instead participated probabilistically (Fig. 2a). To quantify the degree of participation, we first extracted the protosyllables based on syllable duration (see Syllable classification and labeling above) and examined the fraction of protosyllables in which at least one spike occurred (time-window between 30 ms prior to protosyllable onset to 10 ms after protosyllable offset). The fraction of protosyllables in which the neuron was active was obtained for all the HVC projection neurons recorded during the protosyllable stage that showed a significant rhythmic bursting (Extended Data Fig. 2p).

Analysis of simultaneously recorded pairs of neurons (Extended Data Fig. 2q, r)

To test whether probabilistic bursting of neurons in the protosyllable stage is coordinated across many neurons, we analyzed the correlation between pairs of simultaneously recorded neurons (Fig. 2a, bottom). This analysis was restricted to pairs of neurons that were rhythmically bursting (n=11 pairs, 3 birds). Bursting activity of each neuron was converted to a binary string corresponding to its participation in each protosyllable (for the definition of protosyllables, see Syllable classification and labeling above). The activity of a neuron was assigned a ‘1’ for a protosyllable if the neuron exhibited activity in a time-window between 30 ms prior to protosyllable onset to 10 ms after protosyllable offset, and ‘0’ if it did not. Only activity during protosyllables was analyzed to avoid including the highly variable subsong syllables, which are likely generated by circuits outside HVC^27,34. For simultaneously recorded pairs of neurons, this procedure resulted in two binary strings corresponding to the protosyllable-related activity of each neuron. We then calculated the coefficient of determination r² by taking the square of the Pearson’s correlation coefficient r between the two binary strings calculated for each neuron in the pair. The distribution of coefficient of determination is shown in Extended Data Fig. 2q (median r²=0.072, 11 pairs).

We also carried out a mutual information analysis to quantify whether the activity of one neuron was predictive of the set of protosyllables for which the other neuron was active. Using the same binary representation described above, we calculated the joint probability distribution describing the four possible states of activity (neither neuron spikes, neuron A spikes, neuron B spikes, both neurons spike). The mutual information was computed from this joint distribution (Extended Data Fig. 2r, median mutual information=0.056 bits, 11 pairs).

Both the correlation and mutual information were extremely low, suggesting that different projection neurons participated on relatively independent sets of protosyllables. These findings suggest that individual projection neurons participate probabilistically and largely independently in an ongoing rhythmic protosequence within HVC.

Analysis of coverage by HVC projection neuron bursts (Extended Data Fig. 2s, t)

We wondered whether projection neuron bursts effectively span the entire duration of juvenile song syllables, or whether bursts are highly localized to specific times, leaving other times in the syllable unrepresented²². It is clear from the syllable aligned raster plots that some syllables were completely covered by bursts (e.g. Fig. 3h, syllable ‘C’), while other syllables showed some gaps in the burst coverage (e.g. Fig. 4i, syllable ‘A’). To further quantify this aspect of the HVC representation during singing, we analyzed the fraction of time within the syllables of juvenile birds that were ‘covered’ by the recorded projection neurons bursts (‘covered fraction’). This analysis was restricted to syllables with more than 10 associated bursts.

We first determined the region of the song syllable covered by each HVC projection neuron burst. We generated a histogram of syllable -onset or -offset aligned spike times recorded from a single neuron over every recorded rendition of the song syllable. Initial identification of candidate burst events was determined by smoothing the histogram (9 ms sliding square window, 1 ms steps), and setting a threshold to define a window in which to analyze burst spikes (2 Hz for protosyllable stage birds; 10 Hz threshold for older juveniles). To eliminate low-probability spike events, we only considered bursts for which spiking activity (at least one spike) occurred in the candidate burst window on at least 25% of the renditions for that syllable. Bursts were included only if they occurred between 30 ms prior to syllable onset and 10 ms after syllable offset.

For candidate bursts that met these criteria, all spikes occurring in the burst window were considered as contributing to that burst. Based on earlier measurements of postsynaptic currents and potentials of HVC and RA neurons⁶⁶, each HVC spike in the burst window was conservatively assumed to exert a postsynaptic effect lasting no more than 5 ms. Thus, each spike in the dataset was replaced with a 5 ms postsynaptic square pulse (beginning at the spike time). We considered a region of the syllable to be ‘covered’ by this burst if at least three of these post-synaptic pulses overlapped at that time within the burst, across renditions of the syllable. This procedure yielded a small ‘patch’ of time covered by the burst. The patches associated with each different neuron were combined with a logical ‘OR’ operation to determine the total coverage time of the syllable (again in a window from 30 ms prior to syllable onset to 10 ms after syllable offset). The covered time was divided by the duration of the syllable window to determine the covered fraction. Only syllables that had more than 10 neurons bursting within the syllable window were analyzed. This criterion excluded syllables from Bird 3 (shown in Extended Data Fig. 8), from which relatively few neurons were recorded.

While most syllables had nearly complete burst coverage (>90%), one syllable had coverage of only 73% (Extended Data Fig. 2t), which could potentially be due to the relatively smaller number of neurons recorded in this bird. Thus, we asked whether the measured coverage is consistent with sparse sampling of the recorded bursts from a large number of uniformly placed bursts. To simulate this, we calculated the covered fraction for 1,000 surrogate datasets in which the ‘covered patches’ for each burst were randomly shuffled within the syllable. A random offset was added to the time of each patch, and a circular shift was used, allowing the patches to wrap around the edges of the syllable window. The distribution of covered fractions was determined over all shuffled surrogate datasets, and the 2.5–97.5 percentiles (95% confidence interval) of this distribution were determined (shown as vertical gray bars in Extended Data Fig. 2t).

Shared and specific neurons

To examine whether a given HVC projection neuron was active during multiple syllable types (‘shared’ neuron) or was active only during a specific syllable type (‘specific’ neuron), we first constructed a syllable-onset aligned histogram (1 ms bin, smoothed over 20 bins) for each syllable type. Spike times were linearly time warped⁶⁷ to the mean duration of that syllable to reduce the trial-to-trial variability in the spike timing associated with the variation in the syllable duration. Next, we found the peak in the firing rate histogram in the interval between 30 ms before syllable onset and 10 ms after syllable offset. We visually inspected the syllable-aligned histograms, and adjusted the interval if necessary to avoid same burst being detected twice (i.e. being associated with an offset of one syllable and an onset of the next syllable). The significance of this peak was determined by comparing it with the peak size obtained from the shuffled histogram using the same method described above (Syllable-related neural activity).

We defined ‘shared’ and ‘specific’ neurons in the context of a particular syllable differentiation process (e.g. β and γ from Bird 1 in Fig. 3; α and β from Bird 2 in Fig. 4; B and D from Bird 1 in Extended Data Fig. 7). ‘Specific’ neurons were defined as neurons that had a significant peak in the syllable-aligned histogram for only one syllable type, whereas ‘shared’ neurons were defined as neurons that had significant peaks for both syllable types. We took a conservative approach and only considered a neuron to be shared if the peak was significant for both syllable types. However, some neurons classified as specific had weak activity for the other syllable that did not reach significance (e.g. Extended Data Fig. 6f). In other words, we believe this method likely underestimated the fraction of neurons with shared activity.

Our method likely underestimated the incidence of shared neurons for another reason as well. Specifically, we defined shared and specific neurons in the context of a particular pair of syllables undergoing differentiation. For example, in a bird that exhibited hierarchical differentiation (Bird 1; Extended Data Fig. 7), we saw examples of neurons that were B-specific when considering B-C differentiation but shared when considering B-D differentiation. Thus, when considering all the syllables in the motif, our definition of shared and specific neuron based on syllable pairs will underestimate the fraction of shared neurons and overestimate the fraction of specific neurons.

Quantification of the similarity of latencies in shared neurons (Extended Data Fig. 4a–d, Extended Data Fig. 8i, j)

To test whether shared neurons were active at similar latencies for multiple syllable types, we first calculated the latency of the peak in the syllable onset- or offset-aligned histograms. We then plotted the latency of the peak for one syllable against that of another syllable (Extended Data Fig. 4a–d). When a shared neuron was active for three or more syllables, two syllables associated with two highest firing rates were chosen. To quantify whether shared neurons were active at similar latencies for two syllable types, we calculated the Pearson’s correlation coefficient r between two latencies, and the P-value under the null hypothesis that r=0.

For the bird whose song was segmented based on the phase of the rhythm (Bird 3, Extended Data Fig. 8), we asked whether bursts of shared neurons during different syllables occurred at similar phases in the rhythm. To quantify the phase of the neural activity, we first detected the burst times during singing, and for each burst, we assigned an instantaneous phase extracted from the song using the Hilbert transform (see the section on phase segmentation above). Then, mean phase of all the bursts produced during a particular syllable type was calculated (φ_i where i = 1, 2, …, 5 indicates syllables). Finally, the two syllable types were chosen for which the neuron participated most reliably, and the difference between the mean phases for these two syllables (|Δφ| = |φ_m − φ_n|, where m and n are syllable indices) was obtained (Extended Data Fig. 8i). We tested the significance of this value by comparing the value of |Δφ| against that obtained from the shuffled data where the pairing of phases were randomized across all shared neurons (Extended Data Fig. 8j; 1,000 shuffles). P-values were obtained by analyzing the frequency with which |Δφ| of surrogate data was smaller than that of the real data, and P<0.05 was considered significant.

Quantification of the activity level difference in shared neurons (Extended Data Fig. 4i, j)

To quantify the difference in the activity level for multiple syllable types in the shared neurons, we calculated the ‘bias’ defined as follows:

$$\mathit{\text{Bias}}=1-\frac{\text{min}(r_1,r_2)}{\text{max}(r_1,r_2)}$$

where r_i is the peak firing rate in the syllable-aligned histogram for syllable i. Bias of 0 indicates equal activity level for both syllable types, whereas bias of 1 indicates exclusive activity for only one of the syllable types (Extended Data Fig. 4j).

Analysis of acoustic features associated with bursts of shared neurons (Extended Data Fig. 5)

We wondered if the bursts of shared neurons were associated with different acoustic signals in the shared syllables at the time of the bursts. (An alternative possibility is that shared neurons burst only at times within the emerging syllable types when the acoustic signals are identical.) An example of a neuron analyzed here is shown in Extended Data Fig. 5a (from the same data shown in Fig. 3e). This neuron bursts just after the onset of both syllables β and γ. We analyzed the acoustic differences in a 0–50 ms analysis window after the burst time, but were most interested in acoustic differences in a narrower premotor window (10–40 ms), as this corresponds to the premotor latency for which one expects HVC neurons to exert an effect on vocal output^29,58,68.

For each neuron analyzed, all syllables in which the neuron generated a burst were identified. The analysis was carried out for every syllable rendition on which the neuron burst, and was restricted to only those syllables. Syllables had previously been labeled by type (i.e. β and γ). We first directly visualized the spectral differences between the two syllable types using a sparse contour representation^69,70, which is suitable for constructing an ‘average’ spectrogram. The analysis was carried out on the sound signal extracted from a 50 ms window after each burst. In many cases, this spectral representation revealed consistent differences between the different syllable types in this analysis window (Extended Data Fig. 5b, c).

One complication is that some of the shared neurons burst prior to syllable onsets or immediately before syllable offsets such that the 10–40 ms window after the bursts was obscured by silent gaps (9 of 24 HVC_RA neurons and 59 of 120 HVC_X neurons were obscured). These neurons were excluded from the analysis of acoustic difference.

We further quantified differences in the acoustic signals by extracting time varying acoustic and spectral features in a window 0–50 ms after burst time (see subsection Definition of bursts). We used 8 acoustic features previously established to analyze birdsongs (Wiener entropy, spectral center of gravity, spectral width, pitch, pitch goodness, sound amplitude, amplitude modulation, frequency modulation)^51,55. The 8-dimensional vector of features was calculated in 1 ms steps over the 50 ms analysis window (Extended Data Fig. 5d, e).

Because each syllable was labeled, we could determine if the feature trajectories were significantly different for syllables labeled β and those labeled γ, and to make this determination at every time step in the analysis window (Extended Data Fig. 5d, e; s.e.m. indicated by shaded region around mean trajectory). Rather than quantify the difference in these trajectories one feature at a time, we used Fisher’s discriminant analysis⁷¹ to project the 8-dimensional acoustic feature vector onto a single dimension that gives maximum separability between the two syllable types. The projected direction is determined independently at each time point, and the feature vectors of all syllable renditions are projected, at each time point, to yield a distribution of projected samples. For most neurons, the different syllable types produce visibly different distributions of projected samples (Extended Data Fig. 5f) indicating distinct acoustic structure. The separability of the distributions (in one dimension) of projected samples for different syllable types was quantified using the d-prime metric (d’), corresponding to the distance between the means of the distributions, normalized by the pooled variance⁷⁰:

$$d\prime =\frac{{\mu }_A-{\mu }_B}{\sqrt{\frac{1}{2}({\sigma }_A^2+{\sigma }_B^2)}}$$

Because the features evolve in time, this analysis is carried out independently at each 1 ms step in the 50 ms analysis window, and the d’ was plotted as a function of time (Extended Data Fig. 5g). Statistical significance of the d’ trajectory was assessed by randomizing the syllable labels and rerunning the d’ analysis on shuffled datasets (N=1,000 shuffles). For each randomization, the peak value of d’ in 10–40 ms premotor window was recorded; significance threshold was as set as the 95 percentile of the distribution of these peak values. A shared neuron was determined to have significant acoustic difference between the shared syllables only if the d’ trajectory remained above this significance threshold for the entire premotor window of 10–40 ms after the burst. Note that, in the simulated data, none of the 1,000 surrogate runs generated a d’ trajectory that met this stringent criterion.

Statistics

Results are expressed as the mean ± s.d. or s.e.m. as indicated. For χ² tests, if the contingency table included a cell that has an expected frequency less than 5, Fisher’s exact test was used⁷². All tests were two-sided, and P<0.05 was considered significant. Bonferroni correction was used to account for multiple comparisons.

Figure 1(f) The statistical significance of developmental changes in the fraction of HVC neurons that were syllable-aligned was assessed in two different ways: 1) Each stage was compared with the adult stage using the χ² test followed by a post-hoc pairwise test. 2) To quantify the developmental trend in the fraction of syllable-locked neurons, we calculated Pearson’s correlation coefficient r between the binary value for each neuron (0, unlocked; 1, locked) and song stage (subsong: 1, protosyllable: 2, multi-syllables: 3, motif: 4, adult: 5). The P-value was calculated under the null hypothesis that r=0. The significance of the developmental trend for rhythmic bursting was calculated similarly. Similar results were obtained for correlation between these metrics and the age at which each neuron was recorded, rather than song stage.

Figure 1(g) The statistical significance of developmental changes in the period of the HVC rhythm was also assessed in two different ways: 1) Each song stage was compared with the adult stage using the Kruskal-Wallis test followed by a post-hoc pairwise test. 2) To quantify the developmental trend in the period of the HVC rhythm, we calculated Pearson’s correlation coefficient r between burst period and song stage. Similar results were obtained for correlation between burst period and the age at which each neuron was recorded.

Figure 2(c) Wilcoxon rank-sum test was used to test whether the median of the syllable-onset aligned latency distribution was different between subsong and protosyllable stages.

Figure 3(g, h) and 4(h, i) To test whether the fraction shared neurons differed between early and late stages of syllable differentiation, we used the χ² test on a 2 × 2 contingency table (shared/specific, early/late). Significance across all birds: To calculate whether the fraction of shared neurons differed between early and late stages of syllable differentiation over all birds (n=5 syllable pairs in 3 birds), we used the Cochran-Mantel-Haenszel test for repeated tests of independence⁷³.

Extended Data Fig. 1(a) To quantify the relation between song stage and age, we calculated Spearman’s rank correlation coefficient ρ and the P-value under the null hypothesis that ρ=0. (c) We computed the statistical significance of developmental changes in burst width (top) and firing rate during bursts (bottom) by using Kruskal-Wallis test followed by a post-hoc pairwise test to compare each stage with the adult stage.

Extended Data Fig. 2(m–o) To test whether fraction of syllable-locked neurons (m), fraction of rhythmic neurons (n), and period of HVC rhythm (panel o) significantly differed between HVC_RA and HVC_X, we used χ² test for all the pairwise comparisons with Bonferroni correction for multiple comparisons.

Extended Data Fig. 4(a–d) To calculated the relation between latencies of bursts associated with shared neurons, we calculated the Pearson’s correlation coefficient r together with the P-value under the null hypothesis that r=0.

Extended Data Fig. 5(m, n) To test whether mean d’ metric were different between HVC_RA and HVC_X, we used Wilcoxon rank-sum test. Only neurons with d’ trajectories that were significant (continuously from 10–40 ms) were included in this comparison.

Modeling

Binary neuron model

Code used to simulate the model is available as Supplementary Information. To illustrate a potential mechanism of chain splitting, we chose to implement the model as simply as possible. We modeled neurons as binary units and simulated their activity in discrete time steps⁴⁴; at each time step (10 ms), the i-th neuron either bursts (x_i = 1) or is silent (x_i = 0).

Network architecture

A network of 100 binary neurons is recurrently connected in an all-to-all manner, with W_ij representing the synaptic strength from presynaptic neuron j to postsynaptic neuron i. Self-excitation is prevented by setting W_ii = 0 for all i at all times⁴⁴. Synaptic weights are initialized with random uniform distribution such that each neuron receives, on average, its maximum total input. During learning, the strength of each synapse is constrained to be within the interval [0, w_max], while the total incoming and outgoing weights of each neuron are both constrained by the “soft bound” W_max = m * w_max where m represents a target number of saturated synapses per neuron⁴⁴ (see Synaptic plasticity rule section for details).

Network dynamics

The activity of each neuron in the network was determined in two steps; calculating the net feedforward input that comes from the previous time step, and determining whether that is enough to overcome the recurrent inhibition in the current time step.

First, the net feedforward input to the i-th neuron at time step t, $A_i^{\mathit{\text{net}}}(t)$ was calculated by summing the excitation, feedforward inhibition, neural adaptation, and external inputs:

$$A_i^{\mathit{\text{net}}}(t)={[A_i^E(t)-A^{I_{ff}}(t)-A_i^{\mathit{\text{adapt}}}(t)+B_i(t)-{\theta }_i]}_{+}$$

where [z]₊ indicates a rectification (equal to z if z>0 and 0 otherwise). $A_i^E(t)={\sum }_j{W}_{ij}{x}_j(t-1)$ is the excitatory input from network activity on the previous time step. A^I_ff(t) = β∑_jx_j (t − 1) is a feedforward inhibitory input⁴⁴, where β sets the strength of this feedforward inhibition. $A_i^{\mathit{\text{adapt}}}(t)=\alpha y_i$, is an adaptation term⁴⁴ where α is the strength of adaptation, and y_i is a low-pass filtered record of recent activity in x_i with time constant τ_adapt = 40 ms; that is ${\tau }_{\mathit{\text{adapt}}}\frac{d{y}_i}{dt}=-y_i+x_i$. B_i(t) is the external input to neuron i at time t. For seed neurons, this term consists of training inputs (see section on Seed neurons). For non-seed neurons, it consists of random inputs with probability p_in = 0.01 in each time step and size W_max/10. Finally, θ_i is a threshold term used to reduce the excitability of seed neurons, making them less responsive to recurrent input than are other neurons in the network. For seed neurons, θ_i = 10 and for non-seed neurons, θ_i = 0. Including this term improves robustness of the training procedure by eliminating occasional situations in which seed neuron activity may be dominated by recurrent rather than external inputs. In these cases, external inputs may fail to exert proper control of network activity.

Second, we determined whether the i-th neuron will burst or not at time step t by examining whether the net feedforward input $A_i^{\mathit{\text{net}}}(t)$ exceeds the recurrent inhibition A^I_rec(t). We implemented recurrent inhibition by estimating the total activity of the network at time t:

$$A^{I\_\mathit{\text{rec}}}(t)=\gamma {\sum }_i{A}_i^{\mathit{\text{net}}}(t)$$

and feeding it back to all the neurons. Parameter γ sets the strength of the recurrent inhibition. We assume that this recurrent inhibition operates on a fast time scale⁴⁸ (i.e. faster than the duration of a burst). Thus, the final output of the i-th neuron at time t becomes:

$$x_i(t)=\mathrm{\Theta }[A_i^{\mathit{\text{net}}}(t)-A^{I\_\mathit{\text{rec}}}(t)]$$

where Θ [z] is the Heaviside step function (equal to 1 if z > 0 and 0 otherwise). To induce splitting, γ was gradually stepped up to γ_split following a sigmoid with time constant τ_γ and inflection point t₀:

$$\gamma (t)=\frac{{\gamma }_{\mathit{\text{split}}}}{1+e^{-(t-t_0)/{\tau }_{\gamma }}}$$

Seed neurons

A subset of neurons was designated as seed neurons, which received external training inputs used to shape network activity during learning^43,45. The external training inputs activate seed neurons at syllable onsets, reflecting the observed onset-related bursts of HVC neurons during the subsong stage (Fig. 1a). The pattern of these inputs was adjusted in different stages of learning, and each strategy of syllable learning was implemented by different patterns of seed neuron training inputs.

Alternating differentiation (Fig. 5a–e)

Ten neurons were designated as seed neurons and received strong external input (W_max) to drive network activity. In the subsong stage, seed neurons were driven (by external inputs) synchronously and randomly with probability 0.1 in each time step corresponding to the random occurrence of syllable onsets in subsong^27,34. This was done only to visualize network activity; no learning was implemented at the subsong stage. During the protosyllable stage, seed neurons were driven synchronously and rhythmically with a period T = 100 ms. The protosyllable stage consisted of 500 iterations of 10 pulses each. To initiate chain splitting, the seed neurons were divided into two groups and each group was driven on alternate cycles. The splitting stage consisted of 2,000 iterations of 5 pulses in each group of seed neurons (1 second total).

Motif strategy (Extended Data Fig. 10e–h)

This was implemented in a similar manner as alternating differentiation, except that 9 seed neurons were used, and for the splitting stage, seed neurons were divided into 3 groups of 3 neurons, each driven on every third cycle.

Bout-onset differentiation (Extended Data Fig. 10a–d)

Seed neurons were divided into two groups: 5 bout-onset seed neurons and 5 protosyllable seed neurons. At all learning stages, external inputs were organized into bouts consisting of four separate input pulses: Bout-onset seed neurons were driven at the beginning of each bout. Then, 30 ms later, protosyllable seed neurons were driven three times with an interval of T = 100 ms. In the protosyllable stage, inputs to all seed neurons were of strength W_max. In the splitting stage, the input to protosyllable seed neurons was decreased to W_max/10. This allowed neurons in the bout-onset chain to suppress, through fast recurrent inhibition, the activity of protosyllable seed neurons during bout-onset syllables.

Each iteration of the simulation was 5 seconds long, consisting of 10 bouts, as described directly above, with random inter-bout intervals. The protosyllable stage consisted of 100 iterations, and the splitting stage consisted of 500 iterations.

Bout-onset syllable formation (Extended Data Fig. 10i–k)

Input to seed neurons was set high (2.5 * W_max), and maintained at this high level throughout development. This prevented protosyllable seed neurons from being inhibited by neurons in the bout-onset chain. Furthermore, strong external input to the protosyllable seed neurons terminated activity in the bout-onset chain through fast recurrent inhibition, thus preventing further growth of the bout-onset chain, as occurs in bout-onset differentiation.

As in bout-onset differentiation, each iteration of the simulation was 5 seconds long, consisting of 10 bouts with random inter-bout intervals. The protosyllable stage consisted of 100 iterations, and the splitting stage consisted of 500 iterations.

Synaptic plasticity rule

As in previous models^43,44, we hypothesized two plasticity rules in our model: Hebbian spike-timing dependent plasticity (STDP) to drive sequence formation^74,75, and heterosynaptic long term depression (hLTD) to introduce competition between synapses of a given neuron^43,44. STDP is governed by the antisymmetric plasticity rule with a short temporal window (one burst duration):

$${\mathrm{\Delta }}_{ij}^{STDP}(t)=\eta [x_i(t)x_j(t-1)-x_i(t-1)x_j(t)]$$

where the constant η sets the learning rate. hLTD limits the total strength of weights for neuron i, and the summed weight limit rule for incoming weights is given by:

$${\mathrm{\Delta }}_{i*}^{hLTD}(t)=\eta {\left[{\sum }_k\right(W_{ik}(t-1)+{\mathrm{\Delta }}_{ik}^{STDP}(t))-W_{\mathit{\text{max}}}]}_{+}$$

and for outgoing weights from neuron j:

$${\mathrm{\Delta }}_{*j}^{hLTD}(t)=\eta {\left[{\sum }_k\right(W_{kj}(t-1)+{\mathrm{\Delta }}_{kj}^{STDP}(t))-W_{\mathit{\text{max}}}]}_{+}$$

At each time step, total change in synapse weight is given by the combination of STDP and hLTD:

$$\mathrm{\Delta }{W}_{ij}(t)={\mathrm{\Delta }}_{ij}^{STDP}(t)-\epsilon {\mathrm{\Delta }}_{i*}^{hLTD}(t)-\epsilon {\mathrm{\Delta }}_{*j}^{hLTD}(t)$$

where ε sets the relative strength of hLTD.

Model parameters: subsong (Fig. 5a)

In our implementation of the subsong stage, there was no learning. Subsong model parameters were: β = 0.115, α = 30, η = 0, ε = 0, γ = 0.01.

Model parameters: alternating differentiation (Fig. 5b–d)

After subsong, learning progressed in two stages: the protosyllable stage and the splitting stage. Parameters that remained constant over development were: β = 0.115, α = 30, η = 0.025, ε = 0.2. To induce chain splitting, w_max was increased from 1 to 2, m was decreased from 10 to 5, and γ was increased from 0.01 to 0.18 following a sigmoid with time constant τ_γ = 200 iterations and inflection point t₀ = 500 iterations into the splitting stage. No change in parameters occurred prior to the chain-splitting stage.

Model parameters: bout-onset differentiation (Extended Data Fig. 10a–d)

Parameters that remained constant over development were:β = 0.13, α = 30, η = 0.05, ε = 0.14. To induce chain splitting, w_max was increased from 1 to 2, m was decreased from 5 to 2.5, and τ_γ was increased from 0.01 to 0.04 following a sigmoid with time constant τ_γ = 200 iterations and inflection point t₀ = 250 iterations into the splitting stage.

Model parameters: motif strategy (Extended Data Fig. 10e–h)

Parameters that remained constant over development were: β = 0.115, α = 30, η = 0.025, ε = 0.2. To induce chain splitting, w_max was increased from 1 to 2, m was decreased from 9 to 3, and γ was increased from 0.01 to 0.18 following a sigmoid with time constant τ_γ = 200 iterations and inflection point t₀ = 500 iterations into the splitting stage.

Model parameters: formation of a new syllable at bout onset (Extended Data Fig. 10i–k)

Parameters that remained constant over development were: β = 0.13, α = 30, η = 0.05, ε = 0.15. To induce chain splitting, w_max was increased from 1 to 2, m was decreased from 5 to 2.5, and γ was increased from 0.01 to 0.05 following a sigmoid with time constant τ_γ = 200 iterations and inflection point t₀ = 250 iterations into the splitting stage.

Shared and specific neurons

Neurons were classified as participating in a syllable type if the syllable onset-aligned histogram exhibited a peak that passed a threshold criterion. The criteria were chosen to include neurons where the histogram peak exceeded 90% of surrogate histogram peaks. Surrogate histograms were generated by placing one burst at a random latency in each syllable. (For example, in the protosyllable stage, the above criterion was found to be equivalent to having 5 bursts at the same latency in a bout of 10 protosyllables.) During the splitting phase, neurons were classified as shared if they participated in both syllable types, and specific if they participated in only one syllable type.

Visualizing network activity

We visualized network activity in two ways: network diagrams, and raster plots of population activity (e.g. Fig. 5a–d top and bottom panels, respectively). In both cases, we only included neurons that participated in at least one of the syllable types (see Shared and specific neurons above for participation criteria).

Network diagrams

Neurons are sorted along the x-axis based on their relative latencies. Neurons are sorted along the y-axis based on the relative strength of their synaptic input from specific neurons (or seed neurons) of each type (red or blue). Lines between neurons correspond to feedforward synaptic weights, and darker lines indicate stronger synaptic weights. For clarity of plotting, only the strongest six outgoing and strongest nine incoming weights are plotted for each neuron.

Population raster plots

Neurons are sorted from top to bottom according to their latency. Groups of seed neurons are indicated by magenta arrows. Shared neurons are plotted at the top and specific neurons are plotted below. As for network diagrams, neurons that did not reliably participate in at least one syllable type were excluded.

Further details for Figure 5(a–d)

Panels show network diagrams and raster plots at four different stages. (a) subsong stage (before learning), (b) end of protosyllable stage (iteration 500), (c) early chain splitting stage (iteration 992), (d) late chain-splitting stage (iteration 2,500).

Further details for Extended Data Fig. 10(a–d) (a) early protosyllable stage (iteration 5), (b) late protosyllable stage (iteration 100), (c) early chain splitting stage (iteration 130), (d) late chain splitting stage (iteration 600).

Extended Data

Extended Data Figure 1. Bursting and syllable-locked activity in HVC projection neurons of juvenile birds.

a, Range of bird ages at which songs were classified at different developmental stages (Spearman’s rank correlation between age and stage ρ=0.61; red line indicates the median, box indicates the 25–75 percentile, and whiskers indicate 10–90 percentile; n=12, 13, 18, 6 birds, respectively; n=39, 135, 566, 378 neurons, respectively). b, Interspike-interval (ISI) distributions (mean ± s.e.m.) of HVC projection neurons that exhibited spiking during singing, at three stages of vocal development (n=38, 130, 922 neurons). ISI distributions computed with logarithmic binning show bimodal structure: the peak around 3–5 ms indicates inter-spike intervals within bursts, and a broader peak around 100–400 ms indicates intervals between bursts (dashed line indicates the 30 ms threshold used for defining a burst; dotted line indicates peak). Note the refractory period below 1 ms. c, Burst width (top) and firing rate during bursts (bottom) as a function of developmental stage (median ± quartiles; n=39, 135, 566, 378, 32 neurons; **P<0.01, ***P<0.001 post-hoc comparison with adult stage).

d–i, Syllable-onset-aligned raster plots and histograms for neurons recorded during the subsong stage. Syllables are sorted from bottom to top by increasing syllable duration. d, Neuron that did not exhibit significant locking to subsong syllable onsets (HVC_RA, 50 dph, Bird 7). e, Another neuron in the same bird (same neuron as in Fig. 1a; HVC_RA, 51 dph). f–g, Two projection neurons recorded in a different subsong bird (both HVC_X; 47 and 48 dph, respectively; Bird 9). Note different latencies of bursting. h–i, Two projection neurons recorded in a different subsong bird (both HVC_X; 47 and 44 dph, respectively; Bird 10).

j–k, Syllable-onset-aligned raster plots and histograms showing strong locking to protosyllables (Bird 2). j, For the same neuron as in Fig. 1b (HVC_RA; 62 dph). k, For another neuron (HVC_RA; 65 dph).

l–m, Two neurons recorded in the motif stage (Bird 8). l, Neuron locked just after syllable onset (HVC_X neuron; 61 dph). m, Same neuron as in Fig. 1c (HVC_RA; 68 dph) showing locking late in the song syllable.

n, Population raster of 14 neurons aligned to protosyllable onsets (56–59 dph; Bird 1).

Extended Data Figure 2. Further analysis and examples of HVC projection neuron activity.

a–d, Examples of HVC projection neurons showing rhythmic activity during non-rhythmic song. a, Bird 2, HVC_RA neuron, 57dph, b, Bird 12, HVC_X, 53 dph, c, Bird 12, HVC_RA, 57dph, d, Syllable onset-aligned raster plot for neuron shown in panel c. Syllables are sorted in order of increasing duration (bottom to top; blue line indicates syllable offset). Also shown (top) is onset-aligned spike histogram. Note multiple rhythmic bursts during long syllables. Scale bars: (a–c) 1 mV, 100 ms.

e–l, Bout-related activity of HVC projection neurons. e, Bout-onset neuron (HVC_X; 44 dph; Bird 11). f, Bout-onset aligned histogram and raster plot for the neuron shown in (e). g, Bout-onset aligned histogram and raster plot for the neuron shown in Fig. 1d. h, Distribution of pre-bout-onset latencies for all bout-onset neurons (n=187 neurons, 32 birds). i, Bout-offset neuron (HVC_X; 61 dph; Bird 1). j, Bout-offset aligned histogram and raster plot for the neuron shown in (i). k, Bout-offset aligned histogram and raster plot for the neuron shown in Fig. 1e. l, Distribution of post-bout-offset latencies for all bout-offset neurons (n=149 neurons, 32 birds). Vertical scale bars: (e, i) 0.5 mV.

m–o, Developmental progression of HVC activity analyzed separately for HVC_RA and HVC_X neurons. m, Fraction of neurons temporally locked to syllables (mean ± s.e.m.; HVC_RA: 9, 22, 84, 54, 10 neurons analyzed at each stage, respectively; HVC_X: 27, 91, 376, 244, 22 neurons analyzed at each stage, respectively). n, Fraction of neurons that exhibited rhythmic bursts (HVC_RA: 9, 22, 84, 54, 10 neurons, respectively; HVC_X: 27, 91, 376, 244, 22 neurons, respectively). o, Mean period of HVC rhythmicity as a function of song stage (HVC_RA: 0, 16, 51, 41, 7 neurons, respectively; HVC_X: 3, 41, 245, 189, 18 neurons, respectively). Of the 14 comparisons between HVC_RA and HVC_X shown in m–o, only the period of HVC rhythm (panel o) during the motif stage showed significant difference between the cell types (P<0.05 with Bonferroni correction).

p–r, Analysis of probabilistic participation in rhythmic activity during protosyllables. p, Distribution of fraction of protosyllables on which spiking occurred (n=70 neurons). In contrast to the highly reliable bursting of HVC projection neurons in adult birds^19–22, we found that neurons in the protosyllable stage participated probabilistically (mean: 53% of protosyllables; triangle symbol). q, Histogram of the coefficient of determination r² for protosyllable participation across simultaneously recorded pairs of neurons (median r²=0.072; n=11 pairs; see Methods). r, Histogram of mutual information for protosyllable participation across simultaneously recorded pairs of neurons (median 0.056 bits; n=11 pairs; see Methods).

s–t, Analysis of burst coverage by HVC projection neuron bursts. s, Summary histogram of the covered fraction for all analyzed syllables (n=20 syllables, 4 birds). Note that 17/20 syllables had a covered fraction higher than 90%. t, Covered fraction analyzed for 20 syllables for which raster plots are shown in the main or Extended Data figures. Vertical grey bars indicate 95% confidence interval (2.5–97.5%ile) of coverage expected for random uniform shuffling of the observed bursts (see Methods). Note that for all syllables, the observed coverage is within the confidence interval for randomly shuffled bursts. These findings suggest that, even for the three syllables with coverage less than 90% (indicated with red square symbol), the lower coverage was consistent with undersampling due to the smaller number of recorded neurons in these birds.

Note on two models of HVC coding. Our findings bear on several recent models of song representation in HVC. One earlier model hypothesizes that HVC bursts provide timing signals to drive premotor activity^19,58,67 and to control the temporal precision of learning^76–79. This model implies a continuous, though not necessarily uniform, coverage of HVC bursts throughout song, as observed in our data. Overall, given the very large number of HVC neurons in each hemisphere⁸⁰ (>10⁴), our measurements are consistent with a continuous representation of timing signals throughout song syllables.

Another model of HVC coding has emphasized the finding that bursts may occur more often at particular times in the song, related to ‘gestures’ in the vocal control parameters²². Our finding that bursts are more concentrated around syllable onsets early in vocal development suggests that HVC may generate protosyllables as primitive gestures that serve as a scaffold on which later song syllables develop³³. During development, HVC activity appears to evolve such that, as a population, bursts occur more uniformly throughout song syllables (Fig. 2c), while the activity of individual neurons becomes sparser and more precise. At the same time, one might imagine that vocal gestures become more complex and precise as syllables develop into their adult forms. In this view, the emergence of sequential activity in HVC may be viewed to drive an increasingly complex sequence of gestures.

Extended Data Figure 3. Increase in the period of HVC rhythmicity during alternating syllable differentiation.

All data are from Bird 1. a, Paired recording of a shared neuron (top; HVC_RA) and a β-specific neuron (bottom; HVC_X; 69 dph). b, Paired recording of a shared neuron (top; HVC_X) and a C-specific neuron (bottom; HVC_X; 110 dph). c, Neuron switching between shared and specific spiking (HVC_X; 63 dph). d, Same neuron as in c, switching from specific to shared firing. e, A different neuron switching from shared to specific (HVC_p; 68 dph). Scale bars: (a–e) 0.5 mV, 200 ms.

f–i, Inter-burst interval (IBI) distributions for shared and specific neurons. f, for the neuron in Fig. 3c recorded during protosyllable stage. g, for the shared neuron shown in the top panel of Fig. 3f. h, for the β-specific neuron shown in Fig. 3d. i, for a γ-specific neuron (not shown). j, Population summary of the ‘most-probable IBI’ for the neurons recorded during the protosyllable stage (n=9), and during the emergence of syllables β and γ (62–72 dph; shared neurons, n=22; specific neurons, n=83). Note that shared neurons had the same ‘most-probable IBI’ as neurons recorded during the protosyllable stage. Neurons exhibiting an increased burst period by skipping cycles of an underlying rhythm were also observed in Birds 3, 4, and 6 (see Extended Data Fig. 8f–h, 9f, h).

Extended Data Figure 4. Analysis of shared neurons: latency and syllable selectivity.

a–d, Latencies of shared neuron bursts, color-coded by cell type: HVC_RA (red square), HVC_X (blue circle), and HVC_p (green diamond). a, Neurons in Bird 1 shared between syllables β and γ (from Fig. 3) during the early and late stages of syllable differentiation during early (top) and later (bottom) developmental stages. Note strong correlation of burst latencies (early, r=0.91, P<0.001; late, r=0.87, P=0.005). b, Neurons in Bird 1 shared between syllables D and B (Extended Data Fig. 7) during the early and late stages of syllable differentiation (top, early r>0.99, P<0.001; bottom, late r>0.99, P<0.001). c, Neurons in Bird 2 shared between syllables β and α (Fig. 4h) during the early and late stages (top, early r>0.99, P<0.001; bottom, late r>0.99, P<0.001). A shared neuron that had two peaks during the syllable α is shown with an ‘x’ symbol; this point was not included in the calculation of correlation. d, Neurons in Bird 4 shared between syllables ‘b’ and ‘d₁’ (Extended Data Fig. 9l) during early stage (top, r=0.89, P<0.001; neurons that burst in the first part of ‘b’ (syllable ‘b₁’) are shown with ‘x’ symbol, and were not included in the calculation of correlation). Neurons in Bird 4 shared between syllables ‘c’ and ‘d₂’ (Extended Data Fig. 9n) during early stage (bottom, r=0.98, P<0.001).

Bias: As a population, shared neurons exhibited a broad range of selectivity for emerging syllable types—some were equally active for both syllable types while others showed higher activity in one syllable than the other (‘bias’; see Methods). e, Raw spike data (top left) and instantaneous firing rate (bottom left) for a neuron shared between syllables β and γ (HVC_p; 68 dph, Bird 1). Also shown is the syllable-onset-aligned raster plot (bottom right) and histogram (top right) showing similar peak firing rates for both syllables (low bias; bias = 0.07). f, Spike data (left) and syllable-onset-aligned raster plot and histogram (right) for a high-bias shared neuron showing higher peak firing rate for syllable β than γ (bias = 0.63; HVC_RA; 68 dph, Bird 1). g, Low-bias shared neuron (bias = 0.06; HVC_X; 69 dph, Bird 2). h, High-bias shared neuron showing higher peak firing rate for syllable β than α (bias = 0.55; HVC_X; 68 dph, Bird 2). i, Scatter plot of the peak firing rates during two different syllable types, quantified by the height of the peak in the syllable-aligned spike histogram. Each dot is a neuron; shared neurons shown in cyan; neurons near the diagonal have low bias. Specific neurons are colored according to the associated syllable and appear near the axes. j, Distribution of the bias for shared neurons (cyan) and specific neurons (magenta). Bias ranged from 0, representing equal activity, to 1, representing activity exclusive to either one of the syllables (see Methods). Specific neurons exhibited a bias tightly clustered around one (0.96 ± 0.011, mean ± s.d.). In contrast, shared neurons exhibited a broad range of bias (0.28 ± 0.22).

These observations suggest that individual shared neurons can exist in a state intermediate between ‘specific’ and ‘shared’—perhaps reflecting a gradual process by which shared neurons become specific. Scale bars: (e–h) 0.5 mV, 100 ms. Inset in (f, h) shows zoom of bursts indicated by asterisk; scale bar: 5 ms.

Extended Data Figure 5. Analysis of the acoustic differences associated with shared neuron bursts.

One of the distinguishing features of the emergence of new syllable types is an apparent differentiation of the acoustic structure within the emerging syllables. However, it is possible that shared neurons may only be active at times within emerging syllables at which no acoustic differentiation has yet occurred—that is, at times when the emerging syllable types are acoustically identical. To test this possibility, we analyzed the trajectories of acoustic features of emerging syllable types around the times of shared neuron bursts. a, Shared HVC_RA neuron recorded in Bird 1 during alternation between emerging syllable types β and γ (same neuron as Fig. 3e). b–c, Average spectrogram (sparse contour representation; see Methods) computed for syllables β and γ, centered on a 50 ms window immediately after the burst in each syllable. d, Song amplitude as a function of time for syllables β (red) and γ (blue), relative to burst time. Lines show average across all syllable renditions on which the neuron was active. Shading around lines show s.e.m. (for this and several other examples, s.e.m. is too small to be visible). e, Spectral center of gravity as a function of time for syllables β (red) and γ (blue). f, Distribution of projected samples for syllables β (red) and γ (blue), computed by projecting the 8-dimensional vector of spectral features onto a line that yields maximum separability between the two syllables. This distribution is computed at each time (1 ms steps) in the 50 ms analysis window after burst time. Shown is the distribution at t=25 ms. g, d-prime analysis of separability of projected samples for syllables β and γ. The value of d’ is computed as a function of time (1 ms steps; red trace). Also shown is the 95% confidence interval (gray band) computed from surrogate datasets with randomized labels. Dashed horizontal line shows the 95 percentile of the distribution of peak values of d’ in the surrogate data set (identified in the 10–40 ms window). h–j, Acoustic analysis for three additional HVC_RA neurons. Panels are analogous to a–g. k, Plot of d’ trajectories for all shared HVC_RA neurons. Significant d’ values (above the 95 percentile of peak values) are shown in red. Non-significant values shown as gray line. l, Same as (k) but for shared HVC_X neurons. m, Population summary of mean d’ (averaged over the presumptive premotor window 10–40 ms after burst time). Each symbol represents a different shared neuron and each column indicates a different syllable pair. Analysis is shown separately for each neuron type: HVC_RA neurons (green circles) and HVC_X neurons (blue squares). Neurons with no significant acoustic differences are indicated with black symbols. n, Cumulative distribution of mean d’ for shared HVC_RA neurons (green; n=11) and shared HVC_X neurons (blue; n=36). Only neurons with significant d’ metric are included in the cumulative. No significant difference was observed between neuron types (P=0.1). Scale bars: (a, h, i, j) 0.5 mV, 100 ms.

Summary of properties of HVC_RA and HVC_X shared neurons: Shared neurons were found in similar proportion across both HVC_RA and HVC_X neurons (19% and 28%, respectively; P=0.08; averaged over all developmental stages) and shared neurons of both cell types exhibited the property that bursts have similar latencies during the shared syllables (Extended Data Fig. 4a–d). As shown above, for both neuron types, we observed shared neurons that burst at times where there was a significant acoustic difference between the shared syllables. These findings suggest that both projection neuron types participate in shared neural sequences, and that these shared sequences occur during acoustically distinguishable parts of the emerging syllables.

Extended Data Figure 6. Detailed analysis of bout-onset differentiation in Bird 2.

(Fig. 4). a, Song examples throughout song development. Panels: i, subsong (49 dph); ii, emergence of protosyllable α from subsong (60 dph); iii, appearance of bout-onset element ε (63 dph); iv, fusion of ε with first α to form new syllable β (67 dph); v–vi, acoustic differentiation of β and α, and incorporation with γ into song motif CBA (70, 90 dph); vii, tutor song. b, Schematic of syllable formation (same as Fig. 4a), inferred by tracking backward in development the adult syllables C, B and A. Early on, protosyllable (labeled α) is produced rhythmically. The first protosyllable in each bout fuses with a brief bout-onset vocal element ε to form a new emerging syllable type β. Both α and β undergo subsequent acoustic differentiation to form adult syllables A and B, respectively. (An additional syllable γ emerges at bout onset to form adult syllable C). c, Developmental time course of the occurrence probability of different syllable types at bout onsets (mean ± s.e.m.). d, Syllable duration distribution showing three non-overlapping peaks (67 dph). Colored bars indicated syllable duration ranges used for syllable labeling. This separation of durations allowed automatic determination of syllable identity. e, Pitch goodness trajectories of syllables α (red) and β (blue) at three stages of vocal development (median ± quartiles; n=100 syllables per day). Black bar: region used to compute data in Fig. 4b. f, Example of a neuron active during both syllables α and β (HVC_RA; 69 dph). Note that the activity of this neuron during syllable α was weak, and did not quite reach our statistical criterion for being a ‘shared’ neuron.

Extended Data Figure 7. Hierarchical differentiation of syllables.

All data are from Bird 1. a, Song examples during the emergence of syllables B and D from a common precursor syllable β, which had undergone earlier differentiation from a protosyllable α (Bird 1; same bird as Fig. 3). Panels: i (70 dph), After the initial differentiation of the protosyllable into β and γ (at ~62 dph), the bird produced a rhythmic alternation of these two syllables, and the alternating sequence was reliably preceded at bout onsets by a short vocal element ε (ε-β-γ-β-γ-β-γ…). Note that the first repetition of β in each bout (labeled D) is acoustically identical to later repetitions (labeled B); panel ii (80 dph), the first repetition of β in the bout (syllable D) undergoes differential acoustic refinement compared to later repetitions (syllable B); iii, syllable B, C and D, together with bout-onset element ε, crystallize into adult motif EDCB (90 dph), that approximately matches the tutor motif (panel iv). b, Schematic of syllable formation. c, Scatter plot of the mean Wiener entropy showing differential acoustic refinement of syllables B (orange) and D (green) through development (n=100 syllables of each type per day; horizontal jitter added to improve data visibility). d, Wiener entropy trajectory of syllables B and D at three stages of vocal development (median ± quartiles; n=100 syllables of each type per day). Black bar indicates region used to compute data in c. e, Population raster of 60 neurons early in syllable differentiation showing shared (top) and specific (bottom) sequences. f, Same as panel e, but for 70 neurons recorded late in differentiation of D and B.

Evidence for an incomplete splitting of a neural sequence. The pattern of shared and specific neurons observed for these syllables is quite similar to what would be expected in our model during an early/intermediate stage of splitting (Fig. 5c or Extended Data Fig. 10c). Of particular note in this bird is the large fraction of shared neurons that remained in the later recordings (panel f), compared to the smaller fraction of shared neurons at late stages in syllables B and C of the same bird (Fig. 3h). However, syllables B and C differentiated from parent syllable α early in development (~60 dph, Fig. 3b), while D and B differentiated from β at a much later stage (~80 dph, panel c). One might speculate that the splitting of D and B may have failed to reach completion before the bird reached adulthood, possibly preventing further splitting.

Neural evidence (shared burst sequence) for hierarchical differentiation was also observed in Bird 6 (data not shown). Neural evidence (shared burst sequence) for bout-onset differentiation was also observed in Bird 5 (data not shown).

Extended Data Figure 8. Simultaneous formation of multiple syllable types into an entire motif.

All data are from Bird 3. Neural recordings from this bird support the view that, in the ‘motif strategy’, new syllables emerge from a common rhythmic protosequence. a, Song examples during the emergence of a motif. Panels: i, subsong (37 dph); ii, the song began to acquire rhythmic ‘protosyllable’ modulation in song amplitude around 9 Hz (45 dph), iii, over the next five days (47–51 dph), this bird acquired a reliable pattern of 4–5 acoustically distinct elements (‘syllables’), each generated in a different cycle of the 9 Hz rhythm (48 dph); iv, the acoustic structure in each syllable was gradually refined, resulting in an excellent match to the tutor song even at this early age (51 dph); v, tutor song. b, Scatter plot of syllable duration and pitch goodness (n=300 syllables per day; color coded according to syllable identity in panel a). c, Development of the song rhythmicity quantified as spectrum of the sound amplitude³⁸. Gray shade indicates the pass band for the filter used in phase segmentation. d, Phase segmentation based on the rhythmicity in the song. Top: song spectrogram with phase segments (gray boxes). Middle: sound amplitude (blue) and band-pass filtered sound amplitude (magenta). Syllable segmentation based on the sound amplitude is shown as white boxes. Bottom: instantaneous phase (green) of the band-pass filtered sound amplitude. Phase segments (gray boxes) are obtained by detecting threshold crossing (black dotted line) of the instantaneous phase. e, Rhythmic neuron (protosyllable stage; HVC_p; 45 dph). f, Neuron shared between syllables A and B (HVC_RA; 48 dph). g, Neuron shared between B and E (HVC_X; 49 dph). h, Population raster aligned to the five-syllable motif for neurons that were significantly locked to any syllable (n=10 neurons). Each motif and associated spike times were time-warped using a piecewise linear method⁶⁷ based on syllable onsets and offsets. i, Histogram of the absolute phase difference between the two syllables for all shared neurons (n=8 neurons; mean phase difference: 41 ± 33.9 deg, mean ± s.d.). j, Cumulative distribution of the mean absolute phase difference after randomizing the pairing (red dotted line indicates threshold for significance P<0.05; red triangle indicates observed mean absolute phase difference, P=0.013). Statistical details in Methods. Scale bars: (e–g) 30 dB, 0.3 mV, 200 ms.

Extended Data Figure 9. Another example of shared burst sequences during the emergence of new syllable types.

All data are from Bird 4. a, Song examples during the emergence of a motif ABCDF. Note the nearly simultaneous emergence of multiple syllable types in fixed order (52 dph). Tutor song shown at the bottom. Phase segments are shown above the spectrogram for song at 43 dph. b, Top: Song rhythm spectrum calculated in the protosyllable stage (43 dph) and after motif formation (59 dph). Note the pronounced peaks at 5 Hz and 10 Hz in both stages. Bottom: Syllable duration distribution in the protosyllable stage (43 dph) and after motif formation (59 dph) showing two peaks. At 43 dph, the peak at 70 ms indicates short protosyllables corresponding to one cycle of the 10 Hz rhythm, and the peak at 140 ms indicates longer syllables formed by two protosyllables fused across two cycles of the 10 Hz rhythm (doubled protosyllables). Example doubled protosyllables are seen in the first and third syllables of panel a (43 dph; note that boxes at the top of this panel indicate phase segments, not syllable boundaries). c, Hypothesized mechanism of motif construction, based on the examination of acoustic structure and analysis of neural burst sequences (see below). Notably, in this bird, the majority of syllables emerged nearly simultaneously in a relatively fixed order, consistent with a ‘motif strategy.’ d, Scatter plots of syllable duration versus mean spectral center of gravity at four stages of vocal development (each dot represents a single syllable; n=500 syllables per day; color coded according to syllable identity in panel a). e, Neuron bursting at 10 Hz protosyllable rhythm (HVC_X; 48 dph). Phase segments shown above spectrogram. f, Top: neuron bursting at the 10 Hz rhythm (HVC_X; 49 dph). Bottom: Simultaneous recording of a neuron bursting on alternate cycles of 10 Hz rhythm (HVC_RA). g, Shared neuron bursting on second half of syllable ‘b’ (labeled b₂) and first half of syllable ‘d’ (labeled d₁) (HVC_RA; 51 dph). h, Shared neuron bursting rhythmically on first half of ‘b’ (b₁), syllable ‘c’ and second half of ‘d’ (d₂) (HVC_RA; 51 dph). i, Shared neuron bursting on ‘a’ and first half of ‘d’ (d₁) (HVC_RA; 58 dph). j, Shared neuron bursting on second half of ‘d’ (d₂), ‘e’, and last part of ‘f’ (HVC_RA; 57 dph). k, Population raster of 12 neurons that were significantly locked to protosyllable onsets (48–49 dph). Protosyllables were identified using phase segmentation (see Methods). l, Population raster showing neurons active during syllables ‘b’ and/or ‘d’, recorded early in syllable differentiation. Neurons shared between ‘b’ and ‘d₁’ are grouped at top. Neurons specific for ‘b’ are grouped next, and neurons specific for ‘d’ are grouped at bottom. m, Same as panel l but for neurons recorded later in development. n, Population rasters showing neurons active during syllables ‘c’ and/or ‘d’, recorded early in development. o, Same as panel m, but for neurons recorded later in development. Scale bars: (e–j) 0.5 mV, 200 ms.

Neural evidence for hypothesized mechanism of motif construction. Based on an analysis of acoustic signals and neural recordings, we have formulated a hypothesis for how the song of this bird developed, from the formation of the protosyllable to the emergence of the complete motif. We hypothesize that the fundamental protosyllable element corresponds to the prominent 10 Hz peak in the rhythm spectrum and the 70 ms peak in the duration distribution (panel b). This view is further supported by the presence of neurons in the protosyllable stage that generate rhythmic bursts at 10 Hz (panels e, f; 11/18 neurons were rhythmic, 5/11 rhythmic neurons exhibited periodicity at 10 Hz), and the existence of a burst sequence during the protosyllable (panel k).

In this bird, the rhythmic protosyllables differentiated nearly simultaneously, at an early age (52 dph, panel a), into a complete sequence of distinct syllables that subsequently formed the adult song, suggesting this bird employed a ‘motif strategy.’ One complication of this simple view is that there may have been an early partial splitting of the short protosyllable α into two ‘daughter’ protosyllables α₁ and α₂, which alternated to produce the elements of the final motif (panel c). Two lines of evidence based on neural activity support this view: First, many neurons recorded at an early stage (<50 dph) exhibited a prominent 5 Hz periodicity in their rhythmic bursting. (panels f, h; 6/11 rhythmic neurons), rather than the expected 10 Hz period (panel e, f, top). This observation led us to consider the possibility that the 100 ms neural sequence, corresponding to the dominant 10 Hz protosyllable rhythm, underwent a partial splitting during the protosyllable stage—similar to the alternating differentiation described for Bird 1 (Fig. 3; Extended Data Fig. 4). This would result in two distinct alternating protosyllable sequences α₁ and α₂ (panel c). Such splitting would effectively double the period of the protosyllable rhythm, and would account for the ‘doubled’ protosyllables and the 5 Hz peak in the rhythm spectrum (panel b).

The existence of short and doubled protosyllables led us to hypothesize that the short syllables of the adult motif (‘a’, ‘c’, and ‘e’) arose from the short protosyllables, while long adult syllables (‘b’ and ‘d’, and possibly ‘f’) arose from the doubled protosyllables (panel c). Early syllable ‘e’ is later dropped by the juvenile, although it appears in the tutor song.

Furthermore, the analysis of shared sequences (panels l–o) revealed a predominance of shared neurons between syllable elements in alternating cycles of the underlying 10 Hz rhythm. For example, shared neurons were observed between syllables ‘a’, ‘b₂’ and ‘d₁’ (panel i for neuron shared between ‘a’ and ‘d₁’; panel g and l for neurons shared between ‘b₂’ and ‘d₁’). Shared neurons were also observed between syllables ‘b₁’, ‘c’, and ‘d₂’ (panel h for neuron shared between ‘b₁’, ‘c’, and ‘d₂’; panel n for neurons shared between ‘c’ and ‘d₂’). In contrast, many fewer shared neurons were observed between neighboring cycles of the underlying rhythm, although examples of this can be found (panel j).

Extended Data Figure 10. (Model) Other strategies for syllable formation.

a–d, Bout-onset differentiation results from activation of bout-onset seed neurons (blue arrow) followed by rhythmic activation of protosyllable seed neurons (red arrow). Network diagrams show (a, b) protosyllable formation and (c, d) splitting of chains specific for bout-onset syllable β and specific for later repetitions of the protosyllable α (blue and red, respectively; shared neurons: black).

e–h, Model of simultaneous formation of multiple syllable types into an entire motif (‘motif strategy’). e–f, Protosyllable seed neurons (magenta lines) were activated rhythmically to form a protosequence. g, Seed neurons were then divided into three sequentially activated subgroups, resulting in the rapid splitting of the protosequence into three daughter sequences. In intermediate stages (panel g), individual neurons exhibited varying degrees of specificity and sharedness for the emerging syllable types. h, After learning, the population of neurons was active sequentially throughout the entire ‘motif,’ but individual neurons were active during only one of the resulting syllables, forming three distinct non-overlapping sequences.

i–k, Network diagrams and raster plots showing an example of the formation of a new syllable chain at bout onset. In the network diagrams, seed neurons are indicated within magenta boxes, and bout-onset seed neurons and protosyllable seed neurons are indicated by blue and red arrows, respectively. Neurons specific for each emerging syllable type (εand α) are colored blue and red, respectively. The three panels represent the early protosyllable stage, the late protosyllable stage, and the final stage. The training protocol is similar to that for bout-onset differentiation (panel a–d), except that protosyllable seed neurons are driven more strongly throughout the learning process. As a result, protosyllable seed neurons did not become outcompeted by the growing bout-onset chain. Strong activation of the protosyllable seed neurons also terminated activity in the bout-onset chain through fast recurrent inhibition, thus preventing further growth of the bout-onset chain, as occurs in bout-onset differentiation.

General discussion on the role of chain splitting in the formation of new syllable types: In our model, we envision that the formation of daughter chains in HVC is translated into the emergence of new syllable types as follows: During the splitting process, as two distinct sequences of specific neurons develop, their downstream projections can be independently modified^67,77 such that each of the emerging chains of specific neurons can drive a distinct pattern of downstream motor commands, allowing distinct acoustic structure in the emerging syllable types. Such differential acoustic refinement is consistent with the previous behavioral observation that the altered acoustic structure of new syllables emerges in place, without moving or reordering sound components (‘sound differentiation in situ’)³³.

This model naturally explains the apparent ‘decoupling’ of shared projection neuron bursts from acoustic structure in the vocal output—i.e., the fact that the bursts of shared neurons become associated with two distinct acoustic outputs during the differentiation of two syllable types (Extended Data Fig. 5). Specifically, during syllable differentiation, a shared neuron participates with different ensembles of neurons during each of the emerging sequences, and these different ensembles can drive different vocal outputs.