The connectivity domain: Analyzing resting state fMRI data using feature-based data-driven and model-based methods

Abstract

Spontaneous fluctuations of resting state functional MRI (rsfMRI) have been widely used to understand the macro-connectome of the human brain. However, these fluctuations are not synchronized among subjects, which leads to limitations and makes utilization of first-level model-based methods challenging. Considering this limitation of rsfMRI data in the time domain, we propose to transfer the spatiotemporal information of the rsfMRI data to another domain, the connectivity domain, in which each value represents the same effect across subjects. Using a set of seed networks and a connectivity index to calculate the functional connectivity for each seed network, we transform data into the connectivity domain by generating connectivity weights for each subject. Comparison of the two domains using a data-driven method suggests several advantages in analyzing data using data-driven methods in the connectivity domain over the time domain. We also demonstrate the feasibility of applying model-based methods in the connectivity domain, which offers a new pathway for the use of first-level model-based methods on rsfMRI data. The connectivity domain, furthermore, demonstrates a unique opportunity to perform first-level feature-based data-driven and model-based analyses. The connectivity domain can be constructed from any technique that identifies sets of features that are similar across subjects and can greatly help researchers in the study of macro-connectome brain function by enabling us to perform a wide range of model-based and data-driven approaches on rsfMRI data, decreasing susceptibility of analysis techniques to parameters that are not related to brain connectivity information, and evaluating both static and dynamic functional connectivity of the brain from a new perspective.

1. Introduction

There are two widely-used approaches to analyze functional magnetic resonance imaging (fMRI) images in the time domain (i.e. analyzing the spatiotemporal information of fMRI data). The first approach includes model-based methods, such as general linear model (GLM), which show how well a certain model fits to the fMRI data (Friston et al., 1994). The second approach includes data-driven methods, such as principle component analysis (PCA) and independent component analysis (ICA), which are based on feature extraction from fMRI data (Calhoun et al., 2003; Calhoun and Adali, 2012; van den Heuvel and Hulshoff Pol, 2010). In a model-based method, data is compared with a predefined model; therefore, model-based methods are focused on validating a prior hypothesis (the model) based on the data available and improving scientific understanding. Data-driven methods, on the other hand, analyze data in a more flexible manner. These methods are especially desirable when a good model does not exist or is hard to generate. Data-driven methods have the power to identify unanticipated components which can later be used in model-based approaches. Thus, data-driven methods can also be considered as model generating methods (Ford, 1995) since they can be used to obtain a model for data when there is no satisfactory model already available. However, by themselves, data-driven methods are primarily used for scientific discovery and identification of useful features from the data; they are most useful when combined within a statistical testing framework or for tasks such as prediction or classification (Calhoun and Adali, 2012; Erhardt et al., 2011a).

Considering the advantages and limitations of both model-based and data-driven methods, they are complementary to each other. Therefore, in order to analyze data comprehensively and have a better understanding of brain function, it is useful to investigate data using both approaches. In the context of the model-based linear GLM and data-driven linear ICA, both approaches can be conceptualized as X = AS, in which the i^th row of the mixing matrix (A) identifies the contribution of parameters of S to create the i^th value of X. The main difference is that, in the data-driven method, the mixing matrix (A) needs to be estimated, whereas in the model-based method, the mixing matrix is pre-specified (Calhoun et al., 2001; Ford, 1995). This requirement for a pre-specified design matrix makes the application of first-level model-based methods to extract brain networks challenging.

A brain network is defined as a subset of brain regions that interact with each other in a distinguishable way. Brain networks can be identified during the resting state by measuring the blood-oxygenation-level dependent (BOLD) signal from resting state fMRI (rsfMRI) data, which is related to brain activity (Buckner and Vincent, 2007). However, the fluctuations in the BOLD signal in the time domain at a specific time point are not synchronized among subjects for rsfMRI data. Therefore, the time courses of brain networks in rsfMRI are different among subjects. In other words, by considering the general form of X = AS, the mixing matrix (A) that represents the relationship between brain networks (S) with rsfMRI data at different time points (X) is different among subjects, which makes modeling the time-domain aspect of resting fMRI challenging. Consequently, we cannot use the design matrix obtained from one dataset to apply a model-based method such as first-level GLM to identify underlying sources (S) in another dataset, even if matrix A is obtained from the same subjects but at a different sampling (in our work, this means at different scanning sessions). To overcome this limitation, we proposed a new domain, the connectivity domain, in which the mixing matrix A is similar among subjects, which will enable us to perform model-based methods such as GLM to analyze the rsfMRI data.

Transforming data to a new domain requires defining a set of bases for the new domain. In general, each domain is composed of several bases, and by measuring the contribution of data in each of these bases, we can transform and represent the data in the new domain. To accomplish this, we select a set of spatial features that are similar across subjects. Those similar features are here called seed networks, and their time courses are used as the bases of the new domain to construct the connectivity domain. Our proposed connectivity domain is very flexible because various approaches, such as using data-driven seeds, functional seeds, or anatomical seeds, can be used to obtain the bases of the connectivity domain. For example, we can use high model order (number of components = 100) to achieve a “functional parcellation” and apply their corresponding time courses to construct the connectivity domain, which would allow us to investigate a multiscale hierarchical functional organization of the brain.

In general, the time course of any feature which shows similarity across subjects can be used to calculate the connectivity domain. We can use anatomical, cytoarchitectonic and/or functional atlases. We can likewise use the brain networks' time courses to construct the connectivity domain or perform clustering analysis on the rsfMRI data time courses and use the representative time courses of each cluster to construct the connectivity domain. We can also use the functional atlases and ROIs to extract the bases of the connectivity domain (Shirer et al., 2012). However, in this study to show the feasibility, we have chosen to use the simple solution of selecting similar anatomical regions across subjects. In other words, in this preliminary study, we use atlas-derived anatomical locations (seed regions) across subjects to define the corresponding features (seed networks) among subjects and use the time courses of those regions as the basis of the new domain. Thus in this study, the connectivity domain is obtained by calculating the functional connectivity for the anatomical seed networks (seed regions) by measuring a connectivity index (the correlation value) between the correspondent time series of each seed network and the whole brain. The resulting functional connectivity weights are the input data for our proposed domain. In the new proposed domain, (a) the connectivity of the brain can be modeled among subjects and tested for differences among groups (in this example, the relationship between the connectivity of brain regions and brain networks can be calculated and compared among different groups) and (b) with prior knowledge of the contribution of connectivity of seed networks to brain networks, we can directly calculate brain networks using model-based methods such as GLM. This can provide the opportunity to use model-based methods, like first-level GLM, without the handicap of having to estimate the mixing matrix, A, based on the combined group data (making it not a pure model-based method, but a data-informed model-based method). Applying first-level GLM in the connectivity domain can be viewed as similar to first-level GLM in task-based fMRI analysis in which, for each participant, we identify, through modeling, the effects of regressors and create individual subject spatial maps corresponding to those regressors. In other words, we can use a predefined model (a predefined design matrix) to obtain the brain networks of different subjects.

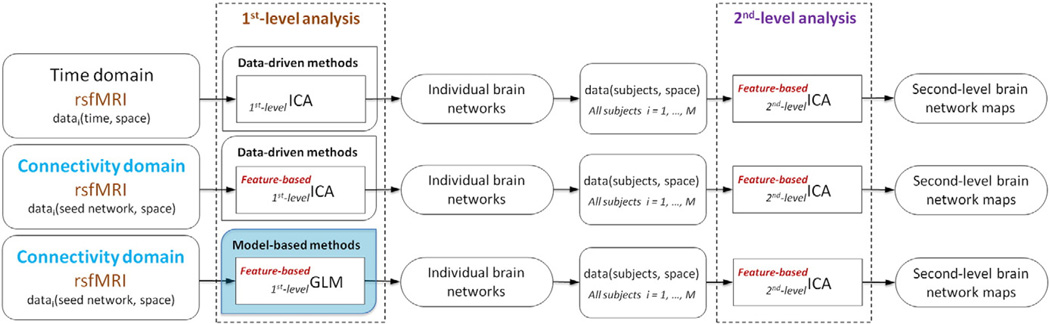
Moreover, the connectivity domain can enhance the usage of data-driven analysis approaches, particularly feature-based ICA (Allen et al., 2011; Smith et al., 2009). Multiple data-driven analysis approaches have been successfully applied to rsfMRI data including clustering (Cordes et al., 2002; van den Heuvel et al., 2008), ICA (Beckmann et al., 2005; Calhoun et al., 2001), graph analysis (Fornito et al., 2013; Rubinov and Sporns, 2010; van Wijk et al., 2010), and sparse coding (Lv et al., 2015). ICA-based methods are some of the more widely used approaches, and their results (i.e., extracted networks) show a high level of consistency in different conditions such as open or closed eyes; task, rest or sleep; and healthy or various mental disorders (Calhoun et al., 2008a, 2008b; Damoiseaux et al., 2006; Garrity et al., 2007; Iraji et al., 2015a; Jafri et al., 2008; Sorg et al., 2007; Stevens et al., 2009; van den Heuvel and Hulshoff Pol, 2010; Whitfield-Gabrieli and Ford, 2012). ICA methods are designed to identify a set of latent spatially independent maps from rsfMRI data. A spatial map can be considered to be an underlying source (i.e. a brain network (Erhardt et al., 2011a)), and the value of each voxel represents the degree to which the voxel belongs to, or is functionally connected to, that source (Calhoun and Adali, 2012; van den Heuvel and Hulshoff Pol, 2010).

Most previous ICA studies have estimated resting state networks (RSNs) by applying first-level ICA on the spatiotemporal information. Some new studies have also suggested the feasibility of calculating patterns of RSNs by applying ICA on features extracted from the spatiotemporal data. Using extracted features from the data rather than the time domain data itself can be useful and important in the study of brain function at the macro-connectome scale, which constitutes the method referred to here as feature-based ICA (Calhoun and Allen, 2013; Kim et al., 2010). One advantage of feature-based ICA is that it removes the need to model the time domain from the fMRI data (Calhoun and Allen, 2013). However, previous feature-based ICA analyses have mostly been limited to second-level analyses, such as applying ICA on the amplitude of low frequency fluctuations (ALFF) map for rsfMRI, t-maps of GLM for task-based fMRI (Calhoun and Allen, 2013), the peak coordinates from meta-analysis (Smith et al., 2009), or even the outputs of the first-level ICA (Wisner et al., 2013). The connectivity domain provides us with the opportunity to use feature-based ICA techniques at both the first level and second level (Fig. 1). While the second-level ICA techniques have been shown to be valid tools for extracting intrinsic networks (Calhoun and Allen, 2013; Smith et al., 2009), they usually have some disadvantages as compared to first-level ICA analysis (Calhoun, 2015). Second-level ICA analysis generates one set of brain networks for all input data by utilizing the covariation among input data, while first-level ICA generates a set of brain networks for each individual by utilizing the information which exists in each individual input data. This provides us the opportunity to perform statistical analyses on brain networks across individuals, such as comparing brain networks between two groups. Furthermore, even if a researcher is only interested in studying the brain networks at the group level, second-level feature-based ICA leads to noisier results as compared to first-level feature-based ICA because 1) second-level feature-based ICA uses highly distilled features and there is a large reduction in data, leading to loss of some related information in data available to the ICA algorithm (Calhoun, 2015), and 2) the ICA algorithm only utilizes the between-subjects variations while first-level feature-based ICA estimates brain networks using both within- and between-subjects variations. Finally, second-level feature-based ICA limits the possible analyses on the input data due to loss of within-subject input data variations. For example, first-level feature-based ICA, unlike second-level feature-based ICA, allows us to investigate dynamic changes in the brain networks. Thus, it is preferable to use a first-level analysis if possible, though there are numerous instances when it is not possible (Calhoun and Allen, 2013). Furthermore, the connectivity domain has uses beyond ICA techniques, and wide ranges of data-driven and model-based approaches can be applied in this domain (Fig. 1).

Fig. 1.

Schematic of analytical approaches which can be applied on rsfMRI data. The connectivity domain, similar to the time domain, allows us to perform a wide range of data-driven methods. The connectivity domain also supports implementing model-based methods such as first-level generalized linear model (GLM) on rsfMRI data (blue box). While feature-based approaches have been performed as second-level analyses, the connectivity domain provides us the opportunity to perform feature-based techniques at both first and second levels.

In this work, we first define one example of a set of seed networks to create the connectivity domain. Then, we present the superiority of the connectivity domain over the time domain by comparing data-driven methods applied in both domains. Lastly, we investigate the feasibility of applying first-level model-based methods in the connectivity domain. One important benefit of the connectivity domain as compared to existing methods for analyzing rsfMRI data is that the connectivity domain enables us to directly perform model-based approaches and empowers us to perform first-level feature-based analyses.

Again, in this manuscript, our purpose is to demonstrate the connectivity domain, a new framework to analyze rsfMRI data, and its feasibility. Neither the approaches to construct the connectivity domain nor the available analytical methods are limited to what we demonstrate here. For instance, the seed networks used to construct the connectivity domain are not limited to canonical seeds or anatomical atlases, and we can identify them using wide range of approaches.

2. Method

2.1. Theory

To illustrate the connectivity domain, we show examples of the same approaches that have been applied in both the time and connectivity domains. The relationship between the two domains can assist us to better explain the connectivity domain and the potential data analysis techniques that can be used in the connectivity domain.

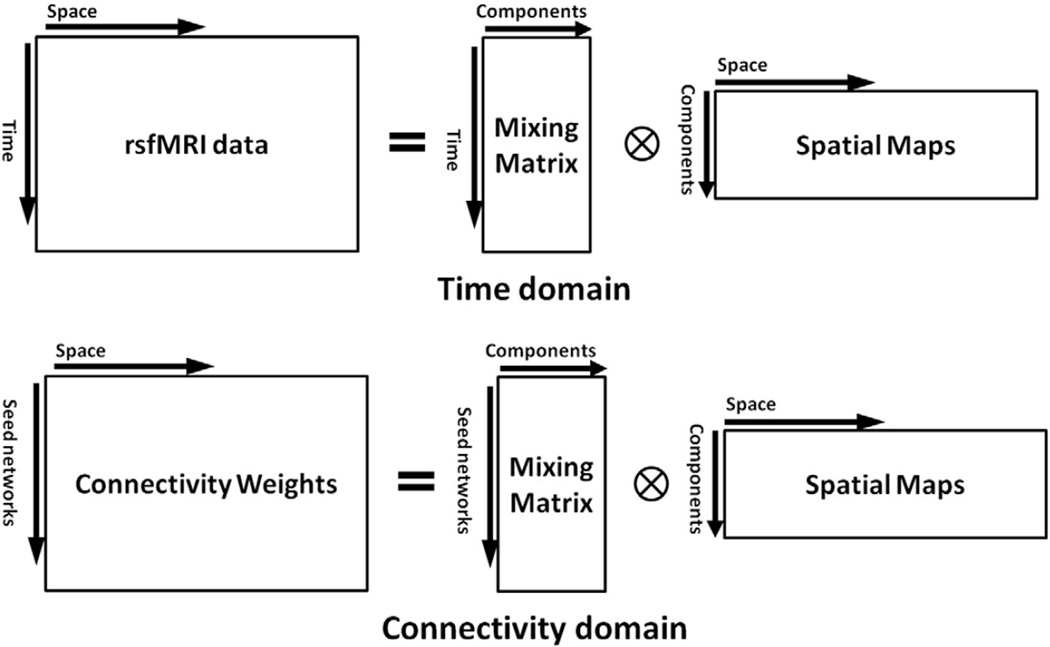
In the connectivity domain, the functional connectivity weights are used as input for data analysis and replace the role of the rsfMRI time series data in the time domain. Fig. 2 shows the analogy between the two domains in the presentation of the general form of X = AS. In the time domain, each row of matrix X is one time point of rsfMRI data, while in the connectivity domain, each row of matrix X represents functional connectivity weights of one seed network. Furthermore, each row of matrix S for both domains is one spatial map (or brain network). Thus, array A(i,j) in the time domain represents the contribution of the brain network j to the voxels' intensities of rsfMRI data at time point i while array A(i,j) in the connectivity domain represents the contribution of the brain network j to the connectivity weights of seed network i (Fig. 2). Considering this analogy, if we measure the connectivity weights, we can apply all existing time-domain data analysis methods in the connectivity domain as well. Of particular note, as we present later in this paper, since the mixing matrix A is similar among (healthy control) subjects in the connectivity domain, the quality and robustness of the result of data-driven approaches are improved as compared with the time domain. Furthermore, the first-level model-based techniques can also be directly applied in the connectivity domain.

Fig. 2.

Analogy for the time and connectivity domains using X = AS equation.

To show the feasibility and advantages of any new domain, we first need to 1) show how the new domain behaves when performing existing analyses as compared to the same analyses in the current domain (the time domain), and then 2) try to evaluate whether we can do a new type of analysis in the new domain that are not feasible in the time domain.

In studying human brain connectivity, it is important to be able to compare and assess findings across different studies. In order to have highly reproducible results which enables us to further compare between studies and make valid conclusions, the results should be less sensitive to the parameters of data collection and the selected analytical approach. Therefore, we should compare the two domains' susceptibility to parameter changes, and a superior domain should be less affected by different parameter variations. Since we are investigating rsfMRI data, we evaluate the impact of parameter variation by comparing the similarity of brain networks obtained for different parameters. In order to have reasonably applicable conclusions in this comparison, we should choose a commonly used and broadly acceptable analysis technique. Thus, we chose ICA for this comparison, as it is one of the most commonly-used and broadly acceptable methods.

In neuroimaging research, first-level model-based methods such as first-level GLM are a key part of fMRI analysis. They allow us to evaluate hypotheses drawn independently from the data being studied. Thus, in studying brain connectivity during rest, it is important to be able to perform investigations using first-level model-based methods. Here, we evaluate whether the connectivity domain can provide us the opportunity to apply first-level model-based methods on rsfMRI data by assessing the feasibility of applying first-level GLM.

ICA can be applied on the rsfMRI data (spatiotemporal information) directly, which is commonly known as first-level ICA, or it can be applied on computed features from the spatiotemporal information, which is commonly known as second-level ICA. While second-level ICA techniques have been shown to be valid tools for extracting intrinsic networks (Calhoun and Allen, 2013; Smith et al., 2009), they usually have some disadvantages as compared with first-level ICA analysis. Loss of information in second-level ICA leads to noisier results and limits the possible analysis on the data, like by preventing us from looking at dynamic changes in the resting state networks (Calhoun, 2015). However, using extracted features from the data rather than the time domain data itself can be useful and important in the study of brain function at the macro-connectome scale, which constitutes the method referred to here as feature-based ICA. One advantage of feature-based ICA is that it removes the need to model the time domain from the fMRI data (Calhoun and Allen, 2013). This study can also be considered as the second attempt to investigate the impact of working with features in ICA analysis. While the first study (Calhoun and Allen, 2013) shows that feature-based ICA methods can provide similar but noisier results, the current study provides a broader context for feature-based ICA analysis. Applying ICA techniques in the connectivity domain, in addition to the superiorities over the time domain which will be presented in this paper, incorporates the benefits of feature-based ICA techniques as well, can be applied using either first or second level estimates.

2.2. Dataset and preprocessing

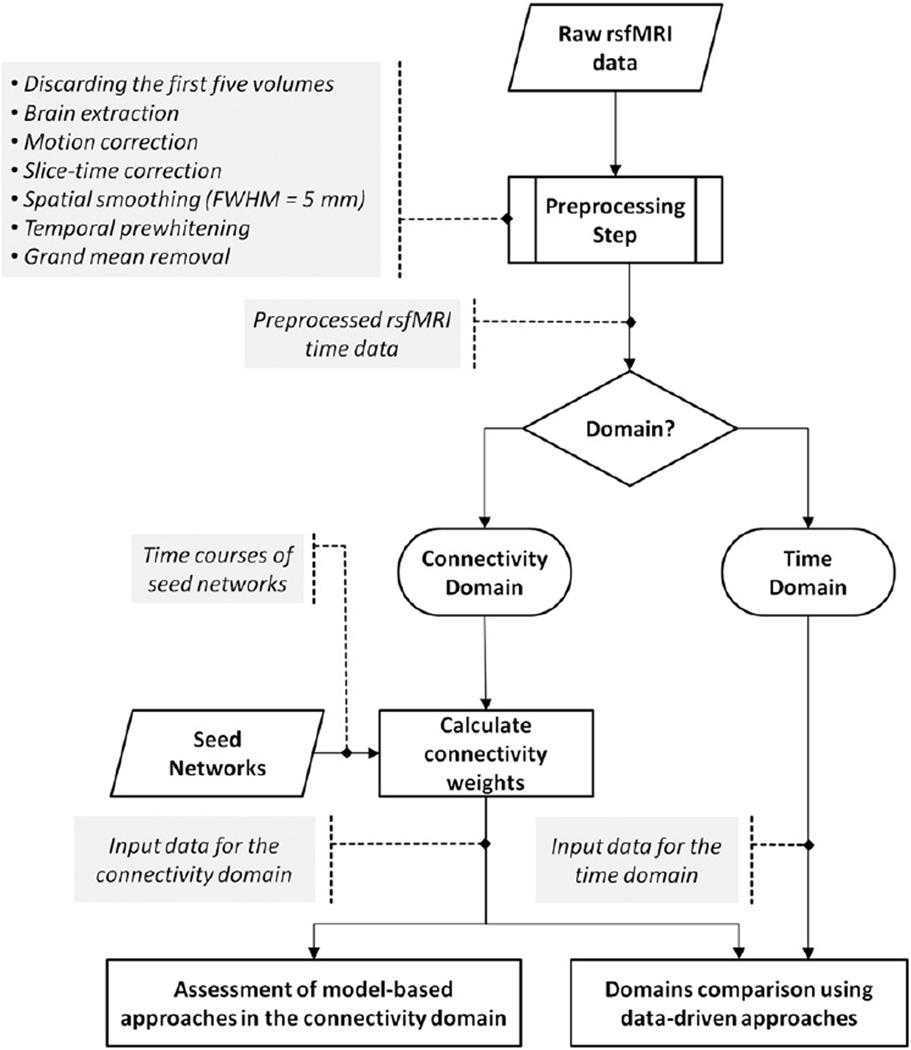
Fig. 3 demonstrates a schematic of the analysis pipeline. Data collection was performed at two independent sites with different image acquisition parameters. The first site was Wayne State University, Detroit, Michigan, USA. MRI data were collected on a 3-Tesla Siemens Verio scanner. Data was collected from 17 healthy subjects (average age: 35.92 ± 8.84; range: 26–56) at two sessions with a 4–6 week interval in between at Detroit Receiving Hospital, an affiliated hospital of the Detroit Medical Center. For rsfMRI data, a gradient echo EPI sequence with following imaging parameters was performed: pixel spacing size = 3.125 × 3.125 mm, slice thickness = 3.5 mm, slice gap = 0.595 mm, matrix size = 64 × 64, TR/TE = 2000/30 ms, flip angle = 90°, 240 volumes for whole-brain coverage, and Number of Excitations (NEX) = 1. During rsfMRI scans, participants were instructed to relax, keep their eyes closed, avoid falling asleep, and not to think about anything specific. The structural high-resolution T1-weighted imaging was collected using the MPRAGE sequence with TR/TE = 1950/2.26 ms, slice thickness = 1 mm, flip angle = 9°, field of view = 256 × 256 mm, matrix size = 256 × 256, and voxel size = 1 mm isotropic. The FSL software package (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) was used for rsfMRI data preprocessing, including discarding the first five volumes for magnetization equilibrium purposes, brain extraction, motion correction, slice-time correction, spatial smoothing with a 5 mm full width at half-maximum (FWHM= 5 mm), prewhitening, and grand mean removal. The data was registered to the Montreal Neurological Institute (MNI) standard space using non-linear registration with 10 mm warp resolution and resampled to 3 mm isotropic voxel size.

Fig. 3.

Schematic of the analysis pipeline. Data was preprocessed, and either kept in the time domain or transformed into the connectivity domain, which involved calculating connectivity weights using seed networks. Similar data-driven approaches were applied in both domains and compared between the two domains. Feasibility of applying model-based methods was evaluated in the connectivity domain.

The second site was Henry Ford Hospital, Detroit, Michigan, USA. MRI data were collected on a 3-Tesla GE scanner. Data was collected from 13 healthy subjects (average age: 27.25 ± 5.97; range: 18–39). For rsfMRI data, a gradient echo EPI sequence with following imaging parameters was performed: pixel spacing size = 3.4375 × 3.4375 mm, slice thickness = 3.5 mm, slice gap = 3.5 mm, matrix size = 64 × 64, TR/TE = 2000/30 ms, flip angle = 90°, 150 volumes for whole-brain coverage, and NEX = 1. The structural high-resolution T1-weighted imaging was collected using the IRSPGR protocol with TR/TE = 10.3/4.3 ms, slice thickness = 1 mm, flip angle = 15, field of view = 256 × 256 mm, matrix size = 256 × 256, and voxel size = 1 mm isotropic. We received already-preprocessed data and were blinded toward the preprocessing steps, which reportedly included elimination of the first five volumes, brain extraction, motion correction, slicing timing, temporal high-pass filtering 100 s, and spatial smoothing (FWHM = 5 mm). The registration step was reported to be similar to that applied to the other dataset, being non-linear with 10 mm warp resolution.

2.3. Seed network selection

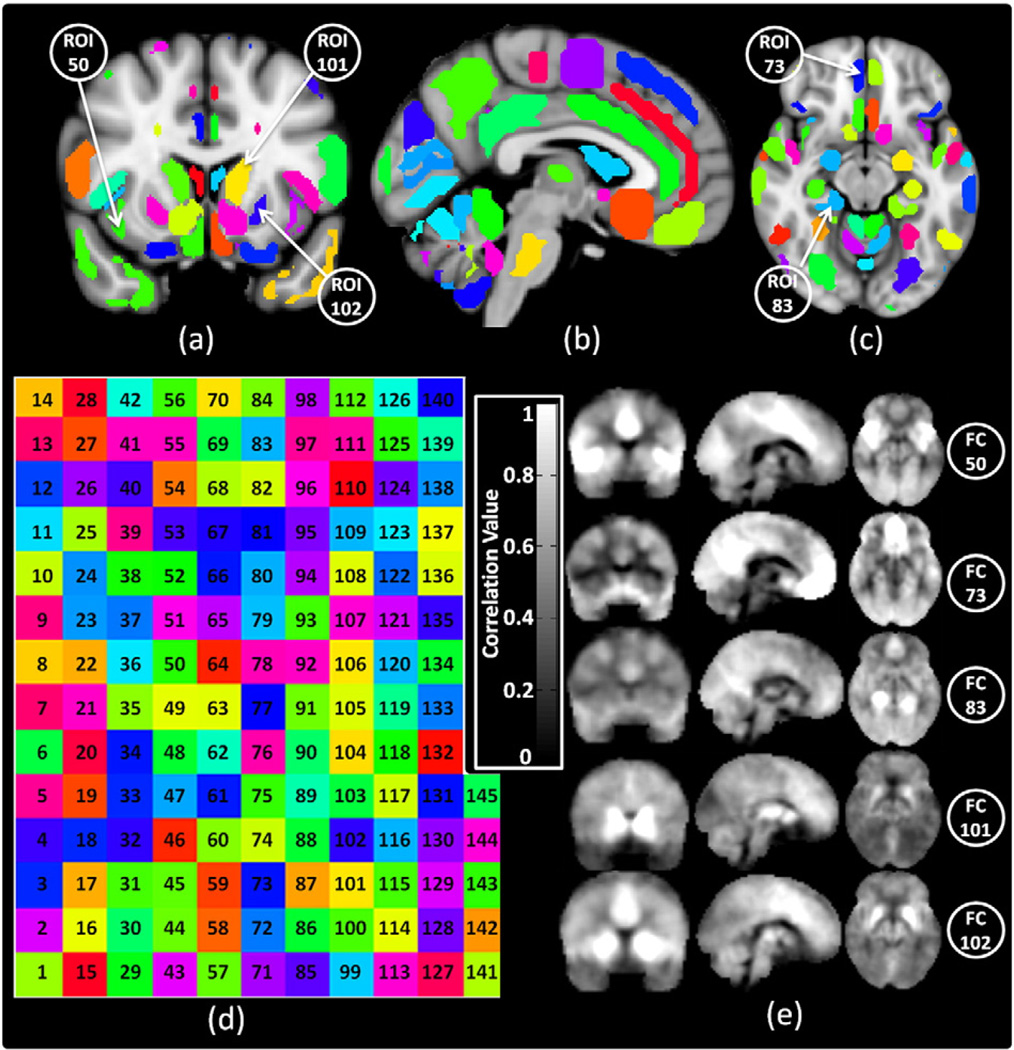
To perform data analysis in the connectivity domain, we first require an appropriate set of seed networks to use their time courses to calculate corresponding connectivity weights among subjects. As mentioned earlier, seed networks can be constructed from any technique that identifies sets of features that are similar across subjects, so that the time courses of those features can be used to construct the connectivity weights that constitute the connectivity domain. For instance, we could use anatomical or functional atlases to identify seed networks and use the time courses of the seed networks to calculate the connectivity weights. We can also use a more individualized set of common cortical landmarks (Iraji et al., 2015b). However, in this study to demonstrate the feasibility of the connectivity domain, we wanted to use common, readily-available atlases to define our seed networks. Accordingly, we chose the Harvard-Oxford cortical and subcortical atlases (Desikan et al., 2006; Frazier et al., 2005) and used anatomical information to identify the seed networks in this demonstration. Time courses from 145 seed networks (seed regions), distributed across the entire brain, were selected to calculate the connectivity weights. Each seed network includes the 100 voxels (2700 mm³) with the highest probability of belonging to the corresponding region. Fig. 4.a, b, and c show some of these regions on the sagittal, coronal and axial views, respectively, on the MNI atlas. The color code of the regions is shown in Fig. 4.d. The functional connectivity (connectivity weights) of five regions of interest (ROIs) shown in Fig. 4.a and Fig. 4.c in three sagittal, coronal and axial views are shown in Fig. 4.e. To demonstrate the importance of selecting an appropriate set of seed regions to construct the connectivity domains, two more sets of seed regions were developed to test the sensitivity of analysis in the connectivity domain to the initial connectivity maps. The second set consisted of the same 145 seed regions from the Harvard-Oxford cortical and subcortical atlases but reduced in volume. The smaller volume was obtained by applying the Gaussian kernel with FWHM = 5 mm on the previous Harvard-Oxford cortical and subcortical masks and thresholding the output at 0.55. For the third set of ROIs, 116 seed regions with a volume equal to 100 voxels were selected from the Automated Anatomical Labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002).

Fig. 4.

Functional connectivity weights calculation. Overlay of 145 ROIs on (a) coronal, (b) sagittal, and (c) axial views of MNI atlas. (d) Color code map of 145 ROIs. (e) Functional connectivity weights of ROIs 50 (right insular cortex), 75 (right subcallosal cortex), 83 (posterior division of parahippocampal gyrus), 101 (left caudate), and 102 (left putamen), respectively; the ROIs are annotated on Fig. 4.a and c. For this study Harvard-Oxford cortical and subcortical structural atlases were used.

2.4. Spatial similarity

Spatial correlation was used as the main parameter to identify corresponding spatial maps and calculate the spatial similarity between two spatial maps. Eq. (1) was used to measure the spatial similarity between the corresponding output maps of a pair of analyses (Calhoun and Allen, 2013; Iraji et al., 2015a). First, to determine which maps best correspond between the two analyses, the spatial similarity was calculated between each output map of the one analysis and every output map of the other analysis. For each output map of the first analysis, the output map of the second analysis with the highest spatial similarity was selected as the corresponding output map. Thus, the pair of output maps with the maximum spatial similarity were identified as corresponding output maps between two analyses. Next, visual inspection was also used to evaluate the accuracy of the previous steps. Upon approval, the correlation value from Eq. (1) was assigned as the spatial similarity between the corresponding output maps of two analyses.

$$r=\frac{{\sum }_i((X_i-{\mathrm{\mu }}_{\mathrm{x}})(Y_i-{\mathrm{\mu }}_{\mathrm{y}}\left)\right)}{\sqrt{{\sum }_i{(X_i-{\mathrm{\mu }}_{\mathrm{x}})}^2\times {\sum }_i{(Y_i-{\mathrm{\mu }}_{\mathrm{y}})}^2},}$$ (1)

where X and Y are spatial maps, and i is an index for corresponding voxels in the spatial maps.

In this manuscript, we will express the spatial similarity as a percentage between 0 to 100%, in which 100% means perfect spatial similarity (r = 1).

2.5. Comparison of the time and connectivity domains for a data-driven analysis

To compare data-driven approaches in the two domains, we used the temporal concatenation group spatial ICA followed by back-reconstruction (TC-BR), the most commonly used data-driven approach (Erhardt et al., 2011b). First, the outputs of TC-BR for the connectivity domain were visually inspected and compared with the output of TC-BR in the time domain. Next, we investigated the impacts of parameter variations of the TC-BR approach on the outcome in both domains while other parameters of the TC-BR algorithm were kept the same. An attractive property of an analysis approach is a higher level of reproducibility, less affected by different parameter variations. The investigated parameters include the number of selected components for prior PCA analysis, the group dataset, and the applied ICA techniques. ICA analysis was performed using the GIFT software package from MIALAB (http://mialab.mrn.org/software/gift/). For TC-BR analysis, the default-selected parameters include: number of IC = 20; ICA algorithm = Infomax; number of iterations for ICASSO = 10, back-reconstruction method = GICA; number of PCA = 2; and number of PC for steps 1 and 2 = 30/20.

The TC-BR approach has been applied on the data of each session separately for each domain with default parameters, and the spatial IC maps of the two domains at two time points were visually inspected to see the feasibility of the connectivity domain to produce the spatial IC maps identifiable as commonly extracted brain networks.

To assess the impact of parameter variation on output results, we began by varying the PCA parameters in our data reduction processing step, a necessary part of ICA analysis (Calhoun et al., 2001; Correa et al., 2007; Erhardt et al., 2011b). PCA is commonly applied at both the subject and group levels to reduce data dimensionality (Calhoun et al., 2001; Correa et al., 2007; Erhardt et al., 2011b). First, the subject-level PCA is applied to the data of each individual separately, which should ideally have a minimum impact on the accuracy of the IC maps and retain 100% of the variance in the data. This data reduction step was evaluated in the two domains by using 30 principle components (the default value) and 45 principle components for two different analyses. Next, the reduced data from individual subjects are temporally concatenated, and the group-level PCA is applied on the aggregated data. The number of principle components for the group-level PCA is usually lower than for the subject-level PCA and usually chosen to be equal to the number of independent components used for the ICA analysis (Calhoun et al., 2001; Erhardt et al., 2011b), so we did not assess the impact of varying this value and set it at 20. The spatial similarities between independent components obtained from the TC-BR analysis using 30 and 45 principle components were measured in each domain.

To assess the sensitivity of the individual subject outcomes to the group data in each domain, we performed the same analysis of individual subject data with two different sets of group data. Because the brains of different individuals are independent from each other and the brain networks of one subject do not influence the brain networks of another subject, the spatial maps of RSNs of one individual should ideally not be dependent on the data of other individuals.

However, because the BOLD signal has low signal-to-noise (SNR) and difficulty in identifying corresponding RSNs among individuals, the TC-BR method uses the aggregated group information to extract the RSNs of each individual. Consequently, RSNs of an individual could be influenced by the group to which the individual belongs, and a preferred method or domain would minimize the influence of the group data on the individual RSNs. To evaluate the influence of the group data on the individual RSNs, the individual RSNs at the first session were compared using two different sets of group data: 1) the group data of only the first session, and 2) the group data from both the first and second sessions. We measured the spatial similarity between each subject's RSNs from the two analyses in each domain.

To assess the impact of varying the ICA methods, we compared two different GIFT ICA options. A more robust domain will result in more similar spatial maps for RSNs when different ICA methods are used in the TC-BR analysis. For this purpose, we compared the spatial maps of RSNs from the TC-BR analysis using Infomax (the default setting in GIFT) and FastICA (Rachakonda et al., 2007). Previous studies on comparison between different ICA algorithms reveals that Infomax and FastICA give the best performance and yield reliable results (Correa et al., 2007, 2005). Both algorithms are iterative and use higher-order statistical information (Correa et al., 2007; Rachakonda et al., 2007); Infomax ICA estimates sources by maximizing the information and minimizing the mutual information among the estimated sources (Correa et al., 2007; Rachakonda et al., 2007), while FastICA uses negentropy as a measure of non-Gaussianity to minimize mutual information (Correa et al., 2007; Rachakonda et al., 2007).

2.6. Assessment of model-based analysis methods in the connectivity domain

To evaluate the feasibility of using first-level model-based data analysis techniques in the connectivity domain, we applied a common model-based method, the GLM. Since we applied the GLM on a feature obtained from the spatiotemporal data, similar to feature-based ICA, we can consider the GLM in the connectivity domain as a feature based GLM. As mentioned in the introduction, when there is no satisfactory model already available, data-driven methods (also known as model generating methods) can be used to generate the model, which is the design matrix, or A, for X = AS. Thus, we can use data-driven methods such as ICA to identify the design matrix (i.e. model). In this study, the average of the individual subject mixing matrices obtained from TC-BR was used as a design matrix for model-based analysis. It is important to mention that a design matrix obtained from small sample of individual subjects is not a good model for model-based analysis. Obtaining a more appropriate model would require a series of data-driven analyses across several data samples. However, since the goal of this part of study is to show the feasibility of applying model-based approaches, producing brain networks using a non-optimal model (the mixing matrix of the ICA analysis) will satisfy our claim. In this study, we first evaluated the possibility of applying model-based techniques in the connectivity domain. Considering the assumption that the relationship between brain networks and the connectivity of the brain regions (i.e. the design matrix in the connectivity domain) is similar among subjects, we should be able to use the average of the individual subject mixing matrices obtained from TC-BR as a design matrix to perform first-level feature-based GLM in the connectivity domain to obtain the brain networks for each subject. This cannot be done in the time domain due to the lack of synchronization of the fluctuations of the contributions of different brain networks across subjects, which leads to dissimilarity of the design matrices. Spatial similarity between the GLM and TC-BR analyses in the connectivity domain was measured to evaluate the application of model-based methods in the connectivity domain.

Next, average design matrices were obtained from each session using TC-BR and used in the first-level feature-based GLM analysis for the first session data in order to investigate the reproducibility of model-based techniques in the connectivity domain. If the model-based techniques are applicable, a design matrix should be similar at both sessions and be insensitive to the time of data acquisition, so using the design matrix from the other session should give a similar result.

Lastly, the reproducibility of model-based analysis methods in the connectivity domain was investigated across different studies and datasets. For this purpose, we investigated the possibility of obtaining the RSN maps from an independent dataset, the Henry Ford Hospital dataset, using a design matrix obtained from the WSU first session group's data using feature-based GLM.

3. Results

3.1. Similar brain networks identified in time and connectivity domains

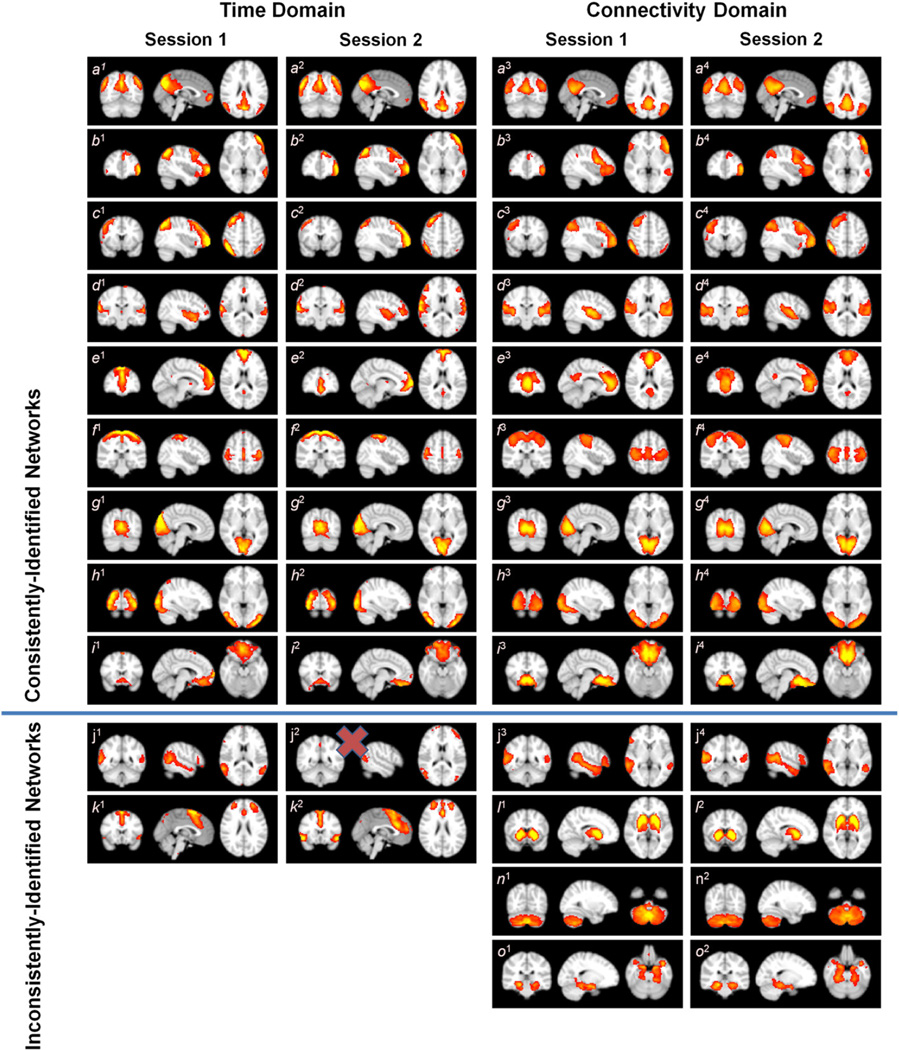
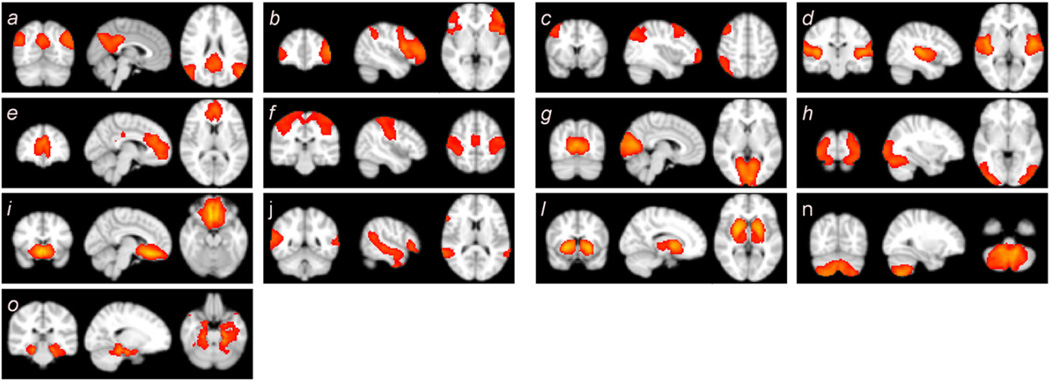
In the initial analyses, 17 healthy subjects at rest, scanned at two separate sessions, were analyzed separately in both the time domain and the connectivity domain. The identified RSNs for both domains at both sessions are shown in Fig. 5. Fig. 5 shows the thresholded t-statistics map obtained for each session and each domain separately. The t-maps, which are one of the outputs of ICA analysis performed using the GIFT software, identify voxels with strong activation across the subjects of each session and of each domain, separately (Allen et al., 2011). Nine well-known brain networks were found in both domains. We labeled these networks as consistently-identified brain networks since they have been identified in both domains and in each session. It is worth mentioning that the term consistent does not refer to high spatial similarity on those brain networks across different analysis but instead refers to those networks that we were able to identify at the group level in both domains and in each session, regardless of their spatial similarity values. The consistently-identified brain networks include the default mode network (DMN) (Allen et al., 2011; Beckmann et al., 2005; Damoiseaux et al., 2008, 2006; De Luca et al., 2006; Smith et al., 2009; van den Heuvel and Hulshoff Pol, 2010; Zuo et al., 2010), left parietal–frontal (working memory) network (Allen et al., 2011; Beckmann et al., 2005; Damoiseaux et al., 2006, 2008; De Luca et al., 2006; van den Heuvel and Hulshoff Pol, 2010; Zuo et al., 2010), right parietal– frontal (working memory) network (Allen et al., 2011; Beckmann et al., 2005; Damoiseaux et al., 2006, 2008; De Luca et al., 2006; van den Heuvel and Hulshoff Pol, 2010; Zuo et al., 2010), auditory network (Allen et al., 2011; Beckmann et al., 2005; Damoiseaux et al., 2008; Smith et al., 2009), frontal default mode network (Allen et al., 2011; Damoiseaux et al., 2006, 2008; de Bie et al., 2012; Kiviniemi et al., 2009; van den Heuvel and Hulshoff Pol, 2010), motor network (Beckmann et al., 2005; Biswal et al., 1995; Damoiseaux et al., 2008; Smith et al., 2009; van den Heuvel and Hulshoff Pol, 2010; Zuo et al., 2010), primary visual network (Allen et al., 2011; Beckmann et al., 2005; Damoiseaux et al., 2006, 2008; De Luca et al., 2006; Smith et al., 2009; van den Heuvel and Hulshoff Pol, 2010; Zuo et al., 2010), secondary visual network (Allen et al., 2011; Beckmann et al., 2005; De Luca et al., 2006; Kiviniemi et al., 2009; Smith et al., 2009; van den Heuvel and Hulshoff Pol, 2010), and subcallosal network (Biswal et al., 2010; Laird et al., 2011; Leaver et al., 2015; Zuo et al., 2010). Fig. 5 j shows an attention network (Allen et al., 2011; Damoiseaux et al., 2006, 2008; de Bie et al., 2012). This network was not appropriately identified in the second session for the time domain (Fig. 5 j²). Therefore, it was not included as one of consistently-identified networks in comparison analyses between two domains. Each domain also yielded several the spatial components that were not present in the other domain (the lower portion of Fig. 5), but which were reproducible at both sessions for each domain. These networks were labeled as inconsistently-identified networks because we could not consistently identify them in both domains. Thus, it is possible that inconsistently-identified networks could show higher spatial similarity between analysis methods in each domain.

Fig. 5.

Spatial maps identified for both domains at both time points presented as thresholded t-statistic map. The upper portion of the figure reveals nine consistently-identified brain networks found in both domains including the default mode network (DMN) (a), left parietal–frontal (working memory) network (b), right parietal–frontal (working memory) network (c), auditory network (d), frontal default mode network (e), motor network (f), primary visual network (g), secondary visual network (h), and subcallosal network (i). An attention network (j) seems consistent between two domains; however, it was not appropriately extracted in the second session for the time domain (j²). The lower portion shows the spatial maps which were identified in one domain but not the other one, or one time point but not the other.

3.2. Connectivity domain analysis is less susceptible to PCA parameters

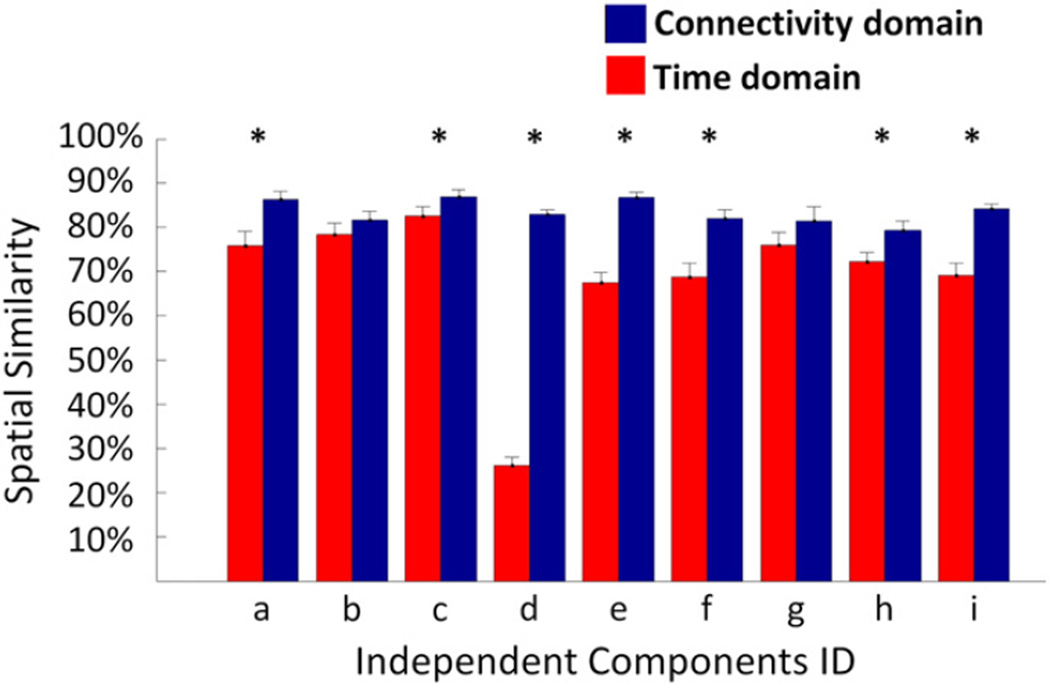
TC-BR analysis was performed with two different data reduction values (30 and 45) for the subject-level PCA. In both domains and every subject, the spatial similarity between the corresponding output maps generated using the two different numbers of principle components was calculated. For the 9 consistently-identified independent components, the spatial similarity was compared between two domains, and the connectivity domain reveals higher spatial similarity (see Fig. 6). A two sample t-test revealed that the connectivity domain has statistically higher spatial similarity for 7 out of 9 consistently-identified ICs including: default mode network (P = 0.06 × 10⁻²), right parietal–frontal network (P = 0.03), auditory network (P = 7.43 × 10⁻¹⁶), frontal default mode network (P = 3.58 × 10⁻⁶), motor network (P = 1.35 × 10⁻⁵), secondary visual network (P = 0.01 × 10⁻¹), and subcallosal network (P= 5.48 × 10⁻⁵).

Fig. 6.

Spatial similarity between consistently-identified independent components (Fig. 5 a to i) in the time (red) and connectivity (blue) domains using 30 and 45 as the number of principle components at the individual level. For each individual, the spatial similarity between spatial maps of each component obtained using 30 and 45 principles was measured. The spatial similarities between independent components obtained from the TC-BR analysis using 30 and 45 principle components is significantly higher in the connectivity domain as compared to the time domain in several spatial maps, identified by *. The low spatial similarity in network d is due to high variability in network d across individuals when change the number of principle components. Fig. S1 shows the network d obtained using different numbers of principle components (30 and 45).

3.3. Connectivity domain analysis is less influenced by the group data

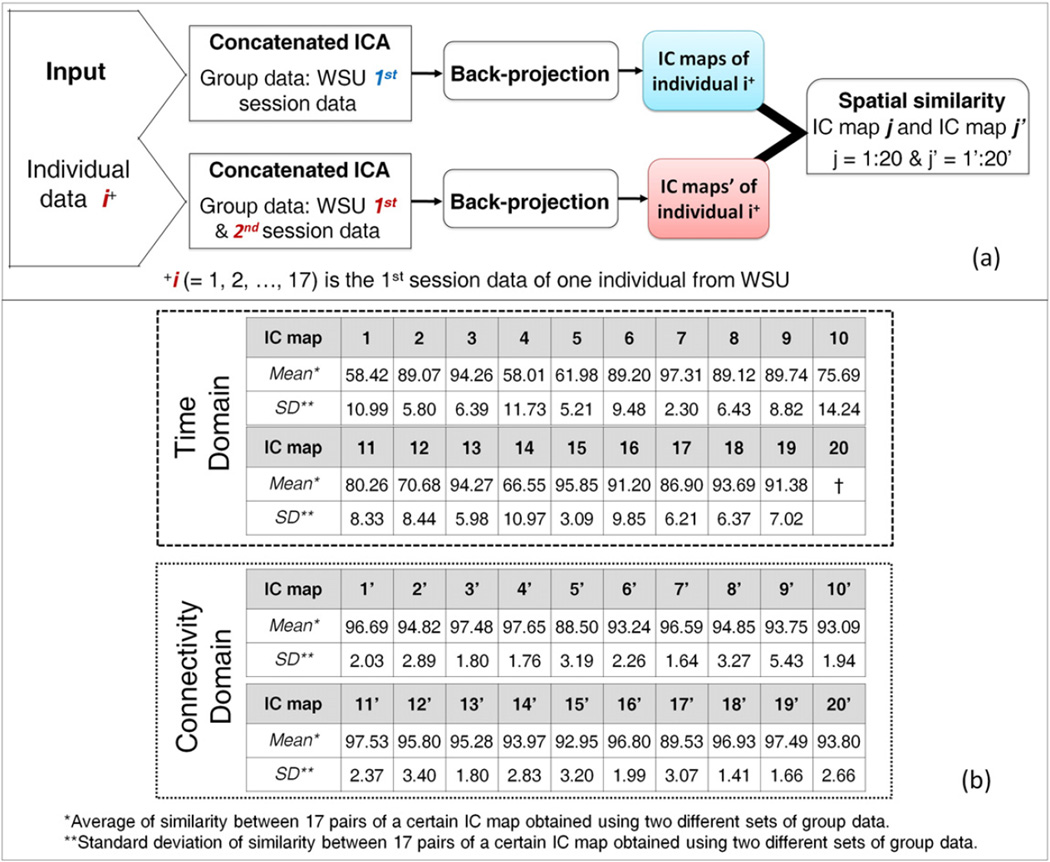
TC-BR was performed with default parameters on the first session data of 17 subjects using either first session group data only (top row of Fig. 7.a) or both sessions combined (bottom row of Fig. 7.a) group data, in both the time and connectivity domains. The similarity between the individual subject IC maps generated using each set of group data was computed and is shown in Fig. 7.b. The spatial similarity between the two analyses is greater in the connectivity domain (average spatial similarity for all spatial components is 94.84 ± 2.56 and for consistently-identified networks is 94.84 ± 2.85) than in the time domain (average spatial similarity for all spatial components is 82.82 ± 13.33 and for consistently-identified networks is 80.79 ± 16.26), indicating that the RSNs of a particular individual are more influenced by the group data in the time domain than in the connectivity domain. Furthermore, the time domain failed to identify one corresponding independent component between the two analyses using different group data. Note that the consistently-identified networks from before (Fig. 5 a–i) match up with IC maps #1–9 and #1′–9′, but that numbers #10 and #10′ and higher represent other components, which may be inconsistently-identified networks or other components.

Fig. 7.

Comparison between time domain and connectivity domain analysis in extracting IC maps of individuals' brain when different group data were used. (a) Flowchart of computation of subject-level spatial similarity between the same data analyzed with different group data and the same analytical approach (i.e. concatenated ICA followed by the back-projection), which was performed in both time and connectivity domains. i (= 1, 2, …, 17) is the 1^st session data of one individual from WSU. (b) Results of the spatial similarity at the subject level in both the time and connectivity domains. “*” indicates the average of similarity between 17 pairs of a certain IC map obtained using two different sets of group data. “**” indicates the standard deviation of similarity between 17 pairs of a certain IC map obtained using two different sets of group data. † indicates that the corresponding independent component has not been identified in the time domain when different group data was used.

3.4. Connectivity domain analysis is less affected by the ICA technique performed

TC-BR analysis was performed with two different ICA techniques, Infomax and FastICA, on the first-session data in both the time and connectivity domains. In each domain, the spatial similarity between the IC maps generated with Infomax and those generated with FastICA was computed. Statistical analysis on all of the nine consistently-identified networks at the subject level shows that spatial similarity across two methods in the connectivity domain is significantly higher than in the time domain (P < 0.005; Fig. S2). To demonstrate this at the group level for all consistently- and inconsistently-identified components, Fig. 8.a. shows the spatial similarity between the average of individual subjects' spatial maps (IC maps) generated from Infomax and FastICA in both domains, with higher average spatial similarity in the connectivity domain than in the time domain (85.62 ± 14.55% in the connectivity domain vs. 71.28 ± 14.53% in the time domain). This greater similarity despite different ICA techniques indicates that the connectivity domain analysis is less affected by the choice of the ICA technique than the time domain analysis.

Fig. 8.

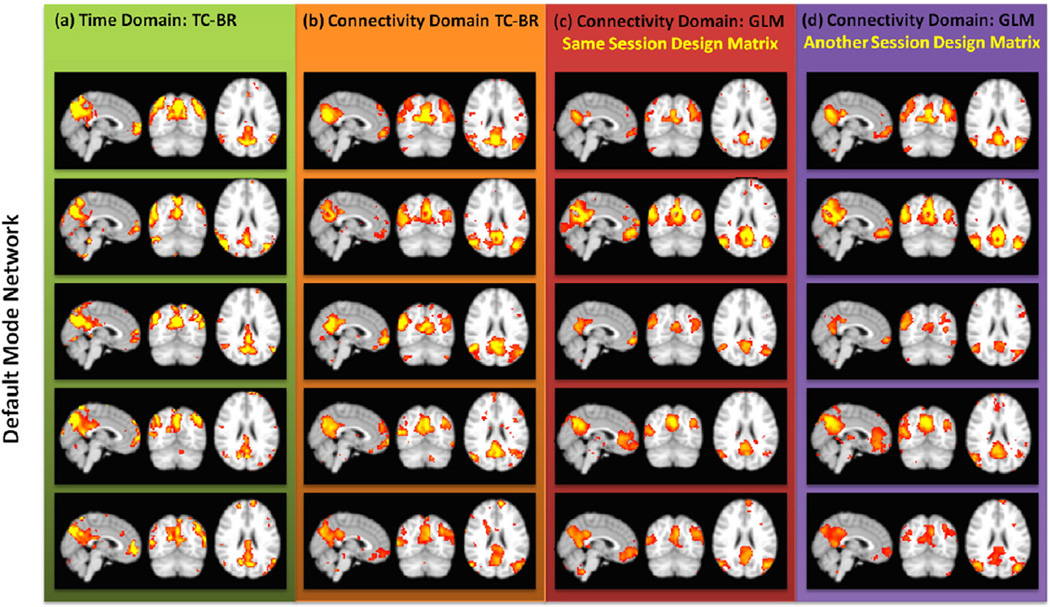
Demonstration of advantages of connectivity domain over time domain. For all results presented for both the time and connectivity domain in this figure, the two methods compared are different first-level analytical techniques that produce spatial maps for each individual subject. The spatial map for each component was averaged across subjects for each method and the spatial similarity between these average maps is reported here as a percentage. (a) Demonstrates the superiority of the connectivity domain for performing TC-BR analyses by comparing the spatial similarity of spatial maps (IC maps) generated with Infomax and FastICA in the time and connectivity domains. (b) Demonstrates the compatibility of model-based methods, such as GLM, with the connectivity domain by assessing the spatial similarity of output maps generated in the connectivity domain using TC-BR and GLM (design matrix 1: design matrix computed from session 1 data), which show good agreement. (c) Demonstrates the consistency of a design matrix over time by assessing the spatial similarity between GLM output maps generated using the 1^st session data and the design matrix from the same session as compared to the design matrix generated from the other session (design matrix 2: design matrix computed from session 2 data).

3.5. In the connectivity domain, a model-based approach identifies similar brain networks

To assess the compatibility of using model-based methods in the connectivity domain, we assessed the spatial similarity between the averages of the individual subject maps generated using a TC-BR approach and a first-level feature-based GLM approach performed on the 1^st session WSU data. Both methods identified the same components in the data. Furthermore, high spatial similarity (91.85 ± 2.10; Fig. 8.b) here indicates that the feature-based GLM method is giving us similar results as the accepted TC-BR methods. Fig. 9 demonstrates this at an individual level; the red column shows examples of 5 randomly-selected individual subject DMN maps obtained using the first-level feature-based GLM approach using the design matrix obtained from same data, while the green and orange columns show the DMN maps obtained using the ICA methods in the time and connectivity domains, respectively. Further examples of individual subject maps of other RSNs can be found in Figs. S3 to S5. Fig. 8.a and Fig. 8.b show that the spatial similarity between the connectivity domain TC-BR and GLM maps is higher than the spatial similarity between the two accepted TC-BR approaches used in the time domain, at only 71.28 ± 14.53. The spatial similarity values demonstrated here represent the spatial similarity between the averaged individual subjects' spatial maps.

Fig. 9.

Individual default mode network (DMN) maps for five randomly-selected subjects obtained using different analyses. The color code is the same as Fig. 8. Example of individual maps of other RSNs can be found at Figs. S3 to S5. This demonstrating the reproducibility of GLM analysis at the individual level using design matrices from different sessions.

3.6. In the connectivity domain, RSN maps are reproducible using the design matrix derived from the same group data but from a different session

To evaluate the consistency of a design matrix over time, we computed the effect of applying different design matrices which were obtained from both the first and second sessions using TC-BR with Infomax. In Fig. 9, the purple column shows some examples of individual subject DMN maps obtained using the first-level feature-based GLM approach using the design matrix obtained from a different session. Example of individual subject maps of other RSNs can be found at Figs. S2 to S4. We assessed the spatial similarity between the output maps of first-level feature-based GLM applied on the first session data using the design matrix from the first session as compared to the output maps of feature-based GLM applied on the first session data using the other design matrix, the design matrix generated from the second session. Both analyses produce the same maps, showing that the design matrices from each session are similar. Moreover, the high spatial similarity of the across-subjects averaged output maps of the two feature-based GLMs which use the information of different sessions (78.65 ± 10.27) is comparable with the result comparing the output maps of the first session data using the two ICA techniques (the second part of Fig. 8.a), showing that the design matrix in GLMis as similar over time.

3.7. In the connectivity domain, RSN maps are reproducible when the design matrix from a different group's data is used

To assess the feasibility of using a common rather than dataset-specific design matrix to extract the RSNs from a dataset using model-based methods in the connectivity domain, we performed an initial analysis in which we evaluated the possibility of obtaining the RSNs maps from a dataset using an independent design matrix obtained from a different group's data. In the initial analysis, the RSNs of a different group's data (n = 13) extracted by applying a GLM model using the design matrix from the first session of the WSU data. The RSNs which were already identified in the WSU data have been identified in the independent dataset and are shown in Fig. 10.

Fig. 10.

The resting state networks (RSNs) identified using a general linear model (GLM) method from the independent dataset. The design matrix that was used for this analysis is from the first session of the WSU dataset (a different group of subjects). Spatial maps were calculated for each individual separately and then averaged. This demonstrates the reproducibility of GLM analysis at the individual level using design matrices from a different group's data.

3.8. The importance of seed selection in the connectivity domain

To recognize the importance of selecting an appropriate set of seed regions for future work, the effect of using different connectivity weights generated from different sets of seed regions was evaluated. We first evaluated the spatial similarity between the RSNs maps generated using the 145 seed regions from the Harvard-Oxford cortical and subcortical atlases with different sizes (ROI set 1 vs ROI set 2). Next, we investigated the effect of selecting different locations for seed regions by measuring the spatial similarity between the RSN maps obtained using the 145 seed regions from the Harvard-Oxford cortical and subcortical atlases and 116 seed regions from AAL atlases (ROI set 1 vs ROI set 3). Table 1 shows the spatial similarity between the average of the individual subjects' spatial maps (IC maps) generated using different ROI sets. Although all of the same RSN maps have been identified with high spatial similarity despite changing the size or location of seed regions, the results show that there is an influence of the ROI set on the final RSN maps, highlighting the necessity of identifying the optimized location for seeds regions.

Table 1.

The spatial similarity of resting state networks (RSNs) map identified in the connectivity domain using different ROI sets.

Network name	Spatial similarity
	ROIs from the Harvard-Oxford atlases with different sizes	ROIs from the Harvard-Oxford atlases vs. ROIs from the AAL atlas
Default mode network (a)	98.42%	95.41%
Left parietal–frontal network (b)	96.55%	86.35%
Right parietal–frontal network (c)	98.87%	95.35%
Auditory network (d)	98.39%	92.02%
Frontal default mode network (e)	99.06%	90.30%
Motor network (f)	98.20%	89.59%
Primary visual network (g)	98.13%	94.17%
Secondary visual network (h)	96.07%	94.12%
Subcallosal network (i)	97.55%	93.31%
Attention Network (j)	98.48%	84.04%
Basal ganglia network (l)	98.76%	93.01%
Cerebellum (n)	97.31%	95.20%
Amygdala and Hippocampus (o)	87.66%	84.40%
Mean ± SD	97.19 ± 3.00%	91.33 ± 4.09%

4. Discussion

In this work, we developed a novel framework, which we called the connectivity domain. Consistent with our hypothesis, the connectivity domain enables us to investigate brain function using data-driven or model-based approaches or both and open a new window to investigate brain function. The connectivity domain demonstrates superior results when it is combined with currently popular methods for analyzing data in the time domain (the brain spatiotemporal rsfMRI data) and offers a new pathway for the use of model-based methods. Furthermore, it provides a unique opportunity to perform feature-based data-driven approaches such as feature-based ICA at the subject level instead of only at the group level (second level).

Using real data from 17 healthy subjects collected at two sessions each, we demonstrated the superiority of the connectivity domain over time domain using both data-driven and model-based analysis methods.

4.1. Data-driven approaches in the connectivity domain vs. time domain

Results demonstrated that the brain networks obtained from the time and connectivity domains using TC-BR are very similar (Fig. 5). In the time domain, we identified 11 brain networks; however, one of these networks (Fig. 5.j²) was not identified correctly in the second session. Therefore, the time domain includes 10 brain networks that were found in both sessions. At the same time, the connectivity domain was able to identify 91% (10 out of 11) brain networks that the TC-BR method detected in the time domain. The connectivity domain also identified three extra brain networks as reported in previous studies (Allen et al., 2011; Biswal et al., 2010; Bolo et al., 2015; Laird et al., 2011; Leaver et al., 2015; Smith et al., 2009); however, these were not detected in our data when we performed the analysis in the time domain. These results indicate the ability of the connectivity domain to extract similar spatial maps as reported in previous studies analyzing data in the time domain. Furthermore, performing TC-BR analysis in both domains using two different sets of group data shows that the brain networks of individuals are more influenced by the group data in the time domain in comparison with the connectivity domain.

We investigated the impacts of variations of parameters in the TC-BR approach on the consistency of results and observed the superiority of the connectivity domain over the time domain for all investigated parameters. In brain connectivity research, one crucial step is the ability to compare and access findings across different studies. In order to have a more valid rationale to compare the results of different studies and make a valid conclusion, the findings of studies should be less susceptible to parameters which are not related to the brain connectivity information. Therefore, a superior domain is less affected by parameter variations of the applied analytical method. For this purpose, we investigated the impact of parameter variations in the TC-BR method on spatial maps of brain networks, as it is one of the most commonly used methods for investigating brain connectivity. Both the number of principal components (a preprocessing step) and the applied ICA techniques (a processing step) show that the connectivity domain is less vulnerable and therefore it is more suitable to produce robust findings. We do note that in order to make this powerful claim we should also investigate and compare the impact of the MRI scanner and other site parameters on individuals' outcomes between two domains.

4.2. Model-based approaches in the connectivity domain

In addition to its strength with data-driven methods, the connectivity domain also provides the ability to use first-level model-based methods. We found the same networks in both data-driven and model-based approaches in the connectivity domain. The ability to obtain similar brain networks using TC-BR and GLM with a high spatial similarity (91.85 ± 2.10%) supports our assumption of the similarity of the relationship between connectivity weights and brain networks among subjects. This opens a new pathway for analyzing brain function using model-based approaches. To further validate our assertion, we demonstrated the result of reconstructing the brain networks using the information, i.e. design matrix, of different studies and datasets.

Using GLM with design matrices obtained from the first and second sessions, the same brain networks were attained. Obtaining the same brain networks shows the reproducibility of model-based techniques when the design matrix from one session is utilized to analyze the data from the other session in the connectivity domain. Furthermore, high spatial similarity (78.65 ± 10.27%) between brain networks obtained using the design matrices of the two sessions shows the consistency of a design matrix over time in the connectivity domain. This could be beneficial in longitudinal studies in which one is interested in minimizing variations in healthy subjects across different time points. This could make the connectivity domain analysis more useful in investigating brain functional alterations and plasticity.

With improving design and obtaining an acceptable model through utilizing several data samples and incorporating statistical analysis, we should be able to obtain RSN maps of a dataset using a design matrix obtained from a different group's data. Although this is a preliminary study without optimum design parameters such as seed choice, we observed that we could obtain similar RSNs for an independent dataset with unknown parameter information using the design matrix extracted from the first session of the WSU dataset (Fig. 10).

We do note that the connectivity domain is affected by the choice of the set of seed regions used to build the domain. Both the number of seed regions and how they are selected are important parts of the connectivity domain to be investigated. For instance, while we are interested in using a larger number of seed networks to retain maximum information, we are also interested in using a smaller number of seed networks so we can transfer the data to the connectivity domain across studies despite a smaller number of time points. At the same time, both size and location of seed regions will change the results and should be selected carefully based on the particular goals of the study. Our primary evaluations using different sizes of the same set of ROIs and different sets of ROIs reveals that the size of ROIs and more importantly the proper location of corresponding seed regions among subjects influences the results. The spatial similarity between brain networks obtained from the same set of seed networks with different sizes was 97.19 ± 3.00%, and the spatial similarity between brain networks obtained from the two different sets of seed networks was 91.33±4.09%. This is especially important in connectomic study where identifying the fine-grained and optimized locations of seed regions is necessary. Note that, although the connectivity domain is biased toward selection of seed networks, this bias is independent to the dataset, and it would have a similar impact on all datasets. Since our aim for this study was to show the feasibility of using the connectivity domain, we reduced the sensitivity to ROI locations by choosing large ROIs and using the average time series of all voxels in each ROI to measure the functional connectivity map.

5. Future work

In order to optimize and improve the connectivity domain and its application, the first step is to identify the optimized corresponding seed networks across individuals. In choosing anatomical locations across the brain as seed networks, the goal is to identify precise, small seed regions, because each location of the brain could be involved in different functions than its neighbors. However, seed networks do not need to be anatomical locations in the brain. Various types of seed selections approaches can be used to identify the seed networks. For example, seed networks can be made from data-driven seeds or functional seeds. Likewise, the bases of the connectivity domain can be obtained from applying PCA or clustering techniques on the temporal information of the data, as long as a measured connectivity index between seed network time courses and spatiotemporal information is able to represent similar characteristics across subjects. Therefore, the connectivity domain can also be useful if we are interested in investigating the interactions between brain networks at different levels of functional hierarchy. Further studies are required to investigate the ability of the connectivity domain in this aspect.

We do note that while, in this preliminary study, we have used the correlation value as the connectivity index, the cross correlation is merely one index among a wide range of mathematical indices which can be used to reconstruct the connectivity domain, including canonical correlation, mutual information, coherence, partial correlation, and indices which have been used for effective connectivity studies. This provides us a unique opportunity to investigate the different types of connectivity and their interaction with brain networks.

After we have identified the corresponding time courses related to seed networks across subjects properly, the next crucial step would be correctly estimating the true value for each array of the design matrix. In other words, the contributions of seed networks to each brain network. This can be achieved through measuring the design matrices obtained from several datasets and performing statistical analysis to identify seed networks that significantly contribute to specific brain networks. This process is not only useful to extract more accurate brain networks using model-based methods but also can be an essential biomarker to discriminate between healthy subjects and patients with different disorders.

We do note that the brain activity at rest has non-stationary behavior and that understanding network dynamics is important to provide rich characteristics of the brain (Calhoun et al., 2013, 2014). Although we implicitly considered that brain functional behavior is constant during the resting state in this study, the connectivity domain also offers a new option to investigate the dynamic characteristics of the brain. For example, one simple way is to use a sliding window approach and calculate the connectivity weights for each interval. As a result, we can evaluate alterations in RSNs and changes in contributions of regions to RSNs over time.

6. Conclusion

In this work, we introduced a new domain, the connectivity domain, to analyze rsfMRI data. We demonstrated several of the advantages of analyzing rsfMRI data in the connectivity domain over the same analyses in the time domain. The connectivity domain also offers a new pathway to apply first-level model-based methods to rsfMRI data and provides a unique opportunity to expand usage of feature-based data-driven approaches, such as feature-based ICA, to the subject-level analyses. Future applications of this domain for both data-driven and model-based analyses will benefit from greater reproducibility and improved ability to compare findings across datasets. Moving forward, this new addition to the rsfMRI analysis toolkit will allow us to perform supplementary assessments of both static and dynamic brain connectivity.