The utility and accuracy of four equations in predicting sodium levels in dysnatremic patients

Abstract

Background

Improper correction of hyponatremia can cause severe complications, including osmotic demyelination syndrome (ODS). The Adrogué–Madias equation (AM), the Barsoum–Levine (BL) equation, the Electrolyte Free Water Clearance (EFWC) equation and the Nguyen–Kurtz (NK) equation are four derived equations based on the empirically derived Edelman equation for predicting sodium at a later time (Na₂) from a known starting sodium (Na₁), fluid/electrolyte composition and input and output volumes.

Methods

Our retrospective study included 43 data points from 31 mostly hyponatremic patients. We calculated Na₂ based on five sets of rules that were progressively more precisely calculated. Sets A–D included all 31 patients and 43 data points and set E was based on 15 patients and 27 data points.

Results

The root mean square error was calculated and found to be between 4.79 and 6.37 mmol/L (mEq/L) for all sets. Bland–Altman analysis showed high variability and discrepancies between the predicted and actual Na₂.

Conclusions

Like similar studies in hypernatremic patients, the data suggest that hyponatremic modeling equations are not reliably accurate in predicting Na₂ from Na₁ and available clinical data regarding sodium, potassium and fluid balance over longer time frames (12–30 h). Our study was retrospective and was done in an inpatient setting and thus was subject to limitations and laboratory measurement variability, but showed that all four equations are not able to reliably predict Na₂ from Na₁ and inputs across a 12–30 h period.

Introduction

The use of mathematical models to predict changes in sodium (Na) dates back to the Edelman equation, which was described nearly 50 years ago [1]. Using isotopic measurements, Edelman et al. defined the relationship between the serum sodium concentration and the body's content of sodium, potassium and total body water [1]. Subsequent derivations of the Edelman equation have resulted in the Adrogué–Madias (AM), Barsoum–Levine (BL), Electrolyte Free Water Clearance (EFWC) and Nguyen–Kurtz (NK) equations. The Nguyen–Kurtz equation is the most developed derivation and includes the original slope of the Edelman equation (1.03) and the original x-intercept of −23.8, which have physiological significance. This would theoretically be expected to lead to better predictions of changes in serum sodium [1–8].

The importance of being able to predict the sodium level at a later time (Na₂) and thus the change in sodium levels clinically is to avoid rapid correction. Correction of serum sodium of >8–12 mmol/day (mEq/day) can result in osmotic demyelination syndrome (ODS) [9–12].

Methods

We designed a retrospective study to compare the predicted Na₂ with the observed Na₂ using four equations. Our resulting cohort was composed of 31 patients: 29 hyponatremic patients and 2 hypernatremic patients. We reviewed 156 charts and included 31 patients, from which 43 data points were calculated. Eight patients had multiple serial non-overlapping data points calculated (between two and four), but only one data point was calculated on 23 of the 31 patients (Table 1).

Table 1.

The Adrogué–Madias, Barsoum–Levine, EFWC and Nguyen–Kurtz equations

Adrogué–Madias equation	Na2 = [(Na1 × TBW) + (Vi × ([Na]i + [K]i)]/(TBW + Vi)
Barsoum–Levine equation	Na2 = [(TBW × Na1) + ((Vi × ([Na]i + [K]i)) − (Vo × ([Na]o + [K]o))]/(TBW + ΔV)
Electrolyte Free Water Clearance equation	Na2 = (Na1 × TBW)/[(TBW − (Vurine*EFWC)], where EFWC = 1 − (([Na]urine + [K]urine)/Na1))
Nguyen–Kurtz equation	Na2 = [[[(Na1 + 23.8) × TBW] + [1.03 × ([Na]i + [K]i) − ([Na]o + [K]o)]]/[(TBW + ΔV)]] − 23.8
Nguyen–Kurtz equation hyperglycemia correction	Add [0.016 × (s[Glucose] − 120)]
Total body water	0.6 × Body Weight

ΔV, net change in volume; EFWC, Electrolyte Free Water Clearance; [K]i, concentration of potassium in input fluid; [K]o, concentration of potassium in output fluid; [K]urine, urinary potassium; Na₁, original sodium; Na₂, predicted sodium; [Na]i, concentration of sodium input fluid; [Na]o, concentration of sodium in output fluid; [Na]urine, urinary sodium concentration; s[Glucose], serum glucose concentration; TBW, total body water; Vi, volume of input fluids; Vo, volume of output fluids; Vurine, volume of urine. All volume units, unless otherwise noted, are as follows: volume as liters, concentration units as millimoles/liter or equivalently as milliequivalents/liter, body weight and total body water weights in kilograms.

To be included in the data set, the patient was required to be dysnatremic at the time of presentation (Na <135 or >145 mmol/L), have been admitted into the step-down unit or the intensive care unit, have available serial chemistry panels and urinary electrolytes including urine sodium and potassium, have available accurate weights and have strict ins and outs recorded. In addition, the electrolyte content and volume of all infused and ingested fluid had to be available, with preference given to patients with little to no intake by mouth (see Table 2). The requirements to be included in the idealized set E were more rigorous, as outlined in Table 2. The serum electrolytes were generally checked every 6–8 h and urine electrolytes had to be checked at least every 12–24 h. Since this was a retrospective study, standardization of serum and urine electrolyte monitoring was not possible. The initial serum sodium on presentation, etiologies of dysnatremia and intravenous fluids given are presented in Table 3. The term intravenous fluids refers to 3%, 0.9%, 0.45% or D5 0.225% normal saline. It is important to note that none of the 31 patients in the study required 3% normal saline.

Table 2.

Inclusion and exclusion criteria for a retrospective, observational study of the hyponatremia correction calculation

Sets A–D: Number of eligible patients 31, number of data points 43, ≥18 years of age, Na <135 or >145 mmol/L, serial chemistry values available between Na1 and Na2, urinary sodium and potassium available, weights available, step-down unit or intensive care unit admission, no blood products. Set E: Number of eligible patients 15, number of data points 27, as well as all the aforementioned criteria and also the ability to calculate all sodium/potassium input and output and to keep track of all fluid infused and eliminated from the patient.

Table 3.

Etiologies of hyponatremia, sodium values, intake data and output data

DP #	Pt #	Na1	Set E?	Etiology of dysnatremia	Wt	uNa	uK	IV fluid	FH2O	Liquid food intake	ONS/TF	K intake	Na intake	UOP	Gluc	Na2	T
1	1	115	No	Hypervolemia	54	10	11	0	0.336 L	0	0	0	0	1.54	7.94 (143)	121	16
2	2	129	No	SIADH	72.9	52	16	3.75 L NS, 0.5 L 1/2NS	0	0	0	0	0	2.3	6.5 (117)	127	12
3	3	119	No	SIADH	56.8	36	24	0.2 L (NS with 40 mmol/L kcl)	0.38 L	0.39 L tea, 0.24 L coffee	0	13.79	0	0.45	6.22 (112)	123	24
4	4	117	Yes	Hypovolemia	70	10	11	0.325 L NS	0.1 L	0.36 L milk	0	17.96	0	2.3	8.78 (158)	125	16
5	5	125	No	Hypervolemia	81.4	10	55	0.5 L NS	0	0	0	0	0	0.1	8.06 (145)	123	23
6	6	128	Yes	Hypovolemia	63.6	10	27	0	0.47 L	0	0	40	0	0.75	11.33 (204)	131	14
7	7	148	No	Free water deficit	40.2	110	12	0.45 L NS, 1.34 L 1/2NS	0.435 L	0	0.48 L Ensure	20.21	0	3.82	5.89 (106)	152	24
8	8	126	No	SIADH	43.7	60	29	0	0.44 L	0.24 L milk	0	11.97	0	1.05	9.78 (176)	126	19
9	9	125	No	SIADH	78.8	125	73	0	1.5 L	0.24 L tea, 0.58 L coffee	0	11.28	0	0.45	8.94 (161)	127	19
10	10	131	No	SIADH	74.3	50	13	0.1 L NS	1.36 L	0.4 L coffee	0	8.48	0	2.65	7.22 (130)	133	24
11	11	121	No	Thiazide induced	51.6	182	18	2.235 L NS	0.1 L	0	0	0	0	1.7	8.33 (150)	137	30
12	12	132	Yes	Hypervolemia	144	15	18	0	1.05 L	0	0	0	0	2.35	8 (144)	135	24
13	13	150	No	Free water deficit	56.7	35	14	1.3 L NS, 3.466 1/2NS	1.2 L	0	0.3 L Ensure	12.64	0	1.73	7.44 (134)	136	24
14	14	115	No	Hypovolemia	45.6	15	54	0.5 L NS	0.42 L	0	0	0	0	0.75	9.39 (169)	118	16
15	15	128	Yes	SIADH	82.7	109	65	3.7 L NS	0.4 L	0	0	0	0	2.71	6 (108)	132	24
16	16	122	No	Thiazide induced	55.5	22	91	1.27 L NS	0.472 L	0.15 L coffee	0	2.68	0	1.07	11.56 (208)	122	24
17	17	115	Yes	SIADH	42.6	93	21	2.375 L NS	0.7 L	0.24 L milk	0	81.97	34.48	2.15	7.28 (131)	120	21
18	18	117	No	SIADH	67.2	31	21	0.335 L NS	0.27 L	0.48 L coffee, 0.72 L milk	0	44.49	0	1.82	5.5 (99)	122	22
19	19	122	Yes	Hypovolemia	58.5	13	60	1 L NS	0.21 L	0	0	0	0	0.5	7.78 (140)	118	18
20	20	124	No	Hypovolemia	68.9	24	21	1.15 L NS, 1.4 L 1/2NS	0.78 L	0.6 L milk, 0.24 L tea	0	150.89	0	1.45	43.78 (788)	129	27
21	21	134	No	SIADH	211	96	22	0.25 L NS	2.375 L	0.18 L tea	0	0.69	0	1.68	5.67 (102)	133	20
22	22	116	No	Hypervolemia	77.8	5	41	0	0.53 L	0.24 L milk, 0.48 L coffee	0	20.54	0	1.58	6.61 (119)	120	23
23	23	128	Yes	SIADH	72.6	100	18	0	0.63 L	0.12 L apple juice	0	4.05	0	2	11.44 (206)	137	12
24	23	137	–	Data point #2, patient #23	72.6	100	18	0	0.7 L	0	0	0	0	2.6	11.44 (206)	130	12
25	24	119	Yes	SIADH	55	67	9.4	1.4 L NS	0.12 L	0.24 L lemonade	0	1.24	0	0.7	5.56 (100)	129	12
26	24	129	–	data point #2, patient #24	55	42	9	0	0	0	0	0	0	0.75	5.56 (100)	128	12
27	25	125	Yes	Hypovolemia	61.4	10	49	1.5 L NS	0.06 L	0.06 L orange juice	0	2.98	17.24	0.6	6.28 (113)	126	12
28	26	112	Yes	Hypovolemia	62.9	17	3.4	1.425 L NS	1.545 L	0	0	0	0	1.65	8.33 (150)	122	12
29	26	122	–	Data point #2, patient #26	62.9	16	3.6	0	0.31 L	0	0	0	0	0.29	6.89 (124)	122	12
30	27	116	Yes	Hypovolemia	44.1	19	18	0.5 L NS	0	0	0	0	0	2	3.94 (71)	122	14
31	27	122	–	Data point #2, patient #27	44.1	41	8.8	0	0	0	0	0	0	0.3	5.61 (101)	125	12
32	28	112	Yes	Hypovolemia	74.2	10	10	0.568 L NS	0.3 L	0	0	0	0	2.34	6.17 (111)	113	12
33	28	113	–	Data point# 2, patient #28	74.2	10	52	0.932 L NS	0.1 L	0	0	0	0	0.42	6.17 (111)	116	12
34	28	116	–	Data point# 3, patient #28	74.8	19	52	1.305 L NS	0.55 L	0	0	0	0	0.73	5.67 (102)	124	12
35	28	124	–	Data point# 4, patient #28	74.8	19	52	1.475 L NS	0.325 L	0	0	0	0	0.56	5.67 (102)	123	15
36	29	120	Yes	SIADH	51	29	53	0.5 L NS	0.63 L	0	0.64 L 2calHN	80	0	0.85	5.11 (92)	118	11
37	29	118	–	Data point #2, patient #29	51	51	25	0.02 L NS	0.184 L	0	0.24 L Osmolyte	12.37	0	0.74	88 (4.89)	122	19
38	30	121	Yes	SIADH	43.7	30	66	0.544 L NS	0.414 L	0.18 L tea	0	0.7	0	0.58	5.33 (96)	119	12
39	30	119	–	Data point #2, patient #30	43.7	10	45	0.457 L NS	0.357 L	0	0	0	0	0.3	9.28 (167)	120	12
40	30	120	–	Data point #3, patient #30	42.9	10	23	1 L NS	0.117 L	0	0	0	7.8	0.56	9.28 (167)	122	14
41	31	118	Yes	Thiazide induced	130	123	85	0.475 L NS	1.105 L	0	0	40	0	5	5.94 (107)	123	12
42	31	123	–	Data point #2, patient #31	130	10	65	0.5 L NS	1.701 L	0	0	40	0	2.27	5.94 (107)	125	14
43	31	125	–	Data point #3, patient #31	129	10	6.3	0	0.61 L	0	0	0	0	1.64	5.94 (107)	126	12

DP #, data point number; Pt#, patient number; Na₁, initial serum sodium (mmol/L); set E?, identifies if data point is in idealized set E; Wt, weight (kg); uNa, urine sodium (mmol/L); uK, urine potassium (mmol/L); IV fluid, IV fluid type and amount (L); FH₂O, free water intake (oral or intravenous); ONS/TF, oral nutritional supplements or tube feeds; K intake, oral potassium intake (mmol); Na intake, oral sodium intake (from sodium tabs or sodium phosphate; mmol) UOP, urine output (L); Gluc, serum glucose (mmol/L and mg/dL); Na₂, final serum sodium; NS, 0.9% normal saline; 1/2NS, 0.45% normal saline; free water, D5W or oral water; KCl potassium chloride; T, time in hours between initial and final serum sodium; Na, sodium; 1 mmol = 1 mEq [standard units] in univalent ions like sodium or potassium.

The predictions were then calculated for all four equations in five sets (A–E) with increasingly complex rules for determining Na₂ from Na₁, input sodium, input potassium and volume inputs of hypotonic fluid as well as infused intravenous fluids. Intravenous fluids are typically the most important determinant of the change of serum sodium. Set A included only intravenous fluids in the calculations. Sets B, C and D use progressively more input information, which is detailed in Table 4.

Table 4.

How sets were calculated

	Fluid volume considered in calculations?	Electrolyte content considered in calculations?
Set A
IV fluids (NS, 1/2NS etc.)	Y	Y
PO/IV KCl repletion	N	N
PO/IV free water	N	N
Sodium content of Na tabs, electrolyte repletion	N	N
Juice/PO liquids (coffee, tea etc.)	N	N
Tube feeds	N	N
IV packing for IV medications	N	N
Solid food intake	N	N
Set B
IV fluids (NS, 1/2NS etc.)	Y	Y
PO/IV KCl repletion	N	Y
PO/IV free water	N	N
Sodium content of Na tabs, electrolyte repletion	N	Y
Juice/PO liquids (coffee, tea etc.)	N	N
Tube feeds	N	N
IV packing for IV medications	N	N
Solid food intake	N	N
Set C
IV fluids (NS, 1/2NS etc.)	Y	Y
PO/IV KCl repletion	Y	Y
PO/IV free water	Y	Y
Sodium content of Na tabs, electrolyte repletion	Y	Y
Juice/PO liquids (coffee, tea etc.)	Y treated as free water	N
Tube feeds	Y treated as free water	N
IV packing for IV medications	Y treated as free water	N
Solid food intake	N	N
Set D
IV fluids (NS, 1/2NS etc.)	Y	Y
PO/IV KCl repletion	Y	Y
PO/IV free water	Y	Y
Sodium content of Na tabs, electrolyte repletion	Y	Y
Juice/PO liquids (coffee, tea etc.)	Y	Y
Tube feeds	Y	Y
IV packing for IV medications	Y treated as free water	N
Solid food intake	N	N
Set E
IV fluids (NS, 1/2NS etc.)	Y	Y
PO/IV KCl repletion	Y	Y
PO/IV free water	Y	Y
Sodium content of Na tabs, electrolyte repletion	Y	Y
Juice/PO liquids (coffee, tea etc.)	Y	Y
Tube feeds	Y	Y
IV packing for IV medications	Y	Y
Solid food intake	Minimal solid food intake	Minimal solid food intake

IV, intravenous; PO, oral; KCl, potassium chloride; NS, 0.9% normal saline; 1/2NS, 0.45% normal saline; Na, sodium; Y, yes; N, no.

For sets A–D, there were 43 data points calculated from the data of 31 patients, which means that for 8 patients multiple non overlapping 12–24 h periods were analyzed and the equations used to make serial predictions about changes in the patient's serum sodium. This varied from two data points for five patients to three data points for two patients and four data points for one patient. The range of initial serum sodium at presentation was 112–132 mmol/L (mEq/L) (sets A–D) for our hyponatremic patients and 148–150 mmol/L (mEq/L) (sets A–D) for our hypernetremic patients.

We then used 27 data points from 15 patients from the aforementioned cohort of 31 patients to make up a set of ‘idealized’ patients where the sodium and potassium intake as well as the fluid intake and output could be most rigorously accounted for (set E). For uniformity, total body water was assessed at 60% of total body weight. For these 15 patients, 7 had one data point and 8 had multiple serial non overlapping data points calculated for their clinical course. For five patients, two non overlapping data points were calculated, for two patients, three data points were calculated and for one patient, four data points were calculated. These 15 patients also did not have significant solid oral intake (liquid oral electrolyte intake was accounted for) or other unaccounted fluid losses.

The range of initial serum sodium on presentation for set E patients was 112–132 mmol/L (mEq/L), but there were no clearly hypernatremic patients in set E. However, there was one patient who had a serum sodium increase from the initial value of 128 to 137 mmol/L (after the first 12 h of therapy), which was faster than optimal guidelines. This patient was corrected downwards with dextrose 5% in water (D5W) (as a hypernatremic patient would be) and this subsequent 12 h period of correction was included in the analysis in set E.

Intermediate calculations and the predicted Na₂ were calculated using Excel 2010 (Microsoft, Redmond, WA, USA) and checked using SAS 9.3 (SAS, Cary, NC, USA). Root mean square errors (RMSEs), R² values and Bland–Altman plots for Na₂ were also calculated using both Excel and SAS. Excel 2010 and Illustrator CS2 (Adobe Systems, San Jose, CA, USA) were used to construct the tables and figures.

RMSE and R² (proportion of variance accounted for) were chosen as the metrics to evaluate the performance of each equation on each data set. RMSE is defined as the square root of the average squared differences (errors) between the observed and predicted Na₂ value. The RMSEs were calculated for sets A–E and for each of the four equations (AM, BL, EFWC and NK). Please see Appendix 1 for details on how the RMSEs were calculated.

The AM equation is an output-independent equation and the EFWC equation is an input-independent equation. The values for sodium concentration, potassium concentration and total input volume used for predicting Na₂ varied depending on the rules of the set. The RMSE for the EFWC equation was identical for sets A–D since this equation is input independent, while set E's RMSE for the EFWC equation differed from the EFWC RMSE for sets A–D only because fewer data points were used.

Results

The data sets consist of 29 hyponatremic patients and 2 hypernatremic patients (sets A–D) and 43 data points derived from their cases. Of the hyponatremic patients, 9 had hypovolemic hyponatremia, 4 had hypervolemic hyponatremia, 13 had the syndrome of inappropriate antidiuretic hormone secretion (SIADH) and 3 had thiazide-induced hyponatremia. Set E consisted of 15 patients with hyponatremia, with no hypernatremic patients, and 27 data points derived from their cases. Of the hyponatremic patients, six had hypovolemic hyponatremia, six had SIADH, two had hypervolemic hyponatremia and one had thiazide-induced hyponatremia.

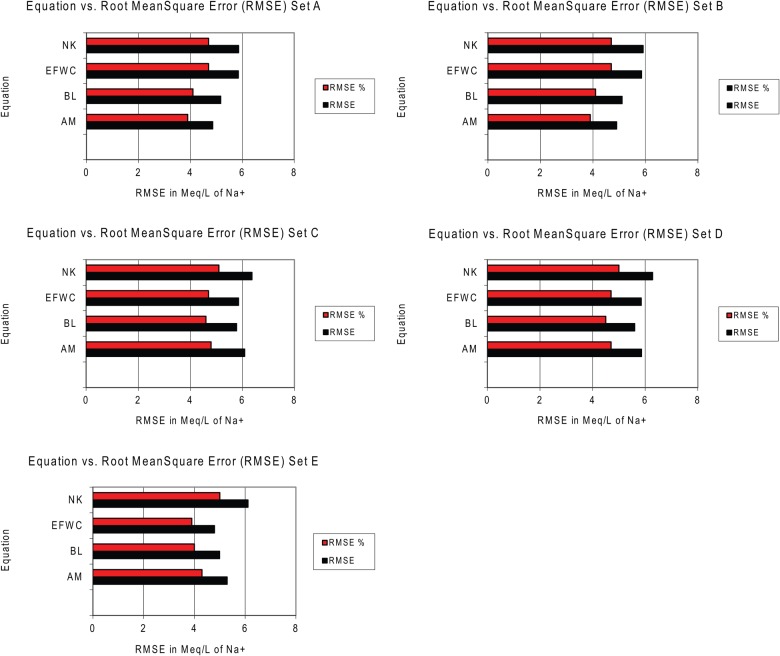
The predicted and calculated serum Na₂ were analyzed to assess the accuracy of the four equations. Accuracy was assessed through Bland–Altman analysis, but more importantly the RMSE was used as the parameter of equation accuracy. The RMSEs are presented in Table 5. Across all five sets, the RMSEs were very consistent, between 4.79 and 6.37 mmol/L (mEq/L), and the RMSEs as a percent of the mean Na₂ were similar, between 3.9 and 5.1%. The RMSEs are all very similar across all four equations for all data sets. The incorporation of more input information did not seem to systematically lower the RMSE. The RMSE remained similar and was actually slightly lower for the AM equation in some of the simpler sets.

Table 5.

Actual Na₂ minus predicted Na₂ differences and statistical analysis for sets A–E

Equation	Set	n	RMSE (RMSE%)	R2
AM	A	43	4.86 (3.9%)	66.2%
BL	A	43	5.17 (4.1%)	58.9%
EFWC	A	43	5.85 (4.7%)	59.3%
NK	A	43	5.86 (4.7%)	57.4%
AM	B	43	4.9 (3.9%)	64.5%
BL	B	43	5.11 (4.1%)	57.5%
EFWC	B	43	5.85 (4.7%)	59.3%
NK	B	43	5.91 (4.7%)	56.8%
AM	C	43	6.09 (4.8%)	64.5%
BL	C	43	5.78 (4.6%)	54.6%
EFWC	C	43	5.85 (4.7%)	59.3%
NK	C	43	6.37 (5.1%)	56.1%
AM	D	43	5.86 (4.7%)	60.9%
BL	D	43	5.6 (4.5%)	53.9%
EFWC	D	43	5.85 (4.7%)	59.3%
NK	D	43	6.28 (5%)	56.7%
AM	E	27	5.29 (4.3%)	50.8%
BL	E	27	4.99 (4%)	44.3%
EFWC	E	27	4.79 (3.9%)	49.8%
NK	E	27	6.11 (5%)	43.2%

AM, Adrogué–Madias equation; BL, Barsoum–Levine equation; EFWC, Electrolyte Free Water Clearance equation; NK, Nguyen–Kurtz equation; RMSE, root mean square error. n, number of data points. Units of RMSE in mmol/L, which is equal to mEq/L.

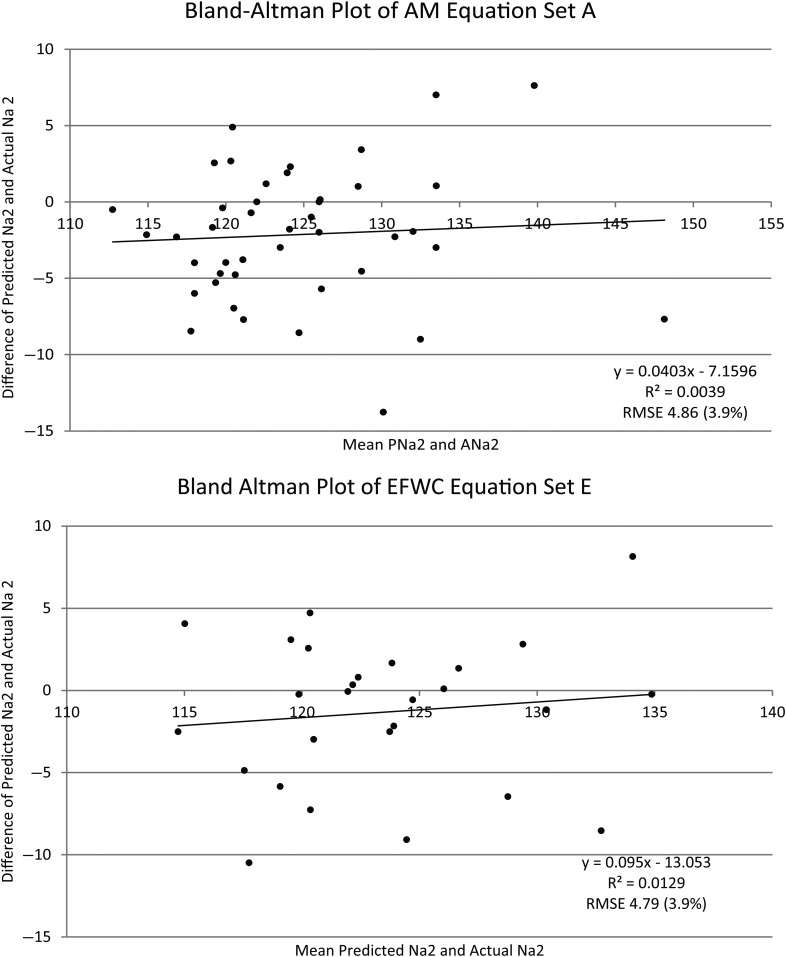
The predicted Na₂ versus actual Na₂ error ranged from −20.19 to +17.19 mmol/L (mEq/L). The average difference in absolute value between Na₂ and Na₁ was 4.09 for sets A–D and 3.93 for set E. The range of change in sodium (Na₂ − Na₁) was −14 to +16 mmol/L (mEq/L). Bland–Altman plots are presented for the two equation data set combinations with the smallest RMSEs (AM equation set A and EFWC equation set E). Even in these best cases, the equation's predictions vary significantly from the observed Na₂ (Figure 1).

Fig. 1.

Bland–Altman plots for AM equation set A and EFWC equation set E. AM, Adrogué–Madias equation; EFWC, Electrolyte Free Water Clearance equation; Na₂, final serum sodium; RMSE, root mean square error.

Figure 2 shows bar graphs of the RMSEs. While the equations themselves do not change, the inputs and outputs for the same patient and observation can differ across data sets since each data set uses progressively more information. In Figure 2 and Table 5, RMSE values were very similar across all equations and across all data sets. Table 6 shows all the data for the 15 patients and 27 data points for set E, including input sodium, potassium, fluid volume intake and fluid volume output.

Fig. 2.

Bar graphs of the root mean square error (RMSE) for sets A–E. AM, Adrogué–Madias equation; BL, Barsoum–Levine equation; EFWC, Electrolyte Free Water Clearance equation; NK, Nguyen–Kurtz equation; Na₂, actual Na₂; RMSE, root mean square error, RMSE units in mmol/L or mEq/L (equivalent metric and standard units).

Table 6.

Set E data

DP #	Pt #	Na1	Wt	uNa	uK	IV fluid	FH2O	Liquid food intake	ONS/TF	K intake	Na intake	UOP	Gluc	T	Na2	PNa2 AM	PNa2 BL	PNa2 EFWC	PNa2 NK
4	4	117	70	10	11.4	0.325 L NS	0.1 L	0.36 L milk	0	17.96	0	2.3	8.78 (158)	16	125	116.65	122.08	122.41	124.87
6	6	128	63.6	10	27.2	0	0.47 L	0	0	40	0	0.75	11.33 (204)	14	131	127.48	129.27	129.8	131.8
12	12	132	144	15	17.9	0	1.05 L	0	0	0	0	2.35	8 (144)	24	135	130.4	133.11	134.75	134.38
15	15	128	82.7	109	65.3	3.7 L NS	0.4 L	0	0	0	0	2.705	6 (108)	24	132	128.84	126.43	125.52	123.05
17	17	115	42.64	93	20.6	2.375 L NS	0.7 L	0.24 L milk	0	81.97	34.48	2.15	7.28 (131)	21	120	118.71	119.16	115.11	110.56
19	19	122	58.51	13	59.6	1 L NS	0.21 L	0	0	0	0	0.5	7.78 (140)	18	118	122.18	122.87	122.71	121.06
23	23	128	72.57	100	18.1	0	0.63 L	0.12 L apple juice	0	4.05	0	2	11.44 (206)	12	137	125.93	126.3	128.46	131.21
24	23	137	72.57	100	18.1	0	0.7 L	0	0	0	0	2.6	11.44 (206)	12	130	134.83	135.88	138.14	142.88
25	24	119	55	67	9.4	1.4 L NS	0.12 L	0.24 L lemonade	0	1.24	0	0.7	5.56 (100)	12	129	119.23	120.1	119.91	115.73
26	24	129	55	42	9	0	0	0	0	0	0	0.75	5.56 (100)	12	128	129	130.81	130.8	130.65
27	25	125	61.4	10	49.2	1.5 L NS	0.06 L	0.06 L orange juice	0	2.98	17.24	0.6	6.28 (113)	12	126	126.27	127.33	126.08	123.53
28	26	112	62.9	17	3.4	1.425 L NS	1.545 L	0	0	0	0	1.65	8.33 (150)	12	122	109.22	112.97	116.15	109.32
29	26	122	62.9	16	3.6	0	0.31 L	0	0	0	0	0.29	6.89 (124)	12	122	121.01	121.79	122.79	121.47
30	27	116	44.1	19	17.6	0.5 L NS	0	0	0	0	0	2	3.94 (71)	14	122	116.7	123.12	122.33	128.51
31	27	122	44.1	41	8.8	0	0	0	0	0	0	0.3	5.61 (101)	12	125	122	122.83	122.82	121.46
32	28	112	74.2	10	10	0.568 L NS	0.3 L	0	0	0	0	2.338	6.17 (111)	12	113	111.79	116.77	117.05	118.44
33	28	113	74.2	10	52.4	0.932 L NS	0.1 L	0	0	0	0	0.42	6.17 (111)	12	116	113.59	114.07	113.48	112.79
34	28	116	74.8	19	52.4	1.305 L NS	0.55 L	0	0	0	0	0.73	5.67 (102)	12	124	115.7	116.4	116.73	113.17
35	28	124	74.8	19	52.4	1.475 L NS	0.325 L	0	0	0	0	0.56	5.67 (102)	15	123	124.08	124.72	124.66	121.01
36	29	120	51	29	52.5	0.5 L NS	0.63 L	0	0.64 L 2calHN	80	0	0.85	5.11 (92)	11	118	119.55	120.57	121.08	116.42
37	29	118	51	51	25.2	0.02 L NS	0.184 L	0	0.24 L Osmolyte	12.37	0	0.735	88 (4.89)	19	122	117.21	118.2	119.01	118.47
38	30	121	43.7	30	65.9	0.544 L NS	0.414 L	0.18 L tea	0	0.7	0	0.575	5.33 (96)	12	119	119.06	119.56	121.55	116.85
39	30	119	43.7	10	44.5	0.457 L NS	0.357 L	0	0	0	0	0.3025	9.28 (167)	12	120	118.02	118.74	119.75	118.31
40	30	120	42.9	10	23	1 L NS	0.117 L	0	0	0	7.8	0.56	9.28 (167)	14	122	121.03	122.91	121.92	122.12
41	31	118	130	123	84.9	0.475 L NS	1.105 L	0	0	40	0	5	5.94 (107)	12	123	117.08	111	112.51	122.5
42	31	123	130	10	64.5	0.5 L NS	1.701 L	0	0	40	0	2.265	5.94 (107)	14	125	123.04	122.44	124.42	122.66
43	31	125	129.4	10	6.3	0	0.61 L	0	0	0	0	1.635	5.94 (107)	12	126	125.01	126.32	127.33	126.57

DP #, data point number; Pt #, patient number; Na₁, initial serum sodium (mmol/L); Wt, weight (kg); uNa, urine sodium (mmol/L); uK, urine potassium (mmol/L); IV fluid, IV fluid type and amount in (L); FH₂O, free water intake (oral or intravenous); ONS/TF, oral nutritional supplements or tube feeds; K intake, oral potassium intake (mmol); Na intake, oral sodium intake (from Na tabs or Na phosphate; mmol); UOP, urine output (L); Gluc, serum glucose (mmol/L and mg/dL); T, time in hours from Na₁ to Na₂; Na₂, final serum sodium; NS, 0.9% normal saline; 1/2NS, 0.45% normal saline; KCl, potassium chloride, 17.24 mEq Na in 1 g sodium chloride tab; Na, sodium, K, potassium; 1 mmol = 1 mEq[standard units] in univalent ions like sodium or potassium; PNa₂, predicted Na₂; AM, Adrogue–Madias equation; BL, Barsoum–Levine equation; EFWC, Electrolyte Free Water Clearance equation; NK, Nguyen–Kurtz equation.

Discussion

The statistical analysis that we have submitted was focused on the RMSE since this is the clinically relevant measure of the prediction's error. In order to be able to predict if the change in sodium will exceed the recommended limit of 8–12 mmol/L/day (mEq/L/day), the Na₂ must be known to within 2–3 mmol/L/day (mEq/L/day) or 1–1.5 mmol/L/12 h (mEq/L/12 h). Since the RMSE or average error of the four studied equations is ∼5–6 mmol/L (mEq/L), this implies that they may not be sufficiently accurate to predict the change in sodium in an inpatient population across 12–24 h time intervals, although one data point had an interval of 30 h. That is, our results show that the RMSEs are too large over the examined time frame to reliably predict the change in serum sodium as precisely as required. For reference, the R² values would need to be >91% for an RMSE of 2–3 mmol/L/day (mEq/L/day), while the observed R² values in Table 5 are only ∼43–66%.

Since we cannot expect to predict Na₂ from Na₁ clinically using these equations over a 12–24 h period, this argues that the equations are not accurate enough to be depended on for prognostication of changes in serum sodium over these time frames. Previous studies have shown that these equations have Pearson coefficient correlations that are highly significant [2], although this may only mean that there is some correlation that is significantly different from zero. It is important that previous studies have shown that these equations are not accurate [2, 13] and that large variations between predicted and observed sodium have long been noted [13]. The RMSE is a better and more clinically relevant parameter for assessing the clinical utility of the equations than correlation coefficients and confirms these observed trends.

The RMSEs observed in the range of 4.79–6.37 mmol/L (mEq/L) of sodium also show that these equations cannot be used to predict a change in sodium in our cohort, where the average observed change in sodium was ∼4 mmol/L (mEq/L) over 12–24 h. Furthermore, since the recommended rate of correction of sodium in hyponatremia is limited to <8–12 mmol/L/day (mEq/L/day), these equations are still too inaccurate to be used alone to calculate an exact infusion rate for intravenous fluids without depending on further close observation of urinary and serum electrolyte parameters. It is also notable that the RMSE did not change as additional factors, such as dietary factors, free fluid intake, etc., were included in the analysis across sets B/C and D/E. Thus, a more rigorous evaluation of input data did not increase the observed correlation or reduce the RMSE of these equations.

This study does not attempt to address the theoretical validity of the four equations used for sodium modeling. Rather, we tested their utility in predicting the change in sodium over a longer time frame (12–24 h) and measured the RMSE as a parameter to evaluate how useful these equations are in clinical practice. Theoretically, these models are based on sound physiology and on the work of Edelman et al. [1] and many other renowned nephrologists. The main problems stem from (i) the difficulty in obtaining input values with the accuracy and precision possible in research laboratory settings; (ii) using constant inputs like urine electrolytes that change over time, although how rapidly they change is unclear and may be different depending on the etiology of hyponatremia and other pathophysiological and physiological factors; and (iii) the possible need for further modifications to one or more of these equations to predict Na₂ from Na₁ over longer time periods or the provision of a time frame where these linear equations can provide an accurate approximation of changes in serum sodium. Of crucial importance is how long urine electrolytes can be assumed to be constant or nearly so.

Many patients with hyponatremia have a dynamic volume status and changing urine electrolytes as the kidneys adjust to treatment (i.e. antidiuretic hormone suppression after volume resuscitation or diuretic withdrawal). Thus, this may limit the usefulness of these equations, which presume static volume status and urinary electrolytes and therefore ignore changes in these parameters over time. Limitations of patient charting and lab error, which are intrinsic to any inpatient setting, must also be taken into account.

Another matter to consider is error related to weight measurement and difficulties in precisely ascertaining the percentage of total body water. For uniformity, total body water was assessed as 60% of total body weight, though in actuality total body water can vary among patients due to physiologic differences of age, gender, volume status, lean body mass, nutritional status and the effects of underlying pathophysiological processes.

Certainly these equations may be accurate or provide a better approximation of the change in sodium in a laboratory setting or if used to predict the change in sodium across a shorter time interval (which would make the assumption of static conditions more accurate). This remains to be seen in other studies, but for now, sodium modeling based on these four equations must be supplemented by frequent laboratory analysis and an attentive nephrologist who will pay close attention to these dynamic conditions.

This is especially important given the greater precision required in correcting hyponatremia that is advocated in recent literature. Previously, a correction of ≤12 mmol/24 h (mEq/24 h) was allotted; now, however, new recommendations are to keep serum sodium correction at ≤10 mmol/L/day (mEq/L/day). There are even more conservative recommendations of maintaining serum sodium correction at <6–8 mmol/24 h (mEq/24 h), since different groups may be at lower or higher risk of complications such as ODS [14–18]. Arginine vasopressin is also being used in patients who have begun to inadvertently overcorrect, or in high-risk cases, as prophylaxis to prevent water diuresis and untoward complications [14, 19]. The risk of overcorrection with the new vasopressin 2 (V2) receptor antagonists is still notable, and ODS has been observed in conjunction with the accompanying water diuresis. Thus, even these new therapeutic options are not exempt from the traditional risks of hyponatremia correction [20, 21].

This points to the importance of preventing inadvertent overcorrection and shows the need for vigilant monitoring of serum electrolytes as the accepted standard of care. The need for better equations, or limits on the use of known equations, to predict Na₂ from Na₁ are still needed in a clinical environment where precise knowledge of the magnitude of sodium correction can be lifesaving. Alternative approaches of frequent sodium monitoring and the use of D5W and desmopressin to prevent, attenuate or reverse overcorrection are helpful for now [14, 19, 22]. New research regarding the use of minocycline and inositol to prevent the clinical development of ODS after overcorrection is ongoing, but these agents have only been used in animal subjects thus far [23, 24].

Limitations

The data presented are from a retrospective, mostly cross-sectional study and are also impaired by the limitations of charting, though we tried to minimize this by using only extremely clearly charted cases. Laboratory error in the measurement of serum and urine sodium and potassium is also a factor in this study. Moreover, the time interval between the collection of Na₁ and Na₂ varied from 12 to 24 h (one measurement at 11 h and one measurement at 30 h) and could vary from observation to observation. Further, monitoring of serum sodium and urinary parameters varied and was not able to be standardized given the retrospective nature of the study.

Future directions

A prospective study of eligible hyponatremic or hypernatremic patients may help evaluate these equations better in the inpatient setting and in obtaining more concurrent longitudinal and cross-sectional data. Also possible is an investigation of how extensively and rapidly urinary electrolytes change in patients with hyponatremia caused by different etiologies. This is an important point since it is an implicit assumption of using these linear equations that the urinary electrolytes are not changing, particularly over longer time periods like 12–24 h. If the urinary electrolytes are changing, the rapidity of their change may help predict how long a laboratory test for urinary sodium and potassium is valid for. Another approach would be to study how different etiologies of hyponatremia respond to repletion, and the validity of these equations in each particular patho physiological cause of hyponatremia. A study that includes patients who have been repleted with 3% normal saline as part of the cohort or one that exclusively uses patients who have been repleted with 3% normal saline may also be helpful.

It may prove to be very challenging to verify these equations in the inpatient setting for the reasons stated above, and more controlled settings may be required. Controlled experimental avenues of validating these theoretically derived equations through animal studies, as was recently successfully done with the Edelman equation [25], may ultimately provide more decisive data regarding their accuracy.

Author contributions

R.M.H. helped guide study design, was primarily responsible for the original research, wrote the paper and is the corresponding author. W.-T.Y. contributed to the original research and analyzed the data. E.A.L. contributed to the original research and analyzed the data. J.N.R. contributed to the original research and analyzed the data. J.W. is the principal investigator of the group, created the concept and helped guide the study design.

Conflict of interest statement

None declared.

Appendix 1

A) Root Mean Square Error (RMSE): a measurement of average variation of predicted from observed values:

$$\mathrm{RMSE}={\sum }_{i=1}^{\mathrm{n}}\sqrt{\frac{{\left(y_{\mathrm{i}}-{\hat{y}}_{\mathrm{i}}\right)}^2}{\mathrm{n}}}$$

where i is the number of an individual data points,

n is the number of the last observed data point or the total number of observed data points,

y_i is the observed value for observation i,

${\hat{y}}_i$ is the predicted value for observation i and

Σ is the sum of the above formula from i = 1 to i = n.

B) Adapting the formula for our calculations :

$$\mathrm{RMSE}={\sum }_{i-1}^{\mathrm{n}}\sqrt{\frac{{\left(\mathrm{N}{\mathrm{a}}_2-\mathrm{PN}{\mathrm{a}}_2\right)}^2}{\mathrm{n}}}$$

where Na₂ is the actual final sodium for a given data point and PNa₂ is the predicted final sodium for a given data point.

(See related article by Sterns. Formulas for fixing serum sodium: curb your enthusiasm. Clin Kidney J (2016) 9: 527–529.)