Mechanical Damage of Tympanic Membrane in Relation to Impulse Pressure Waveform – A Study in Chinchillas

Abstract

Mechanical damage to middle ear components in blast exposure directly causes hearing loss, and the rupture of the tympanic membrane (TM) is the most frequent injury of the ear. However, it is unclear how the severity of injury graded by different patterns of TM rupture is related to the overpressure waveforms induced by blast waves. In the present study, the relationship between the TM rupture threshold and the impulse or overpressure waveform has been investigated in chinchillas. Two groups of animals were exposed to blast overpressure simulated in our lab under two conditions: open field and shielded with a stainless steel cup covering the animal head. Auditory brainstem response (ABR) and wideband tympanometry were measured before and after exposure to check the hearing threshold and middle ear function. Results show that waveforms recorded in the shielded case were different from those in the open field and the TM rupture threshold in the shielded case was lower than that in the open field (3.4±0.7 vs. 9.1±1.7 psi or 181±1.6 vs. 190±1.9 dB SPL). The impulse pressure energy spectra analysis of waveforms demonstrates that the shielded waveforms include greater energy at high frequencies than that of the open field waves. Finally, a 3D finite element (FE) model of the chinchilla ear was used to compute the distributions of stress in the TM and the TM displacement with impulse pressure waves. The FE model-derived change of stress in response to pressure loading in the shielded case was substantially faster than that in the open case. This finding provides the biomechanical mechanisms for blast induced TM damage in relation to overpressure waveforms. The TM rupture threshold difference between the open and shielded cases suggests that an acoustic role of helmets may exist, intensifying ear injury during blast exposure.

1 INTRODUCTION

Exposure to high intensity sound or blast overpressure waves is considered to be an intrinsic situation faced by military personnel involved in most operational activities. The direct consequences of high-intensity noise and blast injuries to the auditory system are acute hearing loss, which immediately affects the normal functioning of soldiers in combat operations, and the resultant long-term hearing disabilities that occur in a significant fraction of veterans (Patterson and Hamernik, 1997 ; Garth, 1994; Karmy-Jones et al., 1994; Gondusky and Reiter, 2005; Fausti et al., 2009).

Blast overpressure is a high intensity disturbance in the ambient air pressure that creates high intensity sound (impulse) over 170 dB SPL. When exposed to a blast, the human auditory system is vulnerable to both peripheral and central damage from the overpressure (Patterson and Hamernik, 1997; Mayorga, 1997). Rupture of the eardrum or tympanic membrane (TM) is the most frequent injury of the ear and has been investigated in animals and humans with wide variability (Hirsch, 1966; Patterson and Hamernik, 1997; Richmond et al., 1989). The literature indicates that mechanical damage to components of the auditory system is the major cause for hearing loss after blast exposure. However, it is not clear how the severity of injury graded by different patterns of TM rupture is related to the overpressure waveforms induced by blast exposure. Particularly, no quantitative study on biomechanical changes of the TM in response to different pressure waveforms has been reported in the literature.

In this paper, we report our currently completed study on relationships between the TM rupture threshold, the TM damage pattern, and the overpressure waveforms using a chinchilla animal model. The chinchilla is a commonly used animal model for auditory research with large TMs, ossicular dimensions, and middle ear spaces for an animal of its size. The chinchilla’s range of hearing is similar to that of humans (Heffner R. and Heffner, H. 1991; Richmond et al., 1989; Hedegaard and Bonding, 1993). In the present study, two groups of animals were exposed to high intensity sound pressure under two conditions: the open field without a shield and the shielded case with a stainless steel cup covering the animal head. By increasing the blast peak pressure level, the TM was finally ruptured and the pressure waveforms at the entrance of the ear canal were recorded simultaneously. The goal of this study was to determine whether there is a change of overpressure waveform under the shield and how the waveform change affects the TM rupture threshold.

In addition to experimental testing in animals, impulse pressure energy spectra analysis of the waveforms recorded under open and shielded conditions was performed to determine signal energy flux over 10 frequency bands. The 3D finite element (FE) model of the chinchilla middle ear recently developed in our lab was employed to calculate the distributions of the stress and strain in the TM with impulse pressure profiles recorded in open and shielded conditions. The FE modeling results reveal that a waveform pattern consisting of both positive and negative pressures in the shield case (under a stainless steel cup) contributes more greatly to TM damage than the positive overpressure in the open case. This finding provides the biomechanical mechanisms for blast induced TM damage in relation to overpressure waveforms. The TM rupture threshold difference between the open and shielded cases suggests that an acoustic role of helmets may exist, intensifying ear injury during blast exposure.

2 METHODS

2.1 Animal study protocol

Eighteen chinchillas (Chinchilla laniger) weighing between 600–800 g were included in this study. The study protocol was approved by the Institutional Animal Care and Use Committee of the University of Oklahoma and met the guidelines of the National Institutes of Health and the United States Department of Agriculture (USDA). All animals were established to be free from middle ear disease, as evaluated by wideband tympanometry.

A well-controlled compressed air (nitrogen)-driven blast apparatus located inside an anechoic chamber in the Biomedical Engineering Laboratory at the University of Oklahoma was used to create a blast overpressure wave or blast exposure in this study (Hawa and Gan, 2014). Polycarbonate film (McMaster-Carr, Atlanta, GA) of varying thickness (130 μm and 260 μm) was employed to generate blast overpressure of at least 30 psi (200 dB SPL). The overpressure level was controlled by varying the distance from the blast reference plate. Figure 1A shows a schematic of the blast apparatus with the animal holder placed at the center.

Figure 1.

(color online) (A) Schematic of animal experimental setup with blast apparatus in the open field testing. (B) Schematic of animal experimental setup in the shielded test with a stainless steel cup. (C) Picture of the animal inside the holder with its head covered by a stainless steel cup in the testing chamber.

The animals were divided into two groups: one group of 9 animals was exposed to blast in an “open field” (Fig. 1A) and another group of 9 animals was exposed to blast with a shield covering the animal head as shown in the schematic of Fig. 1B and the picture of Fig. 1C. The animals in both groups were first tested with the pre-exposure measurements, including middle ear energy absorbance (EA) using wideband tympanometry (Model AT235h, Interacoustics, MN) and auditory brainstem response (ABR) using TDT system III (Tucker-Davis Technologies, Alachua, FL). The EA measurement applied tone-burst stimuli at frequencies of 0.5, 1, 2, 4, and 8 kHz in the ear canal (Guan and Gan, 2011; Jeselsohn et al., 2005; Petrova et al., 2006; Qin et al., 2010). The EA measurement was used as a check of the TM integrity and normal function of the middle ear. The ABR measurements provided the change of hearing threshold of the ear after blast exposure. The animal was anesthetized with mixed ketamine (10 mg/kg) and xylazine (2 mg/kg). To maintain consistent measurement of ABR, tympanometry, and blast pressure level, the pinna was removed.

After pre-exposure testing, the animal was placed into a specially designed animal holder. A pressure sensor (Model 102B16, PCB Piezotronics, Depew, NY) was placed at the entrance of the ear canal (1 cm lateral to the ear canal opening) with the sensing surface facing the blast in both open and shielded conditions. During the shielded test, the entire animal head was covered by a stainless steel cup with a thickness of 2 mm. The edge of the cup was flushed with the sensor which was also covered by the shield (Fig. 1C). Note that the chinchilla head shield was adjustable with relative position from the animal head and there was a distance of about 3 cm from the animal head to the internal top surface of the shield. The stainless steel shield was finally fixed on the animal holder. The animal within the holder was then moved to the testing chamber for blast exposure.

The pressure sensor signal was measured by cDAQ 7194 and A/D converter 9215 (National Instruments Inc., Austin, TX) with the sampling rate of 100k/s (10 μs dwell time). The LabVIEW software package (NI Inc.) was used for data acquisition and analysis. The waveform of each blast test was saved in a PC for further analysis.

It usually took 2–3 iterations of blast tests to reach the TM rupture threshold defined as the peak pressure before the TM rupture. That means if the TM ruptured after the third blast, the threshold was the peak pressure level of the second blast. The initial blast pressure level was selected based on the system calibration using different films and changing the distance between the sensor surface and the blast reference plane. The number of blast tests also varied with individual chinchillas due to the variation among the animals and setups. To confirm the TM damage, an otoscopic examination of both ears was performed first and further verification was done using wideband tympanometry to determine whether the TM was ruptured. When the TM was found without rupture, the next blast test was conducted with an increase of overpressure level. The testing stopped when one ear was ruptured.

Post-exposure measurements included wideband tympanometry to verify whether the TM was ruptured or damaged in both ears and ABR measurement in the ears with intact TMs to determine the hearing threshold shift after exposure. The TM damage pattern was recorded by taking pictures after the animal was euthanized and the bulla was dissected.

2.2 Waveform analysis

Impulse pressure energy spectra analysis on recorded waveforms in the time domain was conducted in MATLAB to determine the signal energy distribution over the frequencies under open and shielded conditions. First, the recorded pressure waveforms were converted to pressure distributions over the frequencies of 20–5000 Hz by using FFT spectral analysis. Next, following the methods of impulse signal energy distribution theory reported by Hamernik et al. (1991a, 1991b, 2001) and Young (1970), the total sound exposure was divided by the standard characteristic impedance of the air ρc as impulse energy flux (energy per unit area) and expressed as:

$$E^{\ast }=\frac{1}{\rho c}\underset{0}{\overset{T}{\int }}{p}^2(t)dt,[\mathrm{J}/{\mathrm{m}}^2]$$ (1)

where p(t) is the instantaneous value of acoustic pressure in Pa or N/m², dt is the time increment for scanning of acoustic pressure in seconds, and ρc = 406 mks rayls to produce a quantity with units of energy flux (i.e., J/m²). Both ρ and c are pressure-dependent in the shock front. The duration of T = 50 ms was used for calculation in the present study.

Eight octave band-pass filters with center frequencies at 125 Hz, 250 Hz, 500 Hz, 1 kHz, 2 kHz, 4 kHz, 8 kHz, and 16 kHz were designed. A low pass filter L125 and a high pass filter H16k were also designed to catch signals at frequencies lower than 125 Hz and higher than 16 kHz. The filtered signals were then generated and the sound energy in each band was calculated as the distribution of pressure energy flux over 10 bands. Instead of directly comparing the energy flux values in the open field and shielded case, the energy in each band was normalized with respect to the total sound energy in that band.

2.3 Finite element modeling prediction

A 3D finite element model of the chinchilla ear has been developed in our lab and is currently under review for publication. The model was built based on X-ray micro-CT images of an entire chinchilla bulla, consisting of the ear canal, TM, middle ear ossicles and suspensory ligaments, and middle ear cavity. In this study, the FE model was used to calculate the distribution of the stress and strain in the TM with impulse pressure waveforms measured under open and shielded conditions. To simplify the modeling process, the ear canal and middle ear cavity were not included in the model as shown in Fig. 2. Figure 2A shows the lateral view of the model with a TM diameter of 8.83 mm along the manubrium or malleus long process and 9.72 mm perpendicular to the manubrium. Surface area of the TM was 74.71 mm² and the thickness was 15 μm. Figure 2B shows the posterior view of the model with a height of cone at 1.65 mm. The TM and ossicles were suspended by the TM annulus (TMA), anterior malleal ligament (AML), posterior incudal ligament (PIL), posterior stapedial tendon (PST), tensor tympani tendon (TTT), and stapedial annual ligament (SAL). In the chinchilla ear, the malleus and incus are fused as the malleus-incus complex and the incus-stapes joint still exists. The mechanical properties of the TM and middle ear tissues are listed in Table A1 in the Appendix.

Figure 2.

(color online) Finite element (FE) model of chinchilla middle ear. (A) Lateral view of the FE model with the tympanic membrane (TM), malleus-incus (M-I) complex, anterior malleal ligament (AML), posterior incudal ligament (PIL), and TM annulus (TMA). (B) Posterior view of the FE model with manubrium, PIL, tensor tympani tendon (TTT), stapes, stapedial annual ligament (SAL), and cochlear load.

The effect of cochlear fluid on acoustic-mechanical transmission through the ossicular chain or cochlear load was modeled as a mass block and 10 dashpots attached between the stapes footplate and fixed boundary. The average cochlear impedance was about 100 GΩ as reported by Slama et al. (2010). The impedance value of 100 GΩ was applied on 2.45 mm² of the stapes footplate to determine the dashpot damping, which resulted in a damping coefficient of 0.06 Nm/s for each dashpot.

Representative pressure waveforms (i.e., same magnitude and impulse duration, but more smooth) analogous to the recorded open and shielded waveforms (pressure vs. time plots) were directly applied on the TM surface and the calculation was performed in ANSYS APDL (ANSYS Inc., Canonsburg, PA). FE modeling of the TM and other soft tissue responses to impulse pressure waves used structural analysis with geometry nonlinearity of the tissues. The analysis was conducted in the time domain, utilizing the automatic time step function offered by ANSYS. Sensitivity analyses resulted in a calculated error of less than 1%. The output from modeling included the stress and strain distributions in the TM and the TM displacement distribution. The FE modeling results characterized mechanical damage of the TM in relation to impulse pressure waveforms.

3 RESULTS

3.1 Experimental results

The damage of the TM observed from chinchilla ears after exposure in both open and shielded conditions showed certain TM rupture patterns. Figure 3 displays otoscopic photographs of chinchilla TMs in a normal or intact ear (Fig. 3A) and injured ears (Figs. 3B–3D). The severity of TM rupture increased from Figs. 3B to 3D. A small split along the radial direction of the TM was shown in Fig. 3B (chin-7s, shielded) and a large split along the radial direction was shown in Fig. 3C (chin-6s, shielded). These damage patterns show that the TM tissue strength varies in radial and circumferential directions and the collagen fibrous structure of the TM results in relatively weak mechanical properties along the circumferential direction. Under high intensity sound or blast overpressure, the TM damage pattern is closely related to variation of mechanical properties across the TM membrane. Figure 3D shows a large perforation about the half of the TM surface in the inferior side (chin-7, unshielded). The TM rupture patterns shown in Fig. 3 were observed in both open and shielded conditions, and in most animals, the both ears were damaged with different patterns. Our observations are similar to those of TM perforations in mice after blast exposure reported by Cho et al. (2013): larger blast pressure did not make larger perforations. Thus, the present study could not provide any relationship between the TM rupture pattern and exposure condition: shielded and unshielded.

Figure 3.

(color online) Otoscopic pictures of chinchilla TMs. (A) Normal chinchilla TM. (B–D) TM ruptured after blast exposure with different severity: (B) a small split along the radial direction; (C) a large split along the radial direction; and (D) severe rupture of the TM.

Figures 4A and 4B show the typical waveforms of pressure amplitude (rupture threshold level) in units of psi over a time of 10 ms recorded from two chinchillas in open field testing. A single positive overpressure peak was observed and peak pressures of 9.8 psi (Fig. 4A) and 11.3 psi (Fig. 4B) were reached within 3 ms as shown in these two figures. The spectral behavior of the waveforms in Figs. 4A and 4B at frequencies of 20–50,000 Hz by FFT analysis is displayed in Figs. 4C and 4D, respectively. There was a plateau of 50–55 dB at low frequencies (<200 Hz), and then the pressure level monotonically decreased to around zero as frequency increased to 50,000 Hz.

Figure 4.

(color online) (A) The overpressure waveform recorded in one chinchilla in open field testing and (C) the impulse pressure spectra obtained from this animal’s waveform. (B) The overpressure waveform recorded in another chinchilla in open field testing and (D) the impulse pressure spectra obtained from this animal’s waveform.

Table 1 lists the measured TM rupture thresholds (positive-peak in both psi and dB SPL) for animals tested in open field. The mean value of the TM rupture threshold measured from 9 animals in open field was 9.1 psi or 190 dB SPL or 62.7 kPa with a standard deviation (S.D.) of ±1.7 psi (N=9).

Table 1.

List of TM rupture thresholds measured from a group of chinchillas tested in open field.

Animal	chin-1	chin-2	chin-3	chin-4	chin-5	chin-6	chin-7	chin-8	chin-9	Mean±S.D.
Positive peak (psi)	10.7	6.9	9.8	11.3	10.2	9.8	9.1	9.0	5.5	9.1±1.7
Positive peak (dB SPL)	191.3	187.5	190.6	191.8	190.9	190.6	189.9	189.8	185.6	189.8±1.9

Figures 5A and 5B show the waveforms of pressure (rupture threshold level) recorded from two animals in shielded testing. The waveform under the shield is obviously different from that in open field. Both positive and negative peaks were reached at less than 3 ms. The peak-to-peak pressure levels were 3.5 psi and 3.4 psi for Figs. 5A and 5B, respectively. This suggests that under the shield, the TM was ruptured at a lower pressure level than that without the shield. The spectral behavior of the waveforms in Figs. 5A and 5B is displayed in Figs. 5C and 5D, respectively. It can be seen that under the shielded test there was no perfect plateau like that observed in open field at lower frequencies (Figs. 4C and 4D) and the peak pressure around 50 dB was reached at about 1000 Hz and decreased to zero as frequency increased to 50,000 Hz.

Figure 5.

(color online) (A) The overpressure waveform recorded in one chinchilla in shielded testing and (C) the impulse pressure spectra obtained from this animal’s waveform. (B) The overpressure waveform recorded in another chinchilla in shielded testing and (D) the impulse pressure spectra obtained from this animal’s waveform.

Table 2 lists the measured TM rupture thresholds for animals tested with the shielded. The positive-peak and negative–peak in psi as well as the peak-to-peak pressures in both psi and dB SPL are included in Table 2. The mean value of the TM rupture thresholds measured from 9 animals with the shield was 3.4 ±0.7 psi (N=9) or 181 dB SPL. Comparing the results listed in Tables 1 and 2, a significant difference in the TM rupture thresholds between the open and shielded cases was revealed. With the shield, the TM rupture occurred at a much lower impulse pressure than that in the open field. This difference shows the biphasic nature of the shielded impulse.

Table 2.

List of TM rupture thresholds measured from a group of chinchillas tested with a shield.

Animal	chin-1s	chin-2s	chin-3s	chin-4s	chin-5s	chin-6s	chin-7s	chin-8s	chin-9s	Mean±S.D.
Positive-peak (psi)	1.5	2.2	1.5	1.5	2.3	2.3	1.8	1.4	1.1	1.7±0.4
Negative peak (psi)	2.6	2.7	1.5	1.3	1.3	1.2	1.6	1.4	1.6	1.7±0.5
Peak-to-peak (psi)	4.1	4.9	3.0	2.8	3.6	3.5	3.4	2.8	2.7	3.4±0.7
Peak-to-peak (dB SPL)	183.0	184.6	180.3	179.7	181.9	181.6	181.4	179.7	179.4	181.3±1.6

Wideband tympanometry was used as an effective tool to detect TM damage in this study. The pre- and post-exposure tympanometry measurements were focused on the change of energy absorbance of the middle ear. The peak EA happens when the pressure of the middle ear equals that of the external ear in a normal ear with intact TM. When there is a perforation, the EA is low and flat. However, if the TM was not ruptured after blast, the EA measured at the pre- and post-blast exposure from 8 ears did not show significant difference between the pre- and post-exposure by paired t-test (detailed results not included here). This indicates that a TM rupture, even a small split, affects the EA measurement substantially.

Hearing threshold shift data were obtained by taking the difference of ABR measurements obtained pre- and post-blast exposure for ears without rupture. The tests were only conducted for animals in the open condition. The threshold shift indicates the hearing loss induced by blast exposure, which may involve outer ear and middle ear disorder. Figure 6 shows the ABR hearing threshold shift obtained from 13 ears (4 animals had both ears tested). The hearing threshold was measured at 5 frequencies: 0.5, 1, 2, 4 and 8 kHz. It can be seen that the blast exposure caused ABR hearing threshold shift, particularly at high frequencies. A 10–20 dB threshold increase was measured at frequencies of 2–8 kHz, which means the high frequency hearing loss is greater than the low frequency hearing loss induced by blast exposure. While there was no mechanical damage observed visibly in the middle ear, damage of the cochlea after blast may contribute to the hearing threshold shift as suggested by Cho et al. (2013).

Figure 6.

(color online) ABR hearing threshold shift at frequencies of 0.5, 1, 2, 4, and 8 kHz obtained from 13 animal ears after exposures to blast waves (open field).

3.2 Impulse energy spectra analysis

The sound pressure signal in the open field (Figs. 4A and 4B) is a shock wave-like impulse and the pressure signal in the shielded case (Figs. 5A and 5B) is a complex wave-like waveform as observed in our experiments. The impulse wave is completely changed under the shield. However, both waveforms are impulse pressure profiles (short duration and non-periodic) and the signal energy flux calculation was performed for all recorded waveforms in open and shielded groups over 10 octave frequency bands. Table 3 lists the calculated normalized energy flux for the open and shielded groups (N=9 for each group) over 10 bands with mean and S.D. Note that the data were normalized with respect to the total signal energy in each group and the total value was 1.0 as shown in the table.

Table 3.

Octave-band energy flux (J/m²) (normalized) for the open and shielded groups.

Octave band CF(kHz)	Open		Shielded
	Mean	±S.D.	Mean	±S.D.
<0.125	0.2557	0.0512	0.0343	0.0225
0.125	0.1797	0.0356	0.0444	0.0157
0.25	0.2159	0.0653	0.1310	0.0285
0.5	0.1628	0.0631	0.3922	0.0417
1.0	0.0935	0.0643	0.3118	0.0914
2.0	0.0421	0.0531	0.0737	0.0615
4.0	0.0211	0.0162	0.0270	0.0177
8.0	0.0113	0.0084	0.0114	0.0109
16.0	0.0121	0.0215	0.0051	0.0019
>16.0	0.0125	0.0278	0.0035	0.0024
Total	1.0066		1.0344

Figure 7 displays the distribution of energy flux (normalized) based on the data in Table 3. It clearly shows the different energy flux over frequencies in the open and shielded cases. Under the open field condition, the majority of energy flux is presented at lower frequencies below 500 Hz. However, under shielded condition, the energy flux is mainly involved at 500 and 1000 Hz. The results demonstrate that the different pressure waveforms in the open and shielded cases implicate the different energy distribution characteristics involved in these two exposures.

Figure 7.

(color online) Comparison of normalized energy flux over 10 frequency bands from below 125 Hz to above 16 kHz between the waveforms recorded in the open and shielded groups of chinchillas.

3.3 FE modeling results

The pressure waveforms recorded from the open field test (Fig. 4B) and the shielded test (Fig. 5B) were selected as blast pressure loading on the TM in the FE model of the chinchilla ear shown in Fig. 2. Two simulations were created: the open case with a positive peak pressure of 11.3 psi and the shielded case with peak pressures of positive 1.7 psi and negative 1.7 psi, or 3.4 psi peak-to-peak. The duration of open case simulation was set to 1 ms, to reflect the majority of the impulse of the measured open waveform. The small initial peak in the measured open waveform was not included in the simulation and the modeling analysis showed that the addition of the initial peak did not alter the results significantly. The shielded case was simulated using 1.5 ms of the experimental waveform so as to capture the initial pressure oscillations.

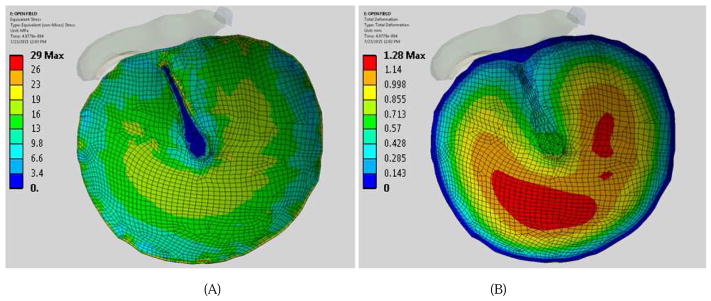
Figure 8 shows the model-derived distributions or contours of stress in the TM (Fig. 8A) and the displacement of the TM (Fig. 8B) in the open case (or under positive pressure waveform) at the time of maximum stress was reached. In this study, the equivalent (von Mises) stress was used as a measure of the stress state of the TM. As shown in Fig. 8A, the stress varied from 29 to 0.13 MPa in the TM. The maximum stress of 29 MPa was at the top of the manubrium or near the flaccida above the handle of malleus. The second high-stress region of the TM was located in the inferior side along the middle region between the annulus and umbo with the stress ranging from 16 to 19 MPa. Figure 8B displays the FE model-predicted TM displacement distribution. The maximum displacement of 1.28 mm was located in the inferior-posterior quadrant, approximately midway between the annulus and umbo. The displacement in the region of the manubrium was the smallest.

Figure 8.

(color online) FE model-derived distributions of the equivalent (von Mises) stress in the TM (A) and the displacement of the TM (B) in the open case at the time when the maximum stress was reached. The recorded pressure waveform is listed in Fig. 4B. The stress and displacement levels are shown by color code.

Figure 9 displays the FE model-derived equivalent stress distribution in the TM (Fig. 9A) and the TM displacement (Fig. 9B) in the shielded case (or under positive-negative pressure waveform) at the time when the maximum stress was reached. The maximum stress occurred as the peak negative pressure was reached. As shown in Fig. 9A, in the superior region of the TM, the location of the maximum stress was the same as that of the open condition, i.e., at the top of the manubrium, and the value of maximum stress was also about 29 MPa. In the inferior side, the maximum stress of the TM was next to the umbo with a value about 15 MPa. The maximum displacement was located in the inferior portion of the TM, directly below the umbo with a value of 1.33 mm.

Figure 9.

(color online) FE model-derived distributions of the equivalent stress in the TM (A) and the displacement of the TM (B) in the shielded case at the time when the maximum stress was reached. The recorded pressure waveform is listed in Fig. 5B. The stress and displacement levels are shown by color code.

A comparison of the results obtained in the shielded case (Fig. 9) with those obtained in open field (Fig. 8) indicates a similar stress distribution on the TM surface in both open and shielded cases, with the maximum stress of about 29 MPa at the top of the manubrium. It is also found that for both open and shielded conditions, the maximum TM displacements were similar, but the location of maximum displacement in the shielded condition was closer to the umbo than that of the open condition. The model-predicted high stress level regions on the TM surface induced by impulse pressure waves recorded in blast tests were generally consistent with the observed TM rupture locations in experiments, suggesting the high stress levels may result in the TM rupture. The calculated location of maximum stress on the TM may not match the common mode of failure as seen in Fig. 3 – a radial tear caused by failure of the TM circumferential fibers. The TM in current model was assumed as an isotropic membrane material, and thus does not capture the intricacies of the physiological, 3-layer membrane. Creation and implementation of a multi-layer TM is a future direction of this study.

Luo et al. (2009) measured the TM failure stress using a miniature split Hopkinson tension bar, and their results showed that the ultimate tensile stress of the TM increased with increasing strain rate, and the orientation of TM sample had a strong influence on the ultimate tensile stress. The mean ultimate stress of TM in the circumferential direction was 7.7 MPa with a strain rate of 772/s, and 13.7 MPa with a strain rate 1353/s. Since the strain rate was not derived from the two waveforms in the present study, the TM strain rate associated with the two waveforms and its effect on the rupture threshold need further investigation.

4 DISCUSSION

4.1 What we found from the chinchilla study?

In this study, mechanical damage of the TM in chinchilla ears after exposure to high intensity sound or blast has been investigated in two groups of animals under two exposure conditions: open field and shielded. The results show that the TM rupture threshold in the shielded case was lower than that in the open field with the mean values obtained from 9 animals in each condition. The waveforms recorded during the tests from these two groups are different: a single positive impulse pressure wave obtained from the open test and the almost equal positive-negative waves obtained from the shielded test. These experimental results provide the evidence that the TM damage induced by blast overpressure is closely related to impulse pressure waveforms at the entrance of the ear canal which determine the energy level and frequency components of the sound signal to be transmitted into to the ear.

4.2 How to explain the results?

Two methods have been used for analysis of the TM damage results in this study with a focus on the relationship between the TM rupture threshold and impulse pressure waveform.

1. The impulse pressure energy spectra for waveforms recorded from each animal was analyzed over 10 octave frequency bands. The normalized energy flux at each band was then calculated from each animal and the mean values with S.D. were derived and displayed in Fig. 7 for both open and shielded groups. The spectra difference between these two groups suggests that the positive-negative pressure waveform in the shielded case carried more energy at higher frequencies than that of the open case. This finding verifies that the spectra behavior of impulse signal energy distribution over frequency bands is different in these two waveforms for the open and shielded conditions. However, the direct analysis of TM mechanical damage in relation to impulse pressure waveform needs further clarification.

2. The 3D finite element model of the chinchilla middle ear (Fig. 2) was used to derive the stress/strain distribution in the TM and the TM displacement when the pressure waves were applied on the TM over a very short time duration (<3 ms, Figs. 4B and 5B). The FE modeling results shown in Figs. 8 and 9 provide the contour distributions of the stress and displacement at the time when the maximum stress was reached, which reflected the stress and movement of the TM at the rupture threshold level. To examine the change of stress in the TM in response to rapid pressure loading, we applied the pressure waves on the TM at four levels: 25%, 50%, 75%, and 100% of the rupture pressure level. The results are shown in Fig. 10 as the variation of TM stress with respect to the impulse pressure level.

Figure 10.

(color online) Plots of FE model-derived stress increase with the peak-to-peak pressure loading in open and shielded cases. The red broken line with symbols was obtained from Fig. 8 in open case and the blue solid line with symbols was obtained from Fig. 9.

As can be seen in Fig. 10, the change of stress in response to change in pressure loading in the shielded case was much higher than that in the unshielded case. This finding reveals that the biomechanical mechanisms for blast-induced TM damage in relation to overpressure waveforms may consist of the following two standard points: 1) the negative pressure component of the shielded waveform may play a crucial role for TM rupture, even though the negative peak is smaller than the positive peak; 2) the sensitivity of TM stress with respect to peak-to-peak pressure amplitude, δσ/δp, may characterize mechanical damage of the TM in relation to the impulse pressure waveform.

4.3 Future studies

This is the first time the TM damage in relation to blast pressure waveforms has been investigated by using the 3D FE model of the chinchilla ear. This approach is based on experimental measurements in animals and the FE mechanical analysis of the TM or middle ear structure response to blast overpressure waves. The results and findings from this study, though limited to two cases, may have general contributions for understanding the mechanisms of TM damage during the blast exposure. In our future studies, we will continue the investigation along this direction on mechanisms of the TM and other ear tissue damages in relation to blast overpressure waveforms. We will also face challenges for development of the failure criteria for TM, a multiple layer, viscoelastic membrane tissue, in response to high intensity sound and blast overpressure.

It is also worth noting that the present study has demonstrated that the TM rupture threshold in the shielded case with the shield covering the animal head was lower than that in the open field, when the animal was exposed to blast overpressure. This suggests that an acoustic role of helmets may exist which intensifies ear injury during blast exposure. However, more studies on a helmet’s effect on possible TM damage are needed in addition to its protection function to traumatic brain injury.

5 CONCLUSIONS

The relationship between the TM rupture threshold and the impulse or overpressure waveform has been investigated in chinchillas. Two groups of animals were exposed to blast overpressure under two conditions: open field and shielded with a stainless steel cup covering the animal head. The waveforms recorded in the shielded case had almost equal positive-negative pressure phases while the waveforms recorded in the open field had the positive pressure only. The average TM rupture threshold measured in the shielded case was lower than that in the open field (3.4 peak-to-peak vs. 9.1 psi or 181 vs. 190 dB SPL, and the positive peak for the shielded case was even smaller). The positive-negative pressure waveform in the shielded case delivered more energy at high frequencies to the ear canal while the positive pressure only waveform in the open case carried energy limited at lower frequencies. The FE modeling results further revealed that the biomechanical mechanisms for blast induced TM damage in relation to the overpressure waveform may consist of two standard points: the role of the negative pressure component and the rate of stress change with respect to impulse pressure loading increasing. The TM rupture threshold difference between the open and shielded cases may suggest that an acoustic role of the helmet may exist which intensifies ear injury during blast exposure.

Research Highlights.

• TM damage in blast exposure was tested in open and shielded cases in chinchillas.

• Rupture threshold of the TM in shielded case was lower than that in open field.

• Waveforms recorded in shielded case delivered more energy at high frequencies.

• The FE model of chinchilla ear predicted the waveform-TM stress relationship.

• Change of stress w.r.t. pressure wave characterized TM damage induced by blast.

List of Abbreviation

ABR

Auditory Brainstem Response

AML

Anterior Malleal Ligament

EA

Energy Absorbance

FE

Finite Element

FSI

Fluid-Structure Interaction

PIL

Posterior Incudal Ligament

PST

Posterior Stapedial Tendon

SAL

Stapedial Annual Ligament

S.D

Standard Deviation

TM

Tympanic Membrane

TMA

Tympanic Membrane Annulus

TTT

Tensor Tympani Tendon

Appendix

Table A1.

Mechanical properties of middle ear soft tissues of chinchilla ear

Structure	Parameters
Tympanic membrane
Elastic modulus (MPa):
Pars tensa	200
Pars flaccida	15
Density (kg/m3)	1100
Damping coefficient	1.00×10−4
Manubrium
Elastic modulus (MPa)	800
Density (kg/m3)	1200
Damping coefficient	7.5×10−5
Incudomalleolar (IS) joint
Elastic modulus (MPa)	6
Density (kg/m3)	1000
Damping coefficient	7.5×10−5
Stapedial annular ligament (SAL)
Elastic modulus (MPa)	0.1
Density (kg/m3)	1000
Damping coefficient	7.5×10−5
Anterior malleal ligament (AML)
Elastic modulus (MPa)	3.2
Density (kg/m3)	1000
Damping coefficient	1.0×10−4
Posterior incudal ligament (PIL)
Elastic modulus (MPa)	2.5
Density (kg/m3)	1000
Damping coefficient	7.5×10−4
Posterior stapedial tendon (PST)
Elastic modulus (MPa)	2.0
Density (kg/m3)	1000
Damping coefficient	7.5×10−5
Tensor tympani tendon (TTT)
Elastic modulus (MPa)	2.0
Density (kg/m3)	1000
Damping coefficient	7.5×10−5
Malleus-incus complex
Elastic modulus (GPa)	14.1
Density (kg/m3)	2000
Mass (mg)	12.05
Damping coefficient	1.5×10−4
Stapes
Elastic modulus (GPa)	14.1
Density (kg/m3)	1300
Mass (mg)	0.55
Damping coefficient	1.0×10−4