Abstract
A review is presented of the physical principles governing the distribution of blood flow and blood pressure in the vascular system. The main factors involved are the pulsatile driving pressure generated by the heart, the flow characteristics of blood, and the geometric structure and mechanical properties of the vessels. The relationship between driving pressure and flow in a given vessel can be understood by considering the viscous and inertial forces acting on the blood. Depending on the vessel diameter and other physical parameters, a wide variety of flow phenomena can occur. In large arteries, the propagation of the pressure pulse depends on the elastic properties of the artery walls. In the microcirculation, the fact that blood is a suspension of cells strongly influences its flow properties and leads to a non-uniform distribution of hematocrit among microvessels. The forces acting on vessel walls include shear stress resulting from blood flow and circumferential stress resulting from blood pressure. Biological responses to these forces are important in the control of blood flow and the structural remodeling of vessels, and also play a role in major disease processes including hypertension and atherosclerosis. Consideration of hemodynamics is essential for a comprehensive understanding of the functioning of the circulatory system.
Introduction
The circulatory system consists of the heart and an extensive branched system of vessels containing blood, whose primary function is the transport of oxygen, nutrients and other substances and heat throughout the body. In medical contexts, the term “hemodynamics” often refers to basic measures of cardiovascular function, such as arterial pressure or cardiac output. In the present review, “hemodynamics” refers to “the physical study of flowing blood and of all the solid structures (such as arteries) through which it flows” (64). According to this definition, the emphasis is on the fluid and solid mechanics of the system. While numerous biological processes have important interactions with hemodynamic effects, these processes are not discussed in depth. Furthermore, the fluid and solid mechanics of the heart are not addressed here, as they are described in other articles in this series.
The study of hemodynamics has a long history. The quantitative reasoning of William Harvey (1578–1657) led in 1628 to the concept that blood continuously circulates (38). However, the complete pathway for the circulation was not identified until Marcello Malpighi (1628–1694) described the frog lung’s capillaries in 1661 (61). In 1733, Stephen Hales (1677–1761) reported direct measurements of arterial pressure (35). Among his many scientific contributions, Thomas Young (1773–1829) established the relationship between the elastic properties of arteries and the propagation speed of the arterial pulse (121,122). Through meticulous experiments, J.L.M. Poiseuille (1797–1869) in 1846 established the fourth-power relationship between flow rate and diameter for a tube subject to a fixed pressure gradient along its length (74). One of the several contributions of Otto Frank (1865–1944) to physiology was his development of the Windkessel model to describe the mechanical interaction between the ejection of blood from the left ventricle during systole and the elasticity of the aorta and the major arteries (25). In this model, the elastic arteries are considered as a single compliant compartment. The modern era of theoretical hemodynamics can be considered to begin in the 1950s with the work of John R. Womersley (1907–1958) and Donald A. McDonald (1917–1973), who observed and analyzed the time-dependent motion of blood in an elastic artery driven by a fluctuating pressure gradient (63,119). “McDonald’s Blood Flow in Arteries” has since become a standard reference in the field (64,71). Its various editions contain detailed reviews of the history of hemodynamics. For further historical information, see also (24,66,102).
This review starts with a discussion of some basic concepts of hemodynamics, considering the relationship between pressures and flows in a network of blood vessels. Next, an introduction to the concepts of continuum mechanics is provided, including fluid and solid mechanics. Aspects of flow mechanics in blood vessels that are applicable to all types of vessels are then considered, including Poiseuille’s law for flow in a tube, the rheological properties of blood, and the overall structure of the systemic circulation as it relates to blood flow. Aspects of blood flow mechanics specific to arteries are considered next, including pulsatile flow, arterial compliance, propagation of the pulse wave, and effects of specific geometrical features of the arteries. Distinctive characteristics of blood flow in the veins are briefly considered. The microcirculation is discussed with emphasis on the consequences of the suspension characteristics of blood, including strong variations in the flow properties of blood and non-uniform distribution of hematocrit in microvessel networks. More detailed discussions of many of the topics mentioned here can be found in several books (7,12,28,64,66,71,73).
Basic concepts of hemodynamics
At a fundamental level, the study of hemodynamics is concerned with the distribution of pressures and flows in the circulatory system. In this context, “pressure” refers to hydrostatic pressure, which is an isotropic compressive stress (see below) and has units of force per unit area. However, pressure can equivalently be considered as internal mechanical energy per unit volume. By pressurizing blood, the pumping heart provides it with this internal energy that is available to drive its motion through the circulation. In a broad sense, the term “flow” refers to the motion of a fluid such as blood. More specifically, “flow velocity” refers to the fluid velocity at a specific point and has dimensions of distance per time, and “(volume) flow rate” refers to the amount of blood passing a given position along the length of a vessel and has units of volume per time. These quantities should be carefully distinguished.
In discussions of hemodynamics, an analogy with electric circuits is commonly introduced. In this analogy, the pressure at a point in the circulation corresponds to the voltage V (energy per unit charge) at a point in a circuit, and the volume flow rate corresponds to the current I (charge per unit time) in the circuit. For a resistive element in a circuit, the resistance R is given according to Ohm’s law by R = V/I where V is the voltage across the element. This leads to the concept of the viscous flow resistance of a blood vessel, defined as the ratio of pressure drop Δp to the volume flow rate Q:
| (1) |
This relationship is strictly valid only when flow does not vary with time. In a time-varying flow, the driving pressure includes a component related to the acceleration of blood. Under a broad range of conditions, the flow resistance of a blood vessel is approximately independent of the flow rate, and depends only on the geometrical properties of the vessel and on the viscosity of blood, as discussed below. In this approximation, the vascular system or a subset of it can be viewed as a network of resistances, fed and drained by known pressures (Figure 1A). The flow rates in each segment of the network can be calculated using basic principles, such as the laws for the combined resistance of resistors connected in series or in parallel, namely
| (2) |
where R1 and R2 are the two resistances and Rseries and Rparallel are the effective resistances of their series and parallel combinations. Many important phenomena in the circulatory system can be understood from the perspective of a network of resistors. For example, an increase in flow resistance of an individual segment, resulting from constriction or from partial blockage by a thrombus or lesion, causes a decrease in flow in all dependent segments of a tree-like vascular structure (Figure 1B). Conversely, a decrease in resistance on a particular flow pathway, resulting for instance from an arteriovenous shunt, causes the flow along other parallel pathways to decrease because flow is “stolen” from them (Figure 1C).
Figure 1.
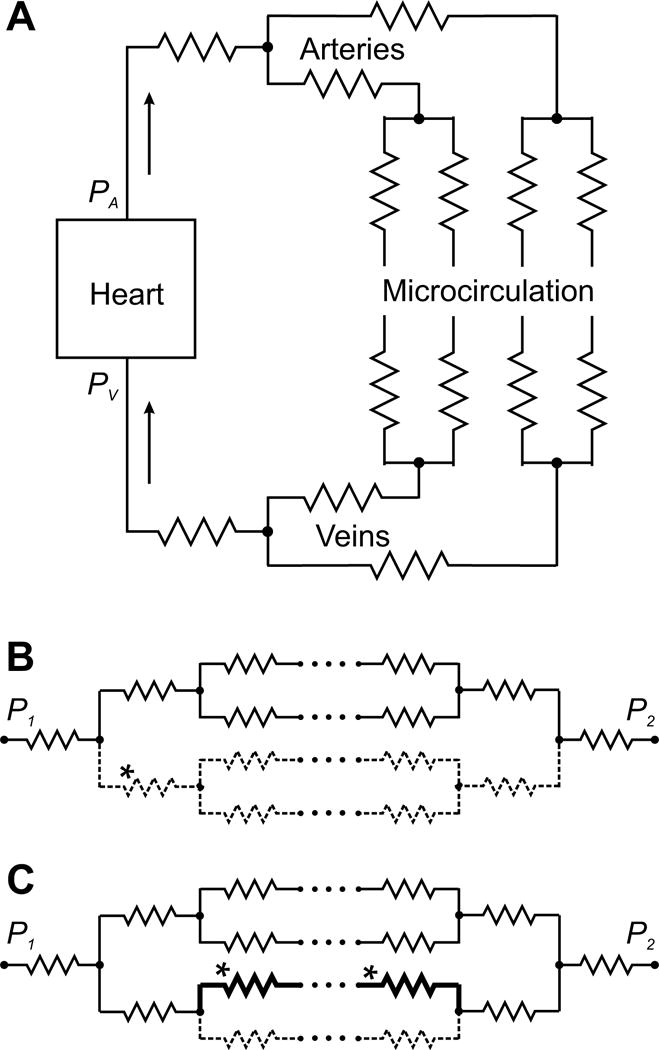
Schematic representation of the systemic circulation as a network of resistances. A. Basic elements of the systemic circulation. The pressure gradient between arterial pressure PA generated by the left heart and venous pressure PV drives blood through a network of blood vessels, consisting of the arteries, the microcirculation and the veins. Vascular segments are indicated by zigzag symbols, as in electrical circuits. The pulmonary circulation (not shown) has the same overall structure. B, C. Hemodynamic interactions within a network of resistances, with flow driven by a pressure difference P1 − P2. Arrays of dots signify additional levels of branching in the network. B. Increased flow resistance in one segment (*) (e.g. due to constriction or occlusion) causes a decrease in flow along all flow pathways containing that segment (dashed lines). C. Decreased flow resistance along one flow pathway (*) (e.g. due to formation of a shunt pathway) causes increased flow on that pathway (heavy black lines) but reduced flow on parallel pathways (dashed lines).
The concept of flow resistance can also be applied to the peripheral circulation as a whole, considered as a single resistance, giving
| (3) |
where TPR is total peripheral resistance, MAP is mean arterial pressure, CVP is central venous pressure and CO is cardiac output. The MAP is often defined as 2/3 of diastolic blood pressure plus 1/3 of systolic pressure, which gives an approximation to the time average of arterial pressure. The total peripheral resistance at any moment depends on the geometric properties of the vascular system, including effects of vascular tone on vessel diameter, and on the flow properties of blood. It determines the pressure that the left heart must generate in order to provide a given level of cardiac output.
An analogous formula can be used to define the resistance of the pulmonary circulation:
| (4) |
where PVR is pulmonary vascular resistance, MPAP is mean pulmonary arterial pressure, defined in the same way as MAP, and PWP is pulmonary wedge pressure. The PWP is measured by wedging a pulmonary catheter with an inflated balloon in a small pulmonary arterial branch, and measuring the pressure downstream of the occlusion. It provides an estimate of pulmonary venous pressure. The pressure drop across the lungs (typically about 10 mmHg) is much lower than the drop across the systemic circulation (typically about 100 mmHg). This implies that PVR is typically about one tenth of systemic TPR (115), although wide variations can occur.
The adequate distribution of blood flow to all parts of the body, so as to meet the changing needs of the tissues for oxygen and other nutrients and for removal of waste products, represents the most essential function of the circulatory system. Considering the circulation as a network of interconnected resistors is simplistic for many reasons, some of which are addressed in the following sections. Nonetheless, it provides an essential basis for understanding how the distribution of blood flow can be controlled by the active contraction or dilation of blood vessels, and how it can be disturbed by disease processes leading to vessel blockage.
Basic concepts of continuum mechanics
The behavior of any mechanical system can in principle be described by applying Newton’s second law, F = ma, to all the particles in the system, where F is the force acting on a particle, m is its mass and a is its acceleration. In practice, this approach is not feasible for a system such as an artery containing flowing blood because the number of molecules in the system is too large. Instead, a continuum approach is generally adopted, in which the physical properties of a material component of the system, such as its velocity, density or temperature, are represented as continuous functions of position. The value of a given variable at a point then represents a local average of the variable over a small region. Fluctuations on smaller scales, arising for example from thermal motion of molecules, are not explicitly represented.
An immediate consequence of this approach is that Newton’s second law cannot be directly applied, because individual particles and the forces acting on them are not identified. Instead, the forces acting in a continuum are described using the concept of stress, as defined below. The stress generally depends on the deformation and/or the rate of deformation of the material. This dependence is expressed in mathematical form using constitutive equations, which depend on the type of material under consideration. Newton’s second law is applied in a continuum by considering the forces acting on a small region of the material, which must equal the product of the mass of the region and its acceleration. The size of the region is then considered to approach zero. In this limit, a system of partial differential equations is derived, relating the stress to the motion at each point in the material. These equations can be combined with the constitutive equations of the material to yield the governing equations of the continuum, which again take the form of partial differential equations.
The discussion of the key concepts of continuum mechanics, as introduced above, is expanded in the following paragraphs. The study of continuum mechanics is necessarily mathematical, requiring the use of vector calculus and partial differential equations to describe the spatial distributions of material motion and deformation. In this review, only a few key elements of the mathematical treatment are introduced. Emphasis is placed on providing physical insights into the phenomena involved, so that mathematical expertise is not essential for gaining an appreciation of the subject. For treatments of continuum mechanics in more mathematical detail, with an emphasis on applications in biomechanics, see (27,40).
Definition of stress
The mechanical forces in a continuum are represented using the concept of stress, which can be defined as follows. In the first step, consider a small surface ΔS within or on the boundary of the material (Figure 2A). The local stress vector or traction T is defined as the force per unit area acting on the surface. More precisely, its value at a point is defined as the limiting value of the force per unit area, as the area ΔS of the surface being considered shrinks to zero around that point. Given a system (x1, x2, x3) of Cartesian coordinates in three dimensions, T can be represented in terms of its components (T1, T2, T3) or briefly as Ti where i is understood to take the values 1, 2 or 3. Generally, T depends on the orientation of the surface being considered. In the second step, the dependence of T at a given point on the orientation of the chosen surface is described by introducing the (Cauchy) stress tensor σ. A tensor is a generalized form of a vector that allows the representation of additional levels of directional information. This particular tensor is of second rank, i.e. it can be described in terms of its components σij, where the two subscripts i and j each take the values 1, 2 or 3, giving a total of nine components. Each component represents the traction force in the ith coordinate direction acting on a surface whose normal vector is in the jth coordinate direction (Figure 2B). Then the traction vector T acting on an arbitrarily oriented surface is given by
| (5) |
where nj are the components of n, the unit vector normal to the surface.
Figure 2.
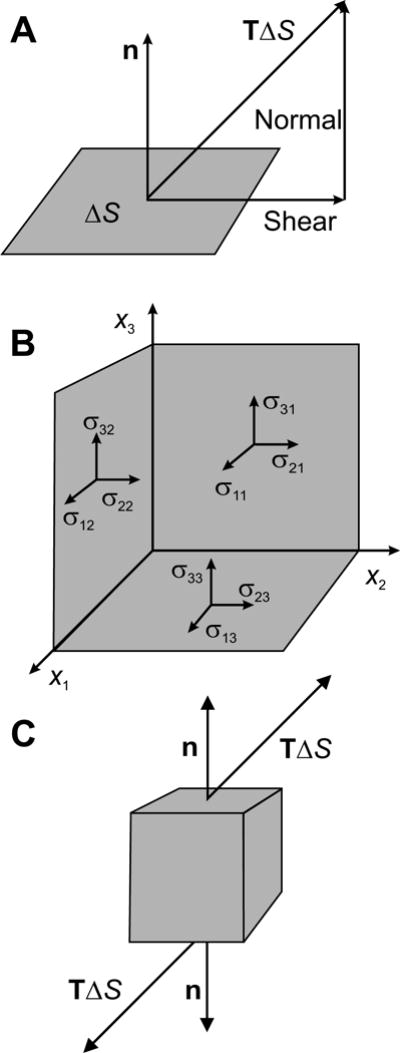
Illustration of concepts underlying the definition of the stress tensor in a material. A. The stress vector or traction T is defined as the force per unit area acting on a small surface ΔS in the material. In general, this vector has components parallel to the surface (shear force) and normal to the surface (normal force). B. The traction acting on an arbitrarily oriented surface can be fully described in terms of the stress tensor σ. Each component σij of the stress tensor represents the i component of the traction acting on a surface oriented perpendicular to the coordinate axis xj. C. The net force on a small cuboid of material resulting from a stress in the material is zero if the stress is uniform, because the traction vectors acting on opposite faces of the cuboid are equal and opposite. However, if the stress distribution is not uniform, the traction vectors do not cancel and a net force is generated.
According to this definition, the stress component σ11 represents a force per unit area in the x1 direction acting on a surface whose normal is oriented in the x1 direction (Figure 2B). Such a stress component is referred to as a normal stress, because it acts normal (perpendicular) to the surface. Likewise, the stress component σ 12 represents a force per unit area in the x1 direction acting on a surface whose normal is oriented in the x2 direction. Such a stress component acts parallel to the surface and is referred to as a shear stress. An important special case is isotropic stress, where the diagonal components σ 11, σ 22 and σ 33 are all equal, and the off-diagonal components are all zero. In a fluid subject only to hydrostatic pressure, the stress is isotropic and σ 11 = σ 22 = σ 33 = −p, where p is the pressure.
Although the definition of the stress tensor does not depend on the specific coordinate system chosen, the components of the tensor do vary according to the choice of coordinates, except in the case of isotropic stress. A normal stress component in one coordinate system may appear as a shear stress component in a different (rotated) coordinate system. Caution is needed in interpreting the physical significance of normal and shear stresses. Besides the Cauchy stress, other measures of stress are commonly used, particular in the study of large deformation elasticity, such as the Piola-Kirchhoff stresses. These are not discussed here. In summary, the stress tensor represents the forces per unit area acting on a small surface at a point in a continuum. Commonly used units of stress include dyn/cm2, N/m2 (i.e. Pa, Pascal), mmHg and cmH2O.
In order to derive the equations of motion for a continuum, Newton’s second law is applied to a small region of the material. This requires consideration of the net force acting on a piece of material, resulting from the stress in the material. In particular, consider a small cuboidal region aligned with the coordinate axes (Figure 2C). Suppose first that the stress tensor is uniform in space, i.e., independent of position. In that case, the forces acting on any two opposite faces of the cuboid are equal and opposite according to Eq. (5), because the stress is the same and the normal vectors (by convention outwards from the region) are opposite on the two faces. All the forces resulting from the stress balance each other and the resultant force is zero. Now consider the case where the stress varies with position in the material. In that case, resultant forces are generated when the stresses on two opposite faces of the cuboid are different. In the limit that the volume of the cuboid goes to zero, it can be shown that the resultant force per unit volume resulting from the stress depends on the gradient of the stress tensor, and its components are:
| (6) |
where ∂σij/∂xj represents the partial derivative of σij with respect to xj. The equation of motion, in the form of Newton’s second law applied per unit volume of the material, therefore gives
| (7) |
at each point, where ρ is the density of the material, a = (a1, a2, a3) is the local acceleration, and F = (F1, F2, F3) is an external “body” force, typically due to gravity, that acts on each part of the material. To complete the equations of motion for the continuum, it is necessary to specify its constitutive equations, which define the dependence of stress on deformation and differ according to the type of material (fluid, solid or viscoelastic).
Constitutive equation for a fluid
In continuum mechanics, a fluid is defined as a material that can be at equilibrium without stress in many different configurations, i.e. it has no preferred shape. A fluid at rest experiences only isotropic stress. Non-isotropic stress causes continuous deformation. Both liquids and gases are fluids according to this definition. The non-isotropic component of stress in a fluid depends on the rate of deformation of the fluid, which is related to the gradient of the fluid velocity. This may be illustrated by considering the flow of a fluid contained between two parallel plates spaced a distance h apart at x2 = 0 and x2 = h, one at rest and one moving parallel to itself in the x1-direction with a constant velocity V (Figure 3). The fluid then moves purely in the x1-direction, with a velocity v(x2) such that dv/dx2 is independent of x2. (Other behaviors are possible under some conditions, but are not considered here for simplicity.) The assumptions of continuum theory imply that a fluid must satisfy the no-slip condition, which states that the velocity of the fluid immediately adjacent to a solid surface moves with the velocity of the surface. It then follows that v(x2) = Vx2/h and the velocity gradient is
| (8) |
The symbol is commonly used to denote the velocity gradient, which has units of inverse time and is also referred to as shear rate. This case is known as simple shear flow. The continuous deformation of the fluid resulting from the velocity gradient is resisted by a shear stress σ12 = τ generated in the fluid, due to the energy that is dissipated as fluid molecules slide past each other. The resistance of the fluid to deformation can be characterized in terms of the viscosity μ, defined as the ratio of the shear stress to velocity gradient
| (9) |
Figure 3.
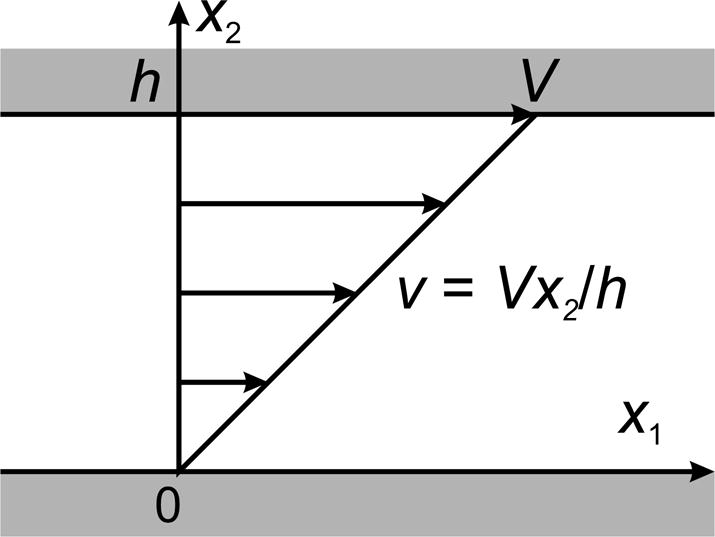
Definition of simple shear flow of a fluid.
The viscosity has units of stress × time, and is measured in units of Pa·s or dyn·s/cm2, also known as P (Poise). For many fluids, including air and water, the viscosity is an intrinsic property of the fluid at a given temperature and pressure. In such cases, the shear stress is proportional to the shear rate. Such materials are called Newtonian fluids. The viscosity of water is about 0.001 Pa·s (1 cP) at 20 C and about 0.0007 Pa·s (0.7 cP) at 37 C. However, biological fluids do not necessarily behave as Newtonian fluids. In particular, blood shows non-Newtonian effects at low shear rates, and the viscosity as defined in Eq. (9) is a function of shear rate . Furthermore, as a concentrated suspension of cells, blood does not behave as a continuum in narrow tubes such as capillaries. The non-Newtonian and non-continuum flow properties of blood are discussed in detail below.
Liquids, including water and blood, have very large resistance to volume changes in response to changes in hydrostatic pressure and can be regarded as incompressible from a hemodynamic perspective. If v(x,t) = (v1, v2, v3) describes the velocity as a vector function of position x = (x1, x2, x3) and time t, then the condition of incompressibility requires that
| (10) |
The hydrostatic pressure p in an incompressible fluid is determined by the overall characteristics of the fluid flow field and not solely by the local conditions at a given point in the fluid. This is in contrast to the situation in a compressible fluid, where the pressure at any point can be defined as a function of the local fluid density. In a Newtonian fluid, the non-isotropic components of stress are proportional to the local velocity gradients. The components of the stress tensor in an incompressible Newtonian fluid are given by the following constitutive equation:
| (11) |
where δij denotes the Kronecker delta, defined to be 1 when i = j and 0 when i ≠ j.
Governing equations for fluid motions
When Eq. (11) is combined with the equation of motion, Eq. (6), it yields the governing equation:
| (12) |
Equations (10) and (12) are referred to as the incompressible Navier-Stokes equations. Their full derivation is found in textbooks on fluid mechanics (4). Generally they must be solved for the unknown variables p and v to predict the fluid motion in a given situation. In the presence of solid boundaries, the no-slip condition applies, i.e. the fluid velocity adjacent to a solid surface must match the velocity of the surface.
A wide range of fluid behaviors is possible under the assumptions of the Navier-Stokes equations, depending on the size and shape of the flow domain and on the parameter values and boundary conditions that apply. The complexity of the behaviors that can occur is increased by the fact that the equations are nonlinear in the velocity, as a result of the terms vj ∂vi/∂xj that describe the acceleration experienced by a fluid as it moves through a non-uniform flow field. This nonlinearity also complicates the solution of these equations by mathematical or computational methods. Under some circumstances, one or more of the terms in Eq. (12) can be neglected, leading to a simplified set of equations. For example, the inertial terms on the left hand side of Eq. (12) may be negligible in very slow or highly viscous flows, whereas if velocities are high and effects of viscosity are small the viscous terms μ ∂2vi/∂xj2 may be neglected in some situations. Insight into the relative importance of the physical effects in the Navier-Stokes equations and the types of flow phenomena that may occur can be obtained by considering the Reynolds number, as discussed next.
Reynolds number and turbulence
In analyzing a physical phenomenon, a common strategy is to construct a dimensionless parameter that indicates the relative importance of various effects that contribute to the phenomenon. In fluid mechanics, the most important such dimensionless parameter is the Reynolds number, which is derived by considering the relative orders of magnitude of the inertial and viscous terms. Suppose that the fluid flow is characterized by a typical velocity V and a typical length L. The magnitude of the inertial and viscous terms may then be estimated as
| (13) |
where ‘~’ means ‘is of the same order of magnitude as’. Here, we are assuming steady flow, for which ∂vi/∂t = 0. The Reynolds number is defined as the ratio of the inertial term to the viscous term, i.e.
| (14) |
When Re is much less than 1, the inertial terms on the left hand side of Eq. (12) are generally negligible. This case is known as Stokes flow. When Re is much larger than 1, inertial effects are dominant, but viscous effects may still strongly influence the flow. In this case, the no-slip condition at solid boundaries has the effect of creating very steep gradients in velocity in narrow regions close to the boundaries. Viscous effects remain important in such regions, which are known as boundary layers. The formation of boundary layers in blood vessels is discussed below, in the section on “Entrance effects.”
The Reynolds number is frequently considered in examining the occurrence of turbulence in a flow system. Fluid flows can generally be classified as laminar or turbulent. In laminar flow, the fluid motion is smooth and orderly. If a laminar flow is unsteady (time-varying), the variation with time is consistent and repeatable under a given set of conditions. In contrast, turbulent flow involves unpredictable fluctuations of velocity. Turbulent flows are fundamentally unstable, such that small random disturbances in the velocity field grow and create a disordered and randomly fluctuating flow distribution. Viscosity (viscous damping) tends to inhibit the growth of such disturbances. At low Reynolds number, this damping effect is large and turbulence cannot develop. With increasing Re, the effect of viscosity diminishes, and turbulence can occur if Re is high enough. The conditions leading to the occurrence of turbulence in cylindrical tubes and in blood vessels are discussed in a later section.
Constitutive equation for a solid
From a continuum mechanics perspective, a solid can be defined as a material that has a unique configuration in the absence of applied stress. In contrast to a fluid, a solid may undergo a deformation when a shear stress is applied, but it does not continuously deform under such a stress. In order to define the constitutive equation of a solid, it is necessary to introduce the concept of strain, a measure of the deformation of a continuum. Suppose that an object is initially in a reference configuration. Often this is a configuration in which the stress is zero. The points in the object are labeled using Cartesian coordinates (X1, X2, X3). The object’s deformed configuration is described by Cartesian coordinates (x1, x2, x3), i.e., the point initially at (X1, X2, X3) moves to (x1, x2, x3), as indicated in Figure 4. Its displacement is given by
| (15) |
Figure 4.
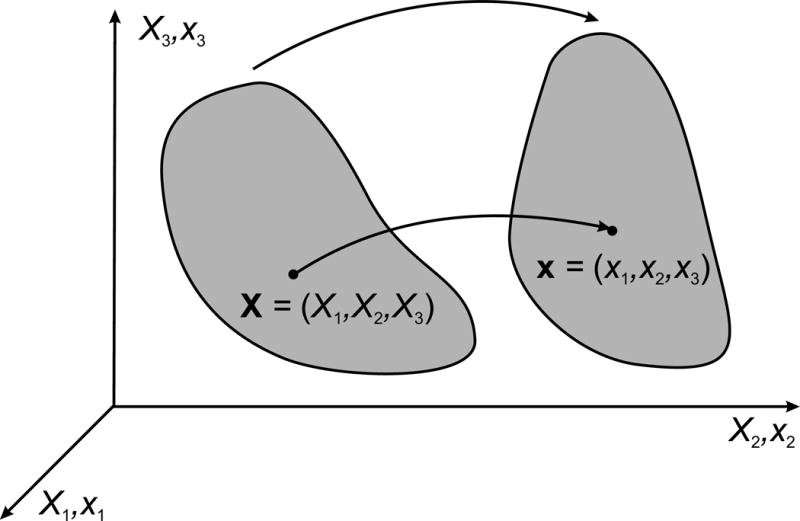
Coordinate systems used to describe the deformation of a body in continuum mechanics.
If the displacement is the same for every point in the object, then it has undergone a translation without any deformation. It follows that the deformation of the object is related to the spatial derivatives of the displacement. Here, for simplicity, we consider the case where the displacements are small, and define Cauchy’s elongation strain tensor (27):
| (16) |
This tensor is dimensionless, resulting from taking the derivative of distance with respect to position. Each element of the tensor describes a specific type of deformation. For example, ε11 refers a stretch in the x1 direction, while ε12 refers to a shear deformation, in which displacement in the x1 direction varies with x2 (or vice versa). The condition for applicability of this tensor is that the strain is small, in the sense that the elements of εij are all much less than 1. If the strain is large, then Cauchy’s elongation strain tensor does not provide a mathematically precise description of the deformation, and other strain tensors must be used, such as Green’s or Almansi’s strain tensor (27).
In an elastic solid, the stress depends only on the deformation of the material at a given moment, and not on the time course of the deformation. The constitutive equation for an elastic solid must therefore specify stress as a function of strain. If the strains are small, then it is often sufficient to represent the material as a Hookean elastic solid, for which the components of stress depend linearly on the components of strain. The simplest such relationship applies to an isotropic material, meaning that its material properties are identical regardless of the orientation of the material. In that case, the stress is given by (27)
| (17) |
where λ is the bulk modulus, G is the shear modulus and δij is the Kronecker delta as defined above. This relationship is often used in inverted form
| (18) |
where ν = ½λ/(λ + G) is the Poisson ratio and E = G(3λ + 2G)/(λ + G) = 2G(1 + ν) is the Young’s modulus. Physical insight into the significance of ν and E can be obtained by considering uniaxial stress, in which a stress σ11 is applied but all the other components of stress are zero, and Eq. (18) reduces to
| (19) |
The strain (elongation) of the material in the direction of tension is proportional to the applied stress divided by the Young’s modulus, while the strain (shortening) in the two perpendicular directions equals the elongation multiplied by the Poisson ratio.
Many biological materials are effectively incompressible under short-term deformations, although they may show changes in volume under long-term stresses as a result of displacement of tissue fluid relative to the cellular structure. In the special case of an incompressible isotropic solid, for which the bulk modulus λ is infinite,
| (20) |
the Poisson ratio is 1/2, and Eq. (17) is replaced by
| (21) |
Here σ0 is an isotropic stress field that is determined by the overall characteristics of the deformation field and not solely by the local conditions at a given point in the solid, analogous to the hydrostatic pressure for an incompressible fluid.
The Young’s modulus is the parameter most frequently used in describing the elastic properties of blood vessel walls. However, it should be noted that blood vessel walls are in reality strongly anisotropic in structure, with highly nonlinear elastic properties when subjected to the stresses produced by blood pressure. Therefore, the Hookean elastic solid model may not be adequate for describing important aspects of hemodynamics. A more general type of constitutive equation for biological solids derives from the concept of a strain-energy function, a scalar quantity that describes the amount of energy per unit volume stored in the material, as a function of the components of (Green’s) strain (27). The stresses are then given by the partial derivatives of the strain-energy function with respect to the components of strain. The nonlinear and anisotropic characteristics of artery walls and other biological tissues can be explicitly represented using this approach, which is well suited for computational simulations using the finite-element method.
The deformation of biological materials such as artery walls generally involves viscous energy dissipation as well as storage of elastic energy, so that they are viscoelastic solids. This behavior may be represented approximately by a Kelvin-Voigt model (also called a Voigt model), in which the stress in the material is the sum of an elastic component dependent on the strain and a viscous component dependent on the rate of strain (66,71). Such a model leads to a single characteristic relaxation time, i.e. the time constant for the approach of the stress to its final value following an abrupt and sustained deformation. Observations of the transient responses of artery walls to deformation on a range of time scales show presence of more than one relaxation time, and provide a basis for application of more elaborate viscoelastic models (27).
The constitutive equations for a solid can be combined with the equations of motion to yield a set of equations governing its deformation. Solution of these equations yields relationships between the load applied to a mechanical system and the resulting deformation. For example, this approach can be used predict the deformation of a blood vessel subjected to a time-varying transmural pressure, as it experiences during each cardiac cycle, and the dependence of the deformation on the material properties of the artery wall, as discussed in more detail below.
Fluid mechanics of flow in blood vessels
Many significant aspects of hemodynamics can be understood by analyzing the associated fluid mechanical phenomena. For example, an analysis of fluid flow in tubes provides insight into the factors determining the flow resistance of a blood vessel. Similarly, fluid mechanical factors determine the distribution of fluid shear stress acting on the endothelial lining of blood vessels, which has important biological effects. The logical starting point for this discussion is the analysis of fluid flow through a uniform cylindrical tube, for which the relationship between driving pressure and flow rate is described by the equation generally known as Poiseuille’s law. A derivation of this equation is presented. This provides a basis for considering a range of fluid dynamical phenomena occurring in the circulatory system.
Steady laminar flow in a uniform tube
In the mid-nineteenth century, J.L.M. Poiseuille (74) sought to understand the physical factors governing blood flow. He performed experiments to determine the relationship between the flow rate Q in a tube of diameter D and length L and the driving pressure Δp. His experimental observations revealed a fourth-power relationship between flow and diameter, Q = KΔpD4/L, where the factor K depended on the type and temperature of the fluid. Subsequent theoretical analysis (34) led to the relationship:
| (22) |
where μ is the fluid viscosity. The history of this relationship, now commonly known as Poiseuille’s law, is discussed by Sutera and Skalak (106).
The derivation of Poiseuille’s law depends on a number of assumptions, namely that the tube is a uniform rigid circular cylinder; the fluid is Newtonian; the flow is steady, i.e., constant in time; the flow is laminar, i.e., not turbulent; and the flow is not subject to entrance effects, i.e., non-uniformities associated with the entrance of fluid into the tube. Although these conditions are violated to some extent in the circulatory system, Poiseuille’s law remains a central result in the area of hemodynamics. A standard mathematical derivation of Poiseuille’s law involves solving Eq. (12) in cylindrical coordinates. Here, an alternative derivation is presented that provides more physical insight into the stresses generated when fluid flows in a tube.
A tube of radius a = D/2 and length L is assumed to be filled with a fluid of fixed viscosity μ. The forces acting on a control volume are considered, where the control volume consists of a cylindrical region of fluid, concentric with the tube, with radius r < a (Figure 5A). Effects of gravity are neglected. The hydrostatic pressures p1 and p2 acting on the ends of the region generate a net force πr2p2 − πr2p1 acting to the right. Although hydrostatic pressure also acts on the curved surface of the cylinder, the resultant forces cancel out and do not produce a net force. As a result of velocity gradients, a uniform shear stress τ acts on the curved surface, here defined as positive to the left. The resultant force is −2πrLτ to the right. Under the assumption of steady flow, the acceleration is zero and so the forces must sum to zero, giving
| (23) |
where Δp = p2 − p1. This result shows that the shear stress in tube flow varies linearly with radial position, from zero at the center-line to a maximum of
| (24) |
at the wall of the tube, where τw is the wall shear stress. The effects of gravity g can be represented by replacing the pressure p with p′ = p + ρgz in this derivation, where ρ is the fluid density and z is the vertical coordinate.
Figure 5.
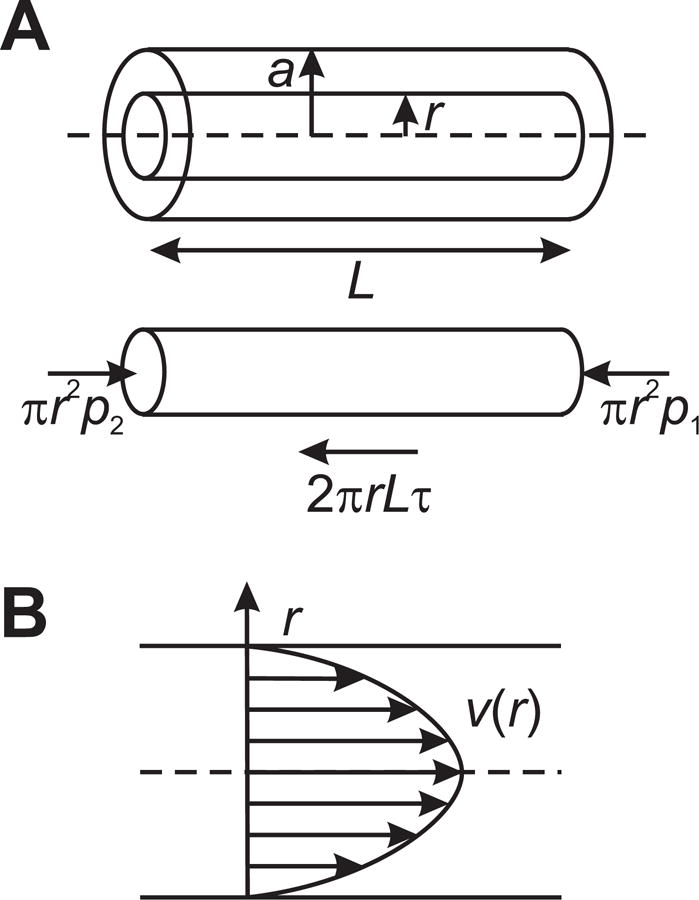
A. Definition of geometry and forces, used in derivation of Poiseuille’s law. B. Parabolic velocity profile in Poiseuille flow.
If the fluid is Newtonian, then according to Eq. (6) the shear stress is given by
| (25) |
where v(r) is the fluid velocity. The minus sign is needed because τ is defined in the negative direction (Figure 5A). Combining Eqs. (23) and (25) gives
| (26) |
According to the no-slip condition, v(a) = 0 and Eq. (26) can be integrated to give
| (27) |
Velocity fields are conventionally represented graphically by plotting velocity as a function of position, giving a velocity profile, which in this case is a parabola with its vertex on the center-line (Figure 5B). The peak velocity occurs on the center-line and is given by
| (28) |
Integrating the velocity across the circular cross-section of the tube gives the volume flow rate Q in the tube:
| (29) |
which is equivalent to Eq. (22) with D = 2a. The mean velocity of flow in the tube is
| (30) |
and equals half of the center-line velocity given by Eq. (28).
Then flow resistance R as defined in Eq. (1) above can be expressed as
| (31) |
This relationship shows that the resistance to blood flow is sensitively dependent on the diameter D, being proportional to 1/D4. An important consequence is that blood flow can be modulated over a wide range by relatively small changes in the diameters of the blood vessels. For example, a 16% decrease in diameter gives a doubling of flow resistance. This also implies that precise control of vessel diameters is needed in order to achieve a given distribution of blood flow rates in a network of vessels. Lack of such control can lead to maldistribution of blood flow. Therefore, the behavior described by Poiseuille’s law is of central importance in understanding how blood flow is controlled and distributed in the circulatory system.
The analysis given here assumes that blood is a Newtonian fluid, with fixed viscosity μ. As discussed in the next section, blood has significant non-Newtonian properties. It should be noted that the result in Eq. (23) regarding the distribution of shear stress in the fluid does not depend on the assumption that the fluid is Newtonian. For non-Newtonian fluids, a similar method of analysis can be used to compute the dependence of flow rate on pressure gradient, with replacing the constant μ in Eq. (25).
Bulk viscosity of blood
Blood is a suspension containing about 45% by volume of cellular components. The suspending medium, plasma, is a solution of proteins and electrolytes and has nearly Newtonian viscous properties. The cellular components include red blood cells (erythrocytes), several types of white blood cells (leukocytes), and platelets. Although the white blood cells and platelets perform vital biological functions, their volume fraction is normally very small and they do not contribute appreciably to the bulk viscosity of blood. The red blood cells have a large effect on blood viscosity, which is dependent on the volume fraction of red blood cells (i.e. hematocrit). The non-Newtonian properties of blood result almost entirely from the biophysical behavior of red blood cells in suspension.
In mammals, mature red blood cells lack a nucleus. Their interiors consist of a concentrated solution of the oxygen-carrying protein hemoglobin. From a hemodynamic perspective, they may be viewed as fluid-filled capsules. The cell membrane is very flexible, and the cells are highly deformable as a result. Red blood cells in flowing blood do not generally retain the characteristic biconcave disk shape that they have under static conditions. In humans and some other mammals, red blood cells under no-flow or low-flow conditions can adhere to each other. This process of aggregation leads to the formation of stacks of cells known as rouleaux. Both deformability and aggregation contribute to the non-Newtonian properties of blood.
The bulk viscosity of a suspension is the viscosity observed when the suspension flows in a region whose dimensions are much larger than the suspended particles. In this case, the suspension can be regarded as a continuum. The standard procedure to determine viscosity as a function of shear rate is to place the fluid in a steady shear flow, as in Figure 3, measure the shear stress and the shear rate, and obtain viscosity as their quotient. For practical reasons, rotational viscometers are generally used, with a shear flow created in the space between two surfaces, one of which is rotating and the other is stationary. The two main types of rotational viscometer are based on coaxial-cylinder (Couette) and cone-and-plate geometries (40).
The dependence of the bulk viscosity of human blood on shear rate and hematocrit was examined by Chien et al. (14) using a coaxial-cylinder viscometer. The dependence of the logarithm of viscosity on hematocrit was fitted using a fifth-order polynomial function for each shear rate tested, ranging from 0.052 to 52 s−1. Figure 6 shows the resulting functions for human blood, plotted from the polynomial coefficients as tabulated (14). Viscosity shows a strong dependence on hematocrit at all levels of shear rate. At the higher levels of shear rate examined (5.2 and 52 s−1), the dependence is almost exponential for hematocrits from zero to 80%, as indicated by the almost linear variation with hematocrit in this semi-log plot. These results also show a large increase in the viscosity of blood at very low shear rates (0.52 and 0.052 s−1).
Figure 6.
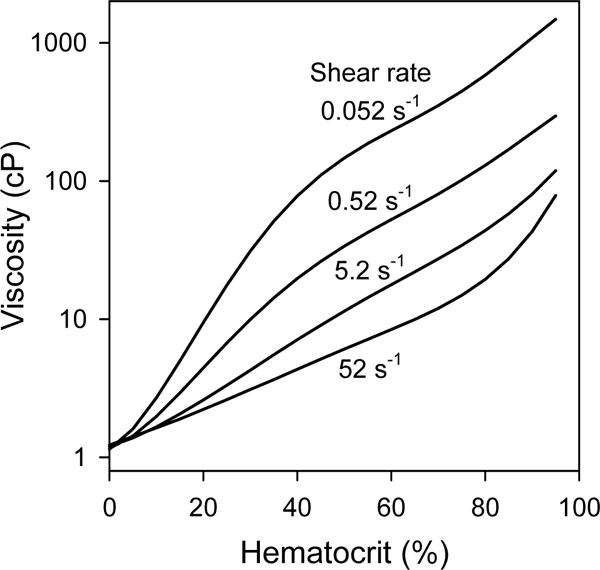
Dependence of the bulk viscosity of human blood on hematocrit, for indicated shear rates. Curves are derived from polynomial expressions given by Chien et al. (14), based on measurements using a coaxial-cylinder viscometer.
The factors underlying the dependence of blood viscosity on shear rate were explored by Chien (13). Viscosity measurements were made for shear rates from 0.01 to 1000 s−1, using suspensions of normal red blood cells in heparinized plasma, normal red blood cells in 11% albumin-Ringer solution, and chemically hardened red blood cells in 11% albumin-Ringer solution. All suspensions were adjusted to a hematocrit of 45%. The results were given in terms of relative viscosity, i.e., measured viscosity divided by suspending medium viscosity, as shown in Figure 7.
Figure 7.
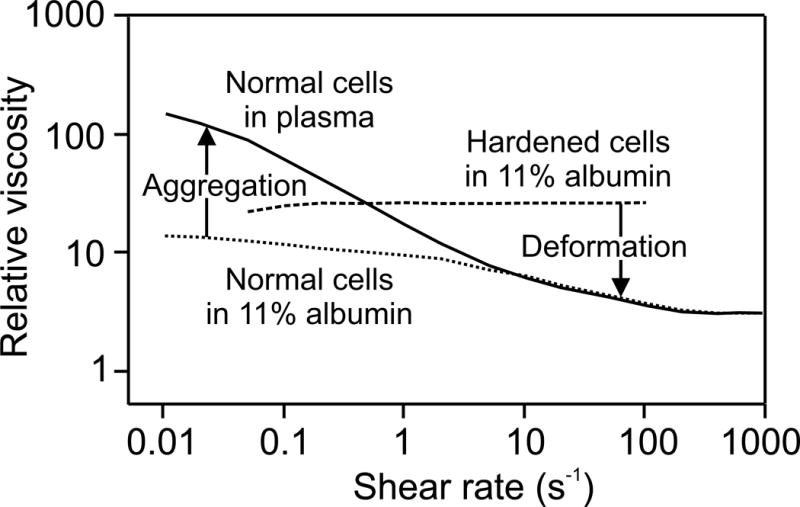
Dependence of the relative bulk viscosity on shear rate for three different types of red blood cell suspensions as described in the text. Vertical arrows indicate effect of aggregation to increase viscosity relative to non-aggregating cells at very low shear rates, and effect of deformation to decrease viscosity relative to rigid cells, an effect that increases with shear rate.
For normal cells in plasma, a strong increase of viscosity with decreasing shear rate was observed, a phenomenon known as shear-thinning, as also shown in Figure 6. The albumin-Ringer solution had the same viscosity as plasma, but did not cause red blood cell aggregation. The increase in viscosity at low shear rates was much less in this suspending medium. This result indicates that aggregation is the main cause of the increase in normal blood viscosity at very low shear rates. For the cells that were hardened (using 0.5% glutaraldehyde solution) the viscosity was almost independent of shear rate and higher than the viscosity of normal red blood cells in the same medium. This result shows that the deformability of red blood cells is mainly responsible for the reduction in blood viscosity at higher shear rates.
These findings can be understood as follows. In general, the increase of viscosity of a suspension, relative to the viscosity of the suspending medium, reflects the extent to which the suspended particles interfere with the shear flow, i.e. impede the ability of fluid at different points across the flow to move at different velocities. The aggregation of red blood cells at low shear rates leads to the formation of rouleaux and networks of rouleaux. Being larger than individual red blood cells, these aggregates extend further across the shear flow and create more interference with the flow. However, aggregates can be broken up by relatively low levels of shear stress. Therefore, the effect of aggregation decreases strongly with increasing shear rate, and is negligible for shear rates larger than 10 s−1 in normal blood (Figure 7). The deformation of red blood cells in flow also depends on the shear rate. At very low shear rates, fluid shear stresses are very low and the cell is only slightly deformed. The viscosity at very low shear rates for non-aggregating cells approaches that of hardened cells, which are almost undeformable for the range of shear rates considered. With increasing shear rates, individual cells are more readily deformed by flow forces. Due to their fluid interiors and highly flexible membranes, they behave analogously to fluid drops, aligning with the flow and continuously deforming so that their impact on the suspension viscosity is reduced (23). As a consequence, the apparent viscosity of blood continues to decrease with increasing shear rate above 10 s−1. Thus, both aggregation and deformation of red blood cells contribute to the reduction of blood viscosity with increasing shear rate, as shown in Figure 7.
In arteries and veins with normal blood flow rates, typical shear rates (in s−1) are in the range of hundreds or thousands. As Figure 7 indicates, normal human blood viscosity approaches an almost constant value for shear rates above about 100 s−1. Therefore, it is appropriate to treat blood as a Newtonian fluid for many situations of interest, such as the analysis of blood flow in arteries. However, if the flow rate in a vessel drops to a very low level, or if very low shear rates are present in local regions of the flow, then non-Newtonian effects may be significant.
The above discussion applies to the flow of blood in vessels with diameters much larger than the size of red blood cells, where blood can be considered to behave as a continuum. As vessel size decreases, non-continuum effects become increasingly important. For example, the flow resistance of vessels with diameters below about 300 μm deviates significantly from that predicted by Eq. (31) as a consequence of such effects. This and related phenomena occurring in the microcirculation are discussed below.
Distribution of flow parameters in the circulatory system
The circulatory system consists of an immense number of blood vessels, connected together in a branched network. Data on the number and geometry of the vessels of the canine systemic circulation (60) are represented graphically in Figure 8, according to class of vessel from the aorta to the vena cava. Several notable features are evident. Vessel lengths and vessel diameters both decrease by about three orders of magnitude from the aorta to the capillaries. Despite the decrease in the cross-sectional area of individual vessels by a factor of 106, the presence of about 109 capillaries has the consequence that the total cross-sectional area of the capillaries is about 1000 times larger than that of the aorta. Since the same cardiac output that flows through the aorta must also flow through the capillaries, the velocity is about 1000 times slower in the capillaries. Figure 8 includes velocity data based on an estimated cardiac output for a dog of 2 l/min, ranging from about 40 cm/s in the aorta to less than 1 mm/s in the capillaries.
Figure 8.
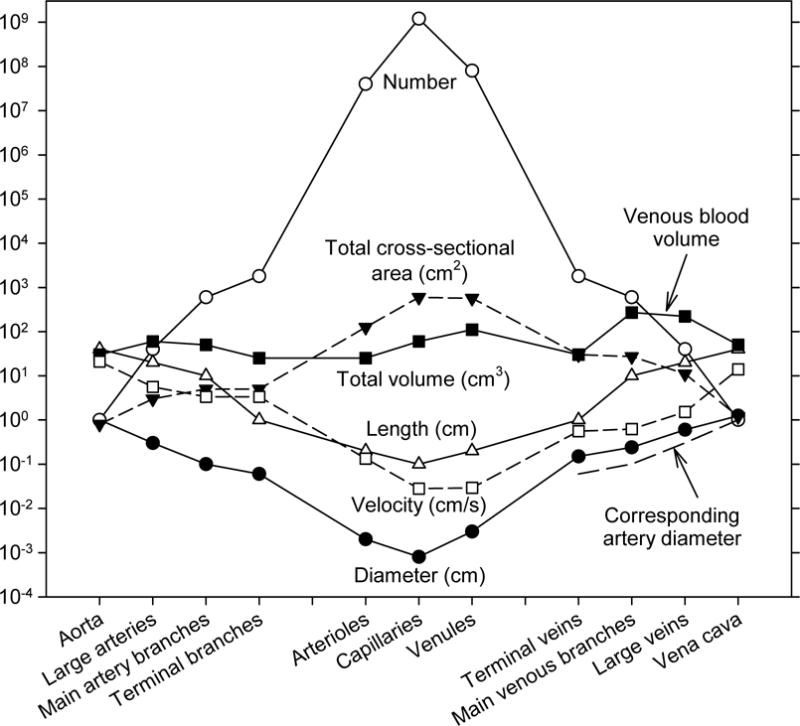
Dimensions and numbers of vessels of various classification in the canine vasculature, based on observations of the mesenteric vascular bed by Mall (7,60). Also included is an estimate of flow velocity in each type of segment, assuming a cardiac output of 2 l/min. Dashed lines at lower right hand side of figure indicate diameters of arteries corresponding to the veins of each classification, to show the difference in diameters between arteries and veins.
Although the data in Figure 8 may appear almost symmetric between the arterial and venous systems, some significant asymmetries exist. In particular, the venous vessels are larger than corresponding arterial vessels, with typically about twice the diameter (see Figure 8). The blood volume in the circulation, and therefore the transit time of blood, is therefore strongly weighted towards the venous side of the vasculature. The flow rates and lengths of corresponding arterial and venous vessels are necessarily virtually equivalent, because they must carry the same flows over the same distances. Therefore, according to Poiseuille’s law (see Eq. (31)), the flow resistance is much larger in the arterial side of circulation than in the venous side, and thus the pressure drop is concentrated on the arterial side, specifically in the small arteries and arterioles. Experimental data on the pressure distribution through the vasculature as a function of vessel diameter are shown in Figure 9, illustrating this arterio-venous asymmetry. If the system were symmetric, the capillary pressure would be the mean of arterial and venous pressures, i.e. about 50 mmHg. A notable consequence of the asymmetry is that capillary pressure is much lower, about 30 mmHg. Since the capillaries have very thin walls with a significant permeability to fluid, the low capillary pressure is important for the maintenance of tissue fluid balance. Also, the fact that most of the flow resistance resides in the small arteries and arterioles is significant with regard to the regulation of blood flow, because it implies that active control of the diameters of these vessels has the potential to modulate blood flow over a wide range.
Figure 9.
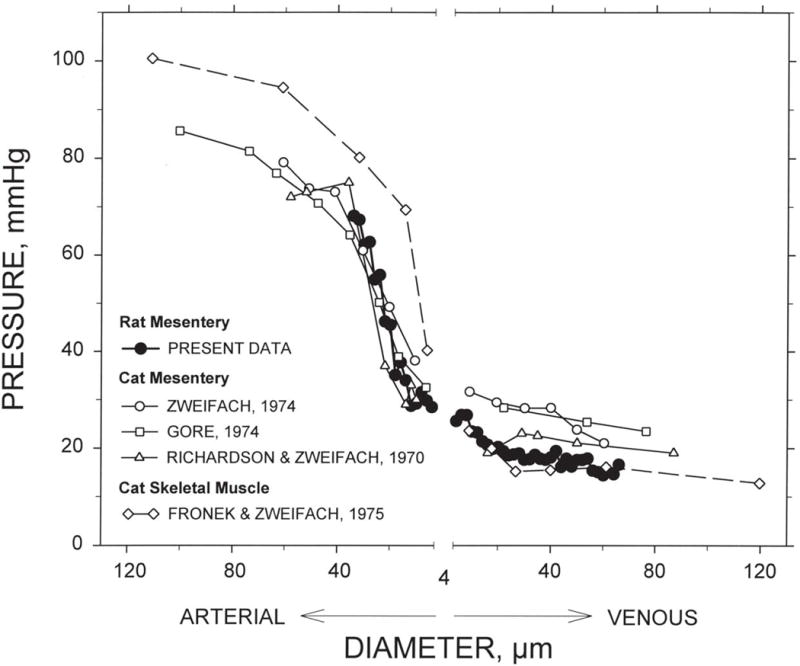
Intravascular pressure as a function of vessel diameter in different tissues and species. The “present data” refers to data obtained from mathematical model calculations for six mesenteric networks (82). The other data are from Zweifach (124), Gore (30), Richardson and Zweifach (90) and Fronek and Zweifach (26). Figure reproduced with permission from Pries et al. (82).
On the arterial side of the circulation, the decline in flow velocity closely parallels the decline in diameter, as indicated in a logarithmic plot (Figure 8). This implies that the ratio of velocity to diameter remains approximately constant. From Eqs. (22), (24) and (30), the wall shear stress in a cylindrical tube is given by
| (32) |
and it follows that the wall shear stress remains roughly constant throughout the arterial tree, down to the capillaries. This finding is consistent with the concept that blood vessels sense and respond to levels of wall shear stress, and that this mechanism plays an important role in determining the structural diameter of blood vessels (91). The typical values of wall shear stress in arteries and arterioles varies with size of mammalian species, from almost 100 dyn/cm2 (10 Pa) in mice and rats to less than 10 dyn/cm2 (1 Pa) in dogs and humans (33). On the venous side, the curves representing velocity and diameter are closer together (Figure 8), implying that levels of wall shear stress are significantly lower in the venous circulation (82).
The data presented in Figure 8 imply an enormous range of Reynolds numbers in the circulatory system. By convention, the Reynolds number for tube flow is based on the tube diameter, i.e. Re = ρVD/μ. For the canine parameters shown, with blood viscosity of 3 cP and blood density 1.06 g/cm3, the Reynolds number ranges from about 740 in the aorta, with a diameter of about 1 cm and a mean blood velocity of about 21 cm/s, to 8 × 10−4 in the capillaries with a diameter of about 8 μm and a velocity of about 0.28 mm/s. The variation is over about six orders of magnitude. In the capillaries, inertial effects are negligible, whereas in the large arteries, inertial effects are dominant and viscous effects are smaller but significant. Because flow is pulsatile in arteries, the peak Reynolds number may greatly exceed the values based on mean velocity. In larger animals and in humans, the Reynolds number in the aorta can reach the low thousands. The significance of these values with regard to the occurrence of flow instability and the development of turbulent flow is discussed in a later section.
Blood flow in arteries
From a hemodynamic perspective, the flow of blood in arteries has several prominent characteristics. (i) It is strongly pulsatile, as a consequence of the alternation between ejection and filling phases during the cardiac cycle. (ii) Artery walls have compliant elastic properties, and the fluctuation of pressure during the cardiac cycle leads to a time-dependent variation in arterial diameter. (iii) The combination of pulsatile flow and compliant vessels results in propagation of the cardiac pulse as a traveling wave along arteries. (iv) Arteries have complex shapes, including taper, curvature, branching, and local variations in diameter. These geometrical characteristics may be altered in pathological states, such as when aneurysms or stenoses develop. (v) The Reynolds numbers of arterial flow are high, in the range of hundreds to low thousands. In this range of Reynolds numbers, flow fields can be complex and sensitive to geometrical irregularities, with the possibility of flow instability and turbulence. Given this range of characteristics, no single theoretical framework exists for describing all aspects of blood flow in arteries. In the following sections, key aspects of blood flow in arteries are considered, including physical arguments and theoretical analyses relevant to each aspect.
Mechanical properties of artery walls
The arterial wall is a layered structure that must provide not only a conduit for passage of blood but also sufficient mechanical strength to resist the forces generated by blood pressure. The wall is customarily described in terms of three main layers, tunica intima, tunica media, and tunica adventitia (89). The innermost layer, the intima, consists of endothelial cells and basement membrane, and may also include other fibrous structures. The intermediate layer, the media, consists of smooth muscle cells and varying arrangements of collagen and elastin fibers. In the larger arteries, elastin is arranged in several sheets known as elastic laminae. Although smooth muscle cells are capable of contraction, they generally behave passively in the large arteries. In small arteries and arterioles, the contractile properties of vascular smooth muscle cells in the media are essential for the regulation of blood flow. The outermost layer, the adventitia, contains elastin and collagen as its main structural elements, as well as nerves and small blood vessels (vasa vasorum) that supply the wall. It serves to connect the artery mechanically with surrounding tissues. The biological components of the wall and their morphological and material properties are discussed in more detail elsewhere (17,89). Here, we focus on the mechanical properties of the wall, the deformations generated by pulsatile blood pressure, and their significance with regard to the propagation of the pressure pulse.
Stress in the artery wall: Thin-wall theory
For a basic analysis of the stress generated in an artery wall by blood pressure, it is helpful to consider first the thin-wall case, in which the thickness of the wall is assumed to be much smaller than the vessel radius. The tension generated in the wall can be computed by considering the forces acting on the part of a vessel segment that lies above a plane containing the center-line, as shown in Figure 10A. If the segment has length L and radius r, the transmural pressure difference Δp = pi − po acts on an area 2RL and generates a net upward force of 2RLΔp. This force must be balanced by the tension T in the wall, which is expressed as force per unit length, and generates a downward force 2LT. Equating these forces leads to the well-known “Law of Laplace” for a cylinder
| (33) |
Figure 10.
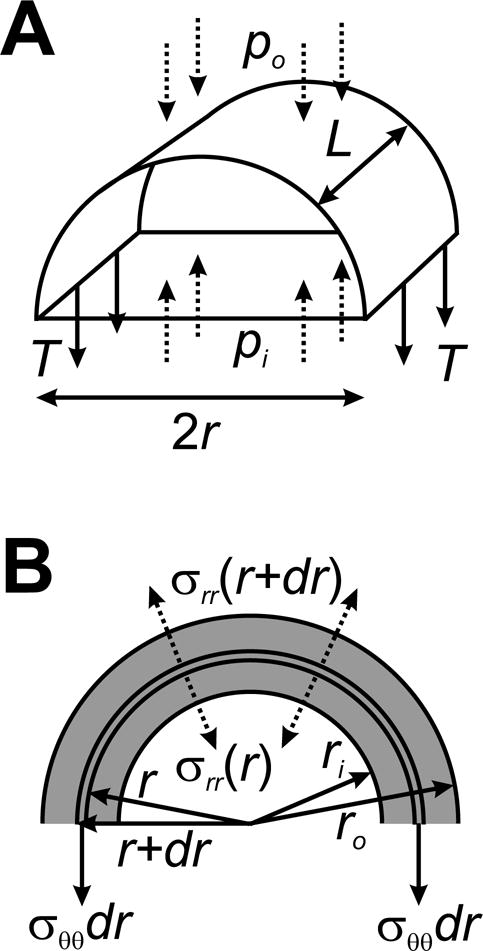
Analysis of stresses in a pressurized cylindrical tube. A. Thin-walled theory, for a segment of length L and radius r. Pressure forces acting on the wall (dashed arrows) must balance tension in the wall (solid arrows), implying the Law of Laplace, T = (pi − po)r. B. Thick-walled theory. The balance of forces is applied to a thin cylindrical shell of radius r and thickness dr. See text for details.
If the wall has thickness h, then the circumferential tensile stress generated in the wall is given by σ = T/h, i.e.
| (34) |
For a typical artery, the ratio r/h is much larger than 1, and the dominant stress is therefore not the radial force exerted by blood pressure, but the resultant circumferential stress generated within the artery wall.
If it is assumed that the vessel is an incompressible isotropic material with Young’s modulus E, and is tethered so that it cannot move longitudinally, then it can be shown (see below) that the change in radius Δr due to a small change in pressure Δp is given by
| (35) |
The ratio of wall thickness to radius varies considerably according to the type of vessel. In the arteries h/r is in the range 0.1 to 0.2, whereas veins have thinner walls, with h/r in the range 0.02 to 0.05 (12). A compilation of data from multiple studies (84) shows that h/r values increase with decreasing vessel diameters in the microcirculation, with smaller ratios in venous vessels than in corresponding arterial vessels. In capillaries, h/r is almost 0.5. Calculations of the circumferential stress in vessel walls according to Eq. (34) show that the stresses are approximately equal in arterial and venous vessels of the same diameter, but decrease strongly with decreasing vessel diameter (84).
Stress in the artery wall: Thick-wall theory
Given this range of h/r values, it is relevant to consider the behavior of a pressurized thick-walled artery, i.e. without assuming that h/r is small. We start by analyzing the case of small strain, assuming that the wall is an isotropic elastic material. We assume that the artery is stress-free in a reference configuration with initial inner radius Ri and outer radius Ro, and is loaded by a transmural pressure difference Δp = pi − po, such that it expands to a final inner radius ri and outer radius ro. We further assume that the wall material is effectively incompressible, and that the artery is tethered longitudinally so that its length is fixed. This analysis could be performed using the general governing equations as described earlier. The alternative approach adopted here is based on a force-balance argument analogous to that used above for the thin-walled case, which provides some physical insight into the mechanics of the system.
A material point in the wall with initial radius R where Ri ≤ R ≤ Ro has final radius r(R) where ri ≤ r(R) ≤ ro. The fact that vessel length and wall volume are both conserved implies that vessel wall-cross-section area is also conserved during the deformation. Applying this condition to the annular region with initial inner radius Ri and outer radius R shows that π(r2 − ri2) = π(R2 − Ri2), which implies that r2 − R2 = ri2 − Ri2. Differentiating with respect to R gives dr/dR = R/r. Also, (r + R)(r − R) = (ri + Ri)(ri − Ri) which implies r(r − R) ≈ ri(ri − Ri) because r ≈ R and ri ≈ Ri when the strain is small. In cylindrical coordinates (r,θ,z), the non-zero components of the Cauchy (small-deformation) strain tensor are therefore
| (36) |
These components sum to zero, which confirms that the deformation conserves volume. Then from Eq. (21) the non-zero components of Cauchy stress are
| (37) |
where is an unknown isotropic stress. Next, we consider the mechanical equilibrium of a thin shell within the wall, of radius r and thickness dr, again considering only the upper half of the vessel (Figure 10B). Similarly to the thin-wall case, the resultant forces per unit length generated by the stress σrr acting on the inner and outer curved surfaces are −2rσrr(r) and 2(r + dr)σrr(r + dr), and the force per unit length resulting from the circumferential stress σθθ is −2σθθ (r)dr. All these forces must sum to zero, i.e.
| (38) |
Dividing by 2dr and taking the limit dr → 0 gives
| (39) |
which may be integrated to give
| (40) |
where c is a constant and σ0(r) = c. The radial component of stress must match the applied pressures at the inner and outer surfaces, i.e. σrr(ri) = −pi and σrr(ro) = −po, and it follows that
| (41) |
and that the change in inner diameter of the vessel as a function of the pressure difference Δp = pi − po is given by
| (42) |
using the fact that G = E/3 when ν = 1/2. Eq. (35) above for a thin-walled tube can be deduced by setting ro − ri = h and ri ≈ r ≈ ro in this equation.
Equation (42) can also be used to deduce the Young’s modulus E from measurements of vessel distension under pressure. For such measurements, the change of outer diameter is usually observed, and the corresponding equation is (71)
| (43) |
Combining these results shows that
| (44) |
In particular, pressurization of a vessel with isotropic elastic properties gives rise to axial tensile stress σzz in the vessel wall if its length is held constant. The analysis of a pressurized thick-walled tube is treated in more detail in the classic book (57).
Other factors affecting arterial compliance
It should be emphasized that the actual behavior of arteries deviates in important respects from the assumptions made in the above analyses, including the assumptions of linear elastic material properties, small strain, isotropy, and the existence of a stress-free reference state. The departures of real arterial properties from these idealized assumptions are discussed next.
Mechanical testing of circumferential strips of arterial walls shows nonlinear passive elastic properties (17,107). As the extension (strain) is increased, tension (stress) increases slowly at first and then more rapidly, often with a roughly exponential dependence on strain. This behavior can be understood in terms of the mechanical properties of the wall structural elements. The molecular structure of elastin allows it to be stretched to more than twice its unstressed length, and its tension increases relatively smoothly with strain. By contrast, collagen fibers are very stiff, but are curved or crimped in the unstressed state of the vessel wall. As the wall is stretched, a relatively low stress is sufficient to straighten collagen fibers, but once they are straightened their high elastic modulus causes a large increase in the effective stiffness of the wall (17).
The linear theory described above can be adjusted to describe deformations of materials with nonlinear elastic properties, as long as the deformations are small. For instance, the change in outer diameter associated with a small change in internal pressure can be described by Eq. (43), but with E redefined as the incremental Young’s modulus, which is determined by the slope of the graph of pressure vs. radius, or more generally the slope of the stress-strain relationship. While this is a useful approximation for some applications, it may not provide an accurate description of the response of arteries to the changes of pressure during the cardiac cycle, because the strains are too large. For human arteries, the change in diameter from diastole to systole, expressed as a percentage of diameter, is typically about 9%, with a range from about 6 to 12% (71). Because of the strongly nonlinear elastic properties of the wall, experimental pressure-diameter curves are nonlinear over the range of pressures in the pressure pulse (17), and the incremental elastic modulus increases significantly from diastole to systole. The implications of this behavior for the propagation of the pressure pulse are discussed below.
The layered structure of the wall gives rise to significantly anisotropic mechanical properties, with different elastic moduli in the axial and circumferential directions. The anisotropy is strongly dependent on the degree of stretch in those two directions, again illustrating the nonlinear properties of artery walls (94,114). The anisotropy of wall mechanics results from the non-random orientations of fiber and sheet structures within the wall. In general, the stiffness is higher in directions in which fibers are preferentially oriented. Theoretical models have been developed that relate the anisotropic properties of the wall to the distribution of fiber orientations (39).
A further deviation from the model described above relates to the assumption of a stress-free reference configuration. When excised arteries are slit open lengthwise, the cut edges generally spring apart, showing the existence of residual stresses in the intact unloaded configuration (29,111). This phenomenon can be interpreted as follows (29). As shown by Eq. (36), the strain generated by pressurization of an artery declines with the inverse square of radial position r. If the strain was zero in the unloaded state, this would lead to a large radial gradient of strain in the loaded state. The observed behavior implies the presence of residual strain in the unloaded state that is negative at the inner surface and positive at the outer surface. When this is superimposed on the changes in strain with pressurization, it results in a more uniform strain state. Underlying this interpretation is the assumption that processes of structural adaptation within the vessel wall lead to equalization of stresses and strains across the wall in the loaded state (10).
When arterial diameter is graphed as a function of pressure during the cardiac pulse, the plotted values form a loop. For a given diameter, the pressure is higher during the increasing phase than during the decreasing phase (17,66). This shows that the arterial wall is not purely elastic and behaves as a viscoelastic material. Energy is dissipated in the wall during each pulse. In a detailed theoretical and experimental analysis of the interaction of a viscoelastic wall with pulsatile blood flow (9), it was shown that a Kelvin-Voigt model provided an adequate description of the wall’s properties.
Pulse propagation in arteries
As a result of the compliance of the arteries, the pressure pulse produced by the heart is not transmitted immediately to all parts of the arterial system, but is propagated along the vessels in the form of a traveling wave. The mechanism of this wave propagation is illustrated schematically in Figure 11. In essence, as a pulse of increased pressure travels along an artery, a negative pressure gradient (with pressure decreasing in the forward direction) is set up at the leading edge, which accelerates the blood. This causes a spatial gradient of flow rate with a larger flow rate entering than leaving a short segment of the vessel. By conservation of mass, this requires an expansion of the vessel, and so the pulse is propagated. The same mechanism also permits the propagation of a pulse wave in the opposite direction, which can arise because of reflection of the primary wave generated by left ventricular systole. The speed of these waves depends primarily on the ratio between the elastic stiffness of the wall and the inertia of the fluid.
Figure 11.
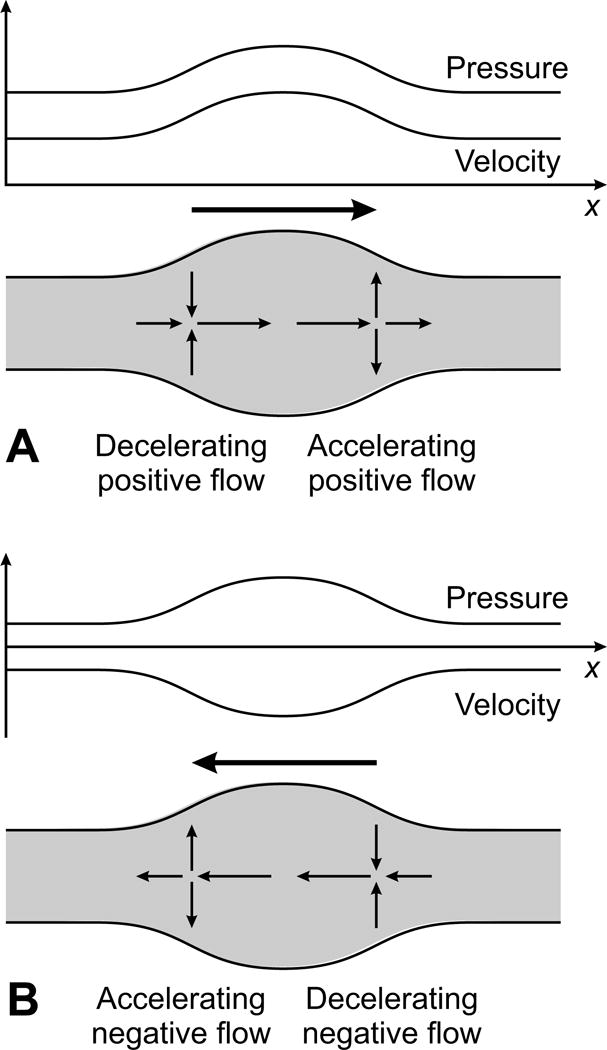
Schematic illustration of the mechanics of pulse propagation in an artery. Graphs show spatial variation of pressure and flow rate. Large arrow shows direction of propagation. Gray area represents artery, and small arrows indicate local fluid velocities. A. Short high-pressure pulse propagating in positive x-direction. At the leading edge of the pulse, fluid is accelerated by the negative pressure gradient. This produces a negative spatial gradient of flow rate. By conservation of mass, fluid accumulates in this region, and wall must move outwards. At the trailing edge of the pulse, fluid is decelerated by the positive pressure gradient, producing a positive spatial gradient of flow rate, and inward wall movement. B. Short high-pressure pulse propagating in positive x-direction. Mechanism is as in A, but with reversed velocities. Note that an arbitrary (positive or negative) x-independent velocity can be superimposed on the indicated velocities without affecting the mechanism. The x-scale is greatly compressed here for illustrative purposes. In reality, the systolic pulse wave is much longer than the diameter (and the length) of the artery.
The theoretical analysis of pulse wave propagation has a long history (72). As early as 1755, the great Swiss mathematician Leonhard Euler formulated the key equations needed for an analysis of this problem (19), although he was apparently frustrated by the difficulty of solving these equations (72). Below, we set out the equations essentially as he wrote them, and show how they may be solved in approximate form to obtain a prediction of the pulse wave velocity (28). First, however, we consider the representation of the pulse in the aorta by the simpler lumped-parameter “Windkessel” model.
Windkessel model for the aorta and large arteries
Stephen Hales in 1733 (35) recognized the role that the compliance of the aorta and large arteries plays in creating a more steady blood flow rate to the tissues than the sporadic ejection provided by the heart. He likened this process to the air chamber (Windkessel) on fire-engines of the time, where the alternate compression and decompression of the air in the chamber produced a relatively steady flow, despite the irregularity introduced by the reciprocating pump driving the flow. This idea was developed mathematically by Frank (25), who expressed the flow from the left ventricle into the aorta as the sum of a flow proportional to the pressure, representing the resistance of the vessels, and a flow proportional to the time derivative of pressure, representing the compliance of the vessels. Such an approach is often called a “lumped-parameter” model. In terms of the electrical analogy introduced earlier, the Windkessel model is simply a resistance and a capacitance in parallel. Despite its simplicity, this model is quite successful in representing the exponential decay of arterial pressure during diastole (64,101). As such, it provides a useful theoretical description of the afterload on the left ventricle, and can also be constructed as a physical device for use in experiments on isolated hearts or artificial pumping devices.
The lumped-parameter approach can be extended to construct more elaborate models (117). In time-varying flows, the acceleration and deceleration of fluid requires pressure drops in addition to those present in a steady flow. In the electrical analogy, these can be represented as inductances. As already mentioned, the variation of volume contained in a compliant vessel is represented by including a capacitance. By combining multiple elements consisting of resistances, inductances and capacitances, electrical circuit configurations can be developed to represent time-dependent blood flow in extensive tree-type models of the arterial system (66). The properties of these circuits can be analyzed using standard theoretical methods of electrical engineering. This type of lumped-parameter representation of circulatory hemodynamics is particularly useful for investigating the mechanical interactions of the systemic and/or pulmonary circulations with the heart (110) or with regulatory mechanisms (18). Such lumped-parameter models are limited in that that they do not readily represent the effects of pulse-wave transmission and reflection in arteries, the nonlinear elastic characteristics of artery walls and nonlinear fluid dynamic effects.
One-dimensional theory of pulse wave propagation
In order to represent pulse wave propagation in arteries, analyses with one spatial dimension are generally used (1). A simplified one-dimensional analysis is presented here, neglecting the effects of blood viscosity and the no-slip condition at the walls. The fluid velocity along the artery is expressed as v(x,t), where x is distance along the artery and radial variations in v are neglected. The cross-section area of the artery is A(x,t) = π[a(x,t)]2 where a(x,t) is the radius, and the volume flow rate is Av. Since blood is effectively incompressible, any increase in volume flow rate with position x implies that the cross-section area must be decreasing with time at that position, and vice versa. In mathematical form, this leads to the equation for conservation of mass
| (45) |
The equation for conservation of momentum follows from Eq. (12) under the assumption of unidirectional flow:
| (46) |
The elastic behavior of the wall is represented by assuming that the radius depends on the internal pressure (relative to the external pressure), i.e., a = a(p). Viscoelastic effects are neglected. This set of nonlinear equations can be solved using the method of characteristics (101), providing the solution that Euler had been unable to find (72).
For the present discussion, a solution is given under further simplifying assumptions. The approximate mathematical approach known as linearization is used, in which it is assumed that all variables have small variations about their reference values, which are a0 for radius, p0 for pressure and zero in the case of velocity. The governing equations are then simplified by neglecting any terms involving products of these small variations. With this approach, Eqs. (45) and (46) reduce to
| (47) |
| (48) |
where the compliance of the artery is represented by
| (49) |
Eqs. (47) and (48) may be combined to give a single partial differential equation governing the pressure:
| (50) |
This is the wave equation in one spatial dimension, which arises in several areas of physics including acoustics and electromagnetics. It is well known to have a general solution
| (51) |
where c = (a0/γρ)1/2 is the wave speed, often referred to as the pulse wave velocity in the context of arterial flow. The unknown functions f and g represent waves traveling in the positive and negative x directions respectively.
For an axially tethered tube with radius a0 and a thin wall of thickness h, composed of an incompressible material with Young’s modulus E, Eq. (35) shows that
| (52) |
and the wave speed is
| (53) |
This differs from the commonly stated result
| (54) |
by a factor of 2/√3 = 1.155. The difference arises because the latter result assumes that the wall is not tethered in the axial direction, whereas the present analysis assumes that it is tethered. The assumption of tethering is probably more appropriate. However, it should be recognized that both results are in any case approximations, because they do not take account of the nonlinear and anisotropic elastic properties of the artery wall. Eq. (54) was first stated in 1808 by Thomas Young (121), and is known as the Moens-Korteweg formula because of subsequent work by those two authors (72). Estimates of the quantities in this equation for the canine aorta are E = 4.8 × 105 Pa, h/2a0 = 0.07 and ρ = 1060 kg/m3, giving c = 5.6 m/s (12).
Observed wave speeds in arteries have been tabulated for various species and anatomical locations (71). In the human aorta, values of 4–6 m/s are typical, with values of 7–9 m/s in the radial, femoral and iliac arteries. With aging, the aorta undergoes substantial structural changes, becoming both larger and stiffer. As shown by Eq. (53), these changes have partially compensating effects on wave speed. The net effect is an approximate doubling of the wave speed between age 20 and old age in healthy subjects (47).
The theory developed above contains numerous simplifications, based on assumptions that are in many cases not well justified under realistic physiological conditions (12,28). As already discussed, the elastic properties of artery walls are strongly nonlinear, such that the effective (incremental) compliance of the wall may vary during the cardiac pulse, being lower at the peak of pressure (systole) and higher at the trough of pressure (diastole). The wave speed then is higher at the peak of pressure than at the trough, causing steepening of the leading edge of the pressure pulse wave. Arterial diameters are not uniform, but decrease with distance downstream, causing amplification of the pulse wave. The linearized analysis is based on the assumption that the blood flow velocity is small compared to the pulse wave velocity. However, the peak velocity during systole may be about 1 m/s, which is not very small compared to a wave velocity in the range 4–6 m/s. In the above analysis, a uniform velocity is assumed across the vessel cross-section, whereas in reality the effects of fluid viscosity and the no-slip condition lead to steep spatial gradients in blood velocity near vessel walls, as discussed below, resulting in viscous energy dissipation. The viscoelastic properties of the wall, as already mentioned, also contribute to the dissipation of the energy in the pulse wave. Theoretical approaches for analyzing these more complex aspects of pulse wave propagation have been reviewed elsewhere (112).
Aortic stiffness is considered to be an important indicator of cardiovascular risk (67), but is difficult to assess directly in human subjects. Pulse pressure and aortic pulse wave velocity are related quantities that are markers of cardiovascular risk (2) and can be measured noninvasively by techniques such as tonometry and ultrasound. According to the Moens-Korteweg equation, pulse wave velocity is proportional to the square root of arterial stiffness, and it is considered one of the more reliable ways to assess this parameter (50). However, caution should be used when making such assessments, because pulse wave velocity is equally dependent on arterial diameter, and because the apparent stiffness is dependent on the pressure to which arteries are exposed, as a result of their nonlinear elastic properties.
Reflection of pulse waves and pulse pressure amplification
The solution to the wave equation given in Eq. (51) is a superposition of waves of arbitrary shape traveling in both directions. In arteries, the dominant wave travels away from the heart, but reflected components are generated at branch points and as a result of variations in vessel diameter or stiffness. Insight into the generation of reflected waves can be gained by considering the case of a traveling wave reaching a diverging arterial bifurcation (12), with the parent vessel labeled 0 and the two branches labeled 1 and 2 as in Figure 12. The vessels are assumed to have cross-sectional areas A0, A1 and A2 and wave speeds c0, c1 and c2. Suppose that pI(t), p1(t), p2(t) and pR(t) are the pressures at the bifurcation associated with the incident wave, the two transmitted waves and the reflected wave, respectively. Then matching of pressures in the branches requires that
| (55) |
Figure 12.
Analysis of wave propagation at an arterial bifurcation. An incident wave in branch zero gives rise to transmitted waves in branches 1 and 2 and a reflected wave in branch 0.
Likewise, suppose that the velocities associated with the incident wave, the two transmitted waves and the reflected wave are vI(t), v1(t), v2(t) and vR(t), where vR(t) is directed in the upstream direction. Conservation of flow then dictates that
| (56) |
For a forward wave, p = f(x − ct) and Eq. (48) shows that
| (57) |
This condition applies to the incident wave at the bifurcation, and so where the dot denotes the time derivative. The same condition holds for the other three wave components, taking account of the fact p = g(x + ct) for the reflected wave, and that its velocity refers to the upstream direction. Taking the time derivative of Eq. (56) and using these conditions gives
| (58) |
where Z0 = ρc0/A0 is termed the impedance of segment 0, and Z1, Z2 are defined similarly. The time derivative of Eqn. (55) gives
| (59) |
Eqs. (58) and (59) can be solved to give the transmitted and reflected pressure waves
| (60) |
where Tw and Rw are the wave transmission and reflection coefficients and Tw − Rw = 1. In the special case for which Z0−1 = Z1−1 + Z2−1, the impedances are said to be matched. Then Rw = 0, there is no reflected wave and the full pressure wave is transmitted to the downstream vessels. The inverse of impedance, Z0−1, is known as the admittance, and the criterion for matching is that the sum of the downstream admittances equals the upstream admittance. Such matching occurs, for example, if the wave speeds satisfy c0 = c1 = c2 and the areas satisfy A0 = A1 + A2. In general, however, this condition is not satisfied, and a reflected wave is generated. If the downstream admittances are less than the upstream admittance, Rw > 0 and the reflected pressure wave has the same sign as the incident wave. In this case, the transmitted pressure wave has higher amplitude than the incident wave. Conversely, if the downstream admittances are greater, the reflected wave is inverted and the transmitted wave has lower amplitude. Both cases are possible; at the aortoiliac bifurcation in humans, the reflection coefficient varies from positive values in youth to negative values in old age (32).
Equation (60) can also be used to describe the behavior at a transition in the diameter or stiffness of a single vessel, simply by omitting the term Z2−1. In that case, a decrease in admittance gives rise to a reflected pressure wave with the same sign as the incident wave and a transmitted pressure wave with increased amplitude. Furthermore, the same argument can be applied to the case where admittance gradually decreases along the vessel, such that an incremental contribution to the reflected wave is generated at each increment of distance along the vessel for which the admittance is varying. For instance, in a tapered vessel with continuously decreasing cross-sectional area and constant or increasing wave speed along its length, admittance continually decreases, such that a positive reflection is generated in a distributed manner along the vessel and the amplitude of the transmitted wave increases with distance.
The mechanism just described is largely responsible for the increase in the amplitude of the pressure pulse with distance peripherally along the arterial tree (71), a phenomenon known as pressure pulse amplification (3). The effect is strongest in young individuals and diminishes with age (71). This amplification has been discussed both in terms of an increase in arterial impedance (58) and in terms of the generation of reflected waves and their summation with the forward wave (92). As the above arguments indicate, these explanations are equivalent, since a reduction in admittance is responsible both for the generation of a positive reflected pressure wave (Rw > 0) and the increase in amplitude of the transmitted wave (Tw = 1 + Rw > 1). A second factor contributing to pulse pressure amplification is the nonlinearity of the elastic properties, leading to steepening of the leading edge of the pressure pulse (42). The decrease in pulse pressure amplification with age can be explained in terms of the increasing stiffness of the aorta, which as mentioned earlier, leads to an approximate doubling of wave speed. This has the effect of more closely matching the impedances of the aorta to more distal arteries, thereby reducing the amplification at distal sites. However, this does not necessarily weaken the reflections returned to the heart, as discussed below.
It has long been generally considered that the entrances to high-resistance arterioles and/or the branching points of major arteries, such as the aortoiliac bifurcation, are the main sites for reflection of the pulse wave (71). However, recent work indicates that the reflections returning to the aortic root are generated in a spatially distributed manner along the aorta and do not have discrete sites of origin (16,99). Such behavior is consistent with the theory of wave reflection in a vessel with spatially varying impedance, as outlined above. The existence of such a phenomenon has in fact been known and discussed for many years (71).
The presence of reflected waves is evident in the pressure waveform observed in the ascending aorta. The earliest time of arrival of the reflected wave is generally apparent as an upwards inflection in the pressure waveform in the ascending aorta. This arrival time varies substantially with age, due to changes in arterial size and stiffness as mentioned earlier (71). In adolescents, the reflected wave arrives during diastole. However, with increasing age, components of the reflected wave arrive earlier in systole, and the arrival time is near the beginning of systole in elderly subjects. This has the important effect of increasing the afterload on the heart. The effect of the reflected wave on the systolic pressure pulse can be quantified by computing an augmentation index, which is obtained by taking the difference between the peak pressure and the pressure at the inflection point and dividing by the pulse pressure (systolic minus diastolic). The augmentation index has often been considered as an indicator of arterial stiffness. However, given that the site of the reflections leading to the augmentation of pulse pressure is not well defined, and that left ventricular contractility influences the pressure wave (100), the augmentation index cannot be considered a direct measure of stiffness (50).
Relationship between wave theory and Windkessel theory
Despite the extensive development of one-dimensional wave theories, the Windkessel model continues to be widely used (117). The relationship between these two theories has been examined in a number of studies. In the “reservoir-wave” approach (109), the arterial pressure is separated into a time-dependent but spatially independent “reservoir pressure” component that corresponds to the Windkessel, and a wave component including forward and backward propagating waves. Subsequent work (70) showed that it is not necessary to invoke a separate “reservoir” component of pressure to explain the occurrence of the Windkessel phenomenon in a wave theory. For example, the aorta during diastole can be modeled as a segment closed at the upstream end and with an abrupt transition to higher impedance at the downstream end. The superposition of multiple reflections occurring within this segment during diastole leads to the generation of an approximately exponential decay in pressure, corresponding to Windkessel behavior. This behavior persists if the abrupt transition in impedance is replaced with a gradual increase along the segment, as discussed above. These studies have clarified the relationship between the two theories, and provide a theoretical basis for deciding whether Windkessel models are appropriate in a given application.
Fluid mechanical phenomena in arteries
In the above analysis of pulse wave propagation, the blood flow velocity in an artery was assumed to be uniform in the cross-section of the vessel. In reality, velocity profiles in arteries are highly variable and affected by several fluid mechanical factors including the no-slip condition at vessel walls, effects of fluid inertia, the strongly time-varying flow, the curvature and non-uniform diameter of vessels, and the presence of bifurcations. This fluid mechanical complexity has significant biological implications. The growth and remodeling of artery walls is strongly influenced by the mechanical stresses that they experience, particularly circumferential stress and wall shear stress (49,69). Furthermore, wall shear stress has an important influence on the development of atherosclerotic lesions, which develop preferentially in regions of low or fluctuating shear stress (59). The spatial and temporal distribution of wall shear stress in arteries is sensitive to the geometry of the vessels as well as the pulsatile nature of the flow. The complex interaction between vascular geometry, blood flow and biological responses has been the subject of a large amount of analysis. Some basic aspects are discussed in the following sections.
Pulsatile flow in arteries
The derivation of the Poiseuille formula for flow in a cylindrical tube, given above, is based on the assumption of steady flow. In arteries, the presence of a strong oscillatory component of flow due to cardiac pulsatility leads to significant differences between arterial flow and steady Poiseuille flow, with regard for example to the relationship between pressure drop and flow rate, the velocity profile in the blood, and the shear stress acting on vessel walls. To characterize the relevant phenomena in pulsatile flow, it is helpful to introduce a dimensionless parameter analogous to the Reynolds number. Suppose that the fluid flow has a typical velocity V, a typical length L and a typical timescale of variations T. In this case, the relevant inertial term is the time-derivative term in Eq. (12), and the magnitudes of the inertial and viscous terms may be estimated as
| (61) |
and the ratio of the inertial term to the viscous term is
| (62) |
If we consider flow in a tube with radius a to be periodic with angular frequency ω (= 2πf where f is frequency), then we let L = a and T = 1/ω and define a non-dimensional parameter
| (63) |
which is known as the unsteadiness parameter or Womersley number. As with the Reynolds number, low values of α imply that the flow is dominated by viscous effects, whereas high values of α imply that inertial effects are important.
The flow waveform generated by the heart is complex, but useful insight may be obtained by considering flow in a uniform cylindrical tube, driven by a sinusoidally varying pressure gradient, with angular frequency ω. For problems of this type, it is helpful to use the complex exponential function
| (64) |
The imposed pressure gradient can then be written as
| (65) |
where Re here denotes the real part of a complex number (and not the Reynolds number). The equations of motion, Eq. (12), can be solved exactly in terms of Bessel functions (64), and the fluid velocity is given by v(r,t) = Re[v′ eiωt] where
| (66) |
and J0 is a Bessel function of the first kind. Examples of resulting velocity profiles at multiple time points over half of a cycle of the oscillation are shown in Figure 13, for several values of α. When α = 1, the velocity profiles are nearly parabolic and the velocity varies with time almost in phase with the pressure gradient. In this case, the flow is quasi-steady, i.e. approximately the same as the steady flow that would be obtained with the pressure gradient fixed at its instantaneous value. The wall shear stress, which is proportional to the velocity gradient near the wall, then varies in phase with pressure gradient. As α is increased, the velocity profiles become increasingly blunted in the interior of the tube and fluid velocity has increasingly sharp variations in amplitude and phase near the wall. The variation of velocity with time in the central region and the variation of wall shear stress with time both lag the variation of pressure gradient. When α is large, the interior velocity lags the pressure gradient by π/2 (90°) and the wall shear stress lags the pressure gradient by π/4 (45°). Conversely, when α is small, both the interior velocity and the wall shear stress are in phase with the pressure gradient.
Figure 13.
Sequences of velocity profiles in a tube with a sinusoidally varying pressure gradient, for indicated values of unsteadiness parameter α. Velocity profiles represent one half of a complete cycle of the oscillation. Bottom profile corresponds to moment of maximum pressure gradient.
The pressure generated by the heart in the root of the aorta is approximately periodic, but has a more complicated variation with time than a simple sinusoidal function. By means of Fourier analysis, such a pressure waveform can be represented as the sum of a steady component, a sinusoid at the fundamental frequency, and harmonics at higher frequencies. The resulting flow in a uniform tube driven can be computed by superimposing the velocity profiles generated by Poiseuille flow for the steady component and by the above analysis for the oscillatory components.
For a specific example, we consider a human aorta of diameter 2.7 cm with heart rate of 60 bpm, blood viscosity of 3 cP and blood density 1.06 g/cm3. The angular frequency of the fundamental frequency component is then ω = 2π s−1, and α = 1.35(2π1.06/0.03)1/2 = 20.1. The velocity profiles therefore correspond to the rightmost panel in Figure 13. Inertial effects are dominant and the pressure gradient drives the acceleration of the flow. The velocity profile is almost uniform across the diameter of the tube, with narrow viscous boundary layers at the walls. The higher harmonic components of the waveform correspond to even higher values of α, and would show similar behavior. Both the spatial and temporal variations of the flow are very different to the predictions of Poiseuille flow, and also differ from a uniform velocity profile, without radial variation in velocity, as assumed in the above discussion of wave propagation in arteries. For a second example, we consider a small artery of diameter 1.35 mm, with other parameters as above. Then α = 0.0675(2π1.06/0.03)1/2 = 1.006, so the flow is quasi-steady, corresponding to the leftmost panel of Figure 13. Thus, the effects of flow pulsatility on velocity profiles in arteries vary widely within the arterial system according to vessel diameter.
In most arteries, the maximum forward flow occurs during systole, but this is not the case in the coronary arteries. The major coronary arteries run over the outer surface of the heart, but their branches penetrate the myocardium where they are subjected to strong compressive forces during systole. This has the effect of impeding or even reversing arterial flow, so that the coronary inflow mainly occurs during diastole, while venous drainage is increased during systole (6,116).
The measurement of blood pressure using the standard method with an inflated cuff wrapped around the arm represents another common situation where pulsatile blood flow is strongly affected by external pressure. When the cuff is fully inflated, the brachial artery is collapsed and flow ceases. As the cuff pressure is decreased, a stage is reached at which the artery opens transiently during systole, permitting a burst of flow with each heartbeat. The length of this interval of flow increases with further decrease in cuff pressure, until the flow continues throughout the cycle. Characteristic (Korotkoff) sounds are associated with the transient flow during each beat and can be detected with a stethoscope and used to determine the pressures associated with systole and diastole in the patient. The sounds are generated as a result of mechanical instability generated by the interaction of the flowing blood with the deformable and partially collapsed wall of the artery (5,12,73).
The above analysis of pulsatile flow is strictly applicable to straight uniform rigid tubes, whereas arteries are in reality curved, non-uniform and deformable. The fluid mechanical effects of oscillatory flow therefore occur in arteries in combination with the fluid mechanical effects resulting from the non-uniformities in arterial geometry, as discussed next.
Entrance effects
One of the assumptions underlying the analysis leading to Poiseuille’s law, Eq. (22), is that effects of the conditions at the entrance to the tube are negligible. Thus, the flow is assumed to be fully developed, in the sense that the distance from the entrance is large enough that the velocity profile is no longer varying with distance along the tube. The distance that must be traveled for this condition to be satisfied within a small tolerance is referred to as the entrance length (12).
The development of the parabolic flow profile with distance along a tube is illustrated in Figure 14, assuming steady flow, for the case when the fluid enters the tube with almost uniform velocity over the cross-section. The no-slip condition at the wall implies that the fluid immediately adjacent to the wall has zero velocity, creating a sharp gradient in velocity at the wall. Viscosity acts to smooth out this velocity gradient as the fluid travels along the tube, creating an increasingly wide region of reduced velocity. This is an example of the fluid mechanical phenomenon known as a “boundary layer” in which the combined effects of fluid viscosity and the no-slip condition produce a region of sharp velocity transition adjacent to a solid surface. Scaling arguments show that the thickness of the layer grows approximately in proportion to the square root of distance along the tube. Since the total flow rate in the tube is a constant, the increase in the width of the boundary layer containing slower moving fluid implies an increase in fluid velocity in the central region. This acceleration is associated with an increased pressure gradient, relative to that needed to drive the fully developed Poiseuille flow. The boundary layer thickness increases until it is comparable to the vessel radius, at which point the flow profile is parabolic and the flow is considered fully developed.
Figure 14.
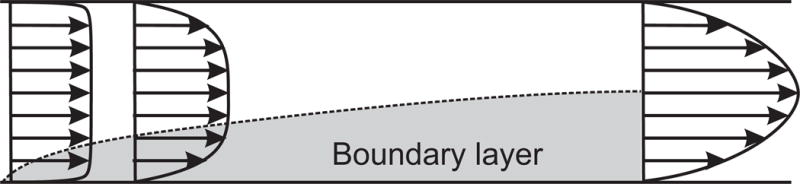
Development of boundary layer (shaded area) in fluid entering a tube. Velocity profiles indicate approach to fully developed flow.
The entrance length depends on the rate at which the boundary layer spreads, which is determined by the viscosity of the fluid. It follows that the entrance length increases with the Reynolds number (Re). For laminar flows, with Re in the range of about 10 to 2000, the entrance length is linearly related to Re and is given approximately by Le ~ 0.03 Re D where D is the diameter (12). At very low Re, the entrance length decreases to a lower limit of about 0.65D (28). In the case of a human aorta with D = 2.5 cm and Re = 2000, Le = 150 cm, and the whole length of the aorta lies within the entry length, so that fully developed Poiseuille flow would not be attained in steady flow. However, for small arteries with diameters in the range of 1 mm, Re is of order 10–30 and the entrance length is much less than the length of the artery, so fully developed flow can be assumed.
The concept of entrance length is less precisely defined under conditions of oscillatory flow. One estimate of the entrance length (12) is obtained by considering the distance at which the thickness of the growing boundary layer (as shown in Figure 14) equals the thickness of the oscillatory viscous boundary layer (see Figure 13 for α = 20), giving Le = 3.4V/ω. Beyond this distance, the thickness of the boundary layer is determined by the oscillatory nature of the flow and not by the distance from the entrance. For the human aorta with a heart rate of 60 bpm and a mean velocity of 20 cm/s, this gives an entrance length of about 10 cm for the oscillatory component of the flow. For pulsatile flow, consisting of an oscillatory component superimposed on a steady mean component, the oscillatory component may be fully developed while the mean component remains subject to strong entrance effects.
Flow in curved, helical and branching arteries
When blood flows through a tube that has a curvature in a single plane, the change in flow direction involves a change in momentum, which is driven by a pressure gradient across the vessel cross-section, with higher pressure at the outside of the curve. The net effect is that fluid near the center-line is driven outwards in the curve, whereas slower-moving fluid near the walls is driven toward the inside of the curve. This sets up a secondary flow in the vessel cross-section, consisting of a pair of vortices (12,28). A further consequence is that the location of peak axial velocity is displaced toward the outer wall, so that the wall shear stress is increased there and reduced on the inner wall (12).
The thoracic aorta has a strong curvature, as it ascends from the heart and then descends to the abdomen. However, its path is more complex than the planar curve described above, and has a significant helical component. This, together with the swirl of the blood flow generated within the left ventricle, generates a helical flow in the aorta (44). The presence of such swirling flows in major arteries and in the heart may have significant fluid mechanical effects by reducing energy dissipation (43), and may also lead to more uniform shear stress acting on artery walls and enhanced transport of solutes between flowing blood and the vessel wall (15).
Flow through bifurcations (branch points) in the arterial tree results in complicated distributions of fluid velocities and wall shear stresses, as illustrated in Figure 15 for flow through the human carotid bifurcation (68). In this example, the relatively high velocity at the center-line of the parent vessel impinges on the flow divider (the surface where the two branches meet). As a consequence, the velocity profiles in the branch vessels are markedly asymmetric, with higher velocities and shear stresses in the regions close to the flow divider. On the opposite sides of the vessels, the velocities and wall shear stresses are much lower. Depending on the specific characteristics of the flow and the bifurcation geometry, flow separation may occur in these areas. In flow separation, the streamlines of fluid moving adjacent to the wall separate from the wall and reattach at downstream points, leading to a region of recirculating flow, with reversed shear stress at the wall. Regions of swirling flow may also be generated, as indicated in Figure 15.
Figure 15.
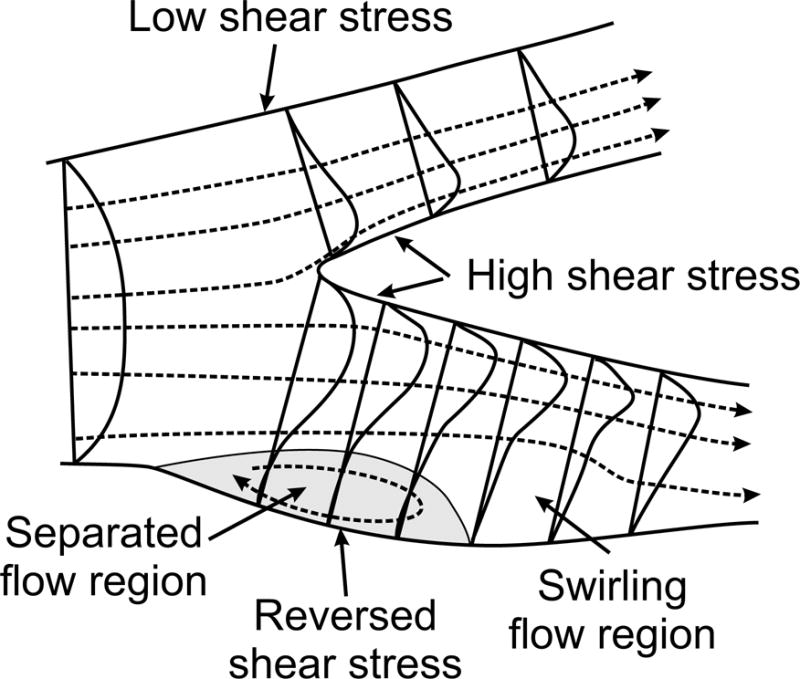
Sketch of flow phenomena occurring during steady flow in a human carotid artery bifurcation, based on observations in a transparent postmortem sample (68). Dashed lines indicate fluid streamlines. Curves across vessel diameters indicate local velocity profiles. Shaded area indicates region of flow separation, with separation point at the upstream end and reattachment point at the downstream end.
Flow instability and turbulence
As discussed earlier, the Reynolds number is useful in describing the characteristics of a fluid flow, providing an indication of the relative importance of inertial and viscous effects in the fluid. In general, low Re implies stable laminar flow, whereas instability and turbulence are possible at high Re. Flow in a long straight cylindrical tube remains laminar up to a Reynolds number of about 2400, beyond which turbulence is observed (12). The fact that the transition occurs at this high Re is suggestive of the fact that Poiseuille flow is relatively stable and only a small amount of viscosity is needed to prevent instability and the development of turbulence.
In other geometries, unstable flow and transition to turbulence can occur at much lower Reynolds numbers. In general, any flow system with the character of a jet, where a stream of faster moving fluid enters a wider region of slower moving fluid, is prone to instability. For instance, when a fluid flows through a narrow orifice, the flow streamlines typically separate from the downstream edge of the orifice, and regions of recirculating flow are formed on each side of the resulting jet. The critical Reynolds number for flow instability and turbulence for such a flow is in the range 300–400 (12). Such conditions can occur in the entrance to the aorta, if the aortic valve is stenosed, or on the downstream side of a stenosis within an artery. Turbulence often results in the generation of characteristic sounds that are useful for the diagnosis of vascular or cardiac abnormalities.
Blood flow in veins
In the veins, blood pressure and flow velocity are relatively low, with increased possibility of thrombus formation, and valves maintain the flow direction. As previously discussed and as indicated in Figure 8, the veins have typically about twice the diameter of corresponding arteries. An increase of diameter by a factor of two implies a 4-fold reduction in flow velocity, a 16-fold reduction in flow resistance (Eq. (31)), and an 8-fold reduction in wall shear stress (Eq. (32)), in veins relative to corresponding arteries. Significant nonlinear rheological effects as a result of aggregation of red blood cells are more likely to occur in veins than in arteries as a consequence of the lower shear stresses and shear rates (45). The walls of veins are thinner than those of corresponding arteries, as expected considering the much lower pressures that they experience. The level of cardiac pulsatility in venous blood flow is generally much lower than in the arteries, because the time varying components of flow are largely damped out during passage through the microcirculation. Nonetheless, pulsatility with respect to both pressure and flow can be observed in venules (52,124). A pulsatile component of pressure can be observed in the superior vena cava, resulting from the oscillatory intake into the right atrium of the heart (118). These and other aspects of venous hemodynamics are discussed by Fung (28).
Gravity has the effect of increasing the hydrostatic pressure in a column of blood by about 0.8 mmHg per cm of height. In a standing human, the resulting hydrostatic pressure difference of 80 to 100 mmHg between the ankle and the right atrium increases the pressure available to drive arterial flow to the lower extremities, but must be overcome in order for blood to return to the heart in the veins. In the absence of any pumping mechanism other than the heart, the pressures in the veins and in the microcirculation of the lower limbs are greatly elevated relative to the rest of the body when standing. Possible consequences include distension of the veins, which can cause orthostatic hypotension and fainting, and increased fluid filtration from microvessels, which can cause edema (51). The primary mechanism available to counteract these effects is the cyclic contraction of the muscles in the legs combined with the presence of valves in the veins, which generates a pumping action to drive blood out of the limbs and reduce intravascular pressures. The pressure changes in the thorax associated with respiration provide an additional pumping effect.
The valves in the veins consist of a pair of thin leaflets attached to the vessel walls with edges that are oriented in the direction of normal flow (towards the heart). When the pressure difference across the valve is positive, i.e., such that it drives flow in the normal direction, the leaflets are pushed apart and flow is not impeded. However, a reversed pressure difference pushes the leaflets together and flow is blocked. Damage to the valves can occur during aging and as a consequence of elevated venous pressure or deep vein thrombosis, both of which can be caused by extended inactivity and/or lack of mobility.
The system of veins in the leg includes both deep and superficial veins that run the length of the leg. These are connected together at intervals by several perforator veins, with valves that direct flow from the superficial veins to the deep veins. Since the superficial veins are not subject to the pumping action of the leg muscle, the perforator veins are important for maintaining blood flow from superficial veins to deep veins where it can be pumped back to the heart. Because of this arrangement, the consequences of venous valve failure depend on the location of valves that are not competent (88,103). Failure of the valves in only the superficial veins does not necessarily lead to impairment of venous return and edema, because the perforating veins continue to drain the superficial veins. However, if the valves in the perforators also fail, then a reflux in the superficial veins can occur, in which blood from the deep veins exits through the perforators and flows in the retrograde direction in the peripheral veins. This can lead to varicose veins, leg edema, and eventually ulcer formation. Such a local circulatory loop in the veins was identified in 1891 and described as a “private circulation” (108).
Blood flow in the microcirculation
Vessels with diameters less than about 300 μm form the microcirculation. Blood flow in the microcirculation has several distinctive features (80). As a consequence of the small diameters and low flow velocities, the Reynolds number is very small, typically much less than one. The flow is laminar and governed by the equations of Stokes flow, i.e. flow at effectively zero Reynolds number. Inertia-dependent phenomena such as flow instability, flow separation, turbulence, and generation of secondary flows in curved tubes do not occur. On the other hand, the suspension characteristics of blood strongly influence flow in the microcirculation. Whereas blood can be considered as a continuum with nonlinear rheological properties in vessels with diameters much larger than the dimensions of individual blood cells, this is not the case in microvessels. Prominent non-continuum effects, including reduction of intravascular hematocrit, variation of the apparent viscosity of blood with tube diameter, and unequal partition of hematocrit between branches of diverging microvascular bifurcations, are generated as a result of the finite size of the suspended elements relative to vessel diameters.
A key phenomenon underlying these non-continuum effects is the tendency for red blood cells flowing near vessel walls to migrate away from the walls, forming a cell-free or cell-depleted layer. This migration occurs as a consequence of the deformability of red blood cells. Opposing the migration away from the walls is the tendency for particles in a concentrated suspension subjected to a shear flow to migrate across the flow (towards the walls) in the direction of decreasing concentration, a phenomenon known as shear-induced dispersion. The eventual thickness of the cell-free layer is governed by the balance between these two effects (97). Although detailed numerical simulations of multiple suspended particles are able to predict formation of the layer (22), the underlying mechanical processes remain incompletely understood and are currently an active area of research (31,37,75).
Insight into the effects of the cell-free layer can be obtained by considering a simple two-phase model of blood flow (113), in which a cylindrical core region of viscosity μc centered on the tube axis is surrounded by a cell-free layer of lower viscosity μp, where λ = 1 − δ/a is the ratio of the core radius to the tube radius, δ is the width of the cell-free layer and a is the tube radius (Figure 16). The analysis presented in Eqs. (23–27) can be used to calculate the velocity profile in the tube, which consists of segments of parabolas, with a blunted profile in the central region where the viscosity is higher:
| (67) |
This model is analyzed in the following sections.
Figure 16.
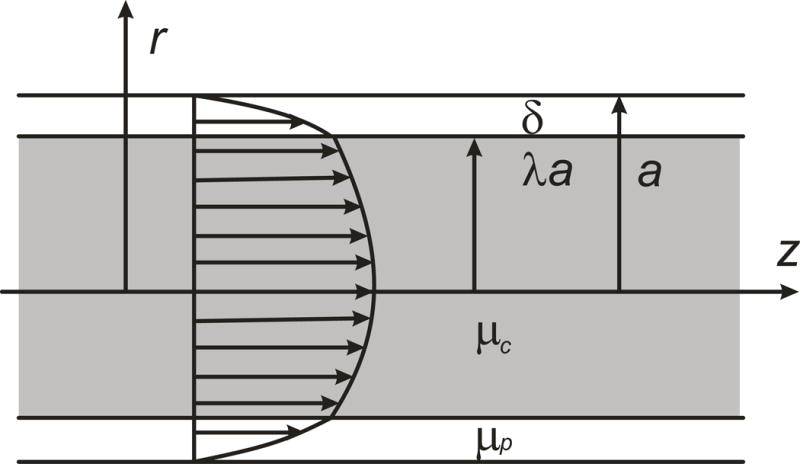
Two-phase model for blood flow in a microvessel, with radius a. A central core region containing red blood cells, with viscosity μc and radius λa, is surrounded by a cell-free or cell-depleted layer, with viscosity μp and width δ. A typical resulting velocity profile is shown.
Hematocrit reduction: The Fåhraeus effect
When blood flows in narrow tubes, the concentration of red blood cells within the tube (tube hematocrit, HT) is observed to be less than the concentration in the blood entering and leaving the tube (discharge hematocrit, HD). This reduction in hematocrit is known as the Fåhraeus effect (20) and can be explained by the fact that red blood cells are more concentrated towards the center of the vessel as a consequence of the formation of the cell-free layer, and therefore travel faster than plasma on average and have shorter transit times. It can be shown that
| (68) |
where Vrbc is the mean velocity of red blood cells within the tube, and Vbulk is overall the mean flow velocity (105). Experimental studies of flow in glass tubes led to an empirical relationship for the dependence of the Fåhraeus effect on tube diameter and hematocrit (77):
| (69) |
where D is measured in μm. The value of this ratio is close to one for a tube diameter near 3 μm (the minimum that allows passage of intact red blood cells), drops to a minimum for a diameter of about 13 μm, and increases to approach one as diameter increases further. The minimum value of the ratio is about 0.72 for a discharge hematocrit of 0.45.
Apparent viscosity in glass tubes: The Fåhraeus-Lindqvist effect
Another consequence of non-continuum effects when blood flows through narrow tubes is that the resistance to blood flow cannot be estimated simply by using Poiseuille’s law, Eq. (22), with the viscosity of blood set equal to its bulk value. To describe this phenomenon, it is useful to rearrange Eq. (22) and define the apparent viscosity of blood by
| (70) |
and the relative apparent viscosity by μrel = μapp/μp where μp is the viscosity of the plasma or other suspending medium. Experiments in which human blood was passed through narrow glass tubes showed a substantial decrease in the relative apparent viscosity as tube diameter is decreased below about 300 μm (Figure 17). This phenomenon is known as the Fåhraeus-Lindqvist effect (21,62,77,98). In very small tubes, with diameter near about 3 μm, apparent viscosity increases steeply, because the cells fit tightly in the tube with a very narrow lubricating layer (36).
Figure 17.
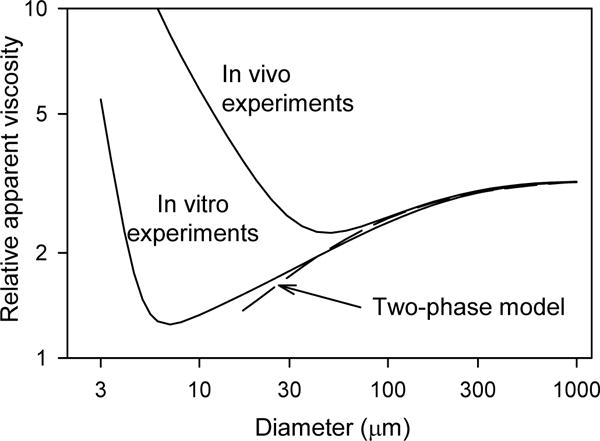
Variation of apparent viscosity with tube diameter for hematocrit HD = 0.45. The lower solid curve represents an empirical fit to experimental in-vitro data (77). The upper solid curve represents the dependence deduced from in-vivo experiments (87). The dashed curve corresponds to a two-phase model with cell-free layer width 1.8 μm, as discussed in the text.
Based on an analysis of multiple experiments using glass tubes, empirical equations were established to describe the variation of μrel with diameter and hematocrit (77):
| (71) |
where
| (72) |
is the relative apparent blood viscosity for a fixed discharge hematocrit of 0.45, and D is the lumen diameter in μm. The coefficient C giving the dependence on hematocrit is governed by:
| (73) |
The dependence of apparent viscosity on diameter when HD = 0.45 is shown in Figure 17 (“In vitro experiments”).
The main cause of this reduction in apparent viscosity of blood in narrow tubes is the formation of a layer of cell-free or cell-depleted plasma near the tube wall, as already discussed. The sensitive dependence of apparent viscosity on the presence of such a layer can be demonstrated using the above two-phase model. By integrating the velocity profile, Eq. (67), to obtain the flow rate, and substituting in Eq. (70), it can be shown that
| (74) |
where λ = 1 − δ/a as before. A good fit to the empirical in-vitro curve for diameters 30 μm and above is obtained by assuming that the width δ of the cell-free layer is independent of tube diameter, with δ = 1.8 μm and , as shown in Figure 17 (96). Physically, the presence of a relatively narrow cell-free layer has a substantial impact on flow resistance, because it results in a lower viscosity in the region near the wall where the shear rate and hence the energy dissipation is highest. For a review of the mechanics of blood flow in smaller tubes, particularly in the diameter range of capillaries, see (97).
Apparent viscosity in vivo
Direct measurements of the apparent viscosity of blood in microvessels in vivo are technically difficult, because of the need to measure pressure drops in individual vessels. A few such measurements (53,54) suggested that apparent viscosity in vivo was substantially higher than expected based on the in-vitro results. Based on a series of studies of the distribution of blood flow and hematocrit in microvascular networks of the rat mesentery, Pries et al. (86,87) deduced a modified empirical relationship to describe the dependence of apparent viscosity on vessel diameter and hematocrit in microvessels:
| (75) |
where
| (76) |
gives the relative apparent blood viscosity for HD = 0.45 and the quantity C is given by Eq. (73) as before. The resulting variation of apparent viscosity HD = 0.45 is shown in Figure 17 (“In vivo experiments”), showing a much higher apparent viscosity in vessels with diameter 30 μm or less, relative to the in-vitro result.
Several explanations of this apparent discrepancy were proposed (86). The main cause was eventually found to be the presence of a relatively thick endothelial surface layer (ESL, or glycocalyx) consisting of macromolecules bound to the inner surface of endothelial cells, with widths of the order of 1 μm (85). In a subsequent analysis (79), the variation of ESL thickness with microvessel diameter and hematocrit was deduced. The resulting relationships for the dependence of Fåhraeus effect and apparent viscosity on diameter and hematocrit provide an alternative to the equations given above.
Phase separation effect in bifurcations
When blood enters a diverging bifurcation in the microcirculation, the partition of the red blood cell flux between the two branches is not generally proportional to the partition of the total flow rate. A low-flow branch tends to draw flow mainly from the peripheral region of the blood stream in the parent vessel, which has a low hematocrit as a consequence of the cell-free layer. Therefore, the lower-flow branch generally receives a lower discharge hematocrit than is present in the parent vessel, while the higher-flow branch generally receives a higher hematocrit.
Based on observations of hematocrit partition in the rat mesentery, a set of empirical equations was proposed to describe the dependence of this phase separation phenomenon on the vessel diameters and on the hematocrit in the parent vessel (76). A slightly modified version of the equations was subsequently developed (79) to give physically reasonable results for extreme combinations of input hematocrit and vessel diameter. These equations relate the fraction FQE of red blood cells entering one branch to the fraction FQB of the total flow in the parent vessel entering that branch:
| (77) |
where logit x = ln(x/(1−x)]. The parameters A, B and X0 are given by:
| (78) |
| (79) |
| (80) |
where Dα, Dβ and DF are the diameters of the two branches and the parent vessel and HD is the discharge hematocrit in the parent vessel.
The resulting behavior is illustrated in Figure 18 for two examples, assuming a discharge hematocrit in the parent vessel HD = 0.4. In a symmetric bifurcation with a parent diameter of 20 μm (Figure 18A), the minimal fraction of the flow that must enter a given branch for it to receive any red blood cells is X0 = 0.029. The fraction of red blood cells entering a given branch then increases nonlinearly with increasing overall flow fraction. Because the bifurcation is symmetric, the behavior is the same for both branches. In a second example (Figure 18B), a parent vessel 10 μm in diameter feeds branches with diameters of 7 and 9 μm, giving X0 = 0.058. The red blood cell fractions in each branch again increase nonlinearly with overall flow fraction. For a given flow fraction, the smaller-diameter branch receives a higher hematocrit. This can be understood as a consequence of the fact that, for any given flow split in the bifurcation, the larger-diameter branch tends to receive flow more from the periphery of the parent vessel, whereas the smaller branch draws from a smaller part of the periphery of the parent vessel and more from the high-hematocrit central core region.
Figure 18.
Red blood cell partition in diverging microvascular bifurcations. Curves giving red blood cell flux fraction in one branch as a function of overall flow fraction entering that branch are derived from empirically derived relationships as described in the text, assuming a discharge hematocrit of 0.4 in the parent vessel. Assumed diameters of parent vessel, DF, and branches, Dα and Dβ, are indicated on each plot. A. Symmetric bifurcation. B. Asymmetric bifurcation.
Hemodynamics of microvascular networks
The above relationships describing the resistance to blood flow in a given segment and the distribution of hematocrit at diverging bifurcations provide a basis for analyzing blood flow in networks of microvessels (55,86). All relevant hemodynamic variables, including hematocrit, velocity, flow rate, pressure and wall shear stress, are found to have highly heterogeneous distributions (83) as a result of the structural heterogeneity of microvessel networks. This structural heterogeneity can be viewed as an inevitable consequence of the geometrical constraints and stochastic mechanisms involved in the growth of microvascular structures. Active biological processes of angiogenesis, structural adaptation and acute flow regulation must compensate for this inherent heterogeneity, in order to achieve adequate and efficient transport functions (81,82).
Conclusion
The study of hemodynamics is a classical area of physiology, with key developments dating back to the sixteenth century. In the second half of the twentieth century, progress in instrumentation for measuring blood flow and pressure, together with increased capabilities for numerical computation, led to a period of rapid development in the study of arterial hemodynamics. During the same period, technical advances in intravital microscopy and measurement techniques also led to progress in characterizing and understanding microcirculatory blood flow. Venous hemodynamics has, however, remained comparatively neglected.
In general, the physical and mechanical aspects of hemodynamics are understood to a considerable extent. The emphasis for future research is likely to be largely on the interaction between hemodynamics and biological processes involving active cellular responses. This interaction occurs in many ways, including the role of hemodynamic forces in vasculogenesis (8), angiogenesis (65) and vascular remodeling (48,78), the contributions of pressure and wall shear stress to local regulation of blood flow (11,41,46), the effects of local variations of wall shear stress in the development of atherosclerotic lesions (120,123), the effect of blood flow patterns on the formation of thromboses (104,120), the interaction between arterial hemodynamics and cardiac function and remodeling (56), the acute control of blood pressure (93), and the role of vascular responses in hypertension (95), to name some prominent examples. Progress in these areas will require advanced biophysical techniques to discover the mechanisms of cellular processes such as mechanotransduction, i.e., the mechanisms by which mechanical signals elicit biological responses in cells. The concepts of hemodynamics, and their basis in the understanding of fluid and solid mechanics, will retain their importance, as they provide the necessary framework for interpreting cellular responses in terms of the integrated structural and functional properties of the circulatory system.
Acknowledgments
This work was supported by NIH grant HL034555. The author thanks Brian Hong for helpful comments.
Reference List
- 1.Alastruey J, Khir AW, Matthys KS, Segers P, Sherwin SJ, Verdonck PR, Parker KH, Peiro J. Pulse wave propagation in a model human arterial network: Assessment of 1-D visco-elastic simulations against in vitro measurements. J Biomech. 2011;44:2250–2258. doi: 10.1016/j.jbiomech.2011.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Asmar R, Rudnichi A, Blacher J, London GM, Safar ME. Pulse pressure and aortic pulse wave are markers of cardiovascular risk in hypertensive populations. Am J Hypertens. 2001;14:91–97. doi: 10.1016/s0895-7061(00)01232-2. [DOI] [PubMed] [Google Scholar]
- 3.Avolio AP, Van Bortel LM, Boutouyrie P, Cockcroft JR, McEniery CM, Protogerou AD, Roman MJ, Safar ME, Segers P, Smulyan H. Role of pulse pressure amplification in arterial hypertension: experts’ opinion and review of the data. Hypertension. 2009;54:375–383. doi: 10.1161/HYPERTENSIONAHA.109.134379. [DOI] [PubMed] [Google Scholar]
- 4.Batchelor GK. An Introduction to Fluid Mechanics. Cambridge University Press; 1967. [Google Scholar]
- 5.Bertram CD, Butcher KS. Possible sources of discrepancy between sphygmomanometer cuff pressure and blood pressure quantified in a collapsible-tube analogue. J Biomech Eng. 1992;114:68–77. doi: 10.1115/1.2895452. [DOI] [PubMed] [Google Scholar]
- 6.Bovendeerd PH, Borsje P, Arts T, van de Vosse FN. Dependence of intramyocardial pressure and coronary flow on ventricular loading and contractility: a model study. Ann Biomed Eng. 2006;34:1833–1845. doi: 10.1007/s10439-006-9189-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Burton AC. Physiology and Biophysics of the Circulation. Chicago: Year Book Medical Publishers; 1972. [Google Scholar]
- 8.Buschmann I, Pries A, Styp-Rekowska B, Hillmeister P, Loufrani L, Henrion D, Shi Y, Duelsner A, Hoefer I, Gatzke N, Wang H, Lehmann K, Ulm L, Ritter Z, Hauff P, Hlushchuk R, Djonov V, van Veen T, le Noble F. Pulsatile shear and Gja5 modulate arterial identity and remodeling events during flow-driven arteriogenesis. Development. 2010;137:2187–2196. doi: 10.1242/dev.045351. [DOI] [PubMed] [Google Scholar]
- 9.Canic S, Tambaca J, Guidoboni G, Mikelic A, Hartley CJ, Rosenstrauch D. Modeling viscoelastic behavior of arterial walls and their interaction with pulsatile blood flow. Siam Journal on Applied Mathematics. 2006;67:164–193. [Google Scholar]
- 10.Cardamone L, Valentin A, Eberth JF, Humphrey JD. Origin of axial prestretch and residual stress in arteries. Biomech Model Mechanobiol. 2009;8:431–446. doi: 10.1007/s10237-008-0146-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Carlson BE, Arciero JC, Secomb TW. Theoretical model of blood flow autoregulation: roles of myogenic, shear-dependent, and metabolic responses. Am J Physiol Heart Circ Physiol. 2008;295:H1572–H1579. doi: 10.1152/ajpheart.00262.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Caro CG, Pedley TJ, Schroter RC, Seed WA. The Mechanics of the Circulation. Oxford: Oxford University Press; 1978. [Google Scholar]
- 13.Chien S. Shear dependence of effective cell volume as a determinant of blood viscosity. Science. 1970;168:977–979. doi: 10.1126/science.168.3934.977. [DOI] [PubMed] [Google Scholar]
- 14.Chien S, Usami S, Taylor HM, Lundberg JL, Gregersen MI. Effects of hematocrit and plasma proteins on human blood rheology at low shear rates. J Appl Physiol. 1966;21:81–87. doi: 10.1152/jappl.1966.21.1.81. [DOI] [PubMed] [Google Scholar]
- 15.Coppola G, Caro C. Arterial geometry, flow pattern, wall shear and mass transport: potential physiological significance. J R Soc Interface. 2009;6:519–528. doi: 10.1098/rsif.2008.0417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Davies JE, Alastruey J, Francis DP, Hadjiloizou N, Whinnett ZI, Manisty CH, Aguado-Sierra J, Willson K, Foale RA, Malik IS, Hughes AD, Parker KH, Mayet J. Attenuation of wave reflection by wave entrapment creates a “horizon effect” in the human aorta. Hypertension. 2012;60:778–785. doi: 10.1161/HYPERTENSIONAHA.111.180604. [DOI] [PubMed] [Google Scholar]
- 17.Dobrin PB. Vascular Mechanics. Compr Physiol Supplement 8: Handbook of Physiology, The Cardiovascular System, Peripheral Circulation and Organ Blood Flow. 2011:65–102. [Google Scholar]
- 18.Ellwein LM, Pope SR, Xie A, Batzel JJ, Kelley CT, Olufsen MS. Patient-specific modeling of cardiovascular and respiratory dynamics during hypercapnia. Math Biosci. 2013;241:56–74. doi: 10.1016/j.mbs.2012.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Euler L. Principia pro motu sanguinis per arterias determinando. In: Fuss PH, Fuss N, editors. Opera posthuma mathematica et physica anno 1844 detecta. Vol. 2. Petropoli: Apund Eggers et Socios; 1775. pp. 814–823. [Google Scholar]
- 20.Fahraeus R. Die Strömungsverhältnisse und die Verteilung der Blutzellen im Gefäβsystem. Zur Frage der Bedeutung der intravasculären Erythrocytenaggregation. Klin Wochenschr. 1928;7:100–106. [Google Scholar]
- 21.Fahraeus R, Lindqvist T. The viscosity of the blood in narrow capillary tubes. Am J Physiol. 1931;96:562–568. [Google Scholar]
- 22.Fedosov DA, Caswell B, Popel AS, Karniadakis GE. Blood Flow and Cell-Free Layer in Microvessels. Microcirculation. 2010;17:615–628. doi: 10.1111/j.1549-8719.2010.00056.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fischer TM, Stohr-Lissen M, Schmid-Schönbein H. The red cell as a fluid droplet: tank tread-like motion of the human erythrocyte membrane in shear flow. Science. 1978;202:894–896. doi: 10.1126/science.715448. [DOI] [PubMed] [Google Scholar]
- 24.Fishman AP, Richards DW. Circulation of the Blood: Men and Ideas. New York: Oxford University Press; 1964. [Google Scholar]
- 25.Frank O. Die Grundform des arteriellen Pulses. Erste Abhandlung. Mathematische Analyse. Zeitschrift für Biologie. 1899;37:483–526. [Google Scholar]
- 26.Fronek K, Zweifach BW. Microvascular pressure distribution in skeletal muscle and the effect of vasodilation. Am J Physiol. 1975;228:791–796. doi: 10.1152/ajplegacy.1975.228.3.791. [DOI] [PubMed] [Google Scholar]
- 27.Fung YC. Biomechanics. Mechanical Properties of Living Tissues. Second. New York: Springer; 1993. [Google Scholar]
- 28.Fung YC. Biomechanics: Circulation. Second. New York: Springer-Verlag; 1997. [Google Scholar]
- 29.Fung YC, Liu SQ. Strain distribution in small blood vessels with zero-stress state taken into consideration. Am J Physiol. 1992;262:H544–H552. doi: 10.1152/ajpheart.1992.262.2.H544. [DOI] [PubMed] [Google Scholar]
- 30.Gore RW. Pressures in cat mesenteric arterioles and capillaries during changes in systemic arterial blood pressure. Circ Res. 1974;34:581–591. doi: 10.1161/01.res.34.4.581. [DOI] [PubMed] [Google Scholar]
- 31.Grandchamp X, Coupier G, Srivastav A, Minetti C, Podgorski T. Lift and down-gradient shear-induced diffusion in red blood cell suspensions. Physical Review Letters. 2013;110 doi: 10.1103/PhysRevLett.110.108101. [DOI] [PubMed] [Google Scholar]
- 32.Greenwald SE, Carter AC, Berry CL. Effect of age on the in vitro reflection coefficient of the aortoiliac bifurcation in humans. Circulation. 1990;82:114–123. doi: 10.1161/01.cir.82.1.114. [DOI] [PubMed] [Google Scholar]
- 33.Greve JM, Les AS, Tang BT, Draney Blomme MT, Wilson NM, Dalman RL, Pelc NJ, Taylor CA. Allometric scaling of wall shear stress from mice to humans: quantification using cine phase-contrast MRI and computational fluid dynamics. Am J Physiol Heart Circ Physiol. 2006;291:H1700–H1708. doi: 10.1152/ajpheart.00274.2006. [DOI] [PubMed] [Google Scholar]
- 34.Hagenbach E. Uber die Bestimmung der Zähigkeit einer Flüssigkeit durch den Ausfluss aus Röhren. Poggendorf’s Annalen der Physik und Chemie. 1860;108:385–426. [Google Scholar]
- 35.Hales S. Statical essays: containing haemosticks, reprinted 1964, No. 22, History of Medicine series, Library of New York Academy of Medicine. New York: Hafner; 1733. [Google Scholar]
- 36.Halpern D, Secomb TW. The squeezing of red blood cells through capillaries with near-minimal diameters. Journal of Fluid Mechanics. 1989;203:381–400. [Google Scholar]
- 37.Hariprasad DS, Secomb TW. Two-dimensional simulation of red blood cell motion near a wall under a lateral force. Physical Review e. 2014;90:053014. doi: 10.1103/PhysRevE.90.053014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Harvey W. Exercitatio Anatomica de Motu Cordis et Sanguinis in Animalibus. 1628. English translation with annotations, C.D. Leake. 4th. Springfield, Ill: Thomas; 1958. [Google Scholar]
- 39.Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity. 2000;61:1–48. [Google Scholar]
- 40.Humphrey JD, Delange SL. An Introduction to Biomechanics. Solids and Fluids, Analysis and Design. New York: Springer; 2004. [Google Scholar]
- 41.Johnson PC. The myogenic response. In: Bohr DF, Somlyo AP, Sparks HV Jr, editors. Handbook of Physiology, Section 2, The Cardiovascular System, Vol II: Vascular Smooth Muscle. Bethesda, MD: American Physiological Society; 1980. pp. 409–442. [Google Scholar]
- 42.Jones CJ, Parker KH, Hughes R, Sheridan DJ. Nonlinearity of human arterial pulse wave transmission. J Biomech Eng. 1992;114:10–14. doi: 10.1115/1.2895433. [DOI] [PubMed] [Google Scholar]
- 43.Kilner PJ, Yang GZ, Firmin DN. Morphodynamics of flow through sinuous curvatures of the heart. Biorheology. 2002;39:409–417. [PubMed] [Google Scholar]
- 44.Kilner PJ, Yang GZ, Mohiaddin RH, Firmin DN, Longmore DB. Helical and retrograde secondary flow patterns in the aortic arch studied by three-directional magnetic resonance velocity mapping. Circulation. 1993;88:2235–2247. doi: 10.1161/01.cir.88.5.2235. [DOI] [PubMed] [Google Scholar]
- 45.Kim S, Popel AS, Intaglietta M, Johnson PC. Effect of erythrocyte aggregation at normal human levels on functional capillary density in rat spinotrapezius muscle. Am J Physiol Heart Circ Physiol. 2006;290:H941–H947. doi: 10.1152/ajpheart.00645.2005. [DOI] [PubMed] [Google Scholar]
- 46.Koller A, Kaley G. Endothelial regulation of wall shear stress and blood flow in skeletal muscle microcirculation. Am J Physiol. 1991;260:H862–H868. doi: 10.1152/ajpheart.1991.260.3.H862. [DOI] [PubMed] [Google Scholar]
- 47.Lakatta EG, Levy D. Arterial and cardiac aging: major shareholders in cardiovascular disease enterprises: Part I: aging arteries: a “set up” for vascular disease. Circulation. 2003;107:139–146. doi: 10.1161/01.cir.0000048892.83521.58. [DOI] [PubMed] [Google Scholar]
- 48.Langille BL. Arterial remodeling: relation to hemodynamics. Can J Physiol Pharmacol. 1996;74:834–841. [PubMed] [Google Scholar]
- 49.Langille BL, O’Donnell F. Reductions in arterial diameter produced by chronic decreases in blood flow are endothelium-dependent. Science. 1986;231:405–407. doi: 10.1126/science.3941904. [DOI] [PubMed] [Google Scholar]
- 50.Laurent S, Cockcroft J, Van BL, Boutouyrie P, Giannattasio C, Hayoz D, Pannier B, Vlachopoulos C, Wilkinson I, Struijker-Boudier H. Expert consensus document on arterial stiffness: methodological issues and clinical applications. Eur Heart J. 2006;27:2588–2605. doi: 10.1093/eurheartj/ehl254. [DOI] [PubMed] [Google Scholar]
- 51.Levick JR. An Introduction to Cardiovascular Physiology. Fourth. London: Hodder Arnold; 2003. [Google Scholar]
- 52.Lindert J, Werner J, Redlin M, Kuppe H, Habazettl H, Pries AR. OPS imaging of human microcirculation: a short technical report. J Vasc Res. 2002;39:368–372. doi: 10.1159/000065549. [DOI] [PubMed] [Google Scholar]
- 53.Lipowsky HH, Kovalcheck S, Zweifach BW. The distribution of blood rheological parameters in the mirovasculature of the cat mesentery. Circ Res. 1978;43:738–749. doi: 10.1161/01.res.43.5.738. [DOI] [PubMed] [Google Scholar]
- 54.Lipowsky HH, Usami S, Chien S. In vivo measurements of “apparent viscosity” and microvessel hematocrit in the mesentery of the cat. Microvasc Res. 1980;19:297–319. doi: 10.1016/0026-2862(80)90050-3. [DOI] [PubMed] [Google Scholar]
- 55.Lipowsky HH, Zweifach BW. Network analysis of microcirculation of cat mesentery. Microvasc Res. 1974;7:73–83. doi: 10.1016/0026-2862(74)90038-7. [DOI] [PubMed] [Google Scholar]
- 56.London GM, Guerin AP. Influence of arterial pulse and reflected waves on blood pressure and cardiac function. Am Heart J. 1999;138:220–224. doi: 10.1016/s0002-8703(99)70313-3. [DOI] [PubMed] [Google Scholar]
- 57.Love AEH. A Treatise on the Mathematical Theory of Elasticity. 4th. New York: Dover; 1944. [Google Scholar]
- 58.Luchsinger PC, Snell RE, Patel DJ, Fry DL. Instantaneous pressure distribution along the human aorta. Circ Res. 1964;15:503–510. doi: 10.1161/01.res.15.6.503. [DOI] [PubMed] [Google Scholar]
- 59.Malek AM, Alper SL, Izumo S. Hemodynamic shear stress and its role in atherosclerosis. JAMA. 1999;282:2035–2042. doi: 10.1001/jama.282.21.2035. [DOI] [PubMed] [Google Scholar]
- 60.Mall FP. Die Blut und Lymphwege in Dunndarm des Hundes. Abhandlungen der Mathematisch-Physischen Classe der Königlich Sachsischen Gessellschaft der Wissenschaften. 1888;14:151–200. [Google Scholar]
- 61.Malpighi M. De Pulmonibus. Observations Anatomicae Bologna. 1661. In: Young J, translator. Proceedings of the Royal Society of Medicine. Vol. 23. 1929. pp. 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Martini P, Pierach A, Schreyer E. Die Strömung des Blutes in engen Gefäβen. Eine Abweichung vom Poiseuille’schen Gesetz. Dt Arch Klin Med. 1930;169:212–222. [Google Scholar]
- 63.McDonald DA. The relation of pulsatile pressure to flow in arteries. J Physiol. 1955;127:533–552. doi: 10.1113/jphysiol.1955.sp005275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.McDonald DA. Blood Flow in Arteries. Second. London: Edward Arnold; 1974. [Google Scholar]
- 65.Milkiewicz M, Brown MD, Egginton S, Hudlicka O. Association between shear stress, angiogenesis, and VEGF in skeletal muscles in vivo. Microcirculation. 2001;8:229–241. doi: 10.1038/sj/mn/7800074. [DOI] [PubMed] [Google Scholar]
- 66.Milnor WR. Hemodynamics. Second. Baltimore: Williams and Wilkins; 1989. [Google Scholar]
- 67.Mitchell GF, Guo CY, Benjamin EJ, Larson MG, Keyes MJ, Vita JA, Vasan RS, Levy D. Cross-sectional correlates of increased aortic stiffness in the community: the Framingham Heart Study. Circulation. 2007;115:2628–2636. doi: 10.1161/CIRCULATIONAHA.106.667733. [DOI] [PubMed] [Google Scholar]
- 68.Motomiya M, Karino T. Flow patterns in the human carotid artery bifurcation. Stroke. 1984;15:50–56. doi: 10.1161/01.str.15.1.50. [DOI] [PubMed] [Google Scholar]
- 69.Mulvany MJ. Small artery remodelling in hypertension. Basic Clin Pharmacol Toxicol. 2012;110:49–55. doi: 10.1111/j.1742-7843.2011.00758.x. [DOI] [PubMed] [Google Scholar]
- 70.Mynard JP, Smolich JJ. Wave potential and the one-dimensional windkessel as a wave-based paradigm of diastolic arterial hemodynamics. Am J Physiol Heart Circ Physiol. 2014;307:H307–H318. doi: 10.1152/ajpheart.00293.2014. [DOI] [PubMed] [Google Scholar]
- 71.Nichols WW, O’Rourke MF. McDonald’s Blood Flow in Arteries. Theoretical, experimental and clinical principles. Fourth. London: Arnold; 1998. [Google Scholar]
- 72.Parker KH. A brief history of arterial wave mechanics. Med Biol Eng Comput. 2009;47:111–118. doi: 10.1007/s11517-009-0440-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Pedley TJ. The Fluid Mechanics of Large Blood Vessels. Cambridge University Press; 1980. [Google Scholar]
- 74.Poiseuille JLM. Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamêtres. Mémoires presentés par divers savants à l’Académie Royale des Sciences de l’Institut de France. 1846;IX:433–544. [Google Scholar]
- 75.Pranay P, Henriquez-Rivera RG, Graham MD. Depletion layer formation in suspensions of elastic capsules in Newtonian and viscoelastic fluids. Physics of Fluids. 2012;24 [Google Scholar]
- 76.Pries AR, Ley K, Claassen M, Gaehtgens P. Red cell distribution at microvascular bifurcations. Microvasc Res. 1989;38:81–101. doi: 10.1016/0026-2862(89)90018-6. [DOI] [PubMed] [Google Scholar]
- 77.Pries AR, Neuhaus D, Gaehtgens P. Blood viscosity in tube flow: dependence on diameter and hematocrit. Am J Physiol. 1992;263:H1770–H1778. doi: 10.1152/ajpheart.1992.263.6.H1770. [DOI] [PubMed] [Google Scholar]
- 78.Pries AR, Reglin B, Secomb TW. Remodeling of blood vessels: responses of diameter and wall thickness to hemodynamic and metabolic stimuli. Hypertension. 2005;46:725–731. doi: 10.1161/01.HYP.0000184428.16429.be. [DOI] [PubMed] [Google Scholar]
- 79.Pries AR, Secomb TW. Microvascular blood viscosity in vivo and the endothelial surface layer. Am J Physiol Heart Circ Physiol. 2005;289:H2657–H2664. doi: 10.1152/ajpheart.00297.2005. [DOI] [PubMed] [Google Scholar]
- 80.Pries AR, Secomb TW. Blood Flow in Microvascular Networks. In: Tuma RF, Duran WN, Ley K, editors. Handbook of Physiology: Microcirculation. Second. San Diego: Academic Press; 2008. pp. 3–36. [Google Scholar]
- 81.Pries AR, Secomb TW. Origins of heterogeneity in tissue perfusion and metabolism. Cardiovasc Res. 2009;81:328–335. doi: 10.1093/cvr/cvn318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Pries AR, Secomb TW, Gaehtgens P. Design principles of vascular beds. Circ Res. 1995;77:1017–1023. doi: 10.1161/01.res.77.5.1017. [DOI] [PubMed] [Google Scholar]
- 83.Pries AR, Secomb TW, Gaehtgens P. Structure and hemodynamics of microvascular networks: heterogeneity and correlations. Am J Physiol. 1995;269:H1713–H1722. doi: 10.1152/ajpheart.1995.269.5.H1713. [DOI] [PubMed] [Google Scholar]
- 84.Pries AR, Secomb TW, Gaehtgens P. Structural autoregulation of terminal vascular beds: vascular adaptation and development of hypertension. Hypertension. 1999;33:153–161. doi: 10.1161/01.hyp.33.1.153. [DOI] [PubMed] [Google Scholar]
- 85.Pries AR, Secomb TW, Gaehtgens P. The endothelial surface layer. Pflugers Arch. 2000;440:653–666. doi: 10.1007/s004240000307. [DOI] [PubMed] [Google Scholar]
- 86.Pries AR, Secomb TW, Gaehtgens P, Gross JF. Blood flow in microvascular networks. Experiments and simulation. Circ Res. 1990;67:826–834. doi: 10.1161/01.res.67.4.826. [DOI] [PubMed] [Google Scholar]
- 87.Pries AR, Secomb TW, Gessner T, Sperandio MB, Gross JF, Gaehtgens P. Resistance to blood flow in microvessels in vivo. Circ Res. 1994;75:904–915. doi: 10.1161/01.res.75.5.904. [DOI] [PubMed] [Google Scholar]
- 88.Recek C. Conception of the venous hemodynamics in the lower extremity. Angiology. 2006;57:556–563. doi: 10.1177/0003319706293117. [DOI] [PubMed] [Google Scholar]
- 89.Rhodin JAG. Architecture of the vessel wall. Compr Physiol Supplement 7: Handbook of Physiology, The Cardiovascular System, Vascular Smooth Muscle. 2011:1–31. [Google Scholar]
- 90.Richardson DR, Zweifach BW. Pressure relationships in the macro- and microcirculation of the mesentery. Microvasc Res. 1970;2:474–488. doi: 10.1016/0026-2862(70)90040-3. [DOI] [PubMed] [Google Scholar]
- 91.Rodbard S. Vascular caliber. Cardiology. 1975;60:4–49. doi: 10.1159/000169701. [DOI] [PubMed] [Google Scholar]
- 92.Safar ME, Levy BI, Struijker-Boudier H. Current perspectives on arterial stiffness and pulse pressure in hypertension and cardiovascular diseases. Circulation. 2003;107:2864–2869. doi: 10.1161/01.CIR.0000069826.36125.B4. [DOI] [PubMed] [Google Scholar]
- 93.Sagawa K. Baroreflex Control of Systemic Arterial Pressure and Vascular Bed. First published in print 1983. Compr Physiol Supplement 8: Handbook of Physiology, The Cardiovascular System, Peripheral Circulation and Organ Blood Flow. 2011:453–496. [Google Scholar]
- 94.Sato M, Hayashi K, Niimi H, Moritake K, Okumura A, Handa H. Axial mechanical properties of arterial walls and their anisotropy. Med Biol Eng Comput. 1979;17:170–176. doi: 10.1007/BF02440925. [DOI] [PubMed] [Google Scholar]
- 95.Schiffrin EL. Vascular remodeling in hypertension: mechanisms and treatment. Hypertension. 2012;59:367–374. doi: 10.1161/HYPERTENSIONAHA.111.187021. [DOI] [PubMed] [Google Scholar]
- 96.Secomb TW. Mechanics of blood flow in the microcirculation. Symp Soc Exp Biol. 1995;49:305–321. [PubMed] [Google Scholar]
- 97.Secomb TW. Mechanics of red blood cells and blood flow in narrow tubes. In: Pozrikidis C, editor. Modeling and Simulation of Capsules and Biological Cells. Boca Raton, Florida: Chapman & Hall/CRC; 2003. pp. 163–196. [Google Scholar]
- 98.Secomb TW, Pries AR. Blood viscosity in microvessels: Experiment and theory. Comptes Rendus Physique. 2013;14:470–478. doi: 10.1016/j.crhy.2013.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Segers P, Mynard J, Taelman L, Vermeersch S, Swillens A. Wave reflection: Myth or reality? Artery Research. 2012;6:7–11. [Google Scholar]
- 100.Sharman JE, Davies JE, Jenkins C, Marwick TH. Augmentation index, left ventricular contractility, and wave reflection. Hypertension. 2009;54:1099–1105. doi: 10.1161/HYPERTENSIONAHA.109.133066. [DOI] [PubMed] [Google Scholar]
- 101.Skalak R. Wave propagation in blood flow. In: Fung YC, editor. Biomechanics Symposium. New York: American Society of Mechanical Engineers; 1966. pp. 20–46. [Google Scholar]
- 102.Skalak R, Keller SR, Secomb TW. Mechanics of blood flow. J Biomech Eng. 1981;103:102–115. doi: 10.1115/1.3138253. [DOI] [PubMed] [Google Scholar]
- 103.Stranden E. Edema in venous insufficiency. Phlebolymphology. 2011;18:3–15. [Google Scholar]
- 104.Strony J, Beaudoin A, Brands D, Adelman B. Analysis of shear stress and hemodynamic factors in a model of coronary artery stenosis and thrombosis. Am J Physiol. 1993;265:H1787–H1796. doi: 10.1152/ajpheart.1993.265.5.H1787. [DOI] [PubMed] [Google Scholar]
- 105.Sutera SP, Seshadri V, Croce PA, Hochmuth RM. Capillary blood flow. II. Deformable model cells in tube flow. Microvasc Res. 1970;2:420–433. doi: 10.1016/0026-2862(70)90035-x. [DOI] [PubMed] [Google Scholar]
- 106.Sutera SP, Skalak R. The History of Poiseuille’s Law. Annual Review of Fluid Mechanics. 1993;25:1–19. [Google Scholar]
- 107.Tanaka TT, Fung YC. Elastic and inelastic properties of the canine aorta and their variation along the aortic tree. J Biomech. 1974;7:357–370. doi: 10.1016/0021-9290(74)90031-1. [DOI] [PubMed] [Google Scholar]
- 108.Trendelenburg F. Über die Unterverbindung der Vena saphena magna bei Unterschenkelvarizen. Beitr Klin Chir. 1891;7:195–210. [Google Scholar]
- 109.Tyberg JV, Davies JE, Wang Z, Whitelaw WA, Flewitt JA, Shrive NG, Francis DP, Hughes AD, Parker KH, Wang JJ. Wave intensity analysis and the development of the reservoir-wave approach. Med Biol Eng Comput. 2009;47:221–232. doi: 10.1007/s11517-008-0430-z. [DOI] [PubMed] [Google Scholar]
- 110.Ursino M. Interaction between carotid baroregulation and the pulsating heart: a mathematical model. Am J Physiol. 1998;275:H1733–H1747. doi: 10.1152/ajpheart.1998.275.5.H1733. [DOI] [PubMed] [Google Scholar]
- 111.Vaishnav RN, Vossoughi J. Residual stress and strain in aortic segments. J Biomech. 1987;20:235–239. doi: 10.1016/0021-9290(87)90290-9. [DOI] [PubMed] [Google Scholar]
- 112.van de Vosse FN, Stergiopulos N. Pulse Wave Propagation in the Arterial Tree. Annual Review of Fluid Mechanics, Vol 43. 2011;43:467–499. [Google Scholar]
- 113.Vand V. Viscosity of solutions and suspensions. I. Theory. J Phys Colloid Chem. 1948;52:277–299. doi: 10.1021/j150458a001. [DOI] [PubMed] [Google Scholar]
- 114.Weizsacker HW, Pinto JG. Isotropy and anisotropy of the arterial wall. J Biomech. 1988;21:477–487. doi: 10.1016/0021-9290(88)90240-0. [DOI] [PubMed] [Google Scholar]
- 115.West JB. Respiratory Physiology – The Essentials. Baltimore: Williams and Wilkins; 1974. [Google Scholar]
- 116.Westerhof N, Boer C, Lamberts RR, Sipkema P. Cross-talk between cardiac muscle and coronary vasculature. Physiol Rev. 2006;86:1263–1308. doi: 10.1152/physrev.00029.2005. [DOI] [PubMed] [Google Scholar]
- 117.Westerhof N, Lankhaar JW, Westerhof BE. The arterial Windkessel. Med Biol Eng Comput. 2009;47:131–141. doi: 10.1007/s11517-008-0359-2. [DOI] [PubMed] [Google Scholar]
- 118.Wexler L, Bergel DH, Gabe IT, Makin GS, Mills CJ. Velocity of blood flow in normal human venae cavae. Circ Res. 1968;23:349–359. doi: 10.1161/01.res.23.3.349. [DOI] [PubMed] [Google Scholar]
- 119.Womersley JR. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J Physiol. 1955;127:553–563. doi: 10.1113/jphysiol.1955.sp005276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Wootton DM, Ku DN. Fluid mechanics of vascular systems, diseases, and thrombosis. Annu Rev Biomed Eng. 1999;1:299–329. doi: 10.1146/annurev.bioeng.1.1.299. [DOI] [PubMed] [Google Scholar]
- 121.Young T. Hydraulic investigations, subservient to an intended Croonian lecture on the motion of the blood. Phil Trans Roy Soc. 1808;98:164–186. [Google Scholar]
- 122.Young T. On the functions of the heart and arteries. The Croonian lecture. Phil Trans Roy Soc. 1809;99:1–31. [Google Scholar]
- 123.Zarins CK, Giddens DP, Bharadvaj BK, Sottiurai VS, Mabon RF, Glagov S. Carotid bifurcation atherosclerosis. Quantitative correlation of plaque localization with flow velocity profiles and wall shear stress. Circ Res. 1983;53:502–514. doi: 10.1161/01.res.53.4.502. [DOI] [PubMed] [Google Scholar]
- 124.Zweifach BW. Quantitative studies of microcirculatory structure and function. II. Direct measurement of capillary pressure in splanchnic mesenteric vessels. Circ Res. 1974;34:858–866. [PubMed] [Google Scholar]


