Abstract
Binary phenotypes commonly arise due to multiple underlying quantitative precursors. Genetic variants may impact multiple traits in a pleiotropic manner. Hence, simultaneously analyzing such correlated traits may be more powerful than analyzing individual traits. Various genotype-level methods, e.g. MultiPhen [O'Reilly et al., 2012], have been developed to identify genetic factors underlying a multivariate phenotype. For univariate phenotypes, the usefulness and applicability of allele-level tests have been investigated. The test of allele frequency difference among cases and controls is commonly used for mapping case-control association. However, allelic methods for multivariate association mapping have not been studied much. We explore two allelic tests of multivariate association: one using a Binomial regression model based on inverted regression of genotype on phenotype (BAMP), and the other employing the Mahalanobis distance between two sample means of the multivariate phenotype vector for two alleles at a SNP (DAMP). These methods can incorporate both discrete and continuous phenotypes. Some theoretical properties for BAMP are studied. Using simulations, the power of the methods for detecting multivariate association are compared with the genotype-level test MultiPhen. The allelic tests yield marginally higher power than MultiPhen for multivariate phenotypes. For one/two binary traits under recessive mode of inheritance, allelic tests are found substantially more powerful. All three tests are applied to two real data and the results offer some support for the simulation study. Since the allelic approaches assume Hardy-Weinberg Equilibrium (HWE), we propose a hybrid approach for testing multivariate association that implements MultiPhen when HWE is violated and BAMP otherwise.
Keywords: Genome-wide association study, multiple phenotypes, multivariate association, allelic tests
Introduction
A clinical trait or disease with a complex end-point is generally characterized by multiple quantitative precursors. In such situations, one can improve statistical power by considering a multivariate phenotype [Lange et al., 2004; Klei et al., 2008; O'Reilly et al., 2012; Stephens, 2013; Zhu et al., 2014]. Moreover, in the presence of association with multiple traits, a multivariate approach is biologically more consistent than a univariate approach. Galesloot et al. [2014] showed that the use of multivariate association analyses can yield higher power compared to univariate analyses even when genetic correlations between traits are weak or when a genetic variant is only associated with one of the phenotypes (that is, when there is no multivariate association). For example, cardiovascular disease (CVD) is characterized by high levels of both low-density serum lipoprotein levels (LDL) and systolic blood pressure (SBP) [Newman et al., 1986]. In order to identify genomic regions associated with CVD, it may be intuitively more appealing and statistically more powerful to carry out association tests with a bivariate phenotype vector comprising LDL and SBP instead of the binary CVD phenotype.
To analyze such data, one can implement a multivariate regression approach such as MANOVA, but this requires that the vector of traits have an approximate multivariate normal distribution. This assumption may be difficult to satisfy for a vector comprising mixed phenotypes, such as, when one trait is binary and the other is continuous. Several methods using variations of generalized estimating equations (GEE) have been developed to incorporate non-normal traits [Zeger and Liang, 1986; Liu et al., 2009]. A log-linear approach [Lee et al., 2011] and a Bayesian network approach [Hartley et al., 2012] have been used to model multiple categorical phenotypes. The linear mixed model approach [Korte et al., 2012] provides a flexible framework to account for the correlation structure between SNPs as well as between individuals in a genome-wide association scan of multiple phenotypes. Other existing methods such as likelihood-based variance components [Almasy and Blangero, 2010] are susceptible to violation in underlying distributional assumptions. Another approach that circumvents the problem of modeling the multivariate phenotype is to obtain a reduced univariate phenotype using principal components [Klei et al., 2008; Minica et al., 2010]. However, association results based on principal components may be difficult to interpret biologically. For example, the first principal component of LDL and SBP is a linear combination of the two traits that explains the highest variability among the traits. However, it is difficult to understand the biological meaning or genetic underpinnings of such a derived trait.
An alternative approach to association mapping of multivariate phenotypes is to reverse the conventional model and regress genotypes on the multivariate phenotype. One such approach has been termed MultiPhen [O'Reilly et al., 2012] and has been shown to yield high power for detecting association with multiple traits [Galesloot et al., 2014]. The advantages of such an approach include the flexibility of incorporating traits of mixed type (binary, discrete or continuous) in the vector of phenotypes, allowing for heterogeneity in both the extent and the direction of association between the genetic variant and each constituent phenotype, robustness to possible violations in underlying distributional assumptions and the possibility of adjustment for covariates simultaneously with the multiple phenotypes.
For univariate traits, allele-level test for association has been investigated comparing its performance with genotype-level test [Guedj et al., 2008; Zheng, 2008; Lee et al., 2013]. To the best of our knowledge, careful studies of allele-level tests for mapping association with multiple traits have not been undertaken. In this article, we explore two allelic tests for association with multiple phenotypes: one based on a binomial regression model (BAMP, Binomial regression-based Association of Multivariate Phenotypes) and the other an extension of the the allelic test for univariate traits proposed by Lee et al. [2013] to include multiple phenotypes (DAMP, Distance-based Association of Multivariate Phenotypes). We can view BAMP as a suitable modification of MultiPhen [O'Reilly et al., 2012] at the allelic level and show that it is equivalent to the classical case control allele-based test of association for binary traits. BAMP is proposed in the framework of inverted regression of genotype on phenotypes whereas DAMP is formulated as a test of difference between the two sample means of vectors of the multivariate phenotype corresponding to the two alleles at a SNP under the usual set-up of regressing phenotype on genotype.
Using simulations under a wide spectrum of multivariate phenotype models, we compare the performance of BAMP and DAMP with MultiPhen. We find that, for multivariate phenotypes, both the allelic tests produce comparable powers, but marginally higher than MultiPhen, in particular, BAMP yields a consistent marginal increase of power over MultiPhen. It is also found that, for a single or two binary traits under a recessive mode of inheritance, the allelic tests offer substantially higher power than MultiPhen. We also demonstrate the advantage of using allelic tests by carrying out association analyses on two real data of multivariate phenotypes: one comprising homocysteine levels, Vitamin B12 levels and coronary artery disease (CAD) status in a North Indian population, and another comprising four case-control phenotypes - hypertension, diabetes type II, cardiovascular disease, and cancers for European-American population in “Resource for Genet Epidemiol Research on Adult Health and Aging” (GERA) cohort data obtained from dbGaP [dbGaP Study Accession: phs000674.v1.p1]. Based on our observations, we propose a hybrid approach for mapping association with multiple traits that uses MultiPhen when variants fail HWE and BAMP otherwise.
Methods
Suppose Y = (Y1, . . . , Yk) denotes a multivariate phenotype vector, where Yj, j = 1, 2, . . . , k, can be either a qualitative or a quantitative trait. We assume that the multivariate phenotype is controlled by a biallelic trait locus with alleles A1 (minor) and A2. Consider a biallelic marker locus with alleles M1 (minor) and M2 such that the coefficient of linkage disequilibrium between the trait locus and the marker locus is δ, which is defined as δ = P(A1M1) – P(A1)P(M1). Suppose X denotes the number of minor alleles (0, 1, or 2) at the marker locus. We denote the frequencies of the alleles A1 and M1 by p and m, respectively. We assume that data are available on the genotypes at the marker locus and on the k-dimensional multivariate phenotype vectors for n unrelated individuals randomly selected from a population. Suppose Yi = (Yi1, . . . , Yik) and Xi represent the multivariate phenotype data and the count of the allele M1, respectively, for the ith individual, i = 1, . . . , n.
MultiPhen
The genotype-level test implemented in MultiPhen, is based on a proportional odds logistic regression model [O'Reilly et al., 2012] given by:
Thus, the conditional distribution of the genotypes given Y = y can be obtained as follows:
with the restriction that α0 ≥ α1 (in order to satisfy that P(X = 1|y) is non-negative). A liklihood ratio test can be performed in this proportional odds logistic regression framework corresponding to versus .
BAMP
We model the conditional distribution of X (the number of minor alleles at the marker locus) given Y = y (the vector of multivariate phenotype) as binomial with parameters 2 and p(y), where p(y) is a logistic link function given by:
It follows that p(y) = P(M1|y). The model implicitly assumes that, conditioned on the vector of multivariate phenotype, the marker locus is in Hardy-Weinberg Equilibrium (HWE). The test for association is equivalent to testing H0 : β1 = . . . = βk = 0 versus H1 : at least one βj ≠ 0, j = 1, . . . , k. Under H0, the minor allele frequency at the marker locus is independent of y and is given by: . The test can be performed using a likelihood ratio statistic which is distributed as chi-square with k degrees of freedom under H0. We note that this test procedure can be viewed as an allelic modification of MultiPhen.
We highlight the following two theoretical properties of BAMP:
Property 1
Testing for H0 : β1 = . . . = βk = 0 vs H1 : at least one βj ≠ 0, j = 1, . . . , k, is equivalent to testing H0 : δ = 0 (no association between the marker locus and the traits) vs H1 : δ ≠ 0 (presence of association).
Property 2
If the phenotype is binary (in a case-control framework), BAMP is equivalent to the usual test of difference in allele frequencies among cases and controls.
The proof of each of the properties is provided in the Appendix. In genome-wide association studies (GWAS), the causal SNPs themselves may not be genotyped, rather the SNPs that are in linkage dis-equilibrium (LD) with them are identified through tests for association. Hence, a detected association between a marker SNP and the phenotypes under consideration is attributed to the non-zero LD between the marker and the causal SNPs. Thus, it is of interest to mathematically prove that testing the null hypothesis of no genotype-phenotype association against the alternative hypothesis of presence of association, is equivalent to testing δ = 0 versus δ ≠ 0.
We note that the proof of Property 1 is based on the assumption that the association between a marker SNP and multivariate phenotypes is induced due to non-zero LD (δ ≠ 0) between the marker SNP and a single causal SNP instead of multiple independent causal SNPs present in nearby genomic regions. This assumption is crucial for the ease of mathematical derivation underlying the proof. Because, the proof is based on the explicit expression of the joint probability of genotypes at one marker and one causal SNP that are in LD. But, the expression of this joint probability for genotypes at the marker and multiple causal SNPs, with each of which the marker is in LD, can be algebraically intractable.
While proving Property 1, δ is used as the definition of LD since it is sufficient for the derivation. Other commonly used formulations of LD, for example, r2 (δ2 divided by the variance of allele frequencies at the two loci) and D′ (δ standardized by its minimum and maximum), are essentially derived based on δ.
DAMP
Motivated by the allelic version of the genotype-level test corresponding to a quantitative phenotype [Lee et al., 2013], we propose a suitable multivariate extension as follows. Suppose (Y1, Y2, . . . , Yn) denote the multivariate phenotype vectors corresponding to n randomly selected individuals in the population. We consider two groups of observations corresponding to the two alleles M1 (minor) and M2 at the marker locus. If the genotype of the ith individual is M1M1, we assign two observations each equal to Yi in the first group, if the genotype is M2M2, we assign two observations each equal to Yi in the second group; and if the genotype is M1M2, we assign one observation equal to Yi in each of the two groups. Hence, if the first group is of size n1 and the second group is of size n2, the total number of observations in the two groups is 2n. If the population means of the multivariate phenotype vector Y conditioned on the two groups are μ1 and μ2, respectively, the test for association can be performed by testing H0 : μ1 = μ2 versus H1 : μ1 ≠ μ2. Assuming that the covariance structure of Y (Σ) is identical in the two groups, for sufficiently large n1 and n2,
The above asymptotic distributions are obtained using the multivariate central limit theorem (MCLT). The test statistic is based on the Mahalanobis distance between the sample mean vectors of the two groups (ȲM1 and ȲM2). If the sample sizes of the two groups (n1 and n2) are sufficiently large, then it follows from the MCLT that, the test statistic (ȲM1 – ȲM2)′S−1(ȲM1 – ȲM2) is asymptotically distributed as chi-square with k degrees of freedom, where S is the combined sample covariance matrix of Y based on the two groups, and hence a consistent estimator of Σ.
For a binary phenotype, the allelic test based on allele frequencies is asymptotically equivalent to the genotype-based trend test under the assumption of HWE [Guedj et al., 2006, 2008; Sasieni, 1997; Zheng, 2008]. We note that the allele-based method proposed by Lee et al. [2013] in the context of a single quantitative trait uses a linear regression of the phenotype on each of the alleles constituting the genotype of an individual. The above method (DAMP) is equivalent to a direct multivariate extension of regressing the vector of phenotypes on the alleles. However, Lee et al. [2013] showed that, considering the allele status (coded as 0 or 1) as a predictor in the linear regression and ignoring the correlation induced by replicating the phenotype data twice, yields marginally lower power compared to using the genotype status (coded as 0, 1 or 2) as a predictor.
Simulation study
We carried out simulation studies to compare the false positive rates and powers of MultiPhen, BAMP, and DAMP for detecting association with multiple traits.
Simulation models
We consider a vector of quantitative traits Y = (Y1, . . . , Yk) that is modulated by a biallelic QTL with alleles A1 and A2, and a random vector of environmental components e = (e1, . . . , ek) having mean vector zero and covariance matrix Σ. We assume that E(Yi|A1A1) = ai, E(Yi|A1A2) = bi, and E(Yi|A2A2) = –ai, i = 1, . . . , k. We denote the vectors (a1, . . . , ak) and (b1, . . . , bk) by a and b, respectively. We assume two possible different distributions of e: multivariate normal and chi-square. We induce different degrees of genetic effects on the traits by varying the choices of a and b. In order to simulate a vector of phenotypes comprising both binary and quantitative traits, we first generate an observation Y according to the above model and then dichotomize some of the components by considering different thresholds so as to fix the prevalence of the binary traits at desired levels.
We also consider a biallelic marker locus with alleles M1 and M2 which is in linkage disequilibrium (LD) with the QTL. The extent of LD is varied to produce different degrees of associations between the marker locus and the vector of phenotypes. The genetic correlation between a pair of traits, say Y1 and Y2, induced by the QTL, is equal to the correlation between E(Y1|G) and E(Y2|G), where G is the genotype at the QTL and is given by:
Combining the genetic correlation between (Y1, Y2) with the correlation ρe between the environmental components modulating (Y1, Y2), the overall correlation induced between Y1 and Y2 can be derived as:
Based on these expressions, for a given choice of a and b vectors and other parameters, we can choose ρe accordingly to fix the final correlation between a pair of traits at a fixed level. Different choices of QTL effects considered in each table are described as footnotes.
Simulation design
We carry out the comparison of MultiPhen, BAMP, and DAMP with respect to the false positive rate and power in testing for association with multiple traits. The type I error rates and powers are calculated based on 2000 individuals and 10, 000 replications. We consider the allele frequency at the QTL to be 0.1. Four different choices of the standardized LD between the marker locus and the QTL are chosen as 0.0, 0.33, 0.66, 0.95. HWE is assumed while generating the genotype data.
Four traits
We first consider a multivariate phenotype that comprises four traits. Since the correlation between the traits may impact power, we consider the overall correlation between a pair of traits at four different levels: 0.0, 0.2, 0.5, 0.8, when the traits are distributed as multivariate normal, and 0.05, 0.2, 0.5, 0.8 when they are distributed as chi-square.
In Table I, we describe the choices of trait specific QTL effects and heritabilities considered in different tables. Initially we assume that the QTL has genetic effects only on the first and the second traits in tables X-XIII. In choices 1, 3, and 4, the heritabilities of the first two traits due to the QTL are fixed at 0.5%. In choice 2, we consider heterogeneity in QTL effects by fixing the genetic heritabilities of the first two non-null traits due to the QTL at two different levels: 0.5% and 1%, respectively. For choice 4, the QTL effects on the two traits are considered to be oppositely directed.
Table I.
Description of simulation scenarios. k: total number of traits, k1: number of associated traits. In tables X-XIII, since the third and the fourth traits are not associated with the QTL, we impose (a3, b3) = (a4, b4) = (0, 0) in each of choices 1-4.
| trait-specific QTL effects and
heritabilities | |||||
|---|---|---|---|---|---|
| Tables | (k, k1) | choice 1 | choice2 | choice 3 | choice 4 |
| X | (4,2) | a1=1.0, b1=0.0 | a1=1.0, b1=0.0 | a1=1.0, b1=0.0 | a1=1.0, b1=0.0 |
| a2=1.0, b2=0.0 | a2=2.0, b2=0.0 | a2=1.0, b2=0.5 | a2=–1.0, b2=0.0 | ||
| XI | (4,2) | same as Table X | same as Table X | same as Table X | same as Table X |
| XII | (4,2) | In Table X, first | continuous trait | is converted to | a binary trait |
| XIII | (4,2) | In Table XI, first | continuous trait | is converted to | a binary trait |
| XIV | (4,4) | a1=1.0, b1=0.0 | a1=1.0, b1=0.0 | a1=1.0, b1=0.0 | a1=1.0, b1=0.0 |
| a2=1.0, b2=0.0 | a2=2.0, b2=0.0 | a2=1.0, b2=0.5 | a2=–1.0, b2=0.0 | ||
| a3=1.0, b3=0.0 | a3=1.0, b3=0.0 | a3=1.0, b3=0.0 | a3=1.0, b3=0.0 | ||
| a4=1.0, b4=0.0 | a4=2.0, b4=0.0 | a4=1.0, b4=0.5 | a4=–1.0, b4=0.0 | ||
While simulating a vector of phenotypes comprising a binary phenotype, we define an individual to be a case if Y1 > C, and a control, otherwise. We replace Y1 by the case or control status of that individual to generate a binary trait. We choose C so as to fix the prevalence of the binary trait at 10%. The rate of Type I error and power are estimated at the level of significance 0.05.
In Table X, we consider the scenario where all the traits are distributed as normal and assume that marker locus allele frequency (= P(M1)) is 0.1. Table XI pertains to the scenario where all four traits are distributed as chi-square under the same simulation parameter values considered in Table X. Under this scenario, we find that the power turns out to be more than 99% for most of the simulation parameter values when P(M1) = 0.1. Since this phenomenon may be attributed to the similarity between the allele frequencies at the marker locus and QTL, we explore the impact of choosing P(M1) = 0.2 on power in Table XI. In Table XII, the first associated trait is dichotomized based on Y1 and converted to a binary trait with the threshold chosen so as to set the prevalence at 10%. The other simulation parameters remain same as in Table X. Similarly, in Table XIII, the first associated trait is binary and is dichotomized based on Y1. All other simulation parameters in Table XIII are the same as in Table XI.
In Table XIV, we consider the scenario where the QTL has genetic effects on all four traits, each of which is distributed as chi-square. We assume that the QTL effects on the third and the fourth traits and the genetic heritabilities of these two traits due to the QTL are the same as those for the first and the second traits, respectively. The other simulation parameters remain the same as in Table XI.
One binary trait
For a binary trait with a recessive mode of inheritance, Wang [2014] showed that MultiPhen produces significantly lower power compared to the regular Armitage trend test. We have proved theoretically that BAMP is equivalent to the usual allelic case control association test, and hence also asymptotically equivalent to the trend test under the assumption of HWE. Thus, for a sample of 2000 individuals under the assumption of HWE, BAMP and the Armitage trend test are expected to be asymptotically equivalent. Thus, we compare the three methods for a binary trait under the same simulation framework considered in Wang [2014] which we briefly describe in the following.
Consider a biallelic locus with two alleles A1 and A2 (minor allele). Let p0, p1, and p2 denote the probabilities of the three genotypes A1A1, A1A2, A2A2, respectively, and f0, f1, and f2 be their penetrances. Corresponding to this locus, the prevalence of the disease is K = p0f0 + p1f1 + p2f2. The genotype probabilities in cases are: and those in controls are: , for j = 0,1,2. Let be the relative risk of genotype i to genotype 0. Let q be P(A2), and so, under HWE, p0 = (1 – q)2, p1 = 2q(1 – q), p2 = q2. A choice of (K, q, γ1, γ2) fully determine all the parameters needed for data generation, because, , f1 = γ1f0, f2 = γ2f0. Power is calculated based on 10,000 replications and 2000 individuals comprising half of them to be cases and the other half to be controls. We consider the same choices of (K, γ1, γ2) as considered in Wang [2014] to encompass a variety of modes of inheritance for the binary trait (recessive, dominant, additive). A recessive model is considered by choosing γ1 = 1, whereas γ1 = γ2 and γ1 = (1 + γ2)/2 represent the dominant and additive models, respectively. The results are provided in Table III. In all the tables, MPhen denotes MultiPhen.
Table III.
Power comparison for a binary trait.
| penetrances | q = 0.2 | penetrances | q = 0.3 | |||||
|---|---|---|---|---|---|---|---|---|
| γ1 = 1, γ2 = 1.5 (recessive) | (f0,f1,f2) | MPhen | BAMP | DAMP | (f0,f1,f2) | MPhen | BAMP | DAMP |
| K = 0.1 | (0.1,0.1,0.15) | 0.16 | 0.28 | 0.28 | (0.1,0.1,0.14) | 0.47 | 0.64 | 0.64 |
| K = 0.01 | (0.01,0.01,0.015) | 0.14 | 0.24 | 0.24 | (0.01,0.01,0.014) | 0.40 | 0.54 | 0.54 |
| γ1 = 1.25, γ2 = 1.5(additive) | ||||||||
| K = 0.1 | (0.09,0.11,0.14) | 0.87 | 0.88 | 0.88 | (0.09,0.11,0.14) | 0.93 | 0.93 | 0.93 |
| K = 0.01 | (0.009,0.011,0.014) | 0.80 | 0.80 | 0.80 | (0.009,0.011,0.013) | 0.88 | 0.87 | 0.87 |
| γ1 = 1.25, γ2 = 1.25 (dominant) | ||||||||
| K = 0.1 | (0.09,0.11,0.11) | 0.76 | 0.71 | 0.71 | (0.09,0.11,0.11) | 0.76 | 0.7 | 0.7 |
| K = 0.01 | (0.009,0.011,0.011) | 0.68 | 0.63 | 0.63 | (0.009,0.011,0.011) | 0.67 | 0.61 | 0.61 |
Two binary traits
We also consider two binary traits with different modes of inheritance. Different choices of penetrances for the two diseases due to a QTL are considered. A marker locus that is in LD with the QTL is also considered. Different choices of allele frequencies at the loci are made to observe difference in powers among the methods. Different choices of simulation parameters, and type I error & power obtained by three methods for each choice are described in Table IV. All the results are based on 2, 000 individuals and 10, 000 replications.
Table IV.
Power comparison for two binary traits. p : allele frequency at the QTL, m : allele frequency at the marker locus. Penetrance vectors (f0,f1,f2) for the disease 1 and 2 are presented in consecutive rows.
| p=0.2,m=0.2 | p=0.1,m=0.2 | |||||||
|---|---|---|---|---|---|---|---|---|
| LD | Penetrances | MultiPhen | BAMP | DAMP | Penetrances | MultiPhen | BAMP | DAMP |
| O(TIerror) | both recessive | 0.051 | 0.052 | 0.052 | both additive | 0.052 | 0.051 | 0.051 |
| 0.33 | (0.25, 0.08, 0.08) | 0.19 | 0.23 | 0.24 | (0.12,0.08,0.04) | 0.15 | 0.15 | 0.17 |
| 0.66 | (0.25, 0.08, 0.08) | 0.52 | 0.69 | 0.71 | (0.12,0.08,0.04) | 0.47 | 0.47 | 0.50 |
| 0.95 | 0.75 | 0.93 | 0.93 | 0.78 | 0.78 | 0.80 | ||
| p=0.1,m=0.3 | p=0.1,m=0.2 | |||||||
|---|---|---|---|---|---|---|---|---|
| LD | Penetrances | MultiPhen | BAMP | DAMP | Penetrances | MultiPhen | BAMP | DAMP |
| 0 (TIerror) | both dominant | 0.052 | 0.051 | 0.051 | recessive,additive | 0.054 | 0.052 | 0.052 |
| 0.33 | (0.1, 0.1, 0.02) | 0.32 | 0.31 | 0.33 | (0.25, 0.08, 0.08) | 0.11 | 0.11 | 0.12 |
| 0.66 | (0.1, 0.1, 0.02) | 0.88 | 0.87 | 0.88 | (0.12, 0.08, 0.04) | 0.28 | 0.29 | 0.31 |
| 0.95 | 0.99 | 0.99 | 0.99 | 0.50 | 0.53 | 0.55 | ||
Results
Four traits
For brevity of space, Tables X-XIV are presented in details in the “Supplementary materials”. The three methods maintain the desired level of significance (corresponding to LD = 0) in all simulation scenarios. With respect to power, we first note some findings observed irrespective of the distribution and type (binary/continuous) of the multiple traits. Of course, the power of detecting association increases as the standardized LD between the marker locus and the QTL increases. We notice that, the power also increases with the degree of correlation among the traits; that is, for a given row in Tables X-XIV with non-zero LD, the power increases with the increase in the value of ρ (correlation between traits), except for choice 3 in Table XIV. In choice 4, when the associated traits have oppositely directed QTL effects, all the methods result in higher power compared to that for choice 1 (QTL effects in same direction). We also note that, as expected, converting the first associated continuous trait into a binary trait decreases power (Table XII compared to Table X). Similarly, due to the dichotomization of the first continuous trait, the overall power in Table XIII is less in comparison to the powers shown in Table XI.
A summary of the comparative performance by the three methods with respect to the power of detecting multivariate association observed in the Tables X-XIV is provided in Table II. In overall, the allelic tests offer marginal increase of power, in particular, BAMP produces a power increase in a range of (1% – 7%) compared to MultiPhen.
Table II.
Summary of the results for the power of detecting multivariate association with four phenotypes by different methods described in Tables X-XIV.
| Tables | Summary |
|---|---|
| Table X | The traits are normally distributed. Both of the allelic tests consistently produce a marginal 1% – 2% increase in power compared to MultiPhen. |
| Table XI | The traits are distributed as chi-square. The performance of MultiPhen is comparable to that of DAMP. However, BAMP performs slightly better than the other two tests offering a 1% – 3% increase of power. |
| Table XII | The first associated continuous trait in Table X is converted into a binary trait. In this scenario, MultiPhen and DAMP perform similarly. But, BAMP performs better than MultiPhen producing an increase in power in the range 1% – 5%. For example, in choice 3, for LD=0.95, the power increase is 2% – 5%. |
| Table XIII | The first associated continuous trait in Table XI is converted into a binary trait. DAMP performs marginally better than MultiPhen while BAMP performs consistently better than the other two methods. It produces higher power than MultiPhen with an increase in the range of 1% – 7%. For example, in choice 3, for LD=0.95, the increase in power of BAMP over MultiPhen is in the range of 5% – 7%. |
| Table XIV | All the traits are associated with the QTL and distributed as chi-square. While DAMP and MultiPhen produce comparable power, BAMP yields a consistent increase in power compared to MultiPhen, ranging from 1% to 3%. |
One binary trait
From Table III, we observe that, for the recessive model of inheritance of the binary trait, the allelic tests produce much higher power compared to MultiPhen with an increase in the range of 10% – 17%. However, for dominant mode of inheritance, MultiPhen produces marginally higher power (5% – 6%) compared to the allelic tests. For the additive model, the three methods yield comparable power.
Two binary traits
We observe from Table IV that, for recessive mode of inheritance of both traits, the allelic tests produce substantially higher power (4% 19%) over MultiPhen. DAMP yields a slight increase of power (2% – 5%) compared to MultiPhen when both the traits follow an additive mode of inheritance, and one follows additive and the other follows a recessive mode of inheritance. In the later scenario, BAMP also produces a marginal increase of power (1% – 3%) in comparison with MultiPhen. All three methods produce similar power when the traits follow other combinations of mode of inheritance: both dominant, one dominant and one additive (results not provided for brevity), one recessive and one dominant (results not provided for brevity).
In summary, for four phenotypes, BAMP and DAMP yield comparable powers, but marginally higher than MultiPhen, in particular, BAMP yields a consistent marginal increase of power in a range of 1% – 7% compared to MultiPhen. For one or two binary traits under a recessive mode of inheritance, the allelic tests offer substantially higher power compared to MultiPhen in a range of 4% – 19%.
Q-Q and test statistics plots
In order to provide a deeper insight of the comparison among the three methods, we present some Q-Q plots and test statistics plots for some selected scenarios from the simulation study.
Some prominent variation in powers are observed in Table XII and XIII related to the situation of mixed (binary and continuous) phenotypes for choice 3 and LD = 0.95. Larger difference in power is observed among the methods for two binary traits with recessive mode of inheritance (Table IV). So, in these three scenarios and for choice 3, LD = 0.66, ρ = 0.5 in Table XI when all four traits are distributed as chi-square, pairwise plots of the test statistics for the three methods are presented in Figure 1 and 2, respectively. Since each of the test statistics follows a chi-square distribution with the same degree of freedom, pairwise plots provide a valid picture of the comparison. For these same choices of simulation scenarios, we consider LD = 0 (H0: no association) between the marker locus and QTL, and present Q-Q plots of -log10(pvalue) obtained by different methods in Figure 3, 4, 5, 6, provided in the “Supplementary materials”.
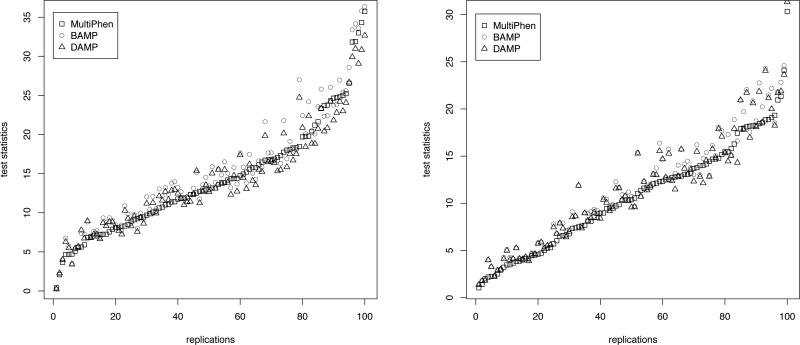
Figure 1.
The figures present the plot of test statistic values obtained by the three methods in 100 replications (ordered in increasing order of the values obtained by MultiPhen) for the following two scenarios: in Table XI for ρ = 0.5, choice 3, LD = 0.66; and in Table XII for ρ = 0.8, choice 3, LD = 0.95, respectively.
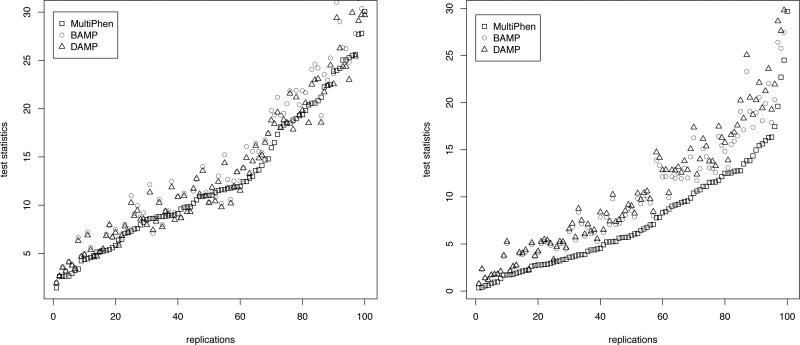
Figure 2.
The figures present the plot of test statistic values obtained by the three methods in 100 replications (ordered in increasing order of the values obtained by MultiPhen) for the following two scenarios: in Table XIII for ρ = 0.8, choice 3, LD = 0.95; and in Table IV for two binary traits with recessive mode of inheritance, respectively.
The Q-Q plots show that, under the null hypothesis of no association, both the allelic tests and MultiPhen produce p-values which approximately follow a uniform distribution. From the pairwise plots of the test statistics under the non-null hypothesis of association, we observe that allelic tests, in particular, BAMP consistently produces larger values than MultiPhen. As expected, the increase for allelic tests is more pronounced in the plot corresponding to two binary traits with recessive mode of inheritance (Figure 2). Thus the Q-Q plots and pair-wise plots of the test statistics in the same simulation scenarios demonstrate the power increase of allelic tests subject to controlling the false positive rate.
Minimum number of minor alleles to implement DAMP
In order for the multivariate CLT to hold in the formulation of DAMP, it is necessary that the count of the minor allele at a SNP must be sufficiently large. In Table X, XI, XII, XIII, the minor allele frequency (MAF) at the marker locus is reduced to 0.01 and 0.0125 (for 2000 individuals) in order to induce an average count of the minor allele to be 40 and 50, respectively. For these two choices of low MAF, simulations for choice 1 in Table X, XI, XII, XIII are repeated. For MAF = 0.01, it is found that the type I error by DAMP is inflated to 0.06 (at level 0.05) for choice 1 and ρ = 0.8 in Table XI when all the traits follow chi square distribution. However, in other cases for MAF = 0.01, the false positive rate by DAMP is controlled reasonably well. For MAF = 0.0125, results for choice 1 in Table XI and XIII are provided in Table V. The results show that the rate of false positive by DAMP is overall maintained. So for using DAMP, the minor allele count is recommended to be at least 50.
Table V.
The minor allele frequency at marker locus is 0.0125. TIerror denotes the type I error and ρ denotes correlation between traits. Type I error (for LD=0) and power (for non-zero LD) obtained by the three methods are rounded to 3-decimal and 2-decimal points, respectively. Results are based on 2,000 individuals and 10,000 replications.
| ρ = 0.0 | ρ = 0.2 | ρ = 0.5 | ρ = 0.8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LD | MPhen | BAMP | DAMP | MPhen | BAMP | DAMP | MPhen | BAMP | DAMP | MPhen | BAMP | DAMP |
| Choice 1 in | Table XI | |||||||||||
| 0(TIerror) | 0.05 | 0.05 | 0.054 | 0.053 | 0.054 | 0.052 | 0.052 | 0.052 | 0.052 | 0.051 | 0.051 | 0.054 |
| 0.33 | 0.17 | 0.17 | 0.10 | 0.17 | 0.17 | 0.10 | 0.16 | 0.16 | 0.10 | 0.20 | 0.20 | 0.14 |
| 0.66 | 0.48 | 0.49 | 0.34 | 0.47 | 0.47 | 0.32 | 0.45 | 0.45 | 0.31 | 0.58 | 0.59 | 0.49 |
| 0.95 | 0.77 | 0.78 | 0.64 | 0.77 | 0.77 | 0.64 | 0.75 | 0.75 | 0.62 | 0.88 | 0.88 | 0.83 |
| Choice 1 in | Table XIII | |||||||||||
| 0(TIerror) | 0.059 | 0.059 | 0.058 | 0.059 | 0.059 | 0.052 | 0.056 | 0.055 | 0.051 | 0.058 | 0.056 | 0.052 |
| 0.33 | 0.12 | 0.12 | 0.07 | 0.12 | 0.12 | 0.068 | 0.12 | 0.13 | 0.07 | 0.15 | 0.15 | 0.10 |
| 0.66 | 0.30 | 0.29 | 0.17 | 0.29 | 0.29 | 0.16 | 0.29 | 0.29 | 0.17 | 0.42 | 0.42 | 0.32 |
| 0.95 | 0.52 | 0.52 | 0.34 | 0.52 | 0.52 | 0.35 | 0.53 | 0.53 | 0.37 | 0.71 | 0.72 | 0.62 |
With respect to power, it is observed in Table V that the power by DAMP was less than that by the other two methods in a range of 4% – 18%. However, for normally distributed traits and mixed traits comprising one binary and others normal, the three methods yield similar power. We also observe in Table V that, for some cases, the type I error of MultiPhen and BAMP are slightly inflated. However, for MAF = 0.01 and larger sample size of 5000 individuals, we checked by simulations for choice 1 in Table XI that all the three methods maintain type I error rate appropriately, but power by DAMP is smaller than that by MultiPhen and BAMP in a range of 3% – 10%. Thus, it is more appropriate to implement DAMP for common variants rather than variants with lower minor allele frequency.
Validity of allelic tests
In GWAS, a two-stage procedure in which the markers are first tested for HWE as a data quality-check step and then evaluated for association is performed. In general, a p-value cut-off in the range (10−3 – 10−5) is used for the genome-wide screening of HWE. Thus, an allelic test can be implemented for a SNP passing through this screening. However, a relevant concern is whether the cut-off of HWE test p-value is sufficient to ensure that HWE holds for a SNP so that the allelic tests can readily be applied. Since it is very difficult to decide on an appropriate cut-off, we explore by simulations the efficiency of the allelic tests in controlling the type I error rate under various degrees of deviation from HWE (in terms of HWE test p-value). We adopt the same simulation design for four traits corresponding to choice 1 and ρ = 0.2 in Table X,XI, and XII, respectively. The results are presented in Table VI. In the last four rows of the table, the QTL has genetic effects on all of the four traits and the simulations corresponding to the first four rows are repeated. For a choice of the genotype frequencies, we generate genotype data at both the marker locus and QTL without assuming HWE. We consider 2000 individuals and zero LD between the marker locus and QTL (no association). Without loss of generality, we also assume the same genotype frequencies at the QTL. The type I error rate is estimated at the level 0.001 based on 20, 000 replications. Let the genotype frequencies at the marker locus be denoted by: q0=P(M2M2), q1=P(M1M2), q2=P(M1M1), respectively. We consider four different choices of (q0, q1, q2) that induces the HWE chi-square test p-value (HWEpv) as 0.048, 0.021, 0.0096, and 0.00014, respectively. We observe that both the allelic tests roughly maintain the desired level for the first choice. But for the other three choices, the allelic tests, in particular, DAMP seems to produce a significantly inflated rate of false positives when the traits are non-normal. The estimated false positive rates for MultiPhen are always less than that obtained for BAMP and DAMP. Since, the allelic tests maintain the rate of type I error satisfactorily for the first choice, we recommend screening for the HWE-test p-values using the cut-off of 0.05 to implement BAMP and DAMP at a genome-wide level.
Table VI.
Type I error rates of the three methods under various degrees of deviation from HWE. k1: number of associated traits, (q0,q1,q2): genotype frequencies, MAF: minor allele frequency.
| k1 = 2 | Normal | Chi-square | Binary and continuous | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (q0,q1,q2) | MAF | HWEpv | MPhen | BAMP | DAMP | MPhen | BAMP | DAMP | MPhen | BAMP | DAMP |
| (0.84,0.149,0.011) | 0.086 | 0.048 | 0.0012 | 0.0014 | 0.0014 | 0.001 | 0.0015 | 0.0016 | 0.0011 | 0.0014 | 0.0015 |
| (0.8,0.183,0.017) | 0.109 | 0.021 | 0.0011 | 0.0016 | 0.0016 | 0.0012 | 0.0016 | 0.0019 | 0.0011 | 0.0017 | 0.0018 |
| (0.85,0.139,0.011) | 0.081 | 0.0096 | 0.0011 | 0.0016 | 0.0016 | 0.0009 | 0.0014 | 0.0021 | 0.0012 | 0.0017 | 0.0019 |
| (0.851,0.137,0.012) | 0.08 | 0.00014 | 0.001 | 0.0018 | 0.0018 | 0.0013 | 0.0018 | 0.0021 | 0.0013 | 0.0018 | 0.002 |
| k1 = 4 | Normal | Chi-square | Binary and continuous | ||||||||
| (0.84,0.149,0.011) | 0.086 | 0.048 | 0.0012 | 0.0015 | 0.0014 | 0.0011 | 0.0013 | 0.0016 | 0.0012 | 0.0014 | 0.0015 |
| (0.8,0.183,0.017) | 0.109 | 0.021 | 0.0012 | 0.0015 | 0.0015 | 0.0012 | 0.0015 | 0.002 | 0.0011 | 0.0017 | 0.0019 |
| (0.85,0.139,0.011) | 0.081 | 0.0096 | 0.0011 | 0.0016 | 0.0016 | 0.0008 | 0.0012 | 0.002 | 0.0012 | 0.0017 | 0.002 |
| (0.851,0.137,0.012) | 0.08 | 0.00014 | 0.0016 | 0.0016 | 0.0016 | 0.001 | 0.0018 | 0.0025 | 0.0014 | 0.0018 | 0.0019 |
Combined strategy of BAMP and MultiPhen
Adopting the commonly used genome-wide significance cut-off 5 × 10−8, a genome-wide strategy can be to apply BAMP for the set of SNPs with a HWE test p-value above 0.05 and to implement a genotype level test (MultiPhen) for the SNPs for which the HWE test p-values lie below 0.05 but above the chosen overall HWE screening cut-off (e.g. 10−5).
For multiple traits, we observed in our simulation study that BAMP always produced marginally higher power compared to MultiPhen. So for multivariate phenotypes, if we assume that- under HWE- the power of BAMP is higher or equal to that of MultiPhen, it can be mathematically shown that the power of the combined strategy of implementing BAMP under HWE and MultiPhen under violated HWE is larger or equal to that by implementing MultiPhen alone.
Let H1 denote that a SNP is associated with the vector of multiple phenotypes. Let RB and RM denote the events that the SNP association is detected by BAMP and MultiPhen, respectively. So, the power for BAMP = PH1(RB), and power for MultiPhen = PH1(RM). We have assumed that PH1(RB|HWE) ≥ PH1(RM|HWE). Also let RBM denote that SNP association is detected by the combined strategy of BAMP and MultiPhen. So, power for the combined strategy = PH1(RBM) = PH1(RB|HWE) × P(HWE)+PH1(RM|HWEc)×P(HWEc) ≥ PH1(RM|HWE)×P(HWE)+PH1(RM|HWEc)×P(HWEc) = PH1(RM). Thus for multiple traits, assuming that BAMP is as good as MultiPhen in terms of power under HWE, the combined strategy of using BAMP and MultiPhen will produce higher or same power compared to implementing MultiPhen alone. Similarly, under H0 (no association), type I error of the combined strategy = PH0(RBM) = PH0(RB|HWE) × P(HWE) + PH0(RM|HWEc) × P(HWEc) = 0.05 × P(HWE) + 0.05 × P(HWEc) = 0.05, since BAMP maintains the appropriate rate of type I error under HWE.
We note that, in the extreme cases, when HWE holds at all associated SNPs, the power of the combined strategy is the same as that of BAMP, and when all the associated SNPs deviate from HWE, the power of the combined strategy becomes the same as MultiPhen. For example, in Table X-XIV, we checked by simulations that the powers by combined strategy and BAMP are the same since HWE was assumed while simulating the genotype data.
It is clear from the above mathematical expressions that the increase in power by the combined strategy over MultiPhen depends on the proportion of associated SNPs at which HWE holds. The expressions reveal that the marginal increase in power of the combined strategy due to BAMP will fade away with the increase in proportion of associated SNPs violating HWE. For a Mendelian disorder, the HWE may deviate at most of the causal SNPs due to the effects of selection at the susceptibility loci. However, for a common complex trait due to numerous variants with small effects, HWE may not be violated at a substantial proportion of causal SNPs. In the real data analysis of multiple common complex traits from the GERA cohort given below, the proportion of genome-wide associated SNPs at which HWE holds is substantially high (for this particular data, an empirical estimate is 80%). Thus, due to the possibility that a substantial proportion of SNPs associated with complex traits may not deviate from HWE, the combined strategy of BAMP and MultiPhen can be used in a GWAS of multivariate complex traits to take the advantage of consistent marginal increases in power by BAMP.
We carry out a simulation study to study the relative performances of the combined strategy and MultiPhen without assuming HWE at the associated markers. In order to consider a set of associated markers at some of which HWE can be violated and vice-versa, we select the top 15 GW-significant SNPs identified by MultiPhen in the real data analysis of GERA cohort which include 3 SNPs (20%) that yield a significant deviation from the HWE at a level of 0.05. This proportion is consistent with the overall percentage (20%) of GW significant SNPs (using a GW threshold 5 × 10−8) deviating from HWE (results reported in Table IX).
Table IX.
Results for GERA cohort data
| Chrom | rsID | HWEpv | BAMP | MultiPhen | HYPER | DIA2 | CARD | CANCER | Gene name |
|---|---|---|---|---|---|---|---|---|---|
| Chr1 | rs 1408420 | 0.51 | 6.20×10–8 | 3.64×10–8 | 0.66 | 0.30 | 0.16 | 3.13×10–9 | RCC2 |
| Chr2 | rs1275988 | 0.81 | 1.38×10–9 | 6.1×10–10 | 1.89×10–11 | 0.78 | 0.84 | 0.84 | KCNK3 |
| Chr2 | rs700635 | 0.68 | 4.55×10–9 | 6.21×10–9 | 0.031 | 0.91 | 0.67 | 9.93×10–11 | CASP8 |
| Chr2 | rs3769823 | 0.11 | 1.06×10–8 | 4.34×10–9 | 0.17 | 0.97 | 0.60 | 7.54×10–11 | ALS2CR12 |
| Chr3 | rs6769511 | 0.16 | 7.65×10–9 | 1.15×10–8 | 0.002 | 1.30×10–9 | 0.67 | 0.02 | MIR548AQ |
| Chr3 | rs7651090 | 0.06 | 1.04×10–8 | 1.8×10–8 | 0.002 | 4.19×10–9 | 0.86 | 0.013 | IGF2BP2 |
| Chr6 | rs12203592 | 0.007 | 3.98×10–46 | 1.52×10–45 | 0.006 | 0.4 | 0.7 | 1.38×10–48 | DUSP22 |
| Chr6 | rs12210050 | 0.51 | 1.0×10–14 | 3.29×10–14 | 0.28 | 0.59 | 0.39 | 4.23×10–17 | EXOC2 |
| Chr7 | rs1708302 | 0.17 | 4.24×10–12 | 6.2×10–12 | 0.11 | 3.51×10–14 | 0.14 | 0.32 | JAZF1 |
| Chr7 | rs849138 | 0.22 | 5.13×10–11 | 7.15×10–11 | 0.051 | 3.95×10–13 | 0.2 | 0.24 | JAZF1 |
| Chr7 | rs10274928 | 0.36 | 1.81×10–10 | 2.03×10–10 | 0.03 | 2.48×10–12 | 0.04 | 0.32 | JAZF1 |
| Chr8 | rs 13266634 | 0.97 | 1.10×10–8 | 5.59×10–8 | 0.28 | 1.30×10–9 | 0.50 | 0.07 | SLC30A8 |
| Chr9 | rs6475606 | 0.16 | 2.80×10–8 | 2.70×10–8 | 0.01 | 0.79 | 7.35×10–8 | 0.004 | |
| Chr9 | rs2383207 | 0.19 | 3.16×10–8 | 2.49×10–8 | 0.0002 | 0.89 | 2.14×10–8 | 0.052 | |
| Chr10 | rs4506565 | 0.95 | 2.04×10–49 | 4.80×10–49 | 0.002 | 1.51×10–55 | 0.17 | 0.87 | TCF7L2 |
| Chr10 | rs55899248 | 0.32 | 1.17×10–40 | 1.32×10–39 | 0.001 | 5.0×10–46 | 0.99 | 0.72 | TCF7L2 |
| Chr10 | rs12255372 | 0.91 | 5.65×10–39 | 2.07×10–38 | 0.016 | 8.25×10–45 | 0.21 | 0.83 | TCF7L2 |
| Chr10 | rs7899529 | 0.73 | 3.93×10–19 | 4.36×10–19 | 0.008 | 1.04×10–22 | 0.15 | 0.34 | TCF7L2 |
| Chr10 | rs61872790 | 0.60 | 1.03×10–14 | 6.51×10–14 | 0.01 | 1.08×10–17 | 0.85 | 0.95 | TCF7L2 |
| Chr10 | rs11196l74 | 0.00005 | 2.81×10–13 | 2.54×10–14 | 0.004 | 1.57×10–16 | 0.35 | 0.79 | TCF7L2 |
| Chr10 | rs7079711 | 0.77 | 1.44×10–10 | 1.24×10–10 | 0.86 | 5.83×10–12 | 0.98 | 0.13 | TCF7L2 |
| Chr10 | rs12255678 | 0.88 | 1.39×10–9 | 7.58×10–10 | 0.003 | 6.72×10–11 | 0.58 | 0.06 | TCF7L2 |
| Chr10 | rs7896811 | 0.005 | 1.38×10–7 | 4.35×10–8 | 0.68 | 6.61×10–9 | 0.9 | 0.24 | TCF7L2 |
| Chr11 | rs67279079 | 0.49 | 1.0×10–8 | 2.78×10–7 | 0.69 | 0.079 | 0.16 | 5.15×10–10 | TYR |
| Chr16 | rs12922197 | 0.006 | 2.52×10–11 | 3.48×10–12 | 0.93 | 0.61 | 0.76 | 6.55×10–14 | ANKRD11 |
| Chr16 | rs74836424 | 0.52 | 1.4×10–10 | 4.87×10–11 | 0.46 | 0.38 | 0.73 | 8.67×10–13 | CDK10 |
| Chr16 | rs 4408545 | 0.02 | 5.69×10–8 | 4.35×10–8 | 0.30 | 0.48 | 0.38 | 9.90×10–10 | CENPBD1 |
| Chr20 | rs4911442 | 0.19 | 9.36×10–10 | 1.38×10–9 | 0.33 | 0.47 | 0.78 | 4.69×10–12 | NCOA6 |
| Chr20 | rs62212235 | 0.86 | 4.78×10–9 | 4×10–9 | 0.84 | 0.41 | 0.38 | 3.64×10–11 | DYNLRB1 |
| Chr20 | rs62211619 | 0.0006 | 5.0×10–8 | 2.27×10–8 | 0.90 | 0.93 | 0.57 | 1.26×10–10 | ACSS2 |
The estimated genotype probabilities at the selected 15 SNPs are used to simulate genotypes without assuming HWE in the simulation study. Each of these SNPs is considered as both the QTL and marker, i.e., the marker is in perfect LD with the QTL having the same genotype probabilities as QTL. We choose choice 1 and 3 from Table XI and XIII. All the simulation parameters for generating phenotypes remain the same except the non-genetic variance of every trait being increased by 100 folds in order to enforce the overall (averaged across the 15 SNPs) powers not reaching 100%. The powers that are described in Table VII are estimated at the level 0.05 using 2000 individuals and 2000 replications. For a better understanding, the percentage of replications in which the combined strategy produces a smaller p-value compared to MultiPhen is also provided. The results show that the combined strategy produces a marginal gain (1% – 4%) in power compared to MultiPhen. It is also observed that, for 58% – 70% of replications across various choices, the combined strategy produces a smaller p-value in comparison with MultiPhen. Thus, the simulation study reveals that, with respect to power of detecting multivariate association, there is no loss but a marginal gain by implementing the combined strategy compared to implementing MultiPhen alone.
Table VII.
Comparison of power between MultiPhen and combined strategy of BAMP and MultiPhen. The combined strategy of BAMP and MultiPhen is denoted by “Comb”, and small.pv presents the percentage of total replications in which the p-value obtained by the combined strategy is smaller than that by MultiPhen. Other abbreviations are as follows- all conti: all the four phenotypes are continuous and distributed as chi-square, mixed: one phenotype is binary and other three are continuous and distributed as chi-square.
| ρ = 0.0 | ρ = 0.2 | ρ = 0.5 | ρ = 0.8 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| all conti | MPhen | Comb | small.pv | MPhen | Comb | small.pv | MPhen | Comb | small.pv | MPhen | Comb | small.pv |
| choice 1 | 0.89 | 0.90 | 62% | 0.88 | 0.89 | 62% | 0.87 | 0.88 | 62% | 0.96 | 0.96 | 62% |
| choice 3 | 0.77 | 0.79 | 66% | 0.75 | 0.78 | 66% | 0.76 | 0.78 | 65% | 0.90 | 0.91 | 66% |
| mixed | ||||||||||||
| choice 1 | 0.65 | 0.67 | 58% | 0.65 | 0.67 | 58% | 0.68 | 0.69 | 58% | 0.88 | 0.89 | 60% |
| choice 3 | 0.36 | 0.38 | 65% | 0.36 | 0.38 | 64% | 0.37 | 0.40 | 65% | 0.55 | 0.59 | 70% |
Application to real data
Indian population
Data description
In a study on hyperhomocysteinemia in a North Indian population, Kumar et al. [2009] analyzed 14 non-synonymous SNPs located in homocysteine metabolism pathway genes. Based on a random sample of 546 individuals selected from the All India Institute of Medical Sciences, two SNPs: rs9001 in the CHDH (Choline Dehydrogenase) gene and rs1801133 in the MTHFR (Methylenetetrahydrofolate Reductase) gene were found to exhibit significant evidence of association (using the Kruskal-Wallis test) with plasma total homocysteine levels, elevated levels of which increase the risk of coronary artery disease (CAD). These associations were validated when an additional 330 individuals from the same population were included in the sample. Moreover, there was a significant interaction of the two SNPs with the nature of diet (vegetarian or non-vegetarian) in modulating the levels of homocysteine. We consider the data on a multivariate phenotype vector comprising three traits: plasma total homocysteine levels, Vitamin B12 levels (which is significantly negatively correlated with homocysteine levels) and the binary CAD status along with the genotypes at the 14 SNPs for all 876 individuals in the combined sample.
Analysis and results
Homocysteine and Vitamin B12 levels are adjusted for the effects of potential confounders: age, gender, and diet using linear regression. We evaluate the relative performances of the three different methods in detecting association between the genotypes at the 14 SNPs and a multivariate phenotype vector comprising CAD status and the residuals of the other two phenotypes obtained via linear regression. None of the SNPs shows any significant deviation from HWE at a level of significance 0.05. Corresponding to three SNPs: rs1801133, rs12676, rs9001, the p-value produced by at least one of the methods is lower than 0.05. The p-values corresponding to these SNPs for the different methods are presented in Table VIII. For the SNPs rs1801133 and rs12676, both the allelic tests produce significantly lower p-values compared to MultiPhen, while for the SNP rs9001, the p-values produced by BAMP and MultiPhen are comparable.
Table VIII.
P-values for the three SNPs each having a p-value less than 0.05 produced by at least one of the three methods.
| SNP ID | rs1801133 | rs12676 | rs9001 |
|---|---|---|---|
| MPhen | 0.072 | 0.049 | 0.0047 |
| BAMP | 0.035 | 0.018 | 0.0051 |
| DAMP | 0.026 | 0.013 | 0.0097 |
GERA cohort
Data description
We analyzed the “Resource for Genet Epidemiol Research on Adult Health and Aging” (GERA) cohort data obtained from dbGaP [dbGaP Study Accession: phs000674.v1.p1]. We analyzed the European-American individuals which constitutes more than 75% of the full data. The data contains genotype data on 657184 SNPs on 22 autosomal chromosomes for 62318 individuals. The data is composed of 22 case-control phenotypes for the individuals along with adjusting covariates and principal components (PCs) of ancestry. For our analysis, we selected four case-control phenotypes: hypertension (HYPER), diabetes II (DIA2), cardiovascular disease (CARD), and cancers. We also adjusted our analysis for potential covariates: age, gender, smoking status, BMI category, and six PCs.
Following Anderson et al. [2010], we ran filtering of the initial data. First we ran individual-wise screening and removed individuals according to the following criteria: discordant sex information using PLINK [Purcell et al., 2007], missing genotype rate more than 3%, genotype heterozygosity rate beyond the six-sigma limit, and screening for relatedness up to first degree relatives using KING [Manichaikul et al., 2010]. This left us with 59458 individuals. Next, we did per marker screening for: excessive missing genotype rate more than 10%, and screening for SNPs with minor allele frequency (MAF) below 0.01, which left us with 635771 SNPs. In the final analysis, we excluded individuals with missing data for adjusting covariates which left us with 53809 individuals. SNPs were screened for deviation from HWE at a level 10−5.
Analysis and results
Since DAMP can not adjust for covariates simultaneously in the model, we executed BAMP and MultiPhen for the joint analysis of the four phenotypes. Adjusting covariates were included along with the phenotypes for both the methods. We also analyzed each of the four binary phenotypes separately by logistic regression of the affection status on genotype adjusting for the same set of covariates incorporated in the joint analysis. Based on the commonly used genome-wide significance level of 5 × 10−8, 54 SNPs were initially found GW-significant by either BAMP or MultiPhen. The SNPs were LD filtered for r2 > 0.7, which left a total of 30 SNPs associated with at least one of the traits or overall. For these SNPs, results of joint and trait-specific analyses are given in Table IX. The p-values for the chi-square test of HWE are also reported for each of the SNPs.
On chromosome 9, rs6475606 would not have been picked up by individual phenotype-wise analysis because of each individual trait's p-value fell below the genome-wide significance cut-off. This demonstrates the advantage of employing a joint analysis for multiple phenotypes. We also note that, for 6 SNPs out of the 30 genome-wide significant SNPs, the HWE test p-value falls below 0.05 (underlined), showing the validity of BAMP for the majority (80%) of the GW-significant SNPs.
Five SNPs, for which only one of the methods produces a p-value below the genome-wide significance cut-off, are highlighted in Table IX. Among these five SNPs, rs7896811 and rs4408545 show significant deviation from HWE at level 0.05, and hence, BAMP is not applicable. For the other three SNPs that satisfy HWE, BAMP marginally misses the single SNP identified by MultiPhen on chromosome 1, and similarly, MultiPhen marginally misses the single SNP identified by BAMP on chromosome 8. But, BAMP produces a genome-wide signal at rs67279079 on chromosome 11, for which MultiPhen yields much weaker signal compared to the genome-wide significance cut-off. Thus, the combined strategy marginally misses the signal on chromosome 1, but identifies both signals on chromosome 8 and 11, which MultiPhen fails to pick up. We further note that, for 16 SNPs (66%) among the 24 SNPs at which the HWE holds, BAMP produces a smaller p-value compared to MultiPhen.
We also map the SNPs in Table IX into genes. Each SNP is located either within the boundaries of a gene or 50KB upstream or downstream of it. Apart from the two SNPs on chromosome 9, every SNP is mapped into one or multiple genes. In Table IX, name of one gene for every SNP is reported. The genes are already known to be associated with a range of phenotypes including blood pressure (hence hypertension), diabetes type II, cardiovascular disease, and multiple type of cancers (breast, lung, prostate, etc.).
Discussion
We have proposed two allelic tests for association with multiple phenotypes extending the models underlying the methods proposed by O'Reilly et al. [2012] and Lee et al. [2013]. We have investigated their performances compared to an established genotype-level approach MultiPhen [O'Reilly et al., 2012] based on simulations and analysis of real data. We also show that BAMP is statistically equivalent to the classical case-control test of association for binary traits at the allelic level.
We observe that for four traits, in comparison with MultiPhen, BAMP yields a consistent marginal increase (1% – 7%) in power for detecting association multiple traits. We also find that, for one or two binary traits under a recessive mode of inheritance, the allelic tests offer much higher power compared to MultiPhen. It is also found that MultiPhen produces marginally higher power for a single binary trait under dominant mode of inheritance.
While the actual frequencies of causal variants with additive, dominant, and recessive genetic effects are somewhat unknown, additive genetic effects are believed to be the most common and the recessive effects be least common [Henn et al., 2015]. Hence, the simulations carried out assuming additive genetic effects for the QTL are most reflective of the overall power difference among the methods.
However, we observe that the allelic tests produce a consistent marginal increase in power for four phenotypes and the increase reaches maximum for two binary traits with recessive mode of inheritance. So, for analyzing multivariate phenotypes, there is no risk of loss in power but marginal gain if one employs the combined strategy of BAMP and MultiPhen instead of implementing MultiPhen alone. Our example using the GERA cohort shows some support for this, since BAMP picked up the only genome-wide signal on chromosome 11 which MultiPhen did not. Both of the real data analyses also demonstrate the possible increase in power in terms of smaller p-values for the majority of top SNPs, that satisfy HWE, produced by the allelic tests in comparison with MultiPhen.
For four traits, the simulation results are provided for a single choice of marker allele frequency. However, we performed simulations for other choices of it and observed similar behavior of the methods (results not provided for brevity). DAMP offers a substantial computational gain over the other two methods, and hence, is a useful alternative for very large GWAS.
We also observe that, for normally distributed phenotypes, DAMP and BAMP produce similar power. However, for non-normal traits, BAMP yields slightly higher power compared to DAMP. It may be due to the fact that, under normality of the phenotypes, the sample means of the multivariate phenotypes within both the groups corresponding to two alleles follow exact multivariate normal distribution, whereas for non-normal traits, the sample means follow multivariate normal asymptotically.
Under the null hypothesis, both the test statistics for MultiPhen and BAMP are distributed as chi-square with k degrees of freedom while testing for k phenotypes. But the number of parameters (intercept) in BAMP is one less than that in MultiPhen and this is the main reason behind the increase in power.
As opposed to MultiPhen and BAMP, DAMP can not directly incorporate covariates in the model. However, it is a common practice to separately adjust for the relevant covariates before the final genome-wide analysis. Yan et al. [2013] has explored the effects of population structure in the inverted regression model of MultiPhen and demonstrated that adjusting for ancestry principal components [Price et al., 2006] in the regression works well to control for population stratification. Since, BAMP is the allelic version of MultiPhen, it is possible to adjust for population structure in similar way. Considering the above issues and the increased power, for mapping association with multivariate phenotypes, we recommend the hybrid approach of employing BAMP and MultiPhen depending on the HWE than implementing MultiPhen alone.
Apart from the methods considered in this article, some other methods also can incorporate phenotypes of mixed type (discrete and continuous). Liu et al. [2009] proposed a method based on the theory of generalized estimating equations (GEE) primarily for two phenotypes that may comprise a binary phenotype as well. The method can be extended for a larger number of traits. However, a practical limitation of the approach is that the continuous phenotypes need to be normally distributed which is not desirable for non-normal traits. He et al. [2013] proposed a flexible framework for analyzing multivariate phenotypes. Instead of jointly modeling the phenotypes directly, the joint test statistic is formulated based on the marginal score statistics for the univariate phenotypes accounting for the covariance matrix of the score statistics. They also extended their approach for family based data. They compared their method with TATES [van der Sluis et al., 2013], which provides an overall p-value of association combining p-values for individual traits while adjusting for correlations between them, and found that TATES competes well with their method. We note that Galesloot et al. [2014] compared six different methods of analyzing multivariate phenotypes including MultiPhen and TATES. Four methods that were found to perform good include both MultiPhen and TATES. Since, in our simulation study, the proposed allelic tests perform consistently better than MultiPhen, we anticipate that the allelic tests would offer competitive performance in comparison with the methods considered in He et al. [2013] and Galesloot et al. [2014]. We also note that, from both theoretical and computational point of view, the methods considered in this article are simpler compared to those proposed in Liu et al. [2009] and He et al. [2013], and yet inherit the flexibility of incorporating phenotypes with arbitrary distribution.
A notable difference between the models underlying BAMP and MultiPhen lies in the interpretation of the regression parameters (β1, . . . , βk) for BAMP and (γ1, . . . , γk) for MultiPhen. The regression parameters in BAMP denote the effects of the individual phenotypes on the minor allele frequency at a SNP and hence captures more relevant information compared to the regression parameters in MultiPhen which denote the effects of the different phenotypes on the genotype frequencies at the SNP. An additional flexibility of BAMP is its statistical basis on a binomial regression model constituted of logistic likelihoods that is much simpler than a proportional odds regression model. It may turn out to be more desirable in a Bayesian framework by placing suitable priors on the regression coefficients since a Bayesian approach involving likelihood based on a logistic regression model rather than a proportional odds regression model is more feasible not only from a methodological but also from a computational point of view.
While BAMP and MultiPhen would provide significant evidence of association even if a SNP is associated with a subset of phenotypes in the multivariate phenotype vector, an advantage of the methods is that these can be simultaneously used to identify the particular subset. One can individually test for the significance of each phenotype considering the rest of the primary traits as adjusting covariates using a similar likelihood ratio test that is distributed as chi-square with one degree of freedom under the null hypothesis of no association. However, it is important to carry out an appropriate correction for multiple testing (such as Bonferroni, Benjamini-Hochberg, or permutations based procedure) to ensure the appropriate overall false positive rate.
Supplementary Material
Acknowledgements
This work was supported by the Council of Scientific and Industrial Research (CSIR) fellowship 09/093(0112)/2008-EMR-I to Arunabha Majumdar, National Institutes of Health grants R01CA088164, R25CA112355, and the UCSF Goldberg-Benioff Program in Cancer Translational Biology. The GERA cohort data came from a grant, the Resource for Genet Epidemiol Research in Adult Health and Aging (RC2 AG033067; Schaefer and Risch, PIs) awarded to the Kaiser Permanente Research Program on Genes, Environment, and Health (RPGEH) and the UCSF Institute for Human Genetics. The RPGEH was supported by grants from the Robert Wood Johnson Foundation, the Wayne and Gladys Valley Foundation, the Ellison Medical Foundation, Kaiser Permanente Northern California, and the Kaiser Permanente National and Northern California Community Benefit Programs. The RPGEH and the Resource for Genet Epidemiol Research in Adult Health and Aging are described in the following publication, Schaefer C, et al., The Kaiser Permanente Research Program on Genes, Environment and Health: Development of a Research Resource in a Multi-Ethnic Health Plan with Electronic Medical Records, In preparation, 2013. The authors sincerely thank Dr. Shantanu Sengupta for providing access to the data on Coronary Artery Disease and two anonymous reviewers for insightful suggestions that improved the manuscript substantially.
Appendix
Proof of property 1
For ease of exposition, we assume that the constituent phenotypes in the multivariate phenotype vector are either all continuous or all binary in nature. HWE is assumed at both the marker and trait loci. We first note that, if f1, f2, and f3 are the joint probability densities (in the case of continuous traits) or joint penetrances (in the case of binary traits) of (Y1, . . . , Yk) conditioned on the three genotypes at the trait locus, it is not possible that f1(y1, . . . , yk) = f2(y1, . . . , yk) = f3(y1, . . . , yk), for all possible values of (y1, . . . , yk). For notational convenience, we denote f1(.) = f1(y1, . . . , yk), f2(.) = f2(y1, . . . , yk), f3(.) = f3(y1, . . . , yk). The expressions of genotype probabilities at the marker locus conditioning on the phenotypes are derived in the following.
If part
In the logistic link function of BAMP:
Using the previous expressions of the probabilities of the genotypes at the marker locus conditioned on (y1, . . . , yk), we obtain the following equations:
Combining the last three equations we derive the following equation:
Now, suppose δ ≠ 0. In order to satisfy the above equation, pf1(.) + (1 – 2p)f2(.) (1 – p)f3(.) must be zero for all possible choices of (y1, . . . , yk), and hence all possible values of f1(.), f2(.), f3(.). But, there must be some choices of (y1, . . . , yk) for which f1(.), f2(.), f3(.) are not equal. Hence, to satisfy the condition, it must hold that p = 0, (1 – 2p) = 0, (1 – p) = 0, which implies that p = 0, p = 1/2, p = 1, simultaneously, and hence a contradiction. The argument is based on the following well known equivalence: ax + by + cz = 0, .
Only if part
Let δ = 0. From the expressions of marker locus genotype probabilities conditioning on the values of traits, we obtain: P(M1M1|y1, . . . , yk) = m2; P (M1M2|y1, . . . , yk) = 2m(1 – m); P(M2M2|y1, . . . , yk) = (1 – m)2. It implies that P(M1|y1, . . . , yk) = m. In BAMP, . Thus, , for all possible (y1,..., yk). Hence, .
Proof of property 2
Suppose Y1 is a binary trait where Y1 takes the value 1 for an affected individual and the value 0 for an unaffected individual. Thus, testing for β1 = 0 versus β1 ≠ 0 in BAMP is equivalent to testing P(M1|case) = P(M1|Y1 = 1) = P(M1|Y1 = 0) = P(M1|control) versus P(M1|case) ≠ P(M1|control).
Next, we derive the expression of the likelihood ratio test (LRT) statistic corresponding to BAMP. Suppose, we have n1 cases and n2 controls. Let n1M1 and n1M2 denote the number of M1 and M2 alleles among cases. Similarly, let n2M1 and n2M2 denote the number of M1 and M2 alleles among controls. Hence, n1M1 + n1M2 = 2n1 and n2M1 + n2M2 = 2n2.
Since the allele frequencies in cases and controls are the same under H0, we define . Under H1, we define the following quantities: and . Thus, the LRT statistic is given by:
Suppose under H0, π0(α) is denoted as p0 (hence, p0 is a 1 – 1 function of α). Then, the numerator of λ(.) is the same as: supp0 p0(n1M1+n2M1) (1 – p0)(n1M2+n2M2). Similarly under H1, denote π1(α,β1) and π2(α,β1), by p1 and p2, respectively [(p1, p2) is a 1 – 1 transformation of (α, β1)]. Hence, the denominator of λ(.) is the same as: supp1,p2 p1n1M1 (1 – p1)n1M2 p2n2M1 (1 – p2)n2M2 and the LRT statistic simplifies to:
where under H0: p0 = P(M1), and under H1: p1 = P(M1|case) and p2 = P(M1|control). Thus, for a binary trait, testing for association using our model is equivalent to the classical test for difference in allele frequencies among cases and controls.
Footnotes
The authors do not have any conflicts of interest.
References
- Almasy L, Blangero J. Variance component methods for analysis of complex phenotypes. Cold Spring Harb Protoc. 2010;2010(5):pdb–top77. doi: 10.1101/pdb.top77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson CA, Pettersson FH, Clarke GM, Cardon LR, Morris AP, Zondervan KT. Data quality control in genetic case-control association studies. Nat Protoc. 2010;5(9):1564–1573. doi: 10.1038/nprot.2010.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galesloot TE, Van Steen K, Kiemeney LA, Janss LL, Vermeulen SH. A comparison of multivariate genome-wide association methods. PloS One. 2014;9(4):e95923. doi: 10.1371/journal.pone.0095923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guedj M, Nuel G, Prum B. A note on allelic tests in case-control association studies. Ann Hum Genet. 2008;72(3):407–409. doi: 10.1111/j.1469-1809.2008.00438.x. [DOI] [PubMed] [Google Scholar]
- Guedj M, Wojcik J, Della-Chiesa E, Nuel G, Forner K. A fast, unbiased and exact allelic test for case-control association studies. Hum Hered. 2006;61(4):210–221. doi: 10.1159/000094776. [DOI] [PubMed] [Google Scholar]
- Hartley SW, Monti S, et al. Bayesian methods for multivariate modeling of pleiotropic SNP associations and genetic risk prediction. Front Genet. 2012;3:1–17. doi: 10.3389/fgene.2012.00176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Q, Avery CL, Lin DY. A general framework for association tests with multivariate traits in large-scale genomics studies. Genet Epidemiol. 2013;37(8):759–767. doi: 10.1002/gepi.21759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henn BM, Botigue LR, Bustamante CD, Clark AG, Gravel S. Estimating the mutation load in human genomes. Nature Rev Genet. 2015 doi: 10.1038/nrg3931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klei L, Luca D, Devlin B, Roeder K. Pleiotropy and principal components of heritability combine to increase power for association analysis. Genet Epidemiol. 2008;32:9–19. doi: 10.1002/gepi.20257. [DOI] [PubMed] [Google Scholar]
- Korte A, Vilhjalmsson BJ, et al. A mixed-model approach for genome-wide association studies of correlated traits in structured populations. Nature Genet. 2012;44(9):1066–1071. doi: 10.1038/ng.2376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar J, Garg G, et al. Single nucleotide polymorphisms in homocysteine metabolism pathway genes association of chdh a119c and mthfr c677t with hyperhomocysteinemia. Circ Cardiovasc Genet. 2009;2(6):599–606. doi: 10.1161/CIRCGENETICS.108.841411. [DOI] [PubMed] [Google Scholar]
- Lange C, Steen KV, Andrew T, Lyon H, DeMeo DL, Raby B, Murphy A, Silverman EK, MacGregor A, Weiss ST, Laird NM. A family-based association test for repeatedly measured quantitative traits adjusting for unknown environmental and/or polygenic effects. STAT APPL GENET MOL. 2004;3:1544–6115. doi: 10.2202/1544-6115.1067. [DOI] [PubMed] [Google Scholar]
- Lee PH, Bergen SE, et al. Modifiers and subtype-specific analyses in whole-genome association studies: a likelihood framework. Hum Hered. 2011;72(1):10–20. doi: 10.1159/000327158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SM, Karrison TG, Cox NJ, Im HK. Quantitative allelic testa fast test for very large association studies. Genet Epidemiol. 2013;37(8):831–839. doi: 10.1002/gepi.21768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Pei Y, Papasian CJ, Deng HW. Bivariate association analyses for the mixture of continuous and binary traits with the use of extended generalized estimating equations. Genet Epidemiol. 2009;33:217227. doi: 10.1002/gepi.20372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manichaikul A, Mychaleckyj JC, Rich SS, Daly K, Sale M, Chen WM. Robust relationship inference in genome-wide association studies. Bioinformatics. 2010;26(22):2867–2873. doi: 10.1093/bioinformatics/btq559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minica CC, Boomsma DI, Sluis SVD, Dolan CV. Genetic association in multivariate phenotypic data: power in five models. Twin Res Hum Genet. 2010;13(6):525. doi: 10.1375/twin.13.6.525. [DOI] [PubMed] [Google Scholar]
- Newman WP, Freedman DS, et al. Relation of serum lipoprotein levels and systolic blood pressure to early atherosclerosis. N Engl J Med. 1986;314(3):138–144. doi: 10.1056/NEJM198601163140302. [DOI] [PubMed] [Google Scholar]
- O'Reilly PF, Hoggart CJ, Pomyen Y, et al. Joint model of multiple phenotypes can increase discovery in GWAS. PLoS One. 2012;7(5):e34861. doi: 10.1371/journal.pone.0034861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association analysis. Nature Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, et al. Plink: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81(3):559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasieni PD. From genotypes to genes: doubling the sample size. Biometrics. 1997:1253–1261. [PubMed] [Google Scholar]
- Stephens M. A unified framework for association analysis with multiple related phenotypes. PloS One. 2013;8(7):e65245. doi: 10.1371/journal.pone.0065245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van der Sluis S, Posthuma D, Dolan CV. Tates: efficient multivariate genotype-phenotype analysis for genome-wide association studies. PLoS Genet. 2013;9(1):e1003235. doi: 10.1371/journal.pgen.1003235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan T, Li Q, Li Y, Li Z, Zheng G. Genetic association with multiple traits in the presence of population stratification. Genet Epidemiol. 2013;37(6):571–580. doi: 10.1002/gepi.21738. [DOI] [PubMed] [Google Scholar]
- Zeger SL, Liang KY. Longitudinal data analysis for discrete and continuous outcomes. Biometrics. 1986;42:121130. [PubMed] [Google Scholar]
- Zheng G. Can the allelic test be retired from analysis of case-control association studies? Ann Hum Genet. 2008;72(6):848–851. doi: 10.1111/j.1469-1809.2008.00466.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Feng T, Tayo BO, Liang J, Young JH, Franceschini N, Smith JA, Yanek LR, Sun YV, Edwards TL, et al. Meta-analysis of correlated traits via summary statistics from GWASs with an application in hypertension. Am J Hum Genet. 2014 doi: 10.1016/j.ajhg.2014.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K. Testing Genetic Association by Regressing Genotype over Multiple Phenotypes. PloS One. 2014;9(9):e106918. doi: 10.1371/journal.pone.0106918. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.