Relative sensitivities of DCE-MRI pharmacokinetic parameters to arterial input function (AIF) scaling

Abstract

Dynamic-Contrast-Enhanced Magnetic Resonance Imaging (DCE-MRI) has been used widely for clinical applications. Pharmacokinetic modeling of DCE-MRI data that extracts quantitative contrast reagent/tissue-specific model parameters is the most investigated method. One of the primary challenges in pharmacokinetic analysis of DCE-MRI data is accurate and reliable measurement of the arterial input function (AIF), which is the driving force behind all pharmacokinetics. Because of effects such as inflow and partial volume averaging, AIF measured from individual arteries sometimes require amplitude scaling for better representation of the blood contrast reagent (CR) concentration time-courses. Empirical approaches like blinded AIF estimation or reference tissue AIF derivation can be useful and practical, especially when there is no clearly visible blood vessel within the imaging field-of-view (FOV). Similarly, these approaches generally also require magnitude scaling of the derived AIF time-courses. Since the AIF varies among individuals even with the same CR injection protocol and the perfect scaling factor for reconstructing the ground truth AIF often remains unknown, variations in estimated pharmacokinetic parameters due to varying AIF scaling factors are of special interest. In this work, using simulated and real prostate cancer DCE-MRI data, we examined parameter variations associated with AIF scaling. Our results show that, for both the fast-exchange-limit (FXL) Tofts model and the water exchange sensitized fast-exchange-regime (FXR) model, the commonly fitted CR transfer constant (K^trans) and the extravascular, extracellular volume fraction (v_e) scale nearly proportionally with the AIF, whereas the FXR-specific unidirectional cellular water efflux rate constant, k_io, and the CR intravasation rate constant, k_ep, are both AIF scaling insensitive. This indicates that, for DCE-MRI of prostate cancer and possibly other cancers, k_io and k_ep may be more suitable imaging biomarkers for cross-platform, multicenter applications. Data from our limited study cohort show that k_io correlates with Gleason scores, suggesting that it may be a useful biomarker for prostate cancer disease progression monitoring.

Graphical abstract

INTRODUCTION

Dynamic-contrast-enhanced MRI [DCE-MRI] is widely used in the study of cancer and other pathologies. It provides high-resolution anatomical [lesion size, shape], microvascular [tumor blood volume, capillary permeability] [1–6] and, potentially metabolic [Na⁺,K⁺ ATPase activity] information [7,8]. The quantitative estimation of DCE-MRI pharmacokinetic parameters requires knowledge of the time-dependences of the plasma and interstitial compartmental contrast reagent (CR) concentrations, [CR_p](t) and [CR_o](t), respectively. The former is commonly referred to as the arterial input function [AIF]. In practice, direct determination of either concentration time-course is not straightforward. Classical methods using radiotracer-labeled CR require frequent blood sampling for [CR_p](t) and sacrificial autoradiography for [CR_o](t) determinations [9,10]. These make them cumbersome and impossible, respectively, for human studies. Furthermore, blood sampling is usually from a large vessel, not a capillary adjacent to the tissue of interest, and autoradiographic estimation of the tissue interstitial distribution volume has considerable systematic uncertainty.

Thus, the common practice is to estimate [CR_p](t) and [CR_o](t) noninvasively, from the DCE-MRI data themselves. However, the accuracy of AIF derived from DCE-MRI data can be influenced by several inherent experimental conditions, such as: 1) partial volume effect (signal from the image voxel, ideally containing only blood, is contaminated with signal from other non-blood tissues); 2) in-flow effect (signals generated by water molecules in the blood that were originally outside of the imaging volume flow in during signal acquisition and impact the final “blood” signal detected); 3) flow-profile dependency (when vessel cross-section contains more than one image voxel, measured voxel blood CR concentration is flow-profile dependent); and 4) no visible vessel in the imaging field-of-view (FOV). These factors can cause errors in the AIF amplitudes computed directly from blood vessel signals, and a scaling factor may be applied to reduce the errors [5,6]. Alternative methods mitigating the challenges of AIF quantification from blood signal have been proposed. Examples of these include reference tissue methods [11–13] and blinded AIF estimation [14–16]. Unfortunately, these approaches also require AIF amplitude scaling after derivation of the AIF time-course curves. The scaling factor (β) is often derived from literature reported tissue properties and generally does not account for individual variations. The AIF scaling uncertainties propagate to errors in the derived DCE-MRI pharmacokinetic modeling parameters. Thus, it is important to understand the effect of AIF scaling variations on modeled parameter values.

In this work, simulated DCE-MRI time-courses based on prostate data were subjected to repeated model fittings with the β of an AIF being the only variable. Repeated fittings of actual prostate region-of-interest (ROI) data were also performed to confirm the simulation findings. We used both the standard Tofts model and the Shutter-Speed model for data fitting. The former ignores intercompartmental water exchange (equivalent to assuming infinitely fast water exchange kinetics [the fast-exchange-limit (FXL)] pertains throughout the CR time-course), while the latter accounts for the effects of intercompartmental water exchange. The FXR (fast-exchange-regime) version of the Shutter-Speed Paradigm (SSP) was used in this study with the parameter k_io (unidirectional equilibrium cellular water efflux rate constant) accounting for transcytolemmal water exchange. Both models return the K^trans (rate constant for plasma/interstitium contrast agent transfer) and v_e (extravascular, extracellular volume fraction) parameters. When comparing all results with the common practice (β=1.0; i.e., using the AIFs determined from reported methods as the reference), our results show that the commonly modeled K^trans and v_e values scale nearly proportionally with β, indicating that cautions should be used comparing K^trans and v_e values among different subjects or across different platforms. By contrast, the k_ep and k_io (SSP specific) variations are much smaller in response to the same β variations. In addition, we show that k_io values correlate with Gleason scores in our limited data set. This indicates that the AIF-scaling insensitive k_io may offer a quantitative way for prostate cancer disease aggressiveness detection or monitoring.

MATERIAL and METHODS

Prostate DCE-MRI data were acquired from 13 subjects under a study protocol approved by the Portland VA Medical Center (PVAMC) and Oregon Health & Science University (OHSU) institutional review boards (IRBs). Each subject was referred for biopsy as standard care and volunteered for our DCE-MRI protocol before that procedure occurred. A prior biopsy was an exclusion criterion. All participants gave written informed consent. Additional details are reported in [5,6].

MRI

All prostate MRI data were acquired with a Siemens TIM Trio (3T) system. RF transmission utilized the instrument whole body coil, while reception employed a combination of flexible body and spine matrix coil arrays. Multi-slice T₂-weighted images (Turbo Spin Echo, TR/TE/FA, 5000 ms/102 ms/90°) were acquired for anatomic contrast and ROI selection [a 320*180*16 matrix size and 360*360 mm² transverse FOV resulted in nominal (1.1)² mm² in-plane resolution: slice thickness, 3 or 3.2 mm]. A near proton density (PD) image of the prostate gland was obtained using a 3D fast low-angle shot (FLASH) pulse sequence with a 256*144*16 matrix size and a 360*203 mm² transverse FOV, resulting in a nominal in-plane resolution of (1.4)² mm². Other parameters were: slice thickness, 3 or 3.2 mm; TR/TE/FA, 200 ms/1.56 ms/8°. For DCE-MRI, the same FLASH sequence was run with the only differences being TR = 5.0 ms and a 15° flip angle, which yielded a 6.28 s imaging inter-sampling interval. The total DCE-MRI acquisition time was ten and a half minutes. A bolus of 0.1 mmol/kg Prohance (Bracco, Inc.) was administered in an antecubital vein ~ 38 s after commencing the DCE-MRI acquisition. It was delivered in 5 to 10 s, at 3.0 mL/s, followed by a 20 mL saline flush.

Prostate Biopsy and Pathology

Subsequent to the DCE-MRI acquisition, each subject underwent a standard ten core “geographic” prostate biopsy procedure performed using (exclusively) ultrasound guidance; i.e., with no MRI input. Pathology examinations of biopsy core specimen fragments revealed Gleason scores ranging from 6 to 8 for five of the subjects. No malignancy was found for the other eight subjects.

Data Preparation

For DCE-MRI analysis, one ROI was selected for each of the 13 subjects [6] resulting in five malignant and eight benign ROI DCE-MRI time-courses. Since the precise biopsy track positions were not recorded, the spatial relationships between the DCE-MRI ROIs and the biopsy loci were restricted to only unilaterality. The experimental AIF was determined from voxels within a femoral artery visible in the FOV [6]. An individual AIF time-course was measureable for each subject except one, due to severe motion during the DCE acquisition in the latter case. A population-averaged AIF, based on the individual AIFs from six other subjects, was used for that individual.

Pharmacokinetic Analyses

In DCE-MRI, ΔR_1t(t) describes the time-course of the ΔR_1t [≡ R_1t(t) - R_1t(0)] value during the bolus CR passage; where R_1t(t) is the measured tissue ¹H₂O longitudinal relaxation rate constant time-course and R_1t(0) denotes the value prior to CR administration. Individual R_1t(0) values were calculated numerically with the Gradient Recalled Echo (GRE) signal expression (Eq. 7) using the average of DCE baseline images and that of the near PD-weighted image. With R_1t(0) determined, the R_1t(t) time-course can be calculated from the DCE-MRI signal time-course using the signal mean from DCE baseline for PD computation. To enhance the k_io detection capability, especially for the fast wash-out malignant lesion cases, only the first 70 time points (7.3 min total) were included in the model fitting for the prostate data. One critical step in quantitative DCE-MRI data analysis is to relate the measured ΔR_1t(t) time-course to the time-course of the interstitial CR concentration time-course, [CR_o](t).

The Shutter-Speed Paradigm

Because most water is inside cells but the CR visits at most the interstitial space, the kinetics of the equilibrium exchange of water molecules across the cell membranes must be taken into account. In this study we used the fast-exchange-regime (FXR)-allowed shutter-speed paradigm model that takes into account this exchange but assumes a single exponential recovery for the ¹H₂O signal [5,17,18]. This is expressed in

$${\mathrm{R}}_{1\mathrm{t}}(\mathrm{t})=\frac{1}{2}\left[{\mathrm{R}}_{1\mathrm{i}}+{\mathrm{r}}_{1\mathrm{o}}[{\text{CR}}_{\mathrm{o}}](\mathrm{t})+{\mathrm{R}}_{1\mathrm{o}0}+{\mathrm{k}}_{\text{io}}+\frac{{\mathrm{k}}_{\text{io}}{\mathrm{v}}_{\mathrm{i}}}{{\mathrm{v}}_{\mathrm{e}}}\right]-\frac{1}{2}{\left\{{\left[{\mathrm{R}}_{1\mathrm{i}}-{\mathrm{r}}_{1\mathrm{o}}[{\text{CR}}_{\mathrm{o}}](\mathrm{t})-{\mathrm{R}}_{1\mathrm{o}0}+{\mathrm{k}}_{\text{io}}-\frac{{\mathrm{k}}_{\text{io}}{\mathrm{v}}_{\mathrm{i}}}{{\mathrm{v}}_{\mathrm{e}}}\right]}^2+\frac{{(2{\mathrm{k}}_{\text{io}})}^2{\mathrm{v}}_{\mathrm{i}}}{{\mathrm{v}}_{\mathrm{e}}}\right\}}^{½}$$ (1)

where R_1i and R_1o0 are, respectively, the longitudinal relaxation rate constants for the intra- and extracellular ¹H₂O signals (in the absence of exchange and CR); r_1o is the interstitial CR relaxivity; k_io is the unidirectional equilibrium cellular water efflux rate constant (reciprocal of the mean intracellular water lifetime, τ_i); and v_i and v_e are the respective intra- and extracellular volume fractions. The absolute difference in R₁ between the extra- and intra-cellular space (|R_1o–R_1i|) is defined as the “shutter-speed”, τ₁⁻¹ [≡ κ₁] [17].

Using the Kety-Schmitt pharmacokinetic rate law, the interstitial CR concentration time course, [CR_o](t), is expressed by Equation (2), where K^trans is the CR transfer rate constant

$$[{CR}_o](T)=K^{\mathit{trans}}·{v_e}^{-1}·\underset{0}{\overset{T}{\int }}\left[{CR}_p\right]\left(t\right)·exp\left(-K^{\mathit{trans}}·{v_e}^{-1}·\left(T-t\right)\right)·dt$$ (2)

and [CR_p](t), the blood plasma [CR] time-course, is the AIF. The MRI experimentally determined AIF can be expressed as in Equation (3):

$$[{\text{CR}}_{\mathrm{p}}](\mathrm{t})=\{{\mathrm{R}}_{1\mathrm{b}}(\mathrm{t})-{\mathrm{R}}_{1\mathrm{b}}(0)\}/\{(1-{\mathrm{h}}_{\mathrm{v}}){\mathrm{r}}_{1\mathrm{p}}\}$$ (3)

where R_1b(t) is the capillary blood ¹H₂O R₁ time-course, R_1b(0) is the pre-CR blood R₁, r_1p is the longitudinal relaxivity for CR in blood plasma and fixed at a literature value of 3.8 mM⁻¹s⁻¹ [19], and h_v (fixed at 0.45) is the microvascular hematocrit.

To systematically account for AIF amplitude scaling, we rewrite Eq. (2) to include the time-independent AIF scaling factor, β, as Equation (4):

$$[{CR}_o](T)=K^{\mathit{trans}}·v_e^{-1}·{\int }_0^T\beta ·\left[{CR}_p\right](t)·exp\left(-K^{\mathit{trans}}·v_e^{-1}·(T-t)\right)·dt$$ (4)

where β is a time-independent scaling factor that quantifies AIF amplitude variations.

The differential form of Eq. (4) is given in Equation (5).

$$\frac{d[{CR}_o]}{dt}+k_{ep}[{CR}_o]=k_{ep}·\beta ·[{CR}_p]$$ (5)

It is important to point out that there is no “extra” β term in any pharmacokinetic model equations. Here, the β factor is added for the purpose of simulating AIF scaling uncertainties, with β = 1.0 representing the “ground truth” AIF. The use of β makes it easier to illustrate parameter changes associated with AIF scaling. That is “β·[CR_p]” is the actual AIF used in each fitting. In Eq. (5), the K^trans/v_e term appearing in Eq. (4) is replaced by k_ep according to its definition.

Standard mathematical approach to solve an inhomogeneous first-order differential equation like Eq. (5) starts with solving its associated homogenous equation (i. e., Eq. (5) with the right-hand-side set to zero, or [CR_p] =0). This immediately reveals that the rate constant (k_ep) is not impulse function ([CR_p]) dependent. Specific to DCE-MRI, as long as the curve shape of [CR_p](t) doesn’t change, then k_ep is independent of β. This observation is associated with the Kety-Schmitt pharmacokinetic rate law and thus applies to both the FXL and FXR models used in this study. In practice, since the AIFs are often determined numerically without an analytical expression, there might be small variations of k_ep following a β change.

The Tracer Paradigm

Very often in the literature the MRI CR is treated as a tracer (i.e., as if it’s directly detected) and, when the blood ¹H₂O contribution to the tissue signal is negligible, the tissue R₁ change, ΔR_1t(t), can be expressed using [CR_o](t), as in Equation (6):

$$\mathrm{\Delta }{\mathrm{R}}_{1\mathrm{t}}(\mathrm{t})={\mathrm{r}}_{1\mathrm{o}}•[{\text{CR}}_{\mathrm{o}}](\mathrm{t})•{\mathrm{v}}_{\mathrm{e}}$$ (6)

which is simpler than Eq. (1). However, Eq. (6) implies a linear [CR_o]-dependence of ΔR_1t, which is experimentally untrue [20,21]. It further implies that equilibrium transcytolemmal water exchange kinetics are effectively infinitely fast [k_io → ∞] [21]. This is usually an incorrect over-simplification. The direct consequences of using tracer paradigm (TP) models are systematic errors in the estimated pharmacokinetic parameters such as K^trans [example below] and v_e [1–3,5–7]. Nevertheless, since tracer models find common use in the literature because of their relative simplicity, we also used one, the standard, fast-exchange-limit (FXL)-constrained Tofts tracer model [22], in addition to the FXR-SSP model in assessing the effects of AIF scaling uncertainty. The k_io parameter is unique to the SSP models and cannot be accessed by any tracer paradigm model because such models effectively assume k_io to approach infinity [k_io → ∞]. Mathematically, Eq. (1) simplifies to the FXL Eq. (6) when κ₁ → 0 [21]. Thus, the SSP-FXR automatically simplifies to the Tofts FXL model if κ₁ (the shutter-speed) never rises sufficiently during a DCE time-course. However, this does not mean that k_io → ∞, only that k_io is indeterminate.

Simulations

The [CR_o] expression in Eq. (4) was used by both the SSP and TP approaches. For a given K^trans, v_e, and k_io (SSP only) parameter set_, R_1t(t) time courses are influenced by AIF scaling through the associated input function β·[CR_p], where [CR_p] (the reference or “true” AIF when β = 1.0) used for the simulation was based on our experimental measurements and further smoothed to mimic a well-determined AIF (see Figure 1A). K^trans, v_e, and k_io values were selected based on those from the prostate data. Unless otherwise stated, we simulated R_1t time-courses using the conventional β =1.0. After the R_1t calculation, Equation (7) suitable for gradient-echo sequence was used to calculate the signal time-courses.

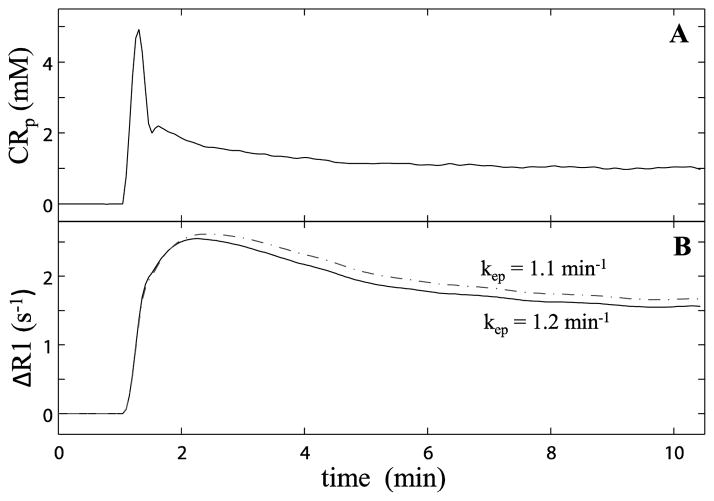
Figure 1.

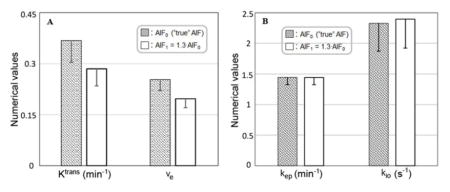
Figure 1A plots the averaged blood plasma concentration ([CR_p]) time-course derived from five individually determined arterial input functions [AIFs]. Under the condition of β =1.3 (i.e., 130% the 1A AIF amplitude), the 1B solid curve plots the ΔR₁(t) time-course calculated with K^trans = 0.36 min⁻¹, v_e = 0.3 (k_ep =1.2 min⁻¹), τ_i = 0.6. The dashed curve traces ΔR₁(t) with a different parameter set: K^trans = 0.35 min⁻¹, v_e = 0.32 (k_ep =1.1 min⁻¹), τ_i = 0.6 s.

$$S=S_0\frac{(1-exp(-TR·R_{1t}))}{(1-exp(-TR·R_{1t})·cos\alpha )}·sin\mathrm{\alpha }$$ [7]

Here, S₀ is proportional to the equilibrium magnetization, TR is the pulse sequence repetition time, α the read pulse flip angle. Noiseless signal time-courses as well as those with added Gaussian white noise were both used to investigate parameter variations under different β values.

Simulated time-courses were fitted with different AIFs defined as β·[CR_p]. Eq. (4) suggests that β interacts inversely with K^trans and proportionately with v_e in data fitting. To investigate parameter variations caused by different AIF scaling, simulations were carried out by fitting pharmacokinetic parameters with β fixed at 13 different values from 0.8 to 2.0 with a step-size of 0.1. A larger than 100% β variation was included for model fittings so that parameter trends in response to AIF scaling can be better observed.

Fitting the simulated time-courses yielded K^trans, v_e, and τ_i (≡ 1/k_io, SSP only) values. In addition, k_ep [≡ K^trans/v_e] [22], and the intracellular volume fraction v_i [≡ 1 – v_e] values were determined. While v_e defines the CR accessible volume fraction, the v_i parameter equals the cell density [ρ] and mean individual cell volume (<V>) product [ρ •<V>], within the ROI or voxel [7].

To avoid local minima in each optimization procedure, 20 different initial guess parameter value sets were used for each β step and each model. Parameters from the best fitting of the 20 trials for each combination were then selected as the fitted results. In addition, two-dimensional grid searches [3,23] were also performed to investigate the K^trans-v_e parameter space to gain insights into the fitting approaches and to provide assurance in avoiding potential local minima during fitting.

RESULTS

Figure 1A plots the averaged blood plasma concentration, [CR_p], time-course derived from five individual AIFs [6]. Under the condition of β =1.3 (i.e., 130% the AIF amplitude as show in 1A), the solid curve in 1B plots the ΔR₁(t) time-course predicted by the shutter-speed approach for k_ep = 1.2 min⁻¹, v_i = 0.70, and k_io = 1.7 s⁻¹ [K^trans = 0.36 min⁻¹, v_e = 0.30, τ_i = 0.60s]. The 1B dashed curve shows the prediction for k_ep = 1.1 min⁻¹, v_i = 0.68, and k_io = 1.7 s⁻¹ [K^trans = 0.35 min⁻¹, v_e = 0.32, τ_i = 0.60 s]. As expected, the ΔR₁(t) wash-out portion is rather sensitive to an only 8% k_ep reduction [there is also a 3% v_i reduction]. Also as expected, the simulated ΔR₁(t) time-courses with either parameter set are lower than the 1B curves when β=1.0 (using the AIF in 1A; not shown).

To investigate K^trans and v_e (and thus k_ep and v_i) parameter sensitivity to AIF scaling, a grid search [23] rather than a non-linear data fitting was selected as the first step of data analysis. Although the former can be tedious and slow, a large searching range can often provide the global solution and avoid local minima that could trap a non-linear optimization.

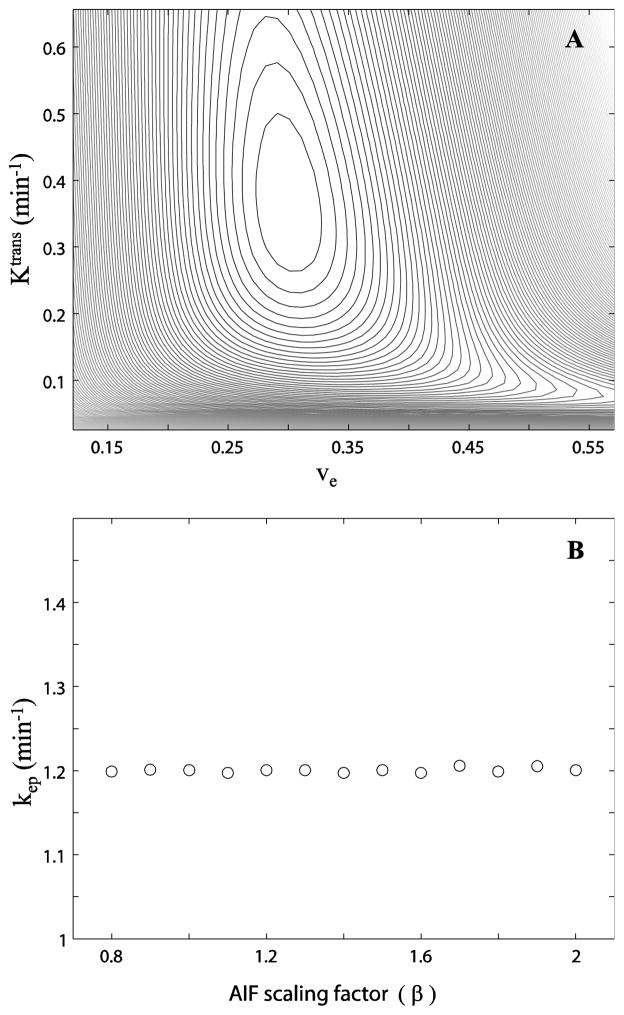
For demonstration, Figure 2A shows a search of the K^trans, v_e error surface. Using the Fig. 1A AIF, and the parameter set of K^trans = 0.36 min⁻¹, v_e = 0.30, and k_io = 1.7 s⁻¹, the reference R_1t and its related reference signal time-course, S_ref(t), were generated. Then, the simulated R₁(t) for each grid point (K^trans,v_e coordinate pair; k_io = 1.7 s⁻¹) and S_grid(t) time-course was calculated and this was compared with S_ref(t). The constant difference square sum {χ² = Σt[S_ref(t) – S_grid(t)]² [3]} value contours decrease to a global minimum at the coordinates K^trans = 0.36 min⁻¹ and v_e =0.30 (k_ep = 1.2 min⁻¹), matching the inputs used in generating the reference curve as expected. The contour lines measure the χ² value (“goodness”) of comparisons with the reference curve of different model curves calculated for the parameter values given by the coordinates [3]. The χ² value decreases as one moves on the surface towards the closed contours. Figure 2B shows the best fitted k_ep values determined at different β. A near constant k_ep [1.2 min⁻¹] is observed over the range of β tested. [Slight k_ep deviations are most likely due to the finite numbers of K^trans and v_e steps (500–600) used in the grid search.]

Figure 2.

Figure 2A shows a K^trans vs. v_e error surface. The contour plot shows the chi square statistic, χ² = Σ[S_ref(t) – S_grid(t)]², for simulated DCE-MRI time-courses from parameters equal to the K^trans,v_e coordinates. The χ² value decreases as the contour lines move towards the center of the closed loops. B shows the best k_ep (≡K^trans/v_e) values determined at different β values. A near constant k_ep is observed within the entire β range tested.

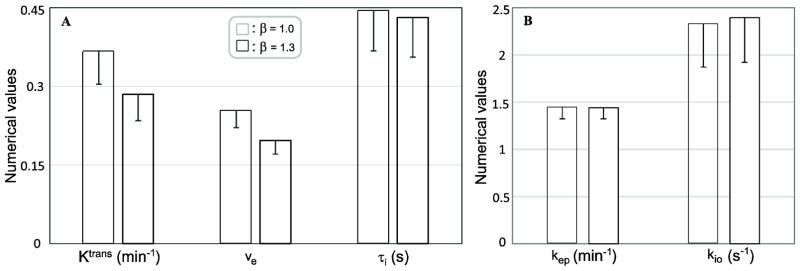
Using shutter-speed simulated data and analyses, Figure 3A shows K^trans, v_e, and τ_i changes associated with a 30% AIF scaling change. The reference parameter values (cross-hatched bars) are: K^trans = 0.36 min⁻¹, v_e = 0.25, and τ_i = 0.45 s. Monte Carlo simulations (using Fig. 1A AIF as the β =1.0 reference) were used to estimate K^trans, v_e, and τ_i accuracy (mean) and precision (SD). 400 fittings were performed with random Gaussian noise (SNR = 10 at baseline, slightly better than the median baseline voxel SNR of 5.3 estimated from the prostate ROI slices of all subjects) added to the simulated time-course each time, and each fitting started with a different initial guess parameter value set. Mean and SD values of k_ep and k_io derived from the 3A fittings are plotted in Figure 3B. Fig. 3A clearly shows that K^trans and v_e decrease proportionally (~ 30%) with the 30% β increase, while the τ_i change is negligibly small (< 3%), well below the standard deviation (~10%) associated with the data SNR. Defined as K^trans/v_e, k_ep is insensitive to β variation (Fig. 3B) as expected. Being the τ_i reciprocal, the rate constant k_io has a similar relative measurement error as τ_i. Except for having different numerical means, v_i and v_e have the same SD values because v_i ≡1-v_e. That is, error propagation for both v_e and v_i is exactly the same. Results of k_io (or τ_i) and k_ep being less sensitive to AIF scaling variations indicate that the values of these parameters are likely to be more consistent despite difficulties in accurate AIF determination in many experimental conditions. We use results from real prostate ROI data in the following figures to illustrate additional aspects also seen with simulations. This provides some validations of the simulation results and adds insights on actual data processing when AIF scaling uncertainty plays a factor in pharmacokinetic model parameters.

Figure 3.

Figure 3A depicts the K^trans, v_e, and τ_i changes associated with a 30% change in β. Monte Carlo simulations were used to estimate K^trans, v_e, and τ_i accuracy (mean) and precision (SD) changes resulting from a 30% β increase. It is seen that K^trans and v_e change proportionately (~ 30%) with β, while the τ_i change is negligibly small (< 3%), well below the standard deviation (>10%) associated with the data SNR. 3B shows the similar plots for k_ep and k_io. Defined as K^trans/v_e, k_ep is insensitive to β variation as discussed in the text. Being the τ_i reciprocal, the rate constant k_io has the same relative error as that of τ_i.

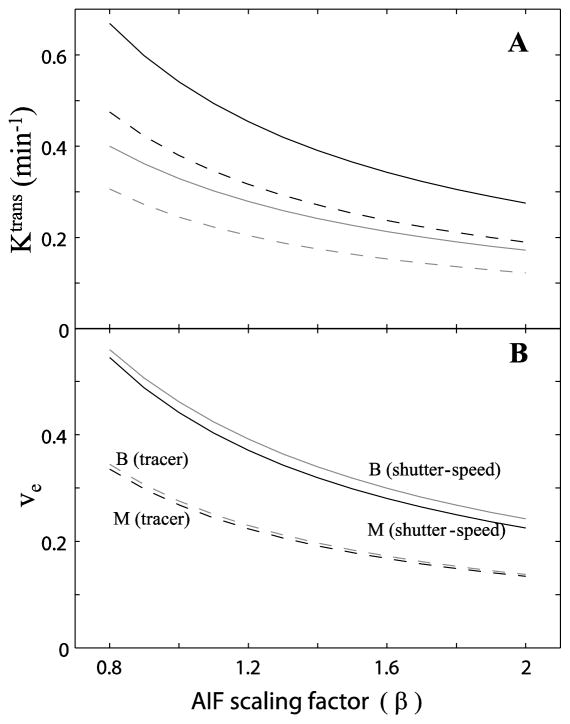
Figure 4A shows representative ROI K^trans variations associated with AIF scaling uncertainty, for malignant (black curves) and benign (gray curves) tissues. The individual AIF (= β·[CR_p]) was used for fitting at each β value, mimicking AIF scaling uncertainty seen in experimental AIF derivation. Each ROI time-course was fitted with shutter-speed (solid curves) and tracer (dashed curves) analyses. The best fitted values returned from the 20 different initial parameter guess sets are plotted. The K^trans values are rather AIF scaling dependent, decreasing with increasing β. Similar findings are observed for the v_e parameter (Figure 4B). Both K^trans and v_e are the most commonly reported parameters in pharmacokinetic model fitting.

Figure 4.

Figure 4A shows representative K^trans changes for malignant (black curves) and benign (gray curves) tissues with increasing β. Each ROI data set was fitted with models from the shutter-speed (solid curves) and tracer (dashed curves) paradigms. The best fitted values from 20 different initial guesses are plotted. The K^trans values decrease with β increase. 4B shows the same trends for v_e.

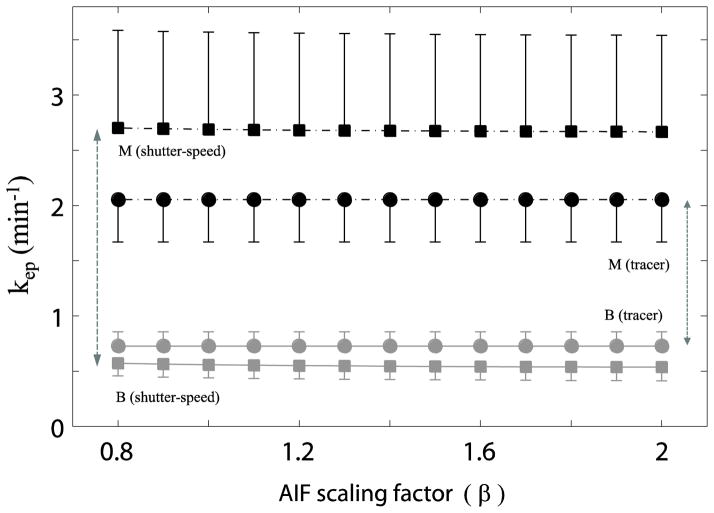
The simulated results in Fig. 2B indicate that k_ep appears to be independent of β scaling. This is confirmed by results from real prostate data (Figure 5). Averaged k_ep values of eight benign and five malignant ROIs (with standard errors), respectively, are plotted versus β values used in this study. For each signal-averaged ROI at each β step, 20 fittings with different initial guess each time were performed and the one with the smallest fitting error was then selected for that ROI. The results from shutter-speed analyses are plotted as square points and those from tracer analyses as circular points. The malignant ROIs are represented by black color vs. gray color for the benign group. Regardless of the analysis paradigm and tissue type, the k_ep within each analysis remains nearly constant at different β values, indicating k_ep is basically unaffected by AIF scaling uncertainty. The apparent malignant/benign discrimination [k_ep(M) – k_ep(B)] is increased with the shutter-speed paradigm (17,18) [double-headed vertical arrows in Fig. 5]. This trend is shown because when compared to their FXL counterparts, k_ep values determined by the FXR often increase for malignant cases and decrease for benign cases. Although this systematic behavior may not be covered by generic statistical tools, we report the Hedges’ g effect size for malignant/benign separation by k_ep to provide a primitive numerical comparison. The computed Hedges’ g values for k_ep mean differences are 1.15 (95% CI: 0.24, 2.07) and 0.82 (95% CI: −0.06, 1.70) for the FXL and FXR approaches, respectively. Future investigation with larger subject cohort is needed to address this issue more thoroughly.

Figure 5.

Figure 5 plots the β-dependence of the mean k_ep values for the five malignant (black) and eight benign (gray) cases. The shutter-speed k_ep values have square symbols while the tracer values have circle symbols. Regardless of the pharmacokinetic paradigm and tissue characteristics, the k_ep value for each model remains constant, indicating k_ep is insensitive to AIF scaling.

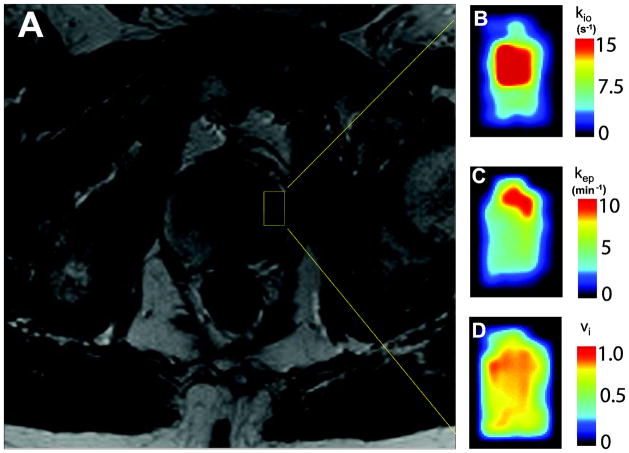
Figure 6A shows a portion of an axial T₂-weighted image of a 66 year old subject with prostate malignancy. Figures 6B–6D show zoomed pharmacokinetic parametric maps (k_io, k_ep, and v_i, respectively) of the lesion area within the prostate, which is generally indicated by the yellow rectangle in Fig. 6a. The black borders in Figs. 6B–6D provide some contrast to the generally cold color of normal-appearing glandular tissue within the rectangular ROI encompassing the lesion. The parametric maps were obtained as the best results from 30 fittings with different initial guess sets. Elevated k_io values are seen in part of the lesion, possibly indicating increased cellular metabolic activity [7] associated with malignancy. Noticeably higher k_ep values reflecting increased vascular leakage are seen only in the anterior portion within the lesion ROI. Besides being on the “warm” portion of the color map (often brighter contrast), v_i is directly proportional to cell density.

Figure 6.

Figure 6A shows a portion of an axial pelvic T₂-weighted image of a 66 year old subject with left prostate malignancy (anterior up). Figures 6B–6D show zoomed parametric maps of a tumor-encompassing ROI in the left prostate indicated by the 6A yellow rectangle. Figure 6B is the k_io map, which displays metabolic activity. Significantly elevated k_io is clearly visible in the anterior half of the ROI. Figure 6C shows increased k_ep in only the most anterior portion of the ROI. The k_ep parameter measures capillary CR permeability. Figure 6D shows v_i slightly elevated in the anterior half of the ROI. This most likely represents increased cell density. Black borders are added in 6B–6D to provide contrast with the elevated parametric color maps.

In Figure 7, lesion ROI-averaged in vivo SSP-only k_io values are plotted against the independently-obtained ex vivo Gleason scores for the five malignant cases. Each voxel within each ROI was fitted 30 times with different initial guess values using both the shutter-speed paradigm and tracer paradigm. The best fitted results from each paradigm were recorded. Then, the commonly used model selection approach, the Akaike information criterion (AIC), was used to determine which model better described the specific voxel time-course. In Figure 7, only those voxels favored by AIC for the shutter-speed paradigm were included in the averaging calculation [the tracer paradigm leaves k_io indeterminate]. Using the lesion ROI (indicated by the yellow rectangle) from Figure 6 as an example, k_io was averaged for 36 out of 38 voxels. The numbers of AIC-favored over the total ROI voxels for the remaining four malignant cases are: 23/56, 13/16, 8/11, and 20/28. A clear trend of increasing k_io with Gleason score (Spearman’s correlation coefficient, r = 0.91; p = 0.03) is observed (the empirical blue dashed curve is intended only to guide the eye). The k_io error bars show standard errors for the analysis of each small lesion. The vertical error bars also reflect our unknown registration of MRI ROI and biopsy locus. That is, without clear knowledge of the latter, voxels from benign tissues can be accidentally included in the lesion ROIs. As CR extravasation is generally lower in non-cancerous tissue, k_io uncertainty increases because of decreased shutter speed [17], which results in larger error bar length compared to an ROI containing more malignant tissue. The horizontal error bars show calculated differences between clinical Gleason scores reported in another study, and the weighted mean Gleason scores given by an expert reviewer [24]. These bars partially illustrate the uncertainties in Gleason pattern reporting (e.g., if no reported Gleason scores differ by two categorical points or larger, a 0.1 bar length then represents 10% of the cases having different Gleason scores). Other fitted parameter values from the same patient group were reported previously [6]. None of the fitted K^trans and v_e values from either paradigm showed a clear correlation with Gleason scores.

Figure 7.

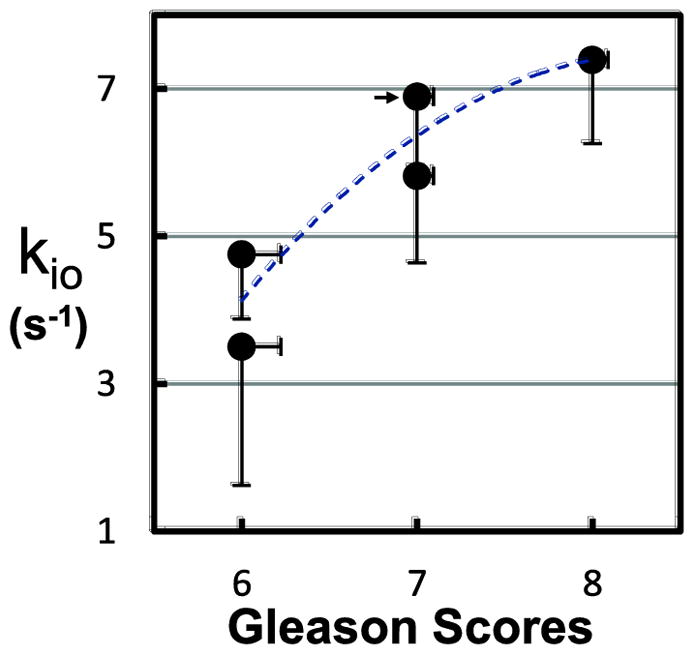
Figure 7 plots lesion ROI-averaged in vivo k_io values against independently obtained ex vivo Gleason scores for the five malignant cases. A clear trend of increasing k_io with Gleason score (Spearman’s correlation coefficient, r = 0.91; p = 0.03) is observed (the empirical blue dashed curve is intended only to guide the eye). The error bars show k_io standard errors and estimated Gleason score errors (see text).

DISCUSSION

Accurate AIF quantification has been one of the primary challenges in quantitative pharmacokinetic analysis of DCE-MRI data. Many AIF derivation methods [5,6,11–16] require an AIF amplitude scaling in the process. Since the ground truth of the scaling factor is often unknown (for example, using muscle as a reference tissue for AIF scaling runs into the problem of varying pharmacokinetic properties of the muscle itself under different physiological conditions), this makes investigation of AIF scaling effects important. By explicitly including an AIF scaling factor (β) into the pharmacokinetic modeling, this work investigated the pharmacokinetic model parameter variations associated with AIF scaling uncertainty. Our results show that the k_ep and the SSP-specific k_io parameters are insensitive to AIF scaling. In a theoretical scenario where k_ep is truly time and [CR] independent, its insensitivity to [CR_p] scaling can be directly predicted from Eq. (5). That is, k_ep insensitivity to AIF scaling is a direct result of the Kety-Schmitt pharmacokinetic rate law. This is the reason that insensitivity of k_ep to AIF scaling is observed for both the TP and the SSP approaches [Fig. 5]. On the other hand, the relative insensitivity of the SSP-specific k_io to AIF scaling is the result of multiple factors. First, k_io quantifies water exchange, which is a separate process independent of CR pharmacokinetics; second, the interstitial CR concentration, [CR_o], generally experiences a more slow-varying temporal feature and reaches its maximum at a much later time when compared with [CR_p] (i.e., [CR_o] is less sensitive to [CR_p] first pass); third, k_io does not appear with [CR_p] in the same term in a pharmacokinetic equation or within a [CR_p] expression. One the other hand, a larger [CR_p] helps reduce k_io uncertainty in CR-extravasating tissues by generating a larger [CR_o] and thus a larger shutter speed [17].

Traditionally, the most common parameters extracted from quantitative DCE-MRI are K^trans and v_e. We found these parameters to be quite sensitive to the AIF scaling factor β over a range from 0.8 to 2.0 for both simulated (Fig. 3) and real prostate ROI data (Fig. 4). This may partially explain the no statistical difference findings [25,26] reported in literature when comparing pharmacokinetic parameters (K^trans and v_e) derived from population averaged AIFs vs. individually measured AIFs -- it is possible that the errors (specially AIF scaling uncertainty) in individually measured AIFs propagate to the fitted K^trans and v_e parameters and thus negatively impact their precisions as quantitative imaging biomarkers. Thus, when AIF amplitude uncertainty is high, the k_io and k_ep parameters are more robust DCE-MRI biomarkers for their relative AIF-scaling insensitivity. As long as the AIF time-course curve shape can be well captured, k_io and k_ep should be the more reproducible parameters than K^trans and v_e. With the recent discovery that k_io is a measure of on-going Na⁺,K⁺-ATPase turnover [7], the capability to quantify k_io using the SSP model potentially ushers DCE-MRI into the emerging field of high-resolution metabolic imaging [8], in addition to its well-known function of quantifying microvascular properties. The parameter k_ep could be a better measure of capillary CR permeation than K^trans. The parameter K^trans usually well-approximates the permeability coefficient capillary surface area product, P_CR^†•S [8,27]. Thus, it can have a significant contribution from the voxel blood volume surface area. In addition, K^trans magnitude closely tracks the initial slope of the tissue enhancement time-course, a feature that describes similar characteristics of v_b•[CR_p] (v_b is the blood volume). This is one reason that K^trans accuracy depends heavily on AIF. On the other hand, k_ep quantification depends more on the washout period of the tissue enhancement time-course. As shown in Figure 1B, a 10% k_ep change causes noticeable difference in only the washout phase. In this case, the K^trans difference is relatively small (~ 3 %) as the rising phase of the curves are nearly indistinguishable.

Figure 7 demonstrates the tumor grading potential of the new k_io biomarker for prostate cancer. Despite the k_io and Gleason score uncertainties shown by the error bars, the data show a strong correlation: k_io increases “hyperbolically” with Gleason scores above 5, the traditional malignancy threshold. The smooth curve drawn through the points serves only to guide the eye. Therefore, the k_io parameter may be a useful noninvasive imaging biomarker that can be potentially used to reduce the number of biopsies performed in current clinical practice.

It is worth noting that even though accurate AIF quantification remains challenging, especially during the CR first pass, an AIF scaling error of less than 30% can be managed from the washout phase, taking into account the total blood volume and CR elimination rate. It is important to point out that the precision in k_io quantification is better when CR extravasation is extensive (large K^trans) [7]. To insure k_io accuracy, we used 30 initial guess sets for each voxel during fitting, and limited our k_io report to voxels with AIC statistics favoring the shutter-speed paradigm.

The uncertainty in [CR_o](t) quantification (because of AIF uncertainty) affects k_io and v_i accuracy, and the maximum [CR_o] magnitude affects k_io precision [6,7]. It has recently been suggested it might be possible to determine k_io and v_i without the use of CR [28]. Though this is not yet established, it would preclude parametric errors due to AIF uncertainty. However, the K^trans and k_ep parameters are not accessible without the use of CR.

With faster imaging speed as a result of ever improving MRI scanner hardware and software, DCE-MRI data acquisition can achieve improved AIF temporal resolution and better tissue curve-shape quantifications. Still, intrinsic challenges, like the in-flow effect, associated with AIF quantification remain. These mostly affect the AIF magnitude. This study only examines the effects of this primary AIF scaling error. Implications of other AIF uncertainties on pharmacokinetic parameters will require separate investigation.

Using a mouse model, a recent study [29] utilizing X-ray fluorescence microscopy showed that gadodiamide (Omniscan) enters normal murine prostatic epithelia and lumens. Although it remains unclear whether CR also enters some tumor cells, this new finding may require to be accounted for with an additional compartment in prostate DCE-MRI pharmacokinetic modeling. It is unclear at this point whether the CR concentration differences between the prostatic epithelia, the lumens, and the EES are large enough to be separately resolved. Still, the new finding may partially explain the large v_e values reported in prostate DCE-MRI literature.

It is interesting to point out that for extracellular Gadolinium based CRs with appreciable extravasation, CR molecules will present in blood plasma and extravascular extracellular space (EES) after a bolus IV injection. The associated compartment-specific relaxivities for the EES and blood plasma are r_1o and r_1p, respectively. In most DCE-MRI studies it is generally assumed that r_1o and r_1p are numerically equal. However, there are some indirect evidences suggesting potential differences [30,31] between the two. Under the condition that r_1o and r_1p are both time-and [CR]-independent_, the effect of unequal r_1o and r_1p on pharmacokinetic model parameter estimations is very similar to that of DCE data modeled under different AIF scaling factors, as was undertaken in this study. The similarity is shown in the APPENDIX.

The data studied here have also been used in two earlier reports [6, 5]. The former showed the shutter-speed K^trans and k_ep as well as the ΔK^trans [≡ K^trans(FXR) - K^trans(FXL)] imaging biomarkers exhibit improved malignant/benign tissue discrimination [6]. The latter paper showed the CA extravasation magnitude effect on commonly modeled DCE parameter (K^trans, v_e, v_b τ_i, τ_b) precisions. Specifically, τ_i (1/k_io) uncertainty and the feasibility of τ_i (1/k_io) mapping of the entire normal prostate were demonstrated [5]. In this paper, after identifying k_ep and k_io as the AIF-scaling-insensitive DCE parameters, the potential for k_io (with its newly discovered metabolic activity nature) as a disease aggressiveness biomarker was shown: a k_io Gleason score correlation.

One limitation of this study is that we investigated the effect of only AIF scaling uncertainty on estimations of pharmacokinetic parameters. Other confounding factors, like variable T₂* effect during CR passage and in-flow effect, etc., can result in AIF curve shape variations, which will cause different variations in the derived k_ep values. Future studies will be needed to address these issues. It is encouraging that a recent multi-center prostate DCE-MRI data analysis study showed that the variations of the k_ep parameter were substantially smaller than those of the K^trans parameter when they were derived from AIFs quantified with different methods, leading to both AIF curve-shape and amplitude differences [32].

CONCLUSIONS

AIF quantification remains a major challenge for DCE-MRI pharmacokinetics. Several AIF derivation approaches require AIF magnitude scaling, which generally suffers from the lack of ground truth knowledge. This simulation work demonstrates that the k_ep and the Shutter-Speed Paradigm specific k_io (1/τ_i) parameters are nearly insensitive to AIF scaling. This supports the notion that both the k_ep and k_io parameters are more robust DCE-MRI biomarkers.

Highlights.

• In DCE-MRI pharmacokinetic modeling, arterial input function (AIF) scaling is often needed for AIF derivation.

• Contrast reagent transfer constant (K^trans) and extravascular, extracellular volume fraction (v_e) model parameters are affected by AIF-scaling.

• The contrast reagent intravasation rate constant (k_ep) is insensitive to AIF-scaling error.

• The unidirectional rate constant for equilibrium cellular water efflux (k_io) is insensitive to AIF-scaling error.

Abbreviations

AIF

arterial input function

AIF scaling factor

β

CR

contrast reagent

[CR_p]

contrast reagent concentration in blood plasma

[CR_o]

contrast reagent concentration in the extravascular, extracellular space

[CR_t]

contrast reagent concentration in tissue

DCE-MRI

dynamic contrast-enhanced magnetic resonance imaging

FOV

field of view

FXL

fast-exchange-limit

FXR

fast-exchange-regime

h_v

microvascular hematocrit

K^trans

rate constant for plasma/interstitium contrast agent transfer

k_ep

= K^trans/v_e, rate constant for contrast reagent intravasation

k_io

= 1/τ_i, unidirectional equilibrium cellular water efflux rate constant

PD

proton density

r₁

longitudinal contrast reagent relaxivity

r_1o

longitudinal relaxivity for CR in the extravascular, extracellular space

r_1p

longitudinal relaxivity for CR in the blood plasma space

R_1b

= 1/T_1b, blood longitudinal relaxation rate constant for blood ¹H₂O

R_1t

= 1/T_1t, tissue longitudinal relaxation rate constant for tissue ¹H₂O

ROI

region of interest

ρ

cell number density [number of cells/unit volume]

SD

standard deviation

SNR

signal-to-noise ratio

SSP

Shutter-Speed Paradigm

SXR

slow-exchange-regime

τ_i

mean intracellular water lifetime

T₁⁻¹

= (|R_1o –R_1i|), the NMR R₁“shutter-speed”, [≡ κ₁]

TP

Tracer Paradigm (Tofts model)

v_e

extravascular, extracellular volume fraction; the EES

v_i

intracellular volume fraction (= 1- v_e, when ignoring blood volume fraction)

APPENDIX

The relaxivity of a contrast reagent (CR) is defined as the slope of the R₁ and [CR] equation as expressed in Eq. (1a),

$${\mathrm{R}}_1={\mathrm{r}}_1·[\text{CR}]+{\mathrm{R}}_{10}$$ (1a)

where r₁ is the relaxivity in unit of (mM⁻¹s⁻¹).

The r₁ values are specific to the compartments occupied by CR molecules. In DCE-MRI, low molecular weight Gadolinium based CR can present in blood plasma and the extravascular, extracellular space (EES).

Eq. (3) can be used to convert measured blood R₁ time-course to that of blood plasma CR concentration time-course, [CR_p].

For the FXR and the FXL models, the relationships of tissue R₁ and the EES CR concentration, [CR_o], is given by Eq. (1) and Eq. (5), respectively.

Because r₁ always appears in the form of r₁•[CR] product in a relaxivity expression, the r_1o•[CR_o] term which quantifies EES R₁ change can be expanded to:

$${\mathrm{r}}_{1\mathrm{o}}[{\text{CR}}_{\mathrm{o}}](\mathrm{t})=\frac{{\mathrm{r}}_{1\mathrm{o}}}{{\mathrm{r}}_{1\mathrm{p}}}·\left(\frac{K^{\mathit{trans}}}{v_e}\right)·\frac{1}{(1-h_v)}·{\int }_0^T(R_{1b}(t)-R_{1b}(0))·exp\left(-\frac{K^{\mathit{trans}}}{v_e}·(\mathrm{T}-\mathrm{t})\right)·\text{dt}$$ (2a)

where r_1o is the longitudinal CR relaxivity for the EES, and r_1p is the longitudinal CR relaxivity for blood plasma. All other parameters are defined in MATERIALS and METHODS section.

It is common practice in DCE-MRI pharmacokinetic modeling to assume that r_1o = r_1p. However, there is some evidence indicating unequal r_1o and r_1p values [30,31].

When both r_1o and r_1p are [CR]- and time-independent, the r_1o/r_1p ratio can be moved to either side of Eq. (2a). That is, r_1o/r_1p ≠ 1.0 has a similar effect as that of employing an AIF scaling factor (β) in pharmacokinetic modeling. Here, the AIF is assumed to be well-characterized and the r_1o/r_1p ratio depends on the compartments the CR molecules occupy. When the r_1o/r_1p ratio is unknown or there is strong evidence indicating that r_1o/r_1p ≠ 1.0, then results from this work show that k_ep can be the parameter preferred over K^trans for characterizing microvasculature. This is because of its insensitivity to AIF scaling uncertainties.