Subrandom Methods for Multidimensional Nonuniform Sampling

Abstract

Methods of nonuniform sampling that utilize pseudorandom number sequences to select points from a weighted Nyquist grid are commonplace in biomolecular NMR studies, due to the beneficial incoherence introduced by pseudorandom sampling. However, these methods require the specification of a non-arbitrary seed number in order to initialize a pseudorandom number generator. Because the performance of pseudorandom sampling schedules can substantially vary based on seed number, this can complicate the task of routine data collection. Approaches such as jittered sampling and stochastic gap sampling are effective at reducing random seed dependence of nonuniform sampling schedules, but still require the specification of a seed number. This work formalizes the use of subrandom number sequences in nonuniform sampling as a means of seed-independent sampling, and compares the performance of three subrandom methods to their pseudorandom counterparts using commonly applied schedule performance metrics. Reconstruction results using experimental datasets are also provided to validate claims made using these performance metrics.

Graphical Abstract

1. Introduction

The use of multidimensional NMR spectroscopy has become a staple of studies that characterize large or complex biomolecules. Following the introduction of two-dimensional acquisition methods [1], and the proliferation of three-dimensional methods for tracing protein backbones and sidechains [2, 3], NMR spectroscopists have utilized atomic connectivities to resolve biomolecular information into multiple dimensions. However, traditional multidimensional NMR acquisition is not without its disadvantages. Spectral resolution along each dimension is dependent on the longest sampled time in that dimension, and achieving high resolution often requires sampling to impractically long times in one or more dimension. Acquiring spectra to acceptable signal-to-noise (SNR) presents similar challenges [4]. Nonuniform sampling (NUS) of a small subset of points from a high-resolution uniform (Nyquist) grid offers a powerful means of simultaneously increasing resolution [5, 6] and sensitivity [7–9] while reducing total experiment time [4, 10].

Collecting a subset of grid points – referred to as a schedule – from a Nyquist grid effectively multiplies the complete uniform time-domain data with that schedule’s indicator function. In the frequency domain, this is equivalent to the convolution of the schedule’s point-spread function (PSF) with the spectrum of the complete data. Naïve application of the discrete Fourier transform to such data (i.e. using the nuDFT) would suffer from this convolution, resulting in drastically reduced signal quality and increased noise and interferences, or artifacts [11]. Consequently, non-Fourier methods of spectrum analysis must be employed to reconstruct the missing time-domain information in NUS datasets. Popular methods include maximum entropy (MaxEnt) estimation or interpolation [5, 12–14], iterative soft thresholding (IST) and its accelerated equivalent NESTA [15, 16], and multidimensional decomposition [17, 18]. Each method approaches the problem of spectrum estimation using a slightly different mathematical model, but all attempt the same result: deconvolution of the sampling schedule’s PSF from the measured data to yield the complete dataset. As a result, the PSF plays an important role as a first-order indicator of signal-to-artifact ratios that may be expected for a given sampling schedule [19–23]. Figures 1 and 2 illustrate representative PSFs of one- and two-dimensional NUS schedules, respectively.

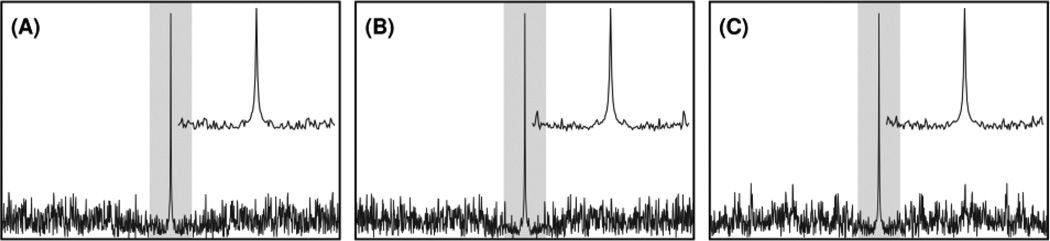
Figure 1.

Comparison of point-spread functions from (A) the lowest-PSR jittered pseudorandom schedule, (B) the highest-PSR jittered pseudorandom schedule, and (C) the jittered subrandom schedule produced from an exponentially weighted 1024-point Nyquist grid at 10% sampling density. Inset plots indicate the shaded central regions of each point-spread function in order to highlight artifacts near the fundamental. As expected for jittered sampling, the variation between each PSF is minimal.

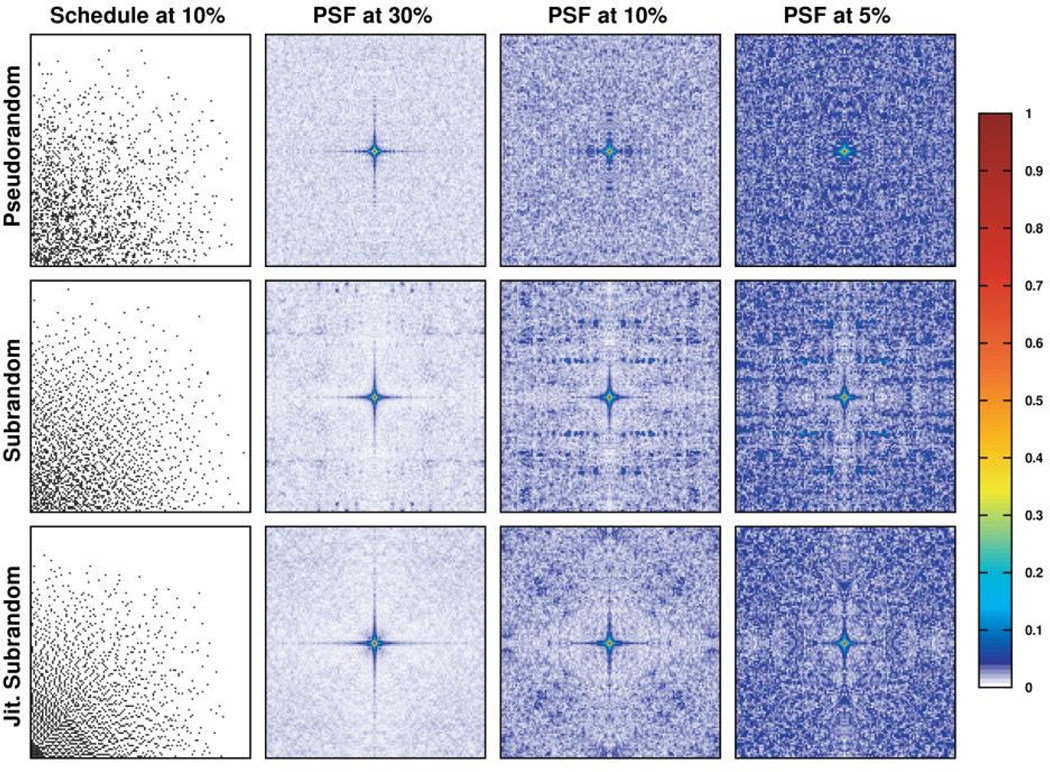
Figure 2.

Comparison of two-dimensional sinusoidally weighted pseudorandom, subrandom and jittered subrandom sampling schedules and their resultant point spread functions (PSFs) at various sampling densities. As sampling density decreases, the μ_PSF metric also increases, indicated by the appearance of more blue-shaded regions in the PSF. At all densities, and especially at 30%, the shape of the PSF fundamental (central region) matches exceedingly well between all three schedules. While subrandom rejection sampling produces substantial sidelobes as sampling density increases, jittered subrandom sampling does not, resulting in PSFs that closely resemble pseudorandom sampling.

Along with the reconstruction method applied, the second most relevant contributor to NUS performance is the sampling schedule itself. While the exact relationship between sampling schedules and reconstructed spectral quality remains unclear, several features of schedules have been linked to high performance. For example, weighting sampled grid points towards regions having higher local signal-to-noise is known to yield sensitivity increases [8, 24]. Minimizing gap lengths between sampled grid points has also been shown to improve spectral fidelity [25, 26]. One interesting feature of effective NUS schedules, known as incoherence, is based on how correlated or coupled sampled grid points are to each other in evolution-time space. In simple terms, the incoherence of a sampling schedule is a measure of how random, aperiodic or non-regular that schedule appears [27, 28]. Artifacts in NUS reconstructions, which result from aliasing of signals within the effective measured bandwidth [19], are substantially diminished by incoherent sampling. As a consequence of this relationship, nearly all contemporary methods of nonuniform sampling employ pseudorandom numbers to produce incoherent schedules.

While the use of pseudorandom numbers is a simple means of constructing incoherent sampling schedules, it adds further complications to the already nontrivial task of selecting a sampling schedule. For any selection of grid size and sampling method, there exists a nearly inexhaustible number of possible pseudorandom schedules, each determined by a seed value. In practice, each schedule in such an ensemble will perform differently and in a manner that cannot be predicted by its seed value [22]. As a result, most efforts to maximize the performance of NUS experiments involve the construction and scoring of a large number of sampling schedules [22, 25, 27, 29–31]. However, such Monte Carlo approaches to schedule optimization are limited in efficacy, as no consensus exists on how to quantitatively score schedule performance. Relative sensitivity (R′) metrics have been introduced to score schedules in the time domain, and metrics such as peak-sidelobe ratio (PSR), line width (λ) and mean artifact intensity (μ_PSF) have been proposed based on schedule point-spread functions [8, 22, 29]. Ultimately, accurate determination of schedule optimality depends on the amplitude, frequency and decay rate distributions of the signals to be measured [11], and thus remains a difficult challenge. For general routine spectroscopy, where these distributions are unknown or poorly specified, Monte Carlo optimizations must be performed to avoid selecting a pseudorandom schedule that performs poorly.

In order to simplify the task of selecting a NUS schedule, substantial effort has been expended towards reducing the dependence of pseudorandom sampling methods on seed values. In all such efforts, constraints are applied to the underlying pseudorandom number generators in order to reduce the number of possible schedules obtained from a given method. For example, jittered sampling draws grid points from a set of equiprobable “jittered regions” based on a specified probability density function [21, 22]. On the other hand, gap sampling draws grid points based on a gap equation that defines the distance between sampled locations [15, 25, 31]. The logical end-game of efforts to reduce pseudorandom seed dependence is apparent: seed-independent sampling schedules that retain the performance and incoherence of pseudorandom methods. Towards that end, seed-independent methods that construct one-dimensional density-based schedules [32] and multidimensional gap-based schedules [31] have been recently proposed. However, no seed-independent method has yet been described to construct incoherent sampling schedules from arbitrary weighting functions on multidimensional Nyquist grids.

This work introduces the use of subrandom number sequences for constructing incoherent NUS schedules on multidimensional Nyquist grids. Three practical seed-independent methods are described as a direct result. The first method is a rejection sampling algorithm derived from quasi-Monte Carlo methods, which use subrandom sequences to efficiently sample the domains of multidimensional integrals [33, 34]. The second method combines subrandom rejection sampling with jittered region determination [22] to yield a seed-independent result. The final method substitutes pseudorandom numbers with subrandom numbers in Knuth’s algorithm [35] in order to construct seed-independent Poisson-gap schedules. A detailed analysis of these methods is performed using multiple grid weighting functions on multiple grid configurations. The presented methods perform comparably to their pseudorandom counterparts according to several metrics of sensitivity and resolution enhancement, and exhibit the incoherence that is expected from NUS schedules. In particular, jittered subrandom rejection sampling offers strong guarantees on spectral quality and obviates the need for Monte Carlo schedule optimization, making it an ideal choice for routine spectroscopic experiments on samples with unknown signal characteristics, especially for multidimensional experiments.

2. Theory

2.1 Subrandom sequences

Pseudorandom sequences are deterministically constructed sequences of numbers that exhibit random character when viewed as a statistical ensemble. Methods of generating pseudorandom sequences must be initialized with a seed number, which will completely pre-determine the sequence of numbers produced by the method. Subrandom sequences are also deterministically constructed, but do not share the statistical randomness of pseudorandom sequences. Nonetheless, subrandom number generators are often used within numerical simulations in place of pseudorandom numbers, and do not require initialization by a seed number. Thus, the replacement of pseudorandom sequences with subrandom sequences is a straightforward means of removing seed-dependence from a sampling method.

Both presented methods operate by replacing pseudorandom numbers uniformly distributed in [0,1) with subrandom Halton sequences [34]. This replacement is an established practice of quasi-Monte Carlo methods, where it is used to substantial positive effect. When used to approximate multidimensional integrals, subrandom sampling boasts lower error bounds than pseudorandom sampling. Because the discrete Fourier transform itself involves the approximation of multidimensional Fourier integrals, it was postulated that the lower error bounds of subrandom sequences could benefit NUS experiments. A one-dimensional Halton sequence having radix b and length M is related to the base-b representation of the sequence of integers m from zero to M − 1, like so:

$$m={\sum }_{j=0}^J{d}_{b,j}(m)b^j$$ (1)

where d_b,j is the j-th base-b digit of m, and J is a large number that sets the maximum representable value. From this representation, the base-b Halton sequence g_b is formed by reversing the radix index in the expansion:

$$g_b(m)={\sum }_{j=0}^J{d}_{b,j}(m)b^{-j-1}$$ (2)

This radix-inverted formula will produce values that uniformly cover the unit interval with increasing density as m increases. Halton sequences generalize naturally to multidimensional spaces: sequences in higher dimensions are constructed by selecting a base for each dimension such that all bases are coprime. For example, the Halton sequence in two dimensions could be formed by the bases (2,3). The selection of small coprime bases ensures a minimal correlation between dimensions, which is essential for constructing incoherent sampling schedules.

2.2 Rejection sampling

Rejection sampling is a method of drawing pseudorandom samples from an arbitrary weighting function f(x) using only uniformly distributed pseudorandom numbers. For each random draw, a trial point x is drawn uniformly from the domain of f, and an associated amplitude u is drawn uniformly between zero and the maximum of f. A trial point x is rejected if its amplitude u falls above f(x), at which point a new pair (x, u) is drawn. Once a pair (x, u) is identified such that u ≤ f(x), the trial point x is accepted and returned as a new sample from the distribution f. To construct a sampling schedule having a density equal to δ using rejection sampling, a set of n random draws are made to satisfy the following equation:

$$n=\lfloor \delta {\prod }_{d=1}^D{N}_d\rfloor$$ (3)

where N_d is the grid size along dimension d of a D-dimensional Nyquist grid. It is important to note that n, and not δ, is the relevant quantity for determining signal-to-noise and signal-to-artifact ratio in nonuniform sampling, as is outlined by Kazimierczuk and colleagues [20]. As a result, all on-grid methods discussed here may be used to construct nearly off-grid schedules by increasing N_d and proportionally decreasing δ.

2.3. Jittered rejection sampling

The jittered sampling algorithm, previously introduced [21] and refined [22] for drawing NUS schedules from density functions, is an effective method of constrained pseudorandom sampling. Rather than drawing each sampled grid point independently from the entire Nyquist grid, jittered sampling establishes a set of non-overlapping regions that have equal total probabilities of holding a sampled grid point. Once a set of jittered regions has been established, a single grid point is drawn from each region using rejection sampling. Jittered region determination does not depend on seed number, and tightly constrains any later pseudorandom sampling that is applied to each region. As a consequence, jittering is an effective general means of reducing seed-dependent variability of NUS schedules [22].

2.4. Poisson-gap sampling

An alternative constrained pseudorandom sampling method, known as Poisson-gap sampling, also achieves reduced seed-dependent variability over pseudorandom rejection sampling [25]. Instead of constraining each sampled point to its own jittered region, gap sampling constrains the distances between sampled points [31] using a gap equation. In particular, distances between sampled points in Poisson-gap schedules follow a Poisson distribution whose rate parameter varies sinusoidally over the Nyquist grid. In pseudorandom Poisson-gap sampling, Knuth’s algorithm is utilized for drawing Poisson random deviates during schedule construction [35]. In short, Knuth’s algorithm simulates a Poisson process by drawing uniform random deviates and counting the number of deviates contained in a defined interval. See Supplementary Code Listing S-1 for an exact description of Knuth’s algorithm as it is used in this work.

2.5. Subrandom sampling

By replacing all pseudorandom draws with numbers from an appropriately constructed subrandom sequence, the rejection sampling method can be transformed into a algorithm that no longer depends on seed numbers. For a schedule having D grid dimensions, a set of D + 1 coprime numbers is selected as the basis set of a Halton sequence [33, 34]. As an example, the bases 2, 3, 5 and 7 would be used for constructing three-dimensional schedules. These four bases would be used in a (2,3,5,7)-Halton sequence that produces uncorrelated values in [0,1)⁴. The first D values in each Halton sequence term are mapped onto trial grid points x, while the last value in each term is used as the amplitude u during rejection sampling. Jittered rejection sampling may similarly be transformed into a seed-independent algorithm using subrandom number sequences. Transforming jittered sampling into a seed-independent method is a straightforward matter of replacing each pseudorandom draw with a subrandom draw from a (2,3)-Halton sequence, which yields a sampling algorithm that performs nearly identically to jittered pseudorandom sampling. Finally, Poisson-gap sampling may be stripped of its seed dependence by replacing its pseudorandom draws in Knuth’s algorithm with subrandom draws from a 2-Halton sequence.

3. Methods

3.1. Schedule construction

In order to evaluate the effectiveness of subrandom number sequences in NUS, a Monte Carlo analysis was performed to compare subrandom schedules with their pseudorandom counterparts. All sampling schedules were constructed using a set of small C programs that use the srand48 and drand48 functions to generate uniform pseudorandom numbers. Exponentially weighted schedules were drawn from the following function:

$$f_{\text{EXP}}(\mathit{x})=\text{exp}\{-{\sum }_{d=1}^D\frac{{\alpha }_d{x}_d}{N_d}\}$$ (4)

where α_d and x_d are the forward-bias and grid index along dimension d, respectively, and D is the grid dimensionality. Gaussian weighted schedules were drawn from a similar function:

$$f_{\text{GAUSS}}(\mathit{x})=\text{exp}\{-{\sum }_{d=1}^D{\alpha }_d{\left(\frac{x_d}{N_d}\right)}^2\}$$ (5)

and sinusoidally weighted schedules were drawn from a quarter-sine function [8]:

$$f_{\text{SIN}}(\mathit{x})={\prod }_{d=1}^D\left\{\text{sin}\right(\frac{\pi }{2}\frac{x_d}{N_d}+\pi )+1\}$$ (6)

A set of 200 pseudorandom schedules was constructed by rejection sampling from each weighting function at 30%, 10% and 5% sampling density. A second set of 200 schedules was constructed by jittered pseudorandom rejection sampling from each weighting function and sampling density. A final set of 200 pseudorandom Poisson-gap schedules was constructed at each sampling density. Nyquist grids having 1024, 64×64, 128×128 and 32×32×32 points were utilized for each weighting function and sampling density, resulting in a total of 16,800 unique pseudorandom schedules. Each group of 200 pseudorandom schedules was paired with a subrandom schedule having equivalent Nyquist grid configuration, grid weighting, sampling density and sampling method.

3.2. Performance metric calculations

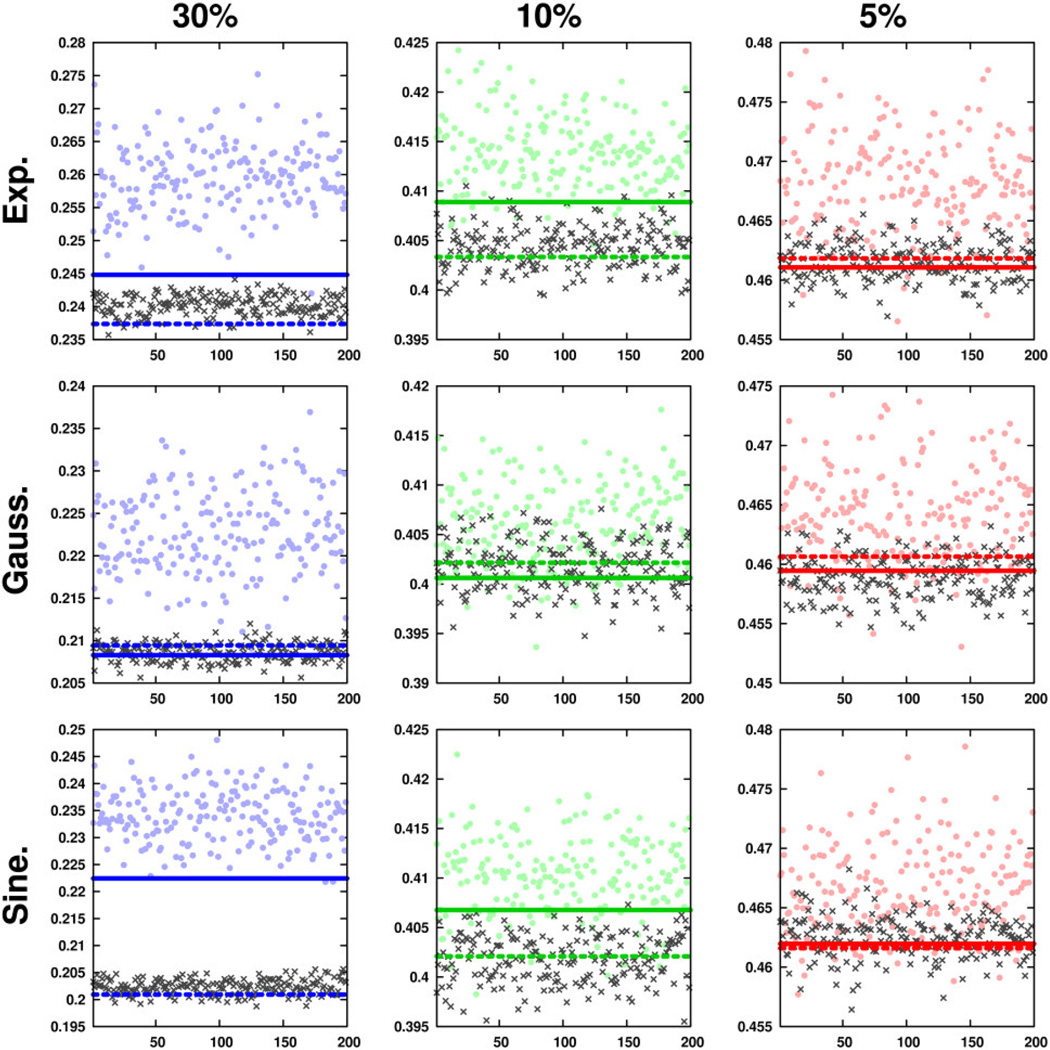
In order to quantify various aspects of performance in each of the compared methods, a battery of several metrics was computed over all constructed sampling schedules. Using each schedule’s indicator function K, the adjusted relative sensitivity R′(K) was computed as previously described [8, 22]. All other metrics were computed using the PSF of each schedule, which was calculated as the magnitude of the hypercomplex multidimensional Fourier transform of each schedule’s indicator function. Each PSF was normalized to a maximum intensity of one. Figures 1 and 2 illustrate several representative PSFs for one- and two-dimensional schedules constructed using exponential and sinusoidal weighting. Further examples are shown in Supplementary Figures S-1 and S-2. The line width (λ) of each schedule’s fundamental (zero frequency component) was estimated from its PSF according to a Lorentzian line shape, and a Lorentzian peak having that line width was subtracted from the PSF to yield only artifacts. Following subtraction of the fundamental, the mean and standard deviation intensity of all remaining artifacts – μ_PSF and σ_PSF, respectively – were computed as previously described [22]. Peak-sidelobe ratios (PSRs) were also computed as the inverse of the maximum artifact intensity (after fundamental removal) for each schedule [11]. Figure 3 summarizes the resulting performance metric computations for rejection-based schedules on one-dimensional grids. Analogous summaries for two- and three-dimensional rejection sampling schedules and gap sampling schedules are provided in Supplementary Figures S-3 through S-7. To simplify interpretation of Figure 3, sidelobe-peak ratios (SPRs) were plotted using the inverses of computed PSR values.

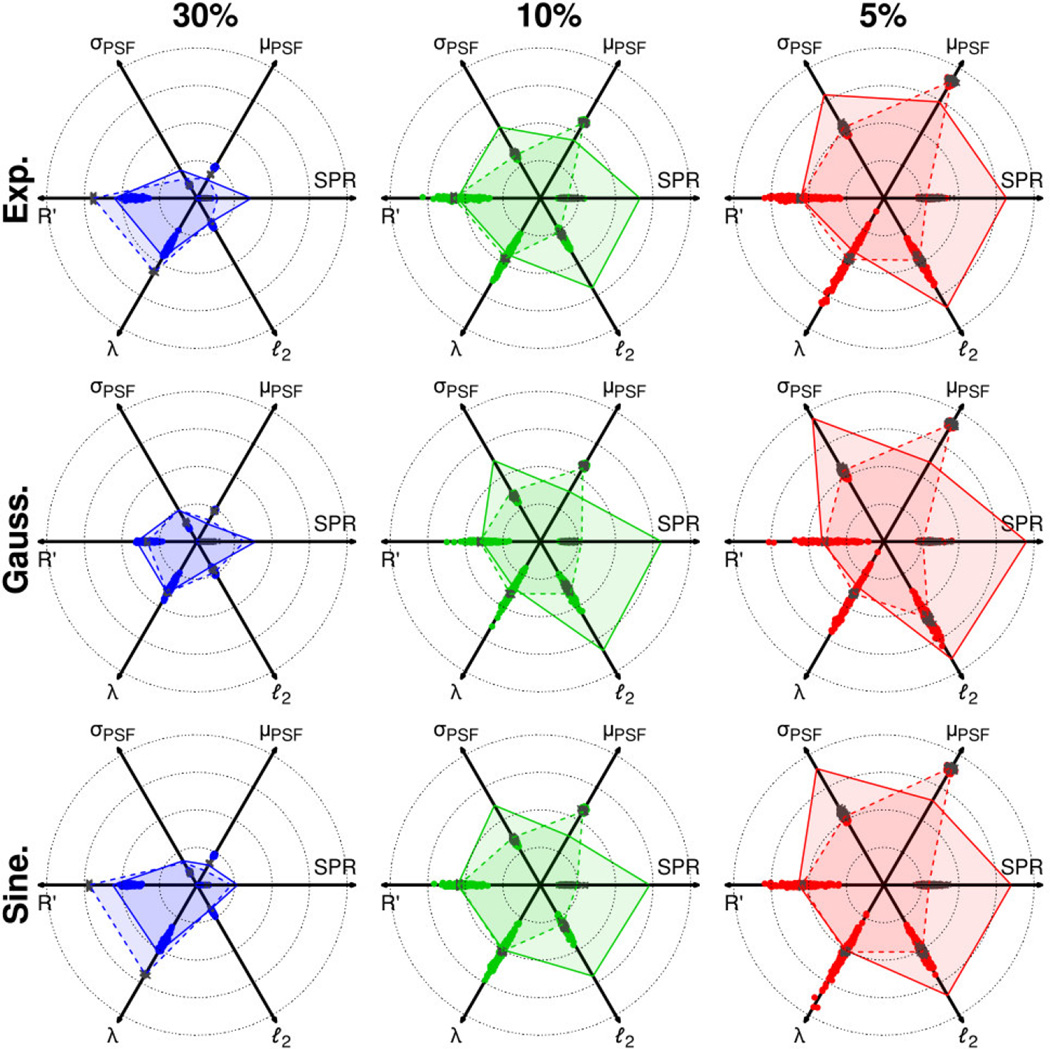
Figure 3.

Radar charts indicating performance metrics for one-dimensional sampling schedules on 1024-point grids. Metrics from pseudorandom, jittered pseudorandom, subrandom and jittered subrandom schedules are indicated by points, crosses, solid lines and dashed lines, respectively. Displayed ranges for each metric are as follows: SPR: 0.08 – 1, μ_PSF: 0.01 – 0.13, σ_PSF: 0.01 – 0.11, R′: 1.1 – 2.2, λ: 0.3 – 1.6, ℓ₂: 0 – 1. Lower values of each range are placed centrally on the charts, and higher values are placed towards the outer radius.

In addition to the data-independent performance metrics described above, one data-dependent metric was computed to compare all methods on one- and two-dimensional grids. Two previously described uniformly collected datasets, a ¹H-¹⁵N HSQC and an HNCA, were used in the computations [31]. For each one-dimensional schedule, the HSQC dataset was subsampled and reconstructed using 500 iterations of convex accelerated maximum entropy reconstruction (CAMERA) [14] in the MINT regime. For each two-dimensional schedule, the HNCA was also subsampled and reconstructed using the same parameters. Each reconstructed dataset was then compared to its uniformly sampled and DFT-processed equivalent using an ℓ₂-norm:

$${\ell }_2(\mathit{A},\mathit{B})=\sqrt{\frac{{\sum }_{i=1}^N{(A_i-B_i)}^2}{{\sum }_{i=1}^N{A_i}^2}}$$ (6)

where A holds the uniform reference spectrum and B holds the CAMERA-reconstructed spectrum. Unlike data-independent performance metrics that focus on the schedule and its PSF, the ℓ₂-norm uniquely includes the effect of noise on schedule performance. In short, the ℓ₂ error metric of a schedule quantifies the ability of CAMERA to reconstruct the true uniform data from its subsampled form in the presence of experimental noise. While the ℓ₂ errors in this work are specific to the CAMERA algorithm, it is wholly expected that any similar reconstruction method (i.e. regularized solvers like IST-D, IST-S, NESTA, or Cambridge/Rowland MaxEnt) would exhibit equivalent figures. Figures 4 and 5 summarize the ℓ₂ errors of one- and two-dimensional rejection sampling schedules, respectively. Equivalent summaries for gap sampling schedules are shown in Supplementary Figures S-8 and S-9.

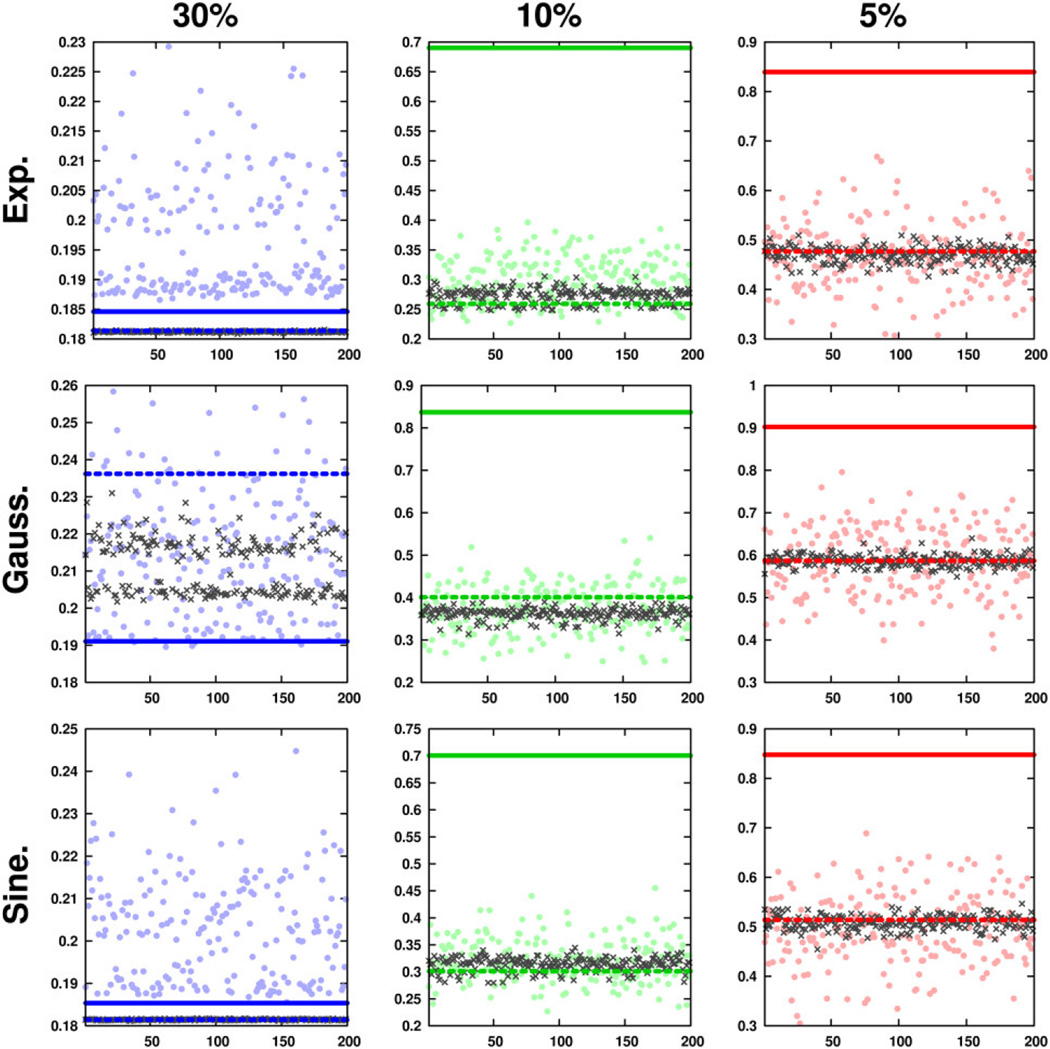
Figure 4.

Expanded view of ℓ₂ reconstruction errors from one-dimensional rejection-based sampling methods. Errors from pseudorandom, jittered pseudorandom, subrandom, and jittered subrandom schedules are indicated by circles, crosses, solid lines, and dashed lines, respectively. The deleterious effects of highly coherent non-jittered sampling are manifest at 10% and 5% sampling densities as high ℓ₂ errors. In all but one case, jittered subrandom sampling performs nearly identically to jittered pseudorandom sampling.

Figure 5.

Expanded view of ℓ₂ reconstruction errors from two-dimensional rejection-based sampling methods. Errors from pseudorandom, jittered pseudorandom, subrandom, and jittered subrandom schedules are indicated by circles, crosses, solid lines, and dashed lines, respectively. The deleterious effects of highly coherent non-jittered sampling are manifest at 10% and 5% sampling densities as high ℓ₂ errors. Jittered subrandom sampling is practically indistinguishable in performance from jittered pseudorandom sampling in all cases.

As a final means of summarizing sampling schedule performance, each HSQC and HNCA reconstruction was peak-picked and subjected to an automated peak matching analysis. For each reconstructed HSQC spectrum, a peak list was generated using the NMRPipe peakHN.tcl utility [36], with a minimum intensity threshold of 3.0 × 10⁷. A greedy algorithm was then used to construct a maximum-cardinality bipartite matching between the reconstruction’s peak list and the peak list of the reference spectrum. Chemical shift windows of 0.015 ppm and 0.08 ppm were used for matching along the ¹H and ¹⁵N dimensions, respectively. The number of peaks matched, lost and gained in the reconstructed spectrum were all counted. Lost peaks were any picked peaks in the reference spectrum without a match in the reconstruction. Gained peaks were any picked peaks in the reconstruction without a match in the reference. The intensities of matched peaks were compared against their true intensities using a Pearson correlation coefficient, r_int, which captures the linearity of reconstructed peak intensities. Finally, root-mean-square chemical shift deviations of all matched peaks along ¹H (d_H) and ¹⁵N (d_N) were also computed. Identical procedures, excepting a peak intensity threshold of 5.5 × 10⁵, were used to generate peak-picking performance figures for ¹H-¹⁵N projections of each reconstructed HNCA spectrum. Performance figures for exponentially sampled HSQC and HNCA spectra are summarized in Tables 1 and 2, respectively. Gaussian, sinusoidal and poisson-gap weighting methods all produced highly similar trends in peak-picking performance.

Table 1.

Summary of overall figures of merit produced from comparing CAMERA-reconstructed (exponentially) subsampled ¹H-¹⁵N HSQC spectra of ubiquitin with their true uniformly sampled spectrum. Matched peak counts are from a total of 121 reference peaks.

Meth.		Matched	Gained	rint	dH / ppm	dN / ppm
PR	30%	117±1.6	2±1.2	0.996±0.014	0.001±0.0003	0.011±0.0016
	10%	95±2.5	1±0.9	0.994±0.011	0.002±0.0003	0.009±0.0022
	5%	89±3.7	3±2.5	0.961±0.024	0.003±0.0004	0.009±0.0023
SR	30%	119	1	0.998	0.002	0.011
	10%	85	79	0.970	0.002	0.007
	5%	53	151	0.956	0.001	0.005
PR+Jit	30%	118±0.9	1±1.0	0.994±0.054	0.002±0.0003	0.011±0.0016
	10%	96±1.3	1±0.8	0.989±0.064	0.002±0.0003	0.010±0.0019
	5%	88±1.4	3±1.8	0.954±0.041	0.003±0.0003	0.008±0.0014
SR+Jit	30%	118	2	0.973	0.002	0.011
	10%	96	0	0.997	0.002	0.010
	5%	88	5	0.960	0.003	0.009

Table 2.

Summary of overall figures of merit produced from comparing CAMERA-reconstructed (exponentially) subsampled ¹H-¹⁵N HNCA spectral projections of ubiquitin with their true uniformly sampled spectral projection. Matched peak counts are from a total of 92 reference peaks.

Meth.		Matched	Gained	rint	dH / ppm	dN / ppm
PR	30%	84±1.7	1±1.0	0.999±0.0007	0.001±0.0003	0.013±0.0021
	10%	77±2.2	2±1.3	0.996±0.0010	0.001±0.0001	0.019±0.0021
	5%	72±2.3	3±1.4	0.990±0.0024	0.001±0.0002	0.021±0.0021
SR	30%	83	2	0.999	0.0004	0.009
	10%	77	3	0.997	0.0008	0.019
	5%	73	2	0.992	0.001	0.023
PR+Jit	30%	89±0.8	1±0.6	0.999±0.00002	0.001±0.0003	0.007±0.0009
	10%	81±1.8	2±1.1	0.995±0.044	0.001±0.0003	0.018±0.0019
	5%	74±2.3	3±1.5	0.994±0.001	0.001±0.0002	0.022±0.0021
SR+Jit	30%	88	0	0.999	0.0004	0.007
	10%	81	2	0.998	0.001	0.015
	5%	71	3	0.995	0.001	0.019

4. Results

According to nearly all utilized performance metrics, subrandom rejection sampling yields comparable NUS schedules to those produced by pseudorandom rejection methods. Examination of Figure 3 and Supplementary Figures S-3 and S-4 provides several intriguing insights, most importantly that jittered subrandom sampling performs identically to it’s equivalent pseudorandom schedules at all dimensionalities. On the other hand, non-jittered subrandom sampling only truly performs equivalently to pseudorandom sampling in two or more dimensions (i.e. for NMR experiments having three or more dimensions). While pseudorandom sampling produces one-dimensional schedules with a range of PSR values, non-jittered subrandom sampling produces highly coherent schedules that exhibit very large artifacts (Figure 3, solid lines). Jittered subrandom sampling reduces artifact intensities in one-dimensional schedules, fully recovering the performance of pseudorandom sampling at δ ≤ 10% (Figure 3, dashed lines). In two dimensions (Supplementary Figure S-3), subrandom sampling performs almost equivalently to pseudorandom sampling, with the exception of PSR, which is once again consistently improved by jittering. Finally, the performance metrics of both jittered and non-jittered subrandom rejection sampling exhibit very tight agreement to pseudorandom sampling in three dimensions (Supplementary Figure S-4). In the cases of two- and three-dimensional sampling, jittering produces a heavier forward weighting of grid points, leading to increased relative sensitivity at the slight expense of line width. The slight forward weighting of jittered sampling is readily observable in schedules having 30% and 10% density, as illustrated in Supplementary Figures S-3 and S-4.

The ℓ₂ reconstruction errors in Figures 4 and 5 shed further light on the performance of each method, and confirm the fundamental challenge of Monte Carlo schedule optimization. In the one-dimensional case, ℓ₂ errors from non-jittered subrandom schedules (Figure 4, solid lines) display a sharp upward trend as δ decreases. This trend is corroborated by PSR values of the same schedules, which clearly indicate that one-dimensional non-jittered subrandom schedules are highly coherent (cf. Supplementary Figure S-2). However, the poor performance of these schedules is remedied by the incorporation of jittering (Figure 4, dashed lines). In all cases, 1D jittered subrandom sampling yields ℓ₂ errors squarely within (if not below) the jittered pseudorandom ensemble. An identical theme was observed for ℓ₂ errors from two-dimensional schedules (Figure 5), where the ℓ₂ errors indicate that jittered subrandom sampling performs identically jittered pseudorandom sampling. In effect, moving from pseudorandom to subrandom jittered rejection sampling has achieved complete seed independence at no cost to schedule performance.

In the case of gap sampling, nearly all performance metrics indicated that subrandom Poisson-gap is a much poorer performer than pseudorandom Poisson-gap sampling (cf. Supplementary Figures S-5 through S-7). In general, subrandom Poisson-gap sampling suffered from larger artifacts and higher ℓ₂ errors than its pseudorandom equivalent (Supplementary Figures S-8 and S-9). Compared to rejection-based methods, Poisson-gap schedules had lower relative sensitivities and PSF line widths, though the latter is largely due to the non-Lorentzian character of Poisson-gap PSF fundamentals (Supplementary Figure S-2). Both pseudorandom and subrandom Poisson-gap sampling tended to produce noticeably “striped” sampling patterns (Supplementary Figures S-10 and S-11) in two or more dimensions. The effect was even more noticeable at 5% sampling density. As sampling densities at or below 5% are becoming increasingly common in three- and four-dimensional NUS NMR [16, 28], this could limit the scope of usefulness of Poisson-gap sampling.

In addition to comparative insights between methods, Figures 3, S-3, and S-4 also offer several general insights into the behavior of pseudorandom nonuniform sampling. As expected, the intensity of artifacts increases as δ is decreased, which is reported by decreasing PSR and increasing μ_PSF and σ_PSF metrics. Furthermore, PSR appears to be a more sensitive reporter of relative artifact intensity, as it takes on a much broader range of values than μ_PSF or σ_PSF. Finally, it is observed that decreasing δ tends to affect the variance of R′ and λ more than it affects their central tendencies. In contrast, μ_PSF and σ_PSF appear to be relatively low-variance metrics that depend primarily on sampling density and less on seed number.

To further underscore the challenges of data-independent Monte Carlo pseudorandom schedule optimization, correlations between all performance metrics and ℓ₂ were computed. Rather intruigingly, patterns of correlation differed as a function of schedule dimensionality, sampling density and weighting function. Correlations from all metrics to ℓ₂ remained within ±0.5 for one-dimensional schedules, with one exception: highly sparse schedules yielded correlations between R′ and ℓ₂ around −0.8. However, the expected negative correlation between PSR and ℓ₂ error was not observed. For exponentially weighted two-dimensional schedules, μ_PSF was found to slightly positively correlate with ℓ₂ (circa 0.7), and R′ was slightly negatively correlated (circa −0.6). No other substantial correlations were observed between data-independent metrics and ℓ₂ errors. In short, data-independent metrics failed to reliably predict reconstruction performance of a real experimental dataset in Monte Carlo analyses of one- and two-dimensional schedules. Given these results, it appears that the intuitive metrics commonly used to score schedule performance (e.g., PSR and R’) may not be robust predictors of practical NUS performance. This lack of consensus among data-independent metrics, as well as between data-independent and data-dependent metrics, is exactly the challenge faced by practicioners of Monte Carlo schedule optimization. Indeed, prior knowledge of the signal characteristics to be measured would greatly improve estimates of schedule optimality.

5. Discussion and Conclusions

Three novel methods of on-grid nonuniform sampling were described based on subrandom number sequences. On one-, two- and three-dimensional Nyquist grids weighted by three common probability density functions, these methods performed almost indistinguishably from pseudorandom schedules, as measured well-established metrics of sensitivity enhancement (R′ and PSR), resolution enhancement (PSF line width), and artifact intensity (PSR, μ_PSF and σ_PSF). In addition, jittered subrandom schedules were found to perform well in concert with CAMERA reconstructions of experimental data. This work confirms previous results that jittered pseudorandom schedules exhibit performance that depends very little on seed value [22], and further demonstrates that jittered subrandom schedules fall within their pseudorandom ensembles. As a consequence, jittered subrandom sampling completes the logical journey from unconstrained sampling, to partially constrained (jittered) sampling, to completely constrained (jittered subrandom) sampling. Jittered subrandom sampling is therefore an ideal method for seed-independent NUS schedule selection.

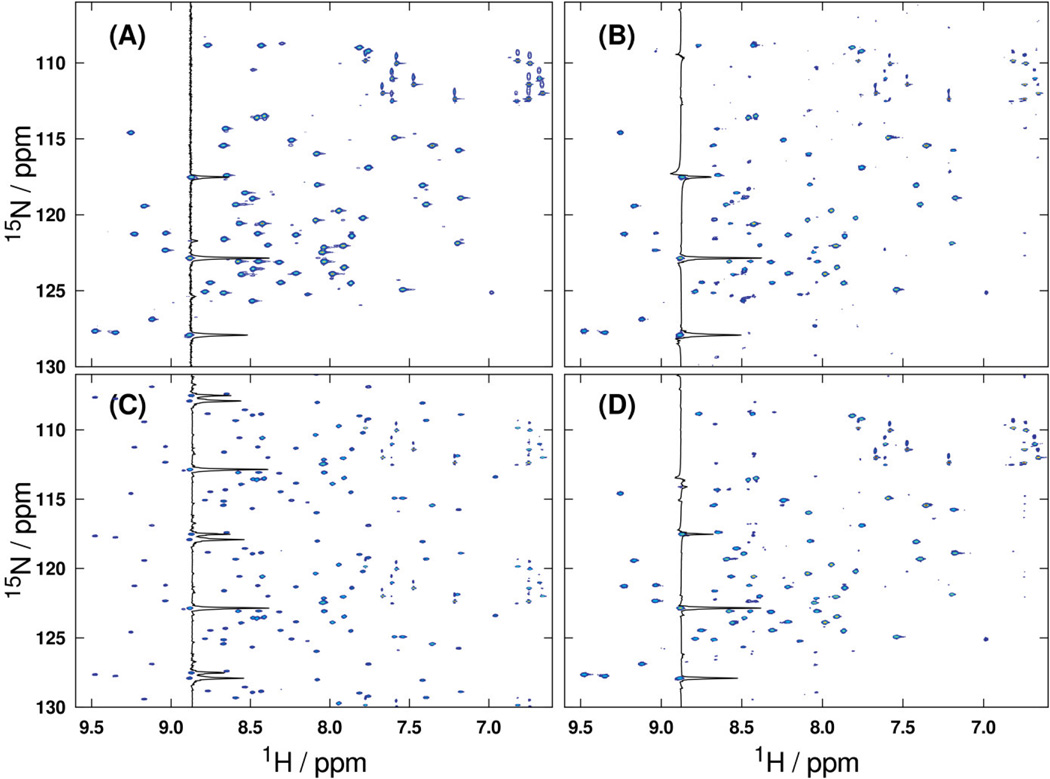
The methods proposed in this work do not perform unequivocally better than their pseudorandom counterparts. Rather, they fall within or near the distribution of performance metrics computed from an ensemble of equivalently weighted pseudorandom schedules. From a statistical viewpoint, this implies that subrandom nonuniform sampling is indistinguishable from pseudorandom nonuniform sampling based on the computed metrics. As the subset of collected grid points is decreased below 10% of the total grid point count, the distinguishability of these methods further decreases (e.g., third columns of Figures 4 and 5). When paired with a suitable reconstruction method, this indistinguishability is also reflected in the final spectra (e.g., Figure 6). Even at 5% sampling density, CAMERA reconstructions of nonuniformly sampled HSQC spectra display remarkable fidelity to the original data, whether sampled via pseudorandom or jittered subrandom schedules. However, as the third panel of Figure 6 illustrates, the high coherence of non-jittered subrandom sampling makes it a poor candidate for practical NUS experiments. Thus, while it is certainly possible to identify a pseudorandom schedule that performs slightly better in one or more of the above utilized metrics, the improvement in reconstructed spectral quality may still be minimal. Accurate determination of schedule optimality still largely depends on the data to be measured [11, 26]. Further studies are still required to determine the proper use of prior knowledge of signal characteristics in schedule construction.

Figure 6.

(A) Uniform reference spectrum from the ¹H-¹⁵N HSQC dataset used for scoring all one-dimensional schedules according to ℓ₂ error. The same data is shown after being subsampled by (B) a pseudorandom schedule, (C) a non-jittered subrandom schedule, and (D) a jittered subrandom schedule, and subsequently reconstructed by CAMERA. All schedules were constructed using an exponential weighting function at 5% sampling density. The high coherence of non-jittered subrandom sampling appears in the form of strong, regular aliasing artifacts in the corresponding reconstruction (C).

Where reproducibility is concerned, it cannot be understated that these new subrandom methods confer no advantages over existing pseudorandom sampling schemes. As long as the complete sampling schedule is provided alongside its measured nonuniform data, exact reproduction of reconstruction results is possible. Instead, the proposed subrandom methods offer increased simplicity and control over experimental design, at the expense of potentially optimizable degrees of freedom found in pseudorandom sequences. As evidenced by the Monte Carlo experiments performed herein, no data-independent metric truly quantitatively captures the concept of schedule optimality for experimental data. Therefore, it is still possible to obtain a schedule with a high PSR or relative sensitivity from Monte Carlo optimization that performs poorly on real, noisy experimental data. Using jittered subrandom sampling, spectroscopists can avoid the task of schedule optimization and still have performance guarantees on their NUS datasets.

An open-source tool for generating sampling schedules using both introduced methods is freely available for download from http://github.com/geekysuavo/nusutils. As defined and implemented, no limitation on Nyquist grid dimensionality exists. The tool has been soft-limited to three-dimensional grids for the sake of computational efficiency, but this limit may be easily relaxed by trivial modifications to its source code.

Highlights.

• Practical uses of subrandom number sequences in nD NUS NMR

• Complete removal of random seed dependence from NUS schedules

• Comparisons between exponential, Gaussian, sinusoidal and Poisson-gap sampling