Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Jul 1;7(14):2722–2729. doi: 10.1021/acs.jpclett.6b00946

Valence and Conduction Band Densities of States of Metal Halide Perovskites: A Combined Experimental–Theoretical Study

James Endres †, David A Egger ‡, Michael Kulbak ‡, Ross A Kerner †, Lianfeng Zhao †, Scott H Silver †, Gary Hodes ‡, Barry P Rand †, David Cahen ‡, Leeor Kronik ‡, Antoine Kahn †,*
PMCID: PMC4959026  PMID: 27364125

Abstract

graphic file with name jz-2016-00946c_0007.jpg

We report valence and conduction band densities of states measured via ultraviolet and inverse photoemission spectroscopies on three metal halide perovskites, specifically methylammonium lead iodide and bromide and cesium lead bromide (MAPbI3, MAPbBr3, CsPbBr3), grown at two different institutions on different substrates. These are compared with theoretical densities of states (DOS) calculated via density functional theory. The qualitative agreement achieved between experiment and theory leads to the identification of valence and conduction band spectral features, and allows a precise determination of the position of the band edges, ionization energy and electron affinity of the materials. The comparison reveals an unusually low DOS at the valence band maximum (VBM) of these compounds, which confirms and generalizes previous predictions of strong band dispersion and low DOS at the MAPbI3 VBM. This low DOS calls for special attention when using electron spectroscopy to determine the frontier electronic states of lead halide perovskites.

The remarkable progress recently made in the development of halide perovskite (HaP)-based solar cells has spurred considerable interest in the electronic structure of these materials.1,2 Interest is amplified by the seemingly simple, solution-based, low-temperature processing that yields HaP films with carrier transport and optical properties comparable to those of standard semiconductors requiring far more constrained and energy intensive processing methods.3 Research efforts have focused, among other things, on the nature of carrier transport and related electronic structure4,5 and the presence of defect states in the gap of these semiconductors.6−8 The determination of the electronic structure and chemical state of HaP interfaces with carrier extraction/blocking interlayers and contacts, which play a key role in the optimization of devices, has also been a major point of interest.9−15 In that regard, the electronic structure of the constituent materials, i.e., the energy positions of valence band maximum (VBM) and conduction band minimum (CBM), density of states (DOS) at frontier electronic states, vacuum level (EVAC), ionization energy (IE) and electron affinity (EA), is of paramount importance for understanding and controlling interfaces and optimizing device performance.

Ultraviolet photoemission spectroscopy (UPS) and inverse photoemission spectroscopy (IPES) are experimental techniques of choice to investigate the semiconductor valence and conduction band DOS, respectively. However, the determination of the VBM and CBM positions for a new material, or for a material affected by structural disorder or defects, is often hindered by the difficulty to distinguish bulk- from surface- or defect-related states, and pinpoint the energy position of the onset of the valence or conduction band states. Early investigations of standard crystalline semiconductor surfaces like Ge(110) or GaAs(110) showed that simulations of photoemission spectra with theoretical VBM DOS could lead to a precise determination of this onset.16 These studies also showed that a good approximation of the photoemission onset could be obtained from a linear extrapolation to zero of the leading edge of the valence band spectrum. This ad hoc procedure was then widely adopted in the last three decades as a practical approach to photoemission studies of most semiconductors, such as conjugated organic semiconductors and organic/inorganic metal halides.17,18 Problems arise, however, for materials that exhibit soft onsets with a nonlinear leading edge of the valence band spectrum, often seen in disordered materials, e.g., polymers, or materials with a significant density of gap states tailing above the VBM. Without theoretical input on the DOS, the determination of the onset on these materials via photoemission becomes difficult and somewhat subjective.

Several groups have reported photoemission spectroscopy data on HaP thin films in the past few years, with the goal of determining electronic parameters (VBM, IE, EA) and the relative position of electronic levels across interfaces. Emara et al. showed significant variations in the IE of methylammonium lead iodide (MAPbI3) as a function of preparation method and film stoichiometry.19 Miller et al. reported X-ray photoemission spectroscopy (XPS) measurements of the valence band of MAPbI3 films deposited on various substrates.20 Schulz et al. reported on UPS and IPES measurements of IE and EA of MAPbI3 and its bromide analogue, MAPbBr3, and associated interfaces.9,10 The data presented in the Supporting Information of this earlier MAPbI3 study9 pointed to the difficulty of evaluating the IE of these materials based on photoemission data, and the need to carefully look at the DOS in order to pinpoint the VBM position.

The present work expands on this point by presenting a combined experimental–theoretical investigation of the DOS of several organic/inorganic metal halides. In addition to providing an identification of the origin of valence and conduction band features, the theoretical simulation of the data helps locate the energy positions of the VBM and CBM and determine IE and EA of organic/inorganic lead halides MAPbI3, MAPbBr3, and cesium lead bromide (CsPbBr3). The combination of valence band experimental and theoretical spectra shows that the DOS at the VBM is remarkably low compared to other semiconductors used in photovoltaics, such as Si or GaAs.16,21 The simple linear extrapolation procedure outlined above, and performed on standard UPS spectra of these materials, misses the VBM and results in an overestimation of IE. The problem is largely corrected by using a logarithmic detection of the photoemission signal, which emphasizes the low DOS part of the valence band photoemission spectrum. By judicious comparison to theoretically computed DOS, based on density functional theory (DFT), it allows for a more accurate definition of the photoemission onset.

Experimental valence band (UPS, He I) and conduction band (IPES) spectra taken on MAPbI3, MAPbBr3 and CsPbBr3 samples made at the Weizmann Institute of Science (WIS) are compared with theoretical simulations in Figures 1–3. The experimental plots are obtained from the UPS and IPES data following subtraction of a cubic spline background (not shown here). Both UPS and IPES energy scales are referenced to the Fermi level EF (0 eV), measured separately on a metallic surface in electrical contact with the samples. The energy of the UPS and IPES electrons involved in probing the valence and conduction bands is in the 5–15 eV range, making these techniques sensitive to the top 3 to 4 lattice planes of the material. The valence and conduction band data can therefore be considered as comprising strong contributions from both the surface and bulk DOS of the material.

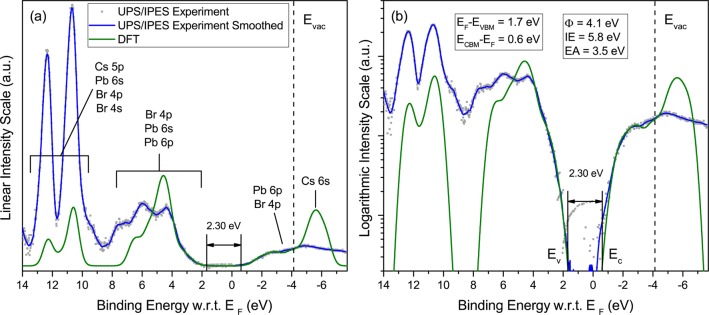
Figure 1.

Figure 1

Open in a new tab

(a) Comparison between UPS and IPES spectra measured from MAPbI3 and DFT-based theoretical simulations, plotted on a linear intensity scale. The energy scale is referenced to the Fermi level, EF (0 eV). The position of the vacuum level EVAC is indicated; major atomic orbital contributions are indicated. (b) Same as panel a for data displayed on a logarithmic intensity scale. The extracted values for IE, EA, the work function ϕ and the energy gap apply to both panels a and b. The 200–300 nm thick MAPbI3 films were grown on compact TiO2/FTO.

Figure 3.

Figure 3

Open in a new tab

Same as Figure 1, for CsPbBr3. The 200–300 nm thick CsPbBr3 films were grown on compact TiO2/ITO.

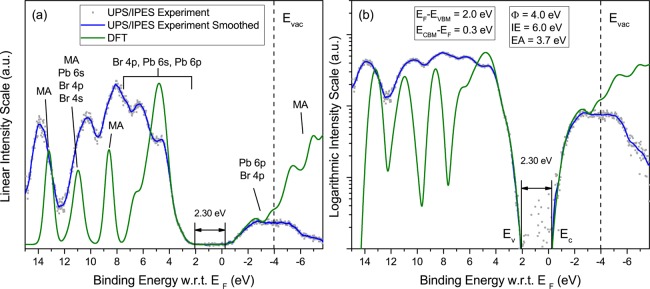
The alignment between experimental and theoretical features is obtained by first shifting the computed VBM and CBM DOS (independently), and stretching them (by <10%), as well as broadening the computed data to experimental resolution, so as to align the main theoretical features with those from experiment. This procedure is well-known to be justified theoretically by a dominantly linear correction between Kohn–Sham eigenvalues and quasi-particle energies, and has been found to be very useful in practice, as discussed previously from various perspectives.22−26 Further details of the procedure are given in the theoretical section. Next, the magnitudes of the UPS and IPES spectra are normalized so as to match the relative magnitude of the corrected DFT DOS near the valence and conduction band edges. The independent shift of the DFT occupied and unoccupied DOS is then fine-tuned to match the valence and conduction band edges of the experimental spectra as closely as possible. Additional details on the alignment procedure are given below when considering the logarithmic representation of the data. The vacuum level (EVAC) and work function (ϕ), determined from the photoemission cutoff (not shown here), and the position of the VBM are indicated for each material.

For all three materials, good alignment over a wide energy range is achieved between the main experimental and theoretical features. For MAPbI3 (Figure 1a), the broad intensity peak near the top of the valence band (2.5 to 5.5 eV binding energy) corresponds predominantly to I 5p levels, with minor contributions from Pb 6s and Pb 6p. Main features at 8, 10.5, and 12.5 eV are dominated by methylammonium molecular states, with additional Pb 6s and minor I 5s and 5p contributions around 10 eV. On the unoccupied side of the spectrum, the bottom of the conduction band is dominated by Pb 6p states with smaller contributions from I 5p states. A similar pattern is found for MAPbBr3 (Figure 2a), with the main Br 4p contribution near the VBM and weak Pb 6s and 6p contributions. Similar to the iodide compound, the main experimental features at 8.5, 11, and 13.2 eV correspond to the methylammonium cation, with some Pb 6s and smaller Br 4s and 4p contributions. The bottom of the conduction band is dominated by Pb 6p states, with smaller components from Br 4p states. For CsPbBr3 (Figure 3a), good alignment between experimental and theoretical features is obtained in the energy range between the VBM and ∼6.5 eV, a region of the valence band dominated by Br 4p states, and for the Cs 5p spin–orbit split doublet at 10.5 and 12 eV. The theoretical simulation of the empty states fits the linear experimental plot very well below EVAC and again shows that the bottom of the conduction band is dominated by Pb 6p states, with smaller components from Br 4p states.

Figure 2.

Figure 2

Open in a new tab

Same as Figure 1, for MAPbBr3. The 200–300 nm thick MAPbBr3 films were grown on compact TiO2/FTO.

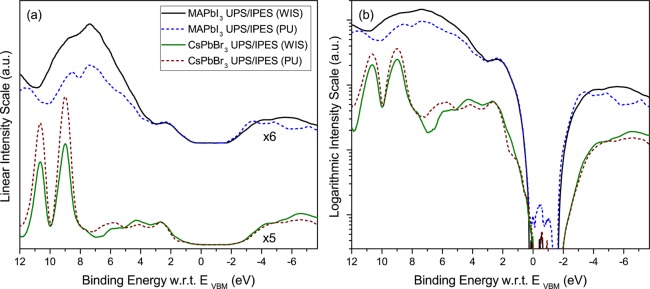
Several minor experimental features are not reproduced by the simulation, particularly the 6.6 eV shoulder in the MAPbI3 valence band, the slight misalignment of the MA features in MAPbBr3, and the 7.5 and 9.4 eV shoulders in CsPbBr3. The origin of these features and the reasons for the discrepancies are unknown at this point, although defects in film structure are likely to have an impact on the details of the DOS.27 However, some information can be gathered from the superposition of the UPS and IPES spectra of MAPbI3 and CsPbBr3 grown at the WIS and at Princeton University (PU), as shown in Figure 4a,b. To facilitate the comparison, the spectra are aligned with respect to the VBM, rather than the Fermi level position, which depends for each film on the substrate work function and on the processing conditions.10 Very good agreement is obtained between these samples of different origin and preparation, including the features not reproduced by theory. While we cannot rule out that these features are intrinsic to the perfect materials, they are more likely linked to defects or different phases known to be present in some concentration in HaP films,28,29 but absent from the theoretical simulation that assumes a perfect HaP crystalline structure. Given the surface sensitive nature of UPS and IPES, surface contamination and/or atomic reconstruction could also be responsible for some of these features. All samples exhibit small levels of adventitious carbon and oxygen on the surface, as measured with XPS, although less so for the PU samples, which were prepared in nitrogen and transferred under nitrogen directly to vacuum. Furthermore, XPS measurements reveal some differences in composition, for example with Cs:Pb:Br normalized core level ratios approximately equal to 0.9:1:2.1 and 1.7:1:3.1 for the WIS and PU samples, respectively, and deviating somewhat from the ideal 1:1:3. Note that these numbers might be disproportionately influenced by the termination at the very top surface of the film, which is certainly influenced by the details of processing. Still, the spectra displayed in Figure 4a,b demonstrate that two groups at two different institutions using different procedures can produce HaP films with overwhelmingly similar electronic features, in particular with regards to the electronically all-important DOS at the band edges.

Figure 4.

Figure 4

Open in a new tab

Comparison between UPS and IPES spectra taken from MAPbI3 (top) and CsPbBr3 (bottom) samples grown at WIS and PU. The PU films, grown on ITO, were 400–500 nm thick. Spectra are referenced to the VBM, EVBM = 0 eV, and plotted on (a) a linear scale and (b) a logarithmic scale. The difference between the band gap energies of the two compounds (1.6 vs 2.3 eV) is clearly visible in panel b.

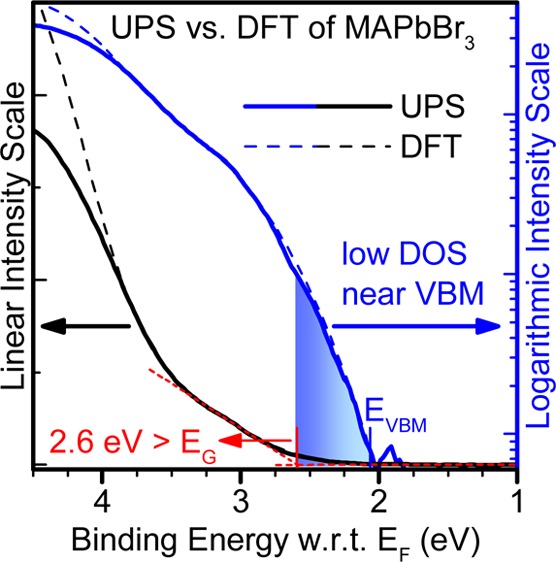
Expanded views of the top of the valence band of each perovskite are presented in Figure 5. The position of the top of the valence band, extracted from the analysis presented below, is indicated in each case. Both experimental data and theoretical simulations point to an unusually low DOS at the VBM, in all cases, as evidenced by the shallow slope at the onset of occupied states. We emphasize that the low photoemission intensity recorded at the VBM is not an experimental artifact of UPS. In fact, the photoionization cross sections for the Br 4p, I 5p and Pb 6s and 6p levels, which dominate the DOS at the top of the valence band, are actually nearly maximized for the He I photon energy used here,30 and are several orders of magnitude larger than those corresponding to high energy (≥1 keV) photons. This peculiar aspect of the occupied DOS was already recognized in theoretical investigations on MAPbI3.31,32 Kawai et al., in particular, showed a large dispersion due to the strong coupling between I 5p and Pb 6s antibonding orbitals, resulting in a low DOS at the top of the MAPbI3 valence band.31 Here, we show that this peculiar aspect is intrinsic to the family of lead-halide perovskites, being largely independent of the nature of A- and X-site ions. From an experimental point of view, the low DOS makes the determination of the VBM via photoemission spectroscopy more difficult for these materials, and precludes, in particular, the conventional use of a simple linear extrapolation of the photoemission onset as means to determine the top of the valence band. As a case in point, recent analyses making use of the linear extrapolation concluded that the VBM position is located at 1.7 eV below the Fermi level for MAPbI3, which is too large for a 1.55–1.6 eV gap semiconductor,19,20 or reported excessive IEs, EAs and exciton binding energies for different methylammonium lead halides.33 Similarly, a linear approximation of the top of the valence band for the data presented here would also yield excessive EF – VBM (IE) values equal to 1.80 eV (5.79 eV), 2.6 eV (6.57 eV) and 2.35 eV (6.47) for MAPbI3, MAPbBr3, and CsPbBr3, respectively. We further note that a recent investigation of quantum dots of a different Pb-containing compound, PbS, similarly concluded that the DOS at the top of the valence band is too low for the determination of the VBM using standard linear extrapolation of UPS/XPS data.34 The strong tailing at the VBM is thus a further similarity between the electronic structure of HaPs and lead-chalcogenides.3

Figure 5.

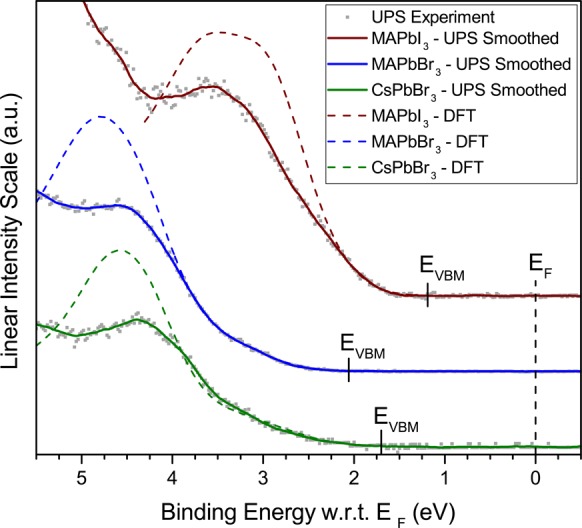
Figure 5

Open in a new tab

UPS and DFT-based theoretical simulation of the top of the MAPbI3, MAPbBr3, and CsPbBr3 valence bands. The VBM (EV) extracted from the analyses of Figures 1–3 is indicated in each case.

We address this issue by analyzing photoemission and inverse photoemission data recorded on a logarithmic scale, with an emphasis on spectral regions of low intensity, as already employed by Schulz et al. in their analysis of the electronic structure of MAPbI3 and MAPbBr3 interfaces.9 Experimental data and theoretical simulations plotted in logarithmic scale are compared in Figures 1b, 2b, and 3b. In all three cases, the excellent fit between experiment and theory at the valence band edge after the alignment procedure explained above allows for a clear definition of the VBM, at a point where the photoemission intensity is more than two and a half orders of magnitude smaller than the first valence band peak. The close fit between IPES experiment and simulation near the bottom of the conduction band leads to energy gaps for MAPbI3 and MAPbBr3 that are within experimental resolution of the expected band gaps of 1.55 and 2.3 eV for these materials, respectively, with no evidence of a significant density of gap states. For CsPbBr3, on the other hand, the fit between experiment and simulation appears to signal a density of states tailing below the CBM, with spectral intensity nearly 2 orders of magnitude smaller than at the top of the first significant peak at −2.5 eV. The origin of this small density of tail states is unknown, but could be related to defects or multiphases present in our films. The presence of tail states also appears to be consistent with the larger than usual separation between EC and EF (0.6 eV) compared to the two methylammonium lead iodide and bromide counterparts (0.33 and 0.24 eV), when deposited on a low work function substrate like TiO2.

The lack of gap states and noise in the simulated spectra make them well suited for determining the VBM and CBM positions as well as the IE and EA values for each material. Given that the exciton binding energy in these materials is small compared to the experimental energy resolution of UPS and IPES,2,35−39 the transport gap measured with these techniques should correspond to the optical gap for each material. Therefore, after aligning the occupied and unoccupied DFT results to achieve best fit with the experiment in both linear and log scales, the VBM and CBM are determined by finding the points on the valence and conduction band spectra that are separated by an energy equal to the known optical band gap. It is important to note that the electronic parameters reported herein, e.g., IE, EA or ϕ, presented in insets in Figures 1–3 and summarized in Table 1, can vary with material processing. As an extreme example, Emara et al. reported excursions of the value of IE of MAPbI3 by more than 600 meV as a function of compositional variations, depending on whether the materials were formed under excess MAI or excess PbI2.19 Furthermore, postprocessing environmental history of the film, as well as measurement probes (UV or X-ray photons, electrons, etc.) and measurement times can cause variations in surface composition,40,4100 often leading to the appearance of metallic Pb.41 Although the films investigated here are largely free of metallic Pb (Figures S1 and S2), composition variations, when present, affect the electronic parameters and must be carefully considered when working on these materials. The numbers extracted from the present analysis are in accord, within experimental resolution, with numbers previously published for MAPbI3 and MAPbBr3.9 The difference between the MAPbBr3 and CsPbBr3 IEs and EAs appear to be beyond the range of experimental uncertainty and could originate with the details of surface termination of the films.

Table 1. Ionization Energy (IE), Electron Affinity (EA), Energy Gap (EG) and Work Function (ϕ) Extracted from the Combined Experimental–Theoretical Study Described in the Text for the Three Materials Investigated Here.

  IE (eV) EA (eV) EG (eV) ϕ (eV)
MAPbI3 5.2 3.6 1.6 4.0
MAPbBr3 6.0 3.7 2.3 4.0
CsPbBr3 5.8 3.5 2.3 4.1
Open in a new tab

As a final note, the low DOS at the VBM of the materials investigated here is a characteristic that is likely common to all Pb halide perovskites and other Pb-containing compounds as well. This tailing of the DOS implies that the dispersion at the band edge of this class of materials is nonparabolic, as noted by Brivio et al.,4 with significant impact on carrier scattering and transport, specifically for hot carriers.31 Beyond the critical issue of correctly determining band edge positions and all energetics of HaPs and their interfaces, the importance of mapping the details of the electronic structure of these materials in order to understand the behavior of devices cannot therefore be overstated.

In summary, we presented here what we believe to be the first comparison between photoemission and inverse photoemission (obtained from samples grown at two different institutions) and DFT-based computations of three metal halide perovskites: MAPbI3, MAPbBr3 and CsPbBr3. Excellent agreement is obtained between theory and the properly analyzed experimental data, allowing a clear definition of the origin of the main spectral features and the position of valence and conduction band edges. This yields the transport gap, critical for the optoelectronic behavior of these materials. The experimental results are found to be independent of the source and preparation process of the materials. We find a remarkably low DOS at the VBM of all three materials, confirming previous theoretical computations for MAPbI3. This result, now extended to additional HaPs, is consistent with strong band dispersion at the VBM due to the coupling between halide p and Pb s antibonding orbitals. The detailed investigation of UPS data around the band edges confirms the absence of significant densities of states tailing into the HaP gaps, with the possible exception of a small DOS tailing below the CsPbBr3 CBM. Further analysis on a range of samples will be necessary to confirm this point.

Experimental Methods

Electron spectroscopy was performed in an ultrahigh vacuum (UHV) analysis chamber (base pressure 10–10 Torr) equipped with an introduction system allowing sample transfer from a nitrogen glovebox without ambient exposure. The analysis chamber was equipped with a He discharge lamp that produces the two standard radiation lines He I (21.22 eV) and He II (40.8 eV) for UPS. Electrons were detected with a double-pass cylindrical mirror analyzer, yielding an overall resolution for the UPS measurements of 0.15 eV. IPES was performed in the same chamber, in the isochromat mode using a setup described elsewhere.42 The overall resolution of the IPES measurements was 0.45 eV. UPS and IPES measurements were performed in sequences designed to minimize photon and electron irradiation time and impact on the electronic structure of the films. Considerable care was taken to minimize all exposure times (to UV or electrons) and to improve the signal-to-noise ratio by averaging measurements over multiple nonpreviously irradiated points of the samples. Surface contamination and sample stoichiometry were investigated via XPS (e.g., for CsPbBr3, Figure S1) after all UPS and IPES measurements were completed, in order to not affect the electronic structure results. Finally, the position of the Fermi level was obtained from the Fermi step measured in both UPS and IPES on a gold surface in electrical equilibrium with the sample.

HaP films with thickness of 200–300 nm were formed via solution-based procedures at the WIS and PU. Detailed fabrication procedures for the WIS MAPbI3 and MAPbBr3 samples (prepared by one-step solution spin-coating) have been given elsewhere.43−45 The WIS CsPbBr3 films were prepared by two-step solution spin-coating on compact TiO2 on ITO. Indium-doped tin oxide (ITO) transparent conducting substrates (Xinyan Technology, XY10S) were cut and cleaned by sequential 15 min sonication in warm aqueous alconox solution, deionized water, acetone, and ethanol, followed by drying in a N2 stream. After a 10 min O2 plasma treatment, a compact ∼60 nm TiO2 layer was applied to the clean substrate by spray pyrolysis of a 30 mM titanium diisopropoxide bis(acetylacetonate) (Sigma-Aldrich) solution in isopropanol using air as the carrier gas on a hot plate set to 450 °C, followed by a two-step annealing procedure at 160 and 500 °C, each for 1 h in air. The CsPbBr3 films were prepared by spin coating. 0.8 M of PbBr2 and CsBr (Sigma-Aldrich) in DMSO were stirred on a hot plate at 75 °C for 1 h in ambient and then filtered using a 0.45 μm pore size PTFE filter and immediately used. The solution was kept at 75 °C during the spin-coating process. For preparation of the CsPbBr3 film, the solution was spin-coated on preheated (75 °C) substrates for 10 s at 500 rpm, 15 s at 1500 rpm, 7 s at 3500 rpm and finally 10 s at 5000 rpm. During the third spin step, 2-propanol was dropped on the spinning substrate. It was then dried on a hot plate at 70 °C for 15 min. Samples were packaged under nitrogen and sent to Princeton for UPS/IPES analysis, where they were transferred under nitrogen directly into vacuum.

The PU MAPbI3 and CsPbBr3 samples were processed as follows: MAI was synthesized by mixing ethanol:methylamine (Sigma-Aldrich) and aqueous HI (Sigma-Aldrich, stabilized) solutions together (equimolar methylamine to HI). The MAI was washed with an ethanol:ether solvent mixture and rotovaped several times to remove the HI stabilizer. Precursor solutions were prepared by mixing PbI2 (Sigma-Aldrich, ≥ 98%) and MAI powders in a 1:1 molar ratio with N,N-dimethylformamide (DMF, Sigma-Aldrich, 99.8% anhydrous) in a single vial to obtain the desired concentrations. Solutions were stirred for at least 30 min. Inorganic CsPbBr3 (PbBr2 and CsBr from Sigma-Aldrich, ≥ 98% and 99.9%, respectively) solutions were prepared in dimethyl sulfoxide (DMSO, Sigma-Aldrich, 99.9%) at 0.5 M concentration and stirred until precursors were fully dissolved. Films were spin coated onto ITO substrates. A 200 nm PTFE filter was used to remove large aggregates prior to spinning. A solvent exchange technique using toluene for the methylammonium perovskite and chloroform for the solvent exchange with DMSO for the cesium perovskite was employed to obtain smooth films with surface RMS of less than 6 nm.46 The MAPbI3 and CsPbBr3 films were annealed at 75 and 100 °C, respectively, for 10 min. Solution preparation and film fabrication were done in a glovebox with an N2 atmosphere. Samples were transferred under nitrogen directly to vacuum for UPS/IPES measurements.

Computational Methods

We performed periodic DFT calculations using the planewave VASP code.47 Convergence criteria of 10–6 eV per unit cell for the total energy in the electronic self-consistent cycle and 10–2 eV/Å for optimizing the forces and unit-cell parameters have been used. Core–valence electron interactions were treated within the projector-augmented wave (PAW) formalism48 using the “normal” (i.e., not “soft”), program-supplied PAW potentials. For Pb, we treated the 5d electrons explicitly. Spin–orbital coupling (SOC) effects, already known to be important for accurate treatment of the electronic structure of metal-halide perovskites,4,35 were accounted for within the noncollinear magnetism framework of the VASP code,49 unless explicitly noted otherwise.

For optimizing the lattice parameters, we employed our previously reported strategy,50 with which we achieved very good agreement between theoretically calculated and experimentally measured structural properties of HaPs: First, exchange and correlation were treated at the generalized-gradient approximation level using the Perdew–Burke–Ernzerhof (PBE) functional,51 augmented by pairwise dispersive corrections with the Tkatchenko-Scheffler scheme52 as implemented in VASP.53,54 To compute accurate stresses, the valence-electron wave functions were expanded on a relatively large planewave basis, using a kinetic-energy cutoff of 700 and 400 eV for the MA and Cs based systems, respectively. In these lattice optimizations, performed with the GADGET tool,55 we did not account for SOC, as this has been shown to have a negligible effect on the calculated lattice parameters of lead-halide perovskites.50 8 × 8 × 8 Γ-centered k-point grids were used for the pseudocubic cell of MAPbBr3, and 6 × 6 × 4 Γ-centered grids for the tetragonal and orthorhombic unit cells of MAPbI3 and CsPbBr3, respectively. For all investigated systems, the structural properties obtained in that fashion are in excellent agreement (deviations of lattice parameters <1%) with experimental data.

Finally, to compute the DOS, we used the screened hybrid functional of Heyd, Scuseria and Ernzerhof (HSE),56,57 which can partially (but not fully) correct for the underestimated DFT band gap and restore some of the “stretching” often needed to align a DFT-computed eigenvalue spectrum with experimental UPS data. To reduce the computational complexity, we evaluated the Fock-like contributions in our HSE calculations on k-grid densities reduced by 50%, and verified that this has no significant effect on the DOS. The HSE gaps were found to be 1.2, 1.5, and 1.5 eV for MAPbI3, MAPbBr3, and CsPbBr3, respectively, i.e., substantially smaller than the experimental values reported in Table 1. After self-consistency, the occupied and unoccupied parts of the computed DOS were shifted independently by a constant energy and stretched (by 3%, 5%, and 9% for the valence band of MAPbI3, MAPbBr3 and CsPbBr3, respectively, no stretch for the conduction bands) so that the main features align with those from experiment. To further ease the comparison between theory and experiment, we additionally broadened the theoretical DOS by a Gaussian with a width of 0.3 eV.

Acknowledgments

This work was supported by a grant from the Princeton Environmental Institute and Andlinger Center; by National Science Foundation Graduate Research Fellowships (JE and RAK, Grant #1148900); and by the US-Israel Binational Science Foundation (AK and DC: Grant #2014357; GH, RAK, BPR, and LZ: Grant #2014199). DAE and LK were supported by the Austrian Science Fund (FWF): J3608–N20 and by a research grant from Dana and Yossie Hollander, in the framework of the WIS Alternative sustainable Energy Initiative, AERI. G.H. and D.C. also thank the Israel Ministry of Science for support. D.C. holds the Sylvia and Rowland Schaefer Chair in Energy Research.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.6b00946.

  • Description of XPS experiments; supplementary figures showing specific core levels of elements used in the evaluation of the composition of the investigated samples (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz6b00946_si_001.pdf (394.6KB, pdf)

References

  1. Gao P.; Grätzel M.; Nazeeruddin M. K. Organohalide Lead Perovskites for Photovoltaic Applications. Energy Environ. Sci. 2014, 7, 2448. 10.1039/C4EE00942H. [DOI] [PubMed] [Google Scholar]
  2. Green M. A.; Ho-Baillie A.; Snaith H. J. The Emergence of Perovskite Solar Cells. Nat. Photonics 2014, 8, 506–514. 10.1038/nphoton.2014.134. [DOI] [Google Scholar]
  3. Brenner T. M.; Egger D. A.; Kronik L.; Hodes G.; Cahen D. Hybrid Organic—inorganic Perovskites: Low-Cost Semiconductors with Intriguing Charge-Transport Properties. Nat. Rev. Mater. 2016, 1, 15007. 10.1038/natrevmats.2015.7. [DOI] [Google Scholar]
  4. Brivio F.; Butler K. T.; Walsh A.; van Schilfgaarde M. Relativistic Quasiparticle Self-Consistent Electronic Structure of Hybrid Halide Perovskite Photovoltaic Absorbers. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 155204. 10.1103/PhysRevB.89.155204. [DOI] [Google Scholar]
  5. Even J.; Pedesseau L.; Jancu J.-M.; Katan C. Importance of Spin–Orbit Coupling in Hybrid Organic/Inorganic Perovskites for Photovoltaic Applications. J. Phys. Chem. Lett. 2013, 4, 2999–3005. 10.1021/jz401532q. [DOI] [Google Scholar]
  6. Yin W.-J.; Shi T.; Yan Y. Unusual Defect Physics in CH3NH3PbI3 Perovskite Solar Cell Absorber. Appl. Phys. Lett. 2014, 104, 063903. 10.1063/1.4864778. [DOI] [Google Scholar]
  7. Yin W.-J.; Shi T.; Yan Y. Unique Properties of Halide Perovskites as Possible Origins of the Superior Solar Cell Performance. Adv. Mater. 2014, 26, 4653–4658. 10.1002/adma.201306281. [DOI] [PubMed] [Google Scholar]
  8. Adinolfi V.; Yuan M.; Comin R.; Thibau E. S.; Shi D.; Saidaminov M. I.; Kanjanaboos P.; Kopilovic D.; Hoogland S.; Lu Z.-H.; et al. The In-Gap Electronic State Spectrum of Methylammonium Lead Iodide Single-Crystal Perovskites. Adv. Mater. 2016, 28, 3406–3410. 10.1002/adma.201505162. [DOI] [PubMed] [Google Scholar]
  9. Schulz P.; Edri E.; Kirmayer S.; Hodes G.; Cahen D.; Kahn A. Interface Energetics in Organo-Metal Halide Perovskite-Based Photovoltaic Cells. Energy Environ. Sci. 2014, 7, 1377. 10.1039/c4ee00168k. [DOI] [Google Scholar]
  10. Schulz P.; Whittaker-Brooks L. L.; MacLeod B. A.; Olson D. C.; Loo Y.-L.; Kahn A. Electronic Level Alignment in Inverted Organometal Perovskite Solar Cells. Adv. Mater. Interfaces 2015, 2, 1400532. 10.1002/admi.201400532. [DOI] [Google Scholar]
  11. Lindblad R.; Bi D.; Park B.; Oscarsson J.; Gorgoi M.; Siegbahn H.; Odelius M.; Johansson E. M. J.; Rensmo H. Electronic Structure of TiO2/CH3NH3PbI3 Perovskite Solar Cell Interfaces. J. Phys. Chem. Lett. 2014, 5, 648–653. 10.1021/jz402749f. [DOI] [PubMed] [Google Scholar]
  12. Wang C.; Wang C.; Liu X.; Kauppi J.; Shao Y.; Xiao Z.; Bi C.; Huang J.; Gao Y. Electronic Structure Evolution of Fullerene on CH3NH3PbI3. Appl. Phys. Lett. 2015, 106, 111603. 10.1063/1.4916079. [DOI] [Google Scholar]
  13. Liu P.; Liu X.; Lyu L.; Xie H.; Zhang H.; Niu D.; Huang H.; Bi C.; Xiao Z.; et al. Interfacial Electronic Structure at the CH3NH3PbI3/MoOx Interface. Appl. Phys. Lett. 2015, 106, 193903. 10.1063/1.4921339. [DOI] [Google Scholar]
  14. Thibau E. S.; Llanos A.; Lu Z. H. A Simple Rule for Determining the Band Offset at CH3NH3PbI3/organic Semiconductor Heterojunctions. Appl. Phys. Lett. 2016, 108, 021602. 10.1063/1.4939744. [DOI] [Google Scholar]
  15. Ryu S.; Noh J. H.; Jeon N. J.; Chan Kim Y.; Yang W. S.; Seo J.; Seok S. Il. Voltage Output of Efficient Perovskite Solar Cells with High Open-Circuit Voltage and Fill Factor. Energy Environ. Sci. 2014, 7, 2614. 10.1039/C4EE00762J. [DOI] [Google Scholar]
  16. Kraut E. A.; Grant R. W.; Waldrop J. R.; Kowalczyk S. P. Precise Determination of the Valence-Band Edge in X-Ray Photoemission Spectra: Application to Measurement of Semiconductor Interface Potentials. Phys. Rev. Lett. 1980, 44, 1620–1623. 10.1103/PhysRevLett.44.1620. [DOI] [Google Scholar]
  17. Hill I. G.; Rajagopal A.; Kahn A.; Hu Y. Molecular Level Alignment at Organic Semiconductor-Metal Interfaces. Appl. Phys. Lett. 1998, 73, 662. 10.1063/1.121940. [DOI] [Google Scholar]
  18. Man G.; Schwartz J.; Sturm J. C.; Kahn A. Electronically Passivated Hole-Blocking Titanium Dioxide/Silicon Heterojunction for Hybrid Silicon Photovoltaics. Adv. Mater. Interfaces 2016, 10.1002/admi.201600026. [DOI] [Google Scholar]
  19. Emara J.; Schnier T.; Pourdavoud N.; Riedl T.; Meerholz K.; Olthof S. Impact of Film Stoichiometry on the Ionization Energy and Electronic Structure of CH3NH3PbI3 Perovskites. Adv. Mater. 2016, 28, 553–559. 10.1002/adma.201503406. [DOI] [PubMed] [Google Scholar]
  20. Miller E. M.; Zhao Y.; Mercado C. C.; Saha S. K.; Luther J. M.; Zhu K.; Stevanović V.; Perkins C. L.; van de Lagemaat J. Substrate-Controlled Band Positions in CH3NH3PbI3 Perovskite Films. Phys. Chem. Chem. Phys. 2014, 16, 22122–22130. 10.1039/C4CP03533J. [DOI] [PubMed] [Google Scholar]
  21. Himpsel F. J. Photoemission Studies of Intrinsic Surface States on Si(100). J. Vac. Sci. Technol. 1979, 16, 1297. 10.1116/1.570144. [DOI] [Google Scholar]
  22. Hybertsen M. S.; Louie S. G. Electron Correlation in Semiconductors and Insulators: Band Gaps and Quasiparticle Energies. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 34, 5390–5413. 10.1103/PhysRevB.34.5390. [DOI] [PubMed] [Google Scholar]
  23. Jones R. O.; Gunnarsson O. The Density Functional Formalism, Its Applications and Prospects. Rev. Mod. Phys. 1989, 61, 689–746. 10.1103/RevModPhys.61.689. [DOI] [Google Scholar]
  24. Stowasser R.; Hoffmann R. What Do the Kohn–Sham Orbitals and Eigenvalues Mean?. J. Am. Chem. Soc. 1999, 121, 3414–3420. 10.1021/ja9826892. [DOI] [Google Scholar]
  25. Chong D. P.; Gritsenko O. V.; Baerends E. J. Interpretation of the Kohn–Sham Orbital Energies as Approximate Vertical Ionization Potentials. J. Chem. Phys. 2002, 116, 1760. 10.1063/1.1430255. [DOI] [Google Scholar]
  26. Kronik L.; Kümmel S. Top. Curr. Chem. 2014, 347, 137–191. 10.1007/128_2013_522. [DOI] [PubMed] [Google Scholar]
  27. Haruyama J.; Sodeyama K.; Han L.; Tateyama Y. Termination Dependence of Tetragonal CH3NH3PbI3 Surfaces for Perovskite Solar Cells. J. Phys. Chem. Lett. 2014, 5, 2903–2909. 10.1021/jz501510v. [DOI] [PubMed] [Google Scholar]
  28. Stamplecoskie K. G.; Manser J. S.; Kamat P. V. Dual Nature of the Excited State in Organic–inorganic Lead Halide Perovskites. Energy Environ. Sci. 2015, 8, 208–215. 10.1039/C4EE02988G. [DOI] [Google Scholar]
  29. Egger D. A.; Rappe A. M.; Kronik L. Hybrid Organic–Inorganic Perovskites on the Move. Acc. Chem. Res. 2016, 49, 573–581. 10.1021/acs.accounts.5b00540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Yeh J. J.; Lindau I. Atomic Subshell Photoionization Cross Sections and Asymmetry Parameters: 1 ⩽ Z ⩽ 103. At. Data Nucl. Data Tables 1985, 32, 1–155. 10.1016/0092-640X(85)90016-6. [DOI] [Google Scholar]
  31. Kawai H.; Giorgi G.; Marini A.; Yamashita K. The Mechanism of Slow Hot-Hole Cooling in Lead-Iodide Perovskite: First-Principles Calculation on Carrier Lifetime from Electron-Phonon Interaction. Nano Lett. 2015, 15, 3103–3108. 10.1021/acs.nanolett.5b00109. [DOI] [PubMed] [Google Scholar]
  32. Quarti C.; Mosconi E.; De Angelis F. Structural and Electronic Properties of Organo-Halide Hybrid Perovskites from Ab Initio Molecular Dynamics. Phys. Chem. Chem. Phys. 2015, 17, 9394–9409. 10.1039/C5CP00599J. [DOI] [PubMed] [Google Scholar]
  33. Li C.; Wei J.; Sato M.; Koike H.; Xie Z.-Z.; Li Y.-Q.; Kanai K.; Kera S.; Ueno N.; Tang J.-X. Halide-Substituted Electronic Properties of Organometal Halide Perovskite Films: Direct and Inverse Photoemission Studies. ACS Appl. Mater. Interfaces 2016, 8, 11526–11531. 10.1021/acsami.6b02692. [DOI] [PubMed] [Google Scholar]
  34. Miller E. M.; Kroupa D. M.; Zhang J.; Schulz P.; Marshall A. R.; Kahn A.; Lany S.; Luther J. M.; Beard M. C.; Perkins C. L.; et al. Revisiting the Valence and Conduction Band Size Dependence of PbS Quantum Dot Thin Films. ACS Nano 2016, 10, 3302–3311. 10.1021/acsnano.5b06833. [DOI] [PubMed] [Google Scholar]
  35. Even J.; Pedesseau L.; Katan C. Analysis of Multivalley and Multibandgap Absorption and Enhancement of Free Carriers Related to Exciton Screening in Hybrid Perovskites. J. Phys. Chem. C 2014, 118, 11566–11572. 10.1021/jp503337a. [DOI] [Google Scholar]
  36. D’Innocenzo V.; Grancini G.; Alcocer M. J. P.; Kandada A. R. S.; Stranks S. D.; Lee M. M.; Lanzani G.; Snaith H. J.; Petrozza A. Excitons versus Free Charges in Organo-Lead Tri-Halide Perovskites. Nat. Commun. 2014, 5, 3586. 10.1038/ncomms4586. [DOI] [PubMed] [Google Scholar]
  37. Miyata A.; Mitioglu A.; Plochocka P.; Portugall O.; Wang J. T.-W.; Stranks S. D.; Snaith H. J.; Nicholas R. J. Direct Measurement of the Exciton Binding Energy and Effective Masses for Charge Carriers in Organic–inorganic Tri-Halide Perovskites. Nat. Phys. 2015, 11, 582–587. 10.1038/nphys3357. [DOI] [Google Scholar]
  38. Sharma V.; Aharon S.; Gdor I.; Yang C.; Etgar L.; Ruhman S. New Insights into Exciton Binding and Relaxation from High Time Resolution Ultrafast Spectroscopy of CH3NH3PbI3 and CH3NH3PbBr3 Films. J. Mater. Chem. A 2016, 4, 3546–3553. 10.1039/C5TA09643J. [DOI] [Google Scholar]
  39. Galkowski K.; Mitioglu A.; Miyata A.; Plochocka P.; Portugall O.; Eperon G. E.; Wang J. T.-W.; Stergiopoulos T.; Stranks S. D.; Snaith H. J.; et al. Determination of the Exciton Binding Energy and Effective Masses for Methylammonium and Formamidinium Lead Tri-Halide Perovskite Semiconductors. Energy Environ. Sci. 2016, 9, 962–970. 10.1039/C5EE03435C. [DOI] [Google Scholar]
  40. Philippe B.; Park B.-W.; Lindblad R.; Oscarsson J.; Ahmadi S.; Johansson E. M. J.; Rensmo H. Chemical and Electronic Structure Characterization of Lead Halide Perovskites and Stability Behavior under Different Exposures—A Photoelectron Spectroscopy Investigation. Chem. Mater. 2015, 27, 1720–1731. 10.1021/acs.chemmater.5b00348. [DOI] [Google Scholar]
  41. Klein-Kedem N.; Cahen D.; Hodes G. Effects of Light and Electron Beam Irradiation on Halide Perovskites and Their Solar Cells. Acc. Chem. Res. 2016, 49, 347–354. 10.1021/acs.accounts.5b00469. [DOI] [PubMed] [Google Scholar]
  42. Sadoughi G.; Starr D. E.; Handick E.; Stranks S. D.; Gorgoi M.; Wilks R. G.; Bär M.; Snaith H. J. Observation and Mediation of the Presence of Metallic Lead in Organic–Inorganic Perovskite Films. ACS Appl. Mater. Interfaces 2015, 7, 13440–13444. 10.1021/acsami.5b02237. [DOI] [PubMed] [Google Scholar]
  43. Wu C. I.; Hirose Y.; Sirringhaus H.; Kahn A. Electron-Hole Interaction Energy in the Organic Molecular Semiconductor PTCDA. Chem. Phys. Lett. 1997, 272, 43–47. 10.1016/S0009-2614(97)00481-8. [DOI] [Google Scholar]
  44. Kojima A.; Teshima K.; Shirai Y.; Miyasaka T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. 10.1021/ja809598r. [DOI] [PubMed] [Google Scholar]
  45. Edri E.; Kirmayer S.; Mukhopadhyay S.; Gartsman K.; Hodes G.; Cahen D. Elucidating the Charge Carrier Separation and Working Mechanism of CH3NH3PbI3–xClx Perovskite Solar Cells. Nat. Commun. 2014, 5, 3461. 10.1038/ncomms4461. [DOI] [PubMed] [Google Scholar]
  46. Kulbak M.; Gupta S.; Kedem N.; Levine I.; Bendikov T.; Hodes G.; Cahen D. Cesium Enhances Long-Term Stability of Lead Bromide Perovskite-Based Solar Cells. J. Phys. Chem. Lett. 2016, 7, 167–172. 10.1021/acs.jpclett.5b02597. [DOI] [PubMed] [Google Scholar]
  47. Kerner R. A.; Zhao L.; Xiao Z.; Rand B. P. Ultrasmooth Metal Halide Perovskite Thin Films via Sol–gel Processing. J. Mater. Chem. A 2016, 4, 8308–8315. 10.1039/C6TA03092K. [DOI] [Google Scholar]
  48. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  49. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  50. Hobbs D.; Kresse G.; Hafner J. Fully Unconstrained Noncollinear Magnetism within the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 62, 11556–11570. 10.1103/PhysRevB.62.11556. [DOI] [Google Scholar]
  51. Egger D. A.; Kronik L. Role of Dispersive Interactions in Determining Structural Properties of Organic–Inorganic Halide Perovskites: Insights from First-Principles Calculations. J. Phys. Chem. Lett. 2014, 5, 2728–2733. 10.1021/jz5012934. [DOI] [PubMed] [Google Scholar]
  52. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  53. Tkatchenko A.; Scheffler M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. 10.1103/PhysRevLett.102.073005. [DOI] [PubMed] [Google Scholar]
  54. Al-Saidi W. A.; Voora V. K.; Jordan K. D. An Assessment of the vdW-TS Method for Extended Systems. J. Chem. Theory Comput. 2012, 8, 1503–1513. 10.1021/ct200618b. [DOI] [PubMed] [Google Scholar]
  55. Bučko T.; Lebègue S.; Hafner J.; Ángyán J. G. Tkatchenko-Scheffler van Der Waals Correction Method with and without Self-Consistent Screening Applied to Solids. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 064110. 10.1103/PhysRevB.87.064110. [DOI] [Google Scholar]
  56. Bučko T.; Hafner J.; Ángyán J. G. Geometry Optimization of Periodic Systems Using Internal Coordinates. J. Chem. Phys. 2005, 122, 124508. 10.1063/1.1864932. [DOI] [PubMed] [Google Scholar]
  57. Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 2003, 118, 8207. 10.1063/1.1564060. [DOI] [Google Scholar]
  58. Heyd J.; Scuseria G. E.; Ernzerhof M. Erratum: “Hybrid Functionals Based on a Screened Coulomb Potential” [J. Chem. Phys. 118, 8207 (2003)]. J. Chem. Phys. 2006, 124, 219906. 10.1063/1.2204597. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz6b00946_si_001.pdf (394.6KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES