ABSTRACT
Bacillus subtilis subsp. niger spore and Staphylococcus albus are typical biological indicators for the inactivation of airborne pathogens. The present study characterized and compared the behaviors of B. subtilis subsp. niger spores and S. albus in regard to inactivation by chlorine dioxide (ClO2) gas under different gas concentrations and relative humidity (RH) conditions. The inactivation kinetics under different ClO2 gas concentrations (1 to 5 mg/liter) were determined by first-order and Weibull models. A new model (the Weibull-H model) was established to reveal the inactivation tendency and kinetics for ClO2 gas under different RH conditions (30 to 90%). The results showed that both the gas concentration and RH were significantly (P < 0.05) and positively correlated with the inactivation of the two chosen indicators. There was a rapid improvement in the inactivation efficiency under high RH (>70%). Compared with the first-order model, the Weibull and Weibull-H models demonstrated a better fit for the experimental data, indicating nonlinear inactivation behaviors of the vegetative bacteria and spores following exposure to ClO2 gas. The times to achieve a six-log reduction of B. subtilis subsp. niger spore and S. albus were calculated based on the established models. Clarifying the kinetics of inactivation of B. subtilis subsp. niger spores and S. albus by ClO2 gas will allow the development of ClO2 gas treatments that provide an effective disinfection method.
IMPORTANCE Chlorine dioxide (ClO2) gas is a novel and effective fumigation agent with strong oxidization ability and a broad biocidal spectrum. The antimicrobial efficacy of ClO2 gas has been evaluated in many previous studies. However, there are presently no published models that can be used to describe the kinetics of inactivation of airborne pathogens by ClO2 gas under different gas concentrations and RH conditions. The first-order and Weibull (Weibull-H) models established in this study can characterize and compare the behaviors of Bacillus subtilis subsp. niger spores and Staphylococcus albus in regard to inactivation by ClO2 gas, determine the kinetics of inactivation of two chosen strains under different conditions of gas concentration and RH, and provide the calculated time to achieve a six-log reduction. These results will be useful to determine effective conditions for ClO2 gas to inactivate airborne pathogens in contaminated air and other environments and thus prevent outbreaks of airborne illness.
INTRODUCTION
The recent Ebola virus, Middle East respiratory syndrome coronavirus (MERS-CoV), and severe acute respiratory syndrome coronavirus (SARS-CoV) outbreaks highlighted the public health risk due to highly pathogenic microbial contaminants (1–3). Most people live and work in densely populated environments that increase their exposure to airborne pathogens (4). The disinfection of airborne biological contaminants is important for eliminating transmission routes and ensure human safety (5).
Standard biological indicators are typically used to evaluate the sterilizing effect of indoor environments. Bacillus subtilis subsp. niger (ATCC 9372) is one of the most common spore-forming strains and has the strongest resistance to sanitizers among the different types of airborne pathogens. This strain has been used as a biological indicator in several evaluations of disinfection efficiency (6–8). In addition to spores, the vegetative forms of bacteria are also major components of airborne pathogens. Staphylococcus albus (China Center of Industrial Culture Collection [CICC] 10897) displays typical vegetative growth and is always used as a criterion for air sterilization (9, 10). Paper is one of the most classical carriers of biological indicators and is widely used for the validation of space decontamination (11, 12), and a previous study showed that spores on paper had more resistance to disinfectant than spores on wood, epoxy, and plastic (13). Therefore, using paper as the carrier of microorganisms can ensure the typicality and reliability of evaluations of inactivation effects.
Chlorine dioxide (ClO2) gas is a novel and effective fumigation agent with strong oxidization ability and a broad biocidal spectrum (14, 15). Compared with liquid chemicals and UV irradiation, ClO2 gas is ideal for indoor decontamination due to its high penetrability and good diffusivity. The antimicrobial efficacy of ClO2 gas has been evaluated in previous studies, and ClO2 gas was proven to effectively decontaminate different environments, such as hospital rooms (16, 17), ambulances (18), biosafety level 3 laboratories (19), biological safety cabinets (20), cafeterias (21), and entire buildings (22).
Inactivation kinetics are combined with microbial knowledge, experimental data, and mathematical techniques to construct mathematical models that can describe and predict the inactivation behaviors of microorganisms under specific treatment conditions (23). The first-order kinetics model is a classical model used to represent microbial inactivation and provides a linear inactivation curve that is related only to time (24). However, several studies have discovered that the inactivation kinetics of microorganisms occasionally deviate from the linear model (25, 26). Microbial inactivation curves frequently show nonlinear phenomena such as tailing, shoulder, and sigmoid effects (27). Many nonlinear models, such as the logistic model (28), the Hom model (29), and the Weibull model (30), have been used to describe these nonlinearities. The Weibull model, which is the simplest of all of the above-mentioned models, has been successfully used to model nonlinear inactivation for many microorganisms under different sterilization conditions (31–33).
The gas concentration, relative humidity (RH), and exposure time have been shown to significantly affect sterilization by ClO2 gas (34, 35). RH is a specific factor of the gas sanitizer; an increase in the RH enhances the antimicrobial effect of the ClO2 gas. However, few studies have investigated the inactivation tendency and kinetics for ClO2 gas relative to different RH conditions. A previous study indicated the influence of RH on the antimicrobial effect of ClO2 gas against foodborne pathogens on spinach leaves, but the results of that study were applicable mainly for the food industry (36). To the best of our knowledge, there are presently no published models that can be used to describe the kinetics of inactivation of airborne pathogens by ClO2 gas under different gas concentration and RH conditions. These models are needed to clarify the process of sterilization by ClO2 gas and to predict the range of treatment conditions that can achieve effective inactivation.
Therefore, the main goals of this study were (i) to characterize and compare the behaviors of B. subtilis subsp. niger spores and S. albus in regard to inactivation by ClO2 gas, (ii) to determine the inactivation kinetics under different ClO2 gas concentrations (1, 2, 3, and 5 mg/liter) using the first-order and Weibull models, and (iii) to reveal the inactivation tendency and kinetics for ClO2 gas under different RH conditions (30, 50, 70, and 90%) by establishing a new model, named the Weibull-H model.
MATERIALS AND METHODS
Bacterial cultures.
Two strains were selected based on their resistance to the sterilizer and their ability to survive in air over time. B. subtilis subsp. niger was regarded as a typical spore-forming strain, and S. albus was selected as a classical example of a vegetative bacterium. Stock cultures of B. subtilis subsp. niger and S. albus were obtained from the China Center of Industrial Culture Collection for this study.
Suspension preparation.
The suspension of S. albus was prepared according to the standard culture method for vegetative bacteria (37). The strain of S. albus from the cryogenic vial was aseptically transferred onto tryptone soy agar (TSA) (CM0131; Oxoid, Basingstoke, United Kingdom) and incubated for 24 h at 37°C. Bacterial suspensions were prepared by inoculating 25-ml tubes containing 10 ml of nutrient broth (NB) (CM0001; Oxoid) with a single colony from the TSA plate and incubated at 37°C for 24 h with continuous agitation (150 rpm) on an incubator shaker (HNY-2102C; Honor, Tianjin, China) to obtain a bacterial suspension. Spores were prepared according to the slightly modified standard method (38) to obtain a spore suspension. Cultures were grown in NB (CM0001; Oxoid) on an incubator shaker (HNY-2102C; Honor) at 37°C for 18 to 24 h to obtain a working culture. An aliquot (1 ml) of working culture was spread on sporulation agar plates at 37°C for 7 days. The medium contained, per liter, 30 g nutrient agar (CM0003; Oxoid), 8 mg MnSO4 · H2O (Jiangtian Ltd., Tianjin, China), and 1 g CaCl2 · H2O (Jiangtian Ltd., Tianjin, China). Spores were gently dislodged from the plate using a sterile L-shape spreader and collected in a sterile centrifuge tube. The spores were washed three times with sterile distilled water and treated at 65°C for 30 min to kill the vegetative cells. A spore population of >90% was verified via a spore straining method and microscopic analysis. The initial concentration of spore or bacterial suspension was determined by the measurement of the optical density at 600 nm (OD600) using an UV-visible spectrophotometer (UV1700; Shimadzu Corp., Kyoto, Japan). A measured volume of sterile tryptone physiology solution (TPS) which contained 1 g tryptone (LP0042; Oxoid) and 8.5 g NaCl (Jiangtian Ltd., Tianjin, China) per liter was added to the suspensions of both the S. albus and B. subtilis subsp. niger spores, bringing the final concentration to 5 × 108/ml.
Inoculation of coupons.
A spot inoculation method was used to inoculate the chosen bacteria on sterile filter paper coupons (1 cm by 1 cm) (7). A total of 10 μl of bacterial or spore suspension prepared was spotted on the coupon in a biosafety cabinet. The coupons were then air dried for 1 h at 23°C in the biosafety cabinet. The prepared coupons were used within 24 h of inoculation.
ClO2 gas treatment system.
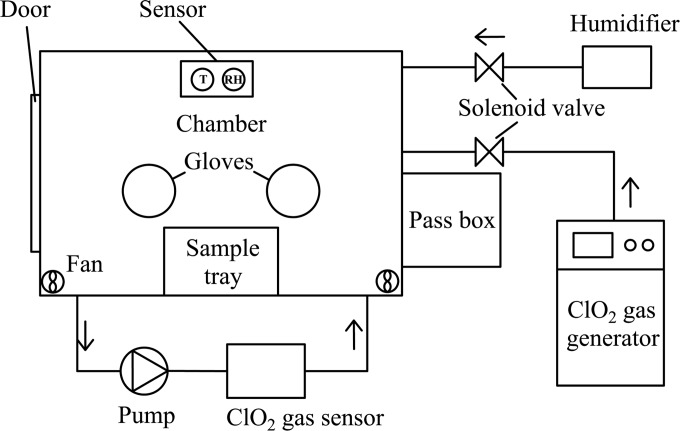
Figure 1 shows the ClO2 gas treatment system used in this experiment. ClO2 gas was produced by a ClO2 gas-generating system (Lab-01; National Bio-Protection Engineering Center, Tianjin, China). The generated ClO2 gas was transported into the test chamber (1.25 m by 0.8 m by 1 m [length by width by height]) equipped with a door and gloves. A pass box was connected to the chamber. Four electric fans (HSL-2; Emicorcom, Leqing, China) were installed in the corner of the chamber to mix the fumigant. The concentration of ClO2 gas in the chamber was continuously monitored using a ClO2 gas sensor (AF26F; Optex Inc., Tokyo, Japan). An ultrasonic humidifier (PW103, Povos, Shanghai, China) was used to control the RH in the test chamber. A thermohygrometer (CHT3W1TLD; Honeywell, USA) was placed inside the chamber to measure the temperature and RH.
FIG 1.
Structure of the test chamber used for the inactivation experiment.
ClO2 gas treatment.
Each inoculated paper coupon was placed in a sealed and sterile centrifuge tube (50 ml; Corning Inc., Morris Plains, NJ, USA) and placed inside the chamber within reach of the gloves. Coupons were inactivated under various gas concentrations and RH conditions. The temperature in the test chamber remained constant at 22 to 24°C. When the desired ClO2 gas concentration, RH, and temperature were stabilized as designed, the centrifuge tubes were opened to expose the coupons, and the exposure period began. At the predetermined time point, the treated coupons were removed via the pass box and were used to determine the surviving cell population.
Microbial enumeration.
An inoculated, untreated control was used to calculate the initial number of CFU in each coupon. Both controls and treated coupons were aseptically placed into sterile tubes containing 10 ml of phosphate-buffered saline (PBS) (BR0014; Oxoid), 0.1% Tween 80 (Jiangtian Ltd., Tianjin, China), and a magnetic stir bar. The tubes were stirred (3 min) on a magnetic stirrer (RH Basic; IKA Inc., Staufen, Germany) until the filter paper disintegrated into pulp to aid the removal of bacteria from the coupons. The tubes containing the coupons were vortexed (1 min) at a speed of 1,000 rpm (MS1 Minishaker; IKA Inc.).
Serial dilutions (1 in 10) to 10−4 were prepared using sterile TPS. Aliquots (1 ml) of the appropriate dilution were pipetted and spread on nutrient agar (CM0003; Oxoid) plates in duplicate. These plates were incubated for 48 h at 37°C, and then the colonies were enumerated. Viable counts were expressed as log CFU per coupon.
Experimental design.
The data used in this study were obtained from 16 separate survival curves. Eight of the survival curves showed the inactivation of B. subtilis subsp. niger spores and S. albus treated with 1, 2, 3, and 5 mg/liter of ClO2 gas at a constant RH of 70%. To evaluate the inactivation kinetics under different RH conditions, additional survival curves were obtained from the inactivation of two chosen strains at RHs of 30, 50, 70, and 90% and a constant gas concentration of 2 mg/liter. Each survival curve was generated from an experiment that consisted of five to seven samples taken at time zero (immediately before inactivation) and at selected time points during inactivation. These inactivation curves were designed to achieve final population reductions of at least 6 log CFU.
Mathematical models.
The first-order model assumes that the cells and spores in a population have the same resistance and that the relationship between the decline in the number of survivors over the treatment time is linear. The model can be written as log10(N/N0) = −kt, where N0 is the initial number of cells (CFU/ml), N is the number of survivors after an exposure time t (CFU/ml), k is the rate parameter, and t is the treatment time (min). The D value, a typical index of inactivation kinetics, is the decimal reduction time in minutes (time required to kill 90% of the organisms) and can be calculated by the parameter k as shown by the equation D = 1/k.
The Weibull model assumes that the survival curve is a cumulative distribution of lethal effects (30). The cumulative form of the Weibull distribution is given by log10(N/N0) = −btn, where b and n are the scale and shape parameters, respectively. When the shape parameter n is greater than or less than 1, the shape of the survival curve will present a shoulder or tailing, respectively. When n = 1, the cumulative form of the Weibull distribution reduces to the first-order rate equation.
For the Weibull model, the parameter td, which is analogous to the traditional D value, was determined. td is the time required for d log reductions of the number of microorganisms and was calculated by the parameters b and n as shown in the equation td = (d/b)1/n, where d is the desired log reduction.
Because no specific mathematical model was used to indicate the influence of RH changes on inactivation by ClO2 gas, the Weibull-H model, which includes a parameter related only to the RH, was established based on the Weibull model. The model can be written as log10(N/N0) = −bϕtn, where ϕ is the RH parameter. This model was used to describe the survival curves for the different RH conditions used in this study. The value of ϕ was set to 1 when the RH was 70%, and the parameters b and n were regarded as constants with the same values as in the established Weibull model. The parameter td can be obtained from the equation td = (d/bϕ)1/n.
Survival curves were fitted using the function Linear Fit in OriginPro (version 8.5.0; Origin Lab Corporation, USA) for the first-order model and the function Nonlinear Curve Fit in OriginPro for the nonlinear models. The model parameters are presented as the mean value and standard error. The mean square error (MSE) was used as the index of residual analysis. The smaller the MSE value is, the more accurate the model is. The coefficient of determination (R2) was used as the index of goodness-of-fit statistics for the models. The larger the R2 value is, the better the fit of the model to the experimental data is.
Statistical analysis.
All experiments were repeated three times using two samples per experiment, for a total of six data points per treatment. The data are presented as the mean values and standard deviations. Differences between samples were determined using the analysis of variance with the SAS Statistics software (version 9.1.3; SAS Institute Inc., USA) and were considered to be statistically significant when the P value was <0.05.
RESULTS
Inactivation of B. subtilis subsp. niger spores under different gas concentrations.
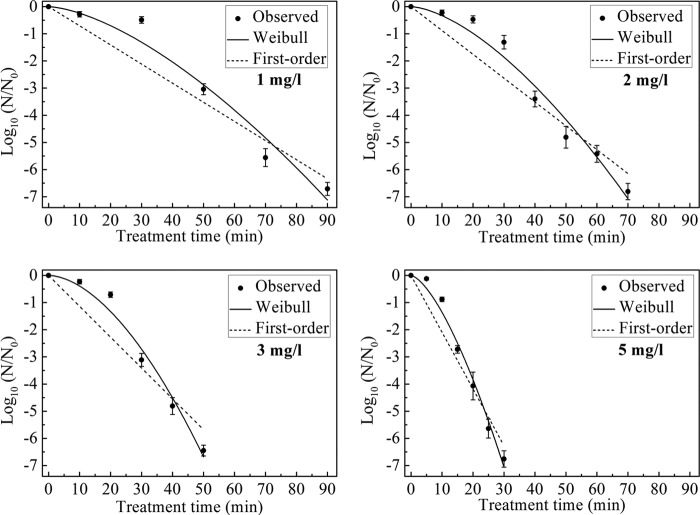
The survival curves for B. subtilis subsp. niger spores in the test chamber with 1, 2, 3, and 5 mg/liter ClO2 gas and a constant RH of 70% are shown in Fig. 2. A greater-than-six-log reduction of spores was achieved after 90, 70, 50, and 30 min of treatment with 1, 2, 3, and 5 mg/liter ClO2 gas, respectively.
FIG 2.
Survival curves for B. subtilis subsp. niger spores treated with different concentrations of ClO2 gas (1, 2, 3, and 5 mg/liter) at 70% RH. The curves are fitted using the first-order and Weibull models.
The inactivation kinetics were determined using the first-order and Weibull models, and the inactivation parameters obtained from each model are shown in Table 1. The time to a 1-log reduction for B. subtilis subsp. niger spores was expressed as the td = 1 value in the Weibull model and as the D value in the first-order model. The td = 1 values were in the range of 25.50 to 8.16 min, and the D values were in the range of 14.19 to 4.78 min. Both the td = 1 values and D values exhibited a significant decrease concomitant with the increase in the ClO2 gas concentration (P < 0.05). The R2 values ranged from 0.89 to 0.93 for the first-order model and from 0.97 to 0.99 for the Weibull model. The shape parameter n of the Weibull model was greater than 1, and there was a downward concavity (shoulder) in the survival curve.
TABLE 1.
Coefficients of the first-order and Weibull models for the survival curves for B. subtilis subsp. niger spores treated with different concentrations of ClO2 gas at 70% RH
| Gas concn (mg/liter) | Weibull model |
First-order model |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| b (mean ± SE) | n (mean ± SE) | td = 1 (min) | R2 | MSE | k (mean ± SE) | D (min) | R2 | MSE | |
| 1 | 0.68 × 10−2 ± 0.93 × 10−2 | 1.54 ± 0.30 | 25.50 | 0.97 | 0.28 | 0.07 ± 0.01 | 14.19 | 0.92 | 0.72 |
| 2 | 0.88 × 10−2 ± 0.66 × 10−2 | 1.58 ± 0.18 | 20.23 | 0.97 | 0.19 | 0.09 ± 0.01 | 11.39 | 0.91 | 0.64 |
| 3 | 0.67 × 10−2 ± 0.58 × 10−2 | 1.76 ± 0.22 | 17.02 | 0.98 | 0.14 | 0.11 ± 0.01 | 8.80 | 0.89 | 0.80 |
| 5 | 4.28 × 10−2 ± 1.95 × 10−2 | 1.50 ± 0.14 | 8.16 | 0.99 | 0.10 | 0.21 ± 0.02 | 4.78 | 0.93 | 0.49 |
Inactivation of S. albus under different gas concentrations.
The survival curves for S. albus in the test chamber treated with 1, 2, 3, and 5 mg/liter ClO2 gas and a constant RH of 70% are shown in Fig. 3. Maximum reductions of 6.15 ± 0.60, 6.82 ± 0.23, 6.46 ± 0.40, and 6.34 ± 0.39 logs were achieved after treatment with 1, 2, 3, and 5 mg/liter ClO2 gas for 70, 50, 30, and 21 min, respectively. The coefficients of the first-order and Weibull models for the survival curves are shown in Table 2. The concentration of ClO2 gas had a significant effect on the td = 1 values and the D values for the concentration range studied (P < 0.05). The td = 1 values and D values obtained for S. albus were smaller than those for B. subtilis subsp. niger spores under the same experimental conditions. For the Weibull model shown in Fig. 3, the survival curve for S. albus contained a tailing (shape parameter n < 1) and represented an inactivation process different from that for B. subtilis subsp. niger spores.
FIG 3.
Survival curves for S. albus treated with different concentrations of ClO2 gas (1, 2, 3, and 5 mg/liter) at 70% RH. The curves are fitted using the first-order and Weibull models.
TABLE 2.
Coefficients of the first-order and Weibull models for the survival curves for S. albus treated with different concentrations of ClO2 gas at 70% RH
| Gas concn (mg/liter) | Weibull model |
First-order model |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| b (mean ± SE) | n (mean ± SE) | td = 1 (min) | R2 | MSE | k (mean ± SE) | D (min) | R2 | MSE | |
| 1 | 0.67 ± 0.08 | 0.52 ± 0.03 | 2.16 | 0.99 | 0.03 | 0.10 ± 0.01 | 9.94 | 0.78 | 0.84 |
| 2 | 0.68 ± 0.10 | 0.58 ± 0.04 | 1.94 | 0.99 | 0.05 | 0.15 ± 0.01 | 6.68 | 0.84 | 0.73 |
| 3 | 0.86 ± 0.14 | 0.58 ± 0.05 | 1.29 | 0.99 | 0.06 | 0.23 ± 0.02 | 4.28 | 0.88 | 0.54 |
| 5 | 0.87 ± 0.13 | 0.63 ± 0.06 | 1.24 | 0.98 | 0.08 | 0.32 ± 0.02 | 3.17 | 0.90 | 0.45 |
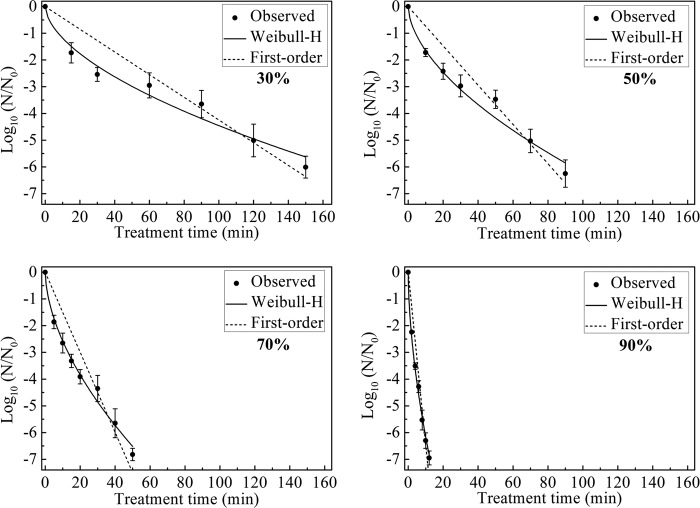
Inactivation of B. subtilis subsp. niger spores under different RH conditions.
The survival curves for B. subtilis subsp. niger spores in the test chamber with 30, 50, 70, and 90% RH and a constant ClO2 gas concentration of 2 mg/liter are shown in Fig. 4. The maximum log reductions for each survival curve were 6.28 ± 0.31 following 180 min of treatment with 30% RH, 6.76 ± 0.17 following 120 min of treatment with 50% RH, 6.81 ± 0.30 following 70 min of treatment with 70% RH, and 6.87 ± 0.26 following 30 min of treatment with 90% RH.
FIG 4.
Survival curves for B. subtilis subsp. niger spores treated with different RH conditions (30, 50, 70, and 90%) and 2 mg/liter ClO2 gas. The curves are fitted using the first-order and Weibull-H models.
Based on the Weibull model established with 2 mg/liter ClO2 gas and 70% RH, the Weibull-H model was built to describe the survival curves under different RH conditions. The parameters b and n of the Weibull-H model were set to 0.0088 and 1.58, respectively, which were same as the values in the second line of Table 1.
Table 3 summarizes the fitting results of the first-order and Weibull-H models for the experimental data. The maximum R2 values were 0.93 for the first-order model and 0.99 for the Weibull-H model. Because n was >1, the inactivation of spores under different RH conditions also showed a shoulder phenomenon. The increase in the RH led to changes in the parameter ϕ from 0.20 to 3.93, in the td = 1 value from 55.74 to 8.48 min, and in the D value from 32.57 to 4.68, indicating a greater rate of kill of spores.
TABLE 3.
Coefficients of the first-order and Weibull-H models for the survival curves for B. subtilis subsp. niger spores treated with different RH conditions and 2 mg/liter ClO2 gas
| RH (%) | Weibull-H model |
First-order model |
||||||
|---|---|---|---|---|---|---|---|---|
| ϕ (mean ± SE) | td = 1 (min) | R2 | MSE | k (mean ± SE) | D (min) | R2 | MSE | |
| 30 | 0.20 ± 0.01 | 55.74 | 0.99 | 0.08 | 0.03 ± 0.01 | 32.57 | 0.91 | 0.51 |
| 50 | 0.44 ± 0.02 | 34.16 | 0.98 | 0.18 | 0.05 ± 0.01 | 19.08 | 0.93 | 0.50 |
| 70 | 1 | 20.23 | 0.97 | 0.19 | 0.09 ± 0.01 | 11.39 | 0.91 | 0.64 |
| 90 | 3.93 ± 0.21 | 8.48 | 0.96 | 0.29 | 0.21 ± 0.02 | 4.68 | 0.91 | 0.72 |
Inactivation of S. albus under different RH conditions.
The survival curves for S. albus in the test chamber with 30, 50, 70, and 90% RH and a constant ClO2 gas concentration of 2 mg/liter are shown in Fig. 5. The largest reductions of 6.01 ± 0.41, 6.25 ± 0.51, 6.82 ± 0.23, and 6.95 ± 0.26 logs were achieved after treatment with 30, 50, 70, and 90% RH for 150, 90, 50, and 12 min, respectively. Similar to the case for B. subtilis subsp. niger spores, the inactivation effect of ClO2 gas against S. albus increased with the increasing RH. The resistance of S. albus against ClO2 gas treatment was weaker than that of spores based on the lower td = 1 and D values. The Weibull-H models in Table 4 were constructed when b was 0.68 and n was 0.58. The shapes of the survival curves were in accordance with the survival curves of S. albus under treatment with different concentrations of ClO2 gas.
FIG 5.
Survival curves for S. albus treated with different RH conditions (30, 50, 70, and 90%) and 2 mg/liter ClO2 gas. The curves are fitted using the first-order and Weibull-H models.
TABLE 4.
Coefficients of the first-order and Weibull-H models for the survival curves for S. albus treated with different RH conditions and 2 mg/liter ClO2 gas
| RH (%) | Weibull-H model |
First-order model |
||||||
|---|---|---|---|---|---|---|---|---|
| ϕ (mean ± SE) | td = 1 (min) | R2 | MSE | k (mean ± SE) | D (min) | R2 | MSE | |
| 30 | 0.46 ± 0.02 | 7.50 | 0.97 | 0.12 | 0.04 ± 0.01 | 23.26 | 0.87 | 0.52 |
| 50 | 0.64 ± 0.03 | 4.20 | 0.97 | 0.15 | 0.07 ± 0.01 | 13.61 | 0.90 | 0.44 |
| 70 | 1 | 1.94 | 0.99 | 0.05 | 0.15 ± 0.01 | 6.68 | 0.84 | 0.73 |
| 90 | 2.39 ± 0.03 | 0.43 | 0.99 | 0.03 | 0.66 ± 0.04 | 1.55 | 0.91 | 0.45 |
Relationship between the RH and ϕ value.
For Tables 3 and 4, the inactivation of B. subtilis subsp. niger spores and S. albus was conducted under different RH conditions, and the Weibull-H model was used to describe the survival curves. The RH parameter ϕ of the Weibull-H model reflected the influence of ClO2 gas on the inactivation speed. The relationship between the RH and ϕ value is shown in Fig. 6. There was a nonlinear increase in the ϕ value as the RH increased from 30% to 90%. Thus, the efficiency of killing of the vegetative bacteria and the spores improved faster under a high RH (>70%) than under a low RH (<70%).
FIG 6.
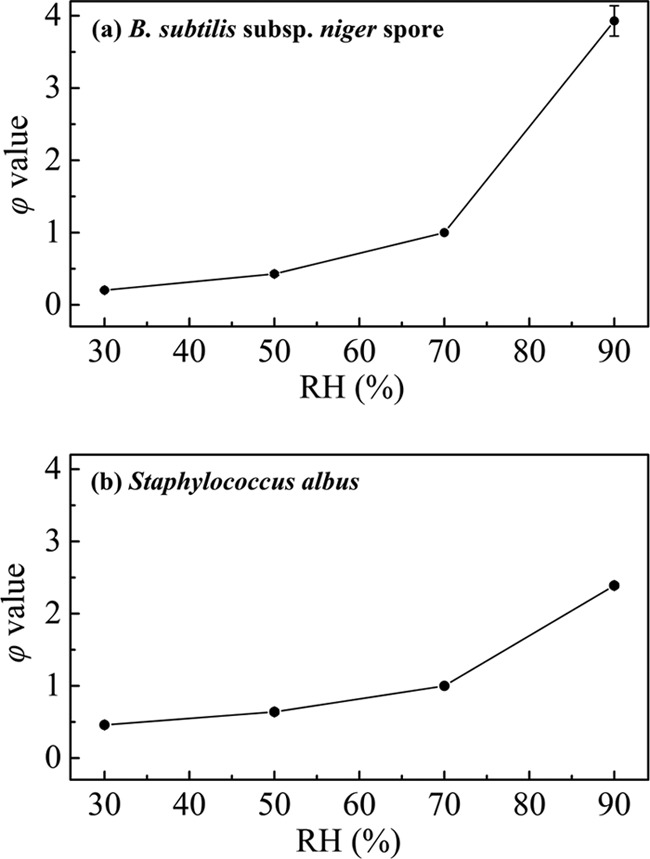
Relationship between the RH and ϕ value in the inactivation of B. subtilis subsp. niger spores (a) and S. albus (b).
Calculated time to achieve a six-log reduction.
Because a one-log reduction is rarely used as a target in air sterilization, we calculated a six-log reduction, which is often used as the standard for effective inactivation. The time required to achieve a six-log reduction is equal to the 6D value for the first-order model and td = 6 for the Weibull or Weibull-H model. Based on the inactivation kinetics models established above, we calculated the required treatment time to achieve a six-log reduction with different ClO2 gas concentrations (1, 2, 3, and 5 mg/liter) and RH conditions (30, 50, 70, and 90%) (Table 5).
TABLE 5.
Calculated treatment times to achieve a six-log reduction for the first-order and Weibull (Weibull-H) models for B. subtilis subsp. niger spores and S. albus during ClO2 gas inactivation
| Gas concn (mg/liter) | RH (%) | Time (min) |
|||
|---|---|---|---|---|---|
|
B. subtilis subsp. niger spores |
S. albus |
||||
| First-order model | Weibull (Weibull-H) model | First-order model | Weibull (Weibull-H) model | ||
| 1 | 70 | 85.14 | 81.57 | 59.64 | 68.68 |
| 2 | 70 | 68.34 | 63.14 | 40.08 | 43.29 |
| 3 | 70 | 52.80 | 47.15 | 25.68 | 28.17 |
| 5 | 70 | 28.68 | 26.93 | 19.02 | 21.32 |
| 2 | 30 | 195.42 | 173.99 | 139.56 | 167.22 |
| 2 | 50 | 114.48 | 106.62 | 81.66 | 93.79 |
| 2 | 90 | 28.08 | 26.47 | 9.30 | 9.56 |
DISCUSSION
In this study, the ability of ClO2 gas at four different concentrations (1, 2, 3, and 5 mg/liter) to inactivate B. subtilis subsp. niger spores and S. albus was evaluated in the test chamber. A higher concentration of ClO2 gas resulted in a shorter time to obtain a specific log reduction and better inactivation efficiency. These results are similar to previous findings in various contaminated indoor environments (11, 16, 18).
Kinetic models are usually used to describe the shape of the survival curve and to determine the mechanism of microbial inactivation. Several studies reported the kinetics of inactivation of inoculated Escherichia coli O157:H7, Listeria monocytogenes, and Salmonella on fruit by ClO2 gas at different concentrations using the first-order model (39) and the Weibull model (9). However, there have been few reports concerning the kinetics of inactivation of airborne pathogens in previous evaluations of the use of ClO2 gas as an air disinfectant. Both the first-order model and the Weibull model were built to evaluate the kinetics of inactivation of B. subtilis subsp. niger spores and S. albus according to the experimental data shown in Tables 1 and 2. Compared with the first-order model, the Weibull model had larger R2 values and smaller MSE values and thus demonstrated a better fit for the observed data. Therefore, the inactivation of B. subtilis subsp. niger spores and S. albus was closer to nonlinear behavior. Similarly, Pottage et al. demonstrated a nonlinear process in the inactivation of three spore-forming Bacillus spp. at a ClO2 gas concentration of 396 ppm for 60 min, although that study did not measure the inactivation kinetics using a nonlinear model (26).
One unique aspect of the inactivation behaviors of B. subtilis subsp. niger spores and S. albus observed in our study was the difference in the shapes of the nonlinear curves. A downward concavity (shoulder) appeared in the curve for B. subtilis subsp. niger spores, which suggested that the resistance of spores to the ClO2 gas was stronger during the early period of inactivation (Fig. 2 and 4). In contrast, the curve for S. albus contained an upward concavity (tailing), which indicated a higher inactivation rate at the beginning of the ClO2 gas treatment (Fig. 3 and 5). This phenomenon demonstrated the different inactivation tendencies for the vegetative bacteria and the spores. There are several possible explanations for this, as follows. (i) Bacterial spores are protected by thick and firm spore coats (40). Thus, the ClO2 gas primarily destroys the structure of the outer coats but does not directly kill the spores during the initial phase. (ii) The sensitivity to ClO2 gas differs for the same type of vegetative bacteria. The weaker or more sensitive members of the population are destroyed relatively faster, leaving behind survivors with higher resistance (31). (iii) The lethal target is different for the vegetative bacteria and the spores. Therefore, the mechanisms of inactivation by the ClO2 gas are distinct.
RH is an important factor in the inactivation effect of ClO2 gas. Lowe et al. reported that a decrease in the RH (<65%) or an airflow restriction reduced the inactivation of Bacillus anthracis, Francisella tularensis, and Yersinia pestis treated with 377 to 385 ppm ClO2 gas for 120 min in a hospital patient care suite (41). Morino et al. reported that the log reduction of feline calicivirus in the dry state was less than 1.0 at 45 to 55% RH and was 6.1 at 75 to 85% RH when the organism was treated with 0.26 ppm ClO2 gas for 24 h (42). Several studies also obtained an effective inactivation under conditions of high RH (>70%) (17, 22). However, there have been no published mathematical models to evaluate the inactivation tendency and kinetics for ClO2 gas under different RH conditions. In our study, the Weibull model established at 2 mg/liter ClO2 gas was modified to the Weibull-H model. The Weibull-H model was used to describe the survival curves, together with the first-order model. The results in Tables 3 and 4 showed that the Weibull-H model produced a better fit to the survival curves, based on the R2 values (close to 1) and low MSE. The increase in the RH accelerated the inactivation process but did not change the concavity of the curve. This finding indicated that the RH had a significant influence on the speed of inactivation of the vegetative bacteria and spores by ClO2 gas but did not change the overall trend of the inactivation process.
The RH parameter ϕ was specifically added in the Weibull-H model to reflect the tendency of the inactivation speed to be affected by the change in RH. Figure 6 shows that the increase in the inactivation speed was not constant when the RH increased from 30% to 90%. There was a rapid improvement in the inactivation efficiency under a high RH (>70%). This phenomenon may be attributed to the following factors. In a high-humidity environment, water vapor may condense onto the surface to surround the vegetative bacteria and spores (26). ClO2 gas is easily soluble in water (39). Thus, the condensed water likely acts as the carrier of the ClO2 gas. An increase in the RH allows more ClO2 to act on the organism and consequently improves the microbicidal effect. Moreover, the ϕ value for B. subtilis subsp. niger spores exhibited a larger increase in the range from 70% to 90% than that for S. albus (Fig. 6). Westphal et al demonstrated that Bacillus thuringiensis spores swelled in response to an increase in the RH (43). Swelling of a spore increases the diameter of the channel for access of gases into spores and expands the spore coat to improve penetrability, which may account for this phenomenon.
For both models, the required process time to achieve a six-log reduction is shown in Table 5. Under each treatment condition, the results obtained showed that B. subtilis subsp. niger spores were more resistant to the ClO2 gas and required longer treatment times for effective inactivation than S. albus. The calculated time could be used as a reference to determine a treatment condition to achieve effective sterilization by ClO2 gas. However, the materials of the coupon significantly affected the inactivation effect. It is important to note that the calculated results are based on one particular carrier of microorganisms and that the use of different surfaces and/or treatment conditions may result in altered inactivation characteristics. Further validation should be conducted before application to real-world settings. On the whole, the exact understanding of the behavior of airborne bacteria and spores in regard to inactivation by ClO2 gas would be useful for the development of an effective disinfection technique and to control outbreaks associated with airborne pathogens.
In summary, this study demonstrated the kinetics of inactivation of B. subtilis subsp. niger spores and S. albus by ClO2 gas. The results showed that the Weibull model produced a better fit to the survival curve than the first-order model under different concentrations of ClO2 gas. A new model (the Weibull-H model) was established to reveal the tendencies and kinetics of inactivation by ClO2 gas under different RH conditions. The behavior of the vegetative bacteria and spores in regard to inactivation by ClO2 gas was nonlinear, and the time to achieve a six-log reduction was calculated based on the established models. The results of this study will be useful for clarifying the effective conditions for ClO2 gas that are required to inactivate airborne pathogens in contaminated air and other environments.
ACKNOWLEDGMENTS
This work was supported by the National Science and Technology Major Project of China (no. 2012ZX10004801) and the National High Technology Research and Development Program of China (no. 2014AA021405).
REFERENCES
- 1.Althaus CL, Low N, Musa EO, Shuaib F, Gsteiger S. 2015. Ebola virus disease outbreak in Nigeria: transmission dynamics and rapid control. Epidemics 11:80–84. doi: 10.1016/j.epidem.2015.03.001. [DOI] [PubMed] [Google Scholar]
- 2.Petersen E, Hui DS, Perlman S, Zumla A. 2015. Middle East respiratory syndrome—advancing the public health and research agenda on MERS: lessons from the South Korea outbreak. Int J Infect Dis 36:54–55. doi: 10.1016/j.ijid.2015.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Smith RD. 2006. Responding to global infectious disease outbreaks: lessons from SARS on the role of risk perception, communication and management. Soc Sci Med 63:3113–3123. doi: 10.1016/j.socscimed.2006.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bolashikov ZD, Melikov AK. 2009. Methods for air cleaning and protection of building occupants from airborne pathogens. Build Environ 44:1378–1385. doi: 10.1016/j.buildenv.2008.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Aygun G, Demirkiran O, Utku T, Mete B, Urkmez S, Yilmaz M, Yasar H, Dikmen Y, Ozturk R. 2002. Environmental contamination during a carbapenem-resistant Acinetobacter baumannii outbreak in an intensive care unit. J Hosp Infect 52:259–262. doi: 10.1053/jhin.2002.1300. [DOI] [PubMed] [Google Scholar]
- 6.Spilimbergo S, Bertucco A, Lauro FM, Bertoloni G. 2003. Inactivation of Bacillus subtilis spores by supercritical CO2 treatment. Innov Food Sci Emerg Technol 4:161–165. doi: 10.1016/S1466-8564(02)00089-9. [DOI] [Google Scholar]
- 7.Li YJ, Zhu N, Jia HQ, Wu JH, Yi Y, Qi JC. 2012. Decontamination of Bacillus subtilis var. niger spores on selected surfaces by chlorine dioxide gas. J Zhejiang Univ Sci B 13:254–260. doi: 10.1631/jzus.B1100289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhang Y, Zhou L, Zhang Y. 2014. Investigation of UV-TiO2 photocatalysis and its mechanism in Bacillus subtilis spore inactivation. J Environ Sci 26:1943–1948. doi: 10.1016/j.jes.2014.07.007. [DOI] [PubMed] [Google Scholar]
- 9.Cui SY, Zhao KY, Liu WJ, Li ZY, Sun QH, Xu BP. 2008. Evaluation of the efficacy of purifying disinfector in air disinfection and purification. Chin J Disinfect 25:366–368. [Google Scholar]
- 10.Li BJ, Li BS, Li W, Yang DH, Meng H, Xu XD. 2014. Evaluation of the sterilizing effect of an optimized photocatalytic air purifier with nano-sized TiO2 on Staphylococcus albus. Mod Prev Med 41:359–361. [Google Scholar]
- 11.Jeng DK, Woodworth AG. 1990. Chlorine dioxide gas sterilization under square-wave conditions. Appl Environ Microbiol 56:514–519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jia HQ, Li YJ, Sun B, Zhao SQ, Yi Y, Zhao M, Zhang ZX, Pan X, Qi JC. 2013. Evaluation of vaporized hydrogen peroxide fumigation as a method for the bio-decontamination of the high efficiency particulate air filter unit. Biomed Environ Sci 26:110–117. doi: 10.3967/0895-3988.2013.02.005. [DOI] [PubMed] [Google Scholar]
- 13.Han Y, Applegate B, Linton RH, Nelson PE. 2003. Decontamination of Bacillus thuringiensis spores on selected surfaces by chlorine dioxide gas. J Environ Health 66:16–20. [PubMed] [Google Scholar]
- 14.Aieta EM, Berg JD. 1986. Review of chlorine dioxide in drinking water treatment. J Am Water Works Assoc 78:62–72. [Google Scholar]
- 15.Gómez-López VM, Rajkovic A, Ragaert P, Smigic N, Devlieghere F. 2009. Chlorine dioxide for minimally processed produce preservation: a review. Trends Food Sci Technol 20:17–26. doi: 10.1016/j.tifs.2008.09.005. [DOI] [Google Scholar]
- 16.Lowe JJ, Gibbs SG, Iwen PC, Smith PW, Hewlett AL. 2013. Impact of chlorine dioxide gas sterilization on nosocomial organism viability in a hospital room. Int J Environ Res Public Health 10:2596–2605. doi: 10.3390/ijerph10062596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Luftman HS, Regits MA, Lorcheim P, Czarneski MA, Boyle T, Aceto H, Dallap B, Munro D, Faylor K. 2006. Chlorine dioxide gas decontamination of large animal hospital intensive and neonatal care units. Appl Biosaf 11:144–154. doi: 10.1177/153567600601100306. [DOI] [Google Scholar]
- 18.Lowe JJ, Hewlett AL, Iwen PC, Smith PW, Gibbs SG. 2013. Evaluation of ambulance decontamination using gaseous chlorine dioxide. Prehosp Emerg Care 17:401–408. doi: 10.3109/10903127.2013.792889. [DOI] [PubMed] [Google Scholar]
- 19.Lowe JJ, Gibbs SG, Iwen PC, Smith PW. 2012. A case study on decontamination of a biosafety level-3 laboratory and associated ductwork within an operational building using gaseous chlorine dioxide. J Occup Environ Hyg 9:196–205. [DOI] [PubMed] [Google Scholar]
- 20.Luftman HS, Regits MA, Lorcheim P, Lorcheim K, Paznek D. 2008. Validation study for the use of chlorine dioxide gas as a decontaminant for biological safety cabinets. Appl Biosaf 13:199–212. doi: 10.1177/153567600801300403. [DOI] [Google Scholar]
- 21.Hsu CS, Lu MC, Huang DJ. 2014. Effect of gaseous chlorine dioxide on student cafeteria bioaerosols. Clean 42:12–19. [Google Scholar]
- 22.Wood JP, Blair Martin G. 2009. Development and field testing of a mobile chlorine dioxide generation system for the decontamination of buildings contaminated with Bacillus anthracis. J Hazard Mater 164:1460–1467. doi: 10.1016/j.jhazmat.2008.09.062. [DOI] [PubMed] [Google Scholar]
- 23.Zimmermann M, Schaffner DW, Aragão GMF. 2013. Modeling the inactivation kinetics of Bacillus coagulans spores in tomato pulp from the combined effect of high pressure and moderate temperature. LWT Food Sci Technol 53:107–112. doi: 10.1016/j.lwt.2013.01.026. [DOI] [Google Scholar]
- 24.Chick H. 1908. An investigation of the laws of disinfection. J Hyg 8:92–158. doi: 10.1017/S0022172400006987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sigstam T, Rohatschek A, Zhong Q, Brennecke M, Kohn T. 2014. On the cause of the tailing phenomenon during virus disinfection by chlorine dioxide. Water Res 48:82–89. doi: 10.1016/j.watres.2013.09.023. [DOI] [PubMed] [Google Scholar]
- 26.Pottage T, Macken S, Giri K, Walker JT, Bennett AM. 2012. Low-temperature decontamination with hydrogen peroxide or chlorine dioxide for space applications. Appl Environ Microbiol 78:4169–4174. doi: 10.1128/AEM.07948-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen H. 2007. Use of linear, Weibull, and log-logistic functions to model pressure inactivation of seven foodborne pathogens in milk. Food Microbiol 24:197–204. doi: 10.1016/j.fm.2006.06.004. [DOI] [PubMed] [Google Scholar]
- 28.Cole M, Davies K, Munro G, Holyoak C, Kilsby D. 1993. A vitalistic model to describe the thermal inactivation of Listeria monocytogenes. J Ind Microbiol 12:232–239. doi: 10.1007/BF01584195. [DOI] [Google Scholar]
- 29.Hom LW. 1972. Kinetics of chlorine disinfection in an ecosystem. ASCE J Sanit Eng Div 98:183–194. [Google Scholar]
- 30.Peleg M, Cole MB. 1998. Reinterpretation of microbial survival curves. Crit Rev Food Sci 38:353–380. doi: 10.1080/10408699891274246. [DOI] [PubMed] [Google Scholar]
- 31.Buzrul S, Alpas H, Bozoglu F. 2005. Use of Weibull frequency distribution model to describe the inactivation of Alicyclobacillus acidoterrestris by high pressure at different temperatures. Food Res Int 38:151–157. doi: 10.1016/j.foodres.2004.09.006. [DOI] [Google Scholar]
- 32.Bozkurt H, D'Souza DH, Davidson PM. 2014. A comparison of the thermal inactivation kinetics of human norovirus surrogates and hepatitis A virus in buffered cell culture medium. Food Microbiol 42:212–217. doi: 10.1016/j.fm.2014.04.002. [DOI] [PubMed] [Google Scholar]
- 33.Mahmoud BSM, Vaidya NA, Corvalan CM, Linton RH. 2008. Inactivation kinetics of inoculated Escherichia coli O157: H7, Listeria monocytogenes and Salmonella Poona on whole cantaloupe by chlorine dioxide gas. Food Microbiol 25:857–865. doi: 10.1016/j.fm.2008.05.009. [DOI] [PubMed] [Google Scholar]
- 34.Han Y, Guentert A, Smith R, Linton R, Nelson P. 1999. Efficacy of chlorine dioxide gas as a sanitizer for tanks used for aseptic juice storage. Food Microbiol 16:53–61. doi: 10.1006/fmic.1998.0211. [DOI] [Google Scholar]
- 35.Han Y, Floros JD, Linton RH, Nielsen SS, Nelson PE. 2001. Response surface modeling for the inactivation of Escherichia coli O157: H7 on green peppers (Capsicum annuum L.) by chlorine dioxide gas treatments. J Food Prot 64:1128–1133. [DOI] [PubMed] [Google Scholar]
- 36.Park S-H, Kang D-H. 2015. Antimicrobial effect of chlorine dioxide gas against foodborne pathogens under differing conditions of relative humidity. LWT Food Sci and Technol 60:186–191. doi: 10.1016/j.lwt.2014.09.031. [DOI] [Google Scholar]
- 37.Gayan E, Condon S, Alvarez I, Nabakabaya M, Mackey B. 2013. Effect of pressure-induced changes in the ionization equilibria of buffers on inactivation of Escherichia coli and Staphylococcus aureus by high hydrostatic pressure. Appl Environ Microbiol 79:4041–4047. doi: 10.1128/AEM.00469-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rastogi VK, Wallace L, Smith LS, Ryan SP, Martin B. 2009. Quantitative method to determine sporicidal decontamination of building surfaces by gaseous fumigants, and issues related to laboratory-scale studies. Appl Environ Microbiol 75:3688–3694. doi: 10.1128/AEM.02592-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mahmoud BS, Bhagat AR, Linton RH. 2007. Inactivation kinetics of inoculated Escherichia coli O157:H7, Listeria monocytogenes and Salmonella enterica on strawberries by chlorine dioxide gas. Food Microbiol 24:736–744. doi: 10.1016/j.fm.2007.03.006. [DOI] [PubMed] [Google Scholar]
- 40.McKenney PT, Eichenberger P. 2012. Dynamics of spore coat morphogenesis in Bacillus subtilis. Mol Microbiol 83:245–260. doi: 10.1111/j.1365-2958.2011.07936.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lowe JJ, Gibbs SG, Iwen PC, Smith PW, Hewlett AL. 2013. Decontamination of a hospital room using gaseous chlorine dioxide: Bacillus anthracis, Francisella tularensis, and Yersinia pestis. J Occup Environ Hyg 10:533–539. doi: 10.1080/15459624.2013.818241. [DOI] [PubMed] [Google Scholar]
- 42.Morino H, Fukuda T, Miura T, Lee C, Shibata T, Sanekata T. 2009. Inactivation of feline calicivirus, a norovirus surrogate, by chlorine dioxide gas. Biocontrol Sci 14:147–153. doi: 10.4265/bio.14.147. [DOI] [PubMed] [Google Scholar]
- 43.Westphal AJ, Price PB, Leighton TJ, Wheeler KE. 2003. Kinetics of size changes of individual Bacillus thuringiensis spores in response to changes in relative humidity. Proc Natl Acad Sci U S A 100:3461–3466. doi: 10.1073/pnas.232710999. [DOI] [PMC free article] [PubMed] [Google Scholar]