Abstract
We study the effect of a driving force F on drift and diffusion of a point Brownian particle in a tube formed by identical cylindrical compartments, which create periodic entropy barriers for the particle motion along the tube axis. The particle transport exhibits striking features: the effective mobility monotonically decreases with increasing F, and the effective diffusivity diverges as F→∞, which indicates that the entropic effects in diffusive transport are enhanced by the driving force. Our consideration is based on two different scenarios of the particle motion at small and large F, homogeneous and intermittent, respectively. The scenarios are deduced from the careful analysis of statistics of the particle transition times between neighboring openings. From this qualitative picture, the limiting small-F and large-F behaviors of the effective mobility and diffusivity are derived analytically. Brownian dynamics simulations are used to find these quantities at intermediate values of the driving force for various compartment lengths and opening radii. This work shows that the driving force may lead to qualitatively different anomalous transport features, depending on the geometry design.
Graphical abstract
I. INTRODUCTION
This paper deals with entropic effects in diffusive transport of noninteracting particles in a static fluid, caused by spatial restrictions of the individual particle motion. More specifically, we study the effect of a uniform driving force F on drift and diffusion of a point Brownian particle in a tube formed by identical cylindrical compartments (see Figure 1a), which effectively create periodic entropy barriers for the particle motion along the tube axis. The model considered here is a fairly simple example of transport through quasi-one-dimensional (1D) structures (tubes or channels) of varying cross-section, in which transfer along the structure axis is coupledwithdiffusion in transverse directions. Despite its simplicity, the model provides qualitative insight into how the system geometry affects biased diffusion.
Figure 1.
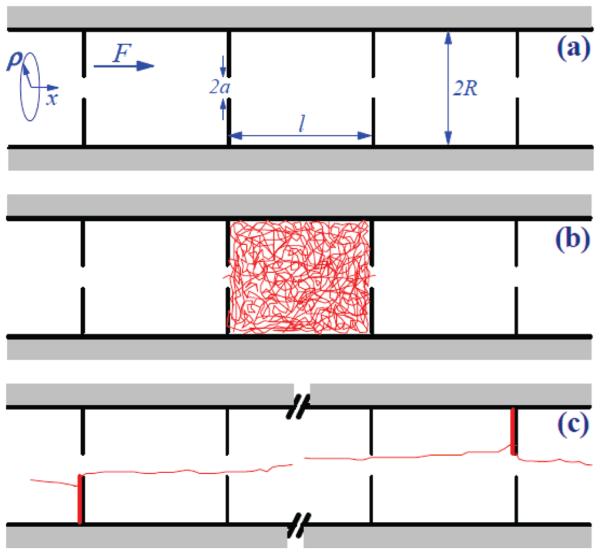
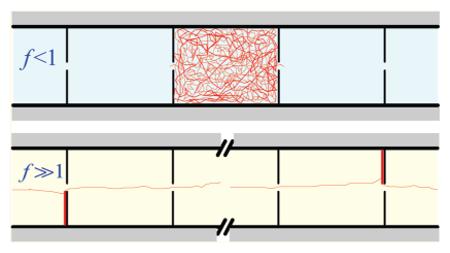
(a) Schematic representation of the model. A Brownian particle moves in a tube formed by identical cylindrical compartments of radius R and length l under the action of uniform driving force F. The particle, with coordinates x (along the tube axis) and ρ (in the radial direction), goes from one compartment to another through circular openings of radius a in the centers of infinitely thin partitions separating the compartments. (b) A typical pattern of particle motion through a compartment at zero or small forcing, illustrating the homogeneous scenario. (c) A typical pattern of particle motion through a tube at strong forcing, illustrating the intermittent scenario. The “break” symbol is used to emphasize the fact that an overwhelming majority of particle transitions between neighboring openings occur while the particle remains in the cylinder of radius a. Long series of fast transitions are interrupted by rare slow transitions during which the particle moves outside the cylinder, diffusing along the partition wall.
The problem of diffusion in a tube of varying cross-section arises in various contexts, including particle transport in porous solids1 and different complex media such as soils,2 translocation of ions through artificial nanopores3 and channels in biomembranes,4 and development of architectures and technologies for controllablemass transfer on the nanoscale.5 The essential physics of the problem is associated with a spatial dependence of the diffusing particle entropy, induced by a variation in the tube cross-sectional area along the propagation direction.6 The particle transport in such a tube evolves through entropy barriers (tube constrictions) and entropy wells (tube expansions).
The problem has been extensively studied by several approaches of varying rigor and sophistication.1,6–13 In a force-free situation (i.e., purely diffusive transport), the most common approach consists in reducing the essentially 3D (or 2D) geometrically restricted Brownian motion to an effective 1D diffusion along the tube axis.6–8 The resulting kinetic equation for the effective 1D distribution is known as the Fick–Jacobs equation,8 which is the Smoluchowski equation with the entropy potential that accounts for changes in the space accessible for the diffusing particle. This dimension reduction scheme relies on the assumption of equilibration in the transversal directions, which implies an instantaneous transverse relaxation. In the modified Fick–Jacobs equation,6,7 finiteness of the transverse relaxation time is taken into account by introducing a renormalized longitudinal spatial-dependent diffusion coefficient. A more general procedure of reduction to the effective 1D description has been developed in ref 9. The validity of the modified Fick–Jacobs equation for force-driven transport in tubes of periodically varying cross-section has been studied both analytically and numerically.10 With this approximation, the problem is reduced to the well-known problem of Brownian motion in a tilted periodic potential, for which exact results for both the effective mobility14 and effective diffusivity15 are available in the case when the potential is of energetic origin. Remarkable similarities and striking differences, mainly in the temperature behavior, between conventional transport in 1D periodic energetic potential and entropic transport have been found and discussed.10 As demonstrated in numerous studies,6,7,9,11 the Fick–Jacobs approach is only applicable to systemswith smooth enough variations in the confining cross-section, but even then it fails at strong forcing.10 Alternative approaches are available allowing one to treat the problem for systems with sharp geometries.12
The present work is concernedwith the effect of the driving force F on the Brownian particle transport through a tube of periodically varying cross-section. The key quantities characterizing the process are the effective mobility μ(F) and the effective diffusivity D(F). It is known that for a Brownian motion in a 1D tilted periodic energetic potential (i) the effective mobility μ(F) monotonically increases with force F between the values μ(0) < μ0 and μ(∞) = μ0,14 where μ0 is the mobility in the absence of the periodic potential, and (ii) the effective diffusivity exhibits a nonmonotonic dependence on F:15 first it increases from the valueD(0),which is less than the bare (potential-free) diffusion coefficient D0; then it reaches a maximum exceeding D0, and finally approaches D0 from above. A similar behavior of μ(F) and D(F) has been reported in several recent studies of driven diffusion in 2Dchannels of periodically varying width10,13 and in a 3D tube formed by spherical compartments,16,17 where an entropy potential is involved. From these observations, one might draw a conclusion that (i) the effect of an external driving force on transport through a tube (channel) of varying cross-section is qualitatively the same as for the Brownian motion in a 1Denergetic potential, and this holds true independently of the tube geometry, and (ii), in particular, the entropic effects in diffusive transport are always suppressed by strong forcing, so that in the limit F → ∞ the effective mobility and diffusivity attain the values μ0 and D0, characterizing potentialfree, unrestricted Brownian motion. However, such a conclusion would be wrong as has been demonstrated recently in studies of driven diffusion in periodically compartmentalized tubes16,18a (or channels18b,c). More precisely, as pointed out in ref 16, (i) the impact of the driving force on the transport through a tube formed by identical compartments may be qualitatively different depending on the compartment shape, and (ii) in a tube formed by cylindrical compartments (see Figure 1a), the effective mobility monotonically decreases with increasing F and the effective diffusivity diverges as F → ∞, so that the driving force enhances, rather than suppresses, the entropic effects.
With the present work, we continue the study of driven diffusion in a periodically compartmentalized tube shown in Figure 1a and explain in more detail the brief report in ref 16. Our consideration is based on two different scenarios of the particle motion in the weak and strong-forcing regimes, respectively. These scenarios are deduced from the careful analysis of statistics of the particle transition times between neighboring openings, using Brownian dynamics simulation. At zero or weak forcing, a transition from one compartment to another is a rare event in the sense that the transition time is much greater than all other characteristic times involved in the problem,19 so that the particle uniformly explores the volume of each compartment before moving to the next one, as schematically shown in Figure 1b. This scenario, which we call homogeneous, suggests using a coarse-grained approach,12 making the problem analytically treatable. With this approach, complemented by a version of the effective medium approximation called boundary homogenization,20 a 3D motion of the particle in the tube is mapped into a 1D nearest-neighbor continuous-time random walk. At strong forcing, one gets a new hierarchy of times (see Figure 1c). In particular, the time characterizing the overwhelming majority of intercompartment transitions is much smaller than all other characteristic times of the problem. In addition, there are very rare, slow transitions associated with the particle diffusion along a cross-wall, which are however very important due to their dominating contribution to the transition time average. In other words, the driving force induces the so-called intermittency21 in the particle transitions between neighboring compartments, which is manifested most clearly in a progressive growth of the corresponding statistical moments with respect to their order. Thus in this regime, a different scenario for the particle motion occurs, which we call hereafter intermittent. In what follows, we discuss these two scenarios in detail and, on their grounds, analytically derive both the small-F and large-F limiting behaviors of the effective mobility and diffusivity. Brownian dynamics simulations are used to find the transport coefficients at intermediate values of the driving force for various compartment lengths and opening radii.
The outline of the paper is as follows. In the next section, we formulate the model and define the basic quantities of interest. In sections III and IV, we consider the limiting cases of weak and strong forcing, respectively: heuristic arguments for the homogeneous and intermittent scenarios are presented and supported by the careful analysis of transition time statistics, using Brownian dynamics simulations. Section V is devoted to the exploration of the transport properties in the whole range of the problem parameters. Finally, our findings are summarized in the last section.
II. MODEL
Consider a point-like Brownian particle moving in a static fluid at temperature T, filling the tube, shown in Figure 1a, under the action of external uniform force F directed toward the right along the tube axis. Periodic zero-thickness partitions divide the cylindrical tube of radius R into identical compartments of length l. Each partition bears a circular opening of radius a, through which the particle can go from one compartment to another. To concentrate on entropic effects in diffusive transport, the model leaves out additional complexities such as interactions among particles and particle–wall interactions, just as previous models of entropic transport traditionally do.
The particle dynamics is governed by the overdamped Langevin equation
| (1) |
complemented by reflecting boundary conditions on the tube and partition walls. Here r(t) is the position vector of the particle at time t; γ is the friction coefficient; a dot refers to time derivative; kB is the Boltzmann constant; a vector F is pointing along the x axis; and ξ(t) denotes a standard 3D Gaussian white noise, with zero mean and correlation for i,j = x,y,z. Equivalently, the particle motion can be described in terms of a probability density of the particle position P3D(x,ρ;t|f), where ρ is the radius vector in cylindrical coordinates (x,ρ); f = βFR is the dimensionless parameter characterizing the force strength; and β = (kBT)−1. The probability density satisfies a 3D diffusion equation with a drift term, complemented by the condition that the normal component of the probability current vanishes at both the lateral tube surface and the partitions. The distinctive feature of the present model is that the zero-thickness partitions do not affect the equilibrium uniform distribution of the particle over the tube cross-section, so that the radial probability density is given by
| (2) |
for any value of the driving force.
We focus on long times when the particle’s displacement significantly exceeds the compartment length l. At these times the particle’s transport along the tube axis is conveniently characterized by the effective mobility μ(f) and diffusivity D(f), defined via the long-time asymptotics of the mean and variance of the particle’s displacement Δx(t|f) = x(t|f) – x(0)
| (3) |
| (4) |
Evidently, in the limiting cases a/R = 1 or l/R = ∞, which correspond to a tube without partitions, the mobility and diffusivity are equal to μ0 = 1/γ and D0 = kBT/γ independently of the driving force. In the force-free case, we have μ(0) < μ0 and D(0) < D0 because of the entropy barriers the particle has to overcome. In contrast to previous reports,10,13,17 here the effect of spatial restrictions on the particle motion is enhanced with application of an external force. As shown in the next sections, μ(f) monotonically decreases from μ(0) to μ(∞), and D(f) diverges as f → ∞.
A further quantity of our interest is the particle transition time between neighboring openings τ. The statistics of τ are distinctly different at weak and strong forcing. In the former case, the distribution is characterized by a single time scale, the mean lifetime in a compartment, which is independent of the driving force. In the latter case, two characteristic time scales are involved that differ widely: τd = l/(μ0F), associated with the particle drift over the period l, and tR = R2/D0, characterizing diffusive motion in the radial direction, with tR >> τd as f → ∞. This suggests two distinctly different scenarios for the particle motion in the tube, homogeneous and intermittent (see Figures 1b and 1c). On the basis of these scenarios, the asymptotic behaviors of the effective mobility and effective diffusivity in the regimes of weak and strong forcing are derived in sections III and IV.
Our goal is to study the effective mobility, eq 3, diffusivity, eq 4, and the transition time statistics as functions of the driving force in a wide range of the model parameters. The conventional Fick–Jacobs approach is inapplicable here because the tube cross-section varies abruptly and the driving force can be arbitrarily large. It is thus necessary to exploit alternative methods, which are discussed in detail below. The essential part of this work is devoted to the extensive Brownian dynamics simulations, carried out to bear out our intuitive guess about plausible scenarios of the particle motion, to test approximations made in the theory, and to bridge the gap between the analytically treatable limits. Technical details of the simulations are presented in Appendix 1.
III. WEAK FORCING REGIME
It is intuitively appealing to formulate the problem of a 3D particle motion in the periodically compartmentalized tube in terms of a 1D nearest-neighbor continuous-time random walk. With such a coarse-grained approach,12 the details of the particle motion in each compartment are disregarded, and what we need to proceed is only the distribution of the transition time between neighboring openings. Generally, the problem of finding this distribution is too difficult to be solved analytically due to mixed boundary conditions on the partition walls. However, at zero or very weak forcing, where we guess the homogeneous scenario of the particle motion (see Figure 1b), the problem can be solved using an approximation called boundary homogenization.20 The approximation is based on replacing the actual nonuniform boundary condition at the cross-wall by an effective uniform radiation boundary condition with a properly chosen trapping rate κ.
A. Transition Time Statistics
With this in mind, we begin with the transition time distribution in the force-free situation, which serves as the reference point for our analysis of small-f behavior. The distribution is characterized by the probability density that a transition occurs in the time interval (τ, τ + dτ). In Appendix 2 we have shown that its Laplace transform, , is given by
| (5) |
with α = D0/(κl). A very accurate approximated formula for the effective trapping rate κ was obtained in ref 22 by means of a computer-assisted boundary homogenization procedure
| (6) |
We have compared q0(τ) found by numerically inverting the Laplace transform, eq 5, with τ-distribution obtained from Brownian dynamics simulations at different values of a/R (from 0.1 to 0.9) and l/R (from 0.1 to 2.0). The comparison has shown that the theoretical distribution of τ perfectly agrees with the simulated distribution in the whole range of the opening radius, providing that the period is not too small, l ≥ R. This is in agreement with the conclusion of refs 20d and 23a where the validity of the homogenization procedure was tested by comparing only the mean values of τ (theoretical and simulated). Equation 5 also agrees with a solution of the similar problem, obtained for a slightly different geometry.20d
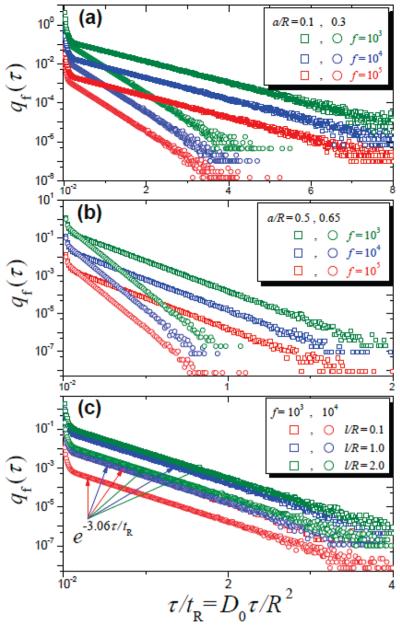
Examples illustrating the τ-distribution at different values of geometric parameters l/R and a/R are given in Figure 2 and Table 1. Along with the probability density q0(τ) calculated from eq 5, in Figure 2 we present the probability density qf(τ) found in simulations for a few nonzero values of f. Comparison of the curves shows that the distribution remains almost unchanged at very weak forcing, f ≤ 0.1. Noticeable changes take place at f > 1. Figure 2 and Table 1 show that with increasing f the maximum (and the average) is shifting toward lower values of τ, which is accompanied by the appearance of a high, narrow peak. The moment ratios presented in Table 1 also indicate that the distribution becomes narrower as the driving force increases (the k-th moment is defined as ). Such a behavior of the moment ratios takes place only if f is not too large. At strong forcing, the situation is completely different, as shown in the next section: in addition to a delta-function-like peak, qf(τ) has a long tail; because of this tail the moment ratios grow, and the distribution becomes more dispersive as f increases. The larger a/R is (or the smaller l/R is), the greater the critical value fc, at which the change in the behavior occurs. As Table 1 indicates, when l/R = 2 the critical value fc is of the order of unity at a/R = 0.1, of the order of 10 at a/R = 0.5, and of the order of 100 at a/R = 0.9.
Figure 2.
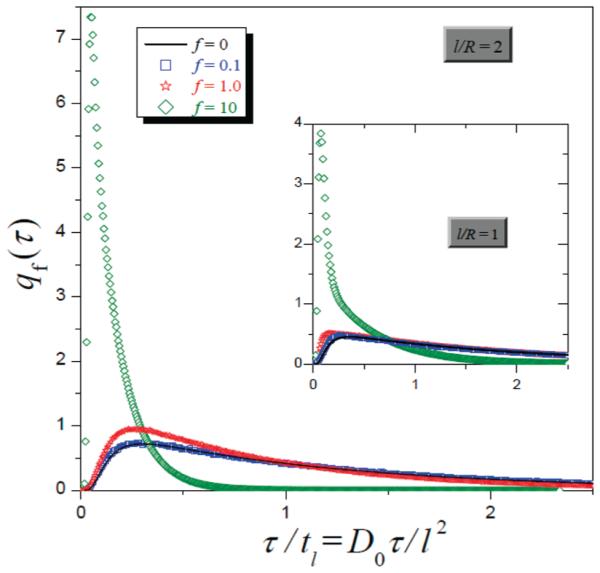
Probability density of the transition time between neighboring openings at weak forcing. The force-free case is represented by the solid (black) line, calculated by numerically inverting the Laplace transform given by eq 5. Histograms for different values of the dimensionless parameter f = βFR are obtained from Brownian dynamics simulations (the symbols are described in the legend). The curves in the main graph and in the inset are obtained at l/R = 2 and l/R = 1, respectively, and at a/R = 0.3 for both.
Table 1.
Average (scaled by ) and the Moment Ratios of the Transition Time for Different Values of a/R and f = βFR at l/R = 2a
| a/R | f | ||||
|---|---|---|---|---|---|
| 0.1 | 0 | 1.00 | 1.92 | 5.52 | 21.2 |
| 0.1 | 0.90 | 1.80 | 4.52 | 14.2 | |
| 1.0 | 0.68 | 1.74 | 4.18 | 12.2 | |
| 10 | 0.11 | 1.86 | 5.14 | 18.8 | |
| 0.5 | 0 | 1.00 | 1.71 | 4.29 | 14.4 |
| 0.1 | 0.99 | 1.71 | 4.28 | 14.4 | |
| 1.0 | 0.76 | 1.65 | 3.95 | 12.6 | |
| 10 | 0.11 | 1.39 | 2.63 | 6.55 | |
| 100 | 0.018 | 3.78 | 28.5 | 295 | |
| 0.9 | 0 | 1.00 | 1.67 | 4.07 | 13.2 |
| 0.1 | 0.99 | 1.66 | 4.06 | 13.1 | |
| 1 | 0.76 | 1.59 | 3.62 | 11.0 | |
| 10 | 0.10 | 1.10 | 1.33 | 1.77 | |
| 100 | 0.010 | 1.03 | 1.10 | 1.24 | |
| 1000 | 0.0011 | 1.44 | 4.70 | 31.2 |
The results in the force-free case are calculated from eqs A2.4–A2.7 and 6. The other results are obtained from Brownian dynamics simulations.
Good agreement between the transition time statistics obtained from simulations and predicted by theory provides strong support for the homogeneous scenario of the particle motion at weak forcing. On the basis of this scenario and the results of this section, one can easily find the transport coefficients.
B. Effective Diffusivity and Effective Mobility
We start again with the force-free situation, where analytical results are available. To find the effective diffusivity D(0), we need only the mean transition time between neighboring openings, ❬τ❭0, which is given in eq A2.4. Following this way, we arrive at the known result23
| (7) |
The small-f limit of the effective mobility can be obtained from the effective diffusivity via the Einstein relation. This leads to16
| (8) |
Equations 7 and 8 perfectly agree with μ(0) and D(0) found in simulations in the whole range of the parameter a/R, providing that l/R ≥ 1 (as, for example, shown in Figure 3 for l/R = 2). However, when l/R < 1, the boundary homogenization procedure fails, and these equations are practically useless.
Figure 3.
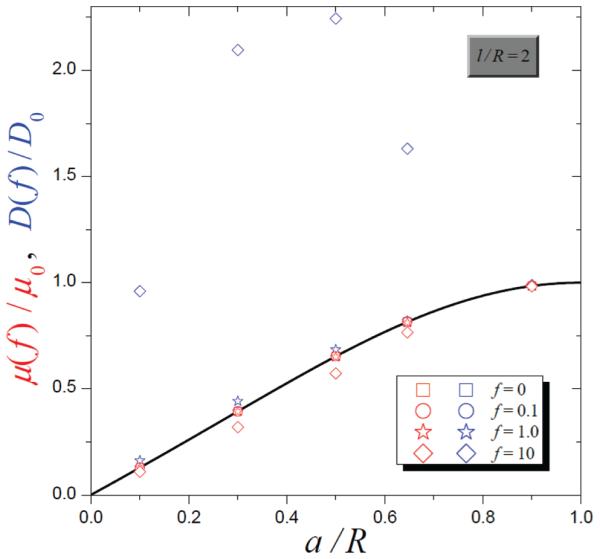
Effective mobility and diffusivity at different values of a/R and f = βFR. The solid line represents the dependence of μ(0)/μ0 = D(0)/D0 on a/R, as calculated from eqs 6–8. Red (blue) symbols represent the results for the effective mobility (diffusivity) obtained from Brownian dynamics simulations. The symbols are described in the legend.
Figure 3 illustrates the effect of the driving force on the transport coefficients at small f. First, note that eq 8 provides reasonable estimates for μ(f) if f ≤ 10. The effective diffusivity appears to be more sensitive to the forcing than the effective mobility: the estimate given by eq 7 becomes inadequate at values of f smaller than the estimate given by eq 8. Deviations from the limiting values μ(0) and D(0), caused by the forcing, are more pronounced at intermediated values of a/R. Next, as Figure 3 shows, the effective diffusivity increases with increasing f, D(f) > D(0), as one might expect because the forcing leads to a decreased average transition time. Qualitatively, such behavior of D(f) at weak forcing is universal (insensitive to the tube geometry).
Finally, the most intriguing observation is that the effective mobility decreases with the application of force. The origin of the unusual behavior observed is attributed to the special geometry of the tube. Indeed, the previous studies10,13,17 dealt with tubes with curved (e.g., spherical17) compartments. In these tubes, the force not only pushes the particle in the x-direction but also drives it inward toward the tube axis that leads to localization of the particle in the cylinder connecting the openings and, as a result, to a higher mobility. The distinctive feature of the tube composed of cylindrical compartments is that the driving force does not affect the uniform particle distribution over the tube cross-section (see eq 2). However, the uniform longitudinal distribution of the particle in each compartment is modified by the force, so that the probability becomes higher to find the particle near the right cross-wall. As a result, the slowing-down effect of the right cross-wall increases with the force, which leads to a lower mobility.
IV. STRONG FORCING REGIME
At strong forcing, the particle motion along the tube changes qualitatively, in that it becomes intermittent (see Figure 1c). The particle randomly switches between two states, “running” and “locked”. In the running state, it moves in the cylinder of radius a surrounding the tube axis, with the drift velocity vd = μ0F. When the particle is outside the cylinder, it is in the locked state, in which it does not move along the tube, being pressed to one of the cross-walls. The state of the particle is determined by its radial position. Switching between the states occurs due to radial diffusion. Since the particle distribution over the tube cross-section is uniform at any forcing level (see eq 2), the probability to find the particle in the running state equals (a/R)2, so that the effective drift velocity of the particle reads
| (9) |
A. Transition Time Statistics
1. Fast and Slow Transitions
We begin with consideration of statistics of transition times, which is significantly different from that we have seen in the weak forcing regime. As Brownian dynamics simulations show, the overwhelming majority of intercompartment transitions take time of the order τd = l/(μ0F) = f−1(l/R)tR. This time scale is associated with the particle drift over the period l. As f → ∞, τd is much smaller than all other characteristic times of the problem. Moreover, the fraction of these fast transitions rises as the driving force increases. For example, it is 0.80 at f = 104 and 0.98 at f = 105 (for a/R = 0.5 and l/R = 2).
In addition to the fast transitions, there are also transitions taking longer, which can be subdivided into “intermediate” and “slow”. While the fast transitions are associated with the particle’s stay in the running state, both intermediate and slow transitions occur due to switching between the running and locked states, or, in other words, due to particle’s visits outside the cylinder connecting the openings. The intermediate transitions are related to short-lived excursions outside the cylinder, so that their characteristic time is comparable with τd. The slow transitions are caused by the long-lasting excursions, during which the particle being pressed to a cross-wall diffuses in the annulus bounded by the two concentric circles of radii a and R. These excursions maintain the uniform particle distribution over the tube cross-section (see eq 2). The characteristic time scale of slow transitions is of the order of tR = R2/D0, tR >> τd as f → ∞. The slow transitions are rare but very important because of their dominating contribution to the mean and especially to higher moments of τ.
The slowest intercompartment transitions are responsible for the far tail of the τ-distribution. Figure 4 gives the far tails of the probability density qf(τ) obtained from Brownian dynamics simulations. Panels (a) and (b) show the results at different values of a/R and f but at a fixed value of l/R. Panel (c) presents the results obtained at different values of l/R and f but at a fixed value of a/R. All curves in the figure clearly exhibit an exponential decay, , at τ ≳ tR. The values of the dimensionless decay rates found in simulations are given in Table 2. As this table and Figure 4 indicate, the values of are independent of f and l/R and are solely determined by the radius ratio a/R.
Figure 4.
Far tail of the transition time distribution qf(τ) obtained from Brownian dynamics simulations at strong forcing (the symbols are described in the legends). The initial part of the distribution (up to τ/tR = 10−2), responsible for fast and intermediate transitions, is not shown. Panels (a) and (b) show the results obtained at different values of a/R (0.1, 0.3, 0.5, and 0.65) and f (103, 104, and 105) but at fixed l/R = 2. These results clearly indicate that at long times the probability density qf(τ) decays exponentially, , where is the dimensionless decay rate. The values of obtained from simulations, as well as the decay rates calculated from eq A3.5, are presented in Table 2. Panel (c) shows the results at different values of l/R (0.1, 1, and 2) and f (103 and 104) but at fixed a/R = 0.3. The probability density decays at the same rate , which is independent of the parameters f and l/R.
Table 2.
Dimensionless Long-Time Decay Rates of the Particle Lifetime Probability Density, k1 (See Appendix 3), and of the Transition Time Probability Density, (see Figure 4)a
| a/R | k1 | |||
|---|---|---|---|---|
| 0.1 | 1.22 | 1.21 | 1.22 | 1.22 |
| 0.3 | 3.06 | 3.06 | 3.07 | 3.07 |
| 0.5 | 7.41 | 7.39 | 7.40 | 7.41 |
| 0.65 | 16.4 | 16.5 | 16.4 | 16.2 |
| 0.9 | 236 | 233 | 236 | 235 |
The values of k1 are calculated from eq A3.5, and the values of are obtained from simulations for different values of f and a/R at l/R = 2.
This observation suggests that the slow transitions, corresponding to the far tail of qf(τ), are controlled by the radial diffusion along a cross-wall: as soon as the particle reaches the opening, a transition to the next compartment immediately occurs due to strong forcing. To test this surmise, in Appendix 3 we analyze the survival of a Brownian particle in the annulus bounded by two concentric circles of radii a and R > a, with absorbing (reflecting) boundary condition on the inner (outer) circle. We find that the particle lifetime probability density w(t) decays as a single exponential, w(t) ∝ exp(−k1τ/tR) as t → ∞, with the dimensionless rate k1 defined by eq A3.5. The values of k1 as calculated from eq A3.5 are presented in Table 2 for different values of radius ratio a/R. A perfect agreement between the long-time decay rates k1 and for different parameters of the model (see Table 2) corroborates our surmise.
2. Probability Density
On the basis of the heuristic arguments and simulation results discussed above, we assume that as f → ∞ the transition time probability density, qf(τ), can be presented as a sum of two terms. The first term is associated with the contribution of the fast transitions, the probability density of which can be approximated by the δ-function, qfast(τ)δ(τ – τd). The second term represents the contribution of the slow transitions. Following the observation made in the previous section that the slow transitions are controlled by the diffusion of a particle along the partition wall, we assume that the corresponding probability density, qslow(τ), can be approximated by the lifetime probability density for this particle, w(τ), which is independent of f, i.e., qslow(τ)w(τ). Thus, we have
| (10) |
where λ(f) and 1 – λ(f) are the fractions of the slow and fast transitions, respectively. Note that the second term in eq 10 depends on f only through the coefficient λ(f). In writing eq 10, we have neglected the intermediate transitions: their fraction is negligible as compared to the fast ones, and on the other hand, their contribution to the averages is much smaller than that from the slow transitions.
The fraction of the slow transitions, λ(f), is found by comparing two expressions for the mean transition time ❬τ❭f. The first follows directly from the definition of ❬τ❭f and eq 10
| (11) |
In writing eq 11, we have neglected τd as compared to the mean lifetime of the particle diffusing along the partition, , which is of the order of tR >> τd, if a is not too close to R. The second expression for ❬τ❭f is obtained from eq 9 for the effective velocity
| (12) |
By equating eqs 11 and 12, we get
| (13) |
This formula shows that the fraction of the slow transitions vanishes as , which is in agreement with the simulation results.
Our last remarks in this section concern eq 12. First, note that ❬τ❭f is (R/a)2 times larger than τd (characterizing the overwhelming majority of transitions), which emphasizes a significant contribution of the slow transitions. Second, the estimate for ❬τ❭f given by eq 12 is in reasonable agreement with simulations results at f = 105, as the third column of Table 3 indicates.
Table 3.
Average (Scaled by ) and Moment Ratios of the Transition Time Found in Brownian Dynamics Simulations at Strong Forcing, f = βFR ≥ 103, for Different Values of a/Ra
| a/R | f | ||||
|---|---|---|---|---|---|
| 0.1 | 103 | 53.3 | 14.6 | 334 | 1.0 × 104 |
| 104 | 78.1 | 97.8 | 1.5 × 104 | 3.1 × 106 | |
| 105 | 90.4 | 844 | 1.1 × 106 | 2.0 × 109 | |
| 0.3 | 103 | 8.81 | 31.0 | 1.8 × 103 | 1.3 × 105 |
| 104 | 10.2 | 264 | 1.3 × 105 | 7.9 × 107 | |
| 105 | 10.7 | 2.5 × 103 | 1.1 × 107 | 6.9 × 1010 | |
| 0.5 | 103 | 3.49 | 25.7 | 1.5 × 103 | 1.2 × 105 |
| 104 | 3.77 | 231 | 1.2 × 105 | 8.6 × 107 | |
| 105 | 3.89 | 2.3 × 103 | 1.2 × 107 | 7.9 × 1010 |
τd = l/(μ0F) is the drift time; l/R = 2.
3. Moment Ratios
Consider the moments of the transition time distribution, . Using eqs 10 and 13, we get for the leading term of large-f asymptotic behavior of the k-th moment
| (14) |
where . Equation 14 shows that all the moments of the transition time distribution, irrespective of their order, are proportional to f−1 as f → ∞. As a consequence, there is a progressive growth of the moment ratios with respect to their order
| (15) |
Numerical results for the ratios of the moments of the second, third, and fourth order, presented in Table 3, support the scaling law given in eq 15. This in turn justifies the approximation made in eq 10 for the probability density qf(τ). The divergence of the transition time moment ratios as f → ∞ is a clear manifestation of intermittency in transitions between neighboring openings.
At strong forcing, the effect of the driving force on the moment ratios (see Table 3) is just opposite to what we have seen at weak forcing, where these ratios decrease with increasing f (see Table 1). This is one more argument indicating the difference between the scenarios of the particle motion in these regimes. The force-induced intermittency contrasts qualitatively with previously reported results,10,13,17 predicting qf(τ) → δ(τ – τd) and the moment ratios tending to unity as f → ∞. The origin of unusual transition time statistics is the special geometry of the considered tube.
B. Transport Coefficients
1. Effective Mobility
The analysis of transition time statistics provides convincing support for the intermittent scenario of the particle motion at strong forcing (see Figure 1c). On the basis of this scenario one can easily derive the effective mobility. As follows from eq 9, the large-f limiting value of the effective mobility is given by16,18a
| (16) |
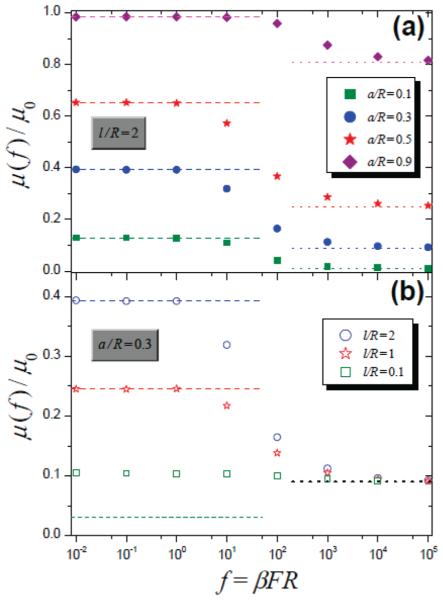
One can check that when l/R ≥ 1 and hence the boundary homogenization procedure is applicable, μ(∞) is less than μ(0), eq 8, at any value of a/R. Figure 5 shows the ratio μ(0)/μ(∞) asa function of a/R for several values of l/R. It is seen that the smaller a/R is or the larger l/R is, the more pronounced the difference between the two limits. In addition, this figure demonstrates very good agreement between the numerical and analytical results in the whole range of a/R.
Figure 5.
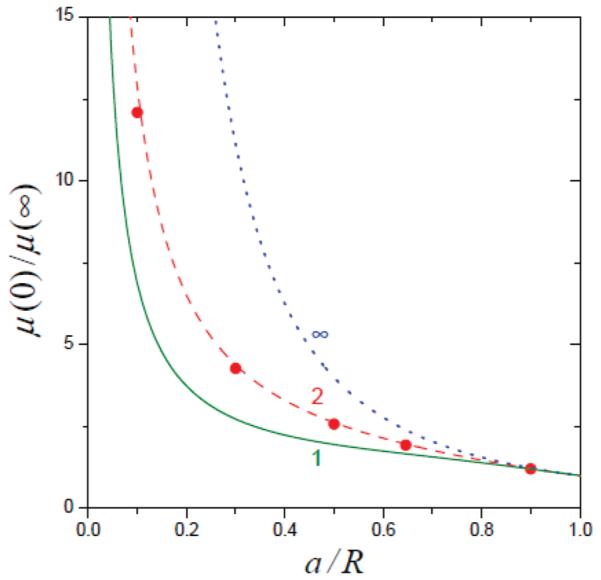
Ratio of limiting values of the effective mobility μ(0)/μ(∞) as a function of a/R. The solid, dashed, and dotted lines corresponding to l/R equal to 1, 2, and ∞, respectively, as indicated by numbers near the curves, are calculated from eqs 7, 8, and 16. Circles represent the ratio μ(0)/μ(105) found in simulations at l/R = 2.
2. Effective Diffusivity
To find the asymptotic behavior of the effective diffusivity as f → ∞, it is convenient to introduce residence time τa(t), spent by the particle in the running state for a sufficiently long observation time t. The mean of this random variable, ❬τa(t)❭ = (a/R)2t, determines the average displacement of the particle, ❬Δx(t|F)❭ = μ0F❬τa(t)❭. This leads to the results for the effective drift velocity, eq 9, and the effective mobility, eq 16. The variance of the residence time, , determines the variance of the particle displacement
| (17) |
since as f → ∞ the main contribution to the width of the particle displacement distribution is due to fluctuations of τa(t). The large-t asymptotic behavior of σ2(t) has been recently found24
| (18) |
Using the definition of D(f), eq 4, and the relations in eqs 17 and 18, we get16
| (19) |
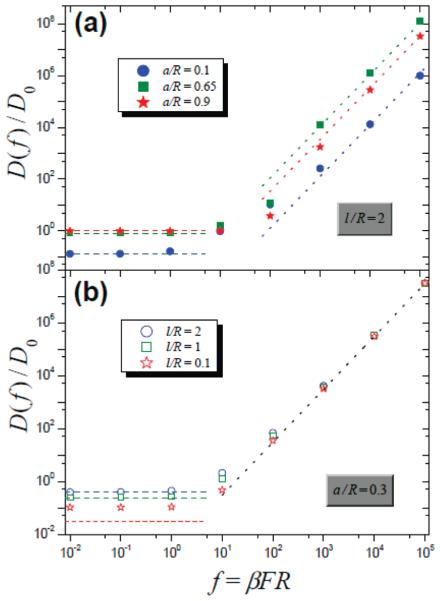
In writing eq 17 we have neglected the contribution from the bare longitudinal diffusion. This contribution is dominant, however, when a/R → 1 (at any finite value of f). In this trivial case, the effect of the cross-walls is negligible and the variance of the particle displacement is equal to 2D0t, so that the diffusivity approaches its unperturbed value D0, independently of the driving force.
Figure 6 compares the effective diffusivity as calculated from eq 19 with that obtained from simulations at various values of f and a/R. There is very good agreement between the analytical and numerical results for sufficiently strong forcing, f ≳ 104. Figure 6 also illustrates a nonmonotonic dependence of D(f) on the parameter a/R, with the maximum at a/R ≈ 0.65. Interestingly, even at a large opening size (e.g., a/R = 0.9), D(f) substantially exceeds D0 as f → ∞, while μ(f) in this case is close to its unperturbed value μ0. Note that both the asymptotic behavior of D(f) and the limiting value of μ(f), as well as the moments of the τ-distribution, do not depend on the other geometric parameter l/R. Moreover, these asymptotic results are applicable to tubes with aperiodic location of cross-walls. The parameter l/R drops out in this regime because the particle, being pressed to a cross-wall, is distributed within a layer of thickness (βF)−1 << l, so that it “feels” the confinement length (βF)−1, rather than the compartment length l. The dimensionless parameter f = βFR compares two lengths characterizing the particle distribution as f → ∞: the confinement length and the tube radius. It plays the determining role at strong forcing, reflecting the combined effect of the force, thermal noise, and the system geometry.
Figure 6.
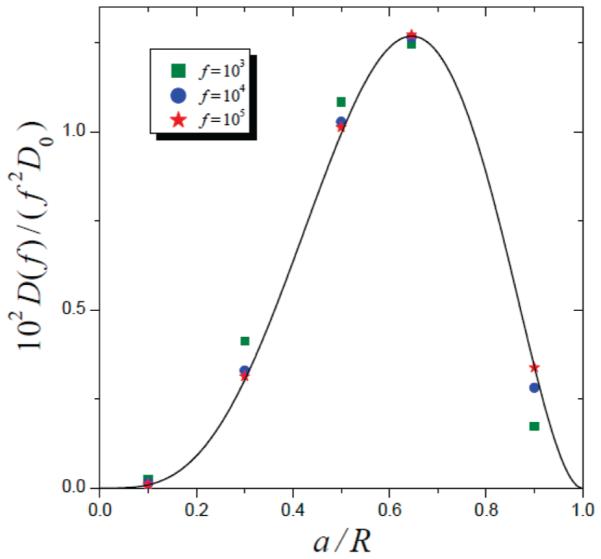
Effective diffusivity D(f) scaled by f2D0 as a function of a/R. The solid line is calculated from eq 19. Points, marked by symbols described in the legend, are obtained from simulations at l/R = 2.
Giant enhancement of the diffusivity predicted by eq 19 arises from the coupling of the transversally modulated longitudinal mobility of the particle and its radial diffusion. The effect has the same origin as the Taylor dispersion25 of a particle diffusing in a laminar flow. The quadratic f-dependence of D(f) as f → ∞, along with the intermittency in the transition time statistics and a decrease of the mobility, μ(∞) < μ(0), is a signature of sharp compartmentalization.
V. TRANSPORT COEFFICIENTS OVER THE ENTIRE RANGE OF F
The limiting small- and large-f behaviors of the effective mobility μ(f) and diffusivity D(f) have been derived and discussed in the previous sections. To find these transport coefficients between the two limits and to ascertain the range of applicability of the asymptotic formulas, we have made use of Brownian dynamics simulations. In this section we present the results and discuss the functions μ(f) and D(f) over the entire range of f at different values of the tube parameters.
The results are presented in Figures 7 and 8, using μ0 and D0 as scaling factors. The ratios μ(f)/μ0 and D(f)/D0 are plotted against f for different values of a/R and l/R = 2 (Figures 7a and 8a) and for different values of l/R and of a/R = 0.3 (Figures 7b and 8b). The periodic entropy barriers slow down the transitions between neighboring compartments. This is why the effective mobility is smaller than μ0 at all f. The smaller the opening size (i.e., the higher the entropy barrier), the stronger the effect. Upon application of the driving force, the slowing-down effect caused by the periodic barriers is enhanced. As Figure 7 shows, the effective mobility μ(f) monotonically decreases between the values μ(0) and μ(∞) < μ(0), in qualitative contrast with the predicted monotonic growth previously reported in studies of transport in 1D tilted periodic energetic potential14 and driven entropic transport.10,13,17 A possible explanation for this unusual behavior has been discussed in the last paragraph of section III. Figure 8 shows that the diffusivity D(f) also exhibits a distinctive behavior: it monotonically increases with f and diverges as f → ∞, while in the previous studies dependence D(f) has been shown to be nonmonotonic and approaching D0 from above at strong forcing.
Figure 7.
Effective mobility as a function of the parameter f = βFR at different values of a/R and l/R = 2 (panel a) and different values of l/R and a/R = 0.3 (panel b). Points, marked by symbols described in the legends, are obtained from simulations. The dashed and dotted lines represent the limiting small-f and large-f behaviors of the effective mobility, as calculated from eqs 8 and 16, respectively.
Figure 8.
Effective diffusivity as a function of the parameter f = βFR at different values of a/R and l/R = 2 (panel a) and different values of l/R and a/R = 0.3 (panel b). Points, marked by symbols described in the legends, are obtained from simulations. The dashed and dotted lines represent the limiting small-f and large-f behaviors of the effective diffusivity, as calculated from eqs 7 and 19, respectively.
We find in Figures 7 and 8 that the small-f behaviors of D(f) and μ(f) are determined by both a/R and l/R, in accordance with the estimates of D(0) and μ(0) given by eqs 7 and 8, respectively. At very weak forcing the theoretical predictions and the simulation data are in very good agreement in the range of applicability of these equations, l > R. However, they can differ widely for short compartments (see the case of l/R = 0.1 in Figures 7b and 8b), which are outside of the validity range of eqs 7 and 8. With increase of the forcing, the simulation data deviate more and more from the force-free values μ(0) and D(0). The larger a/R (or the smaller l/R), the greater the value fw, up to which the description in terms of the weak forcing regime holds. A rough estimate of fw varies from the order of unity up to the order of 100, depending on the tube parameters.
At strong forcing, the effective mobility approaches its limiting value μ(∞), eq 16, and the effective diffusivity approaches the quadratic dependence on f, eq 19. As Figures 7 and 8 indicate, the analytical predictions are in very good agreement with the simulation data for different values of the model parameters. The large-f behaviors of μ(f) and D(f) are solely determined by the ratio a/R. The other geometric parameter l/R determines the level of forcing fs required to reach the asymptotic region: the larger l/R is, the greater fs is (see Figures 7b and 8b). A rough estimate of fs varies from the order of 10 (at l/R = 0.1) up to the order of 100 (at l/R = 2). Figures 7a and 8a show that the forcinginduced decrease in the effective mobility becomes the more pronounced the smaller the opening size (see also Figure 5), whereas the effective diffusivity takes the maximum value at a/R ≈ 0.65 (see also Figure 6).
VI. CONCLUSIONS
We have investigated a driven diffusion of a point particle in a tube formed by identical cylindrical compartments. The analysis of statistics of transition times between neighboring openings, τ, has shown that there are two different scenarios of the particle motion in the tube. At weak forcing, the particle motion in a compartment keeps no memory about the entrance point (provided the compartment length l exceeds the tube radius R), which implies a uniform distribution of the particle within each compartment (homogeneous scenario). At strong forcing, there is intermittency in the transitions, so that the radial distribution becomes uniform as a result of the particle traveling through many compartments (intermittent scenario). We have found and discussed the probability densities and statistical moments of τ in both limiting cases. The analytical predictions are supported by Brownian dynamics simulations. At weak forcing, the effect of the force is to narrow the transition time distribution. In the strong forcing regime, notable observations are: (i) in addition to a delta-function-like peak, attributable to frequent fast transitions, the τ-distribution has a far tail, very important due to its dominating contribution to the mean and especially to higher moments of τ; (ii) the tail is associated with rare slow transitions, which are controlled by the radial diffusion along a cross-wall; (iii) the tail decays as a single exponential as τ f ∞, with the rate independent of the dimensionless force f and the ratio l/R; and (iv) because of the tail there is a progressive growth of the moment ratios with respect to their order as
On the basis of these scenarios, we have derived formulas for the effective mobility and diffusivity in the weak and strong-forcing regimes. Using Brownian dynamics simulations to bridge the gap between the two limits, we have found the transport coefficients over the entire range of the dimensionless driving force at different values of the tube parameters. The results obtained demonstrate that application of the driving force leads to an enhancement of the entropic effects (associated with spatial restrictions of individual particle motion) in the particle transport, which is manifested in a monotonic decrease of the effective mobility between the two limiting values and, especially, in a monotonic unbounded increase of the effective diffusivity, as the dimensionless driving force grows.
To summarize, in the present paper we have demonstrated that spatial restrictions play a significant role in the diffusive transport of driven particles, potentially leading to anomalous transport properties in certain geometry designs. In particular, in a periodically compartmentalized tube, biased diffusion exhibits unusual force-induced features such as decrease of the mobility and divergence of the diffusivity. We have also shown that the statistical mechanism behind such anomalous effects is underpinned by intermittency in the transition time statistics of particle motion through the tube. These results provide a new significant insight into diffusive transport in complex geometries and may find applications in fields as diverse as drug delivery, cellular biology, materials engineering, and development of architectures and technologies for controllable mass transfer on the nanoscale.
ACKNOWLEDGMENT
We are grateful to Sergio Albeverio, Igor Goychuk, Peter Hänggi, Yuri Kondratiev, Fabio Marchesoni, Peter Talkner, and Gerhard Schmidt for the helpful discussions. Yu.A.M. and V.Yu. Z. thank the Russian Foundation for Basic Research for support (Grant No. 10-03-00393). Yu.A.M. was also partially supported by DFG (Grant 436 RUS 113/722). A.M.B. was supported by the Intramural Research Program of the NIH, Center for Information Technology. L.V.B. was partially supported by a Leverhulme Research Fellowship.
APPENDIX 1. DETAILS OF BROWNIAN DYNAMICS SIMULATIONS
In our simulations, particle trajectories were propagated by numerical integration of the dimensionless stochastic equation of motion, equivalent to eq 1, using the forward Euler algorithm. The reflecting boundary conditions were implemented as follows: if a trajectory crossed the lateral tube surface, only the last step displacement along the tube axis was accepted; if a trajectory crossed a cross-wall, only the last step displacement orthogonal to the axis was accepted. We found that different reasonable ways to implement the boundary conditions led to slightly varying results. However, the difference between the results does not exceed the accuracy of our simulations. The effective mobility and diffusivity were calculated according to the definitions given in eqs 3 and 4 as the average over 105 trajectories. The simulation data confirmed that the particle distribution over the tube cross-section remains uniform at any value of the driving force (see eq 2).
The simulations were performed at different values of the dimensionless parameters f = βFR (from 0 to 105), a/R (from 0.1 to 0.9), and l/R (from 0.1 to 2). Different values of the dimensionless time step were taken: from 10−7 at large f or small a/R and l/R to 10−5. The number of steps was also different: from 2 × 107 to 2 × 108, so that the trajectory length (the observation time) varied from 20tR to 200tR. In each simulation, the transition times between neighboring openings τ were collected and used to gain insight into the statistical properties of τ. The number of observed transitions varied from 106 (at weak forcing) to 1010 (at strong forcing).
APPENDIX 2. TRANSITION TIME STATISTICS AT ZERO FORCING
To find the desired probability density q0(τ) of the transition time τ, consider the problem of Brownian particle survival in the interval (0,l). For the particle starting at t = 0 from x = 0, the propagator G(x,t) satisfies the diffusion equation
| (A2.1) |
with the initial condition G(x,0) = δ(x) and the boundary conditions
| (A2.2) |
The effective trapping rate κ is defined by eq 6. The boundary conditions have a simple physical meaning: the boundary condition at x = 0 reflects the problem symmetry, and the radiation boundary condition at x = l models the homogenized boundary.
First, taking the Laplace transform of eq A2.1 and solving the resulting ordinary differential equation, we find the Laplace transform of the propagator. Then, using this result, the Laplace transform of the particle survival probability can be written in the form
| (A2.3) |
where R = D0/(κl). Finally, taking advantage of the relation q0(τ) = −dS(τ)/dτ, we arrive at eq 5 in the main text. From eq 5 one can find the k-th moment of τ using the relation . In particular, the first four moments, which are discussed in the text, are given by
| (A2.4) |
| (A2.5) |
| (A2.6) |
| (A2.7) |
APPENDIX 3. LIFETIME PROBABILITY DENSITY OF A BROWNIAN PARTICLE IN THE ANNULUS
Consider the problem of Brownian particle survival in the annulus bounded by two concentric circles of radii a and R > a, with absorbing (reflecting) boundary condition on the inner (outer) boundary. The probability density for finding the particle at distance ρ from the origin, a ≤ ρ ≤ R, at time t, W(ρ,t), satisfies the 2D diffusion equation
| (A3.1) |
with the initial condition , and the boundary conditions and . A solution for the probability density can be written in terms of the eigenfunctions φn(ρ) and eigenvalues ξn (n = 1,2, …) of the 2D Laplace operator Δ2D that satisfy
| (A3.2) |
The eigenfunctions are the Bessel functions of zero order of the first and second kind, J0(ξnρ) and Y0(ξnρ), respectively. The eigenvalues can be written as ξn = νn/a, where νn is the nth root of the equation26
| (A3.3) |
ordered so that νn+1 > νn > 0. The eigenfunction expansion of the probability density has the form
| (A3.4) |
where coefficients An and Bn can be found from the initial condition, and kn = (νn/a)2.
Then the survival probability of the particle, , as well as its lifetime probability density, W(t)= −dS(t)/dt, can be written as infinite sums of exponentials. At long times, the first terms in the sums are dominant, so that the lifetime probability density decays as a single exponential, W(t) exp(−k1t/tR), with the dimensionless rate k1 determined by the first eigenvalue ξ1
| (A3.5) |
where ν1 is the first (smallest in magnitude) root of eq A3.3. The values of k1 calculated from eqs A3.3 and A3.5, as well as the longtime decay rates of the transition time probability density, , obtained from simulations, are summarized in Table 2 for different values of radius ratio a/R.
REFERENCES
- (1).(a) Petersen EE. AIChE J. 1958;4:343. [Google Scholar]; (b) Michaels AS. AIChE J. 1959;5:270. [Google Scholar]; (c) Goodknight RG, Klikoff WA, Jr., Fatt I. J. Phys. Chem. 1960;64:1162. [Google Scholar]; (d) Käarger J, Ruthven DM. Diffusion in Zeolites and Other Microporous Solids. Wiley; New York: 1992. [Google Scholar]
- (2).(a) Philip JR. Aust. J. Soil Res. 1968;6:1. [Google Scholar]; (b) Pinner A, Nye PH. Eur. J. Soil Sci. 1982;33:25. [Google Scholar]
- (3).(a) Siwy Z, Kosińska ID, Fuliński A, Martin CR. Phys. Rev. Lett. 2005;94:048102. doi: 10.1103/PhysRevLett.94.048102. [DOI] [PubMed] [Google Scholar]; (b) Kosińska ID, Goychuk I, Kostur M, Schmid G, Häanggi P. Phys. Rev. E. 2008;77:031131. doi: 10.1103/PhysRevE.77.031131. [DOI] [PubMed] [Google Scholar]
- (4).(a) Hille B. Ion Channels in Excitable Membranes. 3rd Sinauer Associates; Sunderland, MA: 2001. [Google Scholar]; (b) Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. Garland; New York: 2007. [Google Scholar]
- (5).(a) Saltzman WM. Drug Delivery. Oxford Univ. Press; Oxford: 2001. [Google Scholar]; (b) Häanggi P, Marchesoni F. Rev. Mod. Phys. 2009;81:387. [Google Scholar]; (c) Ai BQ, Xie HZ, Liu LG. Phys. Rev. E. 2007;75:061126. doi: 10.1103/PhysRevE.75.061126. [DOI] [PubMed] [Google Scholar]; (d) Ai BQ. J. Chem. Phys. 2009;131:054111. doi: 10.1063/1.3200923. [DOI] [PubMed] [Google Scholar]
- (6).Zwanzig R. J. Phys. Chem. 1992;96:3926. [Google Scholar]
- (7).Reguera D, Rubí JM. Phys. Rev. E. 2001;64:061106. doi: 10.1103/PhysRevE.64.061106. [DOI] [PubMed] [Google Scholar]
- (8).Jacobs MH. Diffusion Processes. Springer; New York: 1967. [Google Scholar]
- (9).(a) Kalinay P, Percus JK. J. Chem. Phys. 2005;122:204701. doi: 10.1063/1.1899150. [DOI] [PubMed] [Google Scholar]; (b) Kalinay P, Percus JK. Phys. Rev. E. 2005;72:061203. doi: 10.1103/PhysRevE.72.061203. [DOI] [PubMed] [Google Scholar]; (c) Kalinay P, Percus JK. Phys. Rev. E. 2006;74:041203. doi: 10.1103/PhysRevE.74.041203. [DOI] [PubMed] [Google Scholar]; (d) Kalinay P, Percus JK. Phys. Rev. E. 2008;78:021103. doi: 10.1103/PhysRevE.78.021103. [DOI] [PubMed] [Google Scholar]
- (10).(a) Reguera D, Schmid G, Burada PS, Rubí JM, Reimann P, Häanggi P. Phys. Rev. Lett. 2006;96:130603. doi: 10.1103/PhysRevLett.96.130603. [DOI] [PubMed] [Google Scholar]; (b) Burada PS, Schmid G, Reguera D, Rubí JM, Häanggi P. Phys. Rev. E. 2007;75:051111. doi: 10.1103/PhysRevE.75.051111. [DOI] [PubMed] [Google Scholar]; (c) Burada PS, Schmid G, Talkner P, Häanggi P, Reguera D, Rubí JM. BioSystems. 2008;93:16. doi: 10.1016/j.biosystems.2008.03.006. [DOI] [PubMed] [Google Scholar]; (d) Burada PS, Häanggi P, Marchesoni F, Schmid G, Talkner P. ChemPhysChem. 2009;10:45. doi: 10.1002/cphc.200800526. [DOI] [PubMed] [Google Scholar]; (e) Burada PS, Schmid G, Häanggi P. Phil. Trans. R. Soc. A. 2009;367:3157. doi: 10.1098/rsta.2009.0068. [DOI] [PubMed] [Google Scholar]; (f) Schmid G, Burada PS, Talkner P, Häanggi P. Adv. Solid State Phys. 2009;48:317. [Google Scholar]
- (11).(a) Berezhkovskii AM, Pustovoit MA, Bezrukov SM. J. Chem. Phys. 2007;126:134706. doi: 10.1063/1.2719193. [DOI] [PubMed] [Google Scholar]; (b) Dagdug L, Vazquez M-V, Berezhkovskii AM, Bezrukov SM. J. Chem. Phys. 2010;132:034707. doi: 10.1063/1.3431756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).(a) Berezhkovskii AM, Zitserman V. Yu., Shvartsman SY. J. Chem. Phys. 2003;118:7146. [Google Scholar]; (b) Ibid. 2003;119:6991. [Google Scholar]
- (13).Laachi N, Kenward M, Yariv E, Dorfman KD. Europhys. Lett. 2007;80:5009. [Google Scholar]
- (14).(a) Stratonovich RL. Radiotekh. Elektron. 1958;3:497. [Google Scholar]; (b) Risken H. The Fokker-Planck Equation. Springer; Berlin: 1984. [Google Scholar]
- (15).(a) Reimann P, Van den Broek C, Linke H, Häanggi P, Rubi JM, Pérez-Madrid A. Phys. Rev. Lett. 2001;87:010602. doi: 10.1103/PhysRevLett.87.010602. [DOI] [PubMed] [Google Scholar]; (b) Van den Broek C, Linke H, Häanggi P, Rubi JM, Pérez-Madrid A. Phys. Rev. E. 2002;65:031104. doi: 10.1103/PhysRevE.65.031104. [DOI] [PubMed] [Google Scholar]; (c) Lindner B, Kostur M, Schimansky-Geier L. Fluct. Noise Lett. 2001;1:R25. [Google Scholar]; (d) Constantini G, Marchesoni F. Europhys. Lett. 1999;48:491. [Google Scholar]
- (16).Berezhkovskii AM, Dagdug L, Makhnovskii Yu. A., Zitserman V. Yu. J. Chem. Phys. 2010;132:221104. doi: 10.1063/1.3451115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Berezhkovskii AM, Dagdug L. J. Chem. Phys. 2010;133:134102. doi: 10.1063/1.3489375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).(a) Marchesoni F. J. Chem. Phys. 2010;132:166101. doi: 10.1063/1.3402779. [DOI] [PubMed] [Google Scholar]; (b) Marchesoni F, Savel’ev S. Phys. Rev. E. 2009;80:011120. doi: 10.1103/PhysRevE.80.011120. [DOI] [PubMed] [Google Scholar]; (c) Borromeo M, Marchesoni F. Chem. Phys. 2010;75:536. [Google Scholar]
- (19).Grigoriev IV, Makhnovskii Yu. A., Berezhkovskii AM, Zitserman V. Yu. J. Chem. Phys. 2002;116:9574. [Google Scholar]
- (20).(a) Berezhkovskii AM, Makhnovskii Yu. A., Monine MI, Zitserman V. Yu., Shvartsman SY. J. Chem. Phys. 2004;121:11390. doi: 10.1063/1.1814351. [DOI] [PubMed] [Google Scholar]; (b) Makhnovskii Yu. A., Berezhkovskii AM, Zitserman V. Yu. J. Chem. Phys. 2005;122:236102. doi: 10.1063/1.1930827. [DOI] [PubMed] [Google Scholar]; (c) Muratov CB, Shvartsman SY. Multiscale Model. Simul. 2008;7:44. [Google Scholar]; (d) Berezhkovskii AM, Barzykin AV, Zitserman V. Yu. J. Chem. Phys. 2009;131:224110. doi: 10.1063/1.3271998. [DOI] [PMC free article] [PubMed] [Google Scholar]; (e) Makhnovskii Yu. A., Berezhkovskii AM, Zitserman V. Yu. Chem. Phys. 2010;367:110. doi: 10.1016/j.chemphys.2010.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).(a) Zeldovich Ya. B., Molchanov SA, Ruzmaikin AA, Sokolov DD. Sov. Phys. Usp. 1987;30:353. The notion of intermittency was originally coined in hydrodynamics to describe alternation between long periods of a seemingly regular (laminar) behavior and unpredictable short bursts. Later on, it was made popular in dynamical systems theory and nonlinear science, referring to the emergence of highly irregular spatiotemporal structures, featured by a hierarchy of extremely high sparse peaks on a relatively lowprofile background. Intermittency is typical of complex systems and processes in many areas. One can find detailed discussion of various forms of intermittency in. [Google Scholar]; (b) Zeldovich Ya. B., Ruzmaikin AA, Sokolov DD. The Almighty Chance. World Scientific; Singapore: 1990. [Google Scholar]
- (22).Berezhkovskii AM, Monine MI, Muratov CB, Shvarts-man SY. J. Chem. Phys. 2006;124:036103. doi: 10.1063/1.2161196. [DOI] [PubMed] [Google Scholar]
- (23).(a) Makhnovskii Yu. A., Zitserman V. Yu., Berezhkovskii AM. Russ. J. Phys. Chem. B. 2009;3:313. [Google Scholar]; (b) Makhnovskii Yu. A., Berezhkovskii AM, Zitserman V. Yu. J. Chem. Phys. 2009;131:104705. [Google Scholar]
- (24).Berezhkovskii AM. Chem. Phys. 2010;370:253. doi: 10.1016/j.chemphys.2009.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).(a) Taylor GI. Proc. R. Soc. (London) 1953;219:186. A. [Google Scholar]; (b) Aris R. Proc. R. Soc. (London) 1956;235:67. A. [Google Scholar]
- (26).Crank J. The Mathematics of Diffusion. 2nd Clarendon Press; Oxford: 1975. [Google Scholar]