Architecture and Connectivity Govern Actin Network Contractility

SUMMARY

Actomyosin contractility plays a central role in a wide range of cellular processes, including the establishment of cell polarity, cell migration, tissue integrity, and morphogenesis during development. The contractile response is variable and depends on actomyosin network architecture and biochemical composition. To determine how this coupling regulates actomyosin-driven contraction, we used a micropatterning method that enables the spatial control of actin assembly. We generated a variety of actin templates and measured how defined actin structures respond to myosin-induced forces. We found that the same actin filament crosslinkers either enhance or inhibit the contractility of a network, depending on the organization of actin within the network. Numerical simulations unified the roles of actin filament branching and crosslinking during actomyosin contraction. Specifically, we introduce the concept of “network connectivity” and show that the contractions of distinct actin architectures are described by the same master curve when considering their degree of connectivity. This makes it possible to predict the dynamic response of defined actin structures to transient changes in connectivity. We propose that, depending on the connectivity and the architecture, network contraction is dominated by either sarcomeric-like or buckling mechanisms. More generally, this study reveals how actin network contractility depends on its architecture under a defined set of biochemical conditions.

Graphical abstract

INTRODUCTION

Actomyosin contractility plays a central role in a wide range of cellular processes including the establishment of cell polarity, cell migration, tissue integrity, or morphogenesis during development [1, 2]. Contraction is generated by myosin molecular motors that exert forces on actin filaments [3–6]. This active process is complex, in part because actin filaments in contractile networks are assembled in a variety of dynamic organized structures that undergo continuous assembly, disassembly, and overall reorganization [7, 8]. Actomyosin contractility can be reproduced using cell extracts [9, 10] or reconstituted systems [4, 5, 11–14]. In parallel, the molecular mechanism of single myosin motors has been studied extensively over the last decades [15]. Three principal mechanisms of contractility have been proposed for actin filament networks: (1) a sarcomeric-like model, where filaments slide because of structural asymmetry that originates from motor processivity, crosslinker distribution [16, 17] or from contractile versus expansile state stability [18]; (2) an actin filament treadmilling model, where contractility depends on actin filament turnover [19]; and (3) a buckling model, where contractility depends on the mechanical deformation of actin filament under the force exerted by the myosin [20]. However, little is known about how the architecture of the actin structure influences contraction, the molecular mechanism of contraction in complex actin structures, or how network dynamic reorganization affects its deformation.

In a cellular context, actin filaments can be roughly assembled into three categories of dynamical structures, each of them performing specific functions: (1) a nearly orthogonal network at the leading edge of motile cells; (2) parallel bundles in filipodia type of membrane protrusions or at adhesion sites; and (3) anti-parallel contractile actin fibers in the cell cytoplasm [21]. Lamellipodia and filipodia types of actin organization have been extensively studied using a combination of biochemical and cell-biological approaches [21–23]. Although a general consensus emerges from these studies on the mechanism of force generation by actin polymerization and how this can deform or protrude the plasma membrane [21, 24, 25], the role of actomyosin interaction in the remodeling of these structures is far less characterized. Moreover, the mechanism of contraction, which depends on the organization of actin filaments, is largely unknown.

Here, we used our ability to generate well-defined actin organization using surface micropatterning of actin Nucleating Promoting Factor (NPF) [26, 27], to challenge the actin-geometrical principles ruling contractility. We found that the rate of the macroscopic actin deformation due to myosin-contraction depends on network architecture (disordered branched networks, ordered or disordered bundles). Using numerical simulations, we established that in addition of filaments organization, network connectivity modulates the contractile response. We determined the mechanism of contraction leading to macroscopic deformation for the different actin architectures and how it depends on the degree of network connectivity. Finally, using our model, we predicted how dynamic transition upon actin organization can modulate the actomyosin contractile response and validated these predictions using a new experimental system allowing the dynamic and reversible modulation of actin organization during contraction.

RESULTS

Contractile Response of Different Actin Organizations

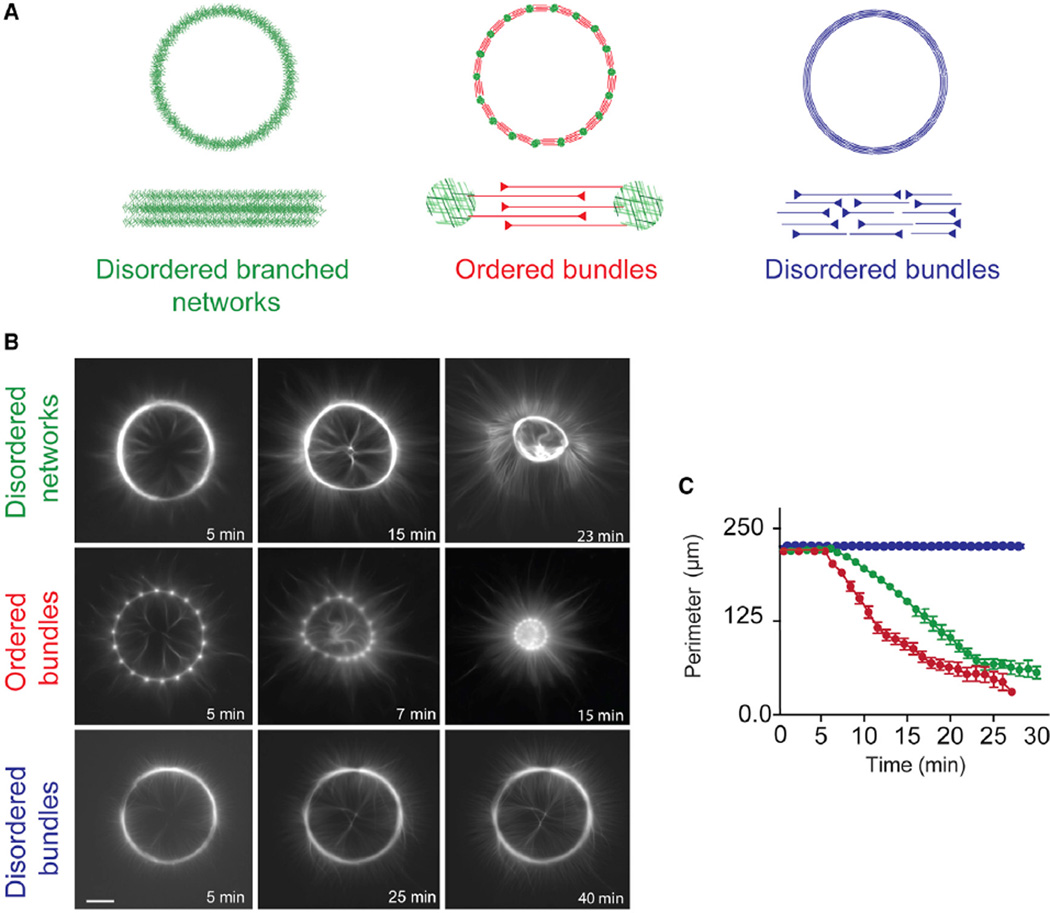
Cellular actin filaments assemble into a variety of structures that are distinct with respect to the orientation of the filaments, as well as their connectivity (ability of one filament to be linked to another filament) [21, 23, 28]. The organization of actin filaments modulates the contractile response of a network. For example, branched networks are less contractile than bundles of anti-parallel filaments [6]. Here, we investigate the factors that govern the coupling between filament spatial arrangement and the degree of crosslinking in the regulation of actomyosin contraction. We evaluated the contractile response of various in vitro reconstituted actin structures, that are branched or not, and in which filaments are either of mixed polarity, or prominently antiparallel (Figure 1). To obtain such diversity in actin architecture, we used surface micropatterning to initiate geometrically controlled actin assembly over 70-µm-wide rings [26]. In this assay, well-defined surfaces coated with Actin Promoting Factor (NPF) trigger actin assembly in a reaction chamber containing a mixture of proteins including the Arp2/3 complex, actin, and profilin. Throughout this study, we varied the architecture and biochemical composition of the overall ring-like network. The perimeter was used as a simple and global readout of contractility (Figure 1).

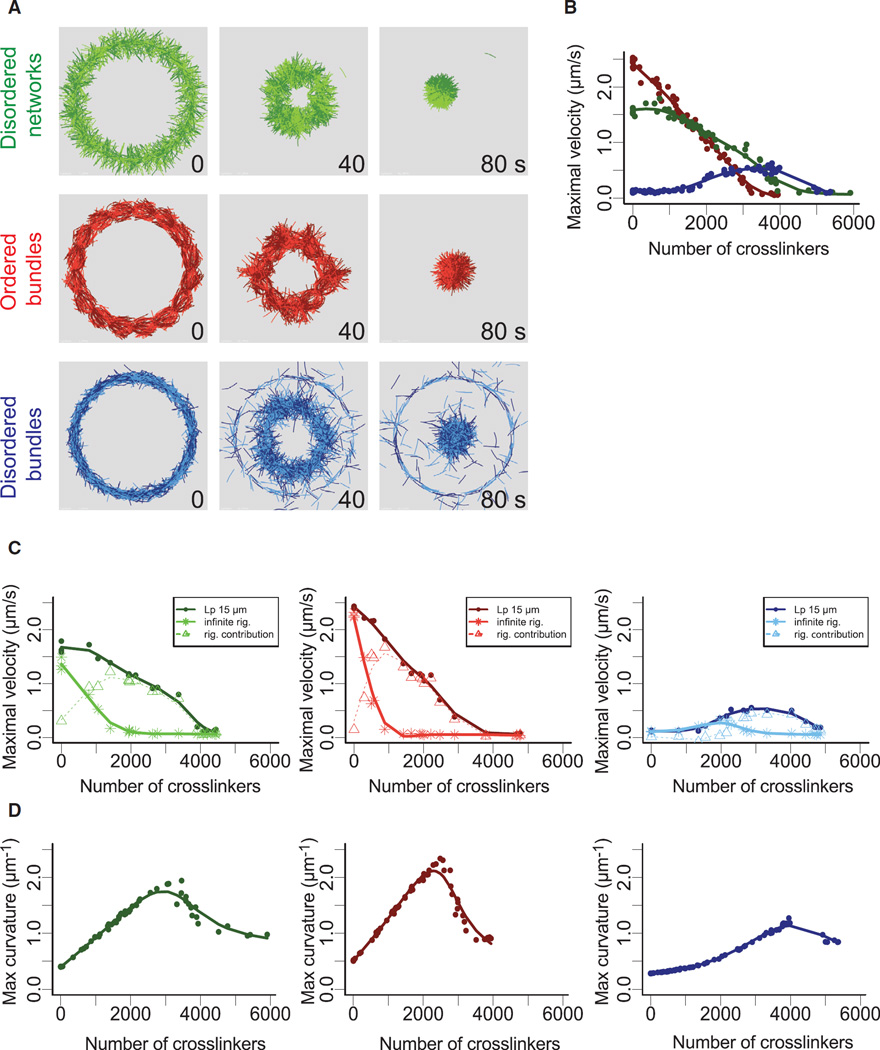
Figure 1. Architecture-Dependent Contractility of Actin Rings.

(A) Schematic representation of the different types of actin architecture: disordered networks, ordered bundles, and disordered bundles, respectively.

(B) Contraction dynamics of the different actin rings, induced by myosin motors. Time is indicated in each picture. Scale bar, 25 µm.

(C) Measured ring perimeter, for each type of ring, as a function of time. The disordered networks (green) and ordered bundles (red) both contract within a few minutes following assembly, whereas disordered bundles (blue) are not contractile within the same time interval. Each curve was obtained by averaging over a dozen of different patterns. Error bars represent SEM. Conditions: 2 µM actin, 6 µM profilin, 100 nM Arp2/3 complex, and 16 nM myosin VI. 300 nM ADF/cofilin was added to the reaction to obtain the ring made of disordered bundles.

See also Figure S1 and Movies S1, S2, and S3.

We generated rings made of three different architectures (Figure 1A) that span the diversity of cellular contractile structures: (1) disordered branched networks (named: disordered networks) mimicking lamella-like structures were assembled from a full ring coated with NPF (Figure 1A, left panel); (2) a series of interconnected, ordered, antiparallel actin bundles (named: ordered bundles), mimicking sarcomeric-like bundles, were generated by a dotted ring where only the dots were coated with NPF (Figure 1A, middle panel); and (3) disordered, mixed polarity actin bundles (named: disordered bundles), mimicking cytokinesis ring-like bundles, were generated by debranching the disordered branched meshwork described above by addition of ADF/cofilin (Figures 1A, right panel, and S1; Movie S1 [for the illustration of ADF/cofilin debranching activity]). The deformation of these actin networks was triggered by the presence of double-headed (heavy-meromyosin (HMM)-like) myosin VI in the reaction mixture. Myosin VI-HMM [6] is a pointed-end directed processive molecular motor [29]. Unlike myosin II, it can trigger continuous contraction and/or filament sliding (Movie S2) without the need to assemble into minifilaments. To generate significant force, myosin VI-HMM must tether two neighboring filaments and slide them with respect to one another (Movie S2). Of course, myosin VI-HMM could stay on a single actin filament for most of the time and act on separate filaments for a small fraction of total stepping events. Thus, using myosin VI-HMM has the advantage that it yields in unprecedented reproducibility of the contractile response, unlike myosin II-based minifilaments, which often vary in length when reconstituted in vitro [6].

The contraction of actin rings by myosins follows three phases [6]: an initial phase corresponding to actin assembly and reorganization by myosins, a second phase characterized by a constant and often fast rate of contraction, and a final phase where actin is slowly compacted at the center of the ring. We measured the contraction rate during the second phase, to quantify the contractile behavior of all systems. This readout was highly reproducible across experiments.

Two types of rings contracted: the rings made of disordered branched networks and the rings made of ordered antiparallel bundles (Figure 1B, top and middle rows). Consistent with previous observations [6], the rings made of ordered antiparallel bundles contract faster than the ones made of branched networks (Figure 1C, cf. green and red curves; Movie S3, cf. top row, left and middle rings). In contrast, the third type of rings, corresponding to disordered bundles, deforms very little over time (Figures 1B, bottom row, and 1C, blue curve; Movie S3, top row, right ring).

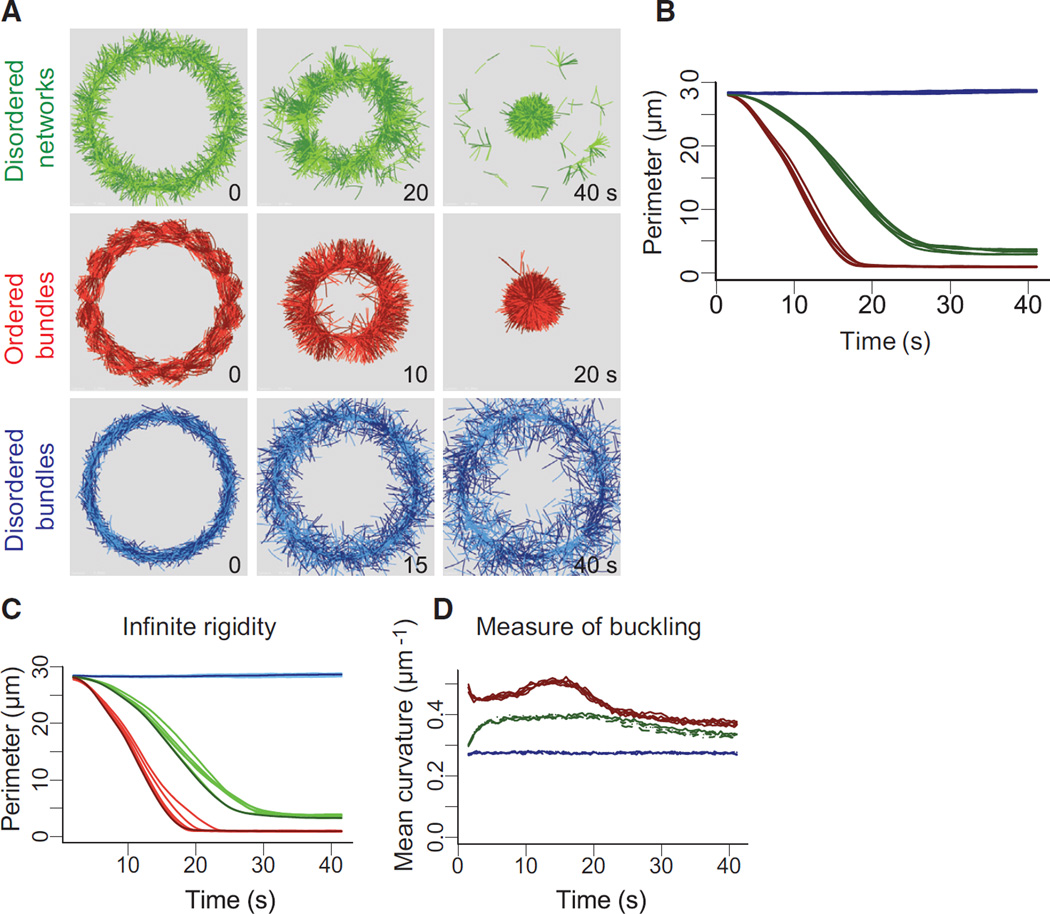
To understand how different actin architectures respond to myosin-induced contraction, we performed detailed simulations of the different types of actin rings—disordered network, disordered and ordered bundles using Cytosim (Figures 2A and S2A; Movie S4; [30, 31]). We implemented our simulation with entities mimicking molecular motors with properties similar to myosin VI (Figures 2A and S2B). Thereby, we could reproduce in silico the diversity of contractile response for various actin architectures (Figures 2A and S2A; Movie S4, left panel, top row) and track individual actin filaments during ring evolution (Movie S4, left panel, bottom row). Disordered bundles do not contract but are nevertheless dynamic. Filaments in them slide with respect to one another (Figure 2A; Movie S4, left panel, bottom row, right ring), leading to local polarity sorting (see Movie S5 for an illustration of this mechanism), suggesting that myosin-produced forces are not transduced into contractile dipoles in this structure. In contrast, inter-connected filaments in disordered network and ordered bundles directly lead to whole-ring contraction (Movie S4, left panel, left and middle rings). The variation of the ring perimeter over time in our simulation was qualitatively similar than in the experiments, in that rings of ordered bundles contract faster than rings of disordered networks and rings made of disordered bundles did not contract (Figure 2B).

Figure 2. Simulation of Architecture-Dependent Contractility of Actin Rings.

(A) Simulated contractility of actin rings with different architectures. The essential features of the three types of actin rings were constructed within the cytosim platform (green, disordered network; red, ordered bundles; blue, disordered bundles) and simulated (see text). The diameter of the rings is 9 µm.

(B) Measured ring perimeter, for each type of ring, as a function of time. The simulated dynamics of ring contraction in the presence of motors were generated from ten simulations in each case.

(C) Effect of polymer rigidity on ring deformation. Simulations were identical as in (A) but with an infinite polymer rigidity. Dark curves correspond to Lp = 15 µm. Light curves were obtained with straight filaments, corresponding to infinite Lp.

(D) Estimation of actin filaments buckling during ring deformation. The curvature (inverse of the radius of curvature) was determined as the average filament curvatures for the entire ring (see Experimental Procedures).

See also Figures S2 and S3 and Movie S4.

Three major mechanisms have been proposed to explain the macroscopic network contraction from the microscopic details: (1) a “sarcomeric-like mechanisms” where the distribution of the crosslinkers and motors are polarized along the actin filaments (see Movie S5 for an illustration of this mechanism and [16]); (2) a “buckling mechanisms” where contraction arises after actin filament mechanical deformation generated by motor contraction see Movie S5 for an illustration of this mechanism and [20]; and (3) a more recent “dynamic mechanism” where contraction emerge by the combined effect of actin turnover and crosslinking [19]. Since our simulations do not need to include actin turnover to obtain macroscopic deformation, we focused on the first two mechanisms. We do not expect major turnover in the experimental conditions, but, since high myosin concentration can induce actin disassembly [6, 32], it will be interesting to investigate in the future if in these conditions the dynamic model would contribute to global deformation.

To discriminate between sarcomeric-like and buckling models during ring contraction, we tested the effect of the polymer rigidity (Figure 2C). Indeed, increasing polymer rigidity should have a minimum impact if ring contraction is dominated by a sarcomeric-like model, where a high polymer rigidity should inhibit contraction driven by buckling. Our simulation revealed that polymer with infinite rigidity (Lp = ∞) support similar ring contraction than polymer with a Lp = 15 µm (cf. Figures 2B and 2C). This suggests that in these conditions ring contraction for the disordered networks and ordered bundles is mainly driven by a sarcomeric-like mechanism. This was further confirmed by the low degree of filament buckling during ring contraction in our simulations (Figure 2D). Other parameters such as motor binding range, actin filament lengths, ring perimeters, and number of myosins can also affect the contractile response but not the qualitative behavior of the different architectures (Figure S3).

α-Actinin Modulates the Contractile Response of Different Actin Organizations

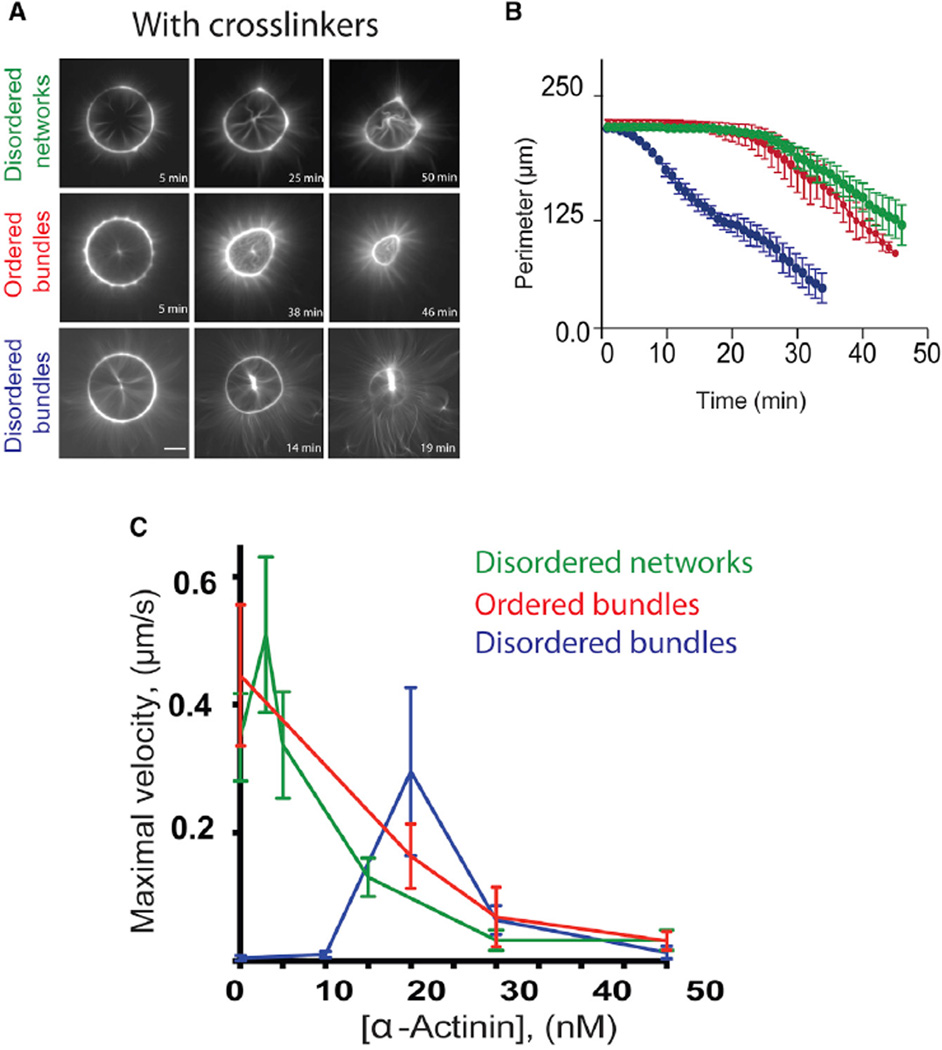
Filament inter-connection in cells is achieved with the help of crosslinking proteins such as α-actinin, fascin, and filamin [33]. Strikingly, non-deforming rings comprising disordered fibers become contractile when α-actinin is added (Figures 3A, bottom row, and 3B, blue curve; Movie S3, bottom row, right). In marked contrast, α-actinin impairs the contraction of the other types of rings (Figures 3A, top and middle rows, and 3B, green and red curves; Movie S3, bottom row, left and middle rings). Therefore, the effects of α-actinin on ring deformation depend on their architecture. Ring deformation also depends on the α-actinin concentration (Figure 3C). In our experimental condition with 2 µM actin monomers, the maximal rate of ring contraction of the disordered network (Figure 3C, green curve) was first increased by low concentration (3 nM) of α-actinin and then decreased progressively for higher α-actinin concentrations (ranging from 5 to 30 nM) displaying undetectable deformation at high α-actinin concentration (>30 nM) over the timescale of our measurements. Increasing the concentration of α-actinin (Figure 3C, red curve) progressively lowered the maximal deformation rate of ordered bundles. At high concentrations (>30 nM), α-actinin blocked the deformation of all types of actin architectures. The complex effect of α-actinin on the rate of myosin-induced contraction in different actin architectures suggests that both the filament organization and their physical interaction are key parameters governing the contractile response. Unfortunately, these parameters cannot be measured experimentally. We could, however, use numerical simulation to study how the amount of crosslinkers and branches affect actomyosin contraction.

Figure 3. Effects of α-Actinin on the Contractility of Actin Rings.

(A) Contraction of one representative example of each actin ring, in the presence of α-actinin: (top row) 15 nM α-actinin for the disordered network; (middle and bottom rows) 20 nM α-actinin for both the ordered and disordered bundles.

(B) Normalized ring perimeters as a function of time are represented. Note that addition of α-actinin induces the disordered bundle ring to contract, whereas it decelerates contraction of the other rings.

(C) Maximal perimeters decrease speed for each type of network, as a function of the concentration of α-actinin. A dozen of ring perimeters were measured as a function of time for each architecture and each α-actinin concentration, and the extracted maximum speeds were averaged. Error bars represent SEM. Conditions: same as in Figure 1 but with addition of α-actinin.

See also Movie S3.

The Mechanism of Ring Contraction Depends on the Number of Crosslinkers

To the simulations containing myosin entities, we added structural elements connecting two actin filaments thereby representing the contribution of α-actinin to the system (Figures 4A and S2B, bottom panel). We then calculated the maximal contraction velocity as a function of the crosslinker number for the three types of ring architectures (Figure 4B). The number of crosslinkers in our simulations ranged from 0 to 6,000, corresponding at most to one crosslinker every 320 nm along filaments, on average. This range is similar to that in our experimental conditions. The contraction rate of the disordered networks, ordered bundles, and disordered bundles (respectively, green, red, and blue; Figure 4B) were qualitatively similar to those obtained experimentally (Figure 3C), indicating that our simulations had reliably modeled the role of filament crosslinkers on the various actin architectures.

Figure 4. Mechanism of Ring Deformation in Presence of Crosslinkers.

(A) Snapshots of simulated actin rings with different architectures: branched network (green), ordered bundles (red), disordered bundles (blue) in presence of 2,500 crosslinkers representing α-actinin.

(B) Maximal rate of ring perimeter decrease, as a function of the number of crosslinkers for each type of ring.

(C) Effect of polymer rigidity on ring deformation. Simulations were performed for two different polymer rigidities (Lp = 15 µm dark curve and ∞ Lp light curve) for the different types of actin architecture as indicated in the different panels. The dashed curves correspond at the difference between the curves for Lp = 15 µm and infinite Lp, respectively.

(D) Estimation of maximal actin filaments buckling during ring deformation. The maximal curvature over time was determined according to filaments curvature (inverse of curvature radius) for the entire ring.

See also Figure S2 and Movies S4 and S5.

To establish the preferred ring contraction mechanism of α-actinin crosslinked networks, we evaluated how the maximal velocity depends on the filament rigidity and crosslinker density (Figure 4C). In contrast to the behavior observed in the absence of crosslinker, the filament rigidity has a major impact of the maximal velocity (cf. Figure 4C, curve Lp~15 µm and Lp~∞). Indeed, the maximal velocity of networks comprising filaments with infinite rigidity drop rapidly with the concentration of crosslinkers, for both disordered networks and ordered bundles (cf. to Lp~15 µm). This shows that buckling is required to allow contraction and suggests that the buckling mechanism is at play under crosslinked conditions. The difference between the curves (Lp~15 µm and Lp~∞) of maximal velocity versus number of crosslinkers illustrated by the dotted curve readily illustrates the rigidity and buckling contributions to contraction (Figure 4C). Contraction of disordered networks and ordered bundles at low crosslinker density is dominated by the sarcomeric-like mechanism. The contribution of buckling to the contraction increased with the crosslinker density and became the main contraction mechanism at intermediate crosslinker concentrations. High concentrations of crosslinkers inhibit filament buckling and therefore reduce the maximal velocity of ring contraction (Figure 4C). For the disordered bundles configuration, the situation is different since its native architecture lacks connection. Therefore, the mechanism driven by myosin switches from polarity sorting at low crosslinker concentrations to buckling at a number of crosslinkers higher than 2,000. High numbers of crosslinkers also inhibit buckling of disordered bundles, and, as a result, ring contraction. To further validate the contribution of the buckling during ring contraction, we measured the maximal filament curvature as a function of the number of crosslinkers for the three different actin organization (Figure 4D). In agreement with our above statement, the maximum curvature of the filament increases for the three type of actin organization as a function of the number of crosslinkers to reach a maximum and then decreases at high number of crosslinkers.

Connectivity Regulates Network Contraction in a Biphasic Manner

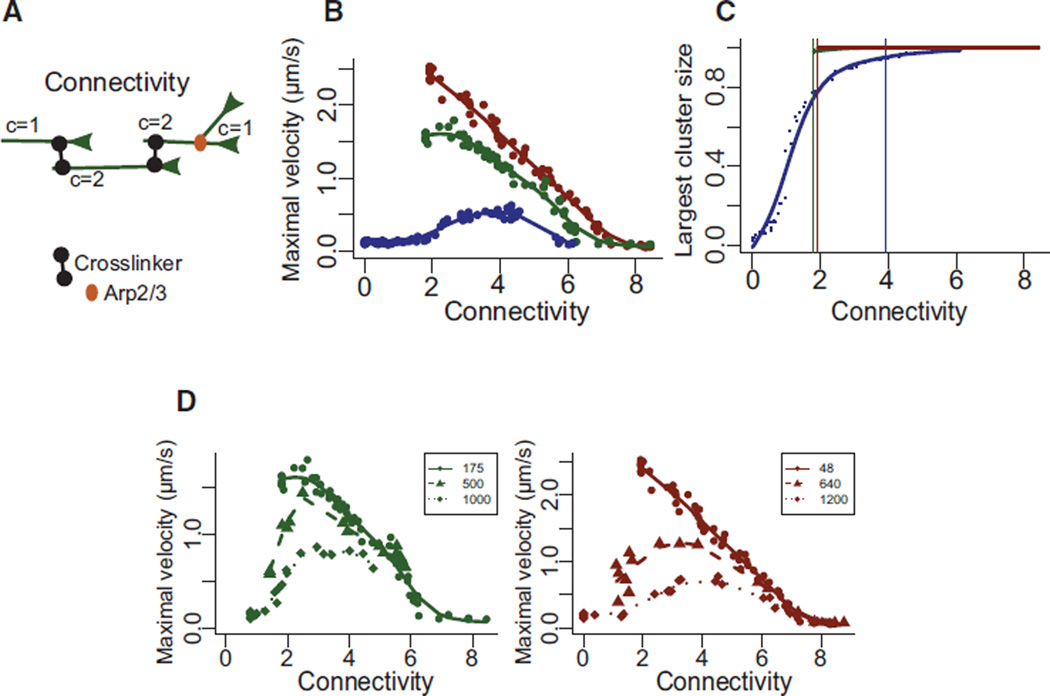
Both crosslinkers and branches act as filaments connectors [11, 34]. We then estimated the global degree of “connectivity,” defined as the average number of connectors per actin filament (Figure 5A, generated by the Arp2/3 complex at branched point and by the bridge made by α-actinin between two filaments). By plotting the contraction velocity with respect to the connectivity for the different actin organizations (Figure 5B), we found that they all reach a maximum centered on an optimal connectivity comprised between 2 and 4. This value corresponds to the percolation threshold (transition point from which all filaments are connected together in one single cluster (Figure 5C; [4]). Below 2 (non-percolated network), many filaments may be unconnected inside the structure. Thus, the deformation is dominated by local events but do not lead to global network contraction. Above 4, filaments get partially or totally blocked and can no longer be moved by myosins. The first important insight gained from this analysis was that Arp2/3 complex is a more efficient connector than α-actinin. By essence, for any given pair of filaments, there can be only one Arp2/3 connection, whereas multiple α-actinin connections are possible. Thus, in terms of percolating the network, Arp2/3 complex entities are more potent than α-actinin crosslinks, because some of the later may be connecting filaments that are already linked otherwise (Figure 5A, branched versus crosslinked connectivity). The second important insight is that, in parallel to curve shape regulation, the contraction rate also depends on the network organization (Figure 5B) and is maximal for ordered bundles (red curve), intermediate for the disordered network (green curve), and minimal for disordered bundles (blue curve). Indeed, ordered bundles have an optimal actin architecture in which filaments are perfectly aligned, oriented, and properly anchored at their pointed ends, allowing efficient transmission of local myosin work throughout the entire structure without adding frictional constraints along the filament. On the other hand, randomly oriented filaments in disordered branched networks resist deformation and are inefficient at propagating myosin-induced translocation. In disordered bundles, a significant fraction of the myosins are not productive, or their work is dissipated in motor displacement rather than filament sliding. Accordingly, both the degree of connectivity and the spatial organization of filaments regulate overall actomyosin response. However, we were not able to directly compare the three different organizations for connectivity values below 2 because the connection made by the Arp2/3 complex in disordered networks (green) and ordered bundles (red) already exceeds this value (Figure 5B). We therefore decrease the number of branches by increasing the number of “primers” in our simulation to maintain the number of filaments constant (Figure 5D). In this case, the contraction velocity with respect to the connectivity for disordered network and ordered bundles forms a bell-shaped curve similarly to disordered bundles organization (Figure 5D, green and red curves). This behavior further confirms that both the architecture and connectivity have an important contribution during contraction.

Figure 5. Connectivity Modulates the Contractile Response of Actin Rings.

(A) Schematic illustration (left) of the connectivity C of different actin filament generated by the Arp2/3 complex (red symbols) and α-actinin (black symbols). The network connectivity is the average of all filament connectivity values. It is expected to increase as a function of the number of connecting crosslinkers present in the system (right).

(B) Maximal velocity of perimeter deformation for the different actin rings as a function of the network connectivity.

(C) Size of the largest percolating cluster (normalized to the total number of actin filaments) as a function of the network connectivity, for branched network (green), ordered bundles (red), and disordered bundles (blue). Vertical lines indicate the threshold at which percolation is considered reached (i.e., 95% of filaments are connected).

(D) Variation of the maximal velocity for a define ring architecture (disordered networks green, ordered bundles red) with different initial configuration (variable number of primers for disordered networks green or ordered bundles red, see Experimental Procedures) as a function of the network connectivity.

Dynamic Modulation of Actin Network Connectivity

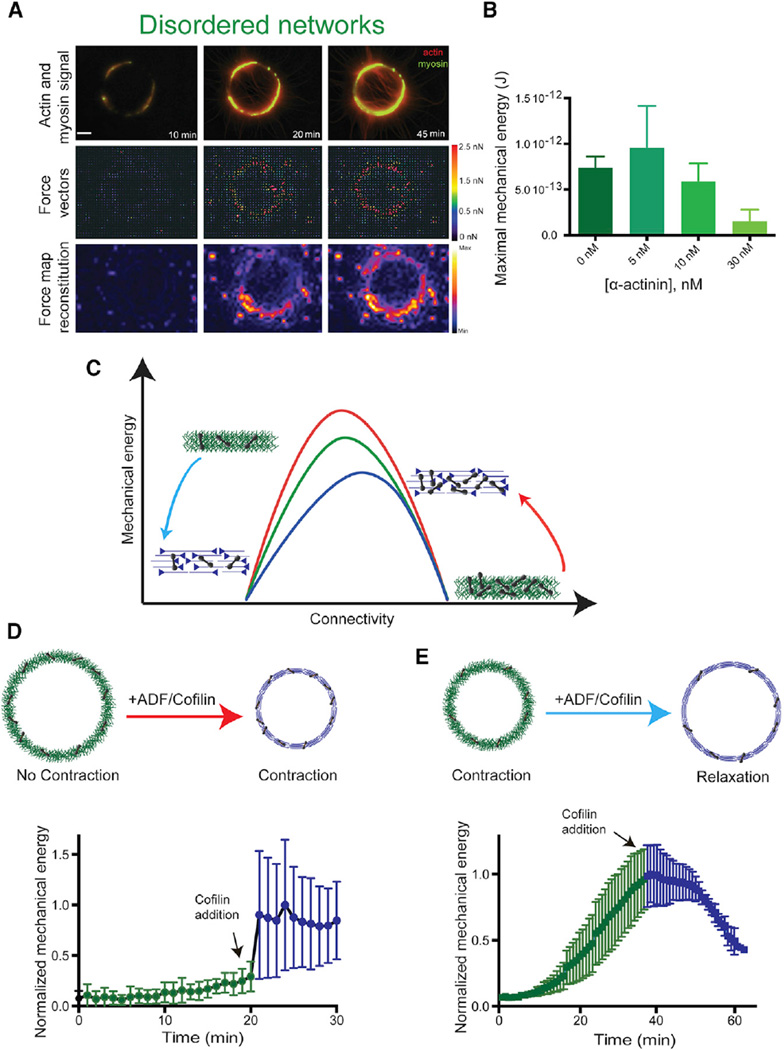
Interestingly, filament connectivity and conformation in adherent motile cells vary as the network evolves from filament nucleation at the cell periphery to filament alignment and crosslinking in transverse arcs, up to filament disassembly in the cell interior [35]. Our work suggests that contractility could change accordingly during these dynamic architectural transitions. Investigating the contractile response of dynamic actin organization required an experimental system where the degree of connectivity or/and the actin filament organization could be modulated over time. One limitation in our initial experimental setup described above is that ring contraction is rapid and the structure collapses when the connectivity is optimal (2–3) or disassembles with minimum deformation when the connectivity is higher than 4. Our ability to modulate the network composition with this setup is therefore limited. To circumvent this limitation, we developed a new method to assemble controlled actin organizations on soft polyacrylamide gels (Figure S4A; [27]). The behavior of actin structures on soft substrate differs drastically from what was previously described with hard substrate. On soft gels, actin rings contract and deform the underlying substrate without detaching from it (Figures 6A and S4B). In these conditions, actin networks do not collapse and disassemble as on hard substrate. Rather, they are maintained in a tensed steady state. By sequentially changing the biochemical conditions, the networks in such steady states are then amenable to dynamic changes. Because the polyacrylamide gels were produced with a defined rigidity, the forces exerted by the various actin structures on the substrate upon myosin-addition could be measured with traction force microscopy (Figures 4A and S4B). Consistent with the variation of the contractile response on hard substrate (Figure 3C), increasing concentrations of α-actinin first enhances (Figures 5 and 6B; 5 nM α-actinin, disordered network) then decreases (Figure 6B; 10 and 30 nM α-actinin) the magnitude of tension forces, resulting in a bell-shape curve for the variation of the mechanical energy in function of the concentration of α-actinin. To modify the connectivity in real time, we designed an open reaction chamber (Figure S4C) that is placed on top of the soft patterned surface. Because of its bell-shape response curve, our numerical model predicts that a given reduction of connectivity can have opposite effects on tensional forces depending of the initial level of network connectivity (Figure 6C). Indeed, if the contractile structure has a high degree of connectivity, a decrease in connectivity should enhance contraction (Figure 6C, red arrow). In contrast, if the structure has an optimal degree of connectivity, reductions in connectivity should block the network deformation and reduce contractility (Figure 6C, blue arrow). We tested these predictions experimentally using ADF/cofilin ability to debranch Arp2/3 network and slightly sever actin filaments, in order to modulate ring connectivity as it contracted (Figures 6D and 6E). As predicted, addition of ADF/cofilin to a highly connected structure increased the magnitude of the contractile forces (Figure 6D). In contrast, addition of ADF/cofilin to an actin organization with optimal connectivity reduced the magnitude of tensional forces (Figure 6E). These experiments showed how the dynamic reorganization of actin network architecture could modulate the contractile mechanical response over time.

Figure 6. Dynamic Variations of Actin Network Connectivity.

(A) Contraction of a branched network ring on a patterned deformable substrate. Combined fluorescence images (top row) show actin and myosin signals, while second and third rows show the corresponding force vectors and the force map reconstitution.

(B) Maximal mechanical energy of the actin disordered branched network, for the indicated α-actinin concentrations. The maximal mechanical energy is defined as the maximal deformation that ring contractions cause on their substrate.

(C) Qualitative contractile behavior for the three different actin rings, as a function of the network connectivity, as predicted by the model (Figure 3D). The red arrow illustrates the effect of reducing connectivity in a highly connected actin network, while the blue arrow indicates a reduction of connectivity in a network with optimal connectivity. The contractility is enhanced in the shift represented by the red arrow, whereas it is reduced in the blue arrow.

(D and E) Cartoon representations (top) of the actin architectures before and after addition of ADF/cofilin and kinetic of the normalized total network mechanical energy as a function of time (bottom). In (D), a highly crosslinked branched actin network (100 nM α-actinin) was de-branched by addition of 100 nM ADF/cofilin. This configuration corresponds to the red arrow. In (E), a network with nearly optimal connectivity (10 nM α-actinin) is debranched by addition of 100 nM ADF/cofilin. This configuration corresponds to the blue arrow. See also Figure S4.

DISCUSSION

In this study, we have investigated the role of network architecture in the contractile response to myosin activity.

Variation in Actomyosin Contractile Response

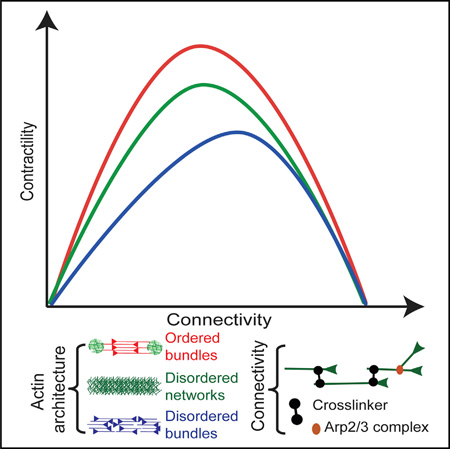
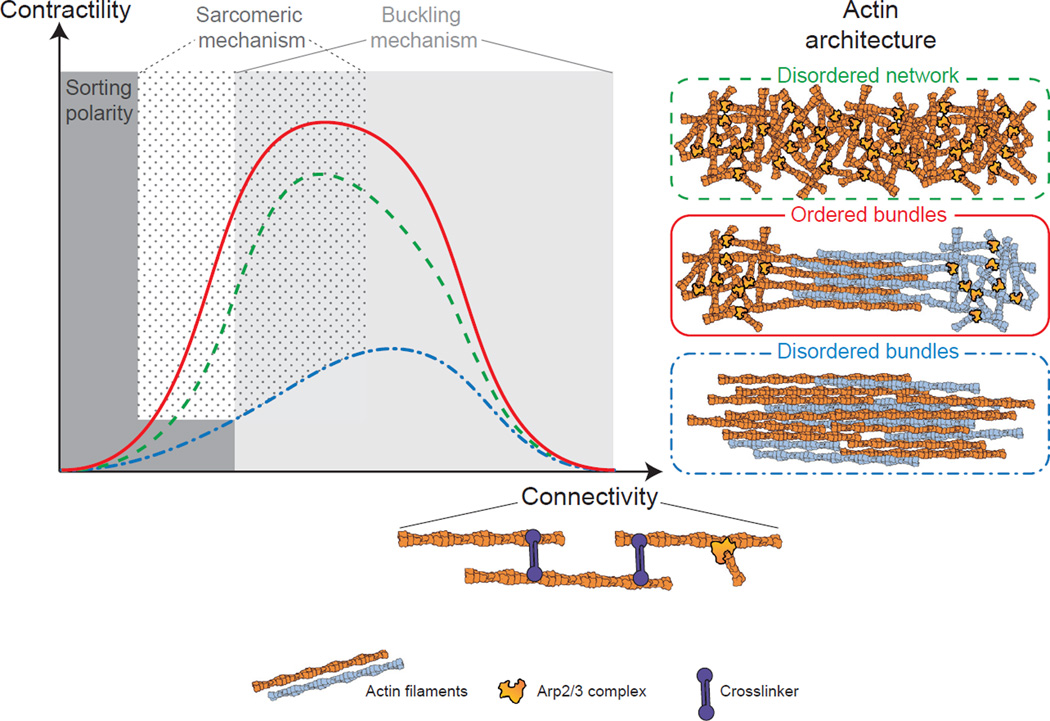
Contractile actomyosin structures in cells have different abilities to generate forces [8]. We found that these variations may result from a combination of two interrelated parameters: the spatial organization of actin filaments (branched, ordered, or disordered bundles) within the network, and their connectivity. The degree of connectivity within the network regulates the type of the contractile response (local sliding, global deformation, or massive freezing). This results in a bell-shape contractile response curve as a function of the connectivity, for all actin architecture tested (Figure 7). This is in agreement with the observation made in disorganized actin network where contractility depends on the degree of crosslinked networks [4, 11]. In addition, we reported here that the network architecture governs the magnitude of the contractile response (Figure 7). In particular, the spatial distribution of the connectors (Arp2/3 complex, crosslinkers) can explain the differences of contractile behavior observed for different architectures at equal connectivity (Figure 7). As other proteins such as fascin or myosin filaments [5, 8] can also act as connectors, it will be interesting to test in the future how these molecules influence the contractile response of the different actin architectures.

Figure 7. Model of Actin Architecture-Dependent Contractile Response.

The contractile response as a function of the connectivity follows a bell-shaped curve for the three different architectures tested (disordered network, ordered bundles, and disordered bundles). However, the amplitude of the contractile response depends on the actin organization, such that it is maximal for ordered bundles, intermediate for disordered networks, and lowest for disordered bundles. Depending on the actin organization and connectivity, the contractile mechanism is dominated by a sarcomeric mechanism at low to intermediate connectivity, or by a buckling mechanism at intermediate to high connectivity. At no or very low connectivity, myosin primarily induces polarity sorting of actin filaments.

Mechanism of Contractility Depends on Network Architecture

Both actin organization and connectivity influence the mode of network deformation (Figure 7). Indeed, contractility of different type of actin organization cannot be described by a unique mechanism of contraction but by a combination of the sarcomeric-like and buckling mechanisms. First, all networks at low connectivity (under percolation threshold) are driven by a local polarity sorting mechanism resulting from the sliding of the actin filaments by the motor without global contraction (Figure 7; Movie S5). When connectivity is mainly generated by Arp2/3 complex-like connections (disordered networks or ordered bundles at initial connectivity), network contraction follows a sarcomeric-like mechanism where the actin filament mechanical property has a minimal impact on the overall contractile response (Figure 7;Movie S5). This is mostly due to the architecture of these arrays that impact on the spatial distribution of the connectivity along the actin filament giving rise to some sarcomericity. As the connectivity increases (due to crosslinkers addition), the contractility of the three different actin organizations is dominated by the buckling mechanism, where the mechanical properties of the filaments play a major role. This could be explained by the fact that the presence of crosslinkers adds frictional constraints anywhere along the filament, thus favoring filament buckling over filament motion (pivoting, sliding, or rotation). For connectivity above 4 in our system, buckling is inhibited and contractility is hindered. This is where we propose that the dynamic of actin network is essential to avoid a full inhibition of the contractile response from excessive connectivity. This could be triggered in the cell by actin filament dynamics, in particular, disassembly mediated by ADF/cofilin, or by myosins [21]. Indeed, we were able to restore contractility of highly crosslinked network using ADF/cofilin as a modulator of connectivity. This revealed how mechanical processes are coupled to biochemical feedbacks.

With this system, we were able to highlight the importance of the network architecture. While the mechanism of contractility has been under study for years, our study reveals the importance of the nature of the connectors (Arp2/3 complex, crosslinkers, others) as a key factor in the contractile behavior of actin networks.

Dynamic Transition in Contractile Networks

The local densities of molecular motors and crosslinkers have been described as key modulators of the transition from contractile to non-contractile organization [5, 10, 11, 36, 37]. Here, we have demonstrated that for a defined set of biochemical parameters the spatial organization of actin filaments can strongly impinge on the rate of contraction and the magnitude of force generation. Moreover, we showed how the contractile properties of an actin network could change drastically, as its conformation is modified. Such behaviors are likely to be important since modulations of the actin architecture are often present in vivo. Modulation occurs, for example, following the maturation of sarcomeres in cardomyocytes [38, 39], during which misoriented actin filaments are transported and sorted by myosins, up to the generation of alternate distribution between myosins and crosslinkers along aligned filaments, an organization that optimizes force production at large scales. Similarly, dynamic changes of connectivity and network architecture occur in the lamella of motile cells, where the protrusive branched network of short filaments is converted to transverse arcs, which are long bundles of aligned and crosslinked fibers, and probably much better suited to produce tension [35]. The possibility to modulate network architecture and composition to finely tune the contractile response provides a large degree of mechanical adaptation and responsiveness to contractile networks. This modularity is crucial for cell-shape changes during migration or tissue development where the mechanical properties and the geometry of the local environment can vary considerably in space and time [40, 41].

EXPERIMENTAL PROCEDURES

Protein expression, purification, and labeling are detailed in Supplemental Experimental Procedures.

Micropatterning

Hard Patterning

Deep UV exposure through a photomask creates micropatterns on polyethylene-glycol-coated coverslip. pWA is adsorbed on the micropatterned regions. In the presence of the actin polymerizing mix, filaments should grow on and out of the micropattern and get contracted.

Soft Surface Patterning

Polyacrylamid gel was prepared as described in detail previously [27] with some modifications. A 20-mm² coverslip was silanized in order to bind the polyacrylamid gel to it. Solution of 40% polyacrylamide and 2% bisacrylamide was mixed to have a solution that contains 4% acrylamide and 0.06% bisacrylamide to have a 1.16 kPa gel rigidity. Beads were added to this mixture and then degased for 15 min. The polymerization solution was added between a coverslip with patterned pWA and the silanized coverslip for 20 min to transfer the protein from the hard to the soft substrate.

Actin Polymerization

Actin polymerization and contraction were induced in a solution containing 2 µM actin monomers (7% labeled with Alexa 568), 6 µM profilin, 100 nM Arp2/3 complex, and 16 nM of HMM-myosin VI (GFP labeled). These proteins mixture were diluted in freshly prepared buffer containing 15 mM imidazole-HCl (pH 7.8), 0.6 mM ATP, 55 mM DTT, 1 mM EGTA, 75 mM KCl, 3.5 mM MgCl₂, 1.5 mg/ml glucose, 10 µg/ml catalase, 50 µg/ml glucose oxidase, and 0.25% w/v methylcellulose. An ATP regenerating system was also added to this medium (2 mM MgATP, 2 mM phosphoenolpyruvate, 2,000 U/ml pyruvate kinase).

TIRF Microscopy, Image Acquisition, and Data Analysis

Time course of actin assembly was acquired on a total internal reflection fluorescence (TIRF) microscope (Roper Scientific) equipped with an iLasPulsed system and an Evolve camera (EMCCD 512 × 512, pixel = 16 µm) using a 60× 1.49 numerical aperture (NA) objective lens. During ring contraction, images were taken using a straight BX61 Olympus microscope equipped with a 40× dry objective (UPLFLN, NA = 0.75), an XY motorized stage (Marzhauser), and a CoolSnap HQ2 camera (Roper Scientific). Microscope and devices were driven by MetaMorph (Molecular Devices). Data were analyzed with ImageJ v.1.48 (see Supplemental Information) and plotted with GraphPad Prism6.

Highlights.

• We generated actin architectures that span the diversity of contractile structures

• These different actin organizations respond differently to myosin-induced contraction

• Actin filament organization and connectivity determine the contractile response

• Network contraction is dominated by either sarcomeric-like or buckling mechanisms

In Brief.

The composition, organization, and geometry of actomyosin networks influence the production of contractile forces. Ennomani et al. describe how modulating network architecture and composition finely tunes the contractile response and provides a large degree of mechanical adaptation and responsiveness to contractile networks.