Analytic expression of fluorescence ratio detection correlates with depth in multi-spectral sub-surface imaging

Abstract

Here we derived analytical solutions to diffuse light transport in biological tissue based on spectral deformation of diffused near-infrared measurements. These solutions provide a closed-form mathematical expression which predicts that the depth of a fluorescent molecule distribution is linearly related to the logarithm of the ratio of fluorescence at two different wavelengths. The slope and intercept values of the equation depend on the intrinsic values of absorption and reduced scattering of tissue. This linear behavior occurs if the following two conditions are satisfied: the depth is beyond a few millimeters, and the tissue is relatively homogenous. We present experimental measurements acquired with a broad-beam non-contact multi-spectral fluorescence imaging system using a hemoglobin-containing diffusive phantom. Preliminary results confirm that a significant correlation exists between the predicted depth of a distribution of protoporphyrin IX (PpIX) molecules and the measured ratio of fluorescence at two different wavelengths. These results suggest that depth assessment of fluorescence contrast can be achieved in fluorescence-guided surgery to allow improved intra-operative delineation of tumor margins.

1. Introduction

In the last decade there has been increased interest in the development of pre-clinical and clinical methods for intra-operative fluorescence-guided resection of tumors (see, e.g., (Pogue et al.) for a review). Application of optical imaging methods in the operating room has the potential to provide surgeons with pertinent tissue information that is complementary to conventional white-light imaging (Troyan et al., 2009; De Grand and Frangioni, 2003). One example is fluorescence-guided surgery for the resection of brain tumors following administration of 5-aminolevulinic acid (ALA). Exogenous administration of ALA overloads the heme biosynthetic pathway, leading to selective accumulation in neoplastic tissues of the fluorescent heme precursor, protoporphyrin IX (PpIX) (Collaud et al., 2004). Accumulated levels of PpIX in certain types of brain tumors is sufficiently high to facilitate visualization through a surgical microscope modified for fluorescence imaging (Stummer et al., 1998b; Stummer et al., 2006; Roberts et al., 2010).

The state-of-the-art methodology for fluorescence-guided resection of brain tumors uses a modified surgical microscope equipped with a broad-beam blue light excitation source. The re-emitted fluorescence is detected using a charged-coupled device (CCD) camera and a long-pass filter (Stummer et al., 1998a). However, strong light absorption in the visible part of the electromagnetic spectrum is an inherent limitation of this in vivo fluorescence imaging method, which severely hampers the ability to identify sub-surface tumor remnants. Near-infrared (NIR) light can penetrate deeper into tissue when compared to visible light. In the NIR range, tissue absorption decreases by two to three orders of magnitude compared to visible light and scattering becomes the dominant light attenuation mechanism. However, despite the resulting increased depth sensitivity, planar epi-illumination NIR images are difficult to interpret because the information they convey is surface-weighted with a strong bias towards fluorescence near the surface (Leblond et al., 2010a).

We present preliminary results in the development of a depth-resolved fluorescence imaging approach that could be integrated with the surgical workflow in brain tumor resection. This imaging methodology has the potential to allow for pixel-by-pixel fluorophore depth estimation at an imaging rate close to real-time and with minimal computational burden. The method exploits the effect of non-uniform attenuation spectra of tissue on propagating fluorescent signals in the NIR by acquisition of two fluorescence images at different wavelengths; it then uses their ratio to estimate the depth of fluorescent sources located beneath the tissue surface. Studies have proposed that a method could be developed allowing for depth-estimation based on multi-spectral data (Swartling et al., 2005; Svensson and Andersson-Engels, 2005). However, the results from those studies are mainly applicable to local fluorescence measurements made using fiber-optics. In those studies, depth is retrieved based on Monte Carlo light transport simulations. Here we present evidence that simple analytical solutions to diffuse light transport could be used for depth-estimation in a non-contact broad-beam imaging system. The depth-retrieval formalism presented here is amenable to wide-field CCD-based photon detection in a manner compatible with existing surgical microscopes. Further, this work fills a gap in the literature by providing closed-form expressions from which the relation between spectral deformations, depth of fluorophores and intrinsic optical properties can be formally understood.

2. Light Transport Modeling Methods

2.1. Relationship between fluorescence ratio and depth

Figure 1(a) illustrates an example of a non-contact configuration for intra-operative multi-spectral imaging. In this configuration, the fluorescence excitation is generated using a broad-beam light source at the excitation wavelength, λ^ex. Remitted fluorescence signals are measured at two wavelengths, λ_1,2 > λ^ex, using band-pass interference filters and a CCD camera. Assuming that tissue absorption due to fluorophores is much smaller than that of other native chromophores (e.g., oxy-hemoglobin, deoxy-hemoglobin), the light signals at each emission wavelength can be modeled using the expression

$${\psi }^{em}(\overrightarrow{R},{\lambda }^{ex},\lambda )\approx Q_F{\epsilon }_F^{em}(\lambda ){\displaystyle \underset{\mathrm{\Omega }}{\int }{d}^{3}r{\psi }^{ex}(\overrightarrow{r})}{C}_F(\overrightarrow{r})G^{em}(\overrightarrow{R},\overrightarrow{r},{\delta }^{\lambda },D^{\lambda }),$$ (1)

where Q_F is the quantum yield, ${\epsilon }_F^{em}(\lambda )$ the emission spectrum and C_F(r) the concentration of fluorophores at location r. Figure 1(b) shows the main geometric variables used in (1), in which light transport is modeled as a diffusive process. The variables R and r_s are used to label the position of the light detection point and the position of the fluorescent source from the origin of the x–y coordinate system, respectively. The indices of refraction of air and tissue are represented by n_air and n_tissue, respectively. The fluence function, ψ^ex, is the excitation light field and G^em is the diffusion equation Green’s function, which corresponds to the radiant exposure in response to a light impulse. In other words, G^em is the solution to the diffusion equation associated with a Dirac delta function source term. For boundary conditions associated with an infinite homogenous medium, it takes the form

$$G_{\infty }^{em}(\overrightarrow{R},\overrightarrow{r},{\delta }^{\lambda },D^{\lambda })=\frac{\text{exp}(-\left|\overrightarrow{R}-\overrightarrow{r}\right|/{\delta }^{\lambda })}{4\pi D^{\lambda }\left|\overrightarrow{R}-\overrightarrow{r}\right|},$$ (2)

where the diffusion constant is $D^{\lambda }=1/3({\mu }_a^{\lambda }+{\mu }_s^{\prime \lambda })$ and the penetration depth is ${\delta }^{\lambda }=\sqrt{D^{\lambda }/{\mu }_a^{\lambda }}$ (Jacques and Pogue, 2008).

Figure 1.

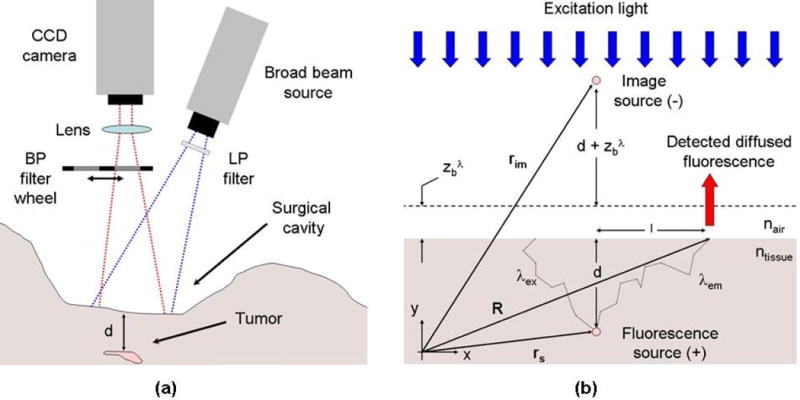
(a) Non-contact multi-spectral imaging instrument used for fluorescence ratio detection. (b) Light transport in tissue is modeled assuming the cavity can be approximated as a semi-infinite diffusive medium with homogeneous optical properties.

A closed form expression is derived from which a depth value can be attributed to each point imaged on the tissue surface. An approximation is made that all of the fluorescence emanating from the surface is from a point-like distribution with molar concentration C_F at r_s. This is equivalent to setting $C_F(\overrightarrow{r})=C_F{\delta }^{(3)}(\overrightarrow{r}-{\overrightarrow{r}}_s)$ in (1), which then takes the form

$${\psi }^{em}(\overrightarrow{R},{\lambda }^{ex},\lambda )\approx C_F{Q}_F{\epsilon }_F^{em}(\lambda ){\psi }^{ex}({\overrightarrow{r}}_s)G^{em}(|\overrightarrow{R}-{\overrightarrow{r}}_s|,{\delta }^{\lambda },D^{\lambda }),$$ (3)

where the depth of the distribution is $|\overrightarrow{R}-{\overrightarrow{r}}_s|=d$ (l = 0 mm in figure 1(b)). To illustrate how fluorescence spectra are affected by varying the depth of the fluorophore distribution, figure 2(a) shows PpIX spectra (normalized to their maximum value) computed with (3) for varying depths up to d = 20 mm for the labeled absorption spectrum spectrum 1 in figure 3(a) and a constant reduced scattering value of μs′ = 1.0 mm⁻¹. As the object lies deeper in the tissue, the optical properties increasingly influence the shape of the spectrum because of the increasing path-lengths traversed by light. The information contained in the distorted spectra may be distilled into a single quantity by calculating the ratio of the signal at two emission wavelengths,

$$\mathrm{\Gamma }=\frac{{\psi }^{em}(\overrightarrow{R},{\lambda }^{ex},{\lambda }_1)}{{\psi }^{em}(\overrightarrow{R},{\lambda }^{ex},{\lambda }_2)}\times \frac{{\epsilon }_F^{em}({\lambda }_2)}{{\epsilon }_F^{em}({\lambda }_1)}=\frac{G^{em}(\overrightarrow{R},{\overrightarrow{r}}_s,{\delta }^{{\lambda }_1},D^{{\lambda }_1})}{G^{em}(\overrightarrow{R},{\overrightarrow{r}}_s,{\delta }^{{\lambda }_2},D^{{\lambda }_2})},$$ (4)

where the intensity values at each wavelength are normalized with the relative signal strength of an undistorted emission spectrum (e.g., the PpIX spectrum labeled 0 mm in figure 2(a)). Normalization with a measured reference spectrum allows direct comparison between ratios computed with (4) and experimental fluorescence ratio data acquired with a multi-spectral instrument. Measurement of a reference spectrum for the specific fluorescent dye of interest (e.g., PpIX or any other fluorescent molecule) should be regarded as an essential component of the calibration procedure which allows comparison of fluorescence ratio experimental data with light transport models. A critical aspect of (4) is that Γ does not depend on the manner in which the surgical field is illuminated. That is, the expression for the excitation light field (ψ^ex) cancels when the ratio is taken. Assuming that the point-like approximation is valid, the equations shown here should be applicable to cases where the surgical field is illuminated with a broad-beam source. By inserting (2) into (4), we find that the logarithm of the fluorescence ratio for an infinite medium is linearly related to the depth of the fluorophores with a slope equal to the difference in penetration depth between wavelengths λ₁ and λ₂,

$$\ln {\mathrm{\Gamma }}_{\infty }=-\left[\frac{1}{{\delta }^{{\lambda }_1}}-\frac{1}{{\delta }^{{\lambda }_2}}\right]\times d+\ln \frac{D^{{\lambda }_2}}{D^{{\lambda }_1}}.$$ (5)

This simple linear relationship suggests that depth can be estimated from a simple measured ratio provided the optical properties (absorption, reduced scattering) of the tissue at the two wavelengths are known. This expression provides a formal theoretical basis for interpreting the results presented in Refs. (Swartling et al., 2005; Svensson and Andersson-Engels, 2005). However, the underlying photon diffusion assumptions used to derive (5) restrict its application to depths for which the diffusion approximation applies, i.e., for objects located more than approximately 1 or 2 mm underneath the surface.

Figure 2.

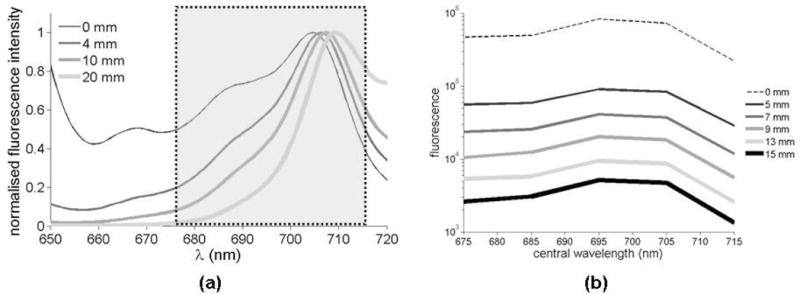
(a) Simulation results showing protoporphyrin IX (PpIX) spectra for molecules located at four different tissue depths. (b) Experimental spectra measured for a tissue-simulating blood phantom using the instrument represented in figure 1(a). The spectra shown in (b) are for different depths ranging from d = 5 mm to d = 15 mm. The curve labeled 0 mm is the reference spectrum measured with the multi-spectral instrument. The highlighted area in (a) represents the spectral domain for which measurements were mare in (b).

Figure 3.

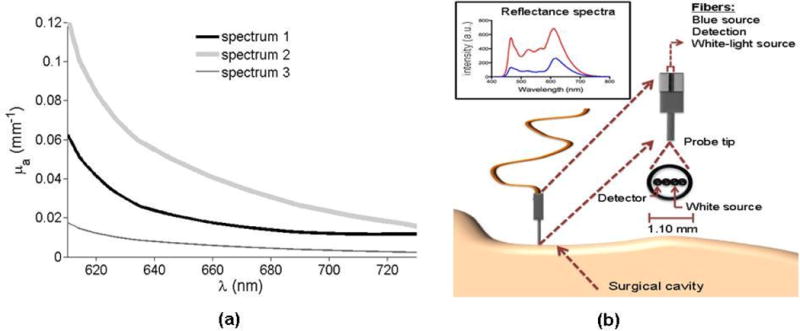
Representative absorption spectra acquired in vivo for normal human brain tissue using the hand-held fiber-optics reflectance probe schematically represented in (b).

In deriving (5), two assumptions were made that could introduce errors in depth estimation: the medium was assumed to be homogeneous and of infinite spatial extent. Quantifying the effects of tissue heterogeneity on depth recovery is difficult and likely to vary for different tissue types. However, the clinical application of interest here is brain tumor resection and fluorescence-guided neurosurgery is performed with an open cranium following skull (i.e., craniotomy) and dura removal (i.e., durotomy). As such, the surgical field is cleared and the brain is imaged directly. Depth imaging will be achieved clinically for depths up to 1–2 cm, and so we can reasonably assume that the volume of interrogated brain tissue (e.g., either grey or white matter) will be relatively homogeneous. A detailed study which analyzes the impact of heterogeneous intrinsic optical properties is desirable but outside the scope of the current study.

The treatment for an infinite case can easily be extended to a more realistic semi-infinite geometry, which more closely represents a surgical imaging configuration, as shown in figure 1(b). In this case, the diffusion equation can be solved given that the fluence vanishes on a planar extrapolated boundary located a distance $z_b^{\lambda }=2A{D}^{\lambda }$ (A ≈ 3 for air-tissue interface) away from the tissue surface (Haskell et al., 1994). The corresponding Green’s function is

$$G_{1/2}^{em}(\overrightarrow{R},{\overrightarrow{r}}_s,{\delta }^{\lambda },D^{\lambda })=\frac{1}{4\pi D^{\lambda }}\left[\frac{\text{exp}(-|\overrightarrow{R}-{\overrightarrow{r}}_s|/{\delta }^{\lambda })}{|\overrightarrow{R}-{\overrightarrow{r}}_s|}-\frac{\text{exp}(-|\overrightarrow{R}-{\overrightarrow{r}}_{im}|/{\delta }^{\lambda })}{|\overrightarrow{R}-{\overrightarrow{r}}_{im}|}\right],$$ (6)

where, for l = 0 mm, the distance between the measurement point and the imaginary negative source, located at r_im, is given by $|\overrightarrow{R}-{\overrightarrow{r}}_{im}|=d+2z_b^{\lambda }$. The expression for the ratio of fluorescence then becomes

$${\mathrm{\Gamma }}_{1/2}={\mathrm{\Gamma }}_{\infty }\times \left\{1-\left(\frac{1}{1+\frac{4A{D}^{{\lambda }_1}}{d}}\right)\text{exp}\left(-\frac{4A{D}^{{\lambda }_1}}{{\delta }^{{\lambda }_1}}\right)/1-\left(\frac{1}{1+\frac{4A{D}^{{\lambda }_2}}{d}}\right)\text{exp}\left(-\frac{4A{D}^{{\lambda }_2}}{{\delta }^{{\lambda }_2}}\right)\right\},$$ (7)

where the second term in brackets is interpreted as a form factor correction to the expression obtained for an infinite medium. The semi-infinite expression in (7) would slightly complicate the depth retrieval procedure derived from (5). This is because the form factor multiplying Γ_∞ in (7) explicitly depends on the depth which makes this a non-linear relationship between Γ_1/2 and d. Depth retrieval based on (7) would require the use of iterative numerical resolution methods. It should be noted that the form factor becomes independent of depth for values that are significantly larger than d_c = 4AD^λ. For example, d_c ≈ 2 mm for tissue with reduced scattering values of μ_s′ = 2 mm⁻¹. This implies that for large enough depths the linear relationship in (5) is retrieved up to a depth-independent scaling factor.

2.2. Predicted variation of fluorescence ratio with depth

As seen in Section 2.1, a critical ingredient for accurate depth estimation is the availability of prior knowledge regarding tissue optical properties (i.e., intrinsic absorption and reduced scattering parameters) at wavelengths for which fluorescence signals are acquired. Inspection of (5) and (7) demonstrates that the slope of the Γ-d relationship is proportional to the difference in the inverse penetration depths at the two measured wavelengths. The ability to use fluorescence ratio detection as a means to discriminate between fluorescent molecules located at different depths depends on whether or not predicted signal variations are large enough to be measured with existing technologies. It should also be noted that these signal changes do not depend on the molecular species of the fluorophore; rather, on the concentrations and relative contributions of the tissue chromophores, e.g., oxy-hemoglobin and deoxy-hemoglobin. It is the non-trivial features of the absorption spectra of the chromophores that are causing the fluorescence ratio to vary with depth. From a mathematical standpoint, the emission spectrum of the fluorophore is only used to normalize the ratio as shown in (4). This allows for direct comparison with light-transport predictions. Of course, signal considerations dictate that wavelengths for which the emission spectrum is larger will lead to more favorable signal-to-noise ratios (S/N).

Initial assessment of fluorescence ratio measurements for depth retrieval depends on measureable depth-dependent signal changes in tissue with optical properties typically encountered in vivo. In order to determine whether or not the proposed fluorescence ratio methodology can be useful for brain tumor resection, we used an intraoperative hand-held fiber optics probe to obtain experimental reflectance spectra. These spectra were used to compute in vivo absorption spectra, with the assumption that the main tissue chromophores are oxy-hemoglobin and deoxy-hemoglobin. The spectra were measured in the scope of a clinical study involving 14 patients undergoing brain tumor resection. Measurements were performed by contacting the probe tip with the tissue (figure 3(b)). As described in detail in Ref. (Kim et al., 2010b), the hand-held probe tip has a diameter of 1.10 mm into which are embedded four optical fibers. Two fibers are connected to a white-light source, a third fiber to a spectrometer, and a fourth fiber to a blue light source for fluorescence excitation. As detailed in (Kim et al., 2010b), using a diffusion model in conjunction with the known absorption spectra of hemoglobin (oxygenated and de-oxygenated), a least-square fitting algorithm is used to match the reflectance spectra with light transport predictions. More precisely, an analytic solution to the diffusion equation for reflectance detection is used. This solution is a function of the tissue absorption and the reduced scattering at all measured wavelengths. The tissue absorption is assumed to be of the form

$${\mu }_a(\lambda )={\epsilon }_{Hb}{C}_{Hb}+{\epsilon }_{\mathit{\text{oxyHb}}}{C}_{\mathit{\text{oxyHb}}},$$ (8)

where ɛ and C are symbols representing the extinction coefficient and the molecular concentration, respectively; and the acronyms Hb and oxyHb represent deoxy-hemoglobin and oxy-hemoglobin, respectively. The spectral constraint used for the reduced scattering coefficient consists in the power law

$${\mu }_s\prime (\lambda )=a{\lambda }^{-b},$$ (9)

where a is the scattering amplitude and b the scattering power. Predictions of the concentration of oxy-hemoglobin and deoxy-hemoglobin were made from which the in situ absorption (μ_a) tissue spectra can be computed. The fitting process also allows recovery of the reduced scattering spectrum (Kim et al., 2010b). Figure 3(a) shows three representative spectra acquired during the clinical study described above. Those spectra, labeled spectrum 1, spectrum 2, and spectrum 3, are representative in the sense that they cover the range of absorption properties typically encountered clinically during brain tumor resection.

The absorption spectra in figure 3(a) are used to characterize the predicted magnitude of in vivo fluorescence ratio variations with depth. Figure 4(a) shows a simulated fluorescence ratio (λ₁ = 650 nm and λ₂ = 670 nm) as a function of depth for those three representative absorption spectra. Fluorescence ratios are computed using (7), i.e., for a semi-infinite diffusive medium. The top curve is the one for which the difference in inverse penetration depth is the smallest. As seen by inspection of figure 3(a), this curve corresponds to the absorption spectrum (spectrum 3) having the smallest difference in absorption between λ₁ = 650 nm and λ₂ = 670 nm. The top curve in figure 4(a) is the one with the most linear Γ-d relationship of the three curves shown. This can be explained by considering the linear limit of (7), i.e., by performing a Taylor expansion in terms of the difference in penetration depth between the two different wavelengths used to compute the ratio. The leading term of this expansion is of the form shown in (5), with higher order corrections becoming increasingly negligible as the difference in penetration depth becomes smaller. This finding explains the observation made in Refs. (Swartling et al., 2005; Svensson and Andersson-Engels, 2005) that the relation between Γ and depth is approximately linear.

Figure 4.

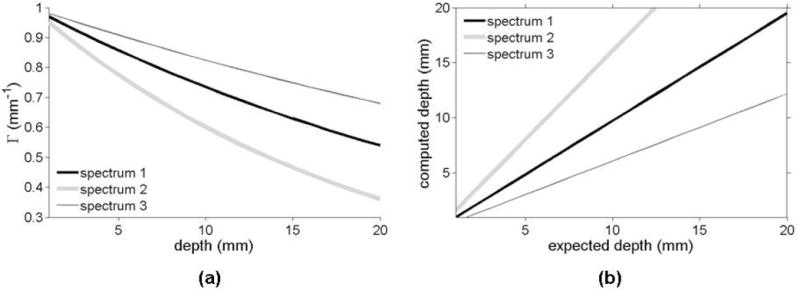
(a) Fluorescence ratio (λ₁ = 650 nm and λ₂ = 670 nm) computed with (7) as a function of depth for the three representative absorption spectra shown in figure 3(a). (b) Expected depth versus computed depth for the different absorption spectra. The curves labeled spectrum 2 and spectrum 3 were computed using (5) assuming that the optical properties were those associated with spectrum 1. Deviations with respect to the darker curve (spectrum 1) should be interpreted as depth errors caused when using the wrong optical properties as input to the depth retrieval algorithm.

The fluorescence ratio expressions (equations (5) and (7)) indicate that the choice of wavelengths used in the ratio affects the sensitivity of Γ to depth. Ideally, the chosen wavelengths should have dramatically different optical properties to emphasize the spectral distortion, which will be manifested as a steeper slope in the Γ-d relationship. An initial assessment of the expected magnitude of the changes with depth considers the linear limit of (5). The resulting analysis is only valid for an infinite diffusive medium and for situations where the difference in penetration depths is small. However, the signal variation predictions derived under those simplifying assumptions still provide useful estimates for the order of magnitude with which the ratio changes with depth. The percentage of Γ-signal change per millimeter (mm) of increased depth is found to be approximately $-\sqrt{3}\left(\sqrt{{\mu }_a^{{\lambda }_1}{\mu \prime }_s^{{\lambda }_1}}-\sqrt{{\mu }_a^{{\lambda }_2}{\mu \prime }_s^{{\lambda }_2}}\right)\times 100\%$, for μ′_s ≫ μ_a. This confirms that using the fluorescence ratio to discriminate between different depths is facilitated when the difference in optical properties is maximized. However, under similar light illumination conditions, tissue that is more absorbing will lead to fluorescence measurements with less favorable signal-to-noise characteristics. This makes it more difficult to detect deeper seated fluorescent distributions. In order to illustrate the signal variations that can be expected in vivo, optical property values derived from the spectra shown in figure 3(a) are used. For the spectrum labeled spectrum 2, if μ_s′ = 1 mm⁻¹ and ${\mu }_a^{\lambda 1}=0.12m{m}^{-1}$ (λ₁ = 610 nm), absorption changes of $\Delta {\mu }_a={\mu }_a^{\lambda 1}-{\mu }_a^{\lambda 2}=0.04{\text{mm}}^{-1}$ (λ₂ = 622 nm), Δμ_a = 0.08 mm⁻¹ (λ₂ = 660 nm) and Δμ_a = 0.105 mm⁻¹ (λ₂ = 730 nm) lead to detected ratio changes of 11%, 25% and 39% per mm, respectively. Similarly, for the spectrum labeled spectrum 1, if μ_s′ = 1 mm⁻¹ and ${\mu }_a^{\lambda 1}=0.06{\text{mm}}^{-1}$ (λ₁ = 610 nm), absorption changes of $\Delta {\mu }_a={\mu }_a^{\lambda 1}-{\mu }_a^{\lambda 2}=0.04{\text{mm}}^{-1}$ (λ₂ = 622 nm), Δμ_a = 0.042 mm⁻¹ (λ₂ = 660 nm) and Δμ_a = 0.05 mm⁻¹ (λ₂ = 730 nm) lead to detected ratio changes of 8%, 19% and 25% per mm, respectively. These variations demonstrate that the choice of wavelengths used can dramatically affect the sensitivity of Γ to depth as well as the permissible level of noise in the signal. Figure 3(a) shows that observed spectral variations for brain tissue should provide an opportunity to generate significant variations allowing signals from different depths to be discriminated. Noteworthy is the large variability of intra-operative normal brain absorption coefficient values, i.e., μ_a = 0.12 mm⁻¹ to μ_a = 0.005 mm⁻¹ across the spectral acquisition domain ranging from 630 nm to 730 nm. Further, to illustrate how fluorescence spectra are affected by varying the depth of the fluorophores, figure 2(a) shows normalized simulated PpIX spectra computed with (3) for various depths of the absorption spectrum labeled spectrum 1 in figure 3(a) (μ_s′ = 1 mm⁻¹). At increasing depths, simulations show the influence of tissue optical properties on the spectrum and its subsequent deformation due to the different light paths traversed.

As explained in Section 2.1, the analytical expression derived for the fluorescence ratio as a function of depth suggests that a methodology could be implemented whereby depth could be estimated based on fluorescence images acquired at two different wavelengths. Depth retrieval based on multispectral fluorescence data requires a priori knowledge of absorption and reduced scattering properties of the interrogated tissue. As a result, the precision with which depth could be evaluated relies on the precision with which those intrinsic optical properties can be measured. As an initial assessment, the algorithm presented here was used to retrieve depth based on incorrect optical property values. To isolate the impact of depth-estimation errors caused by errors in optical property measurements, equation (5) for a semi-infinite medium was used. Figure 4(b) shows curves illustrating the impact of using inaccurate optical properties with (5) to retrieve depth. For the two cases shown (top and bottom curves), the true optical properties were assumed to match those of spectrum 1 in figure 3(a). Using slopes and intercepts derived from (5) for λ₁ = 650 nm and λ₂ = 670 nm, values of depth were recovered using the incorrect properties from spectrum 2 (top curve) and spectrum 3 (bottom curve). Inaccurate optical properties can lead to errors in depth estimation of several millimeters - the magnitude of which increases with depth. The strong reliance on accurate tissue properties suggests that this approach should be implemented with supplemental capabilities to simultaneously determine the optical properties of tissue in the imaging field. This can be accomplished with a system similar to that shown in figure 1(a), where multi-spectral NIR reflectance data is acquired and fitted for absorption and scattering spectra against light transport solutions of the form shown in (6). A simpler approach uses the fibers-optics probe shown in figure 3(b) as a way to estimate the bulk values of tissue optical properties in the surgical cavity prior to imaging using the wide-field multi-spectral instrument.

3. Preliminary Experimental Evaluation

An initial experimental assessment of the proposed depth-resolved imaging method has been performed by designing an instrument (figure 1(a)) for wide-field multi-spectral fluorescence detection. Fluorophore excitation was done with the expanded beam of a diode laser of wavelength λ^ex = 635 nm (Power Technology Inc., Little Rock, Arkansas). Remitted fluorescence is measured at five wavelengths, λ = (675, 685, 695, 705, 715) nm, using 10 nm-wide band-pass interference filters (Omega Optical, Brattleboro, Vermont) inserted into a motorized wheel coupled to an EXi Aqua charge-coupled device (CCD) (QImaging, Surrey, British Columbia). The camera is cooled to 0°C and has a full well-depth of 18,000 e-, a 14 bit digitizer, a dark current of 0.15 e-/pixel/seconds and a read-noise of 6.5 e- when operated at 10MHz readout frequency.

The proposed methodology was evaluated by imaging a tissue-simulating diffusive phantom containing fully oxygenated hemoglobin. A container (dimensions: 150 mm × 75 mm × 61 mm) was filled with water containing a volume fraction of 1% intralipid (Baxter Healthcare Corp., Deerfield, Illinois) and 2% porcine blood. An optically transparent cylindrical inclusion (diameter: 5.5 mm, height: 10 mm) was filled with 20 μg/ml of PpIX (Frontier Scientific, Logan, Utah) dissolved in dimethyl sulfoxide (DMSO). A moving stage allowed the inclusion to be immersed at different depths d. Figure 5(a) shows the optical properties of the medium measured using the fiber-optics reflectance probe described in Refs. (Kim et al., 2010a; Kim et al., 2010b; Valdes et al., 2010; Valdes et al., 2011). The medium was illuminated using an expanded laser beam (diameter: 13 mm, Power = 5.5 mW, λ^ex = 635 nm) and images of the remitted fluorescence emission at five different wavelengths were acquired (d = 1 mm to d = 15 mm). A PpIX spectrum was acquired as a reference, not corrupted by light propagation in the medium, to be used as part of the data calibration procedure described in Section 2.1. A pre-contrast image (inclusion filled with DMSO only) was acquired and subtracted from the corresponding fluorescence image in an effort to account for excitation light filter bleed-through. For all depths, the characteristic shape of the NIR PpIX shoulder was retrieved up to deformations caused by diffusion, as shown in figure 2(b).

Figure 5.

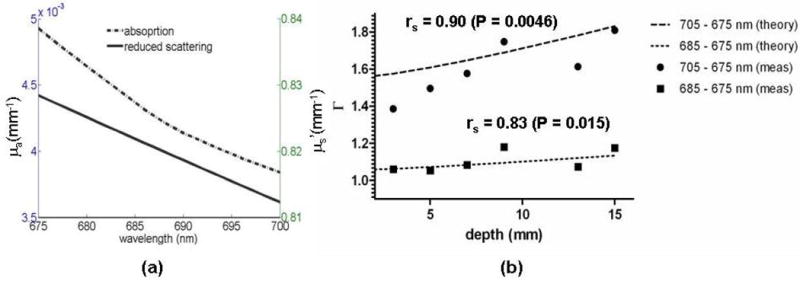
Experimental data acquired using a tissue-simulating blood phantom: (a) Optical properties (absorption and reduced scattering) computed using reflectance data acquired using a fiber-optics probe as shown in figure 3(b). (b) Simulated fluorescence ratios (labeled theory) versus measured fluorescence ratios (labeled meas) for two sets of wavelengths. The simulated ratios are computed using (7) with the optical properties shown in (a) as input parameters. A non-parametric Spearman’s rank correlation test between theory and experiment gives correlation coefficients and P-values of r_s = 0.90, P = 0.0046 (two-tailed) for (λ₁, λ₂) = (675 nm, 685 nm) and r_s = 0.83, P = 0.015 (two-tailed) for (λ₁, λ₂) = (675 nm, 695 nm).

Figure 5(b) shows the measured ratios for two sets of wavelengths: (λ₁, λ₂) = (675 nm, 685 nm) (circles) and (λ₁, λ₂) = (675 nm, 705 nm) (squares). The dotted lines correspond to simulated ratios computed with (7) using the optical properties experimentally retrieved with the fiber-optics probe (figure 5(a)). Qualitative inspection of the data suggests a reasonable match between theory and experiment, although a significant level of noise is observed. Sources of noise in this experiment are either directly associated with the detection system or with the design of the phantom experiment. Since the system has not been fully optimized to minimize the presence of excitation bleed-through in the fluorescence signal, a certain level of noise is expected as a result of pre-contrast image subtraction. Moreover, the magnitude of excitation light delivered to the surface of the phantom was limited, potentially resulting in a non-negligible contribution of photon shot noise. Data acquisition was performed by immersing a fluorescent inclusion in a solution that contained porcine blood. The full dataset collected consisted of images for each wavelength at several depths (range from 0 mm to 15 mm). For each depth, a spectrum of pre-contrast images was acquired with no fluorescence inside the inclusion. Taking into consideration the manipulation time (inserting new liquids, insuring the inclusion is at the desired depth, adjusting camera parameters, etc.), completion of the experiment required several hours. As a result, the optical properties of the hemoglobin solution (absorption and reduced scattering) have changed during the course of the experiment because over time an increasing fraction of the molecules become oxidized and form methemoglobin which has a slightly different absorption spectrum in the NIR. This represents another potential source of noise in the measured fluorescence ratios. In fact, the computed fluorescence-ratio curves shown in figure 5(b) are evaluated using Eq. (7) with, as input parameters, the experimental optical properties evaluated using reflectance data acquired at a single time-point during the experiment. As a result, some of the misfit between theory and experiment may be attributable to the fact that the experimental points were acquired at different times, i.e., for potentially different phantom optical properties. There are no error bars in figure 5(b) because only one data point was acquired per wavelength due to the considerable time required to run the experiment.

Inspection of the fluorescence ratios shown in figure 4(b) suggest that there is a correlation between the experimental data and the fluorescence ratios predicted using (7) based on diffusion light transport modeling. A statistical analysis was conducted in order to quantify how much correlation there is between the measured ratios and the fluorescence ratios predicted by the analytical solution. Using a non-parametric Spearman’s rank correlation test, the correlation coefficients and P-values obtained were r_s = 0.90, P = 0.0046 (two-tailed) for (λ₁, λ₂) = (675 nm, 685 nm) and r_s = 0.83, P = 0.015 (two-tailed) for (λ₁, λ₂) = (675 nm, 695 nm). Based on these results (r_s > 0.8 in both cases), the correlation between theory and experiment is statistically significant. The P-value associated with the likelihood that the observed correlation values would result from chance if no correlation existed between the two datasets further supports the statistically significant linear correlation between theory and experiment. For both sets of wavelengths, values of P<0.05 were obtained which implies that the agreement between theory and experiment is not a result of chance. Further, the significant correlation found between the measured ratios and those predicted by theory occurs despite several approximations made in deriving (7). For example, in deriving the analytic solutions we hypothesized that the fluorescence source was point-like. However, this assumption is clearly not true in the context of the blood phantom experiment, since the fluorescent inclusion is a cylinder with a diameter of 5.5 mm and a height of 10 mm. The preliminary results presented here suggest that the analytical expression (7) has predictive power despite the point-like approximation. However, a future detailed study is warranted in order to precisely characterize how the size of a fluorescent inclusion will affect the predictive power of the analytical model derived here. More comments about this issue can be found in Section 4.

Finally, statistical analyses were performed in order to test whether or not the measured fluorescence ratios as a function of depth were significantly different from a horizontal line (i.e., zero slope line). First, a simple linear regression was performed on the data with goodness-of-fit parameters r² = 0.82 (slope: 0.03 mm^-1) and r² = 0.64 (slope: 0.01 mm⁻¹) for (λ₁, λ₂) = (675 nm, 685 nm) and (λ₁, λ₂) = (675 nm, 695 nm), respectively. An F-test was also performed to test for the presence of a non-zero slope in the relationship between Γ and d. We found that for both sets of wavelengths the data was significantly different from a horizontal line (P<0.05).

4. Discussion

Conventional technique for brain tumor resection uses pre-operative magnetic resonance (MR) images and a surgical microscope spatially co-registered with the surgical field. More recently, intra-operative fluorescence microscopes have been used to provide surgeons with improved guidance for tumor detection. The current state-of-the-art in fluorescence-guided resection of brain tumors uses blue light excitation and, as a consequence, can only detect fluorescent tissue on the surface of the cavity. However, for a large number of cases, even when a lesion has been resected based on MR image features, trained visual inspection, and visible fluorescence, residual tumor remnants remain beneath the surface. Any depth-resolved information beyond what can currently be detected using state-of-the-art fluorescence surgical microscopes is likely to be perceived as a major advance in neurosurgery.

A number of pre-clinical studies have been conducted using NIR fluorescence to guide the resection of tumors. None of the methods introduced allow for intraoperative depth-estimation of fluorescent lesions. However, several depth-resolved NIR imaging techniques have been developed and tested in the past using tissue simulating phantoms and/or small animals. These techniques can be broadly divided into two categories, namely: diffuse reflectance fluorescence tomography and planar reflectance imaging methods. Optical tomography approaches rely on the acquisition of a multitude of NIR measurements used to solve an inverse problem based on a forward model derived from light transport solutions. For example, Refs. (Kepshire et al., 2007; Kepshire et al., 2008) use single-wavelength continuous-wave (CW) fluorescence emission signals acquired with a CCD camera to localize distributions of PpIX. A multitude of measurements are acquired by fluorophore excitation using a raster-scanned laser beam and subsequent binning of the CCD chip. The use of numerous measurements is required to decrease as much as possible the ill-posedness of the corresponding inverse problem (Arridge and Lionheart, 1998; Leblond et al., 2010b). Translation of the raster-scanning technology to the operating room might not be practical. This is in part because the acquisition of a large number of high S/N measurements during surgery might result in imaging times that would significantly disrupt the surgical workflow. The requirement for high S/N measurements is due to the fact that the corresponding inverse problem is hyper-sensitive to even minute levels of stochastic noise. On the other hand, the work presented in (Klose, 2009) introduces a multi-spectral reflectance tomography approach where the burden associated with raster-scanning is relaxed. Several fluorescence images are acquired with a CCD camera at different wavelengths following excitation using a broad-beam light source. Compared with more traditional single-wavelength tomography approaches, this would significantly reduce the imaging time. However, it remains to be shown whether the addition of a finite number of emission wavelengths can result in an inverse problem for which the ill-posedness has been brought to a level comparable to raster-scanning tomography. Other methodologies that were proposed for depth-resolved imaging rely on the use of more sophisticated photodetection techniques such as time-domain (TD) reflectance imaging using single-photon counting methods (Hall et al., 2004; Laidevant et al., 2007; Han and Hall, 2008). In these approaches, TD signals with a resolution of approximately 10 picoseconds are acquired and used to recover planar images in which each pixel is associated with an estimate of the fluorophore depth. As is the case with tomography, a disadvantage of these methods is that measurements are typically acquired one pixel at the time using a photomultiplier tube detector and a laser that must be raster-scanned on the tissue surface. Refs. (Hall et al., 2004; Laidevant et al., 2007; Han and Hall, 2008) have shown that depth-estimation of a fluorophore distribution of finite spatial extent can be achieved with sub-millimeter precision. The authors accomplished this by fitting TD measurements against diffusion equation solutions obtained under the assumption that the fluorophore distribution is point-like.

Similar in spirit to the TD methods from Refs. (Hall et al., 2004; Han and Hall, 2008), the approach presented here shows that a simple relationship between fluorophore depth and fluorescence ratios at two wavelengths could be implemented for intra-operative estimation of deeper seated residual tumor using non-contact fluorescence imaging microscopes. This method has several advantages compared to other methods described above. For example, imaging time should be significantly shorter compared to raster-scanned tomography or planar TD approaches. The fluorescence ratio method requires acquisition of only two fluorescence images of the surgical field which can be accomplished with minimal disruption of the surgical workflow. Also, the technological requirements associated with broad-beam multi-spectral imaging are less stringent than those associated with single-photon counting imaging and raster-scan tomography. Broad-beam multi-spectral fluorescence imaging can be implemented with minimal hardware adaptations, i.e., using the optics associated with a state-of-the-art surgical fluorescence microscope.

We propose an intraoperative approach for depth estimation of fluorescent lesions using a simple analytical solution to a light transport model. Because the approach is based on a normalized signal, there are potentially several important experimental factors that decouple from the solutions presented in Section 2.1. The analytic solutions presented here suggest that the fluorescence ratio expression does not depend on the specific manner in which the surgical cavity is excited (e.g., uniform broad-beam excitation or small area laser excitation). The analytic expression from (7) depends only on the depth d of the fluorophore distribution. This implies that the depth recovery algorithm can potentially provide pixel-by-pixel depth estimates with no geometrical prior knowledge for the three-dimensional profile of the surface. This statement is only valid given that it can be approximated as a semi-infinite medium. However, the significant correlation found in Section 3 between experimental ratios and simulated values support the validity of the approximations made in Section 2.1.

Perhaps the most important approximation made in deriving the analytic expression for the fluorescence ratio is the so-called point-like approximation. The point-like approximation has also been used in the past for localization of fluorescent inclusions using time-domain signals (Hall et al., 2004; Han and Hall, 2008; Laidevant et al., 2007). The analysis presented in Section 3 supports the validity of this approximation by showing a strong correlation between the theoretical model and experimental fluorescence ratio data. It should be clear that depth retrieval based on this approximation cannot be expected to be exact, in part because the distribution of fluorescence emanating from tumors is clearly not point-like. Comments are in order to better explain why this approximation is expected to lend useful depth estimates. In deriving (7), the assumption is made that most of the fluorescence detected over the tissue surface emanates from sources located directly below the surface area where measurements are made. In situations where a tumor of finite spatial extent is present this approximation is clearly not exact. However, the detected signal is expected to be associated mostly with those fluorophores in the tumor that are closest to the detection point; although to a lesser extent, other parts of the tumor can contribute to the signal, so the depth that is actually retrieved from the signal will provide only an approximate value. This value will be a weighted average of the depth from all contributing tumor areas.

Because NIR light is exponentially attenuated in tissue (modified Beer-Lambert law), the information conveyed by epi-illumination imaging is surface weighted. Potential contributions from tissue auto-fluorescence could therefore significantly diminish the ability to image deeply buried sources of fluorescence as well as significantly compromise the validity of the point-like approximation. The majority of auto-fluorescent endogenous molecules have excitation spectra in the visible part of the electromagnetic spectrum. Since excitation in the proposed methodology is in the far-red part of the spectrum (λ_ex = 635 nm), in vivo auto-fluorescence contributions are expected to be relatively small. An oftentimes dominating source of tissue auto-fluorescence is skin. In brain tumor resection this is not an issue, since fluorescence imaging is performed intra-operatively following opening of the cranium (Pogue et al.; Roberts et al., 2010; Valdes et al., 2010). Perhaps more convincing in addressing the issue of auto-fluorescence is the fact that the levels of ALA-induced PpIX fluorescence from brain tumors (including high- and low-grade gliomas, meningiomas and metastases) are two to three orders of magnitude larger when compared to normal adjacent brain tissue. The high specificity of this contrast mechanism is such that fluorescence emanating from areas other than the tumor is in the vast majority of cases negligible (Valdes et al., 2011). We expect that the point-like approximation will not be compromised by the presence of auto-fluorescence and non-specific fluorescence in clinical applications such as ALA-induced PpIX fluorescence-guided resection. Future in vivo studies will be conducted to further validate the precision of this approximation for intraoperative depth retrieval.

5. Conclusion

The relationship between fluorescence ratio and fluorophore depth observed in Refs. (Svensson and Andersson-Engels, 2005; Swartling et al., 2005) was explained using analytical light transport solutions. A simple method was proposed whereby the depth can potentially be retrieved by using a ratio of fluorescence images acquired at two different wavelengths. This approach can only be successful if prior knowledge of the tissue optical properties at the measured wavelengths is available. This is a direct consequence of the relationship between d and Γ (equation (7)), which depends explicitly on those parameters. In this work, those input parameters are retrieved using reflectance spectra acquired with an intra-operative fiber-optics hand-held probe (Kim et al., 2010b; Valdes et al., 2010; Valdes et al., 2011).

In order for the depth retrieval method to be of use in surgery, the absorption and reduced scattering of tissue must lead to ratio changes with depth that can actually be measured despite intrinsic noise characteristics inherent to any imaging system. Using representative absorption spectra measured in vivo, the analysis presented in Section 2.2 demonstrates that the predicted changes of Γ with depth can be large enough to be measured in situations typically encountered during brain tumor resection. However, the experimental analysis presented in Section 3 showed Γ-d relations having relatively small slopes. Attempting to retrieve depth using (7) and the measured ratios shown in figure 5(b) would lead to highly inaccurate values. This is a consequence of both the small observed slopes and the presence of noise in the experimental data. The analysis presented in Section 3 demonstrates a strong correlation between the experimental data and the fluorescence ratios predicted with the analytic equation (7) - despite the several approximations that were made in the derivation presented in Section 2. This suggests that the simple algorithm introduced here could provide reliable depth estimates as long as the sources of measurement noise are minimized. It should also be noted that the blood phantom described in Section 3 is not necessarily representative of the actual chromophore content encountered in vivo. Hemoglobin in the blood phantom is most likely fully oxygenated, which is generally not the case for brain tissue. Also, the absorption coefficient values associated with the tissue-simulating phantom (figure 5(a)) are typically significantly lower than what has been measured in vivo (figure 3(a)).

Future work will test the proposed depth estimation approach during brain tumor resection. To this end, ongoing work consists in the development of an intra-operative depth-resolved fluorescence imaging instrument for which the sources of measurement noise are minimized. This will be addressed through such considerations as: using high-powered light sources, minimizing the filter bleed-through by using optical detection paths where light is collected afocally, and using a CCD chip with improved S/N characteristics and dynamical range.