Common 3-dimensional coordinate system for assessment of directional changes

Abstract

Introduction

The aims of this study were to evaluate how head orientation interferes with the amounts of directional change in 3-dimensional (3D) space and to propose a method to obtain a common coordinate system using 3D surface models.

Methods

Three-dimensional volumetric label maps were built for pretreatment (T1) and posttreatment (T2) from cone-beam computed tomography images of 30 growing subjects. Seven landmarks were labeled in all T1 and T2 volumetric label maps. Registrations of T1 and T2 images relative to the cranial base were performed, and 3D surface models were generated. All T1 surface models were moved by orienting the Frankfort horizontal, midsagittal, and transporionic planes to match the axial, sagittal, and coronal planes, respectively, at a common coordinate system in the Slicer software (open-source, version 4.3.1; http://www.slicer.org). The matrix generated for each T1 model was applied to each corresponding registered T2 surface model, obtaining a common head orientation. The 3D differences between the T1 and registered T2 models, and the amounts of directional change in each plane of the 3D space, were quantified for before and after head orientation. Two assessments were performed: (1) at 1 time point (mandibular width and length), and (2) for longitudinal changes (maxillary and mandibular differences). The differences between measurements before and after head orientation were quantified. Statistical analysis was performed by evaluating the means and standard deviations with paired t tests (mandibular width and length) and Wilcoxon tests (longitudinal changes). For 16 subjects, 2 observers working independently performed the head orientations twice with a 1-week interval between them. Intraclass correlation coefficients and the Bland-Altman method tested intraobserver and interobserver agreements of the x, y, and z coordinates for 7 landmarks.

Results

The 3D differences were not affected by the head orientation. The amounts of directional change in each plane of 3D space at 1 time point were strongly influenced by head orientation. The longitudinal changes in each plane of 3D space showed differences smaller than 0.5 mm. Excellent intraobserver and interobserver repeatability and reproducibility (>99%) were observed.

Conclusions

The amount of directional change in each plane of 3D space is strongly influenced by head orientation. The proposed method of head orientation to obtain a common 3D coordinate system is reproducible.

Acorrect jaw relationship depends on adequate interactions between a series of basal and dentoalveolar adaptations in the sagittal, coronal, and axial planes induced by growth and treatment. Serial cephalometric radiographs^1–3 and cone-beam computed tomography (CBCT)^4,5 have been used for evaluation and understanding of the changes resulting from these interactions.^1,5–7

With the advent of 3-dimensional (3D) evaluations in orthodontics, 3D models generated from CBCT have been used to assess the modifications caused by growth or different kinds of treatment. Facial changes can be quantified by obtaining measurements in cross-sectional slices of scans, in 3D surface models at 2 or more time points, or between scans or surface models registered relative to a stable structure of reference such as the cranial base (a validated voxel-based method to assess posttreatment changes in growing⁸ and adult⁹ patients).

Dental and skeletal displacements and bone remodeling of the maxilla and the mandible can be quantified by 3D linear and angular measurements based on homologous landmarks defined by observers, or by 3D linear surface distances in thousands of triangular meshes in surface models (that can be graphically displayed as color-coded surface maps). Since the original work of Moyers and Bookstein,¹⁰ advanced morphometric methods (ie, that measure morphology or form) using semilandmarks,¹¹ matrices of interlandmark distances (Euclidean Distances Matrix Analysis),¹² curved distances, or tensor-based morphometry¹³ have been proposed. However, those methods involve complex mathematical information that is not easily interpreted by clinicians.

Although 3D linear distances are a simplification of complex morphologic changes, they provide relevant clinical evaluations of changes in the space related to differences between time points. Such 3D distances express different amounts of changes in the 3 axes of the space, and clinical questions require more precise information regarding the location and amount of changes in each direction (x-, y-, and z-axes). In particular, clinicians plan their expected results of treatment based on anterior, posterior, inferior, superior, medial, or lateral movements and displacements.

However, quantification of directional differences in each plane of 3D space (3D components) can be obtained by decomposing the distances between projections of the 3D landmarks in the x, y, and z coordinate system. For any study sample comprising scans with different head orientations, the understanding of the direction of maxillomandibular changes for all patients depends on the establishment of a common coordinate system, so that directional projections can be consistent across patients. Inconsistency of head orientation across patients in a study sample would lead to inconsistent measurements; eg, anterior displacements would become more inferior with the head in clockwise rotation, or would become more lateral with the head in lateral rotation. Additionally, the identification of some landmark locations that depend on head orientation can be affected if the head is rotated or laterally tilted as well (eg, pogonion is the most anterior point of the anterior contour of the symphysis, and it can be misplaced with head rotation).

Reliable and accurate measurements should be used for a precise diagnosis and for assessment of treatment outcomes. Inconsistency in these measurements can adversely affect research conclusions and treatment plans. Some previous studies have investigated the influence of head position before the acquisition on the accuracy of the 3D measurements.^14–16 Those findings indicated that measurements based on 3D CBCT surface images were accurate, and small variations in the patient’s head position did not influence measurement accuracy. However, the rotational angles used in these previous studies do not reflect the actual differences in patient positioning during the CBCT acquisition. The rotations tested were arbitrary because no information was found in the literature with regard to the incidence and extension of patient positioning differences during scan acquisitions.¹⁴ Therefore, clinical studies based on the differences between measurements from 2 time points using the projections of the changes in the x-, y-, and z-axes are still necessary.

This study had 3 objectives: to evaluate the influence of head orientation in the assessment of 3D longitudinal changes and in each plane of 3D space, to propose a method for reaching a common coordinate system using 3D models, and to test the intraobserver and interobserver reproducibility of the proposed method.

MATERIAL AND METHODS

The sample consisted of 30 growing patients (ages, 9–13 years) who had 2 CBCT scans available at 2 time points (T1 and T2) taken at least 18 months apart with a 16 × 22-cm field of view, randomly selected from records (photographs and CBCT volumes) of patients from the Department of Orthodontics of Federal University of Rio de Janeiro in Brazil. Images were selected using the following inclusion criteria: (1) acceptable-quality images and (2) sufficient field of view to include basion, porion, glabella, and chin. The exclusion criteria were (1) motion artifacts, (2) many metallic artifacts, and (3) orthodontic appliances.

This study was approved by the University of Rio de Janeiro institutional review board (971.935).

First, the DICOM files were converted to deidentified gipl files using ITK-SNAP open-source software (http://www.itksnap.org).¹⁷ Then the 3D image analysis procedures followed these steps.

1. Approximation of the T1 and T2 scans. The T1 and T2 scans were approximated by the same observer (A.C.O.R.) having as a reference the best fit of the cranial base outlines in 3D multiplanar cross-sections using the tool transforms in Slicer open-source software (version 4.3.1; http://www.slicer.org).

2. Construction of 3D volumetric label maps of the maxilla (segmentation).¹⁸ The construction of the 3D volumetric label maps for the T1 and T2 scans was performed with the ITK-SNAP software. The automatic segmentation procedures in ITK-SNAP use active contour methods to compute feature images based on the CBCT images’ gray level intensity and boundaries. ITK-SNAP allows adjustment of the parameters for automatic detection of intensities and boundaries as well as user interactive editing of contours.¹⁹ The anatomic structures that were segmented indicated to the software in which areas it should look for corresponding voxels. After registration, the segmentations (volumetric label maps) were used to build 3D surface models that were loaded in VAM software (Vectra; Canfield Scientific, Fairfield, NJ).

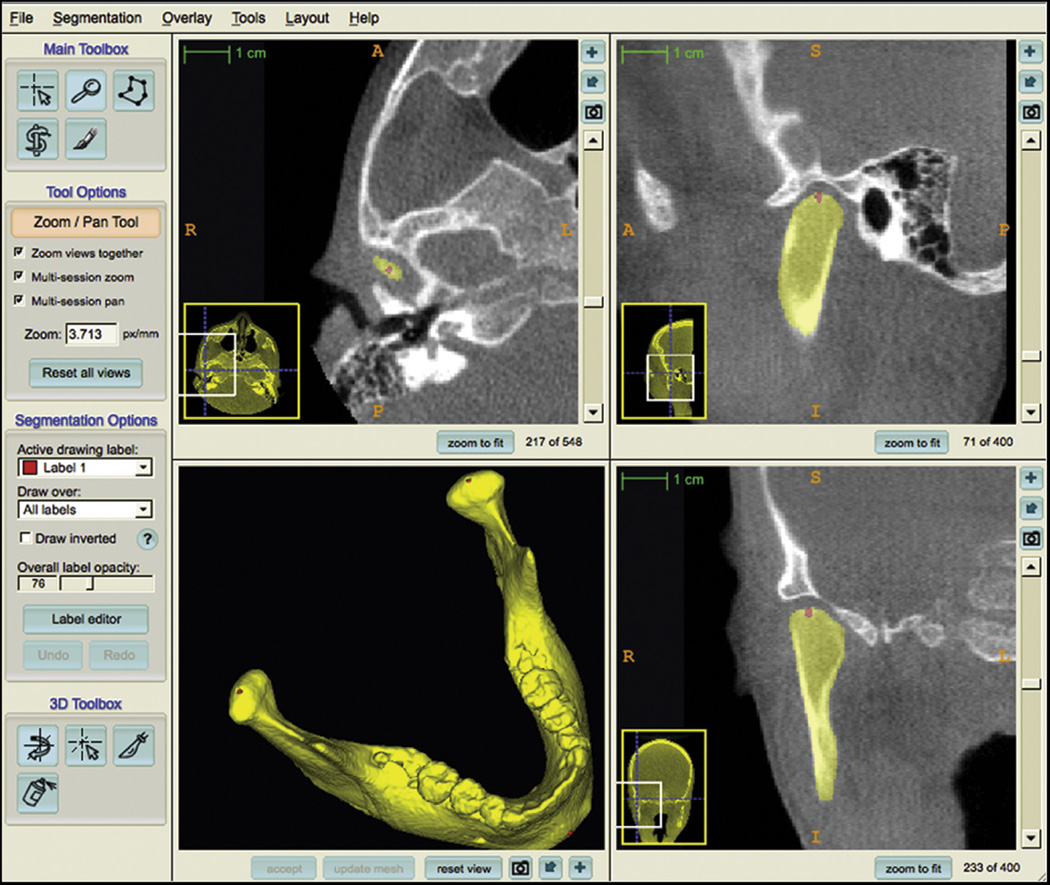
3. Placement of landmarks on the 3D volumetric label maps at T1 and T2. One label with a different color of the 3D volumetric maps was used by 1 observer (A.C.O.R.) to label 4 landmarks in the maxilla and 3 landmarks in the mandible in all T1 and T2 models to prevent any landmark identification errors. The landmarks were (1) anterior nasal spine, (2) posterior nasal spine, (3) maxillary right first molar, (4) maxillary left first molar, (5) right condylion, (6) left condylion, and (7) pogonion. The landmarks were labeled in 2 consecutive slices. Sagittal, axial, and coronal slices as well as the 3D reconstructions of the image were used for landmark positioning in the ITK-SNAP software (Fig 1).²⁰ The 3D models, labeled with the landmarks, were used for the registration procedures to prevent errors caused by segmentation or landmark placement.

4. Voxel-based registration procedures. These procedures used the cranial base anatomic structures as masks for reference, indicating to the software in which stable areas it should look for corresponding voxels. A fully automated voxel-wise rigid growing registration method (that takes into account that the images have different sizes because they are from different times, but applies only 6 degrees of freedom of rotation and translation to the T2 scan) was performed with the Slicer software.^8,21 After registration, the T2 label models resulting from the registration and the T1 label models were saved as surface mesh files (.stl files) with the Slicer software.

5. Landmark-based quantitative assessments in the VAM software. The 3D surface mesh models with landmarks prelabeled were loaded into VAM software, and the coordinates (x, y, and z) were generated for each landmark on the T1 and the registered T2 surface models. Two kinds of quantitative assessments of the differences between landmarks were performed:

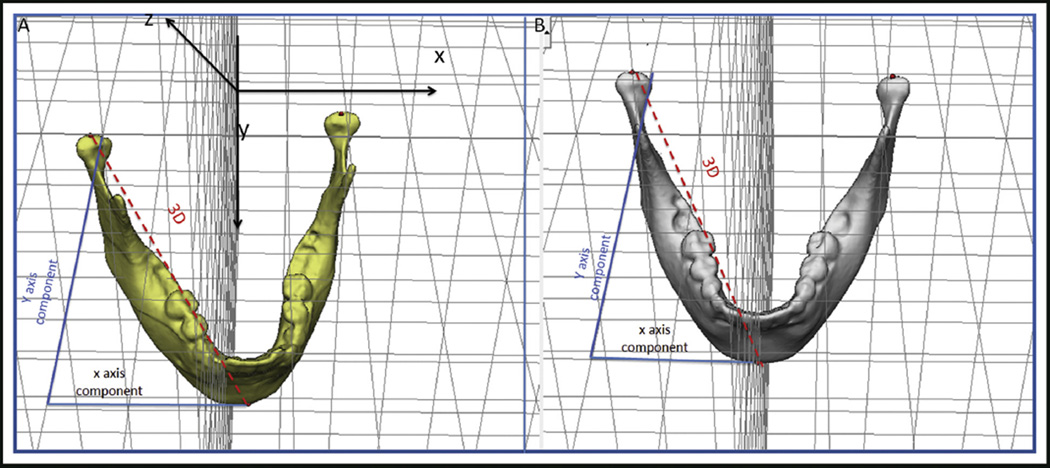
   1. At 1 time point (any time point, initial or follow-up): the 3D distance and its components in each plane of the space were measured for mandibular width and length. The 3D measurements corresponded to the Euclidean distances between the right and left condylions, and the right condylion and pogonion. Changes in each plane of the space were assessed by the distances between the corresponding coordinates of the corresponding landmarks (right and left condylions, and right condylion and pogonion), which represented the transversal (x-axis), anteroposterior (y-axis), and vertical (z-axis) differences (Fig 2).
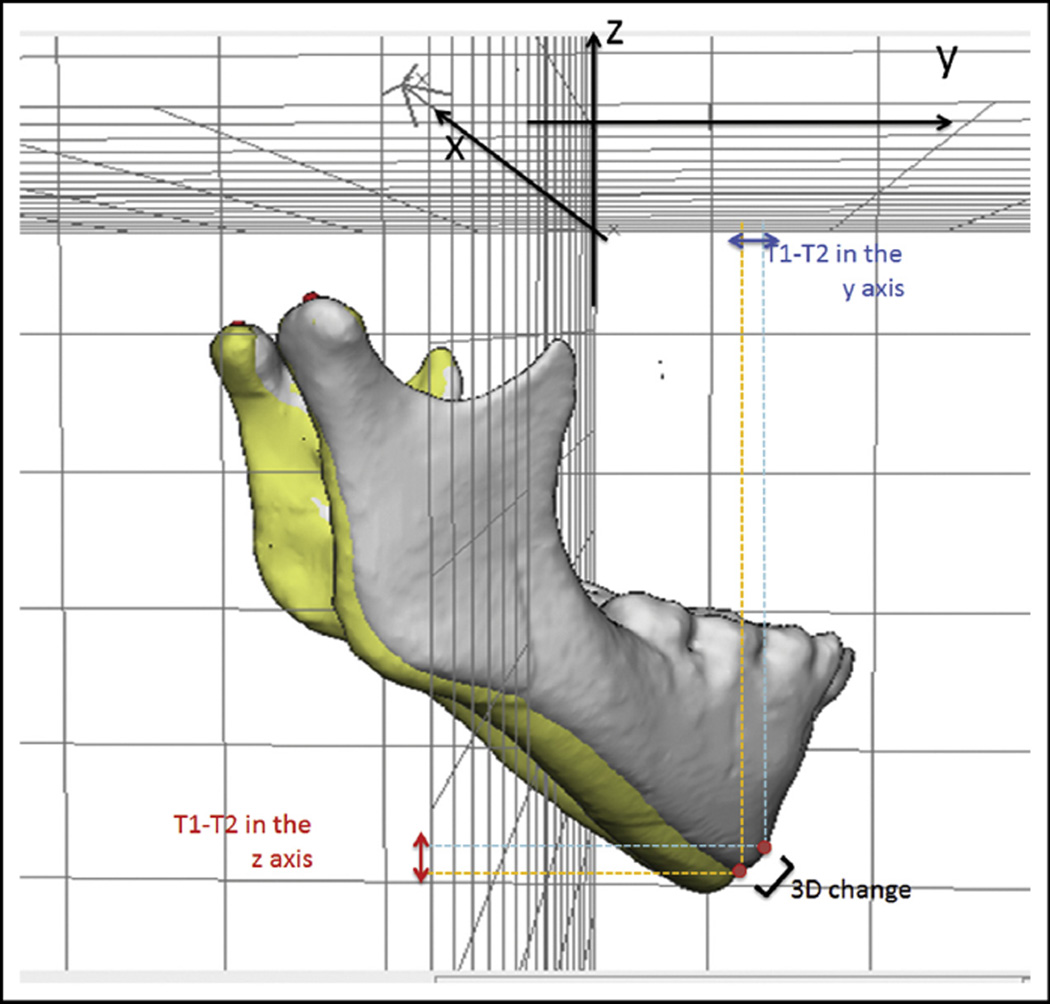
   2. Differences between 2 time points (T1 and T2): the 3D distance and its components in each plane of the space for displacements of the maxilla (distance between anterior nasal spine at T1 and T2) and the mandible (difference between pogonion at T1 and T2) were measured in relation to the cranial base (cranial base registration). The 3D measurements corresponded to the Euclidean distances between the T1 and T2 anterior nasal spine landmarks and the T1 and T2 pogonion landmarks.²² The distances between corresponding coordinates of corresponding landmarks (anterior nasal spine at T1 and T2, and pogonion at T1 and T2), which corresponded to the transversal (x-axis), anteroposterior (y-axis), and vertical (z-axis) displacements were also performed as changes in each plane of space (3D components) (Fig 3).

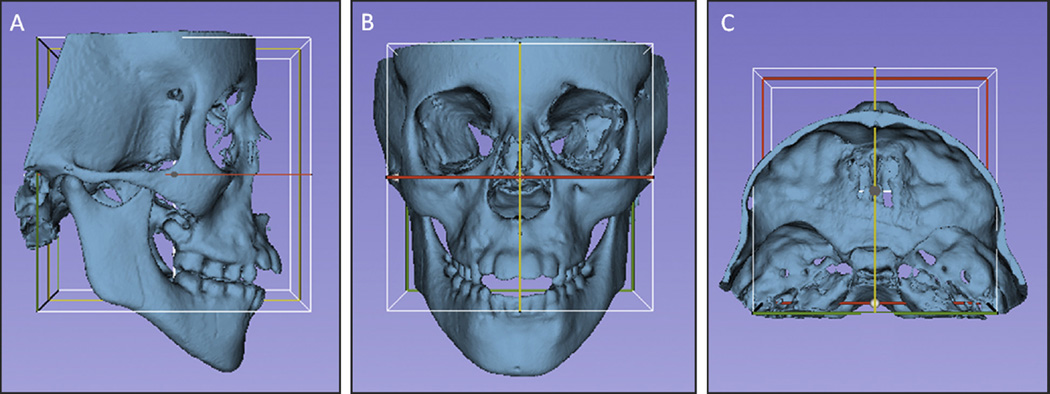
6. Head orientation. The T1 surface models were oriented using the transforms tool in Slicer software (Fig 4). All T1 surface models were moved by orienting its Frankfort horizontal, midsagittal, and transporionic planes to match the axial, sagittal, and coronal planes, respectively, at a common coordinate system in the Slicer software. The 3D orientation was achieved using 3 planes defined by at least 3 landmarks or 2 landmarks and a plane: Frankfort horizontal, midsagittal, and transporionic planes.²³ The midsagittal plane was defined by glabella, crista galli, and basion. The Frankfort horizontal plane was defined bilaterally by the right and left porions and the right and left orbitales. The transporionic plane was defined bilaterally by the porion landmarks and is perpendicular to the Frankfort horizontal plane. The Slicer software displays a fixed 3D coordinate system (red, yellow, and green planes in Fig 4) that was used as the reference to orient the 3D models. Using the axial, coronal, and sagittal views of the 3D models, the T1 model was moved to orient the midsagittal plane vertically and coincident with the yellow (sagittal) plane of the 3D coordinate system. The Frankfort horizontal plane was oriented to match the red (axial) plane. The horizontal transporionic line was oriented to be coincident with the intersection between the red (axial) and green (coronal) planes in both sides of the head. The matrix (file that contains the information relative to translational and rotational movements to obtain the orientation) generated from this step was applied to the T2 registered surface model, reaching the same head orientation. Then the same measurements performed in step 5 (3D components and 3D differences) were repeated for the oriented surface models (T1 and registered T2).

7. Comparisons between measurements at the 1 time point scan, before and after head orientation. Assessments of mandibular width (distance from right to left condylion) and length (distance from right condylion to pogonion) were performed in the 3D surface models to evaluate whether the values were influenced by the head positioning. Threedimensional measurements and 3D components obtained before and after head orientation were compared.

8. Comparisons between longitudinal changes, before and after head orientation based on registered 3D models (cranial base registration). Assessments of the positional changes (displacements caused by growth or treatment) between the 3D surface models (T2-T1) were performed comparing the T2 to T1 changes before head orientation vs the T2 to T1 changes after head orientation to evaluate the head positioning displacement. Two measurements were performed: maxillary (anterior nasal spine displacement) and mandibular displacement (pogonion displacement).

9. Assessment of the intraobserver and interobserver reproducibility. For 16 subjects, the procedure of head orientation was performed at 2 times (orientations 1 and 2) with a 1-week interval between them by 2 observers (A.C.O.R., M.S.Y.), working independently. These observers were trained and calibrated to perform the head orientation using a set of 30 3D surface models not included in this study. To test the interobserver reproducibility, the x, y, and z coordinates (generated by the 2 observers) of corresponding landmarks were compared after each of the 2 orientation procedures. The intraobserver reproducibility was tested by comparing the x, y, and z coordinates from the 2 repeated head orientations for each observer.

Fig 1.

Images showing mandibular 3D volumetric model with 3 prelabeled landmarks (right and left condylions and pogonion) used to obtain reliable landmark identification for comparisons between before and after orientations and for testing the reproducibility of the method.

Fig 2.

Representation of 3D measurements and changes in each component of the 3D space (x and y components). Distances between landmark coordinates (right and left condylions), representing the transversal (x-axis), anteroposterior (y-axis), and vertical (z-axis) differences. A, Before head orientation; B, after head orientation.

Fig 3.

Representation of the 3D differences and changes in each component of the 3D space (y and z components) between 2 time points that were registered on the cranial base.

Fig 4.

Figures illustrating the head orientation procedure: A, lateral view; B, frontal view; and C, superior view. The midsagittal plane of the 3D model was oriented vertically and coincident with the yellow (sagittal) plane, the Frankfort horizontal plane was oriented horizontally to coincide with the red (axial) plane, and the transporionic line was oriented to match with the intersection of the red (axial) and green (coronal) planes. The white box corresponds to the limits of the 3 cited planes, and it was not used as a reference for orientation.

Statistical analysis

Statistical analyses were carried out with MedCalc (version 14.10.2; MedCalc Software, http://www.medcalc.org/). Descriptive statistics of the differences between the before and after head orientations for the 3D changes and their components in each plane of the 3D space included means and standard deviations. The normality of the data was tested using the Shapiro-Wilk test. The comparison of measurements before and after head orientation at the 1 time-point scan was performed by paired t test. The Wilcoxon test was run to compare longitudinal changes before and after head orientation based on the cranial base registration. The statistical significance was set at P < 0.05.

Intraobserver and interobserver agreement was tested with the intraclass correlation coefficient (with 2-way random effects model) and Bland-Altman plots²⁴ of the 95% limits of agreement, average differences ± 1.96 of the standard deviation of the differences, and evaluations of the concordance between corresponding x, y, and z coordinate pairs from corresponding landmarks generated from the 3D surface mesh models after head orientation by both observers.

RESULTS

Table I shows the comparison of measurements before and after head orientation at 1 time point for the 3D distances and 3D components (x, y, and z distances). The 3D distances representing the width and length of the mandible did not show differences caused by head positioning. The measurements based on each of the 3D components, which represent distances in the x-, y-, and z-axes, displayed significant statistical differences in all measurements.

Table I.

Comparisons between measurements before (B.or) and after (A.or) head orientation at baseline for 3D distances and 3D component differences

	Measurement	Mean ± SD (mm)	B.or-A.or (mm)	P value (paired t test)
Mandibular width (Dist RCo−LCo)
3D	B.or	89.94 (±6.69)	0.01	0.88
	A.or	89.95 (±6.74)
x component	B.or	89.26 (±6.70)	0.62	0.00*
	A.or	89.88 (±6.71)
y component	B.or	9.61 (±5.37)	8.15	0.00*
	A.or	1.46 (±1.19)
z component	B.or	2.37 (±1.48)	1.07	0.01*
	A.or	1.30 (±1.15)
Mandibular length (Dist RCo−Pog)
3D	B.or	109.88 (±7.32)	0.25	0.10
	A.or	110.13 (±7.35)
x component	B.or	50.16 (±6.17)	4.73	0.00*
	A.or	45.43 (±4.28)
y component	B.or	57.03 (±15.93)	9.18	0.00*
	A.or	66.21 (±8.23)
z component	B.or	77.44 (±9.32)	2.82	0.01*
	A.or	74.62 (±7.94)

^*P < 0.05 means a significant statistical difference.

Table II displays the comparisons of changes (differences between T1 and T2) before and after head orientation comparing 2 time points previously registered in relation to the cranial base (reference structure) for the 3D distances and 3D components (x, y, and z distances). The means and standard deviations of the 3D changes were similar for the maxillary and mandibular displacements. The means and standard deviations of the 3D components between the 2 time points were small at all axes. However, the changes in the 3D components were statistically significant for the z-axis (maxillary displacement) and y-axis (mandibular displacement).

Table II.

Comparisons between measurements of 3D changes and 3D components changes before (B.or) and after (A.or) head orientation

	Change	Mean ± SD (mm)	B.or–A.or (mm)	P value (Wilcoxon)
Maxillary changes
3D	T2-T1 B.or	5.33 (±5.26)	0.07	0.106
	T2-T1 A.or	5.26 (±5.19)
x component	T2-T1 B.or	0.73 (±1.91)	0.10	0.63
	T2-T1 A.or	0.83 (±1.97)
y component	T2-T1 B.or	0.98 (±3.49)	0.17	0.74
	T2-T1 A.or	1.15 (±3.85)
z component	T2-T1 B.or	3.08 (±3.60)	0.57	0.01*
	T2-T1 A.or	2.55 (±3.56)
Mandibular changes
3D	T2-T1 B.or	4.47 (±2.98)	0.03	0.67
	T2-T1 A.or	4.50 (±2.95)
x component	T2-T1 B.or	1.26 (±2.93)	0.08	0.41
	T2-T1 A.or	1.34 (±2.99)
y component	T2-T1 B.or	1.83 (±2.88)	0.32	0.02*
	T2-T1 A.or	2.15 (±3.43)
z component	T2-T1 B.or	2.04 (±2.41)	0.24	0.49
	T2-T1 A.or	1.81 (±2.39)

^*P < 0.05 means a significant statistical difference.

Table III displays the statistics to test the intraobserver and interobserver agreements relative to the head orientation performed by both observers. The intraclass correlation coefficient between observers and head orientation reproducibility were extremely high (>0.99), resulting in excellent agreement.

Table III.

Measurements of intraobserver and interobserver reproducibility

	Intraclass correlation coefficient (95% CI)
	Anterior nasal spine	Posterior nasal spine	Maxillary right first molar	Maxillary left first molar	Right condylion	Left condylion	Pogonion
Intraobserver
Obs 1, O1 × O2	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)
Obs 2, O1 × O2	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)
Interobserver
Obs 1 × Obs 2, O1	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)
Obs 1 × Obs 2, O2	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)	0.99 (0.99-1)

Obs, Observer; O, observation.

Table IV shows the results from the Bland-Altman limits of agreement. From this table, one would expect that 95% of the differences between corresponding coordinates from corresponding landmarks obtained from the head orientations provided by both observers in this study would be smaller than 0.77, 0.94, 1.22, 1.02, 1.18, 0.95, and 0.85 mm for anterior nasal spine, posterior nasal spine, maxillary right first molar, maxillary left first molar, right condylion, left condylion, and pogion, respectively.

Table IV.

Measurements of intraobserver and interobserver reproducibility: Bland-Altman means (mm), standard deviations, and 95% limits of agreement (LoA, in mm) for comparisons between corresponding x, y, z coordinates

	Results from Bland-Altman: mean (mm) and 95% LoA (mm)
	Anterior nasal spine		Posterior nasal spine		Maxillary right first molar		Maxillary left first molar		Right condylion		Left condylion		Pogonion
	Mean	LoA	Mean	LoA	Mean	LoA	Mean	LoA	Mean	LoA	Mean	LoA	Mean	LoA
Intraobserver
Obs 1, O1 × O2	0.10	−0.53, 0.72	−0.02	−0.94, 0.91	−0.12	−1.22, 0.98	0.10	−0.60, 0.81	0.00	−0.93, 0.93	0.10	−0.71, 0.90	0.04	−0.62, 0.70
Obs 2, O1 × O2	−0.03	−0.67, 0.61	−0.05	−0.65, 0.54	−0.16	−0.98, 0.66	−0.10	−0.84, 0.65	0.02	−0.69, 0.73	0.00	−0.72, 0.72	−0.02	−0.69, 0.65
Interobserver
Obs 1 × Obs 2, O1	0.06	−0.64, 0.76	−0.02	−0.68, 0.64	−0.07	−0.98, 0.85	0.04	−0.78, 0.87	−0.15	−1.18, 0.87	−0.05	−0.91, 0.82	−0.03	−0.75, 0.69
Obs 1 × Obs 2, O2	−0.06	−0.77, 0.64	−0.06	−0.87, 0.75	−0.11	−1.07, 0.85	−0.15	−1.02, 0.72	−0.13	−1.07, 0.81	−0.14	−0.95, 0.67	−0.09	−0.85, 0.67

Obs, Observer; O, observation.

DISCUSSION

Significant effort has been devoted to compare diagnostic and outcome measurements taken from CBCT images.²⁵ The accuracy of 3D reconstructed images has been previously evaluated, and the findings showed that direct 3D measurements are highly accurate with no significant discrepancies from the physical measurements.^26,27

Because our objective was to test errors caused by head orientation, we controlled for errors from landmark identification and location by prelabeling the landmarks in the 3D maps before the head orientation. This was a careful methodologic step to prevent errors because of the choice of landmark locations.

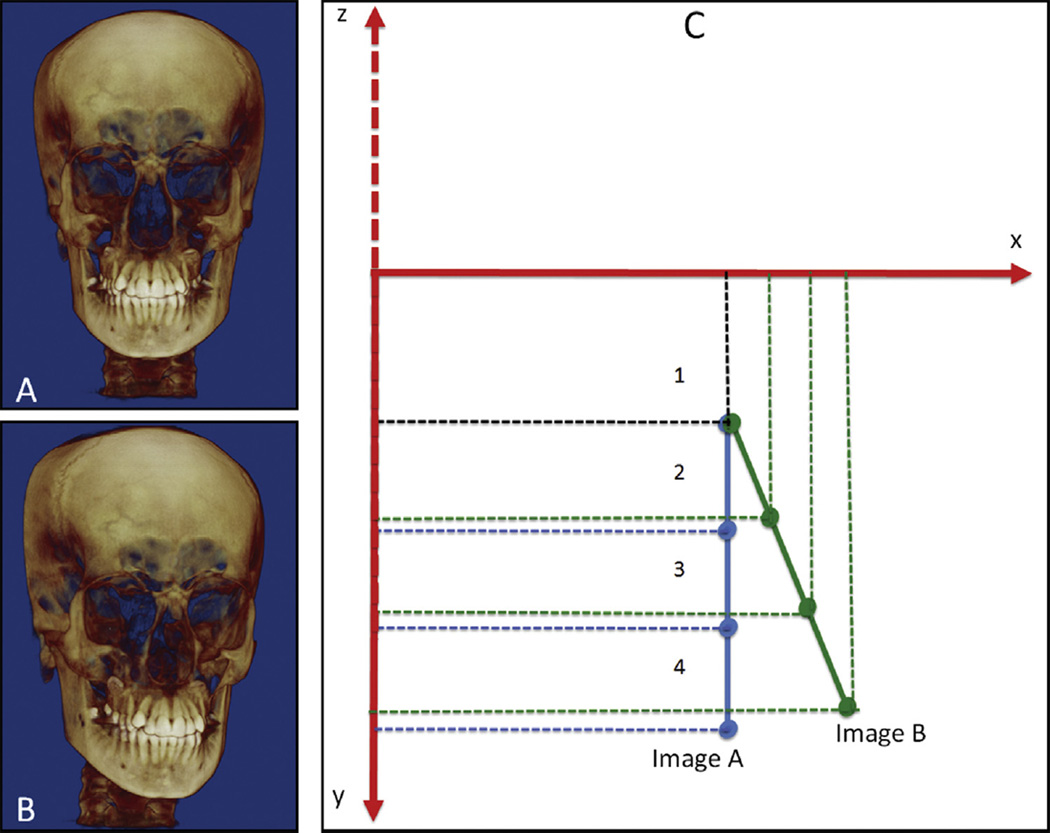
During the acquisition of the 3D facial images, efforts were made to reproduce the natural head position, and commercial and open-source image analysis software also provided tools to adjust and correct the patients’ head positioning after image acquisition. Although the use of mini-3D sensors,²⁸ laser light beams projected on a patient’s face,²⁹ or a gyroscope with fiducials³⁰ has been proposed to register head position longitudinally, a method to establish a common coordinate system for head orientation across patients in a study sample has not been proposed yet. Figure 5, A and B, can represent the same image of 1 patient before and after head orientation (at 2 times in the same patient) or 2 images of 2 patients with different head positioning. Then, the linear displacements based on each component of 3D space (3D components in the x, y, and z coordinates) could be affected because the same landmark (1, 2, 3, or 4) in the same 3D image with 2 head positions might have different x, y, and z coordinates (Fig 5).

Fig 5.

A and B, Images with different head positions; C, simulation of coordinate generations of 4 landmarks from 2 head positions. Linear changes in each component of 3D space based on the x, y, and z coordinates could be affected because the same landmark (1, 2, 3, or 4) in the same 3D model with 2 head positions might have different x, y, and z coordinates.

Comparisons of the measurements before and after head orientation at 1 time point showed that 3D linear distances representing the width and length of the mandible did not have differences caused by the head positioning (Table I). Previous studies have reported reliability of 3D linear distance measurements.^14,16 However, our findings showed that measurements representing the anteroposterior (or horizontal), superoinferior (or vertical), and mediolateral (or transversal) distances based on the 3D components in each plane of space had significant statistical differences in all of the measurements performed. The 3D components of the mandibular measurements would be altered by head orientation.

Our findings showed that the amount of directional differences (3D component differences) at 1 time point can be misinterpreted depending on head positioning: eg, for asymmetry assessments, sample characterizations, or comparisons among different populations in cross-sectional studies. Also, if the same measurements are performed in a follow-up study using 3D models without registration, the comparisons of directional changes between 2 time points can be biased by the lack of a common head orientation, both for each patient and across all patients in a study sample. Depending on the head orientation during the image acquisition, measurements in one direction can be more affected than in another direction.

With the goal of measuring differences between 2 time points, cranial base registration has been advocated in several studies on growth and follow-up evaluations.^4,5,17,31 The 3D registered models resulting from 3D registrations provide the advantage of measuring changes directly between landmarks at different time points (Fig 3).

Our results showed that measurements from 3D surface mesh models registered relative to the cranial base (longitudinal studies) were not affected by the head position (Table II), corroborating findings from previous studies in the orthodontic literature.^14,16,27 The means and standard deviations of the maxillary and mandibular changes were similar for before and after head orientation changes. Hassan et al¹⁴ evaluated the accuracy of linear measurements using 3D CBCT images at 2 head positions and found no significant difference between the linear measurements at the different head positions.

Because the amount and direction of differences or changes are clinically relevant, we also compared the T1 to T2 changes in the 3 planes of the space (3D components), before and after head orientation, as shown in Table II. The means and standard deviations of the changes between the 2 time points, comparing before and after head orientations, were small at all axes because of the use of measures directly between 3D landmarks in the registered models. However, the zaxis for maxillary changes and the y-axis for mandibular changes were statistically different.

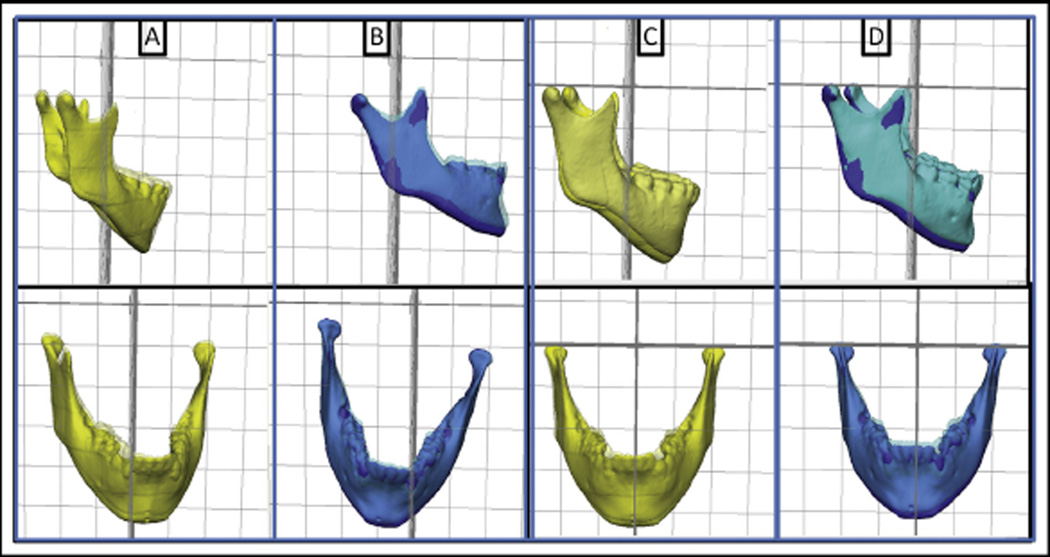
Describing changes between 2 or more time points as horizontal and vertical, or anteroposterior, superoinferior, and transversal, is helpful and common in orthodontics. But are these references in relation to the patient’s face or to a coordinate system based on the true vertical, or on natural head position? If so, it should be important to specify the results (eg, 3 mm of anterior displacement along the patient’s medial sagittal plane) or to standardize the head orientation for comparable cross-sectional evaluations. As we can see in Figure 6, for some subjects in the sample, from T1 to T2, the amount of changes in each axis can have different proportions before and after head orientation.

Fig 6.

Importance of head orientation for cross-sectional studies: A and B, anterior displacements do not mean displacement along the medial sagittal plane for both patients (represented by yellow and blue 3D models); C and D, images after head orientation. Anterior, vertical, and lateral displacements can be compared.

Another crucial point refers to the amount of displacement in each axis when comparing different subjects from 1 sample (eg, the anterior change for 1 patient cannot mean anterior changes for all patients). In Figure 6, anterior (y-axis), vertical (z-axis), and lateral (x-axis) changes for both patients (yellow and blue) do not correspond to the displacements along the medial sagittal plane (Fig 6, A and B). Then, we would be comparing or putting together different things. After head orientation (Fig 6, C and D), anterior, vertical, and lateral changes are comparable. These differences, in millimeters, can be small when the changes between 2 time points are small but are more representative in surgical patients with large displacements such as in distraction osteogenesis.

Extra care should be taken during patient positioning and head orientation after image acquisition if the image evaluation involves the use of measurements based on the 3D components in the x-, y-, and z-axes, or if 2-dimensional images are reconstructed from a 3D data set. The head orientation should be saved, so that every image of every subject has the same reference planes.

Moyers and Bookstein¹⁰ have long correctly affirmed that understanding skeletal growth and changes over time requires direct measurements of shape and size rather than depending on only fixed points (landmarks or implants). They also warned clinicians about the considerable importance of the orientation in cross-sectional studies. We recognize that distances based on landmark methodology still fail in evaluating shape, but the use of 3D components (changes in each component of the 3D space) gives more information than a 3D linear measurement by itself because the 3D components allow better comprehension of the directionality and the amount of the change in the anteroposterior, superoinferior, and transversal directions.

In our study, the 3D surface models were oriented using the 3D hard tissue surface representation, so that the transporionic plane, the Frankfort horizontal plane, and the midsagittal plane were coincident with the x-, y-, and z-axes, respectively. We believe that this orientation is closest to the natural head position and that our results should be based on the natural head position because it is the patients’ most reproducible position. The left and right auditory external meatus and foramen magnum were selected based on their positions and early formation in skeletal growth. It has been reported that most of the cranial base growth (>85%) occurs in the first 5 years of life, with minor changes after this age.³²

Overall, the intraobserver and interobserver reproducibilities of this method of head orientation were excellent based on both the intraclass correlation coefficient (>0.99) and the agreement evaluated by Bland-Altman plots²⁴ that showed small values for limits of agreement and values of the means close to zero (Tables III and IV). By performing the head orientation, the assessments of growth and treatment changes for clinical or research purposes will be supported by precise and consistent measurements.

Since currently there is no totally reproducible head orientation method during scan acquisition, we proposed a method for head orientation after image acquisition to obtain a 3D common coordinate system and comparable measurements from 3D components in any axis of a coordinate system.

CONCLUSIONS

The amount of directional changes in each plane of 3D space is strongly influenced by head orientation. A standardized head orientation and a common coordinate system allow proper anteroposterior, vertical, and transversal assessments. The proposed method of head orientation to obtain a common 3D coordinate system is reproducible.