Simultaneous Cortical Surface Labeling and Sulcal Curve Extraction

Abstract

Automatic labeling of the gyri and sulci on the cortical surface is important for studying cortical morphology and brain functions within populations. A method to simultaneously label gyral regions and extract sulcal curves is proposed. Assuming that the gyral regions parcellate the whole cortical surface into contiguous regions with certain fixed topology, the proposed method labels the subject cortical surface by deformably registering a network of curves that form the boundary of gyral regions to the subject cortical surface. In the registration process, the curves are encouraged to follow the fine details of the sulcal geometry and to observe the shape statistics learned from training data. Using the framework of probabilistic point set registration methods, the proposed algorithm finds the sulcal curve network that maximizes the posterior probability by Expectation-Maximization (EM). The automatic labeling method was evaluated on 15 cortical surfaces using a leave-one-out strategy. Quantitative error analysis is carried out on both labeled regions and major sulcal curves.

1. INTRODUCTION

Extracting and labeling anatomical regions of interest on the human cerebral cortex is important in many neuroscience studies. Automatic labeling methods are typically used since manual delineation is too time-consuming for the analysis of large populations. Because of substantial inter-individual variability of topographic features on the cortical surface, automated labeling methods may lack accuracy and topological consistency.

Various approaches have been taken to automatically or semi-automatically detect regions or features of interest on the cortical surface. Sandor¹ used surface registration to map the anatomical labels from an atlas surface to the subject’s surface. In order to avoid the bias of a single atlas, a probabilistic atlas is often created based on the anatomy of a large number of registered subjects. Fischl² constructed a probabilistic atlas that retains information about each cortical label at each point in atlas space and automatically parcellated the whole cortical surface by maximizing the posterior given the subject surface geometry. Tao³ deforms a network of sulcal curves to match the high curvature region in the subject cortical surface using an active shape model⁴. Watershed transformation based approaches were presented in Lohmann⁵ and Rettmann⁶ to segment the sulcal regions, but they need manual labeling to identify the segmented regions. Graph-based approaches were taken in Goualher⁷ and Shi⁸, in which the relationships between sulci are modeled by graphs and used in the automatic labeling process. Lyu⁹ proposed spectral matching based curve matching method to label and refine the sulcal curve set extracted on the cortical surface.

We are interested in labeling the whole cortical surface with gyral regions and at the same time attaining accurate representation of sulcal curves that form the boundaries of these regions. We assume that the gyral regions parcellate the whole cortical surface into contiguous regions with certain fixed topology and label the subject’s cortical surface by deformably registering a network of curves that form the boundary of these gyral regions to the surface. Using a Bayesian framework for point set registration,¹⁰ the extracted curves follow the high curvature region on the subject’s cortical surface and at the same time preserve the anatomical convention learned from the training data. Our work is related to Tao’s work in [3], in which only a set of a few major sulci were detected. Here we consider a much richer set of connected curves, forming a detailed parcellation of the whole cortical surface.

The rest of the paper is organized as follows: Section 2 gives the outline of the proposed method. In Section 3, we explain how to learn the statistical shape model of sulcal curves from training subjects. The curve deformable registration algorithm is described in Section 4. Experimental results are presented in Section 5 with quantitative accuracy evaluation of automatically extracted gyral regions and major sulci. Finally, conclusions are drawn in Section 6.

2. METHOD OUTLINE

Fig. 1 shows the flattened gyral region map used in this paper; it was designed based on the gyral ROIs defined in [11]. The boundaries of gyral regions is a network of connected curves, referred to as sulcal curve network (SCN) in the following text. Most of the curves coincide with major or minor sulci on the cortical surface. Since the gyral regions and the SCN are mutually dependent, a subject cortical surface can be labeled by locating the SCN on the surface. Fig. 1 also lists the major sulci defined on the SCN.

Figure 1.

Flattened gyral region map and the sulcal curve network (SCN). Major sulci are outlined by thick colored curves.

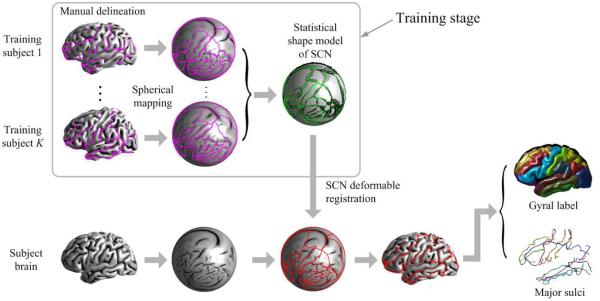
Fig. 2 shows the outline of the proposed method. In the training stage, the SCN is delineated manually according to the gyral region map by a trained rater on the outer cortical surface of each training subject. In order to study the shape statistics of SCN in a common surface manifold, the cortical surfaces of all training subjects are mapped to the unit sphere¹². A statistical shape model (SSM) is computed over the training SCNs on the unit sphere, which includes a mean shape, a set of principal shape modes and feature statistics at each point. Given a subject cortical surface, we first map it to the unit sphere, resulting in a unit sphere with subject feature map, then deform the mean shape of the SCN with the SSM as part of the shape prior to fit the subject feature map. Gyral regions and sulcal curves can be obtained from the registered SCN.

Figure 2.

Outline of the proposed method.

3. STATISTICAL SHAPE MODEL(SSM)

An SCN is represented by a set of ordered landmark points with a feature vector associated with each point. After an SCN is delineated on each training subject, each curve S_i in the SCN is sampled with m_i landmark points, where m_i is determined by the average length of the curve over all training subjects. The SSM consists of two parts:

1) A point distribution model (PDM)⁴ that consists of a mean shape, which is the average of the training shapes, and a set of eigen-modes, which characterizes the range of variation of the shape from the mean shape. We use similar method as in [ 3] to build the SSM on the unit sphere. First, Procrustes alignment is carried out to simultaneously register all the training shapes Y_k, k = 1, 2, …, K, and acquire a mean shape $\stackrel{‒}{\mathbf{Y}}$. Then, each landmark point of a training subject is projected to the tangent plane at the corresponding mean shape point by radial projection, resulting in a local planar coordinate. Principal component analysis (PCA) is carried out on the local planar coordinates of all landmark points. The 2D principal modes thus obtained are converted to the 3D Euclidean space, acquiring a set of 3D shape modes W_i, which can be used directly to form the manifold of highly probable shapes. We define shape manifold Ω as the linear combination of the shape modes, under a rotation transformation on the unit sphere. Ω represents the set of highly probable shapes according to prior knowledge,

$$\Omega =\{{\mathbf{Y}}_p\mid {\mathbf{Y}}_p=(\stackrel{‒}{\mathbf{Y}}+\sum _{i=1}^L{\alpha }_i{\mathbf{W}}_i){\mathbf{R}}^T\},\mathbf{R}\in {\mathbf{SO}}_3,$$

where L is the number of principal shape modes used.

2) Statistics of feature vectors at each point of the SCN. Let f_mk be the feature vector associated with point y_mk on a training shape. In our SSM, the feature vector contains the mean curvature of the subject surface at different levels of inflation. We assume that the feature vector at each landmark point follows a multivariate Gaussian distribution and compute the mean μ_m and covariance matrix Σ_m at each landmark point.

4. DEFORMABLE REGISTRATION

The probabilistic based point set registration framework in [ 10] is used for the deformable registration of the SCN, which has shown to be both accurate and robust in registering two point sets. Here the source point set is formed by points from the SCN and the target point set is sampled from the unit sphere with subject feature map. It considers the registration problem as a probability density estimation problem, where the source point set are the centroids of a Gaussian Mixture Model (GMM) and the target point set are data points, and find the GMM centroids with maximum posterior to fit the data points. Two modifications are made upon the original registration algorithm: 1) In order to consider the feature vector of the SCN points, the vector space in which the GMM lies is the union of 3D Euclidean space and the feature vector space. However, the coordinates of centroids corresponding to the feature vector are fixed as the mean computed in SSM and only the spatial coordinates of SCN are being optimized. 2) We introduce a prior on GMM centroids to enforce smoothness and connections on curves and penalize shape far away from the shape manifold defined by the SSM.

Before describing the algorithm in detail, we list some notations conventions.

X : Target point set, formed by N points x₁, x₂, …, x_N. Each point x_n = {x_n, f_n} in X consists of a coordinate x_n and a feature vector f_n.

Y : Source point set, formed by M points y₁, y₂, …, y_M. Each point y_m = {y_m, μ_m} consists of a spatial coordinate y_m and a fixed feature vector μ_m, which is the mean feature vector learned in Section 3. Since the SCN is formed by a set of curves, the point set has the following structure,

$$y_1^1,y_2^1,\dots ,y_{M_1}^2,y_1^2,y_2^2,\dots ,y_{M_1}^2,\dots ,y_1^S,y_2^S,\dots ,y_{M_S}^S,$$

where S is the number of curves in the shape. M_s is the number of points in the s-th curve. $y_1^s,y_2^s,\dots ,y_{M_1}^s$ are ordered landmark points representing the s-th curve.

X = (x₁, x₂, …, x_N)^T : An N × 3 matrix representing the spatial coordinates of target point set.

Y = (y₁, y₂, …, y_M)^T : An M × 3 matrix representing the spatial coordinates of source point set.

I: Identity matrix.

1: Column vector of all ones.

According to [10], the optimal location of source point set Y can be obtained by maximizing the posterior probability p(Y|X), or equivalently, by minimizing the negative log-likelihood function

$$E\left(\mathbf{Y}\right)=-\sum _{n=1}^N\text{log}p(x_n\mid \mathbf{Y})-\text{log}\mathbf{p}\left(\mathbf{Y}\right)$$ (1)

where $p(x\mid \mathbf{Y})={\sum }_{m=1}^{M+1}\pi \left(m\right)p(x\mid m)$ is a Gaussian mixture density with point set Y as the centroids. Assuming equal isotropic covariances σ² and equal membership probabilities, we have π(m) = 1/M. The Gaussian distribution associated with the m-th centroid in Y is defined as a joint distribution on the union of spatial and feature space,

$$p(x\mid m)=\frac{1}{{\left(2\pi {\sigma }^2\right)}^{3∕2}}\text{exp}\left(-\frac{\parallel \mathbf{x}-{\mathbf{y}}_m{\parallel }^2}{2{\sigma }^2}\right)\frac{1}{\mid {\sum }_m{\mid }^{1∕2}}\text{exp}\left(-\frac{1}{2}{(\mathbf{f}-{\mu }_m)}^T{\Sigma }_m^{-1}(\mathbf{f}-{\mu }_m)\right),{\forall }_m=1,2,\dots ,M.$$

To account for the points in X that do not correspond to any point in Y, called background points, an additional Gaussian distribution is added to the mixture model,

$$p(x\mid M+1)=\frac{1}{N}\frac{1}{\mid {\Sigma }_{\mathbf{M}+1}{\mid }^{1∕2}}\text{exp}\left(-\frac{1}{2}{(\mathbf{f}-{\mu }_{M+1})}^T{\Sigma }_{\mathbf{M}+1}^{-1}(\mathbf{f}-{\mu }_{\mathbf{M}+1})\right)$$

where μ_M+1 and Σ_M+1 are the mean and covariance matrix of the feature vector associated with background points. The complete mixture model can be written as

$$p(x\mid \mathbf{Y})=\omega p(x\mid M+1)+(1-\omega )\sum _{m=1}^M\frac{1}{M}p(x\mid m)$$

where the weight 0 ≤ ω ≤ 1 depends on the percentage of background points in the target point set.

The shape prior p(Y) in Eq.(1) is defined as

$$p\left(\mathbf{Y}\right)=\text{exp}\left(-\frac{{\lambda }_c}{2}{\varphi }_c\left(\mathbf{Y}\right)\right)\text{exp}\left(-\frac{{\lambda }_p}{2}{\varphi }_p\left(\mathbf{Y}\right)\right)$$ (2)

where function

$${\varphi }_c\left(\mathbf{Y}\right)=\parallel \mathbf{LY}{\parallel }_F^2+\sum _{(i,j)\in \Phi }\parallel {\mathbf{y}}_i-{\mathbf{y}}_j{\parallel }^2$$ (3)

regularizes the curves to be smooth and connected to each other. L is a linear operator that evaluates the second order derivative of each curve. It has the following form

$$\mathbf{L}=\left(\begin{array}{cccc}\hfill {\mathbf{L}}_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathbf{L}}_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\mathbf{L}}_S\hfill \end{array}\right),\text{where}{\mathbf{L}}_s=\left(\begin{array}{ccccc}\hfill -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill & \hfill -2\hfill \end{array}\right).$$

The term ${\sum }_{(i,j)\in \Phi )}\parallel {\mathbf{Y}}_i-{\mathbf{Y}}_j{\parallel }^2$ in Eq. (3) enforces connections between end points of curves. A pair of indices (i, j) is in set Φ if point y_i and y_j are connected end points in the SCN. Eq. (3) can be combined as a single linear transformation of Y, φ_c(Y) = $\parallel {\mathbf{L}}^{\prime }\mathbf{Y}{\parallel }_F^2$. Function φ_p(Y) in Eq.(2) is defined as the Euclidean distance between Y and shape manifold Ω introduced in Sec. 3,

$${\varphi }_p\left(\mathbf{Y}\right)=d^2(\mathbf{Y},\Omega )=\underset{{\mathbf{Y}}_p}{\text{min}}\parallel \mathbf{Y}-{\mathbf{Y}}_p{\parallel }_F^2,s.t.{\mathbf{Y}}_p\in \Omega .$$

It restricts the extracted SCN to be close to the learned shape manifold.

To sum up, the negative log-likelihood function in Eq. (1) can be rewritten as

$$E\left(\mathbf{Y}\right)=-\sum _{n=1}^N\text{log}\left(\sum _{m=1}^{M+1}\pi \left(m\right)p(x_n\mid m)\right)+\frac{{\lambda }_c}{2}\parallel {\mathbf{L}}^{\prime }\mathbf{Y}{\parallel }_F^2+\frac{{\lambda }_p}{2}\parallel \mathbf{Y}-{\mathbf{Y}}_p{\parallel }_F^2.$$

Following the Expectation-Maximization (EM) algorithm derivation for GMM estimation, we have:

E-step: Compute posterior or correspondence probabilities

$$P^{old}(m\mid x_n)=\frac{\pi \left(m\right)p(x_n\mid m)}{\sum _{k=1}^{M+1}\pi \left(k\right)p(x_n\mid k)}.$$

M-step: Compute shape Y and Y_p that minimizes

$$Q(\mathbf{Y},{\mathbf{Y}}_p)=-\sum _{n=1}^N\sum _{m=1}^M{P}^{old}(m\mid x_n)\parallel {\mathbf{x}}_n-{\mathbf{y}}_m{\parallel }^2+\frac{{\lambda }_c}{2}\parallel {\mathbf{L}}^{\prime }\mathbf{Y}{\parallel }_F^2+\frac{{\lambda }_p}{2}\parallel \mathbf{Y}-{\mathbf{Y}}_p{\parallel }_F^2,{\mathbf{Y}}_p\in \Omega .$$

Taking the derivative of Q(Y, Y_p) with respect to Y and set it to zero, we get

$$\widehat{\mathbf{Y}}\left({\mathbf{Y}}_p\right)={\left(\frac{1}{{\sigma }^2}diag\left(\mathbf{P}1\right)+{\lambda }_c{\mathbf{L}}^{\prime \mathbf{T}}{\mathbf{L}}^{\prime }+{\lambda }_p\mathbf{I}\right)}^{†}\left(\frac{1}{{\sigma }^2}\mathbf{PX}+{\lambda }_p{\mathbf{Y}}_p\right).$$ (4)

where P is a M × N matrix with entries p_mn = P^old(y_m|x_n). The minimization in the M-step can be solved by first finding the Y_p that minimizes $Q(\widehat{\mathbf{Y}}\left({\mathbf{Y}}_p\right),{\mathbf{Y}}_p)$, which has only L + 3 degrees of freedom, and then computing the optimal Y as in Eq. (4).

We smooth the SCN update with a Gaussian kernel at the end of each iteration, so that the final deformation is a composition of smooth deformations. In this way, a diffeomorphic deformation is encouraged and the topology of the SCN on the unit-sphere is also encouraged. The deformable registration of the SCN can be summarized as follows:

1. Initialize Y⁰ = $\stackrel{‒}{\mathbf{Y}}$.

2. Iterate until convergence:

   1. Compute correspondence probability p_mn.
   2. Solve $\underset{{\mathbf{Y}}_p\in \Omega }{\text{arg}\text{min}}Q(\widehat{\mathbf{Y}}\left({\mathbf{Y}}_p\right),{\mathbf{Y}}_p)$.
   3. Compute ${\mathbf{Y}}^{n+1}≔{(\frac{1}{{\sigma }_2}diag\left(\mathbf{P}1\right)+{\lambda }_c{\mathbf{L}}^{{\prime }^T}{\mathbf{L}}^{\prime }+{\lambda }_p\mathbf{I})}^{†}(\frac{1}{{\sigma }_2}\mathbf{PX}+{\lambda }_p{\mathbf{Y}}_p)$.
   4. Compute Yⁿ⁺¹ := Yⁿ + G ∗ (Yⁿ⁺¹ − Yⁿ).
   5. Project Yⁿ⁺¹ onto the unit sphere.

There are three parameters to be specified at each iteration: σ, λ_c and λ_p. σ controls the size of the neighborhood around a point in the source point set, in which target points have high probability of correspondence. λ_c and λ_p are the weights on preserving the curve network structure and the penalizing the deviation from shape manifold. In order to achieve both robustness and accuracy, the three parameters are changed with each iteration in the following way: σ is set to be large at the beginning in order to search in a large neighborhood for good correspondences, and it decreases with each iteration, since ideally at final stage the corresponding points are very close to the shape points. For the robust of the algorithm, λ_c and λ_p are set to be large at the beginning to regularize the global shape, and then decreases with each iteration so that the shape can follow the fine details of subject feature map at the final stage of registration.

5. RESULTS

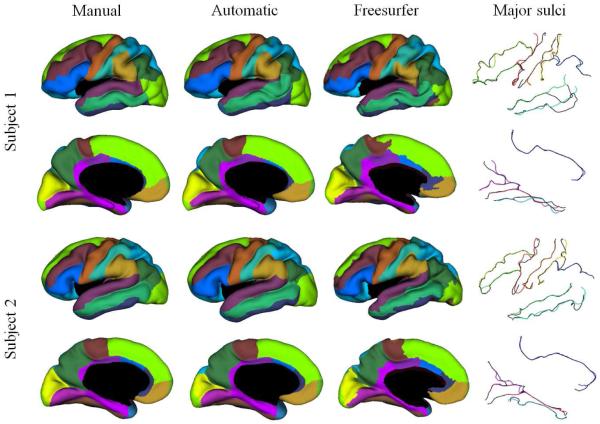
We apply the method to the left hemisphere of 15 subjects obtained from the Open Access Series of Imaging Studies (OASIS) database. Cortical surfaces are extracted from the images using the TOADS-CRUISE^13–15 software available from NITRC (http://www.nitrc.org/projects/toads-cruise/). Mean curvatures are computed on each subject’s surface under different levels of inflation to form a feature vector at each point on the surface. Each subject’s surface is manually delineated by a trained expert. Leave-one-out experiments are carried out on the data set, using each subject as test subject and the remaining 14 subjects to build the SSM. As shown in Fig. 3, the automatically labeled gyral regions show strong resemblance to the manual labeled ones and the extracted sulcal curves align well with manually traced ones. The region boundary detected by the proposed method is much smoother than the gyral regions produced by the Freesurfer software².

Figure 3.

Example results on two subjects. The four columns are in turn the gyral labels from manual delineation, the automatically labeled gyral regions, equivalent gyral labels converted from Freesurfer cortical labeling and the extracted major sulcal curves overlayed with manually traced ones.

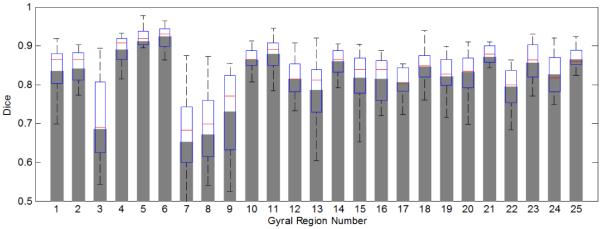
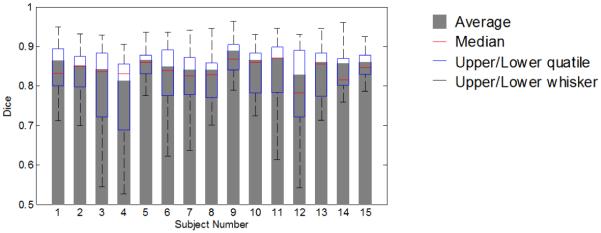
We also compute quantitative statistics on the error of labeled regions and major sulcal curves. Fig. 4 and 5 show the average dice measure for each gyral region and each subject respectively. The overall average dice measure is 85.4%. Table 1 lists quantitative statistics on the distance error of 13 extracted major sulcal curves. Two distances are computed: d_am, the distance from the points on automatically extracted major sulcal curve to the corresponding manual traced curve, and a vice versa distance d_ma. Table 1 shows the statistics on d_am and d_ma. For example, the first number in the column of S1 indicates that 70% of the points on the automatically extracted precentral sulcus are within a distance of 1.7 mm to the manually traced curve. We can see that overall 70% percent of the automatically extracted sulcal curve points are within 3 mm of the manual traced points. The points with large distance errors are caused by the inaccuracy at the ending points of the sulci, which we plan to improve in future work.

Figure 4.

Average dice coefficient for each gyral region over all subjects.

Figure 5.

Average dice coefficient for each subject over all gyral regions (weighted by region area).

Table 1.

Quantile statistics on the error of extracted major sulcal curves.

		S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13
dam(mm)	70%	2.0	1.1	1.6	1.2	1.5	2.4	2.5	2.1	1.6	1.0	2.2	1.6	1.2
	80%	3.7	1.5	2.5	1.9	2.7	3.7	3.7	3.5	2.7	1.5	3.1	2.3	1.9
	90%	7.6	4.7	5.1	3.6	5.2	5.7	6.2	5.9	5.7	2.6	4.9	3.6	3.9
dma(mm)	70%	2.7	1.2	2.6	1.6	2.4	2.8	3.3	2.6	2.4	1.3	2.4	1.5	1.4
	80%	4.5	1.9	4.4	2.5	4.6	4.2	5.0	4.0	3.9	2.0	3.4	2.4	2.2
	90%	7.3	5.4	6.9	4.2	7.2	7.1	7.6	6.6	6.8	3.5	5.2	4.0	4.2

6. CONCLUSION

We propose a method for simultaneously labeling the gyral regions and extracting sulcal curves on the cortical surface. Assuming that the gyral regions parcellate the whole cortical surface into contiguous regions with certain fixed topology, the proposed method labels the subject cortical surface by registering a network of curves (SCN) that form the boundary of gyral regions to the subject cortical surface. Using the framework of probabilistic point set registration method, the deformed SCN follows the fine details of the sulcal geometry of subject cortical surface and also observe the shape statistics learned from the training data. Results show good accuracy in both gyral region labeling and sulcal curve extraction.