Abstract
The aggregates of α-synuclein (αS) are a major pathological hallmark of Parkinson’s disease (PD) making their structure-function relationship important for rational drug design. Yet, the atomic structure of the αS aggregates is unavailable, making it difficult to understand the underlying aggregation mechanism. In this work, based on available experimental data, we examined plausible molecular structures of αS(20/30–110) fibrils for the first time by employing computational approaches. The optimized structure was used to investigate possible interactions with aggregation inhibitors. Our structural models characterize the essential properties of the five-layered fold of the αS fibril. The distribution of the β-strands and the topology of the five β-strands in the relatively stable models are in good agreement with experimental values. In particular, we find that the KTK(E/Q)GV repeat motifs significantly stabilize the αS fibrils. The charged residues within each repeat prefer exposure to the solvent in order to further stabilize the inter-layered interactions by salt-bridges. The organization of the repeat K58T59K60E61Q62V63 between the β2 and β3 layers significantly affects the stability of the non-amyloid-component (NAC) domain. The coupling between the NAC domain and the KTKEGV repeats indicates that both regions can be potential binding sites for inhibitor design. The distinct binding modes of chemical agents that alter αS aggregation highlight the potential of our models in inhibitor design.
Keywords: alpha-synuclein, Parkinson’s disease, fibril structure, molecular dynamics, drug design
Graphical Abstract
1. Introduction
α-synuclein (αS) is a 140-residue protein that is primarily expressed at presynaptic terminals of neuronal brain cells [1, 2]. The aggregation of αS is closely related to several neurodegenerative diseases including Parkinson’s disease (PD) [1, 3]. Recently it was found that αS was present in aggregates of the Krabbe disease and apparently prone to fibrillization in the presence of psychosine [4]. αS adopts different conformations under various environments. Under physiological conditions, αS is characterized as an intrinsically disordered protein, exhibiting a random coil conformation in aqueous solution [3]. In the presence of the membrane, αS displays an α-helical secondary structure as observed from solution NMR structure of micelle-bound αS [5, 6]. Full-length αS can be divided into three distinct domains, the N-terminal domain (residues 1–60) which is amphipathic and responsible for binding to phospholipids [7]; the non-amyloid-β component (NAC) domain (residues 61–95) which is highly hydrophobic and assumed to be essential for αS aggregation [3, 8], and the acidic negatively charged C-terminal domain (residues 96–140) believed to be critical for the chaperone-like activity of αS [9, 10]. The self-assembly of αS is accompanied by conformational transitions [11]; however, the molecular mechanism remains largely unknown partly due to the lack of molecular structures of αS aggregates.
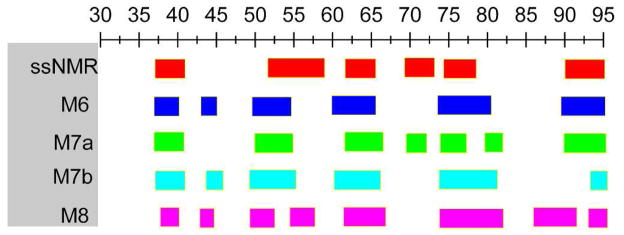
The structural features of αS fibrils have been extensively studied experimentally [12–18]. These studies reveal that both the N-terminal (~20 residues) and C-terminal (~35–40 resides) are highly dynamic and unfolded, whereas ~70 residues have been identified in the ordered fibril core. The folded fibril core of αS shows similar in-register parallel β structures as those observed in the fibrillar structures of amyloid β associated with Alzheimer’s disease [19]. In an earlier study based on site-directed spin labeling and electron paramagnetic resonance spectroscopy, a five-layered model of the αS fibril has been derived by the Langen group. There are five β-strands connected by four loops in this folding pattern (β1-loop-β2-loop-β3-loop-β4-loop-β5) [17]. Later, a similar fibril model was proposed by the Riek group based on NMR experimental studies of αS(30–110) [13]. The five β-strands involve residues 37–43, 52–59, 62–66, 68–77, and 90–95, respectively (Fig. 1). The assignments of β-strands in Riek’s model are largely in agreement with the study of Heise et al.[12] and twisting assemblies of αS in the study of Melki group [16]. The propensity of β1 and β2 is in line with a β-hairpin of αS(35–56) trapped by a β-wrap protein where two β-strands (V37–K43, V48–T54) are connected by a turn (T44–G47) [20]. The β-strand propensity of residues 68–77 is also consistent with previous experimental results which identified residues 71–82 as essential for the αS filament assembly [21]. However, due to different experimental conditions and sample preparation as well as the polymorphic property of the αS fibril structures, an exact consensus from the different experiments cannot be achieved. For example, both studies of Heise and Melki group demonstrate that different strains display distinct distribution of β-sheets along αS sequence [12, 16]. In the NMR study of Wu et al., the C-terminal region (residues 100–140) shows a high β-strand propensity at low temperature (263 K) [18]. In addition, another NMR study at 310 K indicates that the N-terminal of αS fibrils assume a certain extent of β-sheet structures [15].
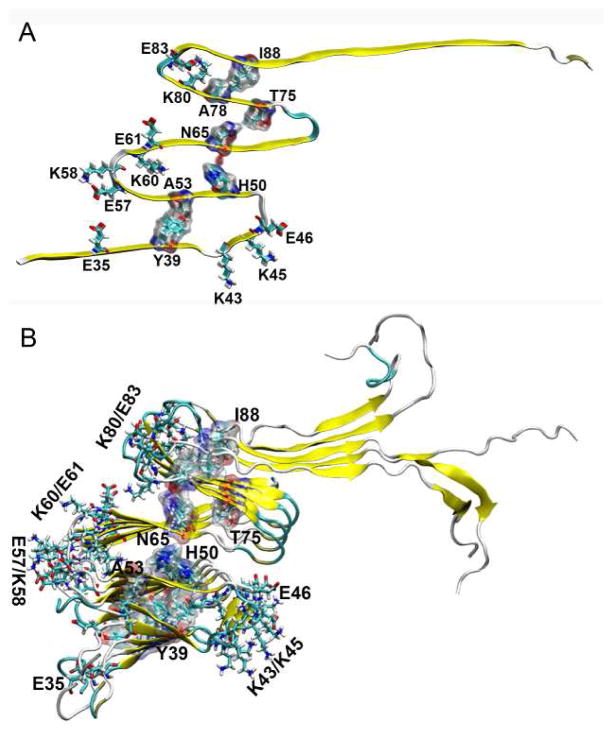
Fig. 1.

The topology of the initial structural models of αS(30–110) fibril. The red region indicates the β-strand. The green spheres represent the distance restraints (Cα distance < 6.0 Å) of inter-layered residues considered in the construction of model structures (Y39-A53, H50-N65, N65-A78, and T75-I88). The initial positions of charged residues in the loops are also shown.
These experimental studies greatly enhanced the understanding of the structure and function of αS fibrils. A partial structural model of NAC (E61–V95) has been proposed recently by computational modeling and simulation [22]. To elucidate the molecular mechanism of αS misfolding and aggregation we aim to construct atomic models of αS fibrils using computational methods based on reported NMR secondary and tertiary structures. We focus on the fold of full-length αS fibrils not only because there are reported experimental results available, but also because there are six familial PD mutations (A30P [23], E46K [24], H50Q [25], G51D [26, 27], A53T [28], and A53E [29]) that have been identified in the N-terminal region. These point mutants can affect membrane binding and aggregation kinetics of αS [30–34]. It is thus important to include the N-terminal region in the structural model. In particular, we carefully examine the role of the imperfect repeat of the KTK(E/Q)GV motif in the stabilization of αS fibrils. There are six such repeats in both the N-terminal and NAC region, which has been suggested to be crucial for lipid binding and aggregation [35–38]. Since both NAC and these repeat are important for αS aggregation, it is also interesting to examine their coupling effect within αS fibrils. Here we propose the first atomic structural models of αS(20/30–110) fibrils, which provide insights into the polymorphic behavior of αS fibrils, the organization of these repeats in the context of fibrils, and the role of the coupling of NAC and these repeats in the stability of αS fibrils.
2. Results and Discussion
2.1 The organization of charged repeats is crucial for the stability of αS fibril models
In the first five-layered αS pentamer structure (M1) (Fig. 2A), we tested the position of residues K43, K45, and E46 between β1 and β2 layers. The possibility of forming E35-K58 salt-bridges to stabilize both β1 and β2 was examined by positioning K60 between β2 and β3.
Fig. 2.
Structural models (M1–M5) of αS fibril. The starting (t=0 ns) and final (t=20 ns) conformations from MD simulations are shown.
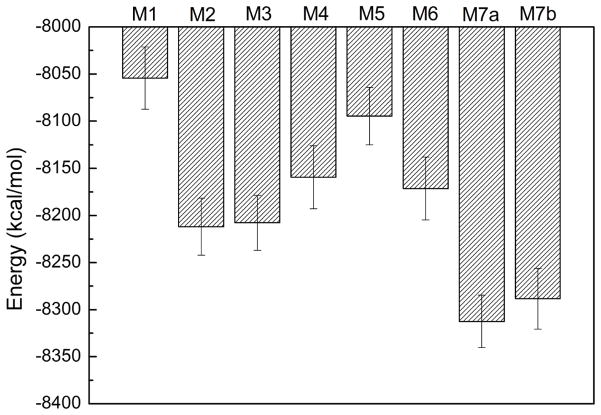
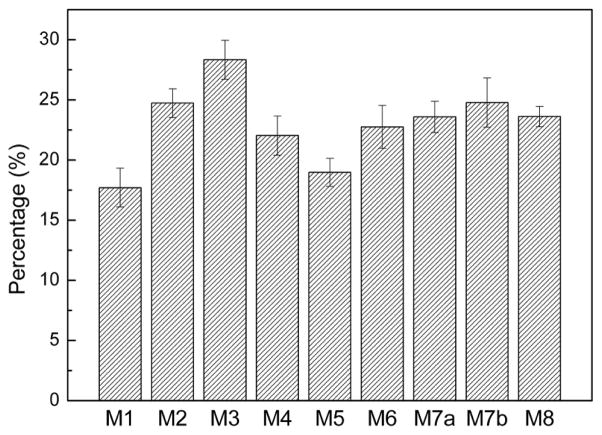
However, after 20-ns MD simulation, the structure collapsed. The layer of β3 moves far away from β4 indicating unfavorable interactions between these two layers. The turn/loop connecting β1 and β2 becomes disordered possibly due to the competing electrostatic interactions between K43 and K45 with E46. Similarly, the loop containing E57, K58, E60, and K61 also becomes disordered. As a result, no stable salt-bridge was observed during the MD simulations. This structural model has the highest GBMV energy (−8054 kcal/mol, Fig. 3) among all structures investigated, implying it is the least stable αS fibril model. Also, it was noted that this fibril model has the lowest β-strand content in its NAC domain (~17%, Fig. 4).
Fig. 3.
Conformational energy calculated in terms of the GBMV method.
Fig. 4.
Percentage of the β-strand in the NAC domain of each fibril model. Only the inner three chains of each pentamer were used for the calculation.
In the second fibril model (M2) (Fig. 2B), we check the possibility of exposing both K43 and K45 to the solvent in order to eliminate the electrostatic repulsion present in M1 but still keep E46 inside the fibril layer. To increase the interaction between different layers, E35 and K58, E61 and K80 initially form salt-bridges, as well as E57 and K60. Different from M1 where H50 was oriented to β3, to examine the interactions between β2 and β3 in this model, H50 was oriented to β1. After 20-ns MD simulation, this model is even less stable than the M1 model, although the interactions between β1 and β2, and between β3 and β4, seem more favorable than those in M1, possibly due to the introduction of inter-layered salt-bridges. The separation of β2 from β3 could indicates that H50 should be oriented to β3 instead of β1 even though this model has a relatively lower GMBV energy (−8212 kcal/mol) than M1, which suggests that inter-layered salt-bridges contribute to the stability of αS fibril structures. In addition, the β-strand in the NAC domain increased to ~25%, indicating that the interaction between E61 and K80 may stabilize NAC.
To further investigate the role of salt-bridges in the loop containing K43, K45 and E46 as observed in the M2 structure, we examined the M3 model (Fig. 2C) where K43 and E46 form a salt-bridge but not K45, which was kept exposed to the solvent. After 20-ns MD simulation, β2 also moves away from β3 as observed in M2. However, the introduction of the salt-bridge between K43 and E46 seems not to be able to stabilize this loop. The structures of β1 and β2 display a globular conformation instead of extended β-strands. Compared to M2, such results imply that the formation of the salt-bridge between K43 and E46 inside the fibril layer will not contribute to the stability of αS fibril structures. As a consequence, this model has a comparative GBMV energy (−8208 kcal/mol) to that of M2. The results are also consistent with the familial variant of E46K promoting amyloid formation [39–41]. If the M3 model contribute to αS fibril formation, the E46K mutation should destabilize the αS fibril. Interestingly, this fibril model has the highest percentage of β-strand in the NAC domain (~28%).
The above results suggest that the repeat K43T44K45E46G47V48 may not form stable salt-bridges inside the fibril layer; as such, we constructed the M4 model where K43, K45 and E46 are exposed to the solvent (Fig. 2D). The organization of the remaining repeats is the same as that in the M3 structure except that H50 was oriented to β3. This model was also used to examine the effect of another charged repeat K58T59K60E61Q62V63 on the stability of αS fibril. After 20-ns MD simulation, the five-layer fold of the αS fibril structure is retained. The repeat K43T44K45E46G47V48 adopts primarily a loop conformation; however, the β-strand of β2 disappears, which could be attributed to the unfavorable electrostatic interactions in the repeat involving E57, K58, K60, and E61. It could also be due to the interactions between β1 and β2. The calculated GBMV energy (−8159 kcal/mol) suggests that it is less stable than M2 and M3, although this model could maintain the fold of the αS fibril structures. In addition, the β-strand content (~22%) in the NAC of this model is also slightly lower than that of M2 (~25%) and M3 (~28%).
Based on M4, we further examined model M5 (Fig. 2E) where both E57 and K58 were exposed to the solvent, so that initially there is no salt-bridge between E57 and K60. Only K60 was kept inside the layer as in M4. We observed that the β-strand of β2 remains relatively stable during 20-ns MD simulation, suggesting that the presence of such salt-bridge between E57 and K60 could affect the stability of the β2 strand. However, the presence of K60 inside the fibril core has a significant effect on the fold of the αS fibril as β2 separates from β3. We speculate that the absence of counter ions results in strong electrostatic interactions between adjacent K60 in different β layers, and the interactions between β2 and β3 are not able to counteract such effect. Other possibility is that neighboring charged residues like K80 could also disrupt the interactions of β2 and β3. Consequently, the M5 model has a relatively high GBMV energy (−8095 kcal/mol, Fig. 3). Unlike M3 where E57 interacts with K60, the β-strand of NAC in this model (~19%) is lower than that of M3 (~28%), implying that electrostatic interactions have a more significant effect on the stability of the NAC domain.
2.2 The relatively stable models characterize the essential secondary and tertiary structures of the αS fibril as observed experimentally
In M5, we examined the possibility that K80 could interact repulsively with K60 and then destabilize the interactions between β2 and β3, although it initially forms a salt-bridge with E61. M6 was used to explore the possibility that K80 establishes a salt-bridge with E83 inside the fibril core (Fig. 5). To increase the hydrophobic interactions between β4 and β5, the orientation of β4 was reversed, leading T75 and A78 to have opposite orientation to that shown in M5. The fold of αS fibril was maintained after 20-ns MD simulation. We then extended the simulation to 40 ns and found that this model structure is relatively stable. However, this fibril model has a higher GBMV energy (−8172 kcal/mol) even than M2 (−8212 kcal/mol, Fig. 3) where the fibril fold collapses. Note that the percentage of β-strand in the NAC domain of M6 is comparable (~23%) to that of M2 (~25%).
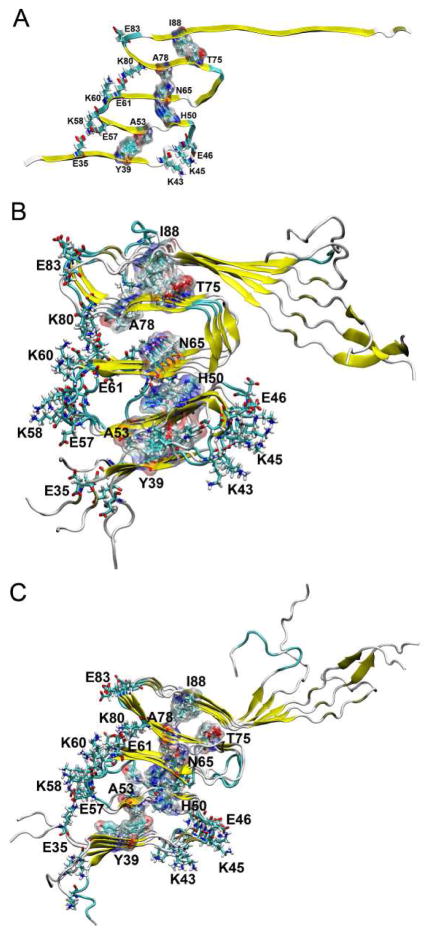
Fig. 5.
Structural model of αS fibril (M6). The initial (A) and final (B) conformations from 40-ns MD simulations are shown.
Although M6 indicates that the fold of the αS fibril structures could be maintained in the presence of inter-layered salt-bridges, such a model structure is energetically less stable. Results from M1 to M3 suggest that charged residues (K43, K45, and E46) in the first loop have a strong tendency to be exposed to the solvent. Taken together, the results of M4 to M6 lead us to conclude that charged resides in all three loops prefer to be exposed to the solvent. We then examined a model M7 (Fig. 6A) that satisfies all the inter-layered distance restraints, and the stabilization factors derived from M1 to M6. Initially, K45 and E46 interact with each other in the loop connecting β1 and β2 due to electrostatic attraction. Similarly, E57 interacts with K58 in the loop connecting β2 and β3. In addition, E35 in β1 may participate in the salt-bridge to further stabilize the interactions between β1 and β2. Similarly, E61 and K80 form a salt-bridge, with K60 also possibly involved. Two independent 40-ns MD simulations were performed (referred as M7a and M7b thereafter) with the same initial conformation but different velocity distribution. Both fibril structures could maintain the αS fibrils fold after 40-ns simulation (Fig. 6B and 6C). Their GBMV energies suggest that both models converged with similar energies, with M7a (−8313kcal/mol) is slightly more favorable than M7b (−8288 kcal/mol, Fig. 3). The two models also display similar percentages of β-strand in their NAC domains (~24% and 25% for M7a and M7b, respectively).
Fig. 6.
Structural model of αS fibril (M7). The initial (A) and final (B and C) conformations from 40-ns MD simulations are shown.
Based on the above three relatively stable fibril structures (M6, M7a, and M7b), we examined the change of the secondary structures during the MD simulations (Fig. S1 and Fig. S2). The average β-strand content of these pentamers is about 39%, 36%, and 33% for M6, M7a, and M7b, respectively; that of the inner core is about 39%, 38%, and 37% for M6, M7a, and M7b, respectively, which is close to the β-strand population (~43%) determined by Riek’s group [13]. The distribution of the β-strand motif for these models was also calculated and summarized in Fig. 7 and Fig. S2. All fibril models display similar distributions of five β-strands as derived from solid-state NMR experiments. The first β-strand comprises residues ~37–41 as indicated by NMR data, however, both M6 and M7b also show a short β-strand consisting of T44–E46, which seems too short to be identified experimentally. Solid-state NMR data suggests that the second β-strand comprises residues ~52–58, whereas all models predict that it contains residues ~49–54. The layout of β1 and β2 in our models is in excellent agreement with the β-hairpin of αS(35–56) trapped by a β-wrap protein where two β-strands (V37–K43, V48–T54) are linked by a turn (T44–G47) [20]. However, it should be noted that β2 lies in the layer involving E57 and K58. Although we have carefully examined the interactions especially of the salt-bridges in this loop, we cannot exclude other possible arrangements of these charged residues that could form stable β-strands. All three models characterize the third β-strand including residues ~62–66, which is in good agreement with the experimental result. As for the fourth β-strand, only M7a exhibits a short β-strand comprising residues 70–72, consistent with NMR data. Interestingly, residues 70–72 in our fibril M7a form a turn connecting β3 and β4. Such arrangement puts residues 72 and 73 in a loop, in agreement with the proposed five-layered β-sandwich by Riek group [13]. For the last β-strand that starts from A90 and ends at V95, a good agreement was obtained between the experimental result and both M6 and M7a.
Fig. 7.
Comparison of the distribution of β-strand between ssNMR assignment and results of MD simulations of M6, M7, and M8.
The tertiary structure of these fibril models was characterized through calculation of the inter-layered distance and compared with available experimental results. However, because the ssNMR experiments were performed at a rather low temperature (273–283 K), and the αS fibril samples were in a dried gel-like state [13], direct comparison between our results from MD simulations performed in aqueous solution at 310 K and experimental data is not straightforward. Here, we compared the most important inter-layered residue distance and validated the consistency between our model structure with available experimental distance restraints [42]. A total of 20 unambiguous distance restraints with Cα-Cα distance within 6 Å were collected from the results of 13C-13C proton-driven spin diffusion spectra. As observed from one of the Aβ fibril structures (PDB ID: 2BEG) [19], the Cα-Cα distance between two β-layers varies from ~8.0–12.0 Å; therefore, a cutoff of 12.0 was used to evaluate the topology of our fibril models. The average Cα-Cα distance of the inner core structures was calculated and shown in Fig. 8.
Fig. 8.
Comparison of the inter-layered distance restraints between ssNMR data and results from MD simulations of M6 (A), M7a (B), M7b (C), and M8 (D). All the inter-layered distance restraints are extracted from the experimental results of Riek group [13].
In all three models, there are at least 12 inter-layered residue distances that are less than 12 Å (Fig. 8), confirming that the proposed model structures are able to maintain the αS fibril fold. Due to the formation of a short β-strand in the region comprising residues 70–72, the distance between β3 and β4 layers is larger than 12 Å in M7a (Fig. 8B). In contrast, the corresponding distances are all less than 8 Å in M7b, and the distance between G67 of β3 and A76 of β4 is even less than 6 Å (Fig. 8C). Also note that the initial distance restraints used to construct these model are all well preserved (Fig. 1), implying that such organization of the five β-strands of the αS fibril could provide favorable inter-residual interactions and such interactions could be further optimized during the MD simulations. In addition, the single-layered αS fibril has been suggested to have a diameter of ~20–35 Å, and a height of ~40 Å (vertical distance between β1 and β5) in its gel-like state. We projected the mass density along x and y direction respectively, from which we could estimate the diameter and height of the αS fibril models (Fig. S3). Using a threshold of 0.05 Da/Å3 to exclude the disordered regions, the dimension of our αS fibril structures is ~45–50 Å, and the height is ~50 Å. Note that such a geometry of αS in aqueous solution is generally larger than the experimental ssNMR data due to the different hydration effect. However, the above dimensions are close or in agreement with other atomic force microscopy (AFM) experiments where samples were prepared in solution (pH 7.5, 310 K). For example, based on observation by AFM, Carter’s group suggested a dimension of 32–44 Å for αS protofilament [43], and the Anderson group obtained a height of 45–60 Å for αS protofilament [44]. In addition, the Bennati group used electron paramagnetic resonance spectroscopy to measure the height of the αS fibril, and obtained a distance of 40–50 Å between the external of β-strands [45]. (Here both protofilament and fibril terms refer to the building block of fibrils).
2.3 Effects of charged repeats on the stability of NAC
It has been shown that the NAC promotes αS aggregation, and the hydrophobic motif of V71–V82 can form filaments alone [21]. Based on our fibril models, we found that the hydrophobic NAC composed of three β layers (β3, β4, and β5) can preserve about ~23%–25% of β-strand conformation in the relatively stable structures (M6, M7, and M8). The presence of charged repeat KTK(E/Q)GV, however, has distinct effects on the stability of the NAC (Fig. 4). In particular, the arrangement of charged residues in K58T59K60E61Q62V63 connecting β2 and β3 has the most significant effect on the stability of NAC.
We also found that the repeat K21T22K23Q24G25V26 in the remote N-terminal may stabilize the NAC domain near to the C-terminal. To test if the secondary and tertiary structures of the above models are also stable in the presence of an additional K21T22K23Q24G25V26 repeat, we extended the N-terminal of M7b to construct a fibril structure of αS(20–110) (M8, Fig. S4), and performed a 40-ns MD simulations under the same conditions. M8 displayed similar secondary structures as the fibril models of αS(30–110) (Fig. 7). However, the strand β5 comprises more ordered residues (residues 85–105) than M7b (residues 94–105) (Fig. 7), suggesting that the presence of the repeat K21T22K23Q24G25V26 increases the stability of the NAC domain (residues 85–95 specifically), although the percentage of β-strand in the NAC of αS(20–110) fibril is comparable to that of αS(30–110) (M6 and M7) (Fig. 4). The tertiary structure of αS(20–110) is also similar to that of αS(30-110) (Fig. 8D), implying that the additional 10 residues have no significant effect on the five-layered topology. These results confirm that the atomic structure models presented here capture the characteristic features of αS fibrils independent of the sequence length.
Shaykhalishahi et al. found that introduction of an intramolecular disulfide bond in the double cysteine mutant G41C/V48C will inhibit amyloid formation [46]. With the G41C/V48C disulfide bond, the Cα-Cα distance range of cysteine disulfide bonds would be around 5.6 Å. However, the average G41/V48 Cα-Cα distances from last 5-ns MD trajectories of the two stable fibril models are much longer, 12.8 Å and 15.9 Å for M7a and M7b, respectively. Clearly, the disulfide bond restriction would destroy the favorite turn conformation for the K43T44K45E46G47V48 repeat and thus inhibit αS amyloid formation.
2.4 Aggregation inhibitors block the NAC region
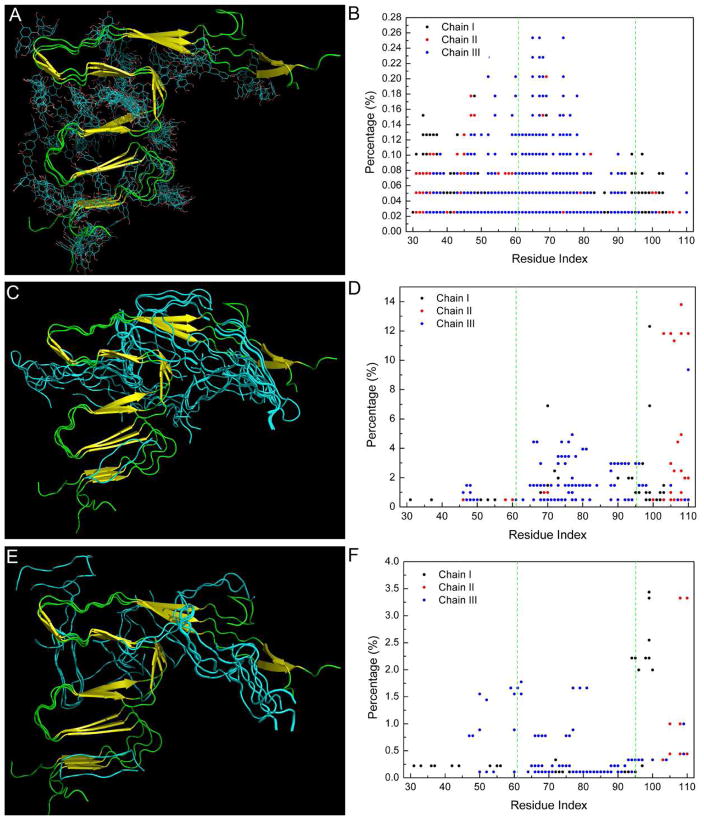
The design of potent inhibitors of αS aggregation provides promising therapeutic strategies. Recent experiments showed that epigallocatechin-3-gallate (EGCG), an abundant catechin in green tea, as well as small β-hairpin peptides, could prevent the formation of αS amyloids in different ways [47–49]. To understand the molecular mechanisms of the interactions between aggregation inhibitors and αS, we used the most stable structure obtained in this study to dock with several αS aggregation inhibitors. First, the EGCG molecule was blindly docked onto the most stable structural model of αS fibril (M7a). Similarly, peptides [48] including WW2 (sequence: KKLTVWIP′GKWITVSA, P′=D-Pro), and cyclo-WW2 (sequence: cyclo- KKLTVWIP′GKWITVSIP′P, P′= D-Pro), were also examined. Gasteiger charges were calculated for all structures. The Lamarckian genetic algorithm was applied to search the docking conformations of EGCG. Flexible and rigid docking experiments were performed for EGCG and β-peptides, respectively (the αS fibril structure is always kept rigid). AutoDock4 and AutoDockTools 4 were used to carry out the docking studies [50]. The distribution of the 100 top ranked conformations of EGCG and β-peptides relative to αS fibrils is shown in Fig. 9. We found that EGCG and β-peptides bind to different sites of the αS fibril. EGCG prefers binding to both N-terminal and NAC domain. A weak binding site in the C-terminal was also observed (Fig. 9A and 9B). In contrast, the β-peptides (WW2 and cyclo-WW2) interact primarily with both NAC and the C-terminal of αS fibril, and the binding of WW2 to the NAC seems particularly favorable (Fig. 9C–9F). The distinct binding modes of the EGCG and β-peptides indicate that they disrupt the formation of the αS fibril through different mechanisms, consistent with recent experimental observations [48].
Fig. 9.
Results of docking of EGCG (A and B), WW2 (C and D), and cyclo-WW2 (E and F) onto αS fibril. Only the central three chains (chain I, chain II, and chain III) of αS fibril were used. The vertical dotted lines in B, D and F indicate the NAC part. The structure of αS fibril was shown in yellow and green, and the docking molecules were shown in cyan. A contact occurs if any atom of EGCG or the center of any residue of β-peptides is within 6 Å of the center of any residue of αS fibril.
In a membrane environment, αS has α-helix-rich conformation [51]. There are energy barriers for conformational transitions from α-helix-rich to β-strand-rich αS conformations. To estimate the energy difference between the α-helix-rich and the β-strand-rich conformations, we simulated a helical dimer of αS(30–110), with each monomer adopting α-helix conformation (the conformation on membrane) [51]. After 20-ns MD simulations, the dimer is still rich in α-helix structures (Fig. S5). Based on the last 5-ns trajectory we calculated the GBMV energy and compared with the value of dimer conformations extracted from trajectories of M7. The obtained conformational energy of a dimer in α-helix conformation is ~−3429 kcal/mol, lower than the dimer in a β sandwich conformation (−3152 kcal/mol and −3136 kcal/mol for dimers extracted from M7a and M7b, respectively). The above result suggests that the formation of αS fibril rich in β-strand needs to overcome a large energy barrier, and inhibitors of EGCG and β-peptides may modulate such process and redirect the aggregation pathway of αS.
3. Conclusions
Because the aggregates of αS are closely associated with PD, the study of the structure-function relationship of αS needs reliable structural models. With sufficient experimental data available, we probed possible fibrillar structures using computational approaches. Although many studies suggest that different αS strains have different structures, aggregation propensity, and levels of toxicity, one of these αS fibrils has been well investigated and its building block unit can adopt a topology with five-layered β-strands. However, the details of how these β-strands organize need to be elucidated, especially how the four imperfect KTK(E/Q)GV repeats arrange in the fibril structures, the interaction with membrane and the αS aggregation mechanism. Adopting a hierarchical strategy, we systematically examined the role of the salt-bridge formed between residues Lys and Glu within each repeat on the stability of model structures of αS(30–110) fibrils. The coupling of these repeats with the NAC domain was specifically investigated. Two obtained models (M6 and M7) are able to preserve the topology of β-strands, with M7a being more energetically stable. One interesting result is that all charged residues in these repeats prefer to be exposed to the solvent and form salt-bridges. The arrangement of charged residues in the repeat K58T59K60E61Q62V63 between the β2 and β3 layers is particularly important for the stability of the NAC domain. Two trajectories of M7 (M7a and M7b) were generated with the same initial conformation but different velocity distributions. Structural characterization suggests that they display somewhat different secondary and tertiary structures. The distribution of β-strand is in better agreement with experimental observations in M7a whereas the distance restraints of adjacent β layers are more consistent with ssNMR data in M7b model. Energetically, the M7a structure was very close to M7b. The stability of M7b was further validated in the context of the model structure αS(20–110) fibril, indicating it also could be a building block for the full-length αS fibrils. In summary, the proposed atomic structures of the αS fibrils not only provide valuable insights into the topology of the αS fibrils, but also offer reliable starting structures for investigations of the assembly mechanism of αS in aqueous or in membrane environments, and of the effect of familial mutations on the structure and aggregation kinetics. Our structural model can also be by examining their molecular interactions useful for rational design of molecules targeting αS aggregates.
4. Materials and Methods
The five-layered model structures of αS(30–110) pentamer were constructed using Chimera software [52]. The five β-strands were assigned according to the NMR results reported by the Riek group [13]. The loop connecting β2 and β3 contains only two residues (K60 and E61) in the original NMR assignments, which makes the turn too narrow and residues in β2 and β3 may collide. We thus extend this loop involving residues 58–61. Similarly, we also extend the loop connecting β3 and β4 that consists of residues 68–73 in order to satisfy the tertiary contact between T64/N65 of β3 and A78 of β4. Other inter-layered distance restraints used to build the model are shown in Fig. 1. These restraints include residue pair Y39-A53, H50-N65, N65-A78, and T75-I88. Note that these restraints are unambiguously assigned between residues based on solid-state NMR (ssNMR) experiment [13]. Other inter-layer distance restraints are also available but not used to build the model structures and will be checked later. We found that not all the “unambiguous” restraints can be applicable to MD simulation simultaneously. For example, ssNMR indicates that Cα of Y39 is within 6 Å of Cα of A53, V55, and E57, suggesting that the inter-layer distance (β1 and β2) is within 6 Å, if we apply these three distance restraints together, β1 and β2 will distort significantly. On the other hand, the normal Cα-Cα distance between two β-layers varies from ~8.0–12.0 Å. Therefore, we applied one distance restraints between each two adjacent layers, and check the other restraints later. Four of the six imperfect KTK(E/Q)GV motifs are present in αS(30–110). Except the K32T33K34E35G36V37 motif, the remaining three repeats (K43T44K45E46G47V48, K58T59K60E61Q62V63, and K80T81V82E83G84A85) have residues in two loops that connect β2 and β3, and β4 and β5, respectively. We thus constructed various models hierarchically in order to investigate the effect of a salt-bridge formed by Glu and Lys on the stability of the αS fibril models (Table 1). The effect of charged residues on the stability of the β-strand has been well recognized [53, 54], thus worth examining in the context of αS fibrils.
Table 1.
Summary of the orientation of charged residues in KTK(E/Q)GV motif. A hierarchical strategy was applied to optimize the structural model of αS(30–110) fibril. Based on M1–M5, K43, K45, and E46 were found to expose to solvent. Further examination of M6 suggested that E57, K58, K60, and E61 prefer to expose to solvent. The final model M7 integrates all these structural features. No stable salt-bridge was found in M7.
| Model structure | Repeats involved | Side-chain orientation | Salt-bridge |
|---|---|---|---|
| M1 | K43T44K45E46G47V48, and K58T59K60E61Q62V63 | Interior: K43 and K45; Surface: E46; H50 towards β3, and A53 towards β1 | |
| M2 | Interior: E46; Surface: K43 and K45; H50 towards β1, and A53 towards β3 | E35-K58; K43-E46 | |
| M3 | Interior: K43 and E46; Surface: K45; H50 towards β1, and A53 towards β3 | E35-K58; K43-E46 | |
| M4 | Surface: K43, K45, and E46; H50 towards β3, and A53 towards β 1 | E35-K58; E57-K60 | |
| M5 | Surface: E57 and K58; Interior: K60 | ||
| M6 | K58T59K60E61Q62V63, and K80T81V82E83G84A85 | Surface: E57, K58, and E61; Interior: K60 | E80-K83 |
| M7/M8 | K43T44K45E46G47V48, K58T59K60E61Q62V63, and K80T81V82E83G84A85 | Surface: K43, K45, E46, E57, K58, K60, E61, K80, and E83 |
Molecular dynamics (MD) simulations have become a powerful tool in drug design and discovery [55–57]. Here we apply this approach to refine our structural models of αS fibril, which could be further used in future studies such as virtual screening of potential drugs targeting PD. All MD simulations were performed in the NPT ensemble using NAMD2 (v2.10) program [58]. Each model structure was represented by CHARMM27 force filed with CMAP correction [59, 60], and solvated in a box filled with TIP3P water molecules [61]. The minimum distance between protein and the edge of water box is at least 15 Å. Each system was neutralized by adding a number of counter-ions. The Langevin piston method and Langevin dynamics were applied to control the pressure at 1 atm and the temperature at 310 K [62]. The Particle Mesh Ewald (PME) method was used to calculate the long-range electrostatics [63]. The hydrogen bonds were constrained by using the SHAKE algorithm [64]. The van der Waals interactions were calculated using a switching function with a twin cutoff of 10 Å and 12 Å. An integration time step of 2 fs was used and trajectory was save every 10 ps. MD simulations were conducted in three successive steps. Each system was first energy minimized for 10000 steps, with the intermolecular hydrogen bonds of the β-strand harmonically restrained with a force constant of 20 kcal/mol. Then the system was heated to 310 K gradually with the same restraints. In the equilibration stage, the force constant was decreased to 10 kcal/mol, 5 kcal/mol, and eliminated entirely. In each step, the system was equilibrated for 2 ns. The production simulation for each system was run for 20–40 ns. If the fibril structures (M1–M6) are not able to maintain the five-fold β-sheet layer, no additional simulations were performed. Additional simulation as performed to verify stable structure (M7a and M7b).
The relative stability of each fibril model was evaluated in terms of the conformational energy calculated by the generalized Born using the molecular volume (GBMV) method implemented in CHARMM program (c37b2) [59, 65]. The standard parameters in the GBMV II algorithm were used. A single-point energy calculation with infinite cutoffs was performed after the structure was minimized 200 steps using the steepest decedent method. For each system, the last 5-ns trajectory (500 frames) was used to obtain the average energy and other analyses.
Supplementary Material
Highlights.
α-synuclein amyloid structures were simulated based on experimental constraints.
Optimized structure was used to investigate interactions with inhibitors.
The KTK(E/Q)GV repeats strongly affect the stability of α-synuclein fibrils.
EGCG and β-peptides modulate the aggregation of α-synuclein in different ways.
Acknowledgments
This project has been funded in whole or in part with Federal funds from the National Cancer Institute, National Institutes of Health, under contract number HHSN261200800001E. This research was supported (in part) by the Intramural Research Program of the NIH, National Cancer Institute, Center for Cancer Research. L. Xu also thanks financial support from China Scholarship Council (CSC201306065001). MD simulations were performed at the high-performance computational facilities of the Biowulf PC/Linux cluster at the NIH (http://biowulf.nih.gov/).
Footnotes
Author contributions
LX, BM designed and simulated structures. LX, BM, RN wrote the paper. All authors have given approval of the final version of the manuscript.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Recchia A. α-Synuclein and Parkinson’s disease. The FASEB Journal. 2004;18:617–626. doi: 10.1096/fj.03-0338rev. [DOI] [PubMed] [Google Scholar]
- 2.Spillantini MG, Schmidt ML, Lee VM, Trojanowski JQ, Jakes R, Goedert M. Alpha-synuclein in Lewy bodies. Nature. 1997;388:839–840. doi: 10.1038/42166. [DOI] [PubMed] [Google Scholar]
- 3.Berrocal R, Vasquez V, Krs SR, Gadad BS, Ks R. α-Synuclein Misfolding Versus Aggregation Relevance to Parkinson’s Disease: Critical Assessment and Modeling. Molecular Neurobiology. 2014;51:1417–1431. doi: 10.1007/s12035-014-8818-2. [DOI] [PubMed] [Google Scholar]
- 4.Smith BR, Santos MB, Marshall MS, Cantuti-Castelvetri L, Lopez-Rosas A, Li G, van Breemen R, Claycomb KI, Gallea JI, Celej MS, Crocker SJ, Givogri MI, Bongarzone ER. Neuronal inclusions of α-synuclein contribute to the pathogenesis of Krabbe disease. The Journal of Pathology. 2014;232:509–521. doi: 10.1002/path.4328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ulmer TS, Bax A, Cole NB, Nussbaum RL. Structure and Dynamics of Micelle-bound Human α-Synuclein. Journal of Biological Chemistry. 2004;280:9595–9603. doi: 10.1074/jbc.M411805200. [DOI] [PubMed] [Google Scholar]
- 6.Rao JN, Jao CC, Hegde BG, Langen R, Ulmer TS. A Combinatorial NMR and EPR Approach for Evaluating the Structural Ensemble of Partially Folded Proteins. Journal of the American Chemical Society. 2010;132:8657–8668. doi: 10.1021/ja100646t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eliezer D, Kutluay E, Bussell R, Jr, Browne G. Conformational properties of alpha-synuclein in its free and lipid-associated states. J Mol Biol. 2001;307:1061–1073. doi: 10.1006/jmbi.2001.4538. [DOI] [PubMed] [Google Scholar]
- 8.Hashimoto M, Takenouchi T, Mallory M, Masliah E, Takeda A. The role of NAC in amyloidogenesis in Alzheimer’s disease. Am J Pathol. 2000;156:734–736. doi: 10.1016/s0002-9440(10)64777-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kim TD, Paik SR, Yang CH. Structural and functional implications of C-terminal regions of alpha-synuclein. Biochemistry. 2002;41:13782–13790. doi: 10.1021/bi026284c. [DOI] [PubMed] [Google Scholar]
- 10.Hong DP, Xiong W, Chang JY, Jiang C. The role of the C-terminus of human alpha-synuclein: intra-disulfide bonds between the C-terminus and other regions stabilize non-fibrillar monomeric isomers. FEBS Lett. 2011;585:561–566. doi: 10.1016/j.febslet.2011.01.009. [DOI] [PubMed] [Google Scholar]
- 11.Deleersnijder A, Gerard M, Debyser Z, Baekelandt V. The remarkable conformational plasticity of alpha-synuclein: blessing or curse? Trends Mol Med. 2013;19:368–377. doi: 10.1016/j.molmed.2013.04.002. [DOI] [PubMed] [Google Scholar]
- 12.Heise H, Hoyer W, Becker S, Andronesi OC, Riedel D, Baldus M. Molecular-level secondary structure, polymorphism, and dynamics of full-length α-synuclein fibrils studied by solid-state NMR. Proceedings of the National Academy of Sciences. 2005;102:15871–15876. doi: 10.1073/pnas.0506109102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vilar M, Chou HT, Luhrs T, Maji SK, Riek-Loher D, Verel R, Manning G, Stahlberg H, Riek R. The fold of α-synuclein fibrils. Proceedings of the National Academy of Sciences. 2008;105:8637–8642. doi: 10.1073/pnas.0712179105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen SW, Drakulic S, Deas E, Ouberai M, Aprile FA, Arranz R, Ness S, Roodveldt C, Guilliams T, De-Genst EJ, Klenerman D, Wood NW, Knowles TPJ, Alfonso C, Rivas G, Abramov AY, Valpuesta JM, Dobson CM, Cremades N. Structural characterization of toxic oligomers that are kinetically trapped during α-synuclein fibril formation. Proceedings of the National Academy of Sciences. 2015;112:E1994–E2003. doi: 10.1073/pnas.1421204112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gath J, Habenstein B, Bousset L, Melki R, Meier BH, Böckmann A. Solid-state NMR sequential assignments of α-synuclein. Biomolecular NMR Assignments. 2011;6:51–55. doi: 10.1007/s12104-011-9324-3. [DOI] [PubMed] [Google Scholar]
- 16.Bousset L, Pieri L, Ruiz-Arlandis G, Gath J, Jensen PH, Habenstein B, Madiona K, Olieric V, Böckmann A, Meier BH, Melki R. Structural and functional characterization of two alpha-synuclein strains. Nature Communications. 2013;4 doi: 10.1038/ncomms3575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Der-Sarkissian A, Jao CC, Chen J, Langen R. Structural Organization of α-Synuclein Fibrils Studied by Site-directed Spin Labeling. Journal of Biological Chemistry. 2003;278:37530–37535. doi: 10.1074/jbc.M305266200. [DOI] [PubMed] [Google Scholar]
- 18.Wu KP, Kim S, Fela DA, Baum J. Characterization of Conformational and Dynamic Properties of Natively Unfolded Human and Mouse α-Synuclein Ensembles by NMR: Implication for Aggregation. Journal of Molecular Biology. 2008;378:1104–1115. doi: 10.1016/j.jmb.2008.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Luhrs T, Ritter C, Adrian M, Riek-Loher D, Bohrmann B, Dobeli H, Schubert D, Riek R. 3D structure of Alzheimer’s amyloid-beta(1-42) fibrils. Proc Natl Acad Sci U S A. 2005;102:17342–17347. doi: 10.1073/pnas.0506723102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mirecka EA, Shaykhalishahi H, Gauhar A, Akgül Ş, Lecher J, Willbold D, Stoldt M, Hoyer W. Sequestration of a β-Hairpin for Control of α-Synuclein Aggregation. Angewandte Chemie International Edition. 2014;53:4227–4230. doi: 10.1002/anie.201309001. [DOI] [PubMed] [Google Scholar]
- 21.Giasson BI, Murray IVJ, Trojanowski JQ, Lee VMY. A Hydrophobic Stretch of 12 Amino Acid Residues in the Middle of α-Synuclein Is Essential for Filament Assembly. Journal of Biological Chemistry. 2000;276:2380–2386. doi: 10.1074/jbc.M008919200. [DOI] [PubMed] [Google Scholar]
- 22.Atsmon-Raz Y, Miller Y. A Proposed Atomic Structure of the Self-Assembly of the Non-Amyloid-β Component of Human α-Synuclein As Derived by Computational Tools. The Journal of Physical Chemistry B. 2015 doi: 10.1021/acs.jpcb.5b03760. 150722124221003. [DOI] [PubMed] [Google Scholar]
- 23.Kruger R, Kuhn W, Muller T, Woitalla D, Graeber M, Kosel S, Przuntek H, Epplen JT, Schols L, Riess O. Ala30Pro mutation in the gene encoding alpha-synuclein in Parkinson’s disease. Nat Genet. 1998;18:106–108. doi: 10.1038/ng0298-106. [DOI] [PubMed] [Google Scholar]
- 24.Zarranz JJ, Alegre J, Gomez-Esteban JC, Lezcano E, Ros R, Ampuero I, Vidal L, Hoenicka J, Rodriguez O, Atares B, Llorens V, Gomez Tortosa E, del Ser T, Munoz DG, de Yebenes JG. The new mutation, E46K, of alpha-synuclein causes Parkinson and Lewy body dementia. Ann Neurol. 2004;55:164–173. doi: 10.1002/ana.10795. [DOI] [PubMed] [Google Scholar]
- 25.Appel-Cresswell S, Vilarino-Guell C, Encarnacion M, Sherman H, Yu I, Shah B, Weir D, Thompson C, Szu-Tu C, Trinh J, Aasly JO, Rajput A, Rajput AH, Jon Stoessl A, Farrer MJ. Alpha-synuclein p.H50Q, a novel pathogenic mutation for Parkinson’s disease. Movement Disorders. 2013;28:811–813. doi: 10.1002/mds.25421. [DOI] [PubMed] [Google Scholar]
- 26.Kiely AP, Asi YT, Kara E, Limousin P, Ling H, Lewis P, Proukakis C, Quinn N, Lees AJ, Hardy J, Revesz T, Houlden H, Holton JL. alpha-Synucleinopathy associated with G51D SNCA mutation: a link between Parkinson’s disease and multiple system atrophy? Acta Neuropathol. 2013;125:753–769. doi: 10.1007/s00401-013-1096-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lesage S, Anheim M, Letournel F, Bousset L, Honore A, Rozas N, Pieri L, Madiona K, Durr A, Melki R, Verny C, Brice A. G51D alpha-synuclein mutation causes a novel parkinsonian-pyramidal syndrome. Ann Neurol. 2013;73:459–471. doi: 10.1002/ana.23894. [DOI] [PubMed] [Google Scholar]
- 28.Polymeropoulos MH, Lavedan C, Leroy E, Ide SE, Dehejia A, Dutra A, Pike B, Root H, Rubenstein J, Boyer R, Stenroos ES, Chandrasekharappa S, Athanassiadou A, Papapetropoulos T, Johnson WG, Lazzarini AM, Duvoisin RC, Di Iorio G, Golbe LI, Nussbaum RL. Mutation in the alpha-synuclein gene identified in families with Parkinson’s disease. Science. 1997;276:2045–2047. doi: 10.1126/science.276.5321.2045. [DOI] [PubMed] [Google Scholar]
- 29.Pasanen P, Myllykangas L, Siitonen M, Raunio A, Kaakkola S, Lyytinen J, Tienari PJ, Poyhonen M, Paetau A. Novel alpha-synuclein mutation A53E associated with atypical multiple system atrophy and Parkinson’s disease-type pathology. Neurobiol Aging. 2014;35:2180 e2181–2185. doi: 10.1016/j.neurobiolaging.2014.03.024. [DOI] [PubMed] [Google Scholar]
- 30.Stefanovic AND, Lindhoud S, Semerdzhiev SA, Claessens MMAE, Subramaniam V. Oligomers of Parkinson’s Disease-Related α-Synuclein Mutants Have Similar Structures but Distinctive Membrane Permeabilization Properties. Biochemistry. 2015;54:3142–3150. doi: 10.1021/bi501369k. [DOI] [PubMed] [Google Scholar]
- 31.Kahle PJ, Nielsen SB, Macchi F, Raccosta S, Langkilde AE, Giehm L, Kyrsting A, Svane ASP, Manno M, Christiansen G, Nielsen NC, Oddershede L, Vestergaard B, Otzen DE. Wildtype and A30P Mutant Alpha-Synuclein Form Different Fibril Structures. PLoS ONE. 2013;8:e67713. doi: 10.1371/journal.pone.0067713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Heise H, Celej MS, Becker S, Riedel D, Pelah A, Kumar A, Jovin TM, Baldus M. Solid-state NMR reveals structural differences between fibrils of wild-type and disease-related A53T mutant alpha-synuclein. J Mol Biol. 2008;380:444–450. doi: 10.1016/j.jmb.2008.05.026. [DOI] [PubMed] [Google Scholar]
- 33.Ghosh D, Mondal M, Mohite GM, Singh PK, Ranjan P, Anoop A, Ghosh S, Jha NN, Kumar A, Maji SK. The Parkinson’s Disease-Associated H50Q Mutation Accelerates α-Synuclein Aggregationin Vitro. Biochemistry. 2013;52:6925–6927. doi: 10.1021/bi400999d. [DOI] [PubMed] [Google Scholar]
- 34.Ghosh D, Sahay S, Ranjan P, Salot S, Mohite GM, Singh PK, Dwivedi S, Carvalho E, Banerjee R, Kumar A, Maji SK. The newly discovered Parkinson’s disease associated Finnish mutation (A53E) attenuates alpha-synuclein aggregation and membrane binding. Biochemistry. 2014;53:6419–6421. doi: 10.1021/bi5010365. [DOI] [PubMed] [Google Scholar]
- 35.Snead D, Eliezer D. Alpha-Synuclein Function and Dysfunction on Cellular Membranes. Experimental Neurobiology. 2014;23:292. doi: 10.5607/en.2014.23.4.292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Harada R, Kobayashi N, Kim J, Nakamura C, Han SW, Ikebukuro K, Sode K. The effect of amino acid substitution in the imperfect repeat sequences of alpha-synuclein on fibrillation. Biochim Biophys Acta. 2009;1792:998–1003. doi: 10.1016/j.bbadis.2009.06.010. [DOI] [PubMed] [Google Scholar]
- 37.Sode K, Ochiai S, Kobayashi N, Usuzaka E. Effect of reparation of repeat sequences in the human alpha-synuclein on fibrillation ability. Int J Biol Sci. 2007;3:1–7. doi: 10.7150/ijbs.3.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Winner B, Jappelli R, Maji SK, Desplats PA, Boyer L, Aigner S, Hetzer C, Loher T, Vilar M, Campioni S, Tzitzilonis C, Soragni A, Jessberger S, Mira H, Consiglio A, Pham E, Masliah E, Gage FH, Riek R. In vivo demonstration that α-synuclein oligomers are toxic. Proceedings of the National Academy of Sciences. 2011;108:4194–4199. doi: 10.1073/pnas.1100976108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pandey N, Schmidt RE, Galvin JE. The alpha-synuclein mutation E46K promotes aggregation in cultured cells. Experimental Neurology. 2006;197:515–520. doi: 10.1016/j.expneurol.2005.10.019. [DOI] [PubMed] [Google Scholar]
- 40.Fredenburg RA, Rospigliosi C, Meray RK, Kessler JC, Lashuel HA, Eliezer D, Lansbury PT. The Impact of the E46K Mutation on the Properties of α-Synuclein in Its Monomeric and Oligomeric States†. Biochemistry. 2007;46:7107–7118. doi: 10.1021/bi7000246. [DOI] [PubMed] [Google Scholar]
- 41.Sahay S, Anoop A, Krishnamoorthy G, Maji SK. Site-Specific Fluorescence Dynamics of α-Synuclein Fibrils Using Time-Resolved Fluorescence Studies: Effect of Familial Parkinson’s Disease-Associated Mutations. Biochemistry. 2014;53:807–809. doi: 10.1021/bi401543z. [DOI] [PubMed] [Google Scholar]
- 42.Kloepper KD, Hartman KL, Ladror DT, Rienstra CM. Solid-state NMR spectroscopy reveals that water is nonessential to the core structure of alpha-synuclein fibrils. J Phys Chem B. 2007;111:13353–13356. doi: 10.1021/jp077036z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Khurana R, Ionescu-Zanetti C, Pope M, Li J, Nielson L, Ramírez-Alvarado M, Regan L, Fink AL, Carter SA. A General Model for Amyloid Fibril Assembly Based on Morphological Studies Using Atomic Force Microscopy. Biophysical Journal. 2003;85:1135–1144. doi: 10.1016/S0006-3495(03)74550-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Apetri MM, Maiti NC, Zagorski MG, Carey PR, Anderson VE. Secondary Structure of α-Synuclein Oligomers: Characterization by Raman and Atomic Force Microscopy. Journal of Molecular Biology. 2006;355:63–71. doi: 10.1016/j.jmb.2005.10.071. [DOI] [PubMed] [Google Scholar]
- 45.Karyagina I, Becker S, Giller K, Riedel D, Jovin Thomas M, Griesinger C, Bennati M. Electron Paramagnetic Resonance Spectroscopy Measures the Distance between the External β-Strands of Folded α-Synuclein in Amyloid Fibrils. Biophysical Journal. 2011;101:L1–L3. doi: 10.1016/j.bpj.2011.05.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shaykhalishahi H, Gauhar A, Wördehoff MM, Grüning CSR, Klein AN, Bannach O, Stoldt M, Willbold D, Härd T, Hoyer W. Contact between the β1 and β2 Segments of α-Synuclein that Inhibits Amyloid Formation. Angewandte Chemie International Edition. 2015;54:8837–8840. doi: 10.1002/anie.201503018. [DOI] [PubMed] [Google Scholar]
- 47.Eidenschink L, Kier BL, Huggins KNL, Andersen NH. Very short peptides with stable folds: Building on the interrelationship of Trp/Trp, Trp/cation, and Trp/backbone-amide interaction geometries. Proteins: Structure, Function and Bioinformatics. 2009;75:308–322. doi: 10.1002/prot.22240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sivanesam K, Byrne A, Bisaglia M, Bubacco L, Andersen N. Binding interactions of agents that alter α-synuclein aggregation. RSC Adv. 2015;5:11577–11590. doi: 10.1039/C5RA00325C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Huggins KNL, Bisaglia M, Bubacco L, Tatarek-Nossol M, Kapurniotu A, Andersen NH. Designed Hairpin Peptides Interfere with Amyloidogenesis Pathways: Fibril Formation and Cytotoxicity Inhibition, Interception of the Preamyloid State. Biochemistry. 2011;50:8202–8212. doi: 10.1021/bi200760h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Morris GM, Huey R, Lindstrom W, Sanner MF, Belew RK, Goodsell DS, Olson AJ. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. Journal of Computational Chemistry. 2009;30:2785–2791. doi: 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Giannakis E, Pacifico J, Smith DP, Hung LW, Masters CL, Cappai R, Wade JD, Barnham KJ. Dimeric structures of alpha-synuclein bind preferentially to lipid membranes. Biochim Biophys Acta. 2008;1778:1112–1119. doi: 10.1016/j.bbamem.2008.01.012. [DOI] [PubMed] [Google Scholar]
- 52.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera--a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 53.Kuo LH, Li JH, Kuo HT, Hung CY, Tsai HY, Chiu WC, Wu CH, Wang WR, Yang PA, Yao YC, Wong TW, Huang SJ, Huang SL, Cheng RP. Effect of Charged Amino Acid Side Chain Length at Non-Hydrogen Bonded Strand Positions on β-Hairpin Stability. Biochemistry. 2013;52:7785–7797. doi: 10.1021/bi400911p. [DOI] [PubMed] [Google Scholar]
- 54.Kuo HT, Liu SL, Chiu WC, Fang CJ, Chang HC, Wang WR, Yang PA, Li JH, Huang SJ, Huang SL, Cheng RP. Effect of charged amino acid side chain length on lateral cross-strand interactions between carboxylate- and guanidinium-containing residues in a β-hairpin. Amino Acids. 2015;47:885–898. doi: 10.1007/s00726-015-1916-2. [DOI] [PubMed] [Google Scholar]
- 55.Zhao H, Caflisch A. Molecular dynamics in drug design. European Journal of Medicinal Chemistry. 2015;91:4–14. doi: 10.1016/j.ejmech.2014.08.004. [DOI] [PubMed] [Google Scholar]
- 56.Milardi D, Pappalardo M. Molecular dynamics: New advances in drug discovery. European Journal of Medicinal Chemistry. 2015;91:1–3. doi: 10.1016/j.ejmech.2014.10.078. [DOI] [PubMed] [Google Scholar]
- 57.Fan HM, Gu RX, Wang YJ, Pi YL, Zhang YH, Xu Q, Wei DQ. Destabilization of Alzheimer’s Aβ42 Protofibrils with a Novel Drug Candidate wgx-50 by Molecular Dynamics Simulations. The Journal of Physical Chemistry B. 2015;119:11196–11202. doi: 10.1021/acs.jpcb.5b03116. [DOI] [PubMed] [Google Scholar]
- 58.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, Schulten K. Scalable molecular dynamics with NAMD. Journal of Computational Chemistry. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. Journal of Computational Chemistry. 1983;4:187–217. [Google Scholar]
- 60.MacKerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiórkiewicz-Kuczera J, Yin D, Karplus M. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins†. The Journal of Physical Chemistry B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 61.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. The Journal of Chemical Physics. 1983;79:926. [Google Scholar]
- 62.Feller SE, Zhang Y, Pastor RW, Brooks BR. Constant pressure molecular dynamics simulation: The Langevin piston method. The Journal of Chemical Physics. 1995;103:4613. [Google Scholar]
- 63.Darden T, York D, Pedersen L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. The Journal of Chemical Physics. 1993;98:10089. [Google Scholar]
- 64.Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. Journal of Computational Physics. 1977;23:327–341. [Google Scholar]
- 65.Lee MS, Feig M, Salsbury FR, Brooks CL. New analytic approximation to the standard molecular volume definition and its application to generalized Born calculations. Journal of Computational Chemistry. 2003;24:1348–1356. doi: 10.1002/jcc.10272. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.