Model-based strategy for cell culture seed train layout verified at lab scale

Abstract

Cell culture seed trains—the generation of a sufficient viable cell number for the inoculation of the production scale bioreactor, starting from incubator scale—are time- and cost-intensive. Accordingly, a seed train offers potential for optimization regarding its layout and the corresponding proceedings. A tool has been developed to determine the optimal points in time for cell passaging from one scale into the next and it has been applied to two different cell lines at lab scale, AGE1.HN_AAT and CHO-K1. For evaluation, experimental seed train realization has been evaluated in comparison to its layout. In case of the AGE1.HN_AAT cell line, the results have also been compared to the formerly manually designed seed train. The tool provides the same seed train layout based on the data of only two batches.

Introduction

The production of biopharmaceuticals for diagnostic and therapeutic applications based on suspension cell culture in bioreactor scales from a few hundred liters up to 20 m³ is state of the art. Regarding this application, a seed train is required to generate an adequate number of cells for inoculation of the production bioreactor. Seed train procedures are time- and cost-intensive but offer potential for optimization.

The cell number has to be increased from small volumes used after cryopreservation or used for cell line maintenance up to production scale while passaging into successively larger cultivation systems. Subcultivation into larger vessels is generally based on monitoring of cell density. A seed train requires many manual operations and the application of various cultivation systems (Li et al. 2006; Chu and Robinson 2001; Schenerman et al. 1999). Examples are T-flasks, roller bottles or shake flasks, small scale bioreactor systems and subsequently larger bioreactors. The production bioreactor is inoculated out of the largest seed train scale. In order to reduce the number of passages within the seed train, the use of bioreactors with a variable filling volume was suggested. After inoculation at volumes that are very small in relation to the maximal filling volume, culture volume is increased stepwise in a so called ‘inoculation’ bioreactor by medium addition (Heidemann et al. 2002, 2003). More and more, disposable technology is applied (Rao et al. 2009), for instance systems with wave-induced agitation or stirred disposable systems.

Regardless of different approaches, a cell culture seed train lasts for a significant period of time and generates corresponding costs. The following Fig. 1 shows a seed train example.

Fig. 1.

Seed train example from a cryopreserved vial into a 10,000 L production bioreactor

As a start, cryopreserved vials are thawed and then cells are cultivated using T-flasks for 5, 15 and 35 mL scale (e.g. T25, T75 and T175), roller bottles or shake flasks for 200 mL scale and bioreactors for 1, 5, 20, 80, 400 and 2,000 L scale. From 5 mL-scale until inoculation of the 10,000 L-scale manual control of cell growth in the range of 20–30 days has to be conducted consistently. Delays caused by unusual low growth rates, contamination of a scale etc. can further increase this time span. The higher the number of seed train steps, the more will the culture be prone to deviations. Moreover, deviation from standard growth rates can enforce the personnel to adapt the typically used seed train to the new growth characteristics. Analysing and optimizing existing seed trains as well as designing new seed trains offers the potential to decrease the time efforts and costs of seed trains. Moreover, failure rates of seed trains may also be reduced. Another important aspect of seed trains is that the quality of inoculum in the first cultivation steps has an impact on the cell performance during the production process. Therefore, keeping the cells in a good state is another criterion for seed trains or the design of new seed trains, respectively.

Seed train layout and optimization

In order to ensure an efficient process, the duration of a seed train protocol and the number of seed train steps should be kept to a minimum. At the same time, good cultivation conditions for the cells should be provided continuously in order to maintain high viability, product titer and growth rate for the production scale. With regard to these parameters, seed train protocols offer scope for optimization. Current studies on seed train optimization in cell culture are focused on process modes, cell line- and media development (Alahari 2009; Pohlscheidt et al. 2013) as well as inoculum cryopreservation (Seth et al. 2013). Additionally, scheduling and minimization of facility equipment using simulation tools have been described (Toumi et al. 2010). Besides the mentioned aspects, the seed train itself can be mathematically described, analysed and optimized or new seed trains can be designed, for example by paying attention to the optimal points in time for passaging or to the choice of inoculation density and culture volume at inoculation. Simultaneously, seed trains using ‘inoculation’ bioreactors are also subject to optimization, e.g. in order to determine when medium is supplemented at which volume and if concentrated feed should be preferred over standard medium. Regarding seed train layout or its optimization, a criterion has to be implemented which triggers cell passaging into the next scale. As mentioned before, often transfer to the next scale is done at a fixed cell density or (in small scales such as T-flasks) at a fixed time interval. Due to the obvious disadvantages, more advanced strategies should be applied. An example is the Space–Time–Yield (STY) as a specific indicator, for instance using viable cells (viable cells per filling volume and time) or produced viable cells (new viable cells per filling volume and time). Concerning the STY during cultivation, its maximum value can be estimated and used as a criterion for cell passaging. Another method is to screen for the latest point in time showing a maximal apparent (effective) growth rate or a certain percentage of the maximal apparent (effective) growth rate. The apparent (effective) growth rate is equal to the growth rate minus death rate. Like this, cells are taken directly out of the exponential growth phase. A combination of both criteria can also be used.

This study presents a method to determine optimized points in time for cell passaging within a seed train, its application and verification on two cell lines at lab scale. Furthermore, the successful application of this tool points to its potential for setting up new seed train protocols and handling a variety of cell lines. The tool is also capable of using different optimization criteria.

Materials and methods

Cells and media

The AGE1.HN_AAT cell line is a human industrial cell line of the company ProBioGen AG (Berlin, Germany) which produces the therapeutic protein α-1-antitrypsin. A detailed description of the cell line was published lately (Niklas et al. 2012). The cells were cultivated in the serum-free 42-Max-UB medium (TeutoCell AG, Bielefeld, Germany). The medium was further supplemented to 5 mM L-Glutamine (PAA Laboratories, Cölbe, Germany).

The CHO-K1 cell line (provided by Prof. Noll, Bielefeld University) was grown in serum and protein free conditions in the chemically defined medium TC-42 (TeutoCell AG, Bielefeld, Germany) supplemented to 4 mM l-Glutamine (PAA Laboratories, Cölbe, Germany).

Analytical methods

Cell counting was performed using a hemocytometer (Brand GmbH, Wertheim, Germany). Viability was determined by applying the Trypan blue exclusion method. Glucose, lactate and glutamine concentrations were analysed enzymatically using the YSI7100MBS (Yellow Springs Instruments, Yellow Springs, Ohio, USA). Ammonia was quantified by using a photometric method (Spectroquant, 1.14752.0001, Merck, Darmstadt, Germany) with measurements at a wavelength of 690 nm (Bio-Rad, SmartSpec Plus, Munich, Germany). The produced protein was not analysed since the expression of α-1-antitrypsin showed no influence on growth and substrate uptake rates of AGE1.HN_AAT cell line (Platas Barradas et al. 2012).

Cultivation parameters and process control system

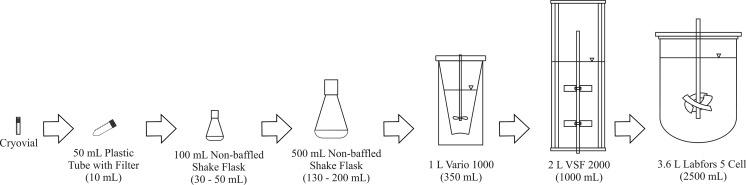
Preculture steps for AGE1.HN_AAT were carried out in 50 mL culture tubes (Biochrom, Berlin, Germany), 100 and 500 mL glass Erlenmeyer shake flasks (Duran Group GmbH, Wertheim/Main, Germany) with working volumes of 10, 30–50 and 130–200 mL, respectively. CHO-K1 cells were cultivated in 50 mL culture tubes (Biochrom, Berlin, Germany) and 250 mL baffled Erlenmeyer flasks (Corning Inc., Germany) with working volumes of 10 and 75 mL, respectively. These preculture steps were operated on an orbital shaker at 225 rpm with oscillation of 10 mm (GFL3005, Omnilab, Bremen, Germany). The incubator atmosphere was regulated at 37 °C and an initial value of 5 % CO₂. A scheduled reduction of the CO₂ partial pressure was carried out routinely according to the externally measured pH-value in culture: CO₂ = 5 % for pH > 7.3, 3 % for 7.1 < pH ≤ 7.3, and 0 % for pH ≤ 7.1. Cells growing exponentially in preculture were centrifuged (125 g, 5 min) and inoculated at initial cell densities from 0.8 × 10⁹–1.2 × 10⁹ cells/L (and 0.3 × 10⁹ cells/L for CHO-K1 respectively). The high initial cell densities were required for the AGE1.HN_AAT cell line. Three different bench-top bioreactors including Vario 1000 (Medorex eK, Nörten-Hardenberg, Germany), VSF 2000 (Bioengineering AG, Wald, Switzerland) and Labfors 5 Cell (Infors AG, Basel, Switzerland) with working volumes of 0.35, 1 and 2–2.5 L were used. The geometric characteristics of the cultivation systems concerning this lab scale seed train example are depicted in Fig. 2 and Table 1.

Fig. 2.

Experimental set-up of the lab scale seed train for the AGE1.HN_AAT cell line

Table 1.

Bioreactor characteristics

Bioreactor	V (10−3 m3)	Bottom	Impeller	di (m)	n (rpm)	utip (m/s)	P/V (W m−3)	Rei (–)
Vario 1000	0.35	Truncated cone	3-MP	0.029	535	0.8	12	10,712
VSF 2000	1	Flat	6-RT	0.048	280	0.7	306	15,360
Labfors 5a	2.5	Curved	3-S	0.084	156	0.7	20	26,208
Labfors 5b	2	Curved	3-S	0.084	156	0.7	26	26,208

V, working volume; 3-MP, 3-blade marine propeller; 6-RT, 6-blade radial-discharging impeller (Rushton); 3-S, 3-blade segment impeller; d_i, impeller diameter; n, agitation speed; u_tip, impeller tip speed; P/V, volume specific power input; Re_i, Reynolds number at impeller tip

^aAGE1.HN_AAT cultivation; ^bCHO-K1 cultivation

The impeller tip speed as well as the mixing time were recently identified as criteria for culture standardization for different bioreactor sizes and geometries (Platas Barradas et al. 2012). Yang et al. 2007, present the selection of mixing models and agitation speeds during scale-up from 3–2500 L for monoclonal antibody production based on a case study. Regarding VSF 2000 and Labfors 5 Cell, stirrer tip velocity was kept constant at 0.7 m/s during cultivation in each bioreactor. In the Vario 1000 bioreactor, stirrer tip velocity was set to 0.8 m/s due to a relatively large working volume and a consequently decreased specific power input and increased mixing time. Further information concerning the bioreactor characteristics are presented in Table 1. Large deviations in specific power input are caused by utilization of different stirrer designs. For cultivation, pH was maintained at 7.15 by adding CO₂ or 0.5 M Na₂CO₃ and dissolved oxygen was set to 30 % air saturation. Total gas flow (Air + O₂ + CO₂) was controlled to a maximum of 0.06 vvm. Therefore, the gas flow of air was increased due to oxygen demand up to the maximum rate; afterwards the proportion of pure oxygen in the gas flow was increased. Off-line sampling was performed at least once per day.

Seed train tool programming

The seed train calculation and layout/optimization tool has been programmed in Matlab 2012a. The programming and its background is further described in literature (Frahm 2014).

Results and discussion

To begin with, the concept of seed train analysis and layout will be presented in this chapter including the applied model and the model parameter identification. Since concept and methodology of a seed train tool for analysis, design and optimization for cell culture has been described recently (Frahm 2014), this study presents the application and verification of this method at lab scale regarding selected optimization criteria. The model-based seed train tool is applied experimentally to AGE1.HN_AAT and CHO-K1 cell line seed trains at lab scale. For both cell lines the seed train set-up has been manually designed in the past by trial and error. This enables a comparison of the tool-designed seed train to the manually designed seed train.

More complex seed train configurations arise in case of influence of ammonia- or lactate inhibition and further from the impact of process parameters such as aeration, shear stress, mixing time, power input, pH-value or feeding rate. Thus, dependencies of these parameters on seed train analysis and therefore on the points in time for passaging cannot be reflected by using a basic fit of the growth curve without an underlying model. The model-based approach is essential in order to determine the end of the exponential growth phase. Especially the transition of the exponential growth phase into the stationary phase/death phase needs to be mathematically described. Only on the basis of such a simulated course of viable cell growth over time, criteria for cell passaging can be applied. A general analysis of a common cell growth curve or a polynomial fit of just the growth phase are not sufficient, since characteristics of different cell lines and different cultivation conditions which both affect the growth curve are not taken into account. The application of the designed tool to the different cell lines (AGE1.HN_AAT and CHO-K1) will illustrate this aspect. The actual course of viable cell growth over time for the used cell line in the applied medium and for the applied cultivation conditions is always required for each seed train scale to analyse the situation, to apply different criteria and to make a decision for seed train layout, e.g. to determine the point in time for cell passaging.

Since this study emphasises on the first implementation and testing of this fast model-based procedure, two standard seed train set-ups of two cell lines based on a corresponding model were used. Of course, the model can be extended for more sophisticated seed train circumstances and used within this seed train tool.

Concept

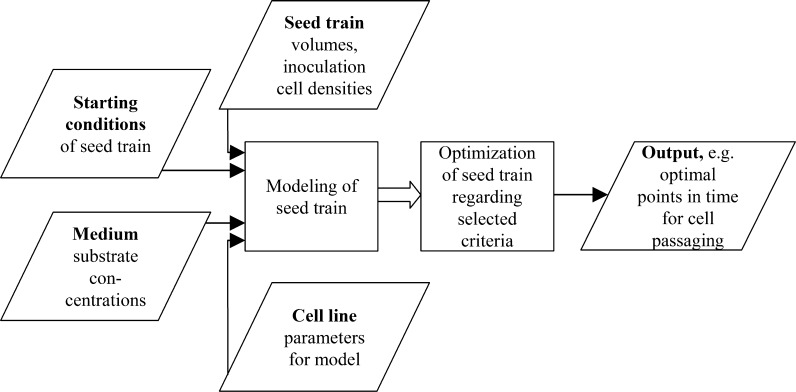
Figure 3 presents the scheme of the tool. Parallelograms illustrate the input information: Concerning the seed train, the filling volumes and inoculation cell densities as well as information regarding the starting conditions is required. The information about the starting conditions includes the initial values of all modeled process variables such as viable cell concentration as well as important substrate and metabolite concentrations. Concerning the medium, relevant substrate concentrations are needed. With respect to the cell line, parameter values for the model equations are necessary. Based on this information, modeling of the seed train is possible.

Fig. 3.

Flow diagram of the model-based seed train optimization tool in Matlab

A general seed train structure for cells growing in suspension has been implemented in the tool with the possibility to enter specific values of different seed trains. The modeling of the seed train in turn allows the optimization regarding the Space–Time–Yield (STY), the latest point in time showing a certain percentage of the maximal apparent (effective) growth rate or any other convincing criteria. The software gives an output of the optimized parameters which are verified experimentally in the laboratory.

Model

Various models for cell growth and metabolism are described in detail in the literature (Pörtner and Schäfer 1996; Zeng et al. 1998; Jang and Barford 2000). For this application, an unstructured, unsegregated model was adopted from Frahm (2014) and Frahm et al. (2002). This simple model structure was chosen because it allows the identification of relevant kinetic parameters from only a few cultivations.

The applied model includes all important parameters for monitoring the seed train such as cell growth and cell death as well as limiting substances. Coupled balance equations for the description of viable and total cell density and all major substrate and metabolite concentrations as well as the kinetics (description of substrate uptake and metabolite production kinetics) are subsumed in the model equations as shown in Table 2. The same model has been applied for both cell lines. The model is based on the following assumptions: The cell specific growth rate µ depends on a two-substrate Monod-type kinetic on glucose and glutamine concentration (Eq. 7). The cell specific death rate is determined by a minimal and a maximal cell specific death rate (Eq. 8). Whereas the minimal cell specific death rate is not affected by any substrate, the maximal cell specific death rate is included in a Monod-type kinetic with glucose as an inhibitor since previous experiments showed an increased death rate in the absence of glucose. Glucose and glutamine uptake rates, q_Glc and q_Gln, depend on their particular concentration according to a kinetic of Monod-type (Eq. 9 and 10). Equation 9 contains an additional term in order to reduce the glucose uptake at low growth rates. Production rates of lactate and ammonia are proportional to the consumption of glucose or glutamine (Eq. 11 and 12), whereby the production rate of lactate is also dependent on the ratio of glucose and lactate concentration. At glucose concentrations below 0.5 mM, an uptake of lactate has been observed. On the basis of these model equations, the courses of viable cell, total cell, glucose, glutamine, lactate and ammonia concentrations can be determined. Furthermore, the balance of the cultivation volume is included in the optimization tool.

Table 2.

Model equations used in the tool simplified to batch mode

Balance equations	Kinetics
Biophase	Growth/death
$\frac{d{X}_v}{dt}=\left(\mathit{\mu }-{\mathit{\mu }}_d\right)·X_v(1)$	$\mathit{\mu }={\mathit{\mu }}_{\text{max}}·\frac{c_{Glc}}{c_{Glc}+K_{S,Glc}}·\frac{c_{Gln}}{c_{Gln}+K_{S,Gln}}(7)$
$\frac{d{X}_t}{dt}=\mathit{\mu }·X_v-K_{Lys}·\left(X_t-X_v\right)(2)$	${\mathit{\mu }}_d={\mathit{\mu }}_{d,\text{min}}+{\mathit{\mu }}_{d,\text{max}}·\frac{K_{S,Glc}}{K_{S,Glc}+c_{Glc}}(8)$
Liquid phase	Substrate uptake/metabolite production
$\frac{d{c}_{Glc}}{dt}=-q_{Glc}·X_v(3)$	$q_{Glc}=q_{Glc,\text{max}}·\frac{c_{Glc}}{c_{Glc}+k_{Glc}}·\left(\frac{\mathit{\mu }}{\mathit{\mu }+{\mathit{\mu }}_{\text{max}}}+0.5\right)(9)$
$\frac{d{c}_{Gln}}{dt}=-q_{Gln}·X_v(4)$	$q_{Gln}=q_{Gln,max}·\frac{c_{Gln}}{c_{Gln}+k_{Gln}}(10)$
$\frac{d{c}_{Lac}}{dt}=q_{Lac}·X_v(5)$	$\begin{array}{c}{q}_{Lac}=Y_{Lac/Glc}·\frac{c_{Glc}}{c_{Lac}}·q_{Glc}-q_{Lac,uptake}\\ c_{Glc}\ge 0.5mM:q_{Lac,uptake}=0\\ c_{Glc}<0.5mM:q_{Lac,uptake}=q_{Lac,uptake,\text{max}}(11)\\ \end{array}$
$\frac{d{c}_{Amm}}{dt}=q_{Amm}·X_v(6)$	$q_{Amm}=Y_{Amm/Gln}·q_{Gln}(12)$

Model parameter identification

For application of this model, model parameters were adjusted in order to find the best fit of modeled courses to cultivation data. Two batch cultivations in shake flasks under equal starting conditions were performed for generation of experimental data for each cell line. These data were fitted by using the simplex algorithm by Nelder and Mead (1965) in order to determine the model parameters. Important final courses of fitted parameters are shown in Fig. 4 for one cultivation each. For the starting conditions and experimental set-up used in this study, metabolite concentrations did not affect the growth and death rate. The Nelder–Mead algorithm needs a set of initial parameter values and corresponding lower and upper bounds. As shown in Table 3, eleven of thirteen model parameters were set free for identification. Monod constants for glucose and glutamine (K_S,Glc and K_S,Gln) affecting the growth rate were fixed at typical values for cell culture. Initial parameters and boundaries were adopted from previous studies (Frahm et al. 2002, 2003). However, impact of initial values could not be observed and boundaries have never been reached (see Table 3).

Fig. 4.

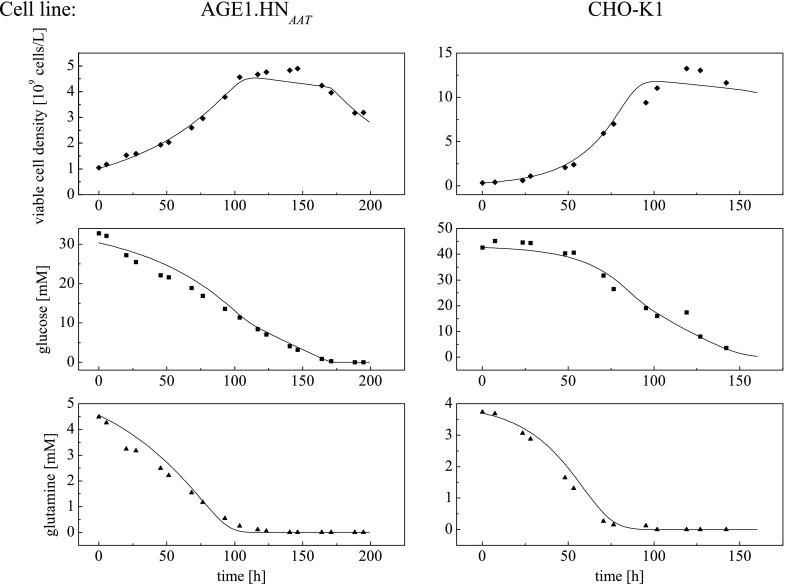
Simulated and experimental data of AGE1.HN_AAT and CHO-K1 cells during shake flask cultivation

Table 3.

Model parameters, initial values and boundaries of the Nelder–Mead algorithm

Parameter	Unit	Initial value	Upper limit	Lower limit	Fitted value AGE1.HNAAT	Fitted value CHO-K1
µ d,min	h−1	0.003	0.03	0	0.0015	0.0017
µ d,max	h−1	0.03	0.3	0	0.0123	0.0360
µ max	h−1	0.05	0.5	0	0.0161	0.0440
k Glc	mmol L−1	0.19	1.9	0	0.0605	1.8501
k Gln	mmol L−1	0.3	3	0	0.4966	3.7363
K Lys	h−1	0.005	0.05	0	0.0021	0.0010
K S,Glc	mmol L−1	0.03 (fixed)
K S,Gln	mmol L−1	0.03 (fixed)
Y Amm/Gln	–	0.4	4	0	0.8889	0.6562
Y Lac/Glc	–	1.5	15	0	0.8326	0.4707
q Glc,max	10−9 mmol cell−1 h−1	0.25	2.5	0	0.0767	0.0726
q Gln,max	10−9 mmol cell−1 h−1	0.085	0.85	0	0.0279	0.0770
q Lac,uptake,max	10−9 mmol cell−1 h−1	0.1	1	0	0.0112	0.0442

Tool-based seed train layout for the AGE1.HN_AAT cell line

The Space–Time–Yield (STY) was selected as optimization criterion that affects the cell passaging from one scale to the next. The number of viable cells per time and volume unit is defined as STY in this case (Eq. 13).

$$STY=\frac{viablecellnumber}{culturevolume\times time}$$ 13

The model parameters affecting the STY time frame are the growth and death kinetics as well as the substrate uptake kinetics. Metabolite production kinetics are important for seed train monitoring but do not influence the STY in case of this cell line. Concerning a specific cell line, the growth kinetics of the model can be extended so as to include metabolite inhibition.

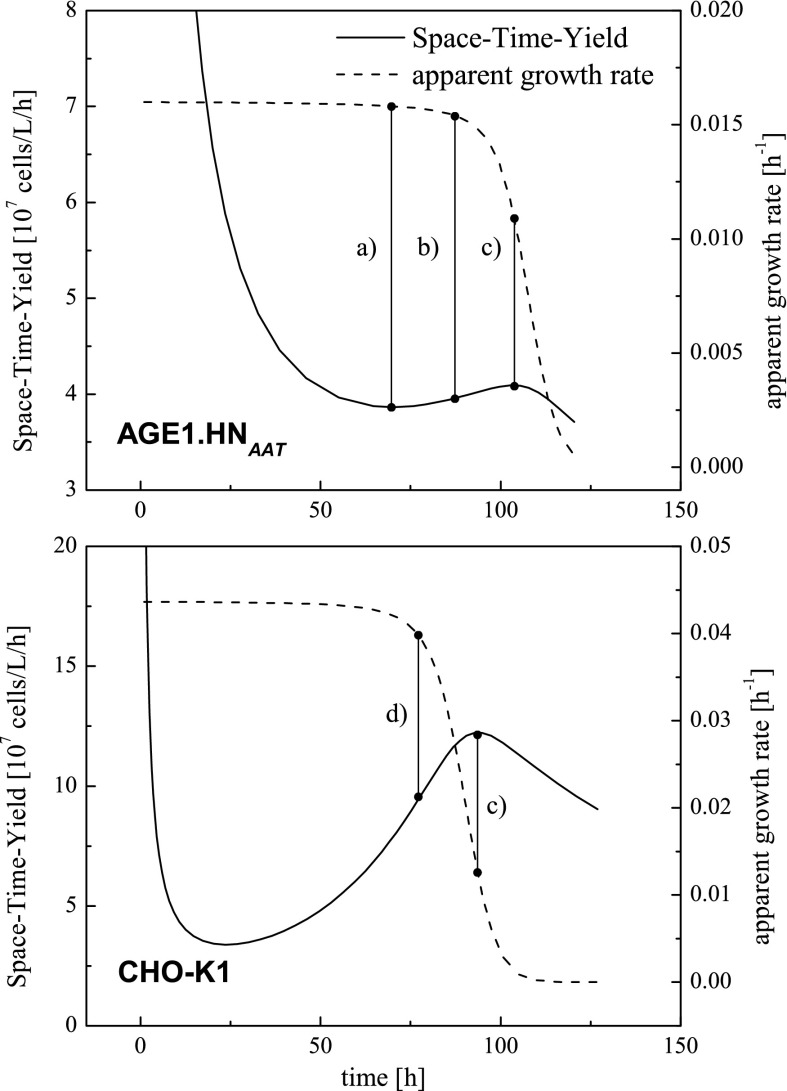
Based on the simulated courses of viable cell density, the STY can be plotted over time for each step of the seed train as shown in Fig. 5.

Fig. 5.

Examples of simulated courses of Space–Time–Yield and apparent (effective) growth rate over time regarding a batch cultivation of AGE1.HN_AAT cell line: a point in time of minimal STY, b average value of points in time of minimal and maximal STY, c point in time of maximal STY. Analog courses regarding a batch cultivation of CHO-K1 cell line: c point in time of maximal STY and d point in time of apparent (effective) growth rate decrease to 90 %

Starting at time approaching to zero STY goes to infinity. Since viable cell concentration increases exponentially whereas time proceeds linear, STY yields a local minimum at the beginning of the cultivation (Fig. 5a). After that, STY increases until one of the substrates is limiting and causes the apparent (effective) growth rate to decrease. This leads to the local maximum of STY which corresponds to the end of the exponential phase. Characteristic points regarding AGE1.HN_AAT cell line are the local minimum and maximum around 70 and 106 h, respectively, in case of a proper inoculation density of 1 × 10⁹ cells/L.

Maximal STY coincided with the end of the exponential growth phase (Fig. 5c), which means that the cells are then passing into the stationary phase. In case cells were passaged at this point in time, the apparent (effective) growth rate would decrease significantly in the following cultivation system (data shown in Fig. 6). Because cells out of this state are not favored for passaging, another optimization criterion was then selected. The mean value of time for minimal and maximal STY according to Eq. 14

$$t=\frac{t_{STY\text{min}}+t_{STY\text{max}}}{2}$$ 14

was implemented as a criterion for cell passaging (Fig. 5b). Thus, cells are taken directly out of the exponential growth phase and buffer time towards the stationary phase is given.

Fig. 6.

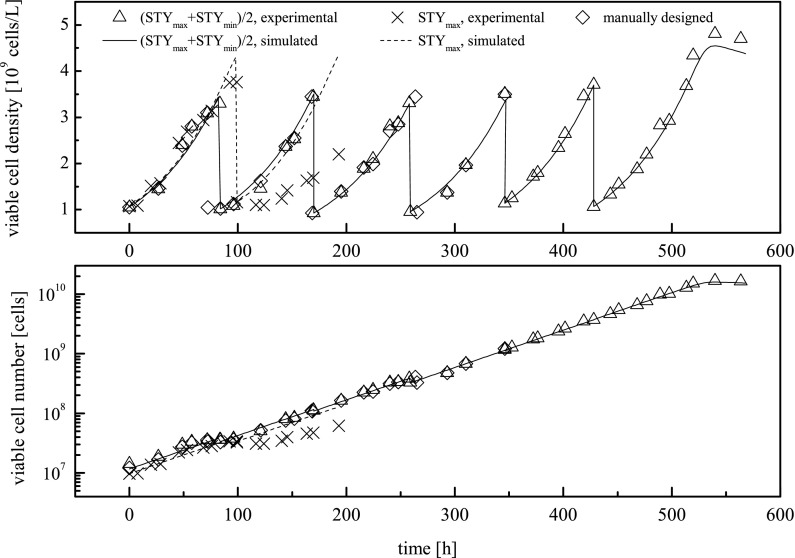
Simulated and experimental time courses of viable cell density and viable cell number during various seed train configurations for AGE1.HN_AAT cell line. These configurations are: seed train conducted based on passaging at the points in time calculated using maximum and minimum Space–Time–Yield (STY) (compare Eq. 14) (=triangles) as well as the corresponding simulation (=line); seed train conducted based on passaging at the points in time calculated using maximum STY (=crosses) as well as the corresponding simulation (=dotted line); seed train conducted according to the manually designed procedure (=rhombs). The seed train steps are: (1) culture tube (0.01 L), (2) shake flask (0.035 L), (3) shake flask (0.13 L), (4) Vario 1000 (0.35 L), (5) VSF 2000 (1 L), (6) Labfors 5 Cell (2.5 L)

Figure 5 also shows the simulated courses of Space–Time–Yield and apparent (effective) growth rate regarding a batch cultivation of CHO-K1 cell line. The differences in the courses of the AGE1.HN_AAT cell line and the CHO-K1 cell line underlines the necessity for this tool-based approach.

However, performing a tool-optimized seed train based on a model without any feedback comprises the same limitations as performing a manually designed seed train based on fixed time intervals without any feedback. Since the modeled data rely only on initial conditions, deviations from model calculation due to unusual cell behavior are not taken into account. In case of unusual cell behavior the optimal point in time for passaging can change significantly. A possibility to avoid the described situation is to perform certain sampling and analytics in order to monitor cell growth and substrate concentrations, for example. If cell growth may differ from model calculation, the model parameters can be adapted to the obtained sampling data. The re-adapted model can then be used for prediction of the coming scale steps.

Verification of tool-based seed train layout by comparison to the manually designed seed train

Due to the consistent cultivations in shake flasks and various bench-top bioreactors the points in time for cell passaging have been determined manually for the AGE1.HN_AAT cell line in the past (Platas Barradas et al. 2012). The pH-value as well as viable and total cell densities were determined as indicators for cell passaging. Cells were passaged at densities between 3.5 and 4.0 × 10⁹ cells/L while the pH and viability should not drop below 6.9 and 90 %, respectively.

The tool-designed seed train and the manually designed seed train have been experimentally realized at lab scale including the previously referred cultivation systems. From starting volumes of 13 mL the working volume was increased to 0.35 and further to 2.5 L in the larger scale experiments. To obtain a fair comparison of the manually designed seed train and the one designed via the tool, parallel seed trains have been performed and compared. Cells out of the same culture vessel were split for both seed train protocols in order to ensure equal starting conditions. The simulation of time courses through the tool was performed by using the starting condition information of each cultivation scale. The experimental courses of viable cell density and cumulative viable cell number of the tool-designed seed train and its experimental realization are presented in Fig. 6 as well as the same parameters for the manually designed seed train.

For the tool-designed seed train, Fig. 6 shows a good compliance of simulation and experiment (comparison of triangles and line). The courses of cell number regarding the criterion concerning the average value of time for minimal and maximal STY show no differences among the tool-designed and the manually designed method (comparison of triangles, line and rhombs). This shows that the tool was able to yield an accurate seed train layout only on the basis of two batches, the underlying model and its parameter identification. Cultivation time for the model-based optimization varies in each step between 82 and 88 h depending on the inoculation density. Differences to the manually designed method extend to a maximum of 12 h. Figure 6 also illustrates for the first two scales, as already discussed in the context of Fig. 5, that maximal STY itself as a criterion for cell passaging is disadvantageous (comparison of crosses and dotted line).

Even in larger bench-top bioreactors the model-based simulation showed reliable results as shown in Fig. 6 starting from hour 350. For these scales no manually designed seed train was established. Concerning the last passaging step, the entirety of cumulated cells could not be transferred into the final scale on account of the maximal working volume of the Labfors 5 (2.5 L working volume, passaging the entirety of cumulated cells would result in 3.5 L). In practical application an additional bioreactor of the same scale or a larger cultivation system would have been used regarding this step.

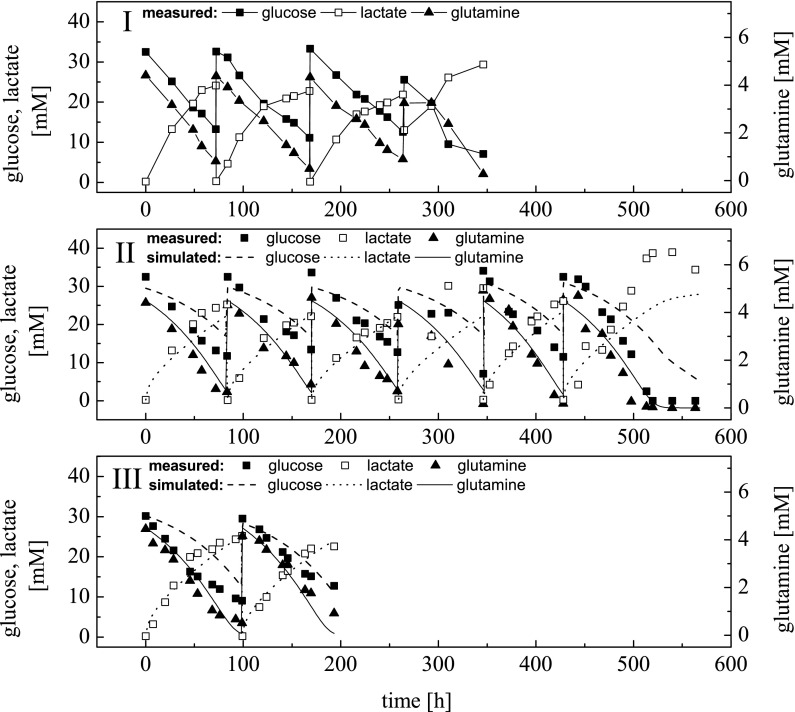
The experimental courses of glucose, lactate and glutamine concentrations for the above configurations are presented in Fig. 7.

Fig. 7.

Simulated and measured glucose, lactate and glutamine concentrations during the seed train configurations for AGE1.HN_AAT cell line of Fig. 6. Part I: seed train conducted according to the manually designed procedure. Part II: seed train conducted based on passaging at the points in time calculated using maximum and minimum Space–Time–Yield (STY) (compare Eq. 14) as well as the corresponding simulation. Part III: seed train conducted based on passaging at the points in time calculated using maximum STY as well as the corresponding simulation. The seed train steps are: (1) culture tube (0.01 L), (2) shake flask (0.035 L), (3) shake flask (0.13 L), (4) Vario 1000 (0.35 L), (5) VSF 2000 (1 L), (6) Labfors 5 Cell (2.5 L)

Simulated and measured glucose, lactate and glutamine concentrations in Fig. 7 agree fairly well except for lactate in the last scale. Since this deviation in lactate was not crucial for the seed train, model refinement has not been carried out.

To conclude, the tool has quickly delivered a seed train layout which could be realized at lab scale. The obtained measured values are in the same range as the tool-predicted values. Comparison to the already existing manually set-up seed train shows that the tool has designed a reasonable seed train.

Tool-based seed train layout for the CHO-K1 cell line

In case of the CHO-K1 cell line, a further advanced optimization criterion has been applied taking Space–Time–Yield (STY) as well as apparent (effective) growth rate into account (Eq. 15).

$$t=\frac{t_{STY\text{max}}+t_{0.9·{\mathit{\mu }}_{\text{max}}}}{2}$$ 15

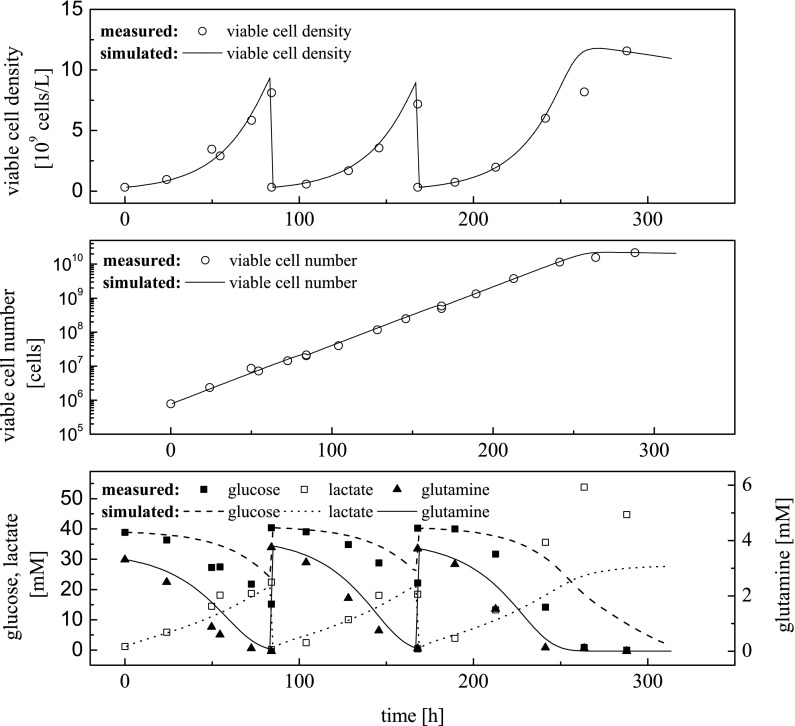
In Eq. 15t_STYmax represents the cultivation time showing the maximal STY and $t_{0.9·{\mathit{\mu }}_{\text{max}}}$ as the latest point in time showing 90 % of the maximal apparent (effective) growth rate (the percentage can be chosen by the user for different applications). This criterion is an advanced version of the criterion given in Eq. 14 and works also for the AGE1.HN_AAT cell line. Whereas Eq. 14 also considered the point in time of the minimum STY, the use of the apparent (effective) growth rate leads to more accurate results. The intention of Eq. 14, which is to include a safety time span between the point in time of cell passaging and the end of the exponential growth phase, is also taken into account by Eq. 15. An example of the simulated courses of Space–Time–Yield and apparent (effective) growth rate over time regarding a batch cultivation of CHO-K1 cell line has already been presented in Fig. 5. The practical application of the presented optimization criterion to the CHO-K1 cell line resulted in the graphs displayed in Fig. 8.

Fig. 8.

Simulated (lines) and experimental (symbols) time courses of viable cell density, viable cell number as well as glucose, lactate and glutamine concentration during tool-based seed train layout for CHO-K1 cell line—seed train steps: (1) culture tube (0.0025 L), (2) shake flask (0.070 L), (3) Labfors 5 Cell (2 L)

Experimental realization of the tool-designed seed train shows a good compliance to its previous layout via simulation. Cultivation time for this model-based optimization varied between 84 and 85 h in each step depending on the inoculation density. No significant decrease of the apparent (effective) growth rate in each cultivation system was detected which shows that the presented optimization criterion is practicable. Contrary to the optimization criterion applied to the AGE1.HN_AAT cell line, the point in time for cell passaging of the CHO-K1 cell line was set closer to the maximal STY, which means the cultivation time in each step was increased. Thereby, a reduction in manual operations and the number of cultivation systems is possible. Moreover, simulated and measured glucose, lactate and glutamine concentrations in Fig. 8 agree fairly well except for lactate in the last scale. Again, since deviation in lactate was not crucial for the seed train, model refinement has not been carried out.

Of course the starting conditions of the seed train modeling are influenced by corresponding measurement errors, e.g. for cell density, substrate and metabolite measurements. This has been investigated for the starting value of the viable cell concentration and the maximum growth rate taken as important values. Table 4 illustrates the sensitivity of point in time of cell passaging and the corresponding viable cell density for a ± variation of 5 % in the starting value of viable cell density and maximum growth rate for an example taken from the CHO-K1 seed train.

Table 4.

Effect of measurement accuracy of viable cell concentration and maximum growth rate on point in time of cell passaging and corresponding viable cell concentration, original values were taken from CHO-K1 scale 1 (cell passaging according to Eq. 15)

Starting value of viable cell concentration (cells L−1)	Model parameter value of maximum growth rate (h−1)	Point in time for cell passaging (h)	Viable cell concentration at cell passaging (cells L−1)
3.15 × 108	0.0440	84.8	9.84·109
2.99 × 108 (−5 %)	0.0440	85.8 (+1.2 %)	9.77·109 (−0.7 %)
3.31 × 108 (+5 %)	0.0440	83.8 (−1.2 %)	9.89·109 (+0.5 %)
3.15 × 108	0.0418 (−5 %)	88.0 (+3.8 %)	9.37·109 (−4.8 %)
3.15 × 108	0.0462 (+5 %)	81.5 (−3.9 %)	10.28·109 (+4.5 %)

For Table 4 the parameters of the presented CHO-K1 cultivation at scale 1 have been used. First of all, the effect of an inaccuracy of ±5 % of the starting value of viable cell concentration was of interest. This is the initial value at time 0 of the scale which is entered into the tool. Therefore the viable cell concentration decreased by 5 % has been employed for a simulation resulting in a point in time for cell passaging of now 85.8 h instead of 84.8 h (+1.2 %). The tool determined the point in time of cell passaging according to Eq. 15 which is an average between the point in time of optimal STY and the point in time of apparent (effective) growth rate decreased to 90 %. An effect of +1.2 % is tolerable which corresponds to a change of −0.7 % in viable cell concentration at cell passaging. An inaccuracy of −5 % of the starting value of viable cell concentration gives corresponding results.

Secondly, the model parameter of the maximum growth rate has also been varied by ±5 %. The model parameter has been determined from data of previous experiments. The ±5 % variation has an effect of +3.8 on the point in time for cell passaging or −3.9 %, respectively, which is also tolerable.

Even if this is acceptable, averaged values of multiple measurements should be used when designing a seed train layout.

When an actual seed train is running that has been modeled and optimized by the software tool, measurement information from this ongoing seed train should be taken into account to see if deviations between designed and actual seed train occur. The software also allows the modeling of running seed trains by adapting the seed train information and entering the current measurement information as starting values into the software.

Conclusions

A tool has been programmed that allows the mathematical description of seed trains based on important characteristics such as cell line, medium and seed train vessel properties. The cell line properties are obtained by using cell line cultivation data to obtain parameters for a cell culture model via the Nelder–Mead algorithm. This seed train tool can be used for analysis and optimization of existing seed trains or the design of new seed trains. In this paper, the tool has undergone first tests by its application to two cell lines at lab scale. Experimental realizations fitted well the tool-designed layouts. Space–Time–Yield (STY) as well as apparent (effective) growth rate have been investigated as indicators to trigger cell passaging into the next scale. For one cell line, the tool-designed seed train has also been compared to the formerly manually designed seed train and showed the same results. Therefore the tool offers a quick and well-directed strategy for seed train layout. The two different cell line examples also illustrated the necessity for such a model-based approach for seed train layout. A general growth curve analysis or polynomial fit of the growth rate is not sufficient to determine the transition of growth phase into stationary phase/death phase for each seed train scale depending on cell line parameters and cultivation conditions which is essential for seed train analysis and layout.

In future research the implementation of online measurements of advances probe technology, e.g. for cell density, as well as further important measurement parameters relevant for the corresponding cell line (e.g. measurements indicating apoptosis) into the software tool will also be a topic.

List of symbols

µ

Cell-specific growth rate (h⁻¹)

µ_d

Cell-specific death rate (h⁻¹)

µ_d,min

Minimum cell-specific death rate (h⁻¹)

µ_d,max

Maximum cell-specific death rate (h⁻¹)

µ_max

Maximum cell-specific growth rate (h⁻¹)

c_Amm

Ammonia concentration (mmol L⁻¹)

c_Glc

Glucose concentration (mmol L⁻¹)

c_Gln

l-glutamine concentration (mmol L⁻¹)

c_Lac

Lactate concentration (mmol L⁻¹)

k_Glc

Monod kinetic constant for glucose uptake (mmol L⁻¹)

k_Gln

Monod kinetic constant for glutamine uptake (mmol L⁻¹)

K_Lys

Cell lysis constant (h⁻¹)

K_S,Glc

Monod kinetic constant for glucose (mmol L⁻¹)

K_S,Gln

Monod kinetic constant for glutamine (mmol L⁻¹)

q_Amm

Cell-specific ammonia production rate (mmol cell⁻¹ h⁻¹)

q_Glc

Cell-specific glucose uptake rate (mmol cell⁻¹ h⁻¹)

q_Glc,max

Maximum cell-specific glucose uptake rate (mmol cell⁻¹ h⁻¹)

q_Gln

Cell-specific glutamine uptake rate (mmol cell⁻¹ h⁻¹)

q_Gln,max

Maximum cell-specific glutamine uptake rate (mmol cell⁻¹ h⁻¹)

q_Lac

Cell-specific lactate production rate (mmol cell⁻¹ h⁻¹)

q_Lac,uptake

Cell-specific lactate uptake rate (mmol cell⁻¹ h⁻¹)

q_{Lac,uptake,max}

Maximum cell-specific lactate uptake rate (mmol cell⁻¹ h⁻¹)

t

Time (h)

t_STYmax

Cultivation time showing the maximal STY (h)

t_0.9 µ max

Latest point in time showing 90 % of the maximal apparent (effective) growth rate (h)

X_t

Total cell concentration (cells mL⁻¹)

X_v

Viable cell concentration (cells mL⁻¹)

Y_Amm/Gln

Kinetic-production-constant (stoichiometric ratio of ammonia production and glutamine uptake) (–)

Y_Lac/Glc

Kinetic-production-constant (stoichiometric ratio of lactate production and glucose uptake) (–)