Multi-Reference Parallel ICA: A Semi-blind Multivariate Approach

Abstract

High data dimensionality poses a major challenge for imaging genomic studies. To address this issue, a semi-blind multivariate approach, multi-reference parallel independent component analysis (pICA-MR), is proposed. pICA-MR extracts imaging and genetic components in parallel and enhances inter-modality correlations. Prior knowledge is incorporated to emphasize genetic factors with specific attributes. Particularly, pICA-MR can investigate multiple genetic references to explore functional interactions among genes. Simulations demonstrate robust performances with Euclidean distance employed as a metric for reference similarity, where components pointed by the same references are reliably identified and the detection power is significantly improved compared to blind methods.

I. Introduction

Imaging genomics is a maturing field which studies associations between genetic variables and neuroimaging traits. While this strategy holds the promise to reveal genetic underpinnings of neuronal functions, novel computational methods are desired to efficiently mine the complex high-dimensional data. One of the most challenging problems is that correction for the huge number of statistical tests in univariate models makes it difficult to identify any small or moderate genetic effect within a practical sample size, as observed in complex polygenic mental disorders [1]. To address this issue, a number of multivariate approaches have been developed to simultaneously assess many variables for an aggregate effect, including principal component regression [2], sparse reduced-rank regression [3], sparse partial lease square [4], parallel independent component analysis (pICA) [5] and sparse canonical correlation [6].

While the aforementioned approaches have shown improved detection power compared to univariate models, their performance could be further advanced through taking prior information into account. For instance, some genes are known to participate in a biological pathway critical to a disease, and they may help elicit a set of genes contributing in a coordinated way to a larger network relevant to the disease. In light of this, we designed a semi-blind multivariate approach, named parallel ICA with reference (pICA-R) [7], where imaging and genomic components are estimated in parallel and inter-modality correlations are enhanced. Particularly, the data decomposition is partially guided by a genetic reference, such that the resulting components highlight the reference variables and other covarying variables.

The application of pICA-R to real imaging genomic data involving one million or so variables has been demonstrated. However, the original design investigates only one single genetic reference. In complex disorders, the capability to simultaneously assess multiple references is desired, given that multiple genes can potentially converge their functional influences on neurobiological traits. To better delineate the underlying genetic architecture, we extended the pICA-R approach to accommodate multiple references.

II. Method

In the proposed multi-reference parallel ICA (pICA-MR), the selected references are organized into a matrix r. Each row represents a reference vector comprising a group of reference loci likely in linkage disequilibrium (LD). The interrelationship among reference vectors is to be investigated in a data-driven manner. The mathematical model for pICA-MR is shown below.

$$X_d=A_d{S}_d\to S_d=W_d{X}_d,A_d=W_d^{-1},d=1,2$$ (1)

$$\begin{array}{l}{Y}_d=\frac{1}{1+e^{-U_d}},U_d=W_d{X}_d+W_{d0}\\ F_1=\mathit{max}\{H(Y_1)\}=\mathit{max}\{-E[ln{f}_{y_1}(Y_1)]\}\\ F_2=\mathit{max}\{\lambda H(Y_2)+(1-\lambda )[-{\sum }_{i=1}^I{\mathit{dist}}^2({\stackrel{\sim }{r}}_i,|{\stackrel{\sim }{S}}_{2k_i}\left|\right)]\}\\ =\mathit{max}\{\lambda (-E[ln{f}_{y_2}(Y_2)])+(1-\lambda )(-{\sum }_{i=1}^I{\Vert \left|W_{2k_i}{\stackrel{\sim }{X}}_2\right|-{\stackrel{\sim }{r}}_i\Vert }_2^2)\}\end{array}$$ (2)

$$\begin{array}{l}{F}_3=\mathit{max}\{{\sum }_{i,j}{\mathit{Corr}}^2(A_{1i},A_{2j})\}\\ =\mathit{max}\{{\sum }_{i,j}\frac{{\mathit{cov}}^2(A_{1i},A_{2j})}{\mathit{Var}(A_{1i})\mathit{Var}(A_{2j})}\}\end{array}$$ (3)

The observed data X (sample × feature) is decomposed into a linear combination of the underlying independent components, or sources, as in (1). S, A and W denote the component, mixing and unmixing matrices, respectively. The subscript d runs from 1 to 2, denoting the data modality. The unmixing matrices W₁ and W₂ are iteratively updated to optimize the objective functions F₁, F₂ and F₃, as in (2). F₁ is the Infomax [8] objective function to maximize the independence of components in modality 1. The inter-modality association function F₃ maximizes the correlations computed over the columns of the loading matrices A₁ and A₂. F₂, the objective function for modality 2, is modified based on Infomax so that components are not only independent but closely resemble the reference matrix r. Specifically, pICA-MR determines the closest component for each reference vector r_i (i^th row of r) and then calculates the Euclidean distance between the reference vector and the matched component only for the reference loci r̃_i, a subvector of r_i. This distance, ( ${\Vert \left|{\stackrel{\sim }{\mathbf{S}}}_{\mathbf{2}{\mathit{k}}_{\mathit{i}}}\right|-{\stackrel{\sim }{\mathbf{r}}}_{\mathit{i}}\Vert }_2^2$), is further minimized, where S̃_2ki represents a subvector of the constrained component S_2ki (the k_i^th row of S₂), computed by W_2ki (the k_i^th row of W₂) multiplying X̃₂ (a submatrix of X₂). ||·||₂ represents the L₂-norm Euclidian distance, and λ is the weight parameter. Through this design, reference loci will be highlighted in the resulting components and non-reference loci will show their own importance driven by the data. Different genetic references may constrain the same component and then be associated with the same imaging trait, suggesting functional convergence. The three objective functions are optimized using gradient maximization and the update functions are similar to [7].

III. Simulations

pICA-MR was evaluated with simulated functional magnetic resonance imaging (fMRI) and single nucleotide polymorphism (SNP) data for its detection power, particularly in the genetic modality. The simulated data consisted of 200 samples. Eight independent vectors (8 × 200) were randomly generated from normal distributions to form a mixing matrix for the fMRI data. Eight diagnosis patterns were then generated through thresholding the linear transformations of the fMRI mixing vectors with random Gaussian noises superimposed. The diagnoses would then be used in PLink [9] for simulating the SNP data. In this way, associations were built between fMRI and SNP modalities.

The fMRI data had a feature dimension of 40K voxels. Eight non-overlapping brain networks were simulated using the SimTB toolbox ([10], http://mialab.mrn.org/software) to serve as the fMRI components. The fMRI data matrix was then obtained as the product of the mixing and component matrices with random Gaussian noises superimposed onto each sample. The SNP data were simulated via PLink [9] with varying SNP dimensionality and causal loci effect size to assess the performance of pICA-MR when components accounted for different amounts of variance in the data. Each component involved 150 causal loci. The dimensionality ranged from 50K to 500K, resulting in the sample-to-SNP ratio from 0.004 (200/50K) to 0.0004 (200/500K). The eight SNP components consisted of 4 pairs, where each pair comprised two components whose causal loci were given the same diagnosis pattern across samples. Note that PLink does not generate SNPs in LD. Thus through linking two components to the same diagnosis pattern, we obtained two groups of independent SNPs associated with the same diagnosis and fMRI loadings. A two-sample t-test showed that the correlations among SNPs linked to the same diagnosis were not significantly different from those among randomly generated SNPs (p = 0.35). Evaluated with explained variances of diagnoses, the effect sizes of individual causal loci ranged from 0.0037 to 0.1926.

We already compared pICA-R with other competing approaches in [7], thus the key point for pICA-MR lies in whether it is able to reliably identify linked references contributing to the same component. We first investigated out of 100 runs, what would be the ratio for pICA-MR to correctly detect the references contributing to the same SNP component and fMRI trait, denoted as linked reference matching ratio (LMR) in the following text. Specifically, a reference matrix was generated, with each vector harboring a set of reference loci derived from one of the two groups of causal loci that were linked to the same diagnosis pattern. The evaluation started with two accurate references, each spanning 20 true causal loci. Then references spanning 40 loci of accuracies from 0 to 0.5 were tested to investigate the performance boundary. Corresponding to LMR, we also evaluated the ratio for pICA-MR to falsely constrain the same component for two isolated references, denoted as isolated reference mismatching ratio (IMR). For this purpose, the reference matrix was generated to consist of two references derived from two groups of causal loci that were linked to distinct diagnosis patterns. Again, the tolerance of reference accuracy was assessed. For proof-of-concept, we conducted the simulations with two references imposed. However, the algorithm is able to deal with more.

Besides LMR and IMR, accuracies of components, loadings, and inter-modality linkages, as well as reference-imposed false discovery rate (RFDR) were also evaluated. SNP component accuracy was assessed with sensitivity, which was the ratio of correctly identified causal loci to the built-in true causal loci. Loading accuracy was reported as the absolute value of the correlation between the diagnosis pattern and the extracted loadings. The correlation between the SNP and fMRI components most resembling the ground truth was calculated and compared with the built-in correlation to reflect link accuracy. RFDR assessed the overfitting by evaluating how many random reference loci were falsely identified as causal. In addition, when testing two isolated references, we compared the performance between a pICA-MR run with two references and two separate pICA-R runs. Due to the computation burden, we conducted this combined versus separate comparison only for one dataset with a SNP dimensionality of 50K and median effect size of 0.059.

pICA-MR requires selection of the component number. In the simulations, the fMRI component number was set to 8, the true component number for the simulated data. For the SNP modality, a true component does not necessarily yield optimal results [11]. This is because a principal component analysis (PCA) data reduction is usually applied before ICA to capture the largest variances in the data. However, genetic components may account for small variances such that the related information can be discarded by PCA. In this work, we chose to set the SNP component number to be 50 given our observation that the semi-blind pICA-R model tends to be robust to over-estimation [7].

IV. Results

Overall, pICA-MR successfully captured the reference structure when two references were assessed simultaneously. Given references spanning 20 true causal loci (accuracy = 1), the LMR was 1 based on 100 runs, regardless of the causal loci effect size or SNP dimensionality, as in Fig. 1. And the resulting component, loading and link accuracies were consistent with those observed for pICA-R [7], which had been shown to yield significant improvement compared to blind methods such as ICA and pICA. Obviously, pICA-MR showed robust performances under various scenarios. The component accuracy remained around 0.5 when the median causal loci effect size decreased to 0.03 with a sample-to-SNP ratio of 0.004; as well as when the sample-to-SNP ratio decreased to 0.0004 (200/500K) given a median casual loci effect size below 0.06.

Figure 1.

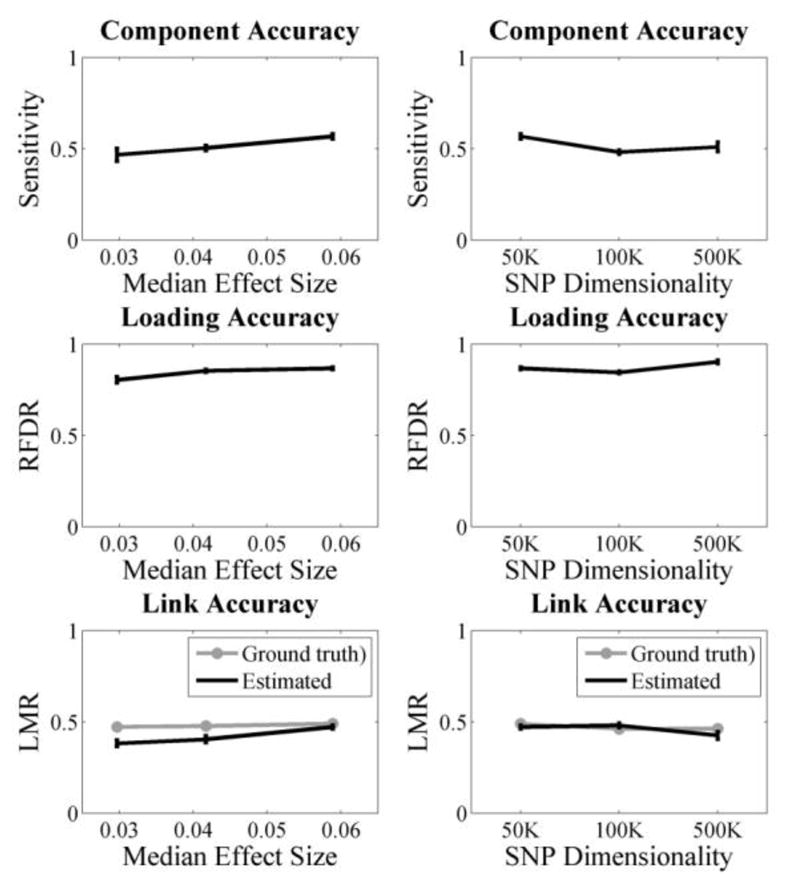
pICA-MR tested with linked 20-loci references of accuracy 1. Left: varying effect sizes when the sample-to-SNP ratio was controlled at 0.004; Right: varying dimensionality from 50K to 500K. The median effect sizes were 0.059, 0.057 and 0.060, respectively. The error bars reflect mean ± SD based on 100 runs.

As expected, LMR was significantly affected by reference accuracies. In Fig. 2, given 40-loci references, when the accuracy was below 0.2, the LMR was around 0.2, indicating that for 80 out of 100 runs, pICA-MR did not constrain the same SNP component for the two references. Meanwhile, a dramatic improvement was generally observed at the reference accuracy of 0.3, where LMR reached 0.9. When the reference accuracy was further increased to 0.5 (including 20 true causal loci), a LMR of 1 was achieved regardless of the causal loci effect size or SNP dimensionality, consistent with that previously observed. The performance of pICA-MR in component accuracy (measured with sensitivity) was comparable to those of pICA-R when the reference structure was correctly identified given relatively high accuracies (≥0.3). On the other hand, larger performance deviations were observed for lower reference accuracies; however the RFDR was not significantly affected, remaining below 0.05 for all the tested scenarios.

Figure 2.

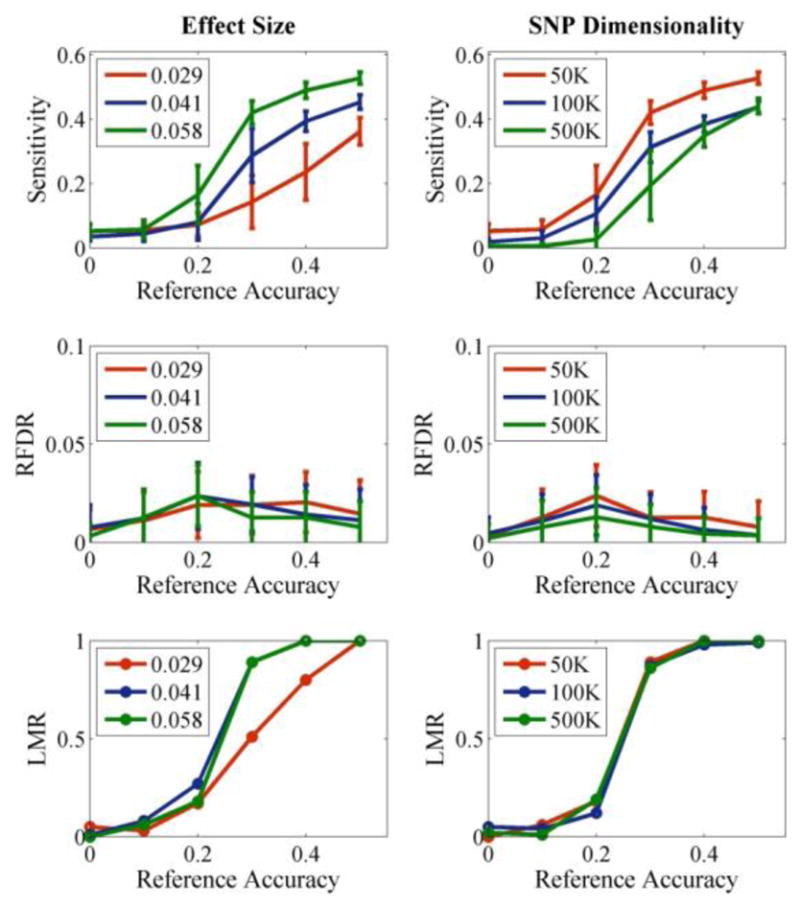
pICA-MR tested with linked 40-loci references of accuracies from 0 to 0.5. Left: varying different effect sizes when the sample-to-SNP ratio was controlled at 0.004; Right: varying dimensionality from 50K to 500K, the median effect sizes were 0.059, 0.057, and 0.060, respectively. The error bars reflect mean ± SD based on 100 runs.

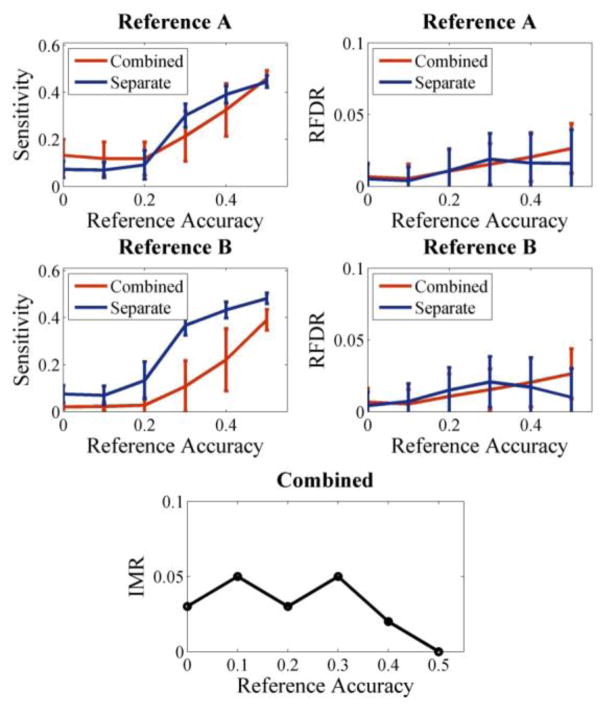
When two isolated references were combined and assessed with pICA-MR, the IMR was no greater than 0.05 for all the tested reference accuracies, as shown in Fig. 3. It was also noted that, the combined run with pICA-MR yielded comparable component accuracies to those obtained from pICA-R for reference A, while degraded accuracies were observed for reference B. Meanwhile, no significant difference in RFDR was observed between combined and separate runs.

Figure 3.

Isolated 40-loci references of different accuracies assessed with pICA-MR (combined) and pICA-R (separate), respectively. The tested dataset had a sample-to-SNP ratio of 0.004 and a median effect size of 0.059. IMR was reported for combined runs. The error bars reflect mean ± SD based on 100 runs.

V. Discussions and Conclusions

The simulation results demonstrated that pICA-MR is able to capture the embedded reference structure in a non-parametric manner. As in Fig. 1, given completely accurate linked references, the algorithm always correctly recognized that they contributed to the same component and applied the constraint. The resulting component, loading and link accuracies were comparable to those previously observed in pICA-R and thus significantly improved compared to blind ICA or pICA. In particular, reliable performance was achieved at a low sample-to-SNP ratio (200/500K) given a median effect size below 0.06, confirming the feasibility of applying pICA-MR to imaging genomic studies to analyze a million or so variables provided that hundreds of subjects are available.

Reference accuracy played an important role in the performance of pICA-MR regarding LMR. As shown in Fig. 2, for a reference accuracy below 0.2, the LMR was around 0.2. This is not surprising, since when random loci are incorrectly selected to be references, the distance between the reference vector and the true component is smeared and no longer distinguishes itself from those randomly observed. On the other hand, it’s encouraging to observe a dramatic improvement of LMR to around 0.9 at the reference accuracy of 0.3, which is likely to achieve when using the strategy of deriving a more homogeneous reference based on moderate LD loci [7].

Besides reference accuracy, causal loci effect size also affected the performance of LMR. As in Fig. 2, degradation was observed for data with lower causal loci effect sizes (0.029), where the LMR only reached 0.5 at a reference accuracy of 0.3. Interestingly, the performance was less vulnerable to the increase of SNP dimensionality. This might be due to the design of the model. Recall that the Euclidean distance is calculated between the component and the reference vector specifically for reference loci. Thus, an increased SNP dimensionality simply results in an increased number of non-reference loci, which might not significantly affect the estimated distance metric. Instead, decrease in effect sizes is expected to increase the distance between the reference vector and the true component, such that other components might by chance be closer to the reference vector and selected for constraint, resulting in in a low LMR.

In contrast, IMR was less affected by reference accuracy, remaining below 0.05 when two isolated references were assessed simultaneously, as shown in Fig. 3. Note that when the reference accuracy was 0, the two isolated references essentially consisted of random loci, which was equivalent to the situation when LMR was evaluated for two references of accuracy 0. In both cases, the chance was below 5% for the algorithm to constrain the same component for the two tested references, as consistently observed in Fig. 2 and 3. When the reference accuracy was increased for the two isolated references, the added true causal loci of one reference were essentially recognized as random loci by the other reference. Consequently, the IMR remained below 0.05, regardless of reference accuracy.

When two isolated references were combined and assessed with pICA-MR, the resulting performances might have been affected by the PCA data reduction. It can be seen in Fig. 3 that, comparable component accuracies were observed between combined and separate runs for reference A, while degradation was observed for reference B. In our simulation, the median causal loci effect size was 0.059 for component A and 0.057 for component B. Thus, more variances related to component A might have been included in PCA when both were assessed together, which resulted in the higher sensitivity.

In summary, pICA-MR is able to assess multiple references simultaneously while the interrelationships are not known. Compared to pICA-R, the extended approach is more flexible in dynamically constraining components for multiple references and allows some extent of heterogeneity in references. Simulation results demonstrated high LMR and low IMR, confirming the validity of Euclidean distance serving as a metric for the assessment of reference structure. Meanwhile, some cautions need to be exercised when conducting a pICA-MR analysis. First, it is recommended to maximize the chance for an accurate reference. A practical strategy is to derive individual references based on LD blocks of genes. In general SNPs in LD are more likely associated with the same trait of interest, hence contributing to the same component. Second, the performance can be affected by PCA data reduction, depending on how much variance in the data is explained by the mechanism of interest. Overall, pICA-MR is most suitable for assessing the architecture of genes which, although previously implicated in the same biological mechanism, still await investigations on their homogeneous or heterogeneous functional influences on neurobiological conditions.