Measurement of an Elasticity Map in the Human Cornea

Abstract

Purpose

The biomechanical properties of the cornea have an important role in determining the shape of the cornea and visual acuity. Since the cornea is a nonhomogeneous tissue, it is thought that the elastic properties vary throughout the cornea. We aim to measure a map of corneal elasticity across the cornea.

Methods

An acoustic radiation force elasticity microscope (ARFEM) was used to create a map of corneal elasticity in the human cornea. This ARFEM uses a low frequency, high intensity acoustic force to displace a femtosecond laser-generated microbubble, while using a high frequency, low intensity ultrasound to monitor the position of the microbubble within the cornea. From the displacement of the bubble and the magnitude of the acoustic radiation force, the local value of corneal elasticity is calculated in the direction of the displacement. Measurements were conducted at 6 locations, ranging from the central to peripheral cornea at anterior and posterior depths.

Results

The mean anterior elastic moduli were 4.2 ± 1.2, 3.4 ± 0.7, and 1.9 ± 0.7 kPa in the central, mid, and peripheral regions, respectively, while the posterior elastic moduli were 2.3 ± 0.7, 1.6 ± 0.3, and 2.9 ± 1.2 kPa in the same radial locations.

Conclusions

We found that there is a unique distribution of elasticity axially and radially throughout the cornea.

The biomechanical properties of the cornea, along with the underlying corneal microstructure, help determine the shape of the corneal surface, and, thus, also determine visual acuity. Since the cornea provides nearly two-thirds of the refractive power of the eye, understanding corneal biomechanics is useful when considering refractive errors in the eye, such as keratoconus and post-LASIK ectasia. Furthermore, a better knowledge of corneal mechanical properties can provide insight into the corneal response to refractive surgery or ultraviolet A (UVA) cross-linking procedures.

Numerous methods have been used to evaluate corneal elasticity, including strip testing, globe inflation, atomic force microscopy, and various ultrasonic methods. Earlier methods, such as globe inflation and strip testing, treated the cornea as a homogenous material, measuring a bulk material property and not localized elastic moduli.^1–8 However, the cornea is a complex, nonhomogenous tissue composed of different layers and varying microstructure radially. There is significant interweaving of stromal lamellae in the central anterior cornea, while this interweaving is absent in the posterior.^9–12 Additionally, the interweaving in the anterior cornea affects the biomechanical properties and interlamellar cohesive strength increases with lamellar interweaving.^13,14 Recently, atomic force microscopy was used to probe varying biomechanical properties through the thickness of the cornea.¹⁵ It was found that Bowman's layer was nearly three times stiffer than the anterior stroma. Similarly, the transverse shear modulus in the anterior cornea was significantly higher than central and posterior layers using torsional rheometry.¹⁶ A study using needle indentation found that the elastic modulus in the anterior cornea was nearly twice that of the posterior.^17,18 Furthermore, this same study also revealed that collagen fiber branching-point density was four times higher in the anterior third of the cornea than in the posterior third. These studies have shown that there is some depth dependence in corneal elasticity. As the cornea approaches the limbus and transitions into sclera tissue, there also is a transition in the microstructure of the tissue. Furthermore, x-ray scattering data suggest that collagen fibril orientation shifts from a preferred orthogonal orientation in the central cornea to a preferred circumferential orientation near the limbus.¹⁹ The nonhomogenous structure of the cornea, through its thickness and radially towards the sclera, suggests that the elastic modulus will vary throughout the cornea. To date, there still is no consensus on regional corneal elastic modulus distribution, especially in the radial direction.

Recently, we used acoustic radiation force elastic microscopy (ARFEM) to measure localized elastic moduli in the human cornea.²⁰ Acoustic radiation force elastic microscopy uses a low frequency, high intensity acoustic force to displace a femtosecond laser-generated microbubble within the cornea, while using a high frequency, low intensity ultrasound to track the position of the microbubble within the tissue.²¹ Importantly, the elasticity measurement is localized to the exact position of the microbubble, which can be created at any position within the cornea. This feature makes ARFEM ideal for probing biomechanical properties throughout the cornea. In this study, ARFEM was used to measure elasticity at varying positions throughout the cornea, with the goal of creating a map of corneal elastic moduli.

Methods

ARFEM Setup

The technical details of the ARFEM system used in this study have been described in detail previously.²⁰ Briefly, the system essentially is comprised of three core components, a femtosecond laser, a dual element ultrasound transducer, and a sample chamber. The laser is a commercial Ti:sapphire femtosecond laser (Coherent Inc., Santa Clara, CA, USA) that produces 130 fs pulses at a wavelength of 800 nm. The ultrasound transducer has two elements, an outer low frequency, high intensity force-generating element, and in an inner low intensity, high frequency tracking, or A-scan element. The outer force-generating, or pushing, element has a central frequency of 1.5 MHz and a spatial peak, pulse average intensity (I_sppa) of 125 Watts/cm². The inner A-scan element has a central frequency of 17 MHz. The elements are confocal and both have a focal length of 41 mm. The A-scan element is driven by a commercial pulser-receiver (Panametrics Model 5072PR, Waltham, MA, USA) at a pulse repetition frequency of 5 kHz. The pushing element is driven by an arbitrary function generator (Model 3314a; Agilent Technologies, Palo Alto, CA, USA) feeding into a 50 dB amplifier (ENI Model 240L; MKS Instruments, Wilmingtom, MA, USA).

Figure 1 illustrates the ARFEM system. The focal point of the laser is fixed in space, while the ultrasound transducer can be moved in three dimensions. To ensure that the optical and ultrasonic elements are confocal, the A-scan signal from a laser-created bubble was maximized by adjusting the alignment of the ultrasonic transducer. The 3-D sample stage then is moved independently of the optical and ultrasonic components, which are focused to the same location. The corneal sample is embedded in gelatin within the sample chamber, while the rest of the chamber is filled with degassed, distilled water for acoustic coupling. The chamber itself is mounted to a 3-D microstage, allowing for the placement of the microbubble anywhere within the cornea. The laser is focused through a 0.3 NA objective creating a microbubble (d = 22 ± 2 μm) within the cornea with a single pulse.²⁰ Once the bubble has been created and confirmed via A-scan, the measurement sequence is initiated manually and the outer element of the ultrasound transducer generates an acoustic radiation force chirp 2 ms in duration. The acoustic force displaces the microbubble within the cornea, while the displacement of the bubble is tracked by the inner ultrasound element with an A-scan at a pulse repetition frequency of 5 kHz. Thus, the position/movement of the bubble in response the acoustic radiation force is measured every 200 μs. The elastic modulus is inversely proportional to the bubble displacement and is calculated using:

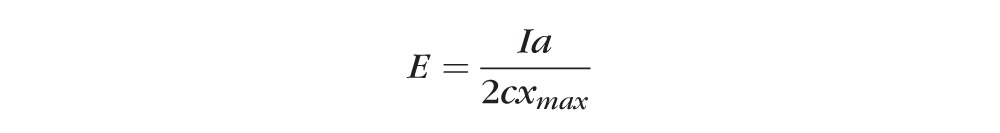where “I” is the acoustic intensity, “a” is the bubble radius, “c” is the speed of sound in the cornea, and “x_max” is the maximum bubble displacement.²² The acoustic intensity and bubble radius are calibrated before the experiment, while maximum bubble displacement is measured experimentally with an A-scan. The raw A-scan RF data are filtered using a 10 MHz high pass filter, and then processed using 1-D cross-correlation between a reference bubble A-scan and the remaining pulse-echoes. The speed of sound “c” in water (1500 m/s) was used in all calculations in place of the speed of sound in cornea for convenience.

Figure 1.

ARFEM experimental setup.

Sample Preparation

Six human cadaver eyes from three donors were obtained from the San Diego Eye Bank. All procedures conformed to the Declaration of Helsinki. The eyes were preserved within 24 hours of death and transported overnight on ice. Samples were refrigerated and measurements were performed within 3 days of death on average, but no later than 5 days. Basic donor data are provided in the Table. Before the experiment, corneas were thinned to a physiologic thickness of 500 to 570 μm by inflating the intact globe with 20% Dextran solution at 20 mm Hg IOP. The samples were placed into a suction holder whereby the posterior portion of the globe created a seal with the holder allowing a mild suction force to hold the sample in place. The sample was oriented such that the central corneal surface was orthogonal to the ultrasonic tip of the pachymeter (Reichert, Inc., Depew, NY, USA) during thickness measurements. The cornea then was excised, leaving a 2-mm scleral rim, and embedded in a 7.5% gelatin gel within the sample chamber. Experiments were performed only when the corneal thickness was in the physiologic 500 to 570 μm range.

Table.

Donor Eye Data

Elasticity Mapping

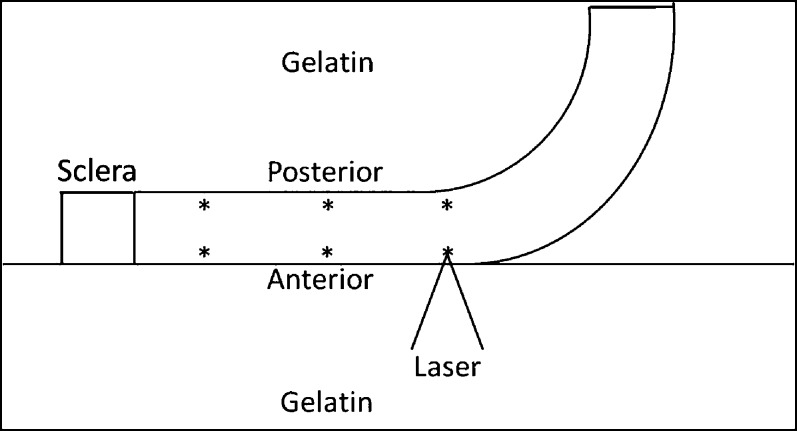
We obtained ARFEM measurements in the central cornea (0 mm), at 2.5 mm (mid), and at 5 mm (peripheral) toward the limbus. At each of these locations, the anterior and posterior 150 μm of the cornea were evaluated. At least five measurements were made in the immediate vicinity of each location. Figure 2 shows the location of the measurements within the cornea. The cornea was placed on the gelatin surface in such a way that half of the cornea was flat against the gelatin surface, with the other half curving upward. Additional gelatin then was poured on top of the sample. This was necessary due to the fact that the corneal surface must be perpendicular to the laser beam for optimal bubble creation. Laying the half cornea flat against the gel allowed measurements to be made in the central and peripheral regions without having to reorient the cornea. During the measurements, the cornea was oriented so that the acoustic force and resultant microbubble displacements were perpendicular to the corneal surface.

Figure 2.

Corneal orientation and ARFEM measurement locations. Measurements are made at 0 (center), 2.5 (mid), and 5 (peripheral) mm. At each radial position, the anterior and posterior regions are interrogated. The sample is flattened against the surface of the gel so that measurements can be made at multiple locations without having to reposition the cornea.

Results

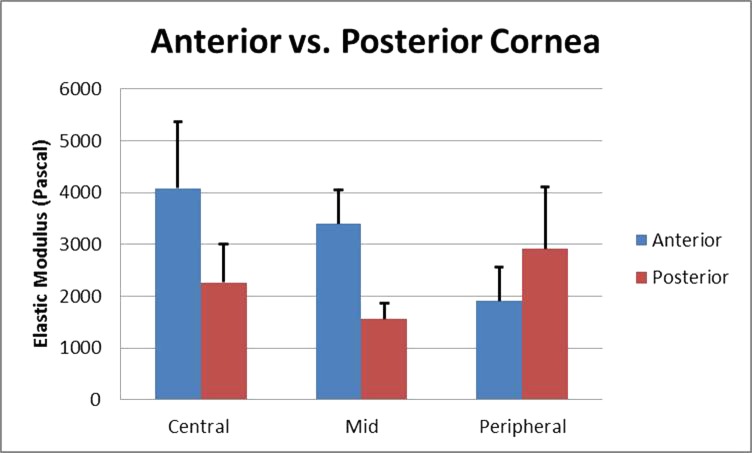
The elastic modulus varied with location in the cornea. In the anterior cornea, the mean elastic moduli were 4.2 ± 1.2, 3.4 ± 0.7, and 1.9 ± 0.7 kPa in the central, mid, and peripheral regions, respectively. These results are summarized in Figure 3. In the posterior cornea, the mean elastic moduli were 2.3 ± 0.7, 1.6 ± 0.3, and 2.9 ± 1.2 kPa in central, mid, and peripheral regions, respectively. These results are summarized in Figure 4. While the anterior cornea was approximately twice as stiff as the posterior cornea in the central and mid cornea, the anterior elastic modulus decreased with respect to the posterior elastic modulus in the peripheral cornea. A direct comparison of the anterior and posterior cornea is presented in Figure 5. Multiple comparisons were performed using ANOVA in MATLAB (MathWorks, Natick, MA, USA) to determine which location-specific elastic moduli means were different from the others. Statistically significant differences in elasticity could be established between the following regions: the central anterior cornea is stiffer than any other region (P = 0.05); the mid anterior cornea is stiffer than the mid posterior, central posterior, and peripheral anterior cornea (P = 0.05); and the peripheral posterior cornea is stiffer than the central posterior, mid posterior, and peripheral anterior cornea (P = 0.05). No statistically significant differences could be established when comparing ARFEM elasticity measurements in between all other regions.

Figure 3.

Elastic modulus in the anterior 150 μm of cornea from the center to the periphery.

Figure 4.

Elastic modulus in the posterior 150 μm of cornea from the center to the periphery.

Figure 5.

The mean elastic moduli for 6 corneal samples.

Discussion

The ARFEM technique used in this study has the significant limitation of being unable to measure the elasticity distribution in the mechanically-loaded cornea and intact globe. Given the nature of the current ARFEM device, the cornea must be excised from the globe and placed between the laser objective and ultrasound. Additionally, the cornea is laid flat against the gelatin surface in such a way that half of the cornea curves unnaturally upward. The mechanical effect of this curvature is assumed to be negligible based on previous measurements of the central cornea with the natural radius of curvature preserved showing the same 2:1 ratio in elasticity between the anterior and posterior regions.²⁰

We found the elasticity in the central anterior cornea to be nearly twice the elasticity in the central posterior cornea. Similar results were found using needle indentation, which revealed the same 2:1 ratio in elastic modulus between the anterior and posterior central cornea.¹⁷ Likewise, the mid anterior cornea was twice as stiff as the mid posterior cornea. Structurally, the anterior cornea possesses highly interwoven collagen structure compared to the relative homogeneity in the posterior. Despite this apparent correlation between microstructure and elasticity in the central and mid cornea, the trend was not observed in the peripheral cornea. The peripheral anterior cornea was approximately half as stiff as the central anterior, while the peripheral posterior cornea was approximately 30% stiffer than the central posterior cornea. It is interesting to note that interlamellar cohesive strength in the stroma is twice as strong in the periphery as it is centrally.¹³ Though ARFEM does not measure interlamellar cohesive strength, both results suggest a biomechanical change in the peripheral cornea. Furthermore, the peripheral anterior elasticity is approximately 2/3 that of the peripheral posterior cornea. It appears as though in the periphery, the anterior and posterior corneas nearly reverse elastic moduli relative to each other. Structural data in the literature are somewhat conflicting in explaining this observation and depend on the imaging modality used.

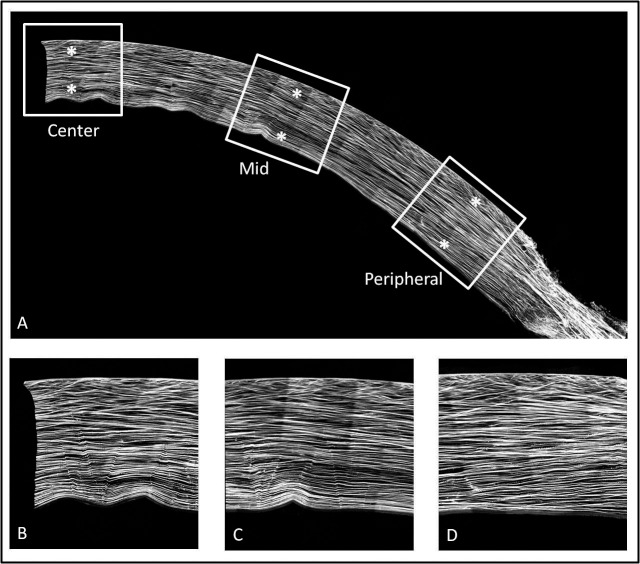
Anterior collagen interweaving, as measured by collagen lamellae angle relative to the corneal surface using nonlinear optical high resolution macroscopy (NLO-HRMac), did not detect a significant difference between the central and peripheral cornea.¹⁸ Figure 6 shows a typical image of the human cornea using NLO-HRMac. The wrinkles on the posterior surface in Figure 6A are artifacts from the mounting of the sample. Figures 6B to 6D show that the anterior interweaving relative to posterior collagen orientation is preserved from the center to the periphery. Structural differences in the periphery of the cornea may be masked by the shifting orientation of lamellae from central to peripheral. Structurally, the cornea is changing as it nears the limbus, with collagen fibers adopting a more tangential (circumferential) orientation in the periphery, as imaged by wide angle x-ray scattering.²³ Collagen fibers in this orientation would not have been detected in the previous work by NLO HRMac, as the technique does not image en face collagen fibers.

Figure 6.

HRMac images of collagen structure in the cornea. (A) Half of a human cornea from the center to the limbus. While the posterior lamellae continue uninterrupted into the sclera, the anterior interwoven region seems to end abruptly at the limbus. (B–D) Center, middle, and peripheral measurement locations, respectively.

Recently, micro focus x-ray scattering data were used to determine the inclination angles of lamellae relative to the corneal surface as a measure of lamellar interweaving.²⁴ As expected, inclination angles in the central anterior cornea were the greatest. The same study found that inclination angles in the posterior peripheral cornea were high when compared to the posterior central cornea, suggesting more interweaving in the posterior peripheral cornea. This finding seems to support our observation of an increasing elastic modulus in the peripheral posterior cornea. The effect of increasing inclination angle in the peripheral stroma along with the effect of tangentially oriented collagen fibers on local elasticity is unknown. As the lamellae exit the cornea and change in orientation, they transition into the structurally unique sclera. The biomechanical effects of the transition or insertion of collagen lamellae into the sclera also are unknown. Furthermore, the periphery may be subject to different swelling conditions because the peripheral edge of the sample is exposed directly to the gelatin medium. The cornea is, indeed, thicker in the periphery and hydration differences between the anterior and posterior could be exacerbated to the proximity of the measurements to the edge of the sample.

In addition to collagen microstructure, proteoglycan (PG) distribution throughout the cornea also may have an effect on local elasticity as measured by ARFEM. Specifically, it is pertinent to explore any differences in PG distribution between the anterior and posterior cornea, centrally and peripherally. A PG consists of a core protein with one or more covalently attached glycosaminoglycans (GAG). The GAG is highly polar, negatively charged, and, as such, binds water. The concentration of keratan sulfate, the most prominent PG in the cornea, increases from anterior to posterior in the central cornea.²⁵ Furthermore, stromal swelling is caused almost entirely by the gel pressure (swelling pressure) generated by negatively charged proteoglycans.²⁶ When these findings are considered along with the highly interwoven structure of the anterior cornea, it seems reasonable that the anterior cornea is resistant to edema compared to the posterior cornea.²⁷

Our results also indicated that the peripheral anterior corneal elasticity is approximately half that of the central anterior cornea. With studies showing conflicting accounts of the amount of interweaving in the periphery, this result is particularly interesting. As with the central cornea, it would be interesting to know the trend in PG distribution in the peripheral cornea. It is possible that local PG concentration and the resultant swelling pressure have an effect on local elasticity as measured by ARFEM. Unfortunately, the literature does not reveal many telling details about the differences in PG concentration between the central and peripheral cornea. One study looked at total soluble protein concentration between the anterior and posterior cornea, traversing across the cornea from the limbus to the central cornea. They found that total soluble protein concentration in the peripheral anterior cornea was nearly twice that of the central anterior cornea.²⁸ Though it may appear that this result corroborates our findings between central and peripheral elasticity, the correlation could be entirely coincidental since they were not specifically measuring PG distribution. To truly resolve this issue, a specific measurement of the axial PG gradient in the peripheral cornea would need to be performed. Such a gradient in PG concentration could affect local hydration, thus affecting elasticity.

Conclusions

We found that there is a unique distribution of elasticity axially and radially throughout the cornea. While ARFEM results in the central cornea are in reasonable agreement with other techniques, including needle indentation and torsional rheometry, lack of mechanical data in the peripheral cornea makes comparisons difficult. However, it is clear that the full picture of corneal biomechanics is quite broad, from complex and inhomogenous collagen microstructure to varying concentration of PG throughout the cornea. A better understanding of these variables along with elasticity measurements, especially in the peripheral cornea, would certainly help in completing the picture. Future modifications of ARFEM to automate the measurement procedure, specifically the movement of the sample with respect to the confocal volume, will result in an elasticity map with greater spatial density and may help provide this information.