Evaluation of a pulsed phase-locked loop system for noninvasive tracking of bone deformation under loading with finite element and strain analysis

Abstract

Ultrasound has been widely used to nondestructively evaluate various materials, including biological tissues. Quantitative ultrasound has been used to assess bone quality and fracture risk. A pulsed phase-locked loop (PPLL) method has been proven for very sensitive tracking of ultrasound time-of-flight (TOF) changes. The objective of this work was to determine if the PPLL TOF tracking is sensitive to bone deformation changes during loading. The ability to noninvasively detect bone deformations has many implications, including assessment of bone strength and more accurate osteoporosis diagnostics and fracture risk prediction using a measure of bone mechanical quality. Fresh sheep femur cortical bone shell samples were instrumented with three 3-element rosette strain gauges and then tested under mechanical compression with eight loading levels using an MTS machine. Samples were divided into two groups based on internal marrow cavity content: with original marrow, or replaced with water. During compressive loading ultrasound waves were measured through acoustic transmission across the mid-diaphysis of bone. Finite element analysis (FEA) was used to describe ultrasound propagation path length changes under loading based on μCT-determined bone geometry. The results indicated that PPLL output correlates well to measured axial strain, with R² values of 0.70 ± 0.27 and 0.62 ± 0.29 for the marrow and water groups, respectively. The PPLL output correlates better with the ultrasound path length changes extracted from FEA. For the two validated FEA tests, correlation was improved to R² = 0.993 and R² = 0.879 through cortical path, from 0.815 and 0.794 via marrow path, respectively. This study shows that PPLL readings are sensitive to displacement changes during external bone loading, which may have potential to noninvasively assess bone strain and tissue mechanical properties.

1. Introduction

Quantitative ultrasound (QUS) has been widely used to nondestructively detect defects, surface roughness and material properties (Bray 1997, Matthews 1994) on materials ranging from metals to ceramics to bone tissues (Bogorosh et al 2009, Qin et al 2008, Xia et al 2007, Qin et al 2003, Chen et al 1998). The adaptability of living bone to its mechanical environment yields great diversity in bone strength and geometry. Both exercise and disease can have a profound effect on bone properties and its ability to perform its necessary functions. Osteoporosis presents unique challenges as its manifestations are being increasingly felt throughout the healthcare system with our aging population (Wang et al 2009, Tanriover et al 2010, Lim et al 2009, Golden et al 2009, NOF 2008, Holroyd et al 2008, Gannon et al 2008, Cole et al 2008, Wehren and Magaziner 2003, Keen 2003, Ethgen et al 2003). With its only symptom being painless bone loss, osteoporosis is known as a ‘silent disease’ and often goes unrecognized as the cause for other medical problems (Harvey et al 2010, Peasgood et al 2009). Osteoporosis is responsible for over 1.5 million fractures annually (NOF 2008), which in turn cause disability and other health problems, greatly increasing the mortality rate within 5 years post-fracture (Deng and Liu 2005, Stewart et al 2006, NOF 2008, Camozzi et al 2007). The most common types of fractures occur at the hip, spine, wrist and ribs (Gardner et al 2006, Peasgood et al 2009). The population affected is ever growing, and currently includes over 10 million Americans, with 34 million more at immediate risk (with osteopenia) (NOF 2008, Xia et al 2007, Golden et al 2009). This includes the 55% of the population over 50 years old diagnosed with osteoporosis; in fact, one in two women and one in four men will suffer from an osteoporotic fracture in their lifetime (Golden et al 2009, NOF 2008). While there is no cure, treatments can mitigate bone loss, lower fracture risk and greatly increase the quality of life. Diagnostics for the disease mainly relies on x-ray bone densitometry which has been shown to correlate relatively well to fracture risk. Recently, QUS has begun to be used to assess bone quality and fracture risk, providing a more informative and safer technique than dual-energy x-ray absorptiometry (DXA) for osteoporosis diagnosis (Qin et al 2002, 2006, Dubs 2002, Falcini et al 1998). Ultrasound has the benefit of physically interacting with the tissue as it propagates. Therefore a relationship between ultrasound velocity and material properties exists, such as $V=\sqrt{E/\rho }$, where E and ρ are the material elastic modulus and density, respectively. Scattering occurs at interfaces between materials, such as the fluid and solid phases of trabecular bone. Therefore energy attenuation is related to the internal architecture of the bone. QUS provides useful information about the bone structure (Yamamoto et al 2009, Lin et al 2009, Muller et al 2008); however, it currently remains mainly a correlative method for quality and fracture risk prediction. More recent applications of Biot theory for wave propagation in a poroelastic medium show the generation of two wave fronts (Haire and Langton 1999), termed ‘fast’ and ‘slow’ waves. These fronts are heavily determined by solid and fluid phases, respectively. In trabecular bone, these wave fronts have been experimentally identified as arriving with temporal separation or isolated with signal processing algorithms (Wear 2010, Nagatani et al 2008, Hosokawa and Otani 1997). The current work focuses on cortical shells from the mid-diaphysis of sheep femurs where the porosity is orders of magnitude lower than that of trabecular bone; thus ‘fast’ and ‘slow’ wave analysis will not be examined here.

Recently pulsed phase-locked loop (PPLL) technology has been proven for accurately tracking ultrasound time-of-flight (TOF) velocity in water (Ueno et al 2003, Froggatt 1995, Yost and Cantrell 1991). The theory of PPLL technology is based on the phase-locked loop, a common IC circuit that provides feedback based on the phase comparison of two signals. The principle is most easily understood by looking at a simplified system containing a multiplier, filter and voltage-controlled oscillator (VCO). The VCO outputs a reference frequency. The multiplier takes in an experimental signal and a reference signal and outputs their product. This product is passed through a filter removing all but the dc component of the result. If the two signals are in quadrature, this dc component will be zero. If not, this dc component feeds back to the VCO and alters the VCO output until quadrature is restored and the dc component drops back to zero. In ultrasound applications, this general technique uses a signal passed through an ultrasound transmitter and receiver compared to the electronic reference signal and requires additional timing circuitry.

The PPLL system used in our work sends an ultrasound pulse through a sample, and compares the received wave to the electronic reference. As the TOF of the ultrasound wave changes, the phase difference between the reference signal and the ultrasound pulse changes. To keep the reference and ultrasound pulse in quadrature, the system adjusts the output frequency of the VCO, which is measured by a frequency counter as the main data collector for the PPLL. Any changes in the TOF should therefore be reflected by changes in measured PPLL reference frequency.

In the current application there are two possible mechanisms for TOF changes of the propagating ultrasound. The first is the result of geometric changes in the sample. Under compressive loading the sample will alter its dimensions, which will cause the ultrasound TOF to change. The second mechanism is a result of altered inherent speed of sound in the material as compressive load changes density and modulus. The following work will be conducted well within the elastic range of the material so changes in modulus are negligible. According to theoretical calculations based on simplified bone geometry, the contribution of density changes to TOF changes is around 1% of the total change seen during loading. Thus the current work will focus on the first mechanism of TOF modulation.

The PPLL technique has been utilized in several applications, including intracranial pressure (ICP) tracking (Ueno et al 1998, 2003, 2005, Steinbach et al 2005,). The variable frequency PPLL has proven sensitive to phase changes due to changes in the ultrasound TOF. In ICP tracking, changes in TOF caused by bulging of the temporal bones in the skull can be detected by the PPLL. This detectable deformation due to small physiologic load is related to the overall structural and material properties of the tissue.

It is the objective of this work to determine if a system based on the PPLL technique is sensitive enough to detect bone deformation during loading. It is hypothesized that the sensitive phase-based TOF measurements by the PPLL can track bone deformation during loading. Measuring deformation at known applied loads can allow calculation of bone strain and then stiffness. Knowing bone properties is a primary factor for overall bone quality and can potentially increase the accuracy of fracture risk prediction and osteoporosis diagnostics. The implication of a noninvasive bone deformation measurement system reaches across the board from exercise, to rehabilitation, to disease diagnostics. In the case of osteoporosis, the technique can provide earlier and more accurate detection of bone changes. Because there is no harmful radiation or other damaging effects, diagnostic scans can be started earlier in at-risk patients, and can be performed more often than DXA with longitudinal assessment.

2. Materials and methods

2.1. Sample preparation

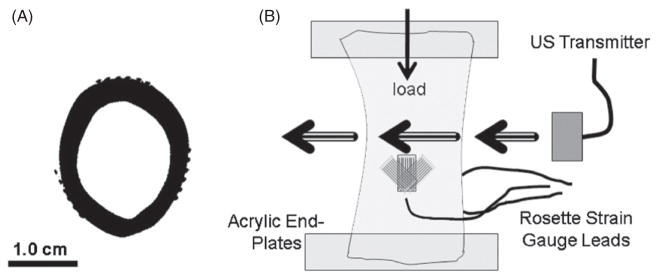
Fourteen cortical shells were cut to 6 cm in height from the mid-diaphysis of fresh-frozen sheep femurs. To determine if internal bone marrow alters ultrasound wave propagation, samples were divided into two main testing groups: group M was tested without removing marrow from the cortical shell while group W was tested after full removal of internal marrow. The 14 cortical shells were divided into two groups as follows: 4 directly into group M, 4 directly into group W and 6 tested first with the marrow inside the cavity for group M, and then again after the marrow was removed for group W. This effectively gives us N = 10 in group M and N = 10 in group W. Samples without marrow inside were filled with degassed water for acoustic coupling. All samples were cut perpendicular to the femur loading axis and contact ends were embedded in self-curing acrylic to ensure uniform loading. In order to obtain local mechanical environment variables, three 3-element rosette strain gauges (WFRA-3-IL-II 120 Ω, Tokyo Sokki Kenkyujo Co., Ltd, Shinagawa-Ku, Japan) were equally distributed around the circumference of the bone 10 mm below the height of ultrasound penetration (figure 1). Each of the ten samples for each group was tested at three different angles of rotation about the longitudinal axis. Due to the geometrical differences around the circumference of bone, the mechanical environment, bone thickness and bone deformation are all largely variable as the bone rotates around the longitudinal axis with respect to ultrasound penetration. In addition, any rigid body translation with respect to the ultrasound penetration can result in altered amounts of energy traveling through the cortical shell, or marrow cavity. Thus any reposition has an effect on overall ultrasound propagation. Therefore, each of these 3 tests was considered independent, yielding a total of N = 30 tests per group.

Figure 1.

(A) Representative cross-sectional μCT scan at 76 μm resolution, showing the six leads of each rosette pattern strain gauge, and the even circumferential gauge distribution. (B) The ultrasound propagation is roughly 10 mm above the top of the strain gauges, eliminating them from ultrasound interference.

2.2. Mechanical loading protocol

All samples were axially loaded with an MTS Mini-Bionix 858 machine (MTS Corporation, Minneapolis, MN) load frame. The static loading protocol began with a 50 N preload to ensure solid contact between the piston and the sample. The loading protocol then consisted of eight 16 s loading periods, with loads from 100 to 800 N in 100 N steps. Each load period was separated with a 16 s reference period where the load was held at 50 N. Previous data show that these loads are well within the elastic range for sheep femurs. Peak values during the loading period are calculated relative to values in the adjacent reference period. The sample was loaded in the axial direction, while the ultrasound transducers were held in the water bath perpendicular to the axial direction. Therefore, any dimensional change detected by the PPLL will be perpendicular to loading. For this reason, finite element analysis (FEA) was used to extract perpendicular dimensional changes in the direction of ultrasound propagation.

2.3. System setup

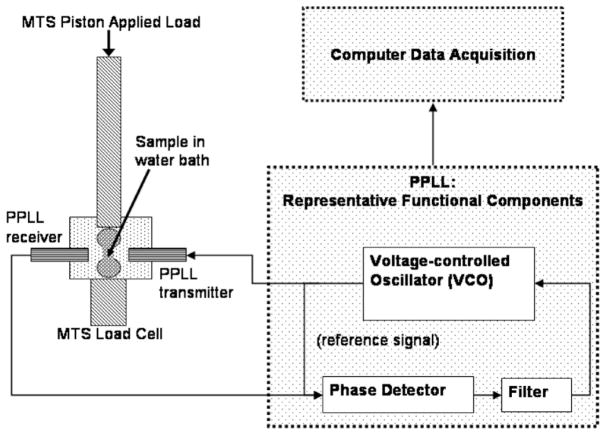
The PPLL system (Luna Innovations Inc., Roanoke, VA) has two 0.5 inch diameter immersion transducers with a central frequency of 2.25 MHz. Transmitted ultrasound signals consist of 15 cycle bursts repeated at 1 kHz. The bone sample and transducers were placed in a small tank of degassed water attached to the MTS load cell (figure 2). Due to mechanical constraints, ultrasound penetration was perpendicular to the loading direction. The output of the PPLL device is read from a frequency counter. In addition to the PPLL and MTS variables, strain gauges were used to determine local strain fields. Data acquisition from the PPLL and strain gauges was controlled by a LabView program. Mechanical loading and data acquisition were synchronized with an external trigger. The data acquired for each test includes: (1) the frequency output from the PPLL, (2) the strain from all three elements in each rosette strain gauge and (3) the load and piston displacement from the MTS.

Figure 2.

Setup schematic. Sample signal and reference signal are phase-compared, filtered and used to modify the VCO. Compressive load is applied perpendicular to ultrasound propagation.

2.4. FEA setup

In this application FEA is used as a tool to elucidate deformations during loading that would be otherwise unobtainable. The models will make the basic simplifying assumption of linear elastic material properties, as is common for cortical bone FEA. To obtain mesh geometry from each individual bone tested, each bone is scanned at 76 μm resolution using a microcomputed tomography scanner (VivaCT40, SCANCO Inc., Switzerland). Custom-written MATLAB scripts were used to mesh the cortical shells at an element side length of roughly 0.4 mm in all directions based on a previous convergence study. The model uses linear elastic, orthotropic material properties, with an axial modulus of 24.76 GPa and a traverse modulus of 17.5 GPa (Liebschner 2004). All simulations were run using ABAQUS (Version 6.5, Simulia, Inc., Providence, RI). The actual load applied by the MTS was used as load input to the FEA at each step. The total load applied by the MTS is distributed to three nodes on the top surface to achieve experimentally seen bending. The values of axial strain recorded from the three strain gauges during each loading period are used to validate these models. Nodes on the surface of the bone in the region of the strain gauge will be used to report axial (ε₃₃) strain. The validation requires the calculation of the 2D strain field in the plane of the gauges using all three gauges, for both experimental and FEA data. In these 2D strain fields the ‘zero-strain’ axis is found and used to compare the experimental and FE data (figure 3). First, the angle of this axis compared to the horizontal must be within 1° of the experimental. Second, the distance of this axis to the bone centroid must be within 2% of the experimental at every load step. In order to obtain a successfully validated model, the load distribution at the top surface is varied in each load step until conditions are met for every step. Each test thus has a different load distribution and validation for each of its eight loading periods, yielding a more accurate approximation of the nonlinear nature of the results during MTS loading.

Figure 3.

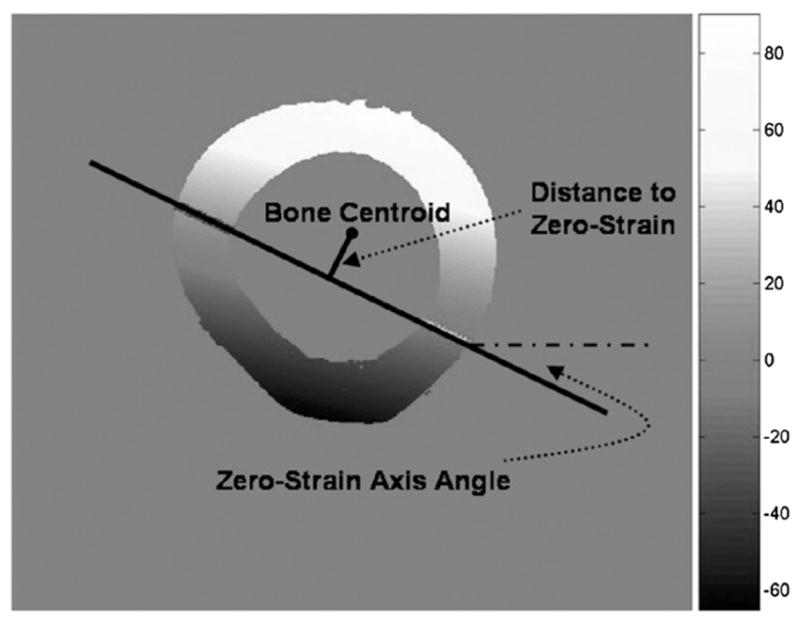
Calculated 2D axial strain field and value bar with parameters for FE validation. The zero-strain angle must be within 1° of that calculated from the strain gauges. The zero-strain distance must be within 2% of that measured experimentally. The scale bar unit is microstrain.

2.5. Data analysis

An average value for the load, MTS piston displacement, local axial strain, local circumferential strain and PPLL output frequency was calculated at each of the eight load steps. Three main correlations are reported: (1) PPLL frequency versus MTS displacement (P-P ΔDisplacement), (2) PPLL frequency versus axial strain, and (3) PPLL frequency versus circumferential strain. The PPLL frequency refers to the unitless quantity of the difference in frequency output divided by the reference level frequency (ΔFrequency/Frequency). Local axial and circumferential strains were determined using the rosette strain gauge data with the assumption that there was a 2D linear strain field in the plane level with the gauges perpendicular to the loading axis. The 2D linear strain field utilizes the planar equation a * x + b * y + c = ε, where a, b, c are constants, x, y are the coordinates in the plane of the bone cross-section and ε is the strain at those coordinates. The x, y planar coordinates were taken from recordings of gauge locations in a cross-sectional slice from the μCT scans. An example 2D strain distribution can be seen in figure 3. For each test, the sum of the inlet and outlet strains along a straight propagation path was correlated with the PPLL frequency at the different mechanical load levels. To obtain a rough estimation of the change in ultrasound path length in bone (ΔL) the cross-sectional image of the bone was used to determine the original thickness of the cortical shell along the straight-line ultrasound path. The average axial strain from all points along the straight-line ultrasound path was translated into transverse ΔL using a Poisson’s ratio of 0.3. This estimated ΔL was then correlated to PPLL frequency.

The ultrasound path through bone is a complex topic; therefore three ultrasound paths will be analyzed in each test. Wave propagation through a circular annulus results in a complicated, multi-path propagation scheme that depends on radii and shell thickness (Liu and Qu 1998). Extending this propagation theory to a cortical bone shell, such as the radius, several wave fronts are present (Floch et al 2008, Kaufman et al 2008). The ‘direct wave’ (termed ‘straight path’ in this work), travels from the transmitter through the cortical shell, into the marrow cavity, through the cortical shell on the other side, and then onto the receiver. The ‘circumferential wave’ at the radius is divided into two separate possible paths in this work: the ‘right path’ and the ‘left path’. In previous work with the sheep femur cortical shells it was shown that not only are these ‘circumferential’ and ‘direct’ waves present, they arrive at the receiver very close temporally, thus making them difficult to separate in the time domain. The change in the ‘straight-line’ path will be calculated as the expansion of the cortical bone shells. While actual propagation through the shell is complex, an ‘average’ length change along the midline between the endosteal and periosteal surfaces will be used. The ΔL from these three paths will be individually correlated to PPLL output and compared to previous strain results.

Finally, using this FEA we can obtain a rough estimation of phase error introduced by the superimposition of the three different ultrasonic paths. Based on absolute node positions, and assumed ultrasound velocities, the phase difference in the signals which travel along the two different paths can be determined. The assumed sound velocity is 3600 m s⁻¹ in bone and 1450 m s⁻¹ in the marrow cavity. If the signals from these two paths mix again before they arrive at the ultrasonic receiving transducer, then the received signal will include artificial phase shift due to this signal interaction. Using the absolute path lengths from ABAQUS, the time of arrival of the signal that travels through each path can be calculated. Then based on the experimental setup the apparent phase of each signal and the combined signal can be found.

3. Results

The PPLL output was well correlated to local mechanical environment variables in most of the tests run. Each of the PPLL frequencies was correlated to MTS displacement, calculated axial strain, calculated circumferential strain and the estimated change in ultrasound path length through bone (figure 4). The average R² values between PPLL frequency and MTS displacement were 0.71 ± 0.28 and 0.60 ± 0.32 for group M (n = 30) and group W (n = 26), respectively. The average R² between PPLL frequency and locally calculated axial strain is 0.70 ± 0.27 and 0.62 ± 0.29 for groups M (n = 29) and W (n = 24), respectively. For PPLL frequency versus locally calculated circumferential strain, the average R² values are 0.61 ± 0.29 and 0.65 ± 0.30 for groups M (n = 29) and W (n = 21), respectively. Using the rough estimation of ΔL, the R² values between PPLL frequency and ΔL are 0.70 ± 0.27 and 0.63 ± 0.28 for groups M (n = 29) and W (n = 24), respectively. While there seems to be a trend of better correlations with marrow rather than water no statistical significance could be found between the marrow and water groups for any of the relationships given above. This is attributed to the high variation and non-normality of the data.

Figure 4.

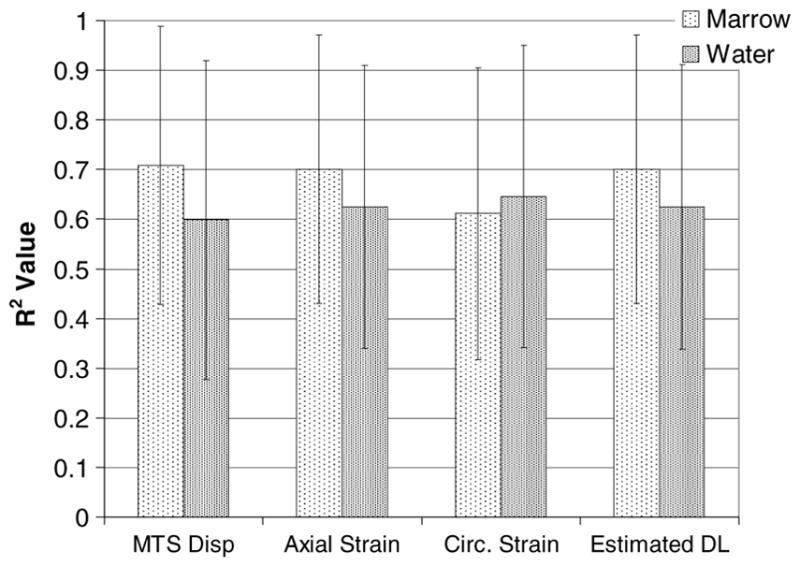
Mean ± standard deviation of R² values for PPLL frequency measurements correlated to given measured or calculated variables.

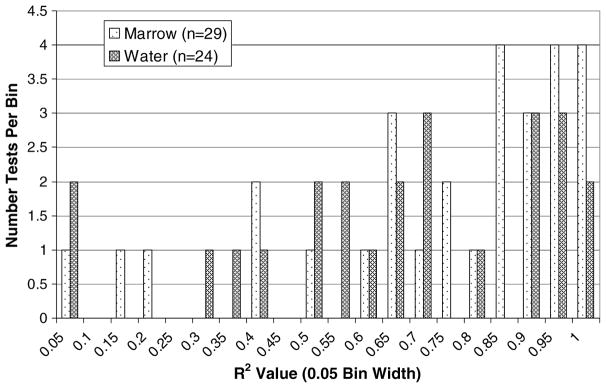
The expected relationships were not always obtained. The linear slopes yielding the reported R² values ranged from −1.61 to 1.29 με Hz⁻¹ with an average of −0.224 ± 0.475 με Hz⁻¹ for PPLL frequency versus axial strain in the water group. Similarly for the marrow group, the slopes were consistently negative despite strong linear response from the PPLL. The slopes ranged from −3.65 to 2.01 με Hz⁻¹ with an average of −0.311 ± 0.841 με Hz⁻¹ in the marrow group. Variation suggests that the PPLL is tracking something very closely related to the axial strain, however not the axial strain itself. Histograms of R² data (figure 5) show that the data are not normally distributed about the mean. There were tests that had very high correlations, with R² values above 0.95, while there were tests that resulted in essentially zero correlation.

Figure 5.

Histograms of R² values for PPLL frequency versus measured axial strain using a 2D strain field.

Due to the extensive validation required, only two models were successfully validated for extraction of data from FEA. These models were separately validated for each load step to ensure high fidelity to experimental results. Data from these two models showed that the ultrasound may travel along an alternate path, and signal convergence and phase artifacts are a reality. The R² values for FE acquired straight (ΔPs), right (ΔPr) and left (ΔPl) path length changes correlated to PPLL frequency are presented in table 1.

Table 1.

R² values for the given variable correlated to the PPLL measured frequency in two representative models.

R2 values	FEA ΔPs	FEA ΔPr	FEA ΔPl	EX Est. ΔCT
M13_1	0.307	0.993	0.987	0.815
W14_3	0.796	0.876	0.866	0.794

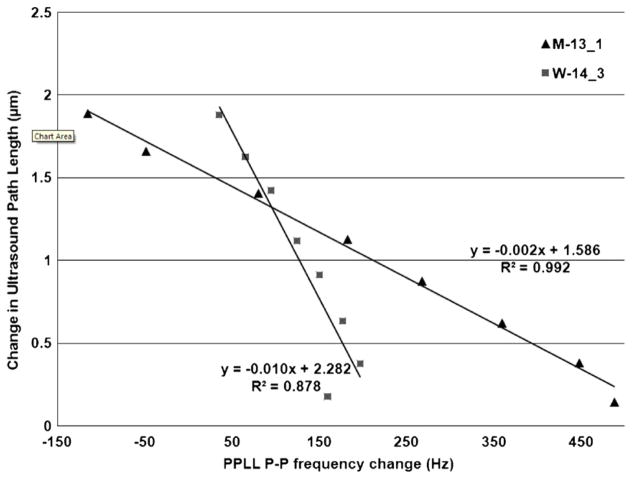
Most notably, the R² of the PPLL frequency measurements versus the right-handed ultrasound path length (ΔPr) jumps to 0.993 and 0.876 for models M-13_1 (Group-Bone #_orientation #) and W-14_3 respectively, while the experimental R² to estimated cortical shell expansion was only 0.815 and 0.794 for the same tests. For the most highly correlated ultrasound path, the path length change is plotted against the P-P frequency change from the PPLL in figure 6.

Figure 6.

FEA (ABAQUS)-determined ultrasound path length change versus P-P change in frequency. Paths used have the highest correlation of various paths analyzed in FEA (right cortical paths in these cases).

At a nominal frequency of 2.25 MHz, the wave period is 0.444 μs, and the time it takes for 15 cycles to propagate past a point is 6.666 μs. The times of arrival for the different pathways in the validated model of the experimental test M-13_1 are 11.874 ± 0.00007, 8.447 ± 0.0002 and 7.339 ± 0.0002 μs, for the straight, right and left paths, respectively. Figure 7 illustrates the selection of the different paths, and how signals converge before being received by the ultrasound transducer. For the validated model of experimental test W-14_3, the times of arrival of the different paths are 11.551 ± 0.0004, 9.292 ± 0.0002 and 8.074 ± 0.0003 μs, for the straight, right and left paths, respectively. The actual time varies with load, since the displacements change; however, as seen, the variations are on the order of tenths of nanoseconds, so only the averages over all steps is presented here. It can be seen that for these two models, there is a delay of between 2 and 5 μs between the arrival of the first wave and the arrival of the last. The superposition of the signals is therefore present, and a phase artifact due to signal addition at these different points will be present. The apparent phase of the signal when all three pathways combine will vary depending on the load. The magnitude of the phase artifact for these two models is up to 2.58° and 2.09° in the M-13_1 and W-14_3 models, respectively.

Figure 7.

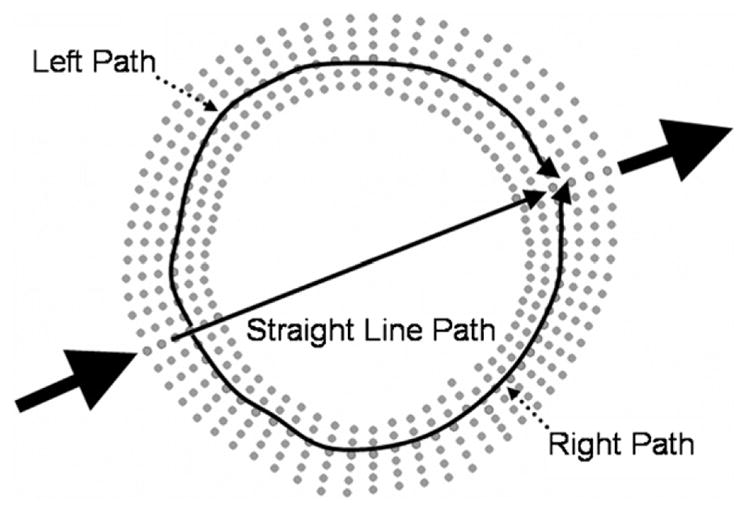
Path selection performed in FEA (solid lines). Node sets are used to determine the path length change for each path independently. Independent path length changes correspond to independent TOF changes, thus phase errors upon superposition.

4. Discussion

To determine whether a system based on the PPLL circuitry could be sensitive enough to detect changes in bone geometry during loading, both experimental and numerical approaches were taken. The system was tested using real bone geometry, and FEA models were created to determine if the PPLL closely tracked dimensional changes seen in bone during loading. Based on experimental work and numerical analysis the PPLL system is able to detect changes in bone during loading.

The PPLL frequency outputs were found to be moderately related to both axial and circumferential strain measurements, regardless of marrow cavity contents (axial strain, M-group R² = 0.70 ± 0.27, W-group R² = 0.62 ± 0.29). This provides good indication that the PPLL is sensitive enough to detect changes in bone during loading; however the variability seen in slopes of these relationships warrants further investigation. Some tests show that the PPLL frequency output almost completely depends on the mechanical loading state, while some tests show absolutely no relation whatsoever. Several reasons for a lack of consistent response are hypothesized; they can be broken down into experimental setup error and ultrasonic signal interference. Other unpublished data using the PPLL for TOF tracking through cortical bone cylinders have also shown similar results; therefore system failure is not the major cause of poorly correlated results. Ultrasonic interference also somewhat depends on the experimental setup, as the burst widths, central frequency and material geometry will all have an effect on the wave propagation. A cortical shell tested with water and then air inside the marrow cavity shows that a significant amount of energy passes through the cortical shell during through transmission. And more importantly, any signal that passes straight through arrives at roughly the same time as any signal that follows the cortical shell in these geometries. This is a cause for concern, as wave energy interference can cause phase shifts and amplitude changes, possibly diminishing the received signal to below noise levels or introducing phase artifacts. Any movement of the sample with respect to fixed transducers will result in altered propagation schemes and different mechanical environment. This high sensitivity to sample repositioning does not necessarily decrease repeatability since each test contains its own reference and does not rely on global calibration.

The PPLL outputs are closely related to the ultrasound path length changes extracted from FEA. The spatial changes seen in the FEA models were on the order of tens of nanometers to several micrometers. The strong PPLL response at such small levels of path length variation shows the great sensitivity of this system. Separating individual propagation paths can yield slightly stronger relationships to the PPLL output, further supporting the idea that ultrasound propagation through the cortical shell takes multiple paths. Using path length changes extracted from FEA, it is seen that wave interference patterns can generate sufficiently large phase artifacts to nullify or reverse any true phase shift due to loading. With phase artifacts that are not necessarily linear, future experimental design must minimize these effects.

Future works can and should be done to better understand the functionality of the PPLL technique in monitoring bone strain. Due to the multiple possible propagation paths and signal interference, great care must be taken in the selection of system lock point, anatomical site and mode of transmission. In future experiments utilizing the PPLL, with its high sensitivity to phase shifts, it is recognized that through transmission is a difficult method to control inside cylindrical shells. Pulse-echo techniques exploring the expansion of a single cortical shell under loading may minimize these artifacts. Through-transmission techniques may prove more consistent at sites containing a large amount of trabecular bone, such as the whole calcaneus. Using a small beam cross-section can allow the majority of energy to propagate relatively straight through the trabecular region, minimizing signal inference. For diagnostic purposes transmission through trabecular regions holds more functionality; therefore through-transmission measurements must be utilized, and suitable sites with minimal signal interference should be found.

While the current work did not generate a relationship between PPLL output and local mechanical variables, it does show that the system is quite sensitive to mechanical changes. The data support the conclusion that the PPLL is sensitive enough to measure bone deformations during elastic loading. The data also highlight complications in cortical shell wave propagation that can cause artifacts in system response. With a proper setup the PPLL technique can noninvasively respond to the local changes in bone during loading, and may prove to be an invaluable tool in both research and diagnostics.